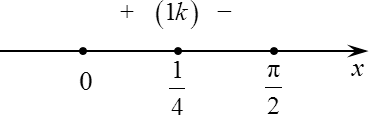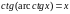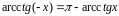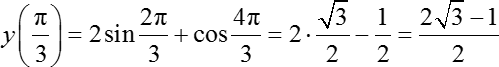Как найти экстремумы функции синус

10 апреля 2014

Сегодня мы продолжаем рассматривать задачи на экстремумы из ЕГЭ по математике. Итак, задача:

Задача B15. Найдите точку максимума на отрезке (0; π/2):

y = (3 − 12x) sin x − 12 cos x + 16

Сразу сделаю небольшое лирическое отступление. Дело в том, что это предпоследний урок из серии уроков, посвященным производным в ЕГЭ по математике. И сразу скажу, что оба эти урока будут посвящены тригонометрии, а точнее, нестандартным задачам на тригонометрию.

Вот и сейчас перед нами довольно-таки нестандартная задача. Хотя, как мы убедимся через пару минут, решается она довольно просто.

Решение задач на точки максимума и минимума

Давайте в первую очередь посмотрим, что от нас требуется. А требуется найти точку максимума. Заметьте: не наибольшее или наименьшее значение, а именно точку максимума. Из этого сразу следует, что наши любимые приемы, чтобы как-то подобрать х, как-то выделить красиво значение функции — в данной задаче эти приемы не работают просто потому, что значение функции нас не интересует.

Давайте работать по старинке. Прежде всего, я запишу общий алгоритм решения подобных задач.

1. В первую очередь нас интересует производная: y‘ = ?
2. Второй шаг — производную мы приравниваем к нулю и решаем полученное уравнение, находим корни. Их редко получается больше, чем две штуки: y‘ = 0; x₁, x₂, …;
3. Третьим шагом мы берем эти корни и оставляем только те из них, которые лежат на интервале, указанном в условии задачи — в нашем случае речь идет об интервале (0; π/2). Итак, интересуют только те корни, которые лежат на обозначенном интервале или отрезке: x₁, x₂ ∈ (0; π/2);
4. Наконец, мы чертим прямую, отмечаем на ней концы отрезка, а также все корни, которые лежат внутри этого отрезка. Затем смотрим знаки. Там, где «плюс» переходит в «минус», будет точка максимума. И наоборот: там, где «минус» переходит в «плюс», будет точка минимума.

Вот и все, что нам нужно знать для решения сегодняшней задачи.

Замечание по поводу тригонометрических функций

Однако некоторые ученики скажут: «На третьем этапе мы отбираем корни только в тех задачах, где требуется найти значение функции, а не точку максимума или минимума. Зачем выполнять отбор корней?»

Согласен, в большинстве задач на поиск точки экстремума отбирать точки не нужно, однако в нашем случае речь идет о тригонометрических функциях, и, как следствие, уравнение y‘ = 0 будет иметь бесконечное множество корней. Вы что будете отмечать множество корней?

А еще нужно искать между ними знаки, смотреть, где «плюс» переходить в «минус». Это бред! Поэтому, когда вы видите, что в задаче требуется найти производную тригонометрической функции, просто запомните для себя: мы в любом случае отбираем корни на интервале, независимо от того, требуется ли от нас найти значение функции или просто точку минимума или максимума.

При вычислении точек максимума/минимума тригонометрической функции отбор корней на отрезке не просто желателен — такой отбор становится необходимостью!

Это замечание существенно упрощает задачу, потому что лучше отметить один или два корня и посмотреть знаки вокруг них, чем бегать по всей числовой прямой и выяснять, где стоят плюсы, а где — минусы.

Решение задачи B15 на тригонометрию

Все, с разъяснениями мы закончили, переходим к решению конкретной задачи.

Производная тригонометрической функции

Итак, первый шаг: нужно найти производную функции:

y‘ = ((3 − 12x) sin x − 12 cos x + 16)’ = ((3 − 12x) · sin x)’ − (12 cos x)’

Первое слагаемое у нас представляет собой произведение двух функций, в каждой из которых присутствует элемент х, следовательно, нам нужно посчитать производную произведения. Напомню формулу производной произведения:

(f · g)’ = f ‘ · g + f · g‘

Запомните, что производная произведения не равна произведению производных. Считаем:

((3 − 12x) · sin x)’ = (3 − 12x)’ · sin x + (3 − 12x) · (sin x)’ = −12 · sin x + (3 − 12x) · cos x

Все, мы посчитали первое слагаемое. Переходим ко второму:

(12 cos x)’ = −12 sin x

Теперь подставляем два значения в нашу исходную формулу. Получим:

y‘ = −12 · sin x + (3 − 12x) · cos x − (− 12 sin x) = (3 − 12x) cos x

Находим точки экстремума

Мы нашли производную и выполнили первый шаг нашего алгоритма. Переходим ко второму шагу:

(3 − 12x) cos x = 0

Произведение равно 0, когда хотя бы один из множителей равен 0. Получаем:

3 − 12x = 0
cos x = 0

Из первого уравнения легко находится х:

x = 3/12 = 1/4

А второе равнение — это обычное тригонометрическое равнение. Мы можем сразу записать ответ:

x = π/2 + πn, n ∈ Z

Прекрасно, второй шаг нашего алгоритма выполнен!

Отбор корней тригонометрического уравнения на отрезке

Итак, мы нашли вес корни. Теперь отбираем те корни, которые лежат на интервале (0; π/2).

Пока отложим корти, которые получились из тригонометрического уравнения, потому что это более сложная конструкция, и таких корней бесконечное множество.

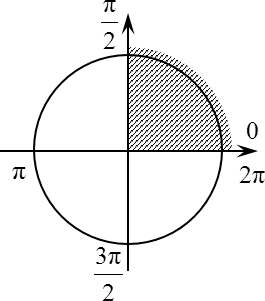
Решать будем с помощью тригонометрического круга. Давайте отметим все точки в пределах (0; π/2):

Нижняя точка нас не устраивает, как и не устраивает верхняя точка, потому что они лежат на концах интервала. А сами концы нас не устраивает просто потому, что в исходном условии задачи концы интервала обозначены выколотыми точками, т. е. круглыми скобками. Следовательно, точка π/2 нас тоже не интересует, и поэтому нужно вычеркнуть весь набор корней.

Остается лишь один корень — 1/4. Возникает вопрос: принадлежит ли он интервалу (0; π/2)? Проверяется это очень просто: приравниваем 1/4 с 0 и π/2:

0 ∨ 1/4 ∨ π/2

То, что 1/4 больше, чем 0, а вот с π/2 придется немного повозиться.

1/4 ∨ π/2 > 2 · 3 = 6
0 < 1/4 < π/2

Следовательно, корень 1/4 принадлежит к интересующему нас интервалу (0; π/2). На этом можно было бы закончить решение, потому что мы нашли единственный корень, который нас интересует и который лежит на рассматриваемом интервале и, следовательно, только он может являться ответом.

Можно записать ответ: 1/4 или 0,25.

Проверка корней тригонометрического уравнения

Однако давайте убедимся, что это действительно точка максимума. Для этого начертим прямую, т. е. перейдем к 4-ому шагу, отметим точку 1/4, а также концы интервала 0 и π/2.

Здесь же отметим знаки. Для этого подставляем любое число в пределах от 0 до 1/4 в изначальную производную. Например, какую-нибудь одну тысячную:

y‘ (0,001) = (3 − 0, 012) ∙ cos 0,001 > 0

Очевидно, что это число будет больше 0. Кроме того, cos x в пределах промежутка (0; π/2) везде положительный.

Произведение двух положительных чисел является положительным числом. Следовательно, в пределах от 0 до 1/4 знак будет «плюс». А число 1/4 является корнем первой кратности, так как у нас нет никаких квадратов, т. е. при переходе через него знак поменяется:

Мы получаем, что в точке x = 1/4 знак производной меняется с «плюса» на «минус». Следовательно, точка x = 1/4 является точкой максимума. Теперь задача точно решена, и мы еще раз убедились, что ответом будет число 0,25.

Особенности решения задач B15 с тригонометрией

Итого, несмотря на довольно угрожающий вид функции, все решается просто и быстро. Главное — не забывайте, по какой формуле считается производная произведения, иначе ответ точно получится неправильный.

Кроме того, настоятельно рекомендую вам потренироваться в отборе корней на интервале, иначе вы замучаетесь отмечать бесконечный набор корней на числовой прямой.

В остальном же это стандартная задача B15 на экстремумы, которая решается классическими приемами из математического анализа и вполне доступна среднестатистическому ученику.

Надеюсь, этот урок поможет тем, кто готовится к ЕГЭ по математике. А у меня на сегодня все. С вами был Павел Бердов. До новых встреч!

Смотрите также:

1. Иррациональные функции в задаче B15: показательная функция и линейная замена
2. Задача B15: Линейные выражения под знаком тригонометрической функции
3. Тест к уроку «Сложение и вычитание дробей» (легкий)
4. Тест: простейшие показательные уравнения (1 вариант)
5. Задача B5: вычисление площади методом обводки
6. Обход точек в стереометрии — 2

Тригонометрическая функция. Продолжаем рассматривать задачи связанные с нахождением точек максимума (минимума). Советую повторить теорию необходимую для решения задач на нахождение наибольшего (наименьшего) значения функции на интервале и на нахождение точек максимума (минимума) функции. В этой статье разберём две задачи в этой теме, рассмотрим тригонометрические функции.  Задачи с логарифмами уже были нами рассмотрены ранее.

Ещё раз запишем алгоритм нахождения точек максимума (минимума) функции:

1. Вычисляем производную функции.

2. Приравниваем её к нулю, решаем уравнение.

3. Полученные корни разбивают числовую ось на интервалы, отмечаем их.

4. Определяем знаки производной на этих интервалах (подставляем произвольные значения из интервалов в производную).

5. Делаем вывод.

77492. Найдите точку максимума функции y = (2x –3) cos x – 2sin x + 5 

принадлежащую промежутку (0;П/2).

Найдём производную функции:

Решаем уравнение:

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, и другие при этом не теряют смысла. Следовательно:

Решаем уравнение      – sin x = 0:

В условии дан промежуток (0;П/2). Ему не принадлежит ни один из полученных корней. *Обратите внимание, что указанные границы исключены (скобки круглые).

Решаем уравнение: 2х – 3 = 0, получим х = 1,5.

Запишем данный промежуток в радианах, получим: (0;1,57), так как

Следовательно полученное значение принадлежит промежутку (0;П/2):

Конечно, нам интуитивно понятно, что полученная точка это и есть точка максимума, и казалось бы в дальнейших вычислениях и рассуждениях нет необходимости. Но любая задача данного типа должна быть решена до конца по указанному алгоритму. Это важно!

Полученное значение х разбивает данный промежуток на два других. Определим знаки производной функции, подставляя произвольные значения из полученных промежутков (0;1,5) и (1,5;1,57) в найденную производную, и изобразим на рисунке поведение функции:

*В подобных случаях необязательно вычислять значения выражений. Важно установить их знаки (положительный либо отрицательный). Например, мы видим, что выражение:

(3,14/2) – 3    имеет отрицательный знак

3,14 – 3    имеет положительный знак

 В целом этого достаточно для определения знака выражения.

Таким образом, в точке х = 1,5 функция меняет знак с положительного на отрицательный.  Это означает, что данная точка является точкой максимума функции на заданном промежутке.

Ответ: 1,5  

77493. Найдите точку минимума функции y = (0,5 – x) cos x + sin x  

принадлежащую промежутку (0;П/2).  

Найдём производную функции:

Решаем уравнение:

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, и другие при этом не теряют смысла. Следовательно:

Решаем уравнение   – sin x = 0:

В условии дан промежуток (0;П/2). Ему не принадлежит ни один из полученных корней.

Решаем уравнение: 0,5 – х = 0,   получим х = 0,5.

Запишем данный промежуток в радианах: (0;1,57).

*Показано в предыдущем примере.

Следовательно полученное значение принадлежит промежутку (0;П/2):

Найденное значение х разбивает данный промежуток на два других. Определим знаки производной функции, подставляя произвольные значения из полученных промежутков (0;0,5) и (0,5;1,57) в найденную производную, и изобразим на рисунке поведение функции:

*Синус 0,3 радиана и синус 1 радиана имеют положительные знаки, так как оба эти угла лежат в пределах от 0 до 90 градусов. А мы знаем, что синусы углов лежащих в первой четверти имеют положительные значения.

Таким образом, в точке х = 0,5 функция меняет знак с отрицательного на положительный.  Это означает, что данная точка является точкой минимума функции на заданном промежутке.

Ответ: 0,5  

Как видите всё просто. Необходимо понимать свойства производной для исследования функций, понимать как «работать» с мерами углов, знать основы тригонометрии.

В будущем мы рассмотрим задачи на нахождение наибольшего (наименьшего) значения тригонометрических функций на заданном интервале, не пропустите!

Посмотрите, что нашёл в интернете. Оказывается, что при извержении вулканов тоже молнии бывают. Да ещё какие!

На том всё. Успехов Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

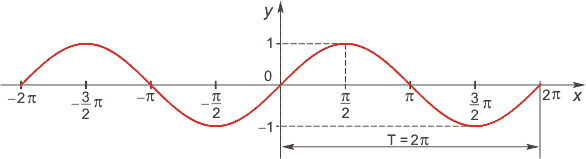
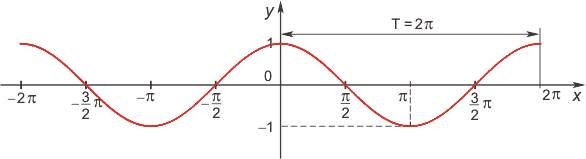
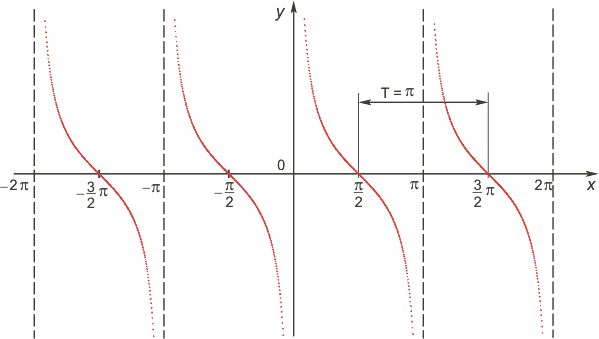
7) Периодическость функции.

Функция
f(x) — периодическая, если существует
такое отличное от нуля число T, что для
любого x из области определения функции
имеет место: f(x+T) = f(x). Такое наименьшее
число называется периодом функции. Все
тригонометрические функции являются
периодическими.

Графиком
функции y = f(x) называется множество
всех точек, у которых абсциссы принадлежат
области определения функции, а ординаты
равны соответствующим значениям
функции.

Другими
словами, график функции y = f (х) — это
множество всех точек плоскости,
координаты х, у которых удовлетворяют
соотношению y = f(x).

21. Основные тригонометрические функции и их св-ва

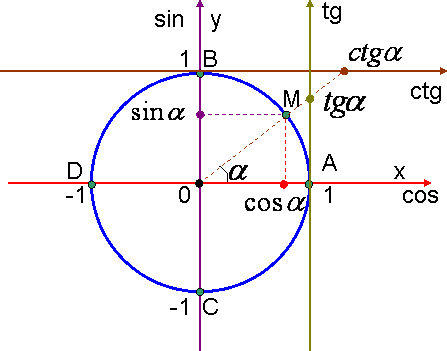
Тригонометрические
функции (функции угла) определяются
следующими равенствами:

синус:
sinα=y, т.е. ордината точки M;

косинус:
cosα=x, т.е. абсцисса точки M;

тангенс:
tgα=x/y, т. е. отношение ординаты к абсциссе
точки M;

котангенс:
ctgα=y/x, т. е. отношение абсциссы к ординате
точки M.

Функция
синус

Функция
косинус

Функция
тангенс

Функция
котангенс

22. Обратные тригонометрические функции, графики, свойства

Функция

на отрезке

имеет обратную функцию, которая
называется арксинусом

Арксинусом
числа
х,
где

называется такое число у,

синус которого равен числу х.
Обозначают:


Таким
образом,

– это угол у,
измеренный в радианах, такой, что


Для
любого

имеем

,

.

2.
Функция

на отрезке

имеет обратную функцию, которая
называется арккосинусом.

Арккосинусом
числа
х,
где

называется такое число у,

косинус которого равен числу х.
Обозначают:


Таким
образом,

– это угол у,
измеренный в радианах, такой, что


Для
любого

имеем

,

.

3.
Функция

на промежутке

имеет обратную функцию, которая
называется арктангенсом.
Арктангенсом
числа
х,

называется такое число у,

тангенс которого равен числу х.
Обозначают:


Таким
образом,

– это угол у,
измеренный в радианах, такой, что


Для
любого

имеем

,

.

4.
Функция

на промежутке

имеет обратную функцию, которая
называется арккотангенсом.
Арккотангенсом
числа
х,

называется число у,

котангенс которого равен числу х.
Обозначается:


Таким
образом,

– это угол
у,
измеренный в радианах, такой, что


Для
любого

имеем

,

.

Функции

,

,

,

называют обратными
тригонометрическими функциями
или аркфункциями.

Некоторые
важные тождества:

,

,

,

,

.

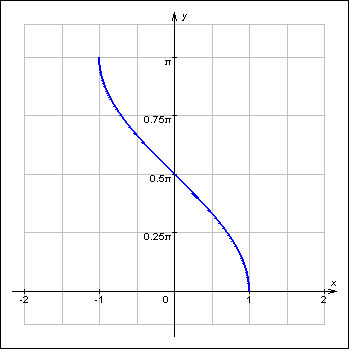
y = arccos x.

y = arcsin x.

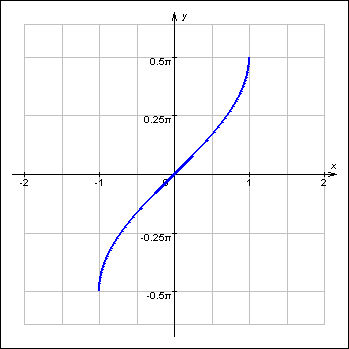
y = arctg x.

2

y = arcctg x.

3. использование свойств функций
для решений уравнений и неравенств

При
решении уравнений и неравенств смешанного
типа приходится применять свойства
элементарных функций: область определения,
область значений, монотонность,
ограниченность, четность и нечетность,
периодичность.

Ограниченность
множества значений функции

Уравнение
f(x)=g(x) равносильно системе уравнений
f(x)=A; g(x)=A, если для всех x€X справедливы
неравенства f(x)≤A и g(x)≥A.

Монотонность
функции

1)
Если функция f возрастает (убывает) на
множестве X, то уравнение f(x)=A на множестве
X имеет не более одного корня.

2) Если функция f
возрастает (убывает), а функция g убывает
(возрастает) на множестве X, то уравнение
f(x)=g(x) на множестве X имеет не более
одного корня.

3) Если f(x) — монотонно
возрастающая функция, то уравнения
f(x)=x и f(f(x))=x равносильны.

Периодичность
функции

1) Сумма двух
функций с соизмеримыми периодами T₁
и T₂
является функция с периодом НОД(T₁,T₂).

2)
Сумма двух функций с несоизмеримыми
периодами является непериодической
функцией.

3)
Не существует периодических функций,
не равных константе, у которой периодами
являются несоизмеримые числа.

Иногда
полезно рассмотреть эскизы графиков
функций

и

,
входящих в уравнение

.
Этот метод, не являющийся строгим
решением, может помочь установить: а)
существуют ли у данного уравнения корни
и сколько их; б) на какие множества
следует разбить область определения
уравнения, чтобы на каждом из этих
множеств использовать свой способ
решения.

Использование
области опр.

В
начале решения уравнения полезно найти
область определения уравнения. Если
она состоит из нескольких точек, то
остается только проверить, какие из
них удовлетворяют уравнению. Если
область определения – пустое множество,
то уравнение не имеет решений. Если же
область определения более сложная или
ее вычисление связано с трудностями,
используется другой метод.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Тригонометрические функции

Основная сложность тригонометрических функций состоит в том, что при решении уравнений возникает бесконечное множество корней. Например, уравнение имеет корни Ну и как отмечать их на координатной прямой, если таких чисел бесконечно много?

Ответ прост: надо подставлять конкретные значения n . Ведь в задачах B15 с тригонометрическими функциями всегда есть ограничение — Поэтому для начала берем а затем до тех пор, пока соответствующий корень не «вылезет» за пределы Аналогично, очень скоро получим корень, который меньше нижней границы.

Несложно показать, что никаких корней, кроме полученных в рассмотренном процессе, не существует. Рассмотрим теперь этот процесс на конкретных примерах.

Задача. Найдите точку максимума функции, принадлежащую

y = sin x − 5 x sin x − 5cos x + 1

y ’ = (sin x − 5 x sin x − 5cos x + 1)’ = . =

Затем решаем уравнение:

y ’ = 0;
(1 − 5 x ) cos x = 0;
.
x ₁ = 0,2;
x ₂ = π /2 + πn , n ∈ Z .

С корнем все понятно, а вот формула требует дополнительной обработки. Будем подставлять разные

Но π /2 > π /3, поэтому корень не входит в исходный отрезок. Кроме того, поэтому нет смысла рассматривать

Но − π /2 < − π /3 — этот корень тоже придется отбросить. А вместе с ним — и все корни

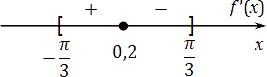
Получается, что на отрезке лежит только корень Отметим его вместе со знаками и границами на координатной прямой:

Чтобы удостовериться, что справа производная действительно отрицательная, достаточно подставить в производную значение Мы же просто отметим, производная меняет знак с плюса на минус, а следовательно, это точка максимума.

Задача. Найдите наибольшее значение функции на отрезке

y = 4 tg x − 4 x + π − 5

y ’ = (4tg x − 4 x + π − 5)’ =

Затем решаем уравнение:

y ’ = 0 ⇒ 4/cos 2 x − 4 = 0 ⇒ . ⇒

Снова выделим из этой формулы корни, подставляя

n = 0 ⇒ x = 0. Этот корень нам подходит.
n = 1 ⇒ x = π . поэтому надо вычеркнуть.
n = −1 ⇒ x = − π . тоже вычеркиваем.

Из всего многообразия корней остался лишь один: Поэтому вычисляем значение функции для Имеем:

y (0) = 4tg 0 − 4 · 0 + π − 5 = π − 5;
y ( π /4) = 4tg π /4 − 4 · π /4 + π − 5 = 1;
y (− π /4) = 4tg (− π /4) − 4 · (− π /4) + π − 5 = . =

Теперь заметим, Получается одно положительное число и два отрицательных. Мы ищем наибольшее — очевидно,

Заметим, что в последней задаче можно было и не сравнивать числа между собой. Ведь из чисел в бланк ответов можно записать лишь единицу.

Действительно, как написать в бланке, скажем, А никак. Это важная особенность первой части ЕГЭ по математике, которая значительно упрощает решение многих задач. И работает она не только в B15.

Случай пустого множества решений

Иногда при исследовании функции возникают уравнения, у которых нет корней. В таком случае задача становится еще проще, поскольку остается рассмотреть лишь концы отрезка.

Однако будьте предельно внимательны, поскольку такие задачи встречаются в ЕГЭ крайне редко. Если в процессе решения выясняется, что корней нет, лучше еще раз проверить все выкладки. И только когда убедитесь, что ошибок нет, можно расслабиться: вам досталась легкая задача!

Задача. Найдите наименьшее значение функции

y = 7sin x − 8 x + 5

Сначала находим производную:

y ’ = (7sin x − 8 x + 5)’ =

Попробуем решить уравнение:

y ’ = 0 ⇒ 7cos x − 8 =

Но значения cos x всегда лежат Поэтому корней нет.

Если корней нет, то и вычеркивать ничего не надо. Переходим к последнему шагу — вычисляем значение функции:

y (−3 π /2) = 7sin (−3 π /2) − 8 · (−3 π /2) + 5 = . =
y(0) = 7sin 0 − 8 · 0 + 5 = 5.

Поскольку число 1 в бланк ответов не записать, остается лишь

, часть 1

Наибольшее и наименьшее значения функции на отрезке

Наибольшее и наименьшее значения функции на множестве
(основные определения)

Пусть X – некоторое множество, входящее в область определения D ( f ) функции y = f (x) .

Определение 1. Значение f (x₀) функции y = f (x) в точкеназывают наибольшим значением функции f (x) на множестве X , если для любой точки выполнено неравенство

Наибольшее значение функции f (x) на множестве X часто обозначают

Определение 2. Значение f (x₀) функции y = f (x) в точке называют наименьшим значением функции f (x) на множестве X , если для любой точки выполнено неравенство

Наименьшее значение функции f (x) на множестве X часто обозначают

Определение 3. Наибольшее значение функции на множестве X часто называют максимальным значением функции f (x) на множестве X или максимумом функции f (x) на множестве X . Наименьшее значение функции на множестве X часто называют минимальным значением функции f (x) на множестве X или минимумом функции f (x) на множестве X .

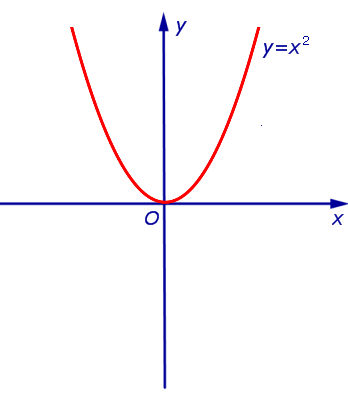
Пример 1. Минимальным значением функции y = x 2 на множестве является число 0 (рис. 1).

Максимального значения функция y = x 2 на множестве не имеет.

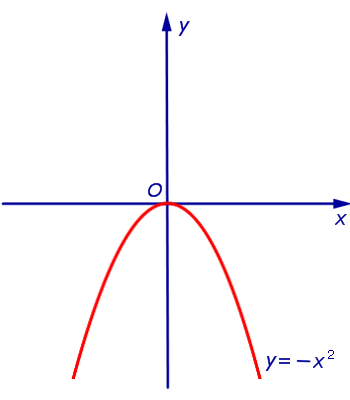
Пример 2. Максимальным значением функции y = – x 2 на множестве является число 0 (рис. 2).

Минимального значения функция y = – x 2 на множестве не имеет.

Пример 3. Функция y = x на множестве не имеет ни максимального, ни минимального значений (рис. 3).

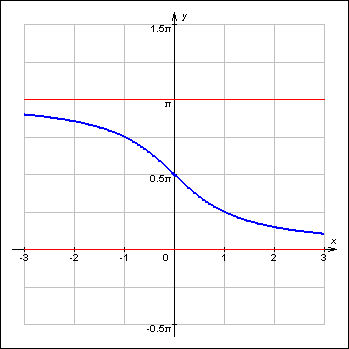
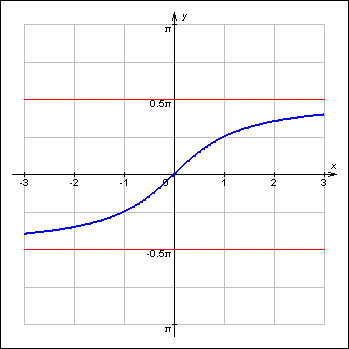
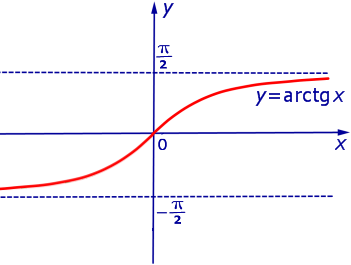
Пример 4. Функция y = arctg x на множестве не имеет ни максимального, ни минимального значений (рис. 4).

Существование наибольшего и наименьшего значений функции на отрезке. Теорема Вейерштрасса

Как мы видели в примерах 1 — 4, даже такие хорошо известные функции, как

не имеют наибольших или наименьших значений на множестве. Однако, если бы в качестве множества X мы взяли произвольный отрезок, то ситуация стала бы принципиально иной, что вытекает из следующей теоремы.

Теорема Вейерштрасса. Если функция непрерывна на отрезке, то на этом отрезке существует точка, в которой функция принимает наибольшее значение, а также точка, в которой функция принимает наименьшее значение.

Доказательство теоремы Вейерштрасса выходит за рамки школьного курса математики и здесь не приводится.

Примеры решения задач

y = 2x 3 + 3x 2 – 36x + 30

(1)

Из формулы (2) получаем, что критическими точками функции (1) являются точки x = – 3 , x = 2, причем только точка x = 2 принадлежит отрезку [–2, 4] . Вычисляя значения функции (1) в критической точке x = 2, а также на концах отрезка x = – 2 и x = 4 , получим:

y (2) = – 14 ,

y (– 2) = 98 ,

y (4) = 62 .

Ответ. Наибольшее значение функции (1) на отрезке [–2, 4] равно 98 , а наменьшее значение функции (1) на отрезке [–2, 4] равно – 14 .

на отрезке [–1, 27] .

Решая уравнение y’ = 0 , получим

Заметим также, что производная (4) функции (3) не существует в точке x = 0 . Следовательно, у функции (3) есть три критические точки: x = 0, и , причем все эти точки лежат на отрезке [–1, 27] . Вычисляя значения функции (3) в критических точках x = 0, и , а также на концах отрезка x = – 1 и x = 27 , получим:

y (0) = 0 ,

y (– 1) = – 1 ,

y (27) = 99 .

Ответ. Наибольшее значение функции (3) на отрезке [–1, 27] равно 99 , а наменьшее значение функции (3) на отрезке [–1, 27] равно – 1 .

Решение. Для того, чтобы найти критические точки функции (5), перепишем правую часть формулы (5), используя определение модуля:

В точке x = 0 производная функции (5) не существует. Критическими точками являются точки

Все критические точки принадлежат отрезку [–1, 6] . Вычисляя значения функции (5) в критических точках x = 0, x = 3, x = 5, а также на концах отрезка x = – 1 и x = 6 , получим:

y (0) = – 4 ,

y (3) = – e 3 ,

y (5) = e 5 ,

y (– 1) = – 5e ,

y (6) = 2e 6 .

Ответ. Наибольшее значение функции (5) на отрезке [–1, 6] равно 2e 6 , а наменьшее значение функции (5) на отрезке [–1, 6] равно – e 3 .

y = (x – 27) e 28 – x

(6)

на отрезке [23, 40] .

Решая уравнение y’ = 0 , получаем, что функция (6) имеет единственную критическую точку x = 28 , причем эта точка лежит на отрезке [23, 40] . При переходе через точку x = 28 производная функции (7) меняет знак с «+» на «–» , откуда вытекает, что точка x = 28 является точкой максимума функции (6) на множестве . Следовательно, точка x = 28 является точкой максимума функции (6) и на отрезке [23, 40] . Найдем значение функции (6) в точке x = 28 :

Задание 11 Профильного ЕГЭ по математике

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции

Найдем производную функции.

Приравняем производную к нулю. Получим:

Исследуем знаки производной.

В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

Определим знаки производной.

В точке производная меняет знак с «минуса» на «плюс». Значит, — точка минимума функции

Исследование сложных функций

3. Найдите точку максимума функции

Перед нами сложная функция Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция монотонно возрастает, точка максимума функции .будет при том же , что и точка максимума функции А ее найти легко.

при . В точке производная меняет знак с «плюса» на «минус». Значит, — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при

4. Найдите абсциссу точки максимума функции

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции является и точкой максимума функции

Это вершина квадратичной параболы

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

Найдем знаки производной.

В точке производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции . Поскольку при функция убывает, В этой задаче значение функции на концах отрезка искать не нужно.

6. Найдите наименьшее значение функции на отрезке

Найдем производную функции и приравняем ее к нулю.

Найдем знаки производной.

Точка — точка минимума функции . Точка не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при Найдем это значение.

7. Найдите наименьшее значение функции на отрезке

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при

Если то Если , то

Значит, — точка минимума функции . В этой точке и достигается наименьшее значение функции на отрезке

8. Найдите наибольшее значение функции на отрезке

Найдем производную функции

Приравняем производную к нулю:

Найдем знаки производной на отрезке

При знак производной меняется с «плюса» на «минус». Значит, — точка максимума функции

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при и

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

9. Найдите наименьшее значение функции на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

Найдем производную функции

При знак производной меняется с «минуса» на «плюс». Значит, — точка минимума функции

10. Найдите наибольшее значение функции на отрезке

Как всегда, возьмем производную функции и приравняем ее к нулю.

По условию, . На этом отрезке условие выполняется только для Найдем знаки производной слева и справа от точки

В точке производная функции меняет знак с «плюса» на «минус». Значит, точка — точка максимума функции . Других точек экстремума на отрезке функция не имеет, и наибольшее значение функции на отрезке достигается при

11.Найдите наименьшее значение функции на отрезке

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при

Значит, наименьшее свое значение функция принимает в левом конце отрезка , то есть при

Способы отбора корней в тригонометрических уравнениях

Класс: 10

Автор проекта:
Шелкова Полина,
Класс: 10

Руководитель:
Злобова Людмила Викторовна,
учитель математики

ВВЕДЕНИЕ

Слово «тригонометрия» греческое, оно переводится как «измерение треугольников» (τρίγονον — «тригон» — треугольник и μετρειν — «метрео» — измеряю).

Тригонометрия, как и всякая другая наука, выросла из практической деятельности человека. Потребности развивающегося мореплавания, для которого требовалось умение правильно определять курс корабля в открытом море по положению небесных светил, оказали большое влияние на развитие астрономии и тесно связанной с ней тригонометрией. Предполагают, что основополагающее значение для развития тригонометрии в эпоху ее зарождения, имели работы древнегреческого астронома Гиппарха Никейского (180-125 лет до н. э.) (прил. №3). Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд (прил. №2). Т.е. таблицы, которые выражают длину хорды для различных центральных углов в круге постоянного радиуса, что является аналогом современных таблиц тригонометрических функций. Впрочем, до нас не дошли оригинальные таблицы Гиппарха, как и почти все, что им написано. И мы, можем составить себе о них представление главным образом по сочинению «Великое построение» или «Альмагесту» знаменитого астронома Клавдия Птолемея, жившего в середине II века н.э.

Несмотря на то, что в работах ученых древности нет «тригонометрии» в строгом смысле этого слова, но по существу они, пользуясь известными им средствами элементарной геометрии, решали те задачи, которыми занимается тригонометрия. Например, задачи на решение треугольников (определение всех сторон и углов треугольника по трем его известным элементам), теоремы Евклида и Архимеда представленные в геометрическом виде, эквивалентны специфическим тригонометрическим формулам. Главным достижением средневековой Индии стала замена хорд синусами. Это позволило вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии, как учению о тригонометрических величинах.

Учёные стран Ближнего и Среднего Востока с VIII века развили тригонометрию своих предшественников. Уже в середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того, как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки. В дальнейшем потребности географии, геодезии, военного дела, способствовали развитию тригонометрии. Особенно усиленно шло ее развитие в средневековое время. Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому ученому Насир ад-Дину ат-Туси (1201-1274), написавшему «Трактат о полном четырехстороннике». Творения ученых этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах еще не была введена необходимая символика. Современный вид тригонометрия получила в трудах Леонарда Эйлера (1707-1783). На основании трудов Эйлера были составлены учебники тригонометрии, излагавшие ее в строгой научной последовательности (прил. №4). Тригонометрические вычисления применяются во многих областях человеческой деятельности: в геометрии, в физике, в астрономии, в архитектуре, в геодезии, инженерном деле, в акустике, в электронике и т.д.

I РАЗДЕЛ (теоретический)

Тема проекта и её актуальность: почему я выбрала тему «Способы отбора корней в тригонометрических уравнениях»?

• Расширить и углубить свои знания, полученные в курсе геометрии 8-9 класса.
• Тригонометрические уравнения рассматриваются в курсе алгебры и начал математического анализа 10-11 класса.
• Тригонометрические уравнения включены в КИМы ЕГЭ по математике.

Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку — это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Немаловажно также знать, тригонометрические формулы, табличные значения тригонометрических функций для решения целого ряда заданий Единого Государственного Экзамена по математике.

Цель проекта: изучить способы отбора корней в тригонометрических уравнениях и выбрать для себя наиболее рациональные подходы для качественной подготовки к ЕГЭ.

Задачи:

• познакомиться с историческими сведениями о возникновении тригонометрии, как науки;
• изучить соответствующую литературу;
• научиться решать тригонометрические уравнения;
• найти теоретический материал и изучить методы отбора корней в тригонометрических уравнениях;
• научиться отбирать корни в тригонометрических уравнениях, принадлежащим заданному промежутку;
• подготовиться к ЕГЭ по математике.

Приёмы отбора корней тригонометрического уравнения на заданном промежутке.

При решении тригонометрических уравнений предлагается провести отбор корней из множества значений неизвестного. В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.

Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.

Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.

Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрической окружности или числовой прямой. Тригонометрическая окружность более удобна, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. В остальных случаях предпочтительнее модель числовой прямой. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого не превосходит 2 или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.

Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.

II РАЗДЕЛ (практический)

Покажу практически три наиболее эффективных и рациональных, с моей точки зрения, метода отбора корней на примере решения следующего тригонометрического уравнения:

sinx−cos2x=0; [применили формулу двойного угла: cos2x = cos 2 x−sin 2 x]

sinx−(cos 2 x−sin 2 x)=0;

sinx−(1−sin 2 x−sin 2 x)=0;

Введем новую переменную: sinx = t, -1 ≤ t ≤1, получим

Вернемся к замене:

б) Рассмотрим три способа отбора корней, попадающих в отрезок .

1 способ: обратимся к единичной окружности. Отметим на ней дугу, соответствующую указанному отрезку, т.е. выполним отбор корней арифметическим способом и с помощью тригонометрической окружности:

2 способ: указанный отрезок соответствует неравенству: Подставим в него полученные корни:

3 способ: разместим корни уравнения на числовой прямой. Сначала отметим корни, подставив вместо n, и нуль (0), а потом добавим к каждому корню периоды.

Нам останется только выбрать корни, которые попали в нужный нам отрезок.

ЗАКЛЮЧЕНИЕ

При работе над моим проектом я изучила методы решения тригонометрических уравнений и способы отбора корней тригонометрических уравнений. Выяснила для себя положительные и отрицательные моменты. При апробации этих подходов в отборе корней тригонометрического уравнения, понимаешь, что каждый из этих способов удобен по-своему в том или ином случае. Например, алгебраический способ (решение неравенством) наиболее эффективен, когда промежуток для отбора корней достаточно большой, в тоже время он дает практически стопроцентное нахождение целочисленного параметра для вычисления корней, а применение арифметического способа приводит к громоздким вычислениям. При отборе корней уравнения, удовлетворяющих дополнительным условиям, т.е. когда корни уравнения принадлежат заданному промежутку, мне проще и нагляднее получить корни с помощью тригонометрической окружности, а проверить себя можно арифметическим способом. Замечу, что при решении тригонометрических уравнений трудности, связанные с отбором корней, возрастают, если в уравнении приходится учитывать ОДЗ. Как показывает практика и анкетирование моих одноклассников, из четырёх возможных методов отбора корней тригонометрического уравнения по дополнительным условиям, наиболее предпочтительным является отбор корней по окружности. Анкетирование проходили 12 респондентов, изучающих тригонометрию (прил. №5). Большинство из них отвечали, что этот раздел математики достаточно сложный: большой объем информации, очень много формул, табличных значений, которые нужно знать и уметь применять на практике. Еще как одна из проблем — небольшое количество времени, отведенное на изучение этого сложного раздела математики. И я разделяю их мнение. При такой сложности, многие считают, что тригонометрия важный раздел математики, который находит применение в других науках и практической деятельности человека.

СПИСОК ЛИТЕРАТУРЫ

1. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К.Потапов, Н.Н.Решетников и др.]-3 -е изд.- М.: Просвещение, 2016.
2. Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова — М. Просвещение, 2017.
3. С.В Кравцев и др. Методы решения задач по алгебре: от простых до самых сложных — М: Издательство: «Экзамен», 2005.
4. Корянов А.Г., Прокофьев А.А. — Тригонометрические уравнения: методы решения и отбор корней. — М.: Математика ЕГЭ, 2012.

Задача B15: Линейные выражения под знаком тригонометрической функции

Сегодня у нас заключительный урок на производные из ЕГЭ по математике. И как всегда по традиции последняя задача будет немножко нестандартной. Итак:

Задача B15. Найдите наибольшее значение функции на отрезке [0; π/3]:

y = 2sin 2 x + cos 4 x

Общая схема вычисления наибольшего значения функции

Перед тем, как мы начнем решать эту задачу, хотел бы напомнить вам общий универсальный алгоритм поиска наибольшего и наименьшего значения функции на отрезке. Он состоит из 4 шагов:

1. Первый шаг состоит в том, что нужно найти производную нашей функции: y ‘ = ?

2. Второй шаг — производную мы приравниваем к нулю в результате решения у нас получится один или несколько корней: x <1>, x <2>, .

3. Затем берем эти корни и оставляем только те из них, которые лежат на отрезке, указанном в условии задачи — в нашем случае речь идет об отрезке [0; π/3]. Другими словами, мы вычеркиваем все корни, которые не лежат на интересующем нас отрезке: x <1>, x <2>∈ [0; π/3].

4. Наконец, подставляем концы отрезка, а также оставшиеся корни в нашей исходное уравнение. Другими словами, мы находим y (0); y (π/3); y ( x ₁); y ( x ₂), т. е. значение функции в нулях производной.

Это стандартная схема, и мы применяли ее уже много раз.

Экстремумы функции на отрезке: пояснение

Естественно, при взгляде на этот алгоритм у многих учеников сразу возникают вопросы. Первый и самый распространенный: «Почему это мы подставляем в нашу функцию концы отрезка? Неужели недостаточно просто посчитать функцию в нулях производной?»

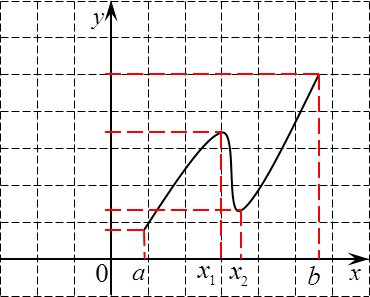
К сожалению, недостаточно. Взгляните вот на такую функцию:

На этом рисунке видно, что наибольшее значение функции достигается именно в правом верхнем конце отрезка — в точке b , а никак не в точке x ₁, которая является точкой максимума и, соответственно, возникает при решении уравнения y ‘ = 0. То же самое и с наименьшим значением — оно достигается в точке a , но ни в коем случае не в точке x ₂, которая также возникнет при решении y ‘ = 0.

Локальный и глобальный экстремум функции: в чем разница?

Вспомните определение производной и точки экстремума: в данном случае точка x ₁ будет являться точкой локального максимума, т. е. на некотором интервале, достаточно небольшом, именно на этой точке будет приниматься наибольшее значение. То же самое касается и точки x ₂. На некотором небольшом интервале, т. е. на определенном отступе от этой точки вправо или влево функция действительно будет принимать наименьшее значение именно в точке x ₂.

Однако на глобальном отрезке никто этого не гарантировал. И часто случается так, что настоящее наибольшее или наименьшее значение функции достигается именно на концах рассматриваемого отрезка. Особенно это качается задач B15, которые любят давать на пробниках и разных демонстрационных ЕГЭ по математике.

Наибольшее или наименьшее значение функции совсем не обязательно достигается в нулях производной. Очень часто такие значения возникают на концах отрезка, где производная отлична от нуля.

В общем, чтобы подстраховаться и не допустить обидных ошибок на настоящем экзамене, настоятельно рекомендую вам считать значения функции не только в нулях производной, но и на концах отрезка, т. е. в нашем случае в точках х = 0 и х = π/3.

Решение задачи B15 с тригонометрией

С теорией разобрались, давайте решать нашу задачу. Для начала нам нужно посчитать производную функции:

y = 2sin 2 x + cos 4 x

Производная тригонометрической функции

y ‘ = (2sin 2 x + cos 4 x )’ = (2sin 2 x )’ + (cos 4 x )’

И вот тут возникает проблема в данной задаче: дело в том, что внутри синуса и косинуса стоит не переменная х, а выражение 2х и даже 4х.

Как поступать с такими конструкциями? Конечно, можно воспользоваться производной сложной функции, посчитать и в итоге получить правильное значение, но давайте не будем лезть в дебри, а вспомним замечательную формулу, которая рассматривалась не нескольких уроках, посвященным подготовке к ЕГЭ по математике. Формула следующая:

x → kx + b
( f ( x ))’ → k ( f ‘ ( kx + b ))

Другими словами, замена переменной функции не проходит для всей функции бесследно. В случае, если вместо х мы подставляем линейную функцию, то перед новой производной появляется коэффициент.

Линейная замена переменной приводит лишь к одному дополнительному множителю в производной. Никаких сложных формул при линейной замене применять не нужно!

Это частный случай производной сложной функции. Однако сложные функции в реальном ЕГЭ не встречаются. Поэтому вам достаточно будет знать упрощенную конструкцию, которую мы записали. Ее очень легко применять.

Производная функции при линейной замене

Давайте посчитаем производную sin 2 x . Для этого вспомним такое:

Тогда производная от sin 2 x будет выглядеть так:

(sin 2 x )’ = 2 · cos 2 x

Все, производная 2sin 2 x найдена. Аналогично давайте разберемся и с производной cos 4 x :

(cos 4 x )’ = 4 · (−sin 4 x ) = −4 sin 4 x

А теперь собираем это все в одну конструкцию и получаем:

y ‘ = 4 cos 2 x − 4 sin 4 x

Считаем нули производной — точки экстремума

Итак, первый шаг нашего алгоритма выполнен, мы нашли производную. Теперь приравниваем эту производную к нулю и решаем полученное уравнение:

2 cos 2 x − 4 sin 4 x = 0

Перед нами обычное тригонометрическое уравнение и все, что нам требуется сделать в нем — это свести все тригонометрические функции к одному и тому же аргументу. Как правило, в таких задачах следует стремиться к наименьшему аргументу. Поэтому вспомним формулу двойного угла:

sin 2λ = 2 sin λ cos λ

В нашем случае это будет выглядеть так:

sin 4 x = sin 2 · 2 x = 2 · sin 2 x · cos 2 x

Обратите внимание! Мы пишем именно 2х, потому что в исходной формуле, которую мы разложили, вместо переменной λ стоит именно 2х.

Итак, с синусом двойного угла мы разобрались, перепишем наше уравнение с учетом этого факта. Получим:

4 cos 2 x − 8 sin 2 x cos 2 x = 0
4 cos 2 x (1 − 2 sin 2 x · 1) = 0

Итак, мы разложили наше уравнение на множители. Теперь вспоминаем: произведение равно нулю, когда хотя бы один из множителей равен нулю. Запишем:

cos 2 x = 0
1 − 2 sin 2 x = 0

Первое уравнение решается элементарно:

2 x = π/2 + π n , n ∈ Z

А со вторым уравнением будет немного посложнее:

sin 2 x = 1/2
2 x = π/6 + 2π n
2 x = π − π/6 + 2π n

Напомню, что решение простейших тригонометрических уравнений, которые содержат синус, лучше записывать как совокупность из двух наборов корней.

Однако на этом решение уравнения еще не закончилось. Взгляните, мы нашли только 2х, а нужно найти просто х. Находим:

x = π/3 + π n /2;
x = π/12 + πn;
x = 5π/12 + π n .

Производная тригонометрической функции: отбор корней на отрезке

Уравнение решено. Переходим к третьему шагу: необходимо отобрать корны, которые лежат на отрезке [0; π/3].

Для этого нам сначала потребуется начертить радар, а потом отметить на мне все три набора корней. На этом же отрезке отмечаем концы отрезка. Получим:

На самом деле из всего этого многообразия нас интересуют лишь две точки: π/4 и π/12. Все, третий шаг выполнен. Мы отобрали корни на отрезке.

Вычисление наибольшего значения функции

А теперь возвращаемся к условию задачи и вспоминаем, что нам нужно найти наибольшее значение функции на отрезке. Т. е. нужно взять функцию

y = 2sin 2 x + cos 4 x

И подставить в нее следующие числа:

1. Оба конца нашего отрезка — числа 0 и π/3
2. А также два корня производной, которую мы нашли: π/4 и π/12

Затем из полученных четырех значений функции надо выбрать наибольшее.

Давайте решать. В первую очередь предлагаю подставить корни нашей производной, т. е. числа π/4 и π/12. Получим:

y (π/4) = 2 · sin 2 · π/4 + cos 4 · π/4 = 2 · sin π/2 + cos π = 2 · 1 − 1 = 1

Подставляем второе число — x = π/12:

y (π/12) = 2 · sin 2 · π/12 + cos 4 · π/12 = 2 · sin π/6 + cos π/3 = 2 · 1/2 + 1/2 = 1,5

Все, с корнями из производной мы разобрались, теперь считаем значение функции на концах отрезка:

y (0) = 2 · sin 0 + cos 0 = 2 · 0 + 1 = 1

Вычисление сложных значений тригонометрической функции

Теперь подставляем правый конец отрезка:

y (π/3) = 2 · sin 2 · π/3 + cos 4 · π/3 = 2 · sin 2π/3 + cos 4π/3

Оба аргумента и в синусе, и в косинусе являются нестандартными значениями (их нет в классической таблице значений тригонометрических функций), поэтому давайте отметим их на тригонометрическом круге:

С помощью полученных данных вычисляем значение функции:

Это иррациональное число, которое нельзя записать в ответ. Следовательно, оно не является ответом к задаче.

Итого нам на выбор осталось три числа: y = 1; y = 1,5; y = 1. Требуется найти наибольшее значение. Следовательно, ответом будет являться y = 1,5. Все, задача решена.

Ключевые моменты в задачах B15 на производную функции

В заключение хотел бы еще раз обратить ваше внимание на два ключевых факта в решении этой задачи. В первую очередь, речь идет о производной сложной функции. В реальных задачах из ЕГЭ по математике встречается лишь упрощенная версия формулы, которую мы записали в самом начале решения задачи.

Итак, запомните: если в табличной производной заменить переменную х на линейное выражение kx + b , то и в самой производной нужно везде вместо х подставить выражение kx + b . Кроме того, перед самой производной нужно добавить множитель k — тот саамый, который стоял перед х во время замены.

Это универсальное правило, и оно работает всегда. Давайте посмотрим. Например, у нас есть следующая функция:

Возьмем большую степень, чтобы у вас не возникало соблазна раскрывать ее по формулам сокращенного умножения. А теперь мы хотим посчитать производную:

Как это сделать? Очень просто. Вспоминаем: производная функции y = x 101 является табличной и легко считается:

Теперь, если вместо переменной х мы хотим подставить выражение kx + b , например, 5х + 7, то получим, что производная такой функции будет равна:

y ‘ = 101 · (5 x + 7) 101 · 5

Последний множитель «5» появился из-за того, что вместо переменной х мы подставили линейную функцию 5х + 7, т. е. выражение, которое при х содержит множитель 5. Если бы перед их стоял коэффициент k = 10, мы умножили бы производную на 10.

При этом второе слагаемое — число b = 7 — никак не влияет на результат. Т.е. на итоговую производную влияет только коэффициент при х. Запомните это.

Особенности записи корней тригонометрического уравнения

Второй важный момент касается отбора корней и решения тригонометрических уравнений, а конкретно — я бы хотел поговорить про решение тригонометрических уравнений, содержащих синус.

Как обычно нас учат записывать решение таких уравнений? Еще в школьных учебниках можно увидеть формулу:

sin x = a → x = (−1) n · arcsin a + π n , n ∈ Z

Естественно, многие ученики спросят: почему мы не используем эту формулу? Зачем разбивать эту формулу на какую-то совокупность, что-то там считать, усложняя себе задачу?

На самом деле такая запись имеет одно единственное преимущество — краткость. Во всем остальном работать с этой записью — сплошное мучение:

1. Непонятно, что делать с множителем (−1) n . Как отмечать постоянно гуляющее то в плюс, то в минус число на тригонометрическом круге?
2. Если вы захотите отбирать корни не с помощью тригонометрического круга, а с помощью двойного неравенства, опять же возникает проблема, потому что слагаемое (−1) n · arcsin a нужно будет вычитать из обеих частей неравенства. Затем полученную конструкцию нужно будет разделить на π, и вот тут возникает проблема: а что делать с множителем (−1) n ? Он снова будет мешать нам и служить источником многочисленных ошибок для большинства учеников.

Чтобы избежать этих многочисленных проблем, просто записывайте решение синуса в виде совокупности из двух уравнений, так, как мы и сделали сегодня при решении нашей задачи.

Вот и все замечания. Я специально детально рассказывал каждый шаг решения — настолько детально, что сам допустил ошибку при вычислении производной. Но ничего страшного, мы заметили ошибку вовремя, и поэтому итоговый ответ и все выкладки получись правильными.:)

Желаю вам удачи при решении сложных задач на ЕГЭ по математике, тренируйтесь в решении задач, смотрите видеоуроки и сдавайте ЕГЭ на «отлично». А у меня на этом все.

Тригонометрические уравнения

Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно. Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.

В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.

Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.

Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.

Понимание раздела «Тригонометрия» в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.

В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:

Знание этих значений необходимо, это «азбука», без которой невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да просто вы именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.

Алгоритм восстановления этих значений прост, он также приведён в теории, полученной вами во втором письме после подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».

Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с использованием угла х для соответствующих уравнений: cosx=a, sinx=a, tgx=a, где х может быть и выражением. В примерах ниже у нас аргумент задан именно выражением.

Итак, рассмотрим следующие задачи:

Найдите корень уравнения:

В ответе запишите наибольший отрицательный корень.

Решением уравнения cos x = a являются два корня:

Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.

Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.

Общая рекомендация для всех подобных задач: для начала берите диапазон n от – 2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: – 3 и 3, – 4 и 4 и так далее.

При n = – 2 х₁= 3 (– 2) – 4,5 = – 10,5 х₂= 3 (– 2) – 5,5 = – 11,5

При n = – 1 х₁= 3 (– 1) – 4,5 = – 7,5 х₂= 3 (– 1) – 5,5 = – 8,5

При n = 0 х₁= 3∙0 – 4,5 = – 4,5 х₂= 3∙0 – 5,5 = – 5,5

При n = 1 х₁= 3∙1 – 4,5 = – 1,5 х₂= 3∙1 – 5,5 = – 2,5

При n = 2 х₁= 3∙2 – 4,5 = 1,5 х₂= 3∙2 – 5,5 = 0,5

Получили, что наибольший отрицательный корень равен –1,5

В ответе напишите наименьший положительный корень.

Решением уравнения sin x = a являются два корня:

Либо (он объединяет оба указанные выше):

Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от – 90 о до 90 о синус которого равен a.

Выразим x (умножим обе части уравнения на 4 и разделим на Пи):

Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n = 0,1,2 …

При n = 0 х = (– 1) 0 + 4∙0 + 3 = 4

При n = 1 х = (– 1) 1 + 4∙1 + 3 = 6

При n = 2 х = (– 1) 2 + 4∙2 + 3 = 12

Проверим при n = –1 х = (–1) –1 + 4∙(–1) + 3 = –2

Значит наименьший положительный корень равен 4.

В ответе напишите наименьший положительный корень.

Решением уравнения tg x = a является корень:

Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90 о до 90 о , тангенс которого равен a.

Выразим x (умножим обе части уравнения на 6 и разделим на Пи):

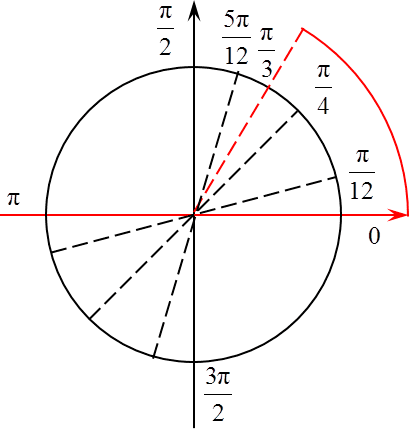
Найдём наименьший положительный корень. Подставим значения n = 1,2,3. Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:

Таким образом, наименьший положительный корень равен 0,25.

Определение котангенса: Арккотангенсом числа a (a – любое число) называется угол x принадлежащий интервалу (0;П), котангенс которого равен a.

Здесь хочу добавить, что в уравнениях в правой части может стоять отрицательное число, то есть тригонометрическая функция от аргумента может иметь отрицательное значение. Если в ходе решения вы не сможете определить угол, например, для

то данные формулы вам помогут:

Спасибо за внимание, учитесь с удовольствием!