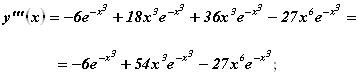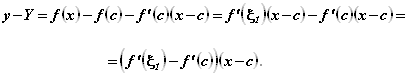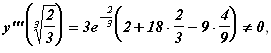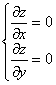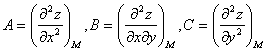Правило для исследования функции на экстремум по второй производной (второй способ)
Для
того чтобы исследовать функцию на
экстремум по второй производной, следует:
-
Найти
область определения функции. -
Найти
– первую производную функции.
-
Определить
критические точки первого рода. -
Исследовать
знак
– второй производной функции – в каждой
точке, найденной в пункте 3. Если окажется,
что в рассматриваемой точке
,
то в этой точке будет минимум, а если
,
то в ней будет максимум. Если же окажется,
что в рассматриваемой точке
,
то исследование надлежит провести по
первому правилу.
Замечание.
Отметим, что исследование знака первой
производной слева и справа от критических
точек совпадает с правилом нахождения
промежутков монотонности функции. Это
связано с тем, что точки экстремума и
разрыва функции разделяют участки ее
возрастания и убывания.
Правило исследования функции на монотонность и экстремумы .
-
Найти область
определения функции. -
Найти
.
-
Определить
критические точки первого рода и
пронумеровать их в порядке возрастания. -
Построить
таблицу I:
|
Интервалы |
|
|
|
и поведение в |
|
|
Поведение функции |
Пример
4. Найти интервалы монотонности
и экстремумы функции
.
▲
Проведем решение
сначала по первому правилу
-
Областью
существования функции является весь
бесконечный интервал.
-
Находим,
что
. -
Решаем
уравнение
,
т. е. уравнение
.
Производная конечна при любом
(в этом случае говорят, что производная
конечна всюду). Поэтому критическими
точками будут только найденные выше.
-
Располагаем
критические точки в порядке возрастания
абсцисс:
. -
Рассмотрим
интервалы
Выберем
внутри каждого из этих интервалов
произвольную точку и определим в этой
точке знак первой производной по
выражению
.
В
интервале
возьмем, например, точку
;
в
интервале
возьмем точку
;
в
интервале
возьмем точку
;
в
интервале
возьмем точку
.
-
Таким
образом, в интервалах первая производная
имеет такую последовательность знаков:
|
+ |
+ |
– |
– |
и
мы приходим к заключению, что в критической
точке
имеет место максимум, а в критических
точках
экстремумов нет.
-
Найдем
теперь локальный максимум функции
.
Построим таблицу
I.
|
–1 |
0 |
1 |
|||||
|
+ |
0 |
+ |
0 |
– |
0 |
– |
|
|
Нет экстремума |
|
Нет экстремума |
Проведем решение по второму правилу Исследуем функцию на экстремум с помощью второй производной.
У
нас критические точки уже определены:
.
Найдем вторую производную функции.
Дифференцируя первую производную,
получаем
,
и
согласно второму правилу определяем
знак второй производной в каждой
критической точке:
;
используем результат по первому правилу,
;
функция имеет максимум;
;
используем результат по первому правилу.
▼
Необходимо отметить,
что исследование, проведенное по второму
способу, было значительно проще. Однако
от исследования функции на экстремум
по первому правилу при помощи первой
производной отказываться не следует,
так как может оказаться, что в критической
точке вторая производная окажется
равной нулю (как в разобранном примере),
а в этом случае нельзя сделать никакого
заключения о наличие экстремума.
Пример
5. Найти интервалы монотонности
и экстремумы функции
.
-
▲
Так как знаменатель
не должен обращаться в нуль, то
. -
Найдем
производную:
.
-
Производная
обращается в нуль в точке
и не существует в точках
.
Точка
не является критической, т. к.
.
Точки
– критически е.
Располагаем
критические точки в порядке возрастания
абсцисс:
.
-
Построим
таблицу I:
|
|
–2 |
|
0 |
|
4 |
|
▼ |
|
|
– |
|
– |
|
+ |
0 |
– |
||
|
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Исследование функции с помощью второй производной
Вторая производная функции, если она существует, может быть так же эффективно использована для исследования на экстремум, определения промежутков выпуклости и вогнутости ее графика, отыскания точек перегиба.
ТЕОРЕМА 1 (ВТОРОЕ ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА). Если для функции в точке
производная
, А в ее окрестности
непрерывна, причем
, то эта точка является точкой ее максимума (минимума).
ДОКАЗАТЕЛЬСТВО.
Пусть в точке с выполняется равенство
И имеет место неравенство
Будучи непрерывной, вторая производная сохраняет свой знак при х, Близких к с. Поэтому для этих x
Но вторая производная функции есть производная от первой производной
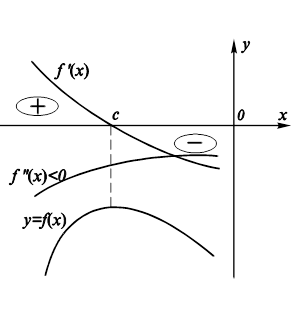
Рис. 11.17. Возможное взаимное расположение графиков функций ,
И
в окрестности точки
Максимума.
Это условие является достаточным признаком для существования экстремума, но не является необходимым. Почему?
Следовательно, есть функция убывающая. По условию теоремы,
. Это означает, что
левее точки с Положительна, а правее – отрицательна. Переходя к самой функции
, можно утверждать, что левее точки С она возрастает, а правее – убывает, то есть с – точка ее максимума, что и требовалось доказать. Аналогично доказывается теорема в случае минимума. На рис. 11.17 приведен возможный вариант взаимного расположения графиков функций
,
И
в окрестности точки с.
Данная теорема может оказаться удобной, когда знак определяется легко. Однако ее недостаток в сравнении с первым достаточным условием экстремума функции очевиден: не все точки, подозрительные на экстремум, могут быть исследованы с помощью данной теоремы. Она неприменима в случаях, когда в точке с первая производная функции обращается в бесконечность или же не определена и, конечно, когда
не существует.
Сформулируем без доказательства некоторое обобщение данной теоремы для случая, когда функция имеет производные порядка .
ТЕОРЕМА 2. Если функция в некоторой окрестности точки С имеет производную до (n+1)-го порядка, непрерывную в самой точке С, причем
то при четном (n+1) функция
имеет максимум, если
и минимум, если
.
Рассмотрим примеры.
Исследуем на экстремум функцию
Находим первую производную:
И приравниваем ее к нулю:
.
Получаем, что x = 0 – Точка, подозрительная на экстремум.
Следовательно, в этой точке функция имеет максимум:
Рассмотрим теперь функцию
Ее первая производная
Также обращается в нуль при .
Легко обнаружить, что , так как
Однако по теореме 2 имеем:
Следовательно, функция при
Экстремума не имеет.
Отсутствие экстремума у данной функции легко установить и без применения производной. Действительно, так как функция всюду возрастает, то функция
Убывает для , то есть экстремум отсутствует. Этот пример еще раз показывает, что при исследовании функций полезно использовать разнообразные приемы.
Применим теперь вторую производную к исследованию на выпуклость и вогнутость графика функции.
Выше, в главе 3, мы определили эти понятия, связывая расположение кривой с расположением хорды, соединяющей две близкие точки этой кривой. Возможен и иной способ описания выпуклости и вогнутости кривой.
Будем называть график функции в точке
вогнутым (выпуклым), если в окрестности точки М он расположен выше (ниже) касательной к кривой в этой точке (рис. 11.18).
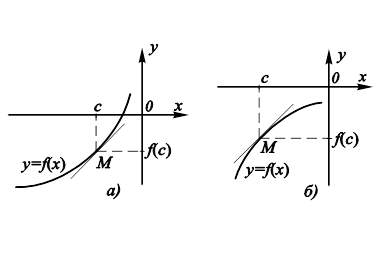
к касательной к ней в точке :
А) расположение касательной к вогнутой кривой;
Б) расположение касательной к выпуклой кривой.
ТЕОРЕМА 3. Если функция в интервале
имеет положительную (отрицательную) вторую производную, то кривая на этом интервале вогнута (выпукла).
ДОКАЗАТЕЛЬСТВО.
Возьмем произвольную точку с в интервале и покажем, что при
точки графика функции, соответствующие значениям аргумента х, близлежащим к с, будут располагаться выше точек касательной к кривой
, Проведенной в точке
(рис. 11.18). Уравнение касательной имеет вид:
Где – Ордината ее произвольной точки.
Найдем разность ординат кривой и касательной к ней при одном и том же значении х, близком к с :
Здесь мы применили теорему Лагранжа к разности ,
К разности , рассматриваемой на отрезке
, снова применим теорему Лагранжа. Получим:
Где .
Если , то
поэтому
,
И при условии, что , имеем
При
И так как , то
Таким образом, любая точка кривой Лежит выше касательной, что и требовалось доказать.
Аналогично доказывается выпуклость графика при
Точка графика функции
называется Точкой перегиба, если при переходе через нее кривая меняет свою выпуклость на вогнутость, или же наоборот. Последующие теоремы определяют критерии существования перегиба.
ТЕОРЕМА 4 (НЕОБХОДИМОЕ УСЛОВИЕ ПЕРЕГИБА). Если функция имеет в окрестности внутренней точки c области определения вторую непрерывную производную и точка
, лежащая на графике функции, является точкой перегиба, то
ДОКАЗАТЕЛЬСТВО.
Может ли точка экстремума совпадать с точкой перегиба?
Предположим противное:
Можно ли утверждать, что между двумя точками экстремума функции лежит хотя бы одна точка перегиба?
В силу непрерывности найдется окрестность точки С, в которой
сохраняет знак, то есть график функции будет либо выпуклым, либо вогнутым, а потому точка
не может быть точкой перегиба. Полученное противоречие доказывает утверждение теоремы
Можно ли утверждать, что между двумя точками перегиба лежит хотя бы одна точка экстремума?
.
Графиком функции на отрезке
является выпуклая кривая, причем
. Может ли она иметь экстремум на этом промежутке?
Данная теорема позволяет отнести к точкам, где следует ожидать перегиб графика функции , те точки ее области определения, в которых
Однако множество точек, подозрительных на перегиб, может быть расширено за счет тех, в которых
обращается в бесконечность или вовсе не существует. На рис. 11.19 указаны возможные случаи перегиба графика функции.
Укажем достаточные условия перегиба графика функции.
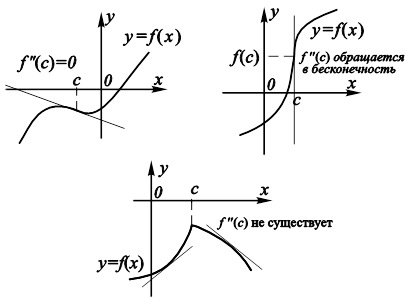
Функции .
ТЕОРЕМА 5 (ДОСТАТОЧНОЕ УСЛОВИЕ ПЕРЕГИБА). Если при переходе через точку c, подозрительную на перегиб графика функции , вторая производная меняет знак, то точка графика
есть точка перегиба.
ДОКАЗАТЕЛЬСТВО.
Из условия теоремы следует, что левее точки – кривая выпуклая (вогнутая), а правее ее – вогнутая (выпуклая). Значит,
– точка перегиба.
Приведем без доказательства еще два признака перегиба графика функции.
ТЕОРЕМА 6. Если функция такова, что в точке с
, а
и конечна, то ее график в точке
имеет перегиб.
Следующая теорема является более общей.
ТЕОРЕМА 7. Если функция в некоторой окрестности точки с имеет производную до (N+1)-го порядка, непрерывную в самой точке С, причем
а
, то при нечетном (n+1) График функции
в точке
будет иметь перегиб.
Рассмотрим примеры.
Найдем точки перегиба функции .
Выше получено:
.
Условие приводит нас к уравнению
Можно ли с помощью второй производной исследовать функцию на монотонность?
Которое имеет решения:
Какая из производных несет большую информацию о свойствах функции – первая или вторая?
Исследуем эти точки, подозрительные на перегиб. Очевидно, что
для
Есть ли функции, у которых:
А) вторая производная изменяется, как и сама функция;
Б) функция не совпадает с первой производной, но первая и вторая ее производные совпадают между собой?
И ;
для
,
Дана функция, являющаяся второй производной некоторой функции. Укажите функции, имеющие такую же вторую производную.
Следовательно, для и
кривая вогнута; для
кривая выпукла, а точки графика
и
являются точками перегиба.
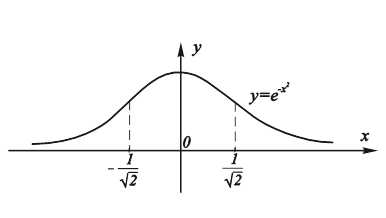
Данная функциональная зависимость встречается часто в теории вероятностей. Она известна под названием кривой Гаусса. Ее график изображен на рис. 11.20.
Рис. 11.20. График функции .
Вернемся теперь еще раз к функции .
Ее вторая производная имеет вид:
Условие
Приводит нас к уравнению
Которое имеет корни
Являющиеся абсциссами точек графика данной функции, подозрительных на перегиб.
Теорема 7 позволяет достаточно просто их исследовать. Имеем:
Следовательно, точка является точкой перегиба графика кривой
.
А потому и точка 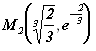
Рис. 11.21. График функции .
| < Предыдущая | Следующая > |
|---|
Экстремум функции двух переменных. Примеры исследования функций на экстремум.
Пусть функция $z=f(x,y)$ определена в некоторой окрестности точки $(x_0,y_0)$. Говорят, что $(x_0,y_0)$ – точка (локального) максимума, если для всех точек $(x,y)$ некоторой окрестности точки $(x_0,y_0)$ выполнено неравенство $f(x,y)< f(x_0,y_0)$. Если же для всех точек этой окрестности выполнено условие $f(x,y)> f(x_0,y_0)$, то точку $(x_0,y_0)$ называют точкой (локального) минимума.
Точки максимума и минимума часто называют общим термином – точки экстремума.
Если $(x_0,y_0)$ – точка максимума, то значение функции $f(x_0,y_0)$ в этой точке называют максимумом функции $z=f(x,y)$. Соответственно, значение функции в точке минимума именуют минимумом функции $z=f(x,y)$. Минимумы и максимумы функции объединяют общим термином – экстремумы функции.
Алгоритм исследования функции $z=f(x,y)$ на экстремум
- Найти частные производные $frac{partial z}{partial x}$ и $frac{partial z}{partial y}$. Составить и решить систему уравнений $
left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$. Точки, координаты которых удовлетворяют указанной системе, называют стационарными. - Найти $frac{partial^2z}{partial x^2}$, $frac{partial^2z}{partial xpartial y}$, $frac{partial^2z}{partial y^2}$ и вычислить значение $Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2$ в каждой стационарной точке. После этого использовать следующую схему:
- Если $Delta > 0$ и $frac{partial^2z}{partial x^2} > 0$ (или $frac{partial^2z}{partial y^2} > 0$), то в исследуемая точка есть точкой минимума.
- Если $Delta > 0$ и $frac{partial^2z}{partial x^2} < 0$ (или $frac{partial^2z}{partial y^2} < 0$), то в исследуемая точка есть точкой максимума.
- Если $Delta < 0$, то в расматриваемой стационарной точке экстремума нет.
- Если $Delta = 0$, то ничего определённого про наличие экстремума сказать нельзя; требуется дополнительное исследование.
Примечание (желательное для более полного понимания текста): показатьскрыть
Пример №1
Исследовать на экстремум функцию $z=4x^2-6xy-34x+5y^2+42y+7$.
Решение
Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:
$$
frac{partial z}{partial x}=8x-6y-34; frac{partial z}{partial y}=-6x+10y+42.
$$
Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:
$$
left { begin{aligned}
& 8x-6y-34=0;\
& -6x+10y+42=0.
end{aligned} right.
$$
Сократим каждое уравнение этой системы на $2$ и перенесём числа в правые части уравнений:
$$
left { begin{aligned}
& 4x-3y=17;\
& -3x+5y=-21.
end{aligned} right.
$$
Мы получили систему линейных алгебраических уравнений. Мне в этой ситуации кажется наиболее удобным применение метода Крамера для решения полученной системы.
$$ begin{aligned}
& Delta=left| begin{array} {cc} 4 & -3\ -3 & 5 end{array}right|=4cdot 5-(-3)cdot (-3)=20-9=11;\
& Delta_x=left| begin{array} {cc} 17 & -3\ -21 & 5 end{array}right|=17cdot 5-(-3)cdot (-21)=85-63=22;\
& Delta_y=left| begin{array} {cc} 4 & 17\ -3 & -21 end{array}right|=4cdot (-21)-17cdot (-3)=-84+51=-33.end{aligned} \
x=frac{Delta_{x}}{Delta}=frac{22}{11}=2; ; y=frac{Delta_{y}}{Delta}=frac{-33}{11}=-3.
$$
Значения $x=2$, $y=-3$ – это координаты стационарной точки $(2;-3)$. Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:
$$
frac{partial^2 z}{partial x^2}=8; frac{partial^2 z}{partial y^2}=10; frac{partial^2 z}{partial x partial y}=-6.
$$
Вычислим значение $Delta$:
$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
8cdot 10-(-6)^2=80-36=44.
$$
Так как $Delta > 0$ и $frac{partial^2 z}{partial x^2} > 0$, то согласно алгоритму точка $(2;-3)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $(2;-3)$:
$$
z_{min}=z(2;-3)=4cdot 2^2-6cdot 2 cdot (-3)-34cdot 2+5cdot (-3)^2+42cdot (-3)+7=-90.
$$
Ответ: $(2;-3)$ – точка минимума; $z_{min}=-90$.
Пример №2
Исследовать на экстремум функцию $z=x^3+3xy^2-15x-12y+1$.
Решение
Будем следовать указанному выше алгоритму. Для начала найдём частные производные первого порядка:
$$
frac{partial z}{partial x}=3x^2+3y^2-15; frac{partial z}{partial y}=6xy-12.
$$
Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:
$$
left { begin{aligned}
& 3x^2+3y^2-15=0;\
& 6xy-12=0.
end{aligned} right.
$$
Сократим первое уравнение на 3, а второе – на 6.
$$
left { begin{aligned}
& x^2+y^2-5=0;\
& xy-2=0.
end{aligned} right.
$$
Если $x=0$, то второе уравнение приведёт нас к противоречию: $0cdot y-2=0$, $-2=0$. Отсюда вывод: $xneq 0$. Тогда из второго уравнения имеем: $xy=2$, $y=frac{2}{x}$. Подставляя $y=frac{2}{x}$ в первое уравнение, будем иметь:
$$
x^2+left(frac{2}{x} right)^2-5=0;\
x^2+frac{4}{x^2}-5=0;\
x^4-5x^2+4=0.
$$
Получили биквадратное уравнение. Делаем замену $t=x^2$ (при этом имеем в виду, что $t > 0$):
$$
t^2-5t+4=0;\
begin{aligned}
& D=(-5)^2-4cdot 1 cdot 4=9;\
& t_1=frac{-(-5)-sqrt{9}}{2}=frac{5-3}{2}=1;\
& t_2=frac{-(-5)+sqrt{9}}{2}=frac{5+3}{2}=4.end{aligned}
$$
Если $t=1$, то $x^2=1$. Отсюда имеем два значения $x$: $x_1=1$, $x_2=-1$. Если $t=4$, то $x^2=4$, т.е. $x_3=2$, $x_4=-2$. Вспоминая, что $y=frac{2}{x}$, получим:
begin{aligned}
& y_1=frac{2}{x_1}=frac{2}{1}=2;\
& y_2=frac{2}{x_2}=frac{2}{-1}=-2;\
& y_3=frac{2}{x_3}=frac{2}{2}=1;\
& y_4=frac{2}{x_4}=frac{2}{-2}=-1.
end{aligned}
Итак, у нас есть четыре стационарные точки: $M_1(1;2)$, $M_2(-1;-2)$, $M_3(2;1)$, $M_4(-2;-1)$. На этом первый шаг алгоритма закончен.
Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:
$$
frac{partial^2 z}{partial x^2}=6x; frac{partial^2 z}{partial y^2}=6x; frac{partial^2 z}{partial x partial y}=6y.
$$
Найдём $Delta$:
$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
6xcdot 6x-(6y)^2=36x^2-36y^2=36(x^2-y^2).
$$
Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(1;2)$. В этой точке имеем:
$$Delta(M_1)=36(1^2-2^2)=-108.$$
Так как $Delta(M_1) < 0$, то согласно алгоритму в точке $M_1$ экстремума нет.
Исследуем точку $M_2(-1;-2)$. В этой точке имеем:
$$Delta(M_2)=36((-1)^2-(-2)^2)=-108.$$
Так как $Delta(M_2) < 0$, то согласно алгоритму в точке $M_2$ экстремума нет.
Исследуем точку $M_3(2;1)$. В этой точке получим:
$$
Delta(M_3)=36(2^2-1^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_3}=6cdot 2=12.
$$
Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(2;1)$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:
$$
z_{min}=z(2;1)=2^3+3cdot 2cdot 1^2-15cdot 2-12cdot 1+1=-27.
$$
Осталось исследовать точку $M_4(-2;-1)$. В этой точке получим:
$$
Delta(M_4)=36((-2)^2-(-1)^2)=108;;; left.frac{partial^2 z}{partial x^2}right|_{M_4}=6cdot (-2)=-12.
$$
Так как $Delta(M_4) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_4} < 0$, то согласно алгоритму $M_4(-2;-1)$ есть точкой максимума функции $z$. Максимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_4$:
$$
z_{max}=z(-2;-1)=(-2)^3+3cdot (-2)cdot (-1)^2-15cdot (-2)-12cdot (-1)+1=29.
$$
Исследование на экстремум завершено. Осталось лишь записать ответ.
Ответ:
- $(2;1)$ – точка минимума, $z_{min}=-27$;
- $(-2;-1)$ – точка максимума, $z_{max}=29$.
Примечание
Вычислять значение $Delta$ в общем случае нет необходимости, потому что нас интересует лишь знак, а не конкретное значение данного параметра. Например, для рассмотренного выше примера №2 в точке $M_3(2;1)$ имеем $Delta=36cdot(2^2-1^2)$. Здесь очевидно, что $Delta > 0$ (так как оба сомножителя $36$ и $(2^2-1^2)$ положительны) и можно не находить конкретное значение $Delta$. Правда, для типовых расчётов это замечание бесполезно, – там требуют довести вычисления до числа 
Пример №3
Исследовать на экстремум функцию $z=x^4+y^4-2x^2+4xy-2y^2+3$.
Решение
Будем следовать алгоритму. Для начала найдём частные производные первого порядка:
$$
frac{partial z}{partial x}=4x^3-4x+4y; frac{partial z}{partial y}=4y^3+4x-4y.
$$
Составим систему уравнений $ left { begin{aligned}
& frac{partial z}{partial x}=0;\
& frac{partial z}{partial y}=0.
end{aligned} right.$:
$$
left { begin{aligned}
& 4x^3-4x+4y=0;\
& 4y^3+4x-4y=0.
end{aligned} right.
$$
Сократим оба уравнения на $4$:
$$
left { begin{aligned}
& x^3-x+y=0;\
& y^3+x-y=0.
end{aligned} right.
$$
Добавим к второму уравнению первое и выразим $y$ через $x$:
$$
y^3+x-y+(x^3-x+y)=0;\
y^3+x^3=0; y^3=-x^3; y=-x.
$$
Подставляя $y=-x$ в первое уравнение системы, будем иметь:
$$
x^3-x-x=0;\
x^3-2x=0;\
x(x^2-2)=0.
$$
Из полученного уравнения имеем: $x=0$ или $x^2-2=0$. Из уравнения $x^2-2=0$ следует, что $x=-sqrt{2}$ или $x=sqrt{2}$. Итак, найдены три значения $x$, а именно: $x_1=0$, $x_2=-sqrt{2}$, $x_3=sqrt{2}$. Так как $y=-x$, то $y_1=-x_1=0$, $y_2=-x_2=sqrt{2}$, $y_3=-x_3=-sqrt{2}$.
Первый шаг решения окончен. Мы получили три стационарные точки: $M_1(0;0)$, $M_2(-sqrt{2},sqrt{2})$, $M_3(sqrt{2},-sqrt{2})$.
Теперь приступим ко второму шагу алгоритма. Найдём частные производные второго порядка:
$$
frac{partial^2 z}{partial x^2}=12x^2-4; frac{partial^2 z}{partial y^2}=12y^2-4; frac{partial^2 z}{partial x partial y}=4.
$$
Найдём $Delta$:
$$
Delta=frac{partial^2z}{partial x^2}cdot frac{partial^2z}{partial y^2}-left(frac{partial^2z}{partial xpartial y} right)^2=
(12x^2-4)(12y^2-4)-4^2=\
=4(3x^2-1)cdot 4(3y^2-1)-16=16(3x^2-1)(3y^2-1)-16=16cdot((3x^2-1)(3y^2-1)-1).
$$
Теперь будем вычислять значение $Delta$ в каждой из найденных ранее стационарных точек. Начнём с точки $M_1(0;0)$. В этой точке имеем:
$$Delta(M_1)=16cdot((3cdot 0^2-1)(3cdot 0^2-1)-1)=16cdot 0=0.$$
Так как $Delta(M_1) = 0$, то согласно алгоритму требуется дополнительное исследование, ибо ничего определённого про наличие экстремума в рассматриваемой точке сказать нельзя. Оставим покамест эту точку в покое и перейдём в иным точкам.
Исследуем точку $M_2(-sqrt{2},sqrt{2})$. В этой точке получим:
begin{aligned}
& Delta(M_2)=16cdot((3cdot (-sqrt{2})^2-1)(3cdot (sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_2}=12cdot (-sqrt{2})^2-4=24-4=20.
end{aligned}
Так как $Delta(M_2) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_2} > 0$, то согласно алгоритму $M_2(-sqrt{2},sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_2$:
$$
z_{min}=z(-sqrt{2},sqrt{2})=(-sqrt{2})^4+(sqrt{2})^4-2(-sqrt{2})^2+4cdot (-sqrt{2})sqrt{2}-2(sqrt{2})^2+3=-5.
$$
Аналогично предыдущему пункту исследуем точку $M_3(sqrt{2},-sqrt{2})$. В этой точке получим:
begin{aligned}
& Delta(M_3)=16cdot((3cdot (sqrt{2})^2-1)(3cdot (-sqrt{2})^2-1)-1)=16cdot 24=384;\
& left.frac{partial^2 z}{partial x^2}right|_{M_3}=12cdot (sqrt{2})^2-4=24-4=20.
end{aligned}
Так как $Delta(M_3) > 0$ и $left.frac{partial^2 z}{partial x^2}right|_{M_3} > 0$, то согласно алгоритму $M_3(sqrt{2},-sqrt{2})$ есть точкой минимума функции $z$. Минимум функции $z$ найдём, подставив в заданную функцию координаты точки $M_3$:
$$
z_{min}=z(sqrt{2},-sqrt{2})=(sqrt{2})^4+(-sqrt{2})^4-2(sqrt{2})^2+4cdot sqrt{2}(-sqrt{2})-2(-sqrt{2})^2+3=-5.
$$
Настал черёд вернуться к точке $M_1(0;0)$, в которой $Delta(M_1) = 0$. Согласно алгоритму требуется дополнительное исследование. Под этой уклончивой фразой подразумевается «делайте, что хотите» :). Общего способа разрешения таких ситуаций нет, – и это понятно. Если бы такой способ был, то он давно бы вошёл во все учебники. А покамест приходится искать особый подход к каждой точке, в которой $Delta = 0$. Ну что же, поисследуем поведение функции в окрестности точки $M_1(0;0)$. Сразу отметим, что $z(M_1)=z(0;0)=3$. Предположим, что $M_1(0;0)$ – точка минимума. Тогда для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) > z(M_1) $, т.е. $z(M) > 3$. А вдруг любая окрестность содержит точки, в которых $z(M) < 3$? Тогда в точке $M_1$ уж точно не будет минимума.
Рассмотрим точки, у которых $y=0$, т.е. точки вида $(x,0)$. В этих точках функция $z$ будет принимать такие значения:
$$
z(x,0)=x^4+0^4-2x^2+4xcdot 0-2cdot 0^2+3=x^4-2x^2+3=x^2(x^2-2)+3.
$$
В всех достаточно малых окрестностях $M_1(0;0)$ имеем $x^2-2 < 0$, посему $x^2(x^2-2) < 0$, откуда следует $x^2(x^2-2)+3 < 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z < 3$, посему точка $M_1(0;0)$ не может быть точкой минимума.
Но, может быть, точка $M_1(0;0)$ – точка максимума? Если это так, то для любой точки $M$ из некоторой окрестности точки $M_1(0;0)$ получим $z(M) < z(M_1) $, т.е. $z(M) < 3$. А вдруг любая окрестность содержит точки, в которых $z(M) > 3$? Тогда в точке $M_1$ точно не будет максимума.
Рассмотрим точки, у которых $y=x$, т.е. точки вида $(x,x)$. В этих точках функция $z$ будет принимать такие значения:
$$
z(x,x)=x^4+x^4-2x^2+4xcdot x-2cdot x^2+3=2x^4+3.
$$
Так как в любой окрестности точки $M_1(0;0)$ имеем $2x^4 > 0$, то $2x^4+3 > 3$. Вывод: любая окрестность точки $M_1(0;0)$ содержит точки, в которых $z > 3$, посему точка $M_1(0;0)$ не может быть точкой максимума.
Точка $M_1(0;0)$ не является ни точкой максимума, ни точкой минимума. Вывод: $M_1$ вообще не является точкой экстремума.
Ответ: $(-sqrt{2},sqrt{2})$, $(sqrt{2},-sqrt{2})$ – точки минимума функции $z$. В обеих точках $z_{min}=-5$.
Экстремум функции двух переменных
Как найти?
Постановка задачи
Найти экстремум функции двух переменных $ z = z(x,y) $
План решения
Экстремумы функции двух переменных возможны в стационарных точках функции. Стационарными точками называются точки $ M(x_1,y_1), M(x_2,y_2)… $, в которых первые частные производные функции равны нулю: $ z(x,y) = 0 $
Для нахождения стационарных точек (подозрительных на экстремум) составляем систему:
$$ begin{cases} z’_x = 0 \ z’_y = 0 end{cases} $$
Решая систему получаем точки $ M(x_1,y_1), M(x_2,y_2)… $, каждую из которых нужно проверить на экстремум.
Проверку осуществляется с помощью подстановки точек в выражение, называемое достаточным условием существования экстремума:
$$ A = z»_{xx} cdot z»_{yy} — (z»_{xy})^2 $$
Если в точке $ M(x_1,y_1) $:
- $ A>0 $ и $ z»_{xx} > 0 $, то $ M(x_1,y_1) $ точка минимума
- $ A >0 $ и $ z»_{xx} < 0 $, то $ M(x_1,y_1) $ точка максимума
- $ A < 0 $, то $ M(x_1,y_1) $ не является точкой экстремума
- $ A = 0 $, то требуется дополнительное исследование (по определению)
Итак, необходимо выполнить действия:
- Найти частные производные первого порядка. Приравнять их к нулю и решить систему уравнений. Получить точки $ M(x_1,y_1), M(x_2,y_2),… $
- Найти частные производные второго порядка в точках $ M(x_1,y_1), M(x_2,y_2),… $
- Используя достаточное условие существования экстремума делаем вывод о наличии экстремума в точках $ M(x_1,y_1), M(x_2,y_2),… $
Примеры решений
| Пример 1 |
| Найти экстремумы функции двух переменных $ z = x^2 -xy +y^2 $ |
| Решение |
|
Находим частные производные первого порядка: $$ z’_x = 2x — y $$ $$ z’_y = -x + 2y $$ Приравниваем полученные выражения к нулю и решаем систему двух уравнений: $$ begin{cases} 2x-y = 0 \ -x + 2y = 0 end{cases} $$ Решив систему получаем стационарную точку (подозрительные на экстремум): $$ M (0,0) $$ Далее вычисляем значения частных производных второго порядка в точке $ M $: $$ z»_{xx} Big |_M = 2 $$ $$ z»_{yy} Big |_M= 2 $$ $$ z»_{xy} Big |_M = -1 $$ Подставляя найденные значения в достаточное условие экстремума функции, проводим исследование знаков: $$ A = Big |_M = z»_{xx} Big |_M cdot z»_{yy} Big |_M — (z»_{xy} Big |_M)^2 = 2 cdot 2 — (-1)^2 = 3 $$ Так как получили $ A > 0 $ и $ z»_{xx} > 0 $, то получается $ M(0,0) $ точка минимума. Наименьшее значение находится в минимуме и равно: $$ z_{min} (0,0) = 0^2 — 0 cdot 0 + 0^2 = 0 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| В точке $ M(0,0) $ находится минимум функции; $ z_{min} = 0 $ |
| Пример 2 |
| Найти экстремумы функции двух переменных $ z = x^3 + y^3 — 15xy $ |
| Решение |
|
Составляем систему уравнений из частных производных первого порядка: $$ begin{cases} z’_x = 3x^2 — 15y = 0 \ z’_y = 3y^2 — 15x =0 end{cases} $$ Получаем стационарные точки $ M_1(0,0) $ и $ M_2(5,5) $, которые необходимо проверить через достаточное условие экстремума. Вычисляем значение частных прозводных второго порядка в точке $ M_1 $: $$ z»_{xx} Big |_{M_1} = 6x Big |_{M_1} = 0 $$ $$ z»_{yy} Big |_{M_1} = 6y Big |_{M_2} = 6y Big |_{M_2} = 0 $$ $$ z»_{xy} Big |_{M_1} = -15 $$ Подставляем данные значения в формулу достаточного условия экстремума: $$ A Big |_{M_1} = 0 cdot 0 — (-15)^2 = -225 $$ Так как $ A < 0 $, то в точке $ M_1(0,0) $ экстремума нет. Получаем значения частных производных 2 порядка в $ M_2 $: $$ z»_{xx} Big |_{M_2} = 6x Big |_{M_2} = 6 cdot 5 = 30 $$ $$ z»_{yy} Big |_{M_2} = 6y Big |_{M_2} = 6 cdot 5 = 30 $$ $$ z»_{xy} Big |_{M_2} = -15 $$ Вычисляем значение выражения достаточного условия экстремума: $$ A = 30 cdot 30 — (-15)^2 = 900 — 225 = 675 $$ Получили $ A > 0 $ и $ z»_{xx} > 0 $, то значит, $ M_2(5,5) $ точка минимума. Наименьшее значение функции $ z = x^3 + y^3 — 15xy $ равно: $$ z_{min} |_{M_2} = 5^3 + 5^3 — 15 cdot 5 cdot 5 = 125 + 125 — 375 = -125 $$ |
| Ответ |
| В $ M_1 (0,0) $ экстремума нет, в $ M_2(5,5) $ минимум функции $ z_{min}=-125 $ |
Экстремум функции двух переменных
Назначение сервиса. Онлайн-калькулятор используется для нахождения в онлайн режиме наибольшего и наименьшего значения функции двух переменных (см. пример). Решение оформляется в формате Word.
- Решение онлайн
- Видеоинструкция
- Оформление Word
Для функции трех переменных можно использовать матрицу Гессе.
Алгоритм исследования функции двух переменных на экстремум
Функция z = f(x,y) имеет максимум в точке M0(x0;y0), если f(x0;y0) > f(x;y) для всех точек (x;y), достаточно близких к точке (x0;y0) и отличных от неё. Функция z = f(x,y) имеет минимум в точке M0(x0;y0), если f(x0;y0) < f(x;y) для всех точек (x;y), достаточно близких к точке (x0;y0) и отличных от неё. Максимум и минимум функции называются экстремумами функции.
Исследование функции двух переменных на экстремум проводят по следующей схеме.
1. Находят частные производные dz/dx и dz/dy.
2. Решают систему уравнений:
и таким образом находят критические точки функции.
3. Находят частные производные второго порядка:
4. Вычисляют значения этих частных производных второго порядка в каждой из найденных в п.2 критических точках M(x0;y0).
5. Делаю вывод о наличии экстремумов:
а) если AC – B2 > 0 и A < 0 , то в точке M имеется максимум;
б) если AC – B2 > 0 и A > 0 , то в точке M имеется минимум;
в) если AC – B2 < 0, то экстремума нет;
г) если AC – B2 = 0, то вопрос о наличии экстремума остается открытым;
Пример №1. Найти экстремумы функции f(x,y)=x3+xy2+x2+y2 и определить по критерию Сильвестра их тип.
Решение.
1. Найдем первые частные производные.
2. Решим систему уравнений.
3x2+2x+y2=0
2xy+2y=0
Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
x = -1
y2+1=0
Данная система уравнений не имеет решения.
б) Из первого уравнения выражаем y и подставляем во второе уравнение:
или
или
Откуда x1 = -2/3; x2 = 0; x3 = -2/3; x4 = 0
Данные значения x подставляем в выражение для y. Получаем: y1 = 0; y2 = 0; y3 = 0; y4 = 0
Количество критических точек равно 2: M1(-2/3;0), M2(0;0)
3. Найдем частные производные второго порядка.
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(-2/3;0)
AC — B2 = -4/3 < 0, то глобального экстремума нет.
Вычисляем значения для точки M2(0;0)
AC — B2 = 4 > 0 и A > 0 , то в точке M2(0;0) имеется минимум z(0;0) = 0
Вывод: В точке M2(0;0) имеется минимум z(0;0) = 0
Пример №2. Исследовать функцию на экстремум классическим методом: Z=8x2+2xy-5x+6.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).