Знаменитая формула, связывающая массу с энергией, является одной из самых известных и популярных в мире. Масса тела — это и есть энергия, содержащаяся в ней. Первым, кто сформулировал этот принцип, был Альберт Эйнштейн. Однако и до него намек на связь энергии с массой встречался в других работах. Итак, как же записывается и формулируется это соотношение?
Энергия покоя объекта равна массе, умноженной на квадрат скорости света в вакууме.
E0 = mc2
Эта формула проста в понимании, получается, что любые тела, объекты — это концентрация огромной энергии. А понятие массы и энергии неразрывно связаны в теории относительности. Попробуем разобраться и понять более подробно, что же все это значит.
Немного про массу

Известно, что при больших скоростях, близких световым, энергия бесконечно возрастает, отсюда как раз и следует недостижимость скорости света. И здесь иногда возникает небольшая путаница: многие по ошибке считают, что масса также возрастает как и энергия. Да, но только релятивистская. Поэтому уточним, дабы избежать путаницы.
Будем использовать только массу покоя в обычном ее понимании, которая является абсолютной величиной и не зависит от скорости. Вместо релятивистской массы будем использовать понятия импульса и энергии.
Связь массы, энергии и импульса
В более общем случае, если тело не покоиться, в связь массы с энергией добавляется импульс. Поэтому окончательный принцип эквивалентности, сформулированный при создании специальной теории относительности для свободно движущейся частицы будет:
E2 — p2 = m2c4
где p — импульс.
Из этого выражения видно что, когда тело покоится (p = 0), энергия тела не становится нулевой. Из этого и вытекает известное соотношение. И можно сделать вывод, что в материи хранятся огромные запасы энергии.
Примеры взаимопревращений
Без конкретных примеров соотношение массы и энергии останется чем-то таинственным. Поэтому приведем примеры, как можно использовать энергию покоя, заключенную в объектах. Сразу после открытия этой эквивалентности появились разговоры о возможных ее практических применениях, что и было сделано в 20 веке.
Превращение массы в энергию
Высвобождение энергии покоя происходит в основном за счет превращения ее в тепловую, то бишь в энергию движения частиц.
Ядерные и термоядерные реакции

В ходе данных реакций (деление или синтез ядер) происходит высвобождение огромной энергии, при котором происходит дефект масс: масса до реакции была больше, чем после и собственно она и превращается в энергию.
Мирное применение нашла только реакция деления ядра, однако работы по укрощению термоядерной реакции активно ведутся. Вполне возможно, что мы скоро увидим новый источник энергии, такой, как на Солнце.
Аннигиляция материи и антиматерии
При данном процессе происходит взаимное уничтожение частиц и античастиц, тем самым высвобождается огромный объем энергии, в основном в виде фотонов.
В настоящий момент практическое применение явления аннигиляции невозможно, так как при нынешних технологиях даже не удалось создать достаточного количества антивещества и хоть немного долго удержать ее. В будущем, вполне вероятно, данный процесс будет использоваться, например, в межзвездных полетах, где потребуется много энергии.
Обратный процесс превращения энергии в массу

Если масса может превращаться в энергию, то может ли происходить обратный процесс? Ответ — да, превращение энергии в массу тоже можно наблюдать, но в реальности это в разы труднее осуществить.
Электромагнитная волна становится электроном
Этот эффект наблюдается тогда, когда у электромагнитной волны такая частота ν, что ее энергия E = hν будет больше, чем энергия покоя электрона. В этом случае волна может превратиться в электрон, либо в античастицу электрона — позитрон.
Столкновение частиц на большой скорости
В массу может превращаться кинетическая энергия частиц, движущихся с околосветовой скоростью в момент их столкновения с другими. В этом случае появляются новые частицы с массой большей, чем масса участвующих частиц до столкновения.

Лишняя масса — это результат перехода кинетической энергии в массу новой частицы. Подобные процессы происходят далеко в космосе или в некоторых коллайдерах.
Заключение
Безусловно, принцип эквивалентности массы и энергии — это одно из значимых открытий начала 20 века, повлиявший на весь ход истории. Соотношение E = mc2 показывает, что в веществе заложены большие запасы энергии и оно нашло практическое применение в военной и энергетической промышленностях.
17 039
Введение
Решение задач — неотъемлемая часть обучения
физике, поскольку в процессе решения задач
происходит формирование и обогащение физических
понятий, развивается физическое мышление
учащихся и совершенствуется их навыки
применения знаний на практике.
В ходе решения задач могут быть поставлены и
успешно реализованы следующие дидактические
цели:
- Выдвижение проблемы и создание проблемной
ситуации; - Обобщение новых сведений;
- Формирование практических умений и навыков;
- Проверка глубины и прочности знаний;
- Закрепление, обобщение и повторение материала;
- Реализация принципа политехнизма;
- Развитие творческих способностей учащихся.
Наряду с этим при решении задач у школьников
воспитываются трудолюбие, пытливость ума,
смекалка, самостоятельность в суждениях, интерес
к учению, воля и характер, упорство в достижении
поставленной цели. Для реализации перечисленных
целей особенно удобно использовать
нетрадиционные задачи.
§1. Задачи по расчету электрических
цепей постоянного тока
По школьной программе на рассмотрение данной
темы очень мало отводится времени, поэтому
учащиеся более или менее успешно овладевают
методами решения задач данного типа. Но часто
такие типы задач встречаются олимпиадных
заданиях, но базируются они на школьном курсе.
К таким, нестандартным задачам по расчету
электрических цепей постоянного тока можно
отнести задачи, схемы которых:
1) содержат большое число элементов –
резисторов или конденсаторов;
2) симметричны;
3) состоят из сложных смешанных соединений
элементов.
В общем случае всякую цепь можно рассчитать,
используя законы Кирхгофа. Однако эти законы не
входят в школьную программу. К тому же, правильно
решить систему из большого числа уравнений со
многими неизвестными под силу не многим учащимся
и этот путь не является лучшим способом тратить
время. Поэтому нужно уметь пользоваться
методами, позволяющими быстро найти
сопротивления и емкости контуров.
§2. Метод эквивалентных схем
Метод эквивалентных схем заключается в том, что
исходную схему надо представить в виде
последовательных участков, на каждом из которых
соединение элементов схемы либо
последовательно, либо параллельно. Для такого
представления схему необходимо упростить. Под
упрощением схемы будем понимать соединение или
разъединение каких-либо узлов схемы, удаление
или добавление резисторов, конденсаторов,
добиваясь того, чтобы новая схема из
последовательно и параллельно соединенных
элементов была эквивалентна исходной.
Эквивалентная схема – это такая схема, что при
подаче одинаковых напряжений на исходную и
преобразованную схемы, ток в обеих цепях будет
одинаков на соответствующих участках. В этом
случае все расчеты производятся с
преобразованной схемой.
Чтобы начертить эквивалентную схему для цепи
со сложным смешанным соединением резисторов
можно воспользоваться несколькими приемами. Мы
ограничимся рассмотрением в подробностях лишь
одного из них – способа эквипотенциальных узлов.
Этот способ заключается в том, что в
симметричных схемах отыскиваются точки с
равными потенциалами. Эти узлы соединяются между
собой, причем, если между этими точками был
включен какой-то участок схемы, то его
отбрасывают, так как из-за равенства потенциалов
на концах ток по нему не течет и этот участок
никак не влияет на общее сопротивление схемы.
Таким образом, замена нескольких узлов равных
потенциалов приводит к более простой
эквивалентной схеме. Но иногда бывает
целесообразнее обратная замена одного узла
несколькими узлами с равными потенциалами, что
не нарушает электрических условий в остальной
части.
Рассмотрим примеры решения задач эти методом.
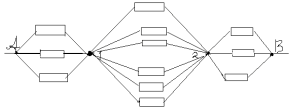
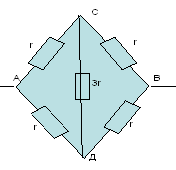
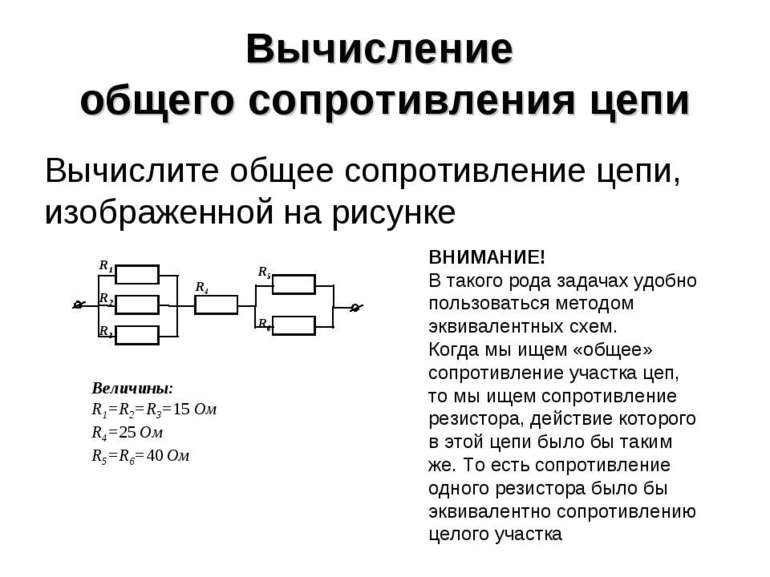
З а д а ч а №1
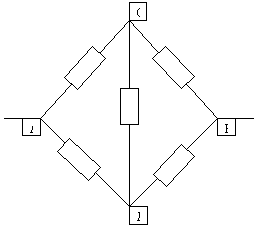
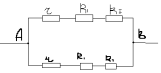
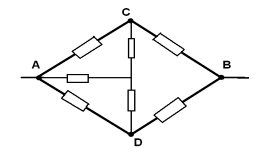
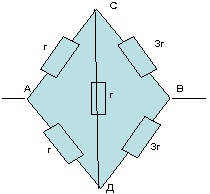
Рассчитать сопротивление между точками А и В
данного участка цепи. Все резисторы одинаковы и
их сопротивления равны r.
Решение:
В силу симметричности ветвей цепи точки С И Д
являются эквипотенциальными. Поэтому резистор
между ними мы можем исключить. Эквипотенциальные
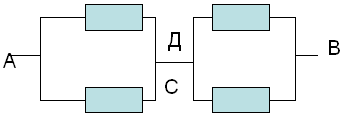
точки С и Д соединяем в один узел. Получаем очень
простую эквивалентную схему:
Сопротивление которой равно:
RАВ=Rac+Rcd=r*r/r*r+r*r/r+r=r.
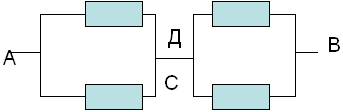
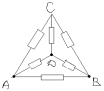
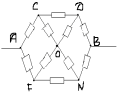
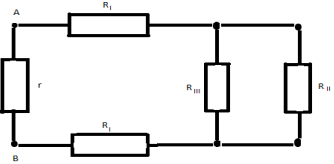
З а д а ч а № 2
Решение:
В точках F и F` потенциалы равны, значит
сопротивление между ними можно отбросить.
Эквивалентная схема выглядит так:
Сопротивления участков DNB;F`C`D`; D`, N`, B`; FCD равны
между собой и равны R1:
1/R1=1/2r+1/r=3/2r
R1=2/3*r
С учетом этого получается новая эквивалентная
схема:
Ее сопротивление и сопротивление исходной цепи
RАВ равно:
1/RАВ=1/r+R1+R1+1/r+R1+R1=6/7r
RАВ=(7/6)*r.
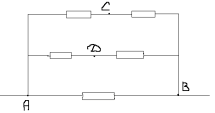
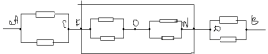
З а д а ч а № 3.
Решение:
Точки С и Д имеют равные потенциалы.
Исключением сопротивление между ними. Получаем
эквивалентную схему:
Искомое сопротивление RАВ равно:
1/RАВ=1/2r+1/2r+1/r=2/r
RАВ=r/2.
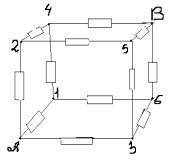
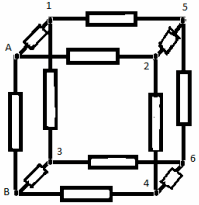
З а д а ч а № 4.
Решение:
Как видно из схемы узлы 1,2,3 имеют равные
потенциалы. Соединим их в узел 1. Узлы 4,5,6 имеют
тоже равные потенциалы- соединим их в узел 2.
Получим такую эквивалентную схему:
Сопротивление на участке А-1, R 1-равно
сопротивлению на участке 2-В,R3 и равно:
R1=R3=r/3
Сопротивление на участке 1-2 равно: R2=r/6.
Теперь получается эквивалентная схема:
Общее сопротивление RАВ равно:
RАВ= R1+ R2+ R3=(5/6)*r.
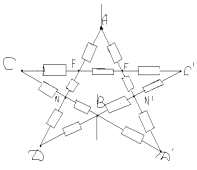
З а д а ч а № 5.
Решение:
Точки C и F-эквивалентные. Соединим их в один
узел. Тогда эквивалентная схема будет иметь
следующий вид:
Сопротивление на участке АС:
Rас=r/2
Сопротивление на участке FN:
RFN =
Сопротивление на участке DB:
RDB =r/2
Получается эквивалентная схема:
Искомое общее сопротивление равно:
RAB= r.
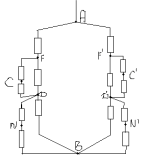
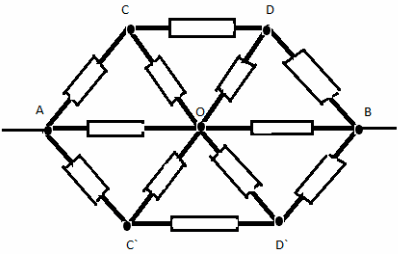
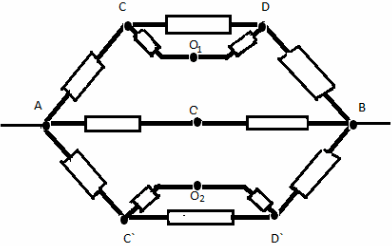
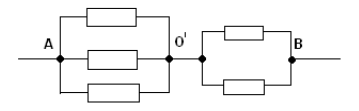
Задача №6
Решение:
Заменим общий узел О тремя узлами с равными
потенциалами О, О1 , О2. Получим
эквивалентную систему:
Сопротивление на участке ABCD:
R1=(3/2)*r
Сопротивление на участке A`B`C`D`:
R2= (8/3)*r
Сопротивление на участке ACВ
R3 = 2r.
Получаем эквивалентную схему:
Искомое общее сопротивление цепи RAB
равно:
RAB= (8/10)*r.
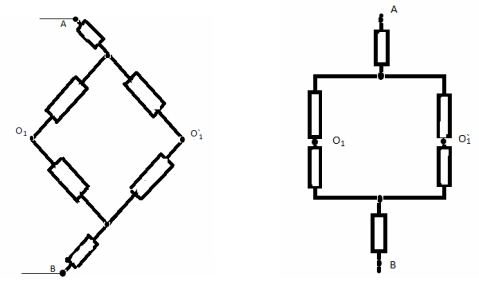
Задача №7.
Решение:
“Разделим” узел О на два эквипотенциальных
угла О1 и О2. Теперь схему можно
представить, как параллельные соединение двух
одинаковых цепей. Поэтому достаточно подробно
рассмотреть одну из них:
Сопротивление этой схемы R1 равно:
R1 = 3r
Тогда сопротивление всей цепи будет равно:
RAB = (3/2)*r
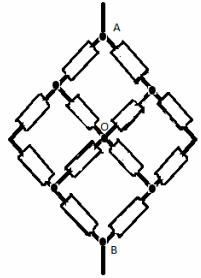
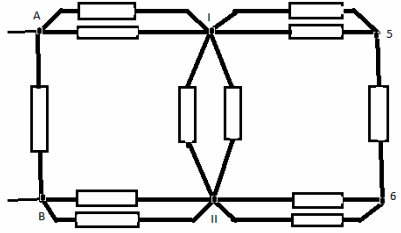
З а д а ч а №8
Решение:
Узлы 1 и 2 – эквипотенциальные, поэтому соединим
их в один узел I. Узлы 3 и 4 также эквипотенциальные
– соединимих в другой узел II. Эквивалентная
схема имеет вид:
Сопротивление на участке A- I равно
сопротивлению на участке B- II и равно:
RI =
Сопротивление участка I-5-6- II равно:
RII = 2r
Cопротивление участка I- II равно:
RIII =
Получаем окончательную эквивалентную схему:
Искомое общее сопротивление цепи RAB=(7/12)*r.
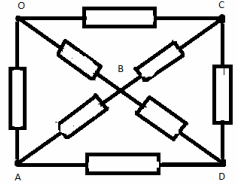
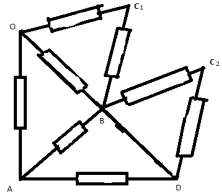
З а д а ч а №9
В ветви ОС заменим сопротивление на два
параллельно соединенных сопротивления по 2r.
Теперь узел С можно разделить на 2
эквипотенциальных узла С1 и С2.
Эквивалентная схема в этом случае выглядит так:
Сопротивление на участках ОСIB и DCIIB
одинаковы и равны, как легко подсчитать 2r. Опять
чертим соответствующую эквивалентную схему:
Сопротивление на участке AOB равно
сопротивлению на участке ADB и равно (7/4)*r. Таким
образом получаем окончательную эквивалентную
схему из трех параллельно соединенных
сопротивлений:
Ее общее сопротивление равно RAB= (7/15)*r
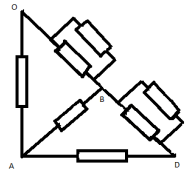
З а д а ч а № 10
Точки СОD имеют равные потенциалы – соединим их
в один узел ОI .Эквивалентная схема
изображена на рисунке :
Сопротивление на участке А ОI равно . На участке
ОIВ сопротивление равно .Получаем совсем
простую эквивалентную схему:
ЕЕ сопротивление равно искомому общему
сопротивлению
RAB=(5/6)*r
Задачи № 11 и № 12 решаются несколько иным
способом, чем предыдущие. В задаче №11 для ее
решения используется особое свойство
бесконечных цепей, а в задаче № 12 применяется
способ упрощения цепи.
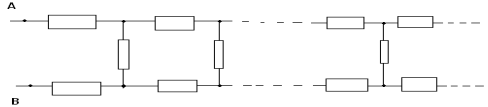
Задача № 11
Решение
Выделим в этой цепи бесконечно повторяющееся
звено, оно состоит в данном случае из трех первых
сопротивлений. Если мы отбросим это звено, то
полное сопротивление бесконечной цепи R не
измениться от этого , так как получится точно
такая же бесконечная цепь. Так же ничего не
измениться, если мы выделенное звено подключим
обратно к бесконечному сопротивлению R, но при
этом следует обратить внимание , что часть звена
и бесконечная цепь сопротивлением R соединены
параллельно. Таким образом получаем
эквивалентную схему :
Получается уравнения
RAB=2ч +
RAB = R
Решая систему этих уравнений, получаем:
R=ч (1+ ).
§3. Обучение решению задач по расчету
электрических цепей способом эквипотенциальных
узлов
Задача – это проблема, для разрешения которой
ученику потребуются логические рассуждения и
выводы. Строящиеся на основе законов и методов
физики. Таким образом, с помощью задач происходит
активизация целенаправленного мышления
учащихся.
В то же время. Теоретические знания можно
считать усвоенными только тогда, когда они
удачно применяются на практике. Задачи по физике
описывают часто встречающиеся в жизни и на
производстве проблемы, которые могут быть решены
с помощью законов физики и, если ученик успешно
решает задачи, то можно сказать, что он хорошо
знает физику.
Для того, чтобы ученики успешно решали задачи,
недостаточно иметь набор методов и способов
решения задач, необходимо еще специально учить
школьников применению этих способов.
Рассмотрим план решения задач по расчету
электрических цепей постоянного тока методом
эквипотенциальных узлов.
- Чтение условия.
- Краткая запись условия.
- Перевод в единицы СИ.
- Анализ схемы:
- установить, является ли схема симметричной;
- установить точки равного потенциала;
- выбрать, что целесообразнее сделать –
соединить точки равных потенциалов или же,
наоборот, разделить одну точку на несколько
точек равных потенциалов; - начертить эквивалентную схему;
- найти участки только с последовательным или
только с параллельным соединением и рассчитать
общее сопротивление на каждом участке по законам
последовательного и параллельного соединения; - начертить эквивалентную схему, заменяя участки
соответствующими им расчетными сопротивлениями; - пункты 5 и 6 повторять до тех пор, пока не
останется одно сопротивление, величина которого
и будет решением задачи. - Анализ реальности ответа.
Подробнее об анализе схемы
а) установить, является ли схема симметричной.
Определение. Схема симметрична, если одна ее
половина является зеркальным отражением другой.
Причем симметрия должна быть не только
геометрической, но должны быть симметричны и
численные значения сопротивлений или
конденсаторов.
Примеры:
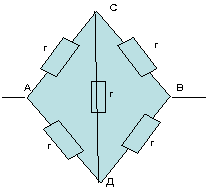
1)
Схема симметричная, так как ветви АСВ и АДВ
симметричны геометрически и отношение
сопротивления на одном участке АС:АД=1:1 такое же,
как и на другом участке СД:ДВ=1:1.
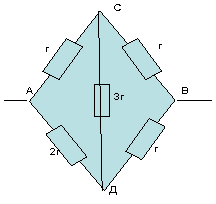
2)
Схема симметричная, так как отношение
сопротивлений на участке АС:АД=1:1 такое же, как и
на другом участке СВ:ДВ=3:3=1:1
3)
Схема не симметрична, так как отношения
сопротивлений численно
не симметричны -1:2 и 1:1.
б) установить точки равных потенциалов.
Пример:
Из соображений симметрии делаем вывод, что в
симметричных точках потенциалы равны. В данном
случае симметричными точками являются точки С и
Д. Таким образом, точки С и Д – эквипотенциальные
точки.
в) выбрать, что целесообразно сделать –
соединить точки равных потенциалов или же,
наоборот, разделить одну точку на несколько
точек равных потенциалов.
Мы видим в этом примере, что между точками
равных потенциалов С и Д включено сопротивление,
по которому ток не будет течь. Следовательно, мы
можем отбросить это сопротивление, а точки С и Д
соединить в один узел.
г) начертить эквивалентную схему.
Чертим эквивалентную схему. При этом получаем
схему с соединенными в одну точку точками С и Д.
д) найти участки только с последовательным или
только с параллельным соединением и рассчитать
общее сопротивление на каждом таком участке по
законам последовательного и параллельного
соединения.
Из полученной эквивалентной схемы видно, что на
участке АС мы имеем два параллельно соединенных
резистора. Их общее сопротивление находится по
закону параллельного соединения:
1/ Rобщ=1/R1+1/R2+1/R3+…
Таким образом 1/RAC=1/r+1/r=2/r,откуда RAC= r/2.
На участке СВ картина аналогичная:
1/RCB= 1/r+1/r =2/r, откуда RCB=r/2.
е)начертить эквивалентную схему, заменяя
участки соответствующими им расчетными
сопротивлениями.
Чертим эквивалентную схему подставляя в нее
рассчитанные сопротивления участков RAC и RCB:
ж)пункты д) и е) повторять до тех пор, пока
останется одно сопротивление, величина которого
и будет решением задачи.
Повторяем пункт д): на участке АВ имеем два
последовательно соединенных сопротивления. Их
общее сопротивление находим по закону
последовательного соединения:
Rобщ= R1+R2+R3+… то есть, RAB=RAC+RCB = r/2+r/2 =2r/2 = r.
Повторяем пункт е): чертим эквивалентную
схему:
Мы получили схему с одним сопротивлением,
величина которого равна сопротивлению исходной
схемы. Таким образом, мы получили ответ RAB = r.
Далее, для проверки усвоения данного материала
можно учащимся предложить задания для
самостоятельной работы, взятые из
дидактического материала. (см. приложение)
Литература
- Балаш. В.А. задачи по физике и методы их решения. —
М: Просвещение,1983. - Лукашик В.И. Физическая олимпиада.- М:
Просвещение, 2007 - Усова А.В., Бобров А.А. Формирование учебных
умений и навыков учащихся на уроках физики.- М:
Просвещение,1988 - Хацет А. Методы расчета эквивалентных схем
//Квант. - Чертов А. Г. Задачник по физике. – М.: Высшая
школа,1983 - Зиятдинов Ш.Г., Соловьянюк С.Г. (методические
рекомендации) г. Бирск,1994г - Марон А.Е., Марон Е.А. Физика. Дидактические
материалы. Москва, “Дрофа”, 2004г
Закон ома
Электроника сейчас получила большое распространение, у всех дома много радиоприёмников, телефонов, компьютеров, планшетов, телевизоров фонариков и т.д. Это всё радиоэлектроника, поэтому некоторые люди заинтересовываются этим хобби, но не знают с чего начать. Наша цель рассказать в данном материале всё о Законе Ома.
Обозначения напряжения, тока, сопротивления
Всё же многие радиолюбители начинают с закона Ома. В закон Ома входят три единицы: напряжение, ток, сопротивление.
- Напряжение измеряется в вольтах (В) и обозначается U.
- Сопротивление измеряется в Омах (Ом) и обозначается R.
- Ток в Амперах (А) и обозначается I.
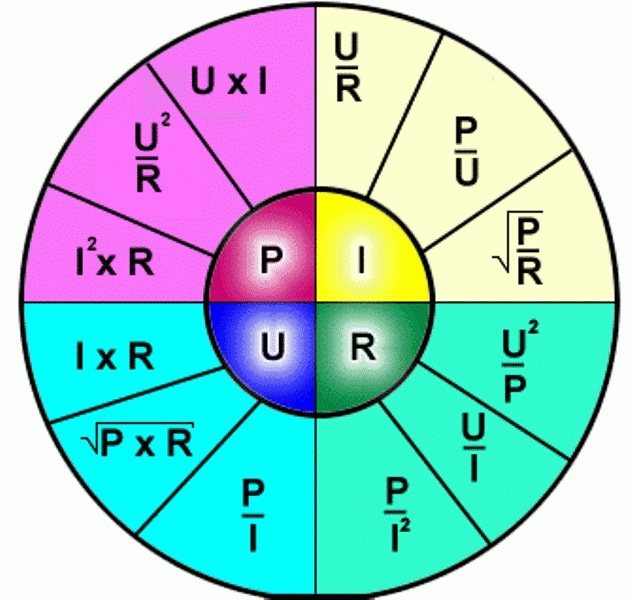
Расчёт напряжения, тока и сопротивления
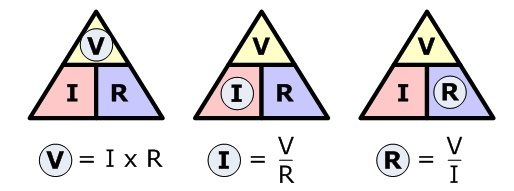
Закон Ома предназначен для того, чтобы найти неизвестную третью, если известны первая и вторая. С этого по подробней, чтобы облегчить закон Ома, будем пользоваться треугольником Ома. Вот этот треугольник:
Давайте разберёмся с напряжением, чтобы найти напряжение, используя треугольник Ома, надо закрыть рукой напряжение — U, остались только I-ток и R-сопротивление, передними стоит вертикальная черта, вертикальная это черта снизу вверх, это вертикальная линия обозначает умножение, значит, чтобы найти напряжение надо ток умножить на сопротивление.
Вот такая формула получилась: U=I*R, где U-напряжение, I-ток, R-сопротивление.
Теперь давайте попробуем найти ток, прикроем рукой I, теперь перед напряжением и сопротивление стоит горизонтальная черта, горизонтальная, это та черта, которая идёт слева направо. Горизонтальная черта означает деление. Значит, чтобы найти ток, надо напряжение разделить на сопротивление.
Формула получилась следующая: I= UR, где I-ток, U-напряжение, R-сопротивление.
Найдём сопротивление, закроем рукой R, то получим опять горизонтальную черту перед напряжением и током, значит нужно делить.
Формула получилась для расчёта сопротивления: R=UI, где R-сопротивление, U-напряжение, I-ток. Итак, мы научились пользовать треугольником Ома и узнали о Законе Ома. Теперь, пожалуй, поучимся на примерах.
Примеры расчётов закона Ома
Давайте, найдём напряжение, если ток равен 0,9 Ампер, а сопротивление 100 Ом, пользуясь треугольником, прикрываем напряжение рукой, смотрим, вертикальная черта, значит умножить. Опять пользуемся той формулой, только подставляем числа, U = 0,9 А * 100 Ом, считаем, получиться 90, значит U = 90 вольт.
Теперь рассчитываем сопротивление, берём те же единицы, только убираем сопротивление, получиться вот такая формула: R = 90 В 0,9 А, получим 100 Ом.
Чтобы рассчитать ток, опять же убираем ток, получаем эту формулу I = 90 В 100 Ом, получаем 0,9 Ампер.
Итак, на этом всё, кстати, закон Ома действует там, где нет катушек индуктивности и конденсаторов, не забивайте голову конденсаторами и катушками индуктивности, просто, запомните, что закон Ома действует, там, где нет катушек индуктивности и конденсаторов. Надеюсь, моя статья была полезной, всем удачи, с вами был Дмитрий Цывцын.
Справочники радиодеталей
ПРОСТОЙ ФОНО-ПРЕДУСИЛИТЕЛЬ
Общие сведения
Прохождение электрического тока через проводник зависит от его проводимости. Это параметр пропорционален силе тока. Другими словами, он определяет способность вещества пропускать через себя электричество без потерь. Зависит проводимость от физических свойств материала, температуры, степени воздействия внешних сил. Обратной ей величиной является сопротивление, то есть характеристика проводника, показывающая его возможность сопротивляться прохождению тока.
Связь между фундаментальными параметрами электротока экспериментально установил Симон Ом. Он выяснил, что сила тока в замкнутой цепи пропорциональна разности потенциалов (напряжению) и обратно пропорциональна сопротивлению: I = U / R. Так, если R равно нулю, то сила тока будет бесконечной.
Способность веществ препятствовать прохождению электротока используется при построении электрических цепей. Так, радиоэлемент, который называется резистором, установленный в определённом месте электроцепи, позволяет получить на нагрузке нужное значение напряжения или тока. Радиодеталь представляет собой двухполюсник, который имеет установленное значение сопротивления или может изменять его.
Расчёт выходных характеристик цепи, а именно величин тока и напряжения, требует знания общего сопротивления всей замкнутой цепочки. Иными словами, все элементы, начиная от источника питания и заканчивая нагрузкой, заменяются эквивалентными резисторами. Для цепи сначала считают общее значение сопротивления, а затем вычисляют нужные характеристики. Относительно источника тока, нагрузки и других элементов каждый резистор может быть подключён:
- последовательно;
- параллельно.
Вид подключения влияет на общее сопротивление. Формула для его нахождения может быть довольно громоздкой из-за смешанного соединения, поэтому чаще расчёт ведётся в несколько этапов, на каждом из которых выполняется объединение одного или нескольких элементов.
Виды устройств и их особенности
Разновидностей штепсельных розеток и блоков довольно много. У каждого типа свои конструктивные особенности и предназначение.
- Скрытые приборы монтируют прямо в стену — в специальные подрозетники.
- Открытые устройства выпускают для тех квартир, где электропроводка не спрятана в стену.
- Выдвижные розеточные блоки монтируют в стол или другую мебель. Их удобство в том, что после эксплуатации приборы легко спрятать от посторонних глаз и шаловливых детских рук.
Приборы отличаются методом зажима контактов. Он бывает винтовым и пружинным. В первом случае проводник фиксируют винтом, во втором — с помощью пружины. Надежность последних больше, однако в продаже их найти не так просто. На стенах устройства закрепляют тремя способами — лапками с зубчатыми краями, саморезами или специальной пластиной — суппортом, который облегчает как установку, так и демонтаж розетки.
Помимо обычных, недорогих устройств существуют модели, оснащенные заземляющими контактами. Это лепестки располагаются в верхней и нижней части, к ним крепят провод заземления. Для обеспечения безопасности выпускают розетки, оборудованные шторкам либо защитными крышками.
Основные популярные типы
К ним относятся:
- вид «С», он имеет 2 контакта — фазу и ноль, обычно покупается, если предназначен для техники малой либо средней мощности;
- тип «F», помимо традиционной пары оснащается еще одним контактом — заземляющим, эти розетки становятся более популярными, так как для квартир в новостройках заземляющий контур стал нормой;
- Вид «Е», отличающийся от предыдущего только формой контакта заземления, это штырь, такой же, как и элементы вилки розетки.
Последний тип встречается реже остальных, так как он менее удобен в эксплуатации: разворот штепселя на 180° при такой розетке невозможен.
Защищенность корпуса — следующее различие моделей. Степень безопасности обозначают индексом IP и двухзначным числом, следующим за этими буквами. Первая цифра обозначает класс защиты от пыли, твердых тел, вторая — от влаги.
- Для обычных жилых комнат достаточно моделей класса IP22 либо IP33.
- IP43 рекомендуют покупать для детских, так как эти розетки оснащены крышками/шторками, блокирующими гнезда, когда техника не используется.
- IP44 — тот минимум, что необходим для ванных комнат, кухонь, бань. Угрозой в них может быть не только сильная влажность, но и брызги воды. Подойдут они для монтажа в подвалах без отопления.
Установка розетки на открытом балконе — достаточное основание для покупки изделия с большей степенью защиты, это как минимум IP55.
Эквивалентные преобразования
При падении напряжения между двумя точками цепи в их разность включают свободное число значений потенциалов, имеющих противоположные знаки. После чего их попарно объединяют.
Готовые работы на аналогичную тему
- Курсовая работа Эквивалентные электрические цепи 470 руб.
- Реферат Эквивалентные электрические цепи 250 руб.
- Контрольная работа Эквивалентные электрические цепи 200 руб.
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость
$Uab = phi a — phi b$, где $a$ и $b$ – точки.
После преобразований у нас получается внушительная формула:
$U_{ab} = phi a — phi b = phi a -phi с +phi с -phi d +phi d -…-phi i +phi i -phi k +phi k-… -phi q +phi q — phi b = (phi a -phi с) + (phi с-phi d) + (phi d -…-phi i) + (phi i -phi k) + (phi k-… -phi q) + (phi q — phi b) = U_{ac}+ U_{cd} + U_{de} +…+ U_{ik} + U_{kl} + U_{lm} +…+ U_{qb} = Ir_1+ Ir_2 + … + Ir_m + E_1 + E_2 +… –E_n = I(r_1 + r_2 + r_3 + … + r_m) + ( E_1 + E_2 +… –E_n) = IR + E$
Всякое последовательное соединения электрической цепи можно преобразовать при помощи последовательного соединения:
- эквивалентного резистора;
- источника электродвижущей силы.
В нашем случае сопротивление эквивалентного резистора равняется сумме сопротивлений, которые входят в соединение. Электродвижущая сила эквивалентного источника будет равна сумме ЭДС источников, входящих в это соединение.
Определение 2
Любые элементы соединения цепи возможно переставлять в разном порядке. Все действия должны осуществляться в пределах соединения. Такой процесс называют свойством коммутативности последовательного соединения элементов.
Нужна консультация преподавателя в этой предметной области? Задай вопрос преподавателю и получи ответ через 15 минут! Задать вопрос
Если взять за основу эквивалентное сопротивление ($R$), которое представляет собой сумму положительных слагаемых, тогда получим, что $R geq r$, где $r$ — максимальное значение из всех сопротивлений, входящих в соединение.
При подключении последовательного соединения к узлам электрической цепи его значение будет равно определению ветви цепи. В этом случае ветвь образовывается исключительно последовательным соединением.
В параллельном соединении элементов совокупность частей электрической цепи не имеет связи с другими узлами, при этом объединена с двумя узлами. Параллельное соединение ветви и элементов параллельного соединения цепи существенно отличается от последовательного соединения.
В параллельное соединение входят также резисторы и источники тока, однако в цепи не могут присутствовать больше одного источника электродвижущей силы.
Преобразования цепей поддерживают еще одну особую задачу в физике. Она состоит в определении сопротивления цепи относительно точек разрыва. Такая ситуация возникает, когда используется метод эквивалентного генератора при анализе электрических цепей, находящихся в неподвижном режиме, а также при решении уравнения для анализа переходных процессов.
Эквивалентное сопротивление является входным сопротивлением определенной цепи. До начала эквивалентных преобразований необходимо в изучаемой цепи заменить источники электродвижущей силы на эквивалентное сопротивление тока и ЭДС. После этого нужно определить само эквивалентное сопротивление. При этом сопротивление источника электродвижущей силы равняется нулю. Сопротивление источника тока имеет бесконечные значения.
Простые электрические цепи содержат исключительно последовательное или параллельное соединение элементов.
Сложный участок цепи содержит последовательное и параллельное соединение элементов (смешанное соединение).
Эквивалентные преобразования имеют смысл, если при их выполнении токи и напряжения не изменяются на конкретных участках цепи. При преобразовании сложных электрических цепей пользуются последовательным методом. Он состоит в последовательном преобразовании участков цепи, которые имеют простое соединение элементов.
Параллельное и последовательное соединение элементов
В разделе электротехники присутствует несколько вариантов того, как подключить детали в электрическую цепь. Есть параллельное и попеременное подсоединения. Их объединяет смешанная схема, которая представлена ниже.
Последовательное подключение — это когда все источники соединяются друг с другом последовательно. Получаемая цепь не обладает никакими разветвлениями. Сила тока в данном случае проходит через каждый источник. Она постоянная, общее напряжение одинаковое.
В случае препятствия резисторов заряду при последовательном подключении получится, что сопротивляемость будет равна сумме всех взаимозаменяемых пассивных элементов цепи. Рассчитывая параметры электротехнической схемы, не нужно применять частные параметры устройств. Их можно заменить одним значением, которое равно их суммарному показателю.
Обратите внимание! Польза взаимозаменяемости компонентов заключается в возможности замены нескольких пассивных элементов электрической сети одним. Параллельное подключение — это такое подсоединение источников, в котором входы всех устройств находятся в одних местах, а выходы — в других
Этими местами служат узлы
Параллельное подключение — это такое подсоединение источников, в котором входы всех устройств находятся в одних местах, а выходы — в других. Этими местами служат узлы.
В случае эквивалентного препятствия заряду при параллельном соединении определить его можно благодаря закону Ома с преобразованием формулировки подсчета. Так, сделать необходимый расчет можно, основываясь на следующей формуле: R · R / N·R = R / N.
Если это соединение нескольких индуктивных катушек, то их индуктивный показатель сопротивляемости будет рассчитываться по той же формуле, что для резисторных устройств.
Важно! В случае с параллельным подключением общий показатель будет меньше любого показателя резистора. При последовательном подсоединении все наоборот
Практическое применение
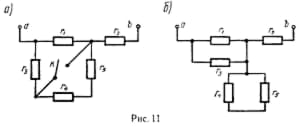
Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.
Простое соединение
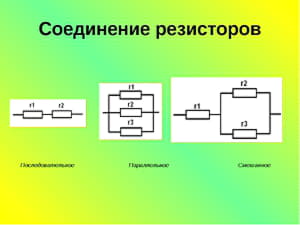
R3 = 1 кОм = 1000 Ом.
Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.
Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:
1/Ro = 1/R1 + 1/R2 +1/R3.
Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).
Подставив исходные данные в эту формулу, получим:
Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.
Комбинированный контур
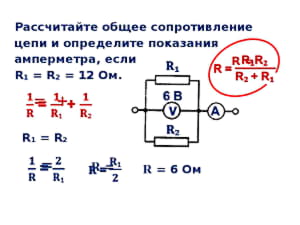
Первоначально понадобится упростить схему. Сопротивления R3 и R4 включены относительно друг друга параллельно. Поэтому находится их объединённое сопротивление:
Rp = (R3*R4)/(R3+R4).
Rp = (10*3)/ (10+3) = 2,3 Ом.
Теперь схему можно перерисовать в виде трёх последовательно включённых резисторов и найти общее сопротивление путём сложения их величин:
Ro = R1+R2+Rp = 5+5+2,3 = 12,3 Ом.
Зная эквивалентное сопротивление, используя закон Ома, несложно вычислить силу тока в цепи и мощность эквивалентного резистора:
I = U/R = 5/2,3 = 2,2 A.
P = I*U = 2,2*5= 11 Вт.
Таким образом, путём постепенного упрощения схемы можно свести цепь из последовательно и параллельно соединённых резисторов к одному элементу. А затем рассчитать его сопротивление и требуемую мощность.
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.
1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.
Эквивалентное сопротивление R eq группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.
Иными словами, проводимость G
параллельно соединенных резисторов равна сумме проводимостей этих резисторов:
Эта формула для R eq и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:
Если параллельно соединены только два резистора, формула упрощается:
Если имеется n
соединенных параллельно одинаковых резисторовR , то их эквивалентное сопротивление будет равно
Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.
Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.
При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.
С количественной
стороны процесс электролиза впервые
был изучен в 30-х годах XIX века выдающимся
английским физиком Фарадеем, который
в результате своих исследований установил
следующие законы электролиза:
I
закон. Масса
образующегося при электролизе вещества
пропорциональна количеству прошедшего
через раствор электричества.
Этот закон вытекает
из сущности электролиза. Как уже
говорилось, в месте соприкосновения
металла с раствором происходит
электрохимический процесс – взаимодействие
ионов или молекул электролита с
электронами металла, так что
электролитическое образование вещества
является результатом этого процесса.
Ясно, что количество вещества, получающегося
у электрода, всегда будет пропорционально
числу прошедших по цепи электронов, т.
е. количеству электричества.
Количество вещества,
выделяющегося при прохождении через
электролит 1 кулона электричества,
называется электрохимическим эквивалентом
(Э).
где Q
– количество электричества, пропущенного
через раствор или расплав электролита:
Q
= I∙t,
где t
‑ время, в сек., I
‑ сила тока.
где МЭ
‑ молярная
масса эквивалента вещества, n
– число электронов в электродном
процессе. Таким образом:
Или, при выделении
газообразных веществ:
Измерениями
установлено, что количество электричества,
обусловливающее электрохимическое
превращение одного эквивалента вещества,
равно 96 485 (округленно 96 500) кулонам.
Величина 96 500 Кл/моль называется постоянной
Фарадея и обозначается буквой F.
II
закон. При
электролизе различных химических
соединений равные количества электричества
приводят к электрохимическому превращению
эквивалентных количеств веществ.
Следовательно,
для восстановления на катоде и окисления
на аноде одного моль-эквивалента любого
вещества необходимо затратить одно и
то же количество электричества, а именно
96500 кулонов.
1.11 Последовательность восстановления частиц на катоде и окисления на аноде
Руководствуясь
таблицей стандартных электродных
потенциалов металлов, можно указать
следующие случаи при электролизе водных
растворов электролитов:
1) На катоде легче
всего разряжаются катионы того металла,
которому отвечает наиболее положительный
потенциал. Так, например, из смеси
катионов Cu2+,
Ag+
и Zn2+
при достаточном напряжении на клеммах
электролизера вначале восстанавливаются
ионы серебра (φ0=+0.79
В), затем меди (φ0=+0.337
В) и, наконец, цинка (φ0=
–0.76 В).
2) Катионы металлов
со стандартным электродным потенциалом,
большим, чем у водорода, расположены в
ряду напряжений после него: Cu2+,
Hg22+,
Ag+,
Pt2+,
…, до Pt4+.
При электролизе они почти полностью
восстанавливаются на катоде и выделяются
в виде металла:
Men+
+ nē
→ Meo
3) Катионы металлов
с малой величиной стандартного
электродного потенциала (металлы начала
ряда напряжений Li+,
Na+,
K+,
Rb+,
… до Al3+
включительно). При электролизе на катоде
они не восстанавливаются, вместо них
восстанавливаются молекулы воды:
2H2O
+ 2ē → H2
+ 2OH—
4) Катионы металлов
со стандартным электродным потенциалом
меньшим, чем у водорода, но большим, чем
у алюминия (Mn2+,
Zn2+,
Cr3+,
Fe2+,
…, до H). При электролизе эти катионы,
характеризующиеся средними величинами
электроноакцепторной способности, на
катоде восстанавливаются одновременно
с молекулами воды:
Men+
+ nē → Meo
2H2O
+ 2ē → H2
+ 2OH—
Процессы, протекающие
на аноде, зависят как от электролита,
так и от материала (вещества), из которого
сделан анод. Нерастворимые аноды не
претерпевают окисления в ходе электролиза.
В определенных условиях роль нерастворимых
анодов могут выполнять Fe, Ni, Pb, Sn и др.
Растворимые аноды в процессе электролиза
могут окисляться (разрушаться) и
переходить в раствор в виде ионов. Они
изготовляются из меди, серебра, цинка,
кадмия, никеля и других металлов.
Растворимые аноды используют при
нанесении металлических покрытий на
изделие (катод).
На нерастворимом
аноде в процессе
электролиза происходит окисление
анионов или молекул воды.
1) На аноде легче
всего окисляются те ионы, у которых
стандартный электродный потенциал
меньше.
2) При электролизе
водных растворов бескислородных кислот
и их солей (кроме HF и фторидов) у анода
будут окисляться (разряжаться) анионы.
Так, например, при электролизе растворов
кислот и их солей (HI, HBr, HCl, H2S
или гидроксидов) на аноде будет окисляться
соответствующий ион передавать свои
электроны во внешнюю цепь электролизера:
2I–
– 2ē → I20
S2-
— 2ē → So
4OH–
– 4ē → 2H2O
+ O2
3) При электролизе
кислородсодержащих кислот и их солей
(SO42–,
NO3–,
PO43–
и т. п.) с максимальной степенью окисления
неметалла на аноде окисляются не анионы,
а молекулы воды с выделением кислорода,
так как потенциал окисления воды
значительно меньше, чем для таких анионов
2H2O
– 4ē
→ O2
+ 4H+
На растворимом
аноде в
процессе электролиза происходит
окисление материала, из которого
изготовлен анод
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
23.11.2019279.04 Кб0n1.doc
- #
- #
Содержание материала
- Последовательное соединение элементов
- Последовательное соединение элементов
- Определение эквивалентного сопротивления
- Параллельное соединение резисторов. Калькулятор для расчета
- Основные преимущества
- Физические формулы и примеры вычислений
- Практическое применение
- Простое соединение
- Комбинированный контур
- Емкость в цепи переменного тока
- Виды устройств и их особенности
- Основные популярные типы
- Как рассчитать сложные схемы соединения резисторов
- Параллельное соединение
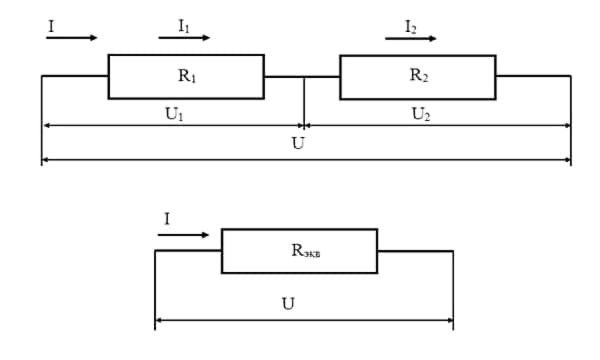
Последовательное соединение элементов
В случае последовательного подключения все приборы соединяются последовательно друг с другом, а собранная цепь не имеет разветвлений.
При таком подключении сила тока, проходящая через каждый резистор, будет одинаковая, а общее падение напряжения складывается из суммарных падений напряжения на каждом из приборов.
Последовательное подключение приборов
Чтобы определить суммарное значение в этом случае, воспользуемся законом Ома, который записывается следующим образом:
I = U/R.
Из вышестоящего выражения получаем значение R:
R = U/I (1).
Поскольку при последовательном соединении:
- I = I1 = I2 =…= IN (2),
- U = U1 + U2 +…+ UN (3),
формула для расчёта эквивалентного сопротивления (Rобщ или Rэкв) из (1) – (3) будет иметь вид:
- Rэкв = (U1 + U2 + …+ UN)/I,
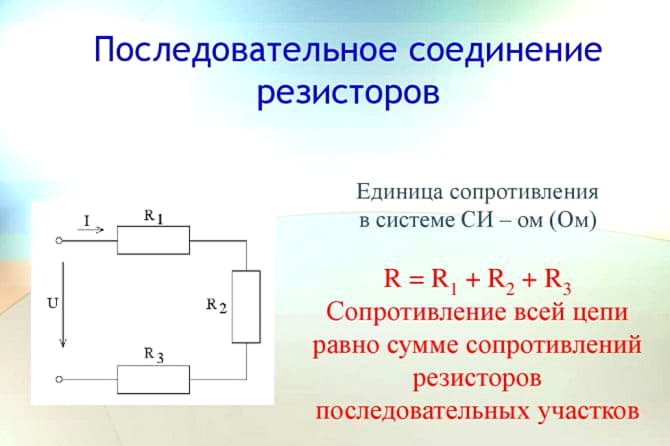
- Rэкв = R1 + R2 + … + RN (4).
Таким образом, если имеется N последовательно соединённых одинаковых элементов, то их можно заменить на одно устройство, у которого:
Rобщ = N·R (5).
Последовательное соединение элементов
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.
В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
Следовательно, рассчитать можно общее:
Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Определение эквивалентного сопротивления
При рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации.
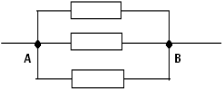
Параллельное соединение резисторов. Калькулятор для расчета
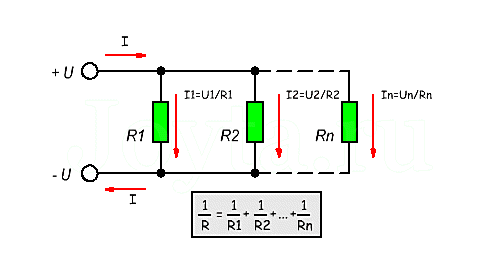
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Основные преимущества
Светодиодные лампы Т8 значительно превосходят альтернативные образцы практически по всем показателям. К достоинствам приборов следует отнести:
- эффективность, высокие значения светового потока;
- экономичность;
- длительный срок службы;
- освещение имеет направленный характер, что позволяет организовать более эффективный и комфортный режим подсветки;
- подключение происходит мгновенно, чего не наблюдается у люминесцентных ламп;
- ровный, без мерцания режим работы;
- есть возможность работы при нестабильности напряжения в сети;
- не создают электромагнитных помех;
- нет вредного излучения в ультрафиолетовом диапазоне;
- попадание частиц жира или иных взвесей, находящихся в воздухе, не создает опасность перегрева и взрыва лампы, характерных для альтернативных конструкций;
- утилизация светодиодных устройств не требует специализированных мероприятий и может быть произведена обычным способом;
- подключать такие светильники можно напрямую к сети 220 В, без промежуточных устройств.
Помимо этих преимуществ, необходимо отметить широкие возможности выбора цветовой температуры ламп. Этот параметр позволяет создать в помещении определенную обстановку, позволяющую повысить концентрацию и увеличивающую работоспособность сотрудников. Такой результат достигается подключением ламп с холодным белым светом.
Если необходимо обеспечить более расслабленную, комфортную обстановку, выбирают экземпляры с теплым светом. Кроме этого, светодиоды хорошо переносят низкие температуры, что позволяет использовать их в неотапливаемых переходах, коридорах и прочих помещениях со сложными условиями эксплуатации.
Физические формулы и примеры вычислений
Формулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
- параллельное присоединение определяют по формуле Rэкв. = (R1*R2)/R1+R2;
- последовательное включение вычисляют, определяя его сумму Rэкв. = R1+R2.
Практическое применение
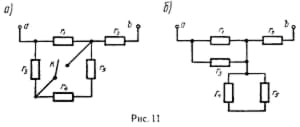
Перед тем как приступить к расчёту эквивалентного сопротивления, вся электрическая цепь разделяется на простые контуры. Как только импеданс каждого такого контура будет подсчитан, схема перерисовывается, но вместо контуров рисуется уже резистор. Затем всё повторяется, и это происходит до тех пор, пока не останется один элемент.
Простое соединение
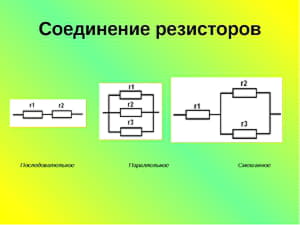
R3 = 1 кОм = 1000 Ом.
Так как соединение последовательное, используется формула: Ro = R1+R2+R3. Подставив известные значения, рассчитывается эквивалентное значение: Ro = 57+57+1000 = 1114 Ом.
Если же те же самые резисторы будут расположены параллельно друг другу, то для расчёта общего сопротивления уже используется другое выражение:
1/Ro = 1/R1 + 1/R2 +1/R3.
Ro = R1*R2*R3 / (R1*R2+R2*R3+R1*R3).
Подставив исходные данные в эту формулу, получим:
Ro = 57*57*1000/ (57*57 +57*1000+ 57*1000) = 3249000/117249 = 27,7 Ом.
Комбинированный контур
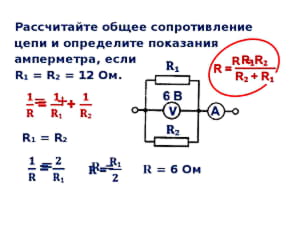
Первоначально понадобится упростить схему. Сопротивления R3 и R4 включены относительно друг друга параллельно. Поэтому находится их объединённое сопротивление:
Rp = (R3*R4)/(R3+R4).
Rp = (10*3)/ (10+3) = 2,3 Ом.
Теперь схему можно перерисовать в виде трёх последовательно включённых резисторов и найти общее сопротивление путём сложения их величин:
Ro = R1+R2+Rp = 5+5+2,3 = 12,3 Ом.
Зная эквивалентное сопротивление, используя закон Ома, несложно вычислить силу тока в цепи и мощность эквивалентного резистора:
I = U/R = 5/2,3 = 2,2 A.
P = I*U = 2,2*5= 11 Вт.
Таким образом, путём постепенного упрощения схемы можно свести цепь из последовательно и параллельно соединённых резисторов к одному элементу. А затем рассчитать его сопротивление и требуемую мощность.
Емкость в цепи переменного тока
При подаче на конденсатор постоянного напряжения он постепенно зарядится до максимальной разности потенциалов на его обкладках. После этого ток через электронный компонент прекратится и, не считая ничтожной утечки, будет равняться нулю. Поэтому в цепи постоянного тока конденсатор имеет огромное сопротивление. При расчетах его величину принимают равной бесконечности.
Реактивное сопротивление имеет вполне исчисляемое значение. Его можно измерить с помощью осциллографа, генератора и постоянного резистора. Для этого потребуется собрать схему. В ней конденсатор образует с резистором делитель напряжения. С помощью осциллографа будет измеряться потенциал, который образуется на выводах ёмкости.
Для данной схемы вычисления имеют следующий вид.
Формула косвенного измерения
Здесь:
- Ur – разность потенциалов на резисторе, В;
- Uc – напряжение на обкладках, В;
- R – сопротивление резистора, ом;
- Xc – сопротивление ёмкости, ом;
- I – ток, протекающий в цепи, А.
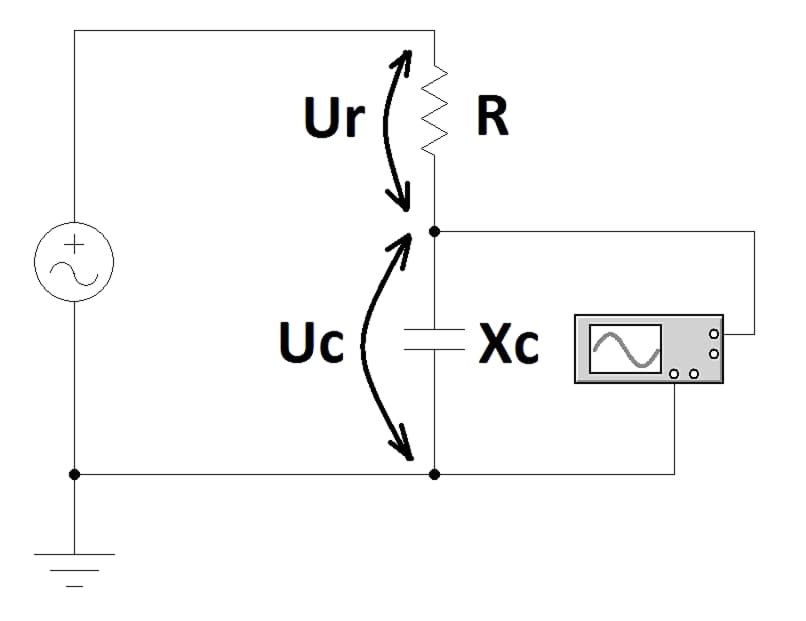
Важно! Электрический кабель также обладает ёмкостью. Поэтому после снятия напряжения на нём остаётся некоторый заряд
Данное явление опасно для человека, особенно, если проводник до отключения находился под потенциалом 1000 В и выше.
Виды устройств и их особенности
Разновидностей штепсельных розеток и блоков довольно много. У каждого типа свои конструктивные особенности и предназначение.
- Скрытые приборы монтируют прямо в стену — в специальные подрозетники.
- Открытые устройства выпускают для тех квартир, где электропроводка не спрятана в стену.
- Выдвижные розеточные блоки монтируют в стол или другую мебель. Их удобство в том, что после эксплуатации приборы легко спрятать от посторонних глаз и шаловливых детских рук.
Приборы отличаются методом зажима контактов. Он бывает винтовым и пружинным. В первом случае проводник фиксируют винтом, во втором — с помощью пружины. Надежность последних больше, однако в продаже их найти не так просто. На стенах устройства закрепляют тремя способами — лапками с зубчатыми краями, саморезами или специальной пластиной — суппортом, который облегчает как установку, так и демонтаж розетки.
Помимо обычных, недорогих устройств существуют модели, оснащенные заземляющими контактами. Это лепестки располагаются в верхней и нижней части, к ним крепят провод заземления. Для обеспечения безопасности выпускают розетки, оборудованные шторкам либо защитными крышками.
Основные популярные типы
К ним относятся:
- вид «С», он имеет 2 контакта — фазу и ноль, обычно покупается, если предназначен для техники малой либо средней мощности;
- тип «F», помимо традиционной пары оснащается еще одним контактом — заземляющим, эти розетки становятся более популярными, так как для квартир в новостройках заземляющий контур стал нормой;
- Вид «Е», отличающийся от предыдущего только формой контакта заземления, это штырь, такой же, как и элементы вилки розетки.
Последний тип встречается реже остальных, так как он менее удобен в эксплуатации: разворот штепселя на 180° при такой розетке невозможен.
Защищенность корпуса — следующее различие моделей. Степень безопасности обозначают индексом IP и двухзначным числом, следующим за этими буквами. Первая цифра обозначает класс защиты от пыли, твердых тел, вторая — от влаги.
- Для обычных жилых комнат достаточно моделей класса IP22 либо IP33.
- IP43 рекомендуют покупать для детских, так как эти розетки оснащены крышками/шторками, блокирующими гнезда, когда техника не используется.
- IP44 — тот минимум, что необходим для ванных комнат, кухонь, бань. Угрозой в них может быть не только сильная влажность, но и брызги воды. Подойдут они для монтажа в подвалах без отопления.
Установка розетки на открытом балконе — достаточное основание для покупки изделия с большей степенью защиты, это как минимум IP55.
Как рассчитать сложные схемы соединения резисторов
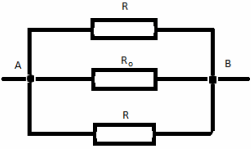
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
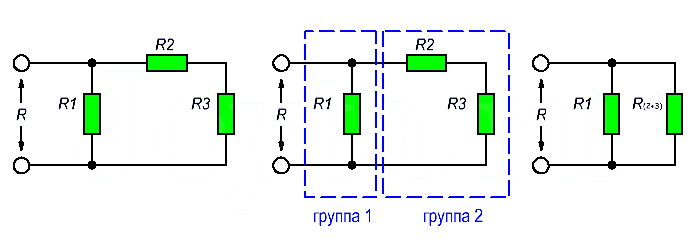
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
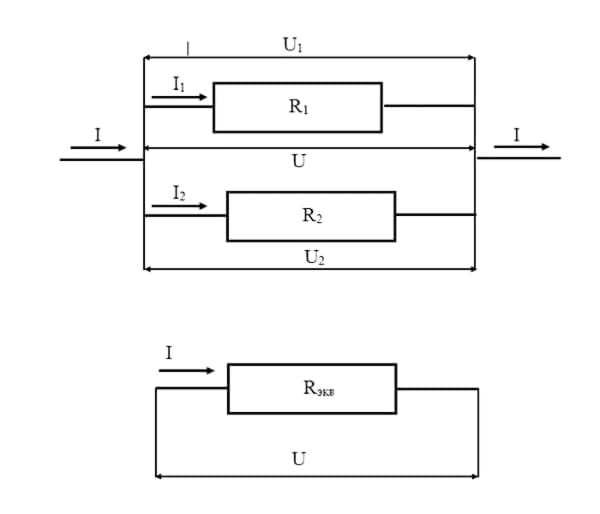
Параллельное соединение
Реактивное сопротивление
При таком подключении входы от всех устройств соединены в одной точке, выходы – в другой точке. Эти точки в физике и электротехнике называются узлами. На электрических схемах узлы представляют собой места разветвления проводников и обозначаются точками.
Параллельное соединение
Расчет эквивалентного сопротивления также выполняем с помощью закона Ома.
В этом случае общее значение силы тока складывается из суммы сил токов, протекающих по каждой ветви, а величина падения напряжения для каждого устройства и общее напряжение одинаковые.
Если имеются N резистивных устройств, подключенных таким образом, то:
I = I1 + I2 + … + IN (6),
U = U1 = U2 = … = UN (7).
Из выражений (1), (6) и (7) имеем:
- Rобщ = U/(I1 + I2 + …+ IN),
- 1/Rэкв = 1/R1 + 1/R2 +…+ 1/RN (8).
Если имеется N одинаковых резисторов, имеющих подключение данного типа, то формула (8) преобразуется следующим образом:
Rобщ = R · R / N·R = R / N (9).
Если соединены несколько катушек индуктивности, то их суммарное индуктивное сопротивление рассчитывается так же, как и для резисторов.