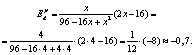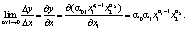Рассмотренные
в предыдущем подразделе экономические
понятия имеют размерность, что не вполне
удобно для анализа взаимосвязи
относительных изменений переменных.
Вводят понятия: эластичность
выпуска по труду EL
и эластичность выпуска по капиталу EK,
определяемые формулами
EL
=;
(2.6)
EK
=.
(2.7)
Безразмерные
показатели EL
и EK
показывают, на сколько процентов
произойдет относительное увеличение
выпуска при относительном увеличении
соответствующего ресурса на 1%.
Сумма
значений эластичности выпуска по всем
ресурсам называется эластичностью
производства:
E
= EK
+ EL.
(2.8)
Для
эластичности
KL
предельной
нормы замещения труда капиталом
справедливо соотношение:
KL
=
(2.9)
Эффективность
производственного процесса (эффект от
масштаба производства) можно оценить
математически, увеличив одновременно
все ресурсы в t
раз. Если
использовать более общую аппроксимирующую
формулу Кобба—Дугласа
Q
= AKL,
получаем: Q
(tK,
tL)
= AKtLt
= tt
Q
(K,
L)
= t+
Q
(K,
L).
Отсюда вытекает, что если
и
в сумме превышают единицу, то говорят,
что производственная функция имеет
возрастающий эффект от масштаба
производства (если ресурсы K
и L увеличиваются
в некоторой пропорции, то выпуск Q
растет в большей пропорции). Если их
сумма меньше, чем единица, то имеет место
убывающий эффект от масштаба производства.
В
своей первой статье Ч. Коббс и П. Дуглас
описывали производственную функцию в
виде (2.1), предполагающем постоянную
отдачу от масштаба:
и
в сумме точно составляют единицу.
Впоследствие они ослабили это допущение,
предпочитая оценивать степень отдачи
от масштаба производства. Как указывалось
нами ранее, при обработке исходных
данных, использованных Ч. Коббсом и П.
Дугласом, методом наименьших квадратов,
получаем значения
= 0,23 и
= 0,81. Сумма
и ,
равная 1,04, лишь несколько превышает
единицу, т.е. первоначальное предположение
Ч. Коббса и П. Дугласа о постоянной отдаче
от масштаба было вполне оправдано.
Пример
4. Рассчитать
эластичность выпуска по труду и капиталу
для производственной функции Q
= K1/4L3/4
в точке K
= 2, L
= 3. Оценить эффект от масштаба производства.
Решение.
Эластичность выпуска по труду определяется
формулой (2.6). Так как предельный продукт
труда
=
=3/4
,
получаем:
EL
==
=
(3/4
)
= (L /
K1/4L3/4)(3/4)
= 3/4.
Эластичность
выпуска по капиталу определяется
формулой (2.7). Так как предельный продукт
капитала
=
=1/4
,
получаем:
EK
==
=
(1/4
)
= (K
/ K1/4L3/4)(1/4)
= 1/4.
Таким
образом, эластичность выпуска по труду
и капиталу в случае производственной
функции Кобба—Дугласа
вида Q
= AKL
не зависит от точки производства и равна
показателям степени при соответствующих
переменных
= 0,75 и
= 0,25 соответственно.
Сумма
значений эластичности выпуска по всем
ресурсам (эластичность производства)
равна
+
= 1, т.е. в данном случае имеет место
постоянная отдача от масштаба производства.
Для
эластичности KL
предельной нормы замещения труда
капиталом в общем случае производственной
функции вида
Q = AKL
получаем:
KL
=

1,
т.е.
для функции Кобба—Дугласа
эластичность предельной нормы замещения
труда капиталом постоянна и равна
единице. Это важнейшее свойство функции
Кобба—Дугласа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Авторы
- Файлы
- Литература
Попова Е.С
1
Дырдасова А.С.
1
1 Самарский государственный экономический университет
1. Предельный анализ в экономике. Эластичность функции [Электронный ресурс]. – Режим доступа: http://www.mathelp.spb.ru/book1/lim_an_ec.htm. – (Дата обращения: 16.12.2015).
2. Яшина Ю.Е, Карнавская Н.В., Чехута В.А. и др. Эластичность функции и ее применение экономике [Электронный ресурс] / Ю.Е. Яшина, Н.В. Карнавская, В.А. Чехута и др./ Международный студенческий научный вестник: эл.науч.журн. – 2015. – №3. – Режим доступа: http://www.eduherald.ru/140–14166. – (Дата обращения:16.12.2015).
На современном этапе развития человечества одну из ведущих ролей в развитии общества играют экономические отношения, поскольку именно они являются той материальной основой, которая в свою очередь делает возможным формирование и развитие различных общественных институтов. Для наиболее полного изучения экономических явлений и процессов, происходящих в обществе, экономическая теория использует различные методы, прибегая к «помощи» других не менее важных наук. Одной из таких наук является математический анализ. Одними из базовых, ключевых понятий в экономической теории являются такие широко известные категории как спрос и предложение, которые, в свою очередь, обладают определенными признаками и свойствами, что и является главным предметом экономической теории. Спрос и предложение товаров обладают различной степенью чувствительности к изменению определяющих их факторов. Мерой такого изменения является эластичность спроса и эластичность предложения. В свою очередь, выделяется несколько основных видов эластичности: ценовая эластичность, эластичность по доходу и перекрестная эластичность.
Ценовая (прямая) эластичность спроса (предложения) показывает, какое процентное изменение спроса (предложения) последует за однопроцентным изменением цены товара.
Эластичность спроса по доходу показывает, какое процентное изменение спроса последует за однопроцентным изменением дохода потребителя.
Перекрестная эластичность спроса показывает, какое изменение спроса на товар A последует за однопроцентным изменением цены товара B, при условии, что товары A и B являются комплементарными (комплементами) или взаимозаменяемыми (субститутами). Количественным выражением эластичности спроса и предложения является коэффициент эластичности E, который рассчитывается в одной точке кривой спроса и предложения или на дуге этой кривой.
Эластичностью функции 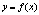
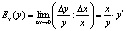
Таким образом, эластичность функции можно вычислить по формуле
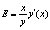
Эластичность функции также называется относительной производной. Эластичность функции по аргументу показывает, на сколько процентов изменится значение функции при изменении аргумента в точке x на 1 %. Пусть спрос задан функцией Q(d)=96–16P+P2, необходимо определить ценовую точечную эластичность спроса по цене при P=4.
Найдем первую производную функции
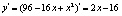
Подставим полученное выражение в формулу эластичности:
Таким образом, при изменении цены на 1 % величина спроса изменяется на 0,7 %. Спрос неэластичен.
Также в качестве примера можно рассмотреть производственную функцию Кобба-Дугласа. Данная функция устанавливает зависимость между величиной созданного общественного продукта и совокупными затратами живого труда, а также суммарным объемом применяемых производственных фондов.
Данная функция имеет следующий вид
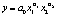
где a0 – коэффициент, 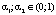
Каждый из используемых ресурсов характеризуется средней и предельной величинами. средняя производительность труда показывает, сколько единиц продукции приходится на единицу труда. Предельная производительность труда показывает, сколько дополнительных единиц продукции приносит дополнительная единица труда.
Рассчитаем вторую частную производную:
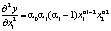
Вторая частная производная отрицательна, а значит, предельная производительность с увеличением 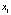
Для производственной функции Кобба-Дугласа предельная производительность всегда меньше средней.
Кроме того, можно определить показатель, характеризующий относительный прирост объема производства на единицу относительно увеличения труда
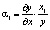
Полученный показатель называется эластичностью выпуска продукции по затратам труда. Он показывает, на сколько процентов увеличивается выпуск продукции при увеличении затрат труда на 1 %.
Подобные показатели можно рассчитать и для производственных фондов. Объем продукции в расчете на единицу производственных фондов называется фондоотдачей. Можно рассчитать среднюю и предельную фондоотдачу. Из функции Кобба_Дугласа имеем
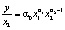
Предельная фондоотдача равна частной производной выпуска продукции по объему фондов:
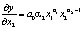
Предельная фондоотдача всегда ниже средней.
Относительная фондоотдача (эластичность выпуска продукции по объему производственных фондов) определяется как
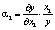
Если производственная функция задана формулой
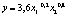
где y – объем продукции в стоимостном выражении, x1 – фонд заработной платы, x2 – стоимость основных производственных фондов. 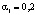
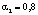
Библиографическая ссылка
Попова Е.С, Дырдасова А.С. ЭЛАСТИЧНОСТЬ В ПРОИЗВОДСТВЕННЫХ ФУНКЦИЯХ // Международный студенческий научный вестник. – 2016. – № 4-4.
;
URL: https://eduherald.ru/ru/article/view?id=16408 (дата обращения: 28.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Примеры решений задач: производственная функция
Производственная функция — экономико-математическая количественная зависимость между величиной выпуска (объемом продукции фирмы) и факторами производства, такими как затраты ресурсов, уровень технологий.
Наиболее известные примеры производственных функций: функция Кобба-Дугласа вида $Y=Acdot L^{alpha}cdot K^{beta}$, в которой предполагается постоянные эластичности ($alpha$ и $beta$) выпуска по факторам производства $K$ и $L$ соответственно (капитал и трудовые затраты); линейная производственная функция: $Y=aK+bL$, функция Леонтьева и т.д.
В этом разделе вы найдете подробно решенные задачи, касающиеся производственной функции (в том числе модели Кобба-Дугласа).
Полезная страница? Сохрани или расскажи друзьям
Производственная функция: задачи с решениями
Задача 1. Производственная функция коммерческого предприятия имеет вид $f=10sqrt{x_1}cdot sqrt{x_2}$, где $f$ — товарооборот, тыс. руб.; $x_1$ — производственная площадь, м ; $x_2$ — численность работников, сотни человек. Рассмотрите изокванту уровня $y_0$ и найдите точку $C_1$ и точку $C_2$. Сделайте вывод о возможности замены ресурсов. Полученные результаты изобразите графически.
Задача 2. Исходные данные. Фирма, производящая продукцию при заданной рынком системе цен по технологии, отображающейся производственной функцией $Q = 20 L^{0,5}$, может продавать любой объем своей продукции по цене Р = 6. Фирма может использовать любое количество труда по цене w = 40.
1. Какой тип производственной функции представлен в задании? В чем ее особенность? Приведите пример подобного производства. Изобразите график заданной производственной функции, а также графики среднего и предельного продуктов переменного фактора (труда).
2. На основе представленных данных выведите функции общих, средних и предельных затрат фирмы, функцию индивидуального предложения фирмы и определите объем предложения при заданной цене блага.
3. Дайте характеристику статуса фирмы на товарном и факторном рынках в представленном примере. Раскройте различия в поведении фирмы-совершенного конкурента и фирмы-монопсониста на рынке фактора. Приведите примеры подобного поведения фирм на рынке труда.
4. Выведите функцию спроса фирмы на труд, если цена блага P = 6 и остается неизменной. Определите объем спроса на труд при w = 40. Решение сопроводите графиком. Укажите несколько факторов (не менее трех), влияющих на спрос фирмы на труд.
Задача 3. Процесс производства некоторого товара описывается с помощью производственной функции $q=f(x_1, x_2)=54x_1^{1/2}x_2^{2/3}$. Для плана (2,5) найти первый второй предельные продукты. Дайте экономическую интерпретацию полученным результатам. Выясните, характеризуется ли ПФ той или иной разновидностью эффекта масштаба. Предполагая, что производитель приобретает ресурсы по ценам (2,7) найдите функцию переменных издержек $C_v(q)$.
Консультируем по решению задач микроэкономики
Модель Кобба-Дугласа: задачи с решениями
Задача 4. Производственная функция фирмы имеет вид: $Q = К^{0,5}cdot L^{0,5}$. Предположим, что в день затрачивается 4 часа труда (L = 4) и 4 часа работы машин (К = 4).
Определить:
1) максимальное количество выпускаемой продукции;
2) средний продукт труда;
3) допустим, что фирма увеличила затраты обоих факторов в два раза. Каков будет объем выпускаемой продукции?
Задача 5. Задана производственная функция Кобба-Дугласа
Изобразить изокванту, соответствующую плану (36,27). Какое количество продукта выпускается при этом плане?
Найти первый, второй предельные продукты для плана (36,27) и дать экономическую интерпретацию полученным результатам.
Каким эффектом от расширения масштабов производства характеризуется производственная функция
Каковы затраты производителя на покупку ресурсов при плане производства (36,27) и заданном векторе цен на ресурсы (3,4)?
Найти самый дешевый (оптимальный) план по ресурсам, обеспечивающий выпуск такого же количества продукции, что и для плана (36,27). Найти аналитически решение этой задачи
методом Лагранжа
методом подстановки.
Сделать геометрическую иллюстрацию решения задачи, изобразив ОДР и целевую функцию линиями уровня.
Задача 6. На основании представленных в таблице ниже данных построить ПФ типа Кобба-Дугласа. Сделать прогноз объема производства отрасли на 2000 год, если планируются увеличение основных фондов на 20% и одновременное уменьшение трудовых ресурсов на 5% относительно предыдущего года. Пусть заданы агрегированные основные показатели некоторой отрасли за четыре года:
Задача 7. Для построенной в самостоятельной работе производственной функции рассчитать предельные производительности, предельные нормы замещения ресурсов в 1993 и 1999 годах, сделать сравнительный экономический анализ. При расчетах предположить, что ресурсы в исследуемом году заданы, объем производства вычисляется.
Задача 8. Пусть производственная функция имеет вид $Y = 0.94 cdot K^{1.17}cdot L^{1.57}$. Для базового года $K_0 = 727$ млн ден. ед., $L_0 = 97.7$ тыс. человек. Для отчётного года $K_1 = 977$ млн ден. ед., $L_1 = 127.7$ тыс. человек. Подсчитать индексы изменения характеристик, масштаб и экономическую эффективность производства. Дать экономическую интерпретацию.
Задача 9. Производственная функция фирмы, выпускающая линолеум, имеет вид $Y=177 K^{0.356} L^{0.644}$.
Здесь $Y$ – сотни м*м, $K$ – тыс. ден. ед., $L$ – сотня рабочих (сот. р.).
Стоимость ресурсов W=5,13 тыс. ден. ед./сот. раб.
q = 10 тыс. ден. ед./тыс. ден. ед.
Издержки производства ограничены суммой C = 1770 тыс. ден. ед.
Найти максимальный выпуск продукции, оптимальное количество рабочих и стоимость капитальных фондов.
Построить график изокванты и изокосты. Отметить оптимальную точку.
Оценить, как изменится выпуск продукции, если:
а) увеличить заработную плату на 8%;
б) уменьшить цену на фонды в два раза;
в) ввести дополнительные инвестиции в производство в количестве 57,7 тыс. ден. ед.
Задача 10. Найти объем продукции, произведенной за период $[0;52]$, если функция Кобба-Дугласа имеет вид: $f(t)=(364+7t)e ^{1/104 t}$
Задача 11. 1. Выпуск продукции фирмой описывается функцией Кобба-Дугласа $Y=AK^{alpha}L^{1-alpha}$. Ставка заработной платы равна $p_L$, норма процента на используемый капитал — $p_K$.
2. По заданному уровню выпуска продукции $Y$ определить объемы факторов $K$ и $L$, при которых общие издержки будут минимальны, и величину этих издержек.
3. По известной величине общих издержек $TC$ определить объем факторов $K$ и $L$, обеспечивающие максимальный выпуск продукции, и соответствующий объем выпуска.
Задача 12. На основании следующих данных построить производственную функцию Кобба-Дугласа.
Здесь $Y_i$ — производственный национальный доход (млрд. руб.), $K_i$ — среднегодовые основные производственные фонды (млрд. руб.), $L_i$ — среднегодовая численность занятых в материальном производстве (млн. чел.). Имеется прогноз на 1997 год: основных производственных фондов $K_{1996}cdot N$ млн. руб. и трудовых ресурсов $L_{1996}cdot N$, где $N$ (номер) млн. чел. На основании полученной производственной функции сделать точечный прогноз национального дохода на 1997 год.
Задача 13. Производственная функция задается формулой $Q = 150 K^{0,9}L^{0,5}$, где Q — выпуск, K – капитал, L — труд.
Найти:
a) Предельные продукты труда и капитала при K=16, L=125.
б) Коэффициенты эластичности выпуска по труду и капиталу и объяснить их экономический смысл для полученных значений.
Заказать решение задач по микроэкономике просто!
Может быть интересно:
|
|
Экономический анализ деятельности предприятия на основе производственной функции Кобба-Дугласа
- Галиаскарова Г.Р.
Стерлитамакский филиал Башкирского государственного университета
кандидат наук,доцент
NovaInfo 61, с.217-221, скачать PDF
Опубликовано 2 марта 2017
Раздел: Экономические науки
Просмотров за месяц: 2
Аннотация
В статье приведен экономический анализ деятельности одной из крупнейших российских химических компаний по производству полиэтилена на основе производственной функции Кобба-Дугласа.
Ключевые слова
КАПИТАЛ, ТРУД, ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ, ЭЛАСТИЧНОСТЬ ВЫПУСКА
Текст научной работы
Эффективное планирование производства, прогнозирование выпуска продукции, повышение конкурентоспособности являются одними из главных задач современных предприятий. Использование математического моделирования помогает выделить и описать наиболее важные, существенные связи экономических объектов, оценить параметры производства.
В целях эффективного управления производством продукции необходимо знание количественных взаимосвязей между величиной вовлекаемых в производство ресурсов и объемом полученной продукции. Данная задача может быть решена с помощью аппарата производственных функций.
Производственная функция — это функция, описывающая зависимость результата производства от затраченных ресурсов.
Производственные функции используются как полезный инструмент, позволяющий проводить аналитические расчёты, определять эффективность использования ресурсов и целесообразность их дополнительного вовлечения в производство, прогнозировать объём выпуска продукции и контролировать реальность плановых проектов. С помощью производственных функций можно оценить эффективность функционирования системы и использования отдельных производственных факторов, определить возможности и последствия замещения одних факторов производства другими, найти влияние масштаба производства на его эффективность, изучить воздействие управленческих и технологических инноваций на производственные процессы.
В микроэкономике используется большое количество самых разнообразных функций производства, но чаще всего двухфакторные функции вида Z=F(x,y), которые легче анализировать в силу возможности их графического представления.
Своеобразным компромиссом между сложностью математической зависимости и областью применимости выступает производственная функция Кобба-Дугласа. Ее безусловными преимуществами являются относительная простота функциональной зависимости при достаточной практической универсальности и адекватности. Она строится на реальных экономических показателях и может быть легко параметризованна. Многочисленные исследования обеспечили ей популярность и широкое применение на практике, о чем свидетельствуют работы многих зарубежных и отечественных авторов [1,2].
Пользуясь программой Excel, подберем производственную функцию Кобба-Дугласа и осуществим экономический анализ одной из крупнейших российских химических компаний по производству полиэтилена.
Наша задача состоит в построении производственной функции Кобба-Дугласа, которая имеет вид:
Y=AK^alpha L^beta,
где — Y выпуск продукции (ВВП); К — капитал (основные фонды); L — труд (который может характеризоваться количеством работников); alpha — константа (коэффициент эластичности производства по капиталу К); beta — константа (коэффициент эластичности производства по труду L); А — коэффициент, который в простейшем случае является константой, которую часто связывают с уровнем технологий, хотя на самом деле, он может зависеть и от других факторов, не относящихся непосредственно к труду, или капиталу.
Будем использовать метод наименьших квадратов. Тогда задача будет выглядеть следующим образом:
sum e_i^2rightarrow min.
ei — есть отклонение расчетного значения от фактического при ограничениях:
alpha +beta =1;
A,alpha, beta > 0.
В качестве исходной базы для расчетов, будем использовать статистические данные предприятия с 2007 по 2016 год (таблица 1).
|
Год |
Выпуск (тн.) |
Труд (чел.) |
Капитал (тыс. руб.) |
|
2007 |
840000 |
9500 |
211400 |
|
2008 |
870000 |
9400 |
221800 |
|
2009 |
810000 |
9100 |
223600 |
|
2010 |
850000 |
9200 |
240100 |
|
2011 |
900000 |
9000 |
248000 |
|
2012 |
970000 |
9300 |
271300 |
|
2013 |
1032000 |
8750 |
260000 |
|
2014 |
1015000 |
8900 |
281500 |
|
2015 |
1260000 |
8700 |
283000 |
|
2016 |
1319000 |
8650 |
279100 |
С помощью Надстройки «Поиск решения» программы Excel, была решена задача оптимизации для нахождения параметров целевой функции. Были получены следующие значения:
A=7.5;
alpha =0.8;
beta =0.2.
Полученные результаты означают, что увеличение капитала на 1% приводит к росту выпуска предприятия на 0,8%, а приращение труда на 1% обусловливало увеличение выпуска на 0,2%. Тогда производственная функция Кобба-Дугласа будет иметь следующий вид:
Y=7.5cdot K^{0.8}cdot L^{0.2}.
Данная функция Кобба-Дугласа обладает известной ограниченностью, как, например, весь прирост продукта приписывается количественному росту факторов, допускается нейтральный технологический прогресс, предполагается единичная эластичность замещения.
Результаты аппроксимации значений Y приведены на рисунке 1, где Yr — значение годового оборота.
Средняя фондоотдача AY_K равна отношению произведенного продукта к величине затраченного капитала:
AY_K=frac{Y(K,L)}{K}=7.5cdot K^{-0.2}cdot L^{0.2}.
Средняя производительность труда AYL равна отношению произведенного продукта к величине затраченного труда:
AY_L=frac{Y(K,L)}{L}=7.5cdot K^{0.8}cdot L^{-0.8}.
Эластичность выпуска по капиталу равна:
varepsilon_K=0.8.
Если эластичность выпуска по фондам alpha больше эластичности выпуска по труду, предприятие имеет трудосберегающий (интенсивный) рост. Если выполняется обратное неравенство иbeta > alpha, то имеет место фондосберегающий (экстенсивный) рост предприятия, когда увеличение трудовых ресурсов на 1% приводит к большему росту объема производства, нежели такое же увеличении фондов.
Т.е. получили, что эластичность выпуска по капиталу равна 0.8, что равно показателю степени при капитале. В свою очередь, как эластичность производственной функции по труду равна 0.2. Следовательно, увеличение затрат капитала на 1% приведет к росту выпуска продукции на alpha процентов, а увеличение затрат труда на 1% приведет к росту выпуска на beta процентов.
По построенной производственной функции Кобба-Дугласа можно сделать вывод, что развитие исследуемого предприятия имеет трудосберегающий (интенсивный) рост. Если труд и капитал увеличиваются в некоторой пропорции, то выпуск растет в большей пропорции.
Читайте также
-
Факторы недооценки первичного публичного размещения
- Локтионов Н.О.
-
Социальная ответственность бизнеса на предприятии
- Артеменко А.П.
- Сабурова Л.В.
-
Проблемы формирования эффективной системы мотивации персонала
- Тимиргалеева Р.Р.
- Кузьмин В.
-
Теоретические подходы к трактовке понятия «инновации»
- Казанцев А.С.
-
Прогнозирование курса валюты на основе нейронных сетей
- Баранова М.А.
- Галиаскарова Г.Р.
Список литературы
- Колемаев В. А. Математическая экономика. – M.:ЮНИТИ-ДАНА, 2002. – 399 c.
- Терехов Л. Л. Производственные функции. – М.: Статистика, 1974. – 128с.
Цитировать
Баранова, М.А. Экономический анализ деятельности предприятия на основе производственной функции Кобба-Дугласа / М.А. Баранова, Г.Р. Галиаскарова. — Текст : электронный // NovaInfo, 2017. — № 61. — С. 217-221. — URL: https://novainfo.ru/article/11575 (дата обращения: 28.05.2023).
Поделиться
Содержание:
- Эластичность функции
- Определение и свойства эластичности функций
- Свойства эластичности функции
- Эластичность спроса относительно цены
- Эластичность предложения относительно цены
Эластичность функции
В экономических исследованиях приросты тех или иных показателей, характеризующих экономические процессы, чаще всего выражают в процентах к базовым значениям. Поэтому и изменение величин, которые связаны с ними функциональной зависимостью, также выражают в процентах. Для этого используют понятие эластичности функции, которое выражается через производную функции.
Определение и свойства эластичности функций
Пусть задана функция y = f (x). Если аргумент x получил приращение Δx и при этом функция y получила приращение Δy, то 

Определение. Предел отношения относительного приращения функции к относительному приращению аргумента при условии, что приращение аргумента стремится к нулю, если существует, называется эластичностью функции.
Обозначают эластичность функции y = f (x) относительно переменной x Ex(y). То есть,
Итак, если в точке x функция имеет производную, то эластичность определяется формулой 
Эластичность выражает приближенный процент приращения функции, который соответствует 1 % приращения аргумента.
Пример. Найти эластичность функции y = x2 – 4 x +7 и вычислить ее при x = 1, x = 2, x = 5.
Решение.
Итак, если x вырастет на 1 % с 1 до 1,01, то y снизится на 0,5 %. Если x вырастет на 1 % с 2 до 2,02, то значение переменной y практически не изменится. Если x вырастет на 1 % с 5 до 5,05, то y вырастет на 2,5 %.
Свойства эластичности функции
ТЕОРЕМА 1. Эластичность произведения двух функций равна сумме эластичности сомножителей:
Ex (U ⋅ V) = Ex (U) + Ex (V).
Доказательство. По определению эластичности
ТЕОРЕМА 2. Эластичность частного двух функций равна разности показателей эластичности делимого и делителя:
Доказательство. По определению эластичности
Эластичность спроса относительно цены
В анализе и прогнозах ценовой политики применяется понятие эластичности спроса и предложения.
Пусть p цена одного изделия, а Q — количество изделий, произведенных и проданных через некоторое время, что определяет спрос. Величина Q зависит от цены, т. е. Q является функцией от p: Q = f (p).
Пусть приращение цены Δp вызывает приращение ΔQ. тогда относительные приращения цены и спроса будут соответственно 
Отношение 
Эластичностью спроса относительно цены называется предел отношения относительного приращения спроса к относительному приращению цены при условии, что приращение цены стремится к нулю.
Эластичность спроса относительно цены приближенно определяет, как меняется спрос на данное изделие, если его цена возрастает на 1 %.
Так, например, если рост цены на 5 % вызывает падение спроса на 8 %, то эластичность будет
Если эластичность спроса η = –0,5, то 10 % роста стоимости товара вызывает падение спроса на (–0,5) 10% = –5%.
Определение. Если процент изменения спроса больше процента изменения цены (η < 1), то спрос называют эластичным, если процент изменения спроса меньше процента изменения цены (-1 < η < 0), то спрос называют не эластичным, а если процент изменения спроса равен проценту изменения цены (η = 1), то спрос называют нейтральным.
Пример. Установлено, что количество произведенных и проданных изделий Q по цене p определяется по формуле Q = 10000 – 500p (0 < p < 20). Определить, при какой цене спрос эластичный, нейтральный, не эластичный.
Решение. Эластичность спроса относительно цены
Спрос будет эластичным, если η < –1, 

Спрос нейтральный при цене p = 10 (руб.). Спрос будет не эластичный, когда -1 < η < 0.
Итак, спрос не эластичный при цене меньшей 10 руб. за изделие.
Пример 2. Установить связь между доходом предприятия и эластичностью спроса от цены.
Решение. Доход определяется как произведение стоимости каждого изделия на количество произведенных и проданных изделий Q : D (Q) = p⋅ Q.
Найдем маржинальный доход, учитывая, что Q есть функция от p.
Если η ≤ –1, то 1 + η < 0, а 
Если –1 < η < 0, то 1 + η > 0, а
То есть функция D (Q) дохода растет с ростом цены p, когда спрос не эластичный.
Эластичность предложения относительно цены
Понятие эластичности можно применять и к другим функциям экономического содержания.
Рассмотрим понятие эластичности предложения S в зависимости от цены товара p. Под предложением понимают количество некоторого товара, который предлагается на продажу за единицу времени. Как правило, предложение какого-либо товара является возрастающей функцией цены. Но бывают случаи, когда предложение повышается со снижением цены. Величина S является функцией от цены товара. То есть, S = S (p).
Пусть Δp — приращение цены, а ΔS — соответствующее приращение предложения. Тогда относительные приращения цены и предложения будут соответственно 

Эластичностью предложения относительно цены называется предел отношения относительного приращения предложения к относительному приращению цены при условии, что приращение цены стремится к нулю.
Эластичность предложения относительно цены приближенно определяет процент приращения предложения на 1 % приращения цены.
Пример 3. Функция предложения некоторого товара 
Решение.
Если p = 2, то
Следовательно, при цене p = 2 увеличение ее на 1 % вызовет увеличение предложения на 0,2 %.
Лекции:
- Разностные уравнения
- Случайная вероятность
- Эквивалентные бесконечно малые функции. Сравнение бесконечно больших функций
- Решение определённых интегралов
- Параллельные прямые
- Экстремум функции многих переменных
- Пределы в математике
- Дифференциал функции
- Объемы подобных фигур
- Алгебра логики