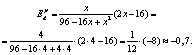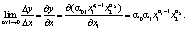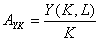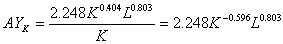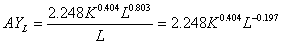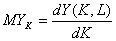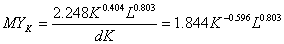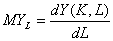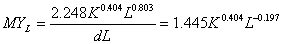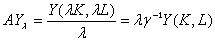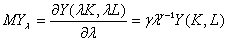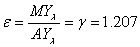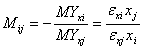Рассмотренные
в предыдущем подразделе экономические
понятия имеют размерность, что не вполне
удобно для анализа взаимосвязи
относительных изменений переменных.
Вводят понятия: эластичность
выпуска по труду EL
и эластичность выпуска по капиталу EK,
определяемые формулами
EL
=;
(2.6)
EK
=.
(2.7)
Безразмерные
показатели EL
и EK
показывают, на сколько процентов
произойдет относительное увеличение
выпуска при относительном увеличении
соответствующего ресурса на 1%.
Сумма
значений эластичности выпуска по всем
ресурсам называется эластичностью
производства:
E
= EK
+ EL.
(2.8)
Для
эластичности
KL
предельной
нормы замещения труда капиталом
справедливо соотношение:
KL
=
(2.9)
Эффективность
производственного процесса (эффект от
масштаба производства) можно оценить
математически, увеличив одновременно
все ресурсы в t
раз. Если
использовать более общую аппроксимирующую
формулу Кобба—Дугласа
Q
= AKL,
получаем: Q
(tK,
tL)
= AKtLt
= tt
Q
(K,
L)
= t+
Q
(K,
L).
Отсюда вытекает, что если
и
в сумме превышают единицу, то говорят,
что производственная функция имеет
возрастающий эффект от масштаба
производства (если ресурсы K
и L увеличиваются
в некоторой пропорции, то выпуск Q
растет в большей пропорции). Если их
сумма меньше, чем единица, то имеет место
убывающий эффект от масштаба производства.
В
своей первой статье Ч. Коббс и П. Дуглас
описывали производственную функцию в
виде (2.1), предполагающем постоянную
отдачу от масштаба:
и
в сумме точно составляют единицу.
Впоследствие они ослабили это допущение,
предпочитая оценивать степень отдачи
от масштаба производства. Как указывалось
нами ранее, при обработке исходных
данных, использованных Ч. Коббсом и П.
Дугласом, методом наименьших квадратов,
получаем значения
= 0,23 и
= 0,81. Сумма
и ,
равная 1,04, лишь несколько превышает
единицу, т.е. первоначальное предположение
Ч. Коббса и П. Дугласа о постоянной отдаче
от масштаба было вполне оправдано.
Пример
4. Рассчитать
эластичность выпуска по труду и капиталу
для производственной функции Q
= K1/4L3/4
в точке K
= 2, L
= 3. Оценить эффект от масштаба производства.
Решение.
Эластичность выпуска по труду определяется
формулой (2.6). Так как предельный продукт
труда
=
=3/4
,
получаем:
EL
==
=
(3/4
)
= (L /
K1/4L3/4)(3/4)
= 3/4.
Эластичность
выпуска по капиталу определяется
формулой (2.7). Так как предельный продукт
капитала
=
=1/4
,
получаем:
EK
==
=
(1/4
)
= (K
/ K1/4L3/4)(1/4)
= 1/4.
Таким
образом, эластичность выпуска по труду
и капиталу в случае производственной
функции Кобба—Дугласа
вида Q
= AKL
не зависит от точки производства и равна
показателям степени при соответствующих
переменных
= 0,75 и
= 0,25 соответственно.
Сумма
значений эластичности выпуска по всем
ресурсам (эластичность производства)
равна
+
= 1, т.е. в данном случае имеет место
постоянная отдача от масштаба производства.
Для
эластичности KL
предельной нормы замещения труда
капиталом в общем случае производственной
функции вида
Q = AKL
получаем:
KL
=

1,
т.е.
для функции Кобба—Дугласа
эластичность предельной нормы замещения
труда капиталом постоянна и равна
единице. Это важнейшее свойство функции
Кобба—Дугласа.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Авторы
- Файлы
- Литература
Попова Е.С
1
Дырдасова А.С.
1
1 Самарский государственный экономический университет
1. Предельный анализ в экономике. Эластичность функции [Электронный ресурс]. – Режим доступа: http://www.mathelp.spb.ru/book1/lim_an_ec.htm. – (Дата обращения: 16.12.2015).
2. Яшина Ю.Е, Карнавская Н.В., Чехута В.А. и др. Эластичность функции и ее применение экономике [Электронный ресурс] / Ю.Е. Яшина, Н.В. Карнавская, В.А. Чехута и др./ Международный студенческий научный вестник: эл.науч.журн. – 2015. – №3. – Режим доступа: http://www.eduherald.ru/140–14166. – (Дата обращения:16.12.2015).
На современном этапе развития человечества одну из ведущих ролей в развитии общества играют экономические отношения, поскольку именно они являются той материальной основой, которая в свою очередь делает возможным формирование и развитие различных общественных институтов. Для наиболее полного изучения экономических явлений и процессов, происходящих в обществе, экономическая теория использует различные методы, прибегая к «помощи» других не менее важных наук. Одной из таких наук является математический анализ. Одними из базовых, ключевых понятий в экономической теории являются такие широко известные категории как спрос и предложение, которые, в свою очередь, обладают определенными признаками и свойствами, что и является главным предметом экономической теории. Спрос и предложение товаров обладают различной степенью чувствительности к изменению определяющих их факторов. Мерой такого изменения является эластичность спроса и эластичность предложения. В свою очередь, выделяется несколько основных видов эластичности: ценовая эластичность, эластичность по доходу и перекрестная эластичность.
Ценовая (прямая) эластичность спроса (предложения) показывает, какое процентное изменение спроса (предложения) последует за однопроцентным изменением цены товара.
Эластичность спроса по доходу показывает, какое процентное изменение спроса последует за однопроцентным изменением дохода потребителя.
Перекрестная эластичность спроса показывает, какое изменение спроса на товар A последует за однопроцентным изменением цены товара B, при условии, что товары A и B являются комплементарными (комплементами) или взаимозаменяемыми (субститутами). Количественным выражением эластичности спроса и предложения является коэффициент эластичности E, который рассчитывается в одной точке кривой спроса и предложения или на дуге этой кривой.
Эластичностью функции 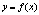
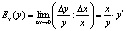
Таким образом, эластичность функции можно вычислить по формуле
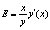
Эластичность функции также называется относительной производной. Эластичность функции по аргументу показывает, на сколько процентов изменится значение функции при изменении аргумента в точке x на 1 %. Пусть спрос задан функцией Q(d)=96–16P+P2, необходимо определить ценовую точечную эластичность спроса по цене при P=4.
Найдем первую производную функции
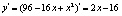
Подставим полученное выражение в формулу эластичности:
Таким образом, при изменении цены на 1 % величина спроса изменяется на 0,7 %. Спрос неэластичен.
Также в качестве примера можно рассмотреть производственную функцию Кобба-Дугласа. Данная функция устанавливает зависимость между величиной созданного общественного продукта и совокупными затратами живого труда, а также суммарным объемом применяемых производственных фондов.
Данная функция имеет следующий вид
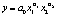
где a0 – коэффициент, 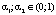
Каждый из используемых ресурсов характеризуется средней и предельной величинами. средняя производительность труда показывает, сколько единиц продукции приходится на единицу труда. Предельная производительность труда показывает, сколько дополнительных единиц продукции приносит дополнительная единица труда.
Рассчитаем вторую частную производную:
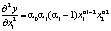
Вторая частная производная отрицательна, а значит, предельная производительность с увеличением 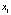
Для производственной функции Кобба-Дугласа предельная производительность всегда меньше средней.
Кроме того, можно определить показатель, характеризующий относительный прирост объема производства на единицу относительно увеличения труда
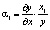
Полученный показатель называется эластичностью выпуска продукции по затратам труда. Он показывает, на сколько процентов увеличивается выпуск продукции при увеличении затрат труда на 1 %.
Подобные показатели можно рассчитать и для производственных фондов. Объем продукции в расчете на единицу производственных фондов называется фондоотдачей. Можно рассчитать среднюю и предельную фондоотдачу. Из функции Кобба_Дугласа имеем
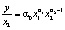
Предельная фондоотдача равна частной производной выпуска продукции по объему фондов:
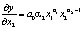
Предельная фондоотдача всегда ниже средней.
Относительная фондоотдача (эластичность выпуска продукции по объему производственных фондов) определяется как
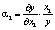
Если производственная функция задана формулой
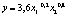
где y – объем продукции в стоимостном выражении, x1 – фонд заработной платы, x2 – стоимость основных производственных фондов. 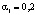
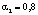
Библиографическая ссылка
Попова Е.С, Дырдасова А.С. ЭЛАСТИЧНОСТЬ В ПРОИЗВОДСТВЕННЫХ ФУНКЦИЯХ // Международный студенческий научный вестник. – 2016. – № 4-4.
;
URL: https://eduherald.ru/ru/article/view?id=16408 (дата обращения: 27.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Инна Смирнова
Эксперт по предмету «Экономика»
преподавательский стаж — 15 лет
Задать вопрос автору статьи
Назначение производственной функции
Определение 1
Производство с точки зрения экономики представляет собой процесс применения технологий и ресурсов для получения продуктов, предназначенных для продажи.
Таким образом, это процесс создания товара и услуги, которая обладает определенной полезностью для покупателей. Любая деятельность по производству товаров и услуг является деятельностью направленной на удовлетворения потребностей отдельных индивидов или общества в целом.
Соотношение платежеспособного спроса на товары и предложения определяет цену товара или услуги. Количественной характеристикой предложения или объема производства и стоимости товаров является производственная функция. Производственный процесс оказывает прямое влияние на благосостояние общества в целом: чем выше степень удовлетворения индивидуальных и общественных потребностей и удельный вес среднего класса в общем численности населения, тем выше уровень национального благосостояния и развития.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Задача производственной функции состоит в том, чтобы объяснить рост благосостояния общества в процессе выпуска товаров и услуг.
Функция Кобба-Дугласа в системе производственных функций
Замечание 1
Значение производственных функций выражается в создании экономико-математических моделей, характеризующих зависимость объема производства от его различных факторов или их соотношения в условиях национального хозяйства.
Эти модели включают в себя такие показатели как объем производства в натуральном или стоимостном выражении, затраченные объемы ресурсов (факторов производства).
Различают две разновидности производственных функций:
- во-первых, однофакторные, устанавливающие зависимость объема производства от одного фактора. К этой разновидности относятся линейная, параболическая, степенная и показательная функции;
- во-вторых, двухфакторные устанавливающие зависимость объема производства от соотношения двух факторов. К этой разновидности относятся функции Кобба-Дугласа, Леонтьева, Солоу, Аллена.
«Производственная функция Кобба-Дугласа» 👇
Особенности производственной функции Кобба-Дугласа
В качестве двух основных факторов производства выступают капитал и труд. Определенная пропорциональность их сочетания создает условия для получения продукта. Назначение производственной функции Кобба-Дугласа состоит в том, чтобы отражать технологическое соотношение объема труда и капитала, необходимое для производства того или иного товара в необходимом количестве.
Данная производственная функция является двухфакторной. Впервые ее предложил шведский экономист Кнут Векселль, но статистическая проверка была выполнена в период с 1927 по 1947 год двумя учеными – Чарльзом Коббом и Полом Дугласом (в 1928 году вышла их работа под названием «Теория производства»). Именно фамилии этих ученых и дали название производственной функции.
Также термин «производственная функция Кобба-Дугласа» в узком смысле применяется для обозначения постоянной отдачи от масштаба.
Производственная функция, разработанная Коббом и Дугласом, представляет собой первую функцию агрегированного производства. Ее применение позволило осуществлять моделирование не только мелкомасштабных процессов, но и целых отраслей экономики. Статистическое подтверждение данной функции стало началом нового этапа макроэкономического развития, позволяющего дать оценку эффективности производства на уровне национального хозяйства.
Формула производственной функции Кобба-Дугласа
В формуле производственной функции Кобба-Дугласа отражается зависимость объем производства определенного товара от сочетания двух факторов производства – труда и капитала.
В общем виде формула имеет следующий вид:
$Q = A • L^α • K^β$, где:
- $Q$ – показатель объема производства, характеризующий реальную стоимость товаров и услуг, произведенных в определенный период времени;
- $A$ – общий показатель технологической продуктивности факторов. Этот показатель является наиболее трудным для определения и предусматривает с определенным уровнем погрешности возможность несовершенства оценки вклада труда и капитала, а также влияние иных факторов;
- $L$ – затраты труда в производство определенного объема продукции, выражающиеся в количестве человеко-часов, отработанных всеми работниками за указанный период времени;
- $K$ – затраты вложенного капитала в производство определенного объема продукции, выражающиеся в реальной стоимости оборудования и машин, используемых в производстве;
- $α$ – технологическая эластичность труда;
- $β$ – технологическая эластичность капитала.
Основу данной формулы составляют статистические расчеты, свидетельствующие о том, что для развитых стран характерны постоянные доли вкладов труда и капитала на протяжении длительного времени. Однако в настоящее время данное утверждение подвергается сомнению.
Эластичность факторов производства в производственной функции Кобба-Дугласа
Важнейшими показателя производственной функции Кобба-Дугласа являются показатели эластичности факторов производства, которые отражают влияние изменения их соотношения на физический объем производства при иных равных условиях.
Возможны три варианта значений, принимаемых коэффициентами эластичности в рамках формулы:
- $α + β = 1$, данное соотношение характеризует постоянную отдачу от масштаба, например, при росте затраченного труда и капитала на 100%, объем производства возрастет на те же 100%, то есть в два раза. производственная функция является линейно однородной;
- $α + β > 1$, данное соотношение характеризует возрастающую отдачу от масштаба, например, при росте затраченного труда и капитала на 100%, объем производства возрастет, допустим, на 120%, то есть более чем в два раза;
- $α + β$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Производственная функция Кобба-Дугласа
Назначение сервиса . Онлайн-калькулятор предназначен для анализа производственной функции Кобба-Дугласа:
- нахождение средней фондоотдачи и средней производительности труда, вычисление предельной фондоотдачи и предельной производительности труда;
- расчет эластичности продукта и эластичности масштаба производства;
- определение предельной нормы замещения факторов производства, построение изоклины.
- Решение онлайн
- Видеоинструкция
- Оформление Word
Свойства производственной функции
- Производственная функция должна задаваться положительно определенной, дважды дифференцируемой по всем своим аргументам функцией.
- Производственная функция обращается в нуль, если отсутствует хотя бы один из ресурсов x1, x2, . ,xn.
Невозможно полностью заменить один фактор производства комбинацией других факторов. Возможно лишь частичное замещение одного фактора другими в некоторой ограниченной области. - С увеличением любого из ресурсов объем производства возрастает dY/dxi.
- При увеличении любого из ресурсов предельная эффективность является убывающей функцией.
- Производство должно обладать свойством масштабируемости: при одновременном увеличении всех затрат в λ раз количество произведенного продукта также должно увеличиться в λ раз.
Пример . Производственные функции, обладающие свойствами 2 – 5, называются неоклассическими.
Y = 2.248K 0.404 L 0.803
Степень однородности этой производственной функции γ = 0.404 + 0.803 = 1.207. Это означает, что при увеличении капитальных и трудовых затрат в λ раз объем производства увеличится в λ 1.207 раз, что характерно для развивающейся экономики.
Средняя фондоотдача AYK равна отношению произведенного продукта к величине затраченного капитала:
Средняя производительность труда AYL равна отношению произведенного продукта к величине затраченного труда L:
Предельная фондоотдача находится как производная объема произведенного продукта Y по величине затраченного капитала K:
Предельную производительность труда, или предельный продукт труда, MYL определим как частную производную продукта Y по величине затраченного труда L:
Эластичность продукта по фактору.
Коэффициентом эластичности продукта по i-фактору называется относительное изменение продукта, выраженное в процентах, при относительном увеличении i-фактора на 1%.
Эластичность по i-фактору равна отношению предельного продукта к среднему продукту по этому фактору.
эластичность производственной функции по фондам равна εK = α = 0.404
эластичность производственной функции по труду равна εL = β = 0.803
Если эластичность выпуска по фондам α больше эластичности выпуска по труду, экономика имеет трудосберегающий (интенсивный) рост. Если выполняется обратное неравенство и β > α, то имеет место фондосберегающий (экстенсивный) рост экономики, когда увеличение трудовых ресурсов на 1% приводит к большему росту объема производства, нежели такое же увеличении фондов.
Эластичность масштаба производства.
Средним продуктом масштаба производства называется отношение продукта, полученное при увеличении факторов производства в λ раз, к коэффициенту масштабирования λ :
AYλ = λ 0.207 2.248K 0.404 L 0.803
Предельный продукт масштаба производства определяется как прирост продукции при изменении масштаба производства на единицу:
MYλ = 0.207 λ 0.207 2.248K 0.404 L 0.803
Коэффициентом эластичности масштаба производства называется отношение предельного продукта масштаба к среднему продукту масштаба:
Таким образом, коэффициент эластичности масштаба производства всегда равен степени однородности производственной функции.
Предельная норма замещения факторов производства.
Предельную норму замещения i-фактора производства j-фактором Mij определим соотношением:
Для нашей модели:
Норма замещения фондов трудовыми ресурсами в явном виде: RSTK,L = L / K
Норма замещения трудовых ресурсов производственными фондами в явном виде: RSTL,K = K / L
Назовем изоклиной множество точек области определения производственной функции, для которых предельная норма замещения i-го фактора производства j-м постоянна.
Для наших данных получаем искомое уравнение семейства изоклин:
K = 1.988MLK • L
Как и следовало ожидать, семейство изоклин является семейством прямых линий, выходящих из начала координат. Каждому значению предельной нормы замещения труда капиталом соответствует своя линия.
На рис. изображены две изоклины семейства для значений MLK = 5 и MLK = 2.
Производственная функция Кобба-Дугласа. Изокванты и изокосты
Факторы производства и производственная функция
В современном мире нам не удастся выжить, орудуя одной лишь «палкой-копалкой», верно служившей нашим далёким предкам. Стол, кресло, компьютер, одежда, посуда, — всё стало настолько сложным, что одному человеку никак не справиться, и одновременно настолько простым, что десятки тысяч этих товаров каждую секунду сходят с конвейеров по всему миру.
Чтобы произвести что-нибудь, нужны ресурсы: сырьё, материалы, оборудование, энергия, информация, деньги, труд людей.
Факторы производства – это используемые в процессе производства ресурсы.
В простейшей модели производства рассматривают два основных фактора:
Результат производства – это некоторое количество Q выпущенного продукта.
Производственная функция – это зависимость количества выпущенного продукта от величины затрат факторов производства:
Пусть $Q = 1,5 sqrt$.
Тогда при затратах K = 100 ед. капитала и L = 16 ед. труда, будет получено $Q = 1,5 cdot sqrt <100 cdot 16>= 1,5 cdot 10 cdot 4 = 60$ ед. продукции.
Степенная производственная функция Кобба-Дугласа
Производственные функции можно строить по-разному.
Часто используется модель, в которой оба фактора – труд и капитал – входят в виде произведения степеней:
где A – технологический коэффициент (зависит от применяемой технологии);
$0 le a le 1$ — коэффициент эластичности.
Такие производственные функции называют функциями Кобба-Дугласа в честь американских исследователей, которые получили:
в 1927 году для обрабатывающей промышленности США.
Свойства производственной функции Кобба-Дугласа:
1. Если K = 0 или L = 0, то Q = 0, т.е. производство невозможно при отсутствии хотя бы одного фактора производства.
2. При увеличении затрат фактора производства, величина выпуска продукции возрастает: $K uparrow Rightarrow Q uparrow, L uparrow Rightarrow Q uparrow$
Тогда при затратах K=81 ед. капитала и L=16 ед. труда, будет получено $Q = 2,5 cdot sqrt[4] <81 cdot 16^3>= 2,5 cdot 3 cdot 8 = 60$ ед. продукции.
Изокванты – линии равного выпуска
Пусть предприятие планирует выпустить $Q_0$ единиц продукции.
В этом случае, мы можем найти зависимость затрат капитала от затрат труда.
Эту зависимость можно изобразить на плоскости LOK в виде кривой.
Для каждого плана выпуска будет отдельная кривая.
Множество точек (L;K) на плоскости LOK, которые соответствуют одному плану выпуска, называют изоквантой или линией равного выпуска .
Построим изокванты для $Q_0 = <25;50;75;100 >$ единиц готовой продукции.
1. Чем больше используется труда, тем меньше нужно капитала для производства заданного количества продукции. И наоборот: чем меньше труда, тем больше капитала. Труд и капитал взаимно заменяют друг друга.
2. Через каждую точку (L;K) проходит единственная изокванта.
3. Изокванты, соответствующие разным количествам продукции $Q_1 neq Q_2$, не пересекаются.
Изокосты – линии равной стоимости
Согласно полученному выше графику, произвести $Q_0$ = 100 единиц продукции можно потратить 50 единиц труда и 20 единиц капитала, или же по 40 единиц труда и капитала, или же множество других сочетаний L и K.
Как нам определить, какое из сочетаний будет самым удачным? Очевидно, исходя из цены каждого ресурса. Пусть r — цена единицы капитала, а w – цена единицы труда. Тогда для некоторого набора ресурсов (L,K ), их общая стоимость:
На плоскости LOK это будет прямая с угловым коэффициентом $k = -frac$.
Множество точек (L;K) на плоскости LOK, которые соответствуют одной величине затрат на ресурсы (бюджету), называют изокостой или линией равной стоимости .
Пусть цена ресурсов r = 5, w = 3.
Построим изокосты для общей суммы затрат C =
$$ frac = frac<3> <5>= 0,6, frac = frac <5>= 0,2C, K = -0,6L+0,2C $$
1. Угловой коэффициент изокосты равен отношению цен на ресурсы $k = -frac$.
2. Изокоста для данного бюджета затрат C проходит через точки $(frac,0)$ и $(0;frac)$.
3. Для заданных цен на ресурсы изокосты для $C_1 neq C_2$ являются параллельными прямыми.
План производства с минимальными затратами на ресурсы
Теперь поставим главную задачу:
При заданном плане производства $Q_0$, известных ценах на ресурсы r и w, найти такое сочетание труда L и капитала K, при котором затраты на эти ресурсы минимальны:
$$ <left< begin Q_0 = A cdot K^a L^ <1-a>\ C = wL+rK rightarrow min end right.> $$
При заданном плане производства $Q_0$, известных ценах на ресурсы r и w, затраты на ресурсы будут минимальными в точке $(L_0,K_0)$, в которой изокоста $C_0 (L_0,K_0)$ является касательной для изокванты $Q_0 (K,L)$, т.е. имеет с ней только одну общую точку.
Величина затрат для оптимальной изокванты:
Оптимальный объем ресурсов:
Пусть $Q = 2,5 cdot K^frac<1> <4>L^frac<3><4>$. План выпуска продукции $Q_0 = 100$ единиц.
Цена ресурсов r = 5, w = 3.
Найти оптимальное отношение труда к капиталу $frac$, при котором затраты на ресурсы будут минимальными.
$$ = 40 cdot 2^2 cdot sqrt[4] <5>= 160 sqrt[4] <5>$$
Оптимальный объем ресурсов:
Объем труда в 5 раз больше объема капитала при оптимальных затратах.
В плоскости LOK:
Таким образом, точка $(40 sqrt[4]<5>;8 sqrt[4]<5>)$ является точкой касания изокосты с минимальным бюджетом затрат $C_0 = 160 sqrt[4]<5>$ и изокванты с планом выпуска $Q_0 = 100$.
Производственная функция Кобба-Дугласа
Вы будете перенаправлены на Автор24
Назначение производственной функции
Производство с точки зрения экономики представляет собой процесс применения технологий и ресурсов для получения продуктов, предназначенных для продажи.
Таким образом, это процесс создания товара и услуги, которая обладает определенной полезностью для покупателей. Любая деятельность по производству товаров и услуг является деятельностью направленной на удовлетворения потребностей отдельных индивидов или общества в целом.
Соотношение платежеспособного спроса на товары и предложения определяет цену товара или услуги. Количественной характеристикой предложения или объема производства и стоимости товаров является производственная функция. Производственный процесс оказывает прямое влияние на благосостояние общества в целом: чем выше степень удовлетворения индивидуальных и общественных потребностей и удельный вес среднего класса в общем численности населения, тем выше уровень национального благосостояния и развития.
Задача производственной функции состоит в том, чтобы объяснить рост благосостояния общества в процессе выпуска товаров и услуг.
Функция Кобба-Дугласа в системе производственных функций
Значение производственных функций выражается в создании экономико-математических моделей, характеризующих зависимость объема производства от его различных факторов или их соотношения в условиях национального хозяйства.
Эти модели включают в себя такие показатели как объем производства в натуральном или стоимостном выражении, затраченные объемы ресурсов (факторов производства).
Различают две разновидности производственных функций:
- во-первых, однофакторные, устанавливающие зависимость объема производства от одного фактора. К этой разновидности относятся линейная, параболическая, степенная и показательная функции;
- во-вторых, двухфакторные устанавливающие зависимость объема производства от соотношения двух факторов. К этой разновидности относятся функции Кобба-Дугласа, Леонтьева, Солоу, Аллена.
Готовые работы на аналогичную тему
Особенности производственной функции Кобба-Дугласа
В качестве двух основных факторов производства выступают капитал и труд. Определенная пропорциональность их сочетания создает условия для получения продукта. Назначение производственной функции Кобба-Дугласа состоит в том, чтобы отражать технологическое соотношение объема труда и капитала, необходимое для производства того или иного товара в необходимом количестве.
Данная производственная функция является двухфакторной. Впервые ее предложил шведский экономист Кнут Векселль, но статистическая проверка была выполнена в период с 1927 по 1947 год двумя учеными – Чарльзом Коббом и Полом Дугласом (в 1928 году вышла их работа под названием «Теория производства»). Именно фамилии этих ученых и дали название производственной функции.
Также термин «производственная функция Кобба-Дугласа» в узком смысле применяется для обозначения постоянной отдачи от масштаба.
Производственная функция, разработанная Коббом и Дугласом, представляет собой первую функцию агрегированного производства. Ее применение позволило осуществлять моделирование не только мелкомасштабных процессов, но и целых отраслей экономики. Статистическое подтверждение данной функции стало началом нового этапа макроэкономического развития, позволяющего дать оценку эффективности производства на уровне национального хозяйства.
Формула производственной функции Кобба-Дугласа
В формуле производственной функции Кобба-Дугласа отражается зависимость объем производства определенного товара от сочетания двух факторов производства – труда и капитала. В общем виде формула имеет следующий вид:
$Q = A • L^α • K^β$, где:
- $Q$ – показатель объема производства, характеризующий реальную стоимость товаров и услуг, произведенных в определенный период времени;
- $A$ – общий показатель технологической продуктивности факторов. Этот показатель является наиболее трудным для определения и предусматривает с определенным уровнем погрешности возможность несовершенства оценки вклада труда и капитала, а также влияние иных факторов;
- $L$ – затраты труда в производство определенного объема продукции, выражающиеся в количестве человеко-часов, отработанных всеми работниками за указанный период времени;
- $K$ – затраты вложенного капитала в производство определенного объема продукции, выражающиеся в реальной стоимости оборудования и машин, используемых в производстве;
- $α$ – технологическая эластичность труда;
- $β$ – технологическая эластичность капитала.
Основу данной формулы составляют статистические расчеты, свидетельствующие о том, что для развитых стран характерны постоянные доли вкладов труда и капитала на протяжении длительного времени. Однако в настоящее время данное утверждение подвергается сомнению.
Эластичность факторов производства в производственной функции Кобба-Дугласа
Важнейшими показателя производственной функции Кобба-Дугласа являются показатели эластичности факторов производства, которые отражают влияние изменения их соотношения на физический объем производства при иных равных условиях.
Возможны три варианта значений, принимаемых коэффициентами эластичности в рамках формулы:
- $α + β = 1$, данное соотношение характеризует постоянную отдачу от масштаба, например, при росте затраченного труда и капитала на 100%, объем производства возрастет на те же 100%, то есть в два раза. производственная функция является линейно однородной;
- $α + β > 1$, данное соотношение характеризует возрастающую отдачу от масштаба, например, при росте затраченного труда и капитала на 100%, объем производства возрастет, допустим, на 120%, то есть более чем в два раза;
- $α + β$
http://reshator.com/sprav/algebra/9-klass/proizvodstvennaya-funkciya-kobba-duglasa-izokvanty-i-izokosty/
http://spravochnick.ru/ekonomika/proizvodstvennaya_funkciya_kobba-duglasa/