Как найти эластичность замещения - Исправление недочетов и поиск решений вместе с Examum.ru

На
основании вышеизложенного можно сделать
вывод о том, что основным вопросом
производственной функции является
вопрос правильной комбинации факторов
производства, при которой уровень
выпуска продукции будет оптимальный,
то есть, приносящий наибольшую прибыль.
В целях поиска оптимальной комбинации,
необходимо ответить на вопрос: На какую
величину надо увеличить затраты одного
фактора при снижении затрат другого на
единицу. Вопрос соотношения затрат
замещающих друг друга факторов
производства решается при помощи
введения такого понятия, как эластичность
замещения факторов производства.

Эластичность
замещения – это соотношение затрат
замещающих друг друга факторов
производства при неизменном объёме
выпуска продукции. Это своего рода
коэффициент, который показывает степень
эффективности замещения одного фактора
производства другим.

Мерой взаимозаменяемости
факторов производства служит предельная
норма технического замещения MRTS (marginal
rate of technical substitution), которая показывает,
на сколько единиц можно уменьшить один
из факторов при увеличении другого
фактора на единицу, сохраняя выпуск
неизменным.

Предельную
норму технического замещения характеризует
наклон изоквант. Более крутой наклон
изокванты показывает что, при увеличении
количества труда на единицу, нужно будет
отказаться от нескольких единиц капитала
для сохранения данного уровня производства.
MRTS выражается формулой:

MRTS_L_,_K=–K/L

Величина	Значение
MRTS_L,K	Предельная норма технического замещения факторов
K	Изменение фактора K (Капитал)
L	Изменение фактора L (труд)

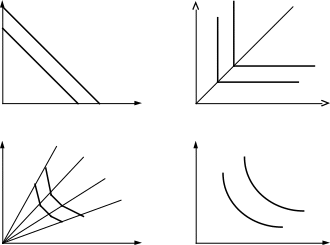
Изокванты могут
иметь различную конфигурацию.

Линейная
изокванты на рисунке 1.2,а предполагает
совершенную замещаемость производственных
ресурсов, то есть, данный выпуск может
быть получен с помощью либо только
труда, либо только капитала, либо с
помощью комбинации этих ресурсов.

Изокванта,
представленная на рисунке 1.2,б характерна
для случая жесткой дополняемости
ресурсов. В этом случае известен лишь
один технически эффективный способ
производства. Такую изокванту иногда
называют изоквантой леонтьевского типа
(см. далее), по имени экономиста В.В.
Леонтьева, предложившего такой тип
изокванты. На рисунке 1.2,в показана
ломаная изокванта, предполагающая
наличие нескольких методов производства
(P). При этом предельная норма технического
замещения при движении вдоль изокванты
сверху вниз убывает. Изокванта подобной
конфигурации используется в линейном
программировании – методе экономического
анализа. Ломаная изокванта реалистично
представляет производственные возможности
современных производств. Наконец, на
рисунке 1.2,г представлена изокванта,
предполагающая возможность непрерывной,
но не совершенной замещаемости ресурсов.

K
а)
K Q₂б)

Q₁

Q₁
Q₂

0
L
0
L

K
P₁в) K
г)

P₂

Q₂

Q₁

Q₁P₃

P₄

0
L
0
L

Рисунок 1.2
Возможные конфигурации изоквант

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

From Wikipedia, the free encyclopedia

Elasticity of substitution is the ratio of percentage change in capital-labour ratio with the percentage change in Marginal Rate of Technical Substitution.^[1] In a competitive market, it measures the percentage change in the two inputs used in response to a percentage change in their prices.^[2] It gives a measure of the curvature of an isoquant, and thus, the substitutability between inputs (or goods), i.e. how easy it is to substitute one input (or good) for the other.^[3]

History of the concept[edit]

John Hicks introduced the concept in 1932. Joan Robinson independently discovered it in 1933 using a mathematical formulation that was equivalent to Hicks’s, though that was not implemented at the time.^[4]

Definition[edit]

The general definition of the elasticity of X with respect to Y is ${displaystyle E_{Y}^{X}={frac {% {mbox{change in X}}}{% {mbox{change in Y}}}}}$ , which reduces to ${displaystyle E_{Y}^{X}={frac {dX}{dY}}{frac {Y}{X}}}$ for infinitesimal changes and differentiable variables. The elasticity of substitution is the change in the ratio of the use of two goods with respect to the ratio of their marginal values or prices. The most common application is to the ratio of capital (K) and labor (L) used with respect to the ratio of their marginal products ${displaystyle MP_{K}}$ and ${displaystyle MP_{L}}$ or of the rental price (r) and the wage (w). Another application is to the ratio of consumption goods 1 and 2 with respect to the ratio of their marginal utilities or their prices. We will start with the consumption application.

Let the utility over consumption be given by and let ${displaystyle U_{c_{i}}=partial U(c_{1},c_{2})/partial {c_{i}}}$ . Then the elasticity of substitution is:

$E_{21} =frac{d ln (c_2/c_1) }{d ln (MRS_{12})} =frac{d ln (c_2/c_1) }{d ln (U_{c_1}/U_{c_2})} =frac{frac{d (c_2/c_1) }{c_2/c_1}}{frac{d (U_{c_1}/U_{c_2})}{U_{c_1}/U_{c_2}}} =frac{frac{d (c_2/c_1) }{c_2/c_1}}{frac{d (p_1/p_2)}{p_1/p_2}}$

where MRS is the marginal rate of substitution. (These differentials are taken along the isoquant that passes through the base point. That is, the inputs $c_{1}$ and $c_{2}$ are not varied independently, but instead one input is varied freely while the other input is constrained to lie on the isoquant that passes through the base point. Because of this constraint, the MRS and the ratio of inputs are one-to-one functions of each other under suitable convexity assumptions.) The last equality presents $MRS_{12} = p_1/p_2$ , where are the prices of goods 1 and 2. This is a relationship from the first order condition for a consumer utility maximization problem in Arrow–Debreu interior equilibrium, where the marginal utilities of two goods are proportional to prices. Intuitively we are looking at how a consumer’s choices over consumption items change as their relative prices change.

Note also that $E_{21} = E_{12}$ :

${displaystyle E_{21}={frac {dln(c_{2}/c_{1})}{dln(U_{c_{1}}/U_{c_{2}})}}={frac {dleft(-ln(c_{2}/c_{1})right)}{dleft(-ln(U_{c_{1}}/U_{c_{2}})right)}}={frac {dln(c_{1}/c_{2})}{dln(U_{c_{2}}/U_{c_{1}})}}=E_{12}}$

An equivalent characterization of the elasticity of substitution is:^[5]

$E_{21} =frac{d ln (c_2/c_1) }{d ln (MRS_{12})} =-frac{d ln (c_2/c_1) }{d ln (MRS_{21})} =-frac{d ln (c_2/c_1) }{d ln (U_{c_2}/U_{c_1})} =-frac{frac{d (c_2/c_1) }{c_2/c_1}}{frac{d (U_{c_2}/U_{c_1})}{U_{c_2}/U_{c_1}}} =-frac{frac{d (c_2/c_1) }{c_2/c_1}}{frac{d (p_2/p_1)}{p_2/p_1}}$

In discrete-time models, the elasticity of substitution of consumption in periods and t+1 is known as elasticity of intertemporal substitution.

Similarly, if the production function is then the elasticity of substitution is:

$sigma_{21} =frac{d ln (x_2/x_1) }{d ln MRTS_{12}} =frac{d ln (x_2/x_1) }{d ln (frac{df}{dx_1}/frac{df}{dx_2})} =frac{frac{d (x_2/x_1) }{x_2/x_1}}{frac{d (frac{df}{dx_1}/frac{df}{dx_2})}{frac{df}{dx_1}/frac{df}{dx_2}}} =-frac{frac{d (x_2/x_1) }{x_2/x_1}}{frac{d (frac{df}{dx_2}/frac{df}{dx_1})}{frac{df}{dx_2}/frac{df}{dx_1}}}$

where MRTS is the marginal rate of technical substitution.

The inverse of elasticity of substitution is elasticity of complementarity.

Example[edit]

Consider Cobb–Douglas production function $f(x_1,x_2)=x_1^a x_2^{1-a}$ .

The marginal rate of technical substitution is

${displaystyle MRTS_{21}={frac {1-a}{a}}{frac {x_{1}}{x_{2}}}}$

It is convenient to change the notations. Denote

${displaystyle {frac {1-a}{a}}{frac {x_{1}}{x_{2}}}=theta }$

Rewriting this we have

${displaystyle {frac {x_{1}}{x_{2}}}={frac {a}{1-a}}theta }$

Then the elasticity of substitution is^[6]

${displaystyle sigma _{21}={frac {dln({frac {x_{1}}{x_{2}}})}{dln(MRTS_{21})}}={frac {dln({frac {x_{1}}{x_{2}}})}{dln(theta )}}={frac {d{frac {x_{1}}{x_{2}}}}{frac {x_{1}}{x_{2}}}}{frac {theta }{dtheta }}={frac {d{frac {x_{1}}{x_{2}}}}{dtheta }}{frac {theta }{frac {x_{1}}{x_{2}}}}={frac {a}{1-a}}{frac {1-a}{a}}{frac {x_{1}}{x_{2}}}{frac {x_{2}}{x_{1}}}=1}$

Economic interpretation[edit]

Given an original allocation/combination and a specific substitution on allocation/combination for the original one, the larger the magnitude of the elasticity of substitution (the marginal rate of substitution elasticity of the relative allocation) means the more likely to substitute. There are always 2 sides to the market; here we are talking about the receiver, since the elasticity of preference is that of the receiver.

The elasticity of substitution also governs how the relative expenditure on goods or factor inputs changes as relative prices change. Let $S_{21}$ denote expenditure on $c_{2}$ relative to that on $c_{1}$ . That is:

$S_{21} equiv frac{p_2 c_2}{p_1 c_1}$

As the relative price p_2/p_1 changes, relative expenditure changes according to:

$frac{dS_{21}}{dleft(p_2/p_1right)} = frac{c_2}{c_1} + frac{p_2}{p_1}cdotfrac{dleft(c_2/c_1right)}{dleft(p_2/p_1right)} = frac{c_2}{c_1}left[1 + frac{dleft(c_2/c_1right)}{dleft(p_2/p_1right)}cdotfrac{p_2/p_1}{c_2/c_1} right] = frac{c_2}{c_1}left(1 - E_{21} right)$

Thus, whether or not an increase in the relative price of $c_{2}$ leads to an increase or decrease in the relative expenditure on $c_{2}$ depends on whether the elasticity of substitution is less than or greater than one.

Intuitively, the direct effect of a rise in the relative price of $c_{2}$ is to increase expenditure on $c_{2}$ , since a given quantity of $c_{2}$ is more costly. On the other hand, assuming the goods in question are not Giffen goods, a rise in the relative price of $c_{2}$ leads to a fall in relative demand for $c_{2}$ , so that the quantity of $c_{2}$ purchased falls, which reduces expenditure on $c_{2}$ .

Which of these effects dominates depends on the magnitude of the elasticity of substitution. When the elasticity of substitution is less than one, the first effect dominates: relative demand for $c_{2}$ falls, but by proportionally less than the rise in its relative price, so that relative expenditure rises. In this case, the goods are gross complements.

Conversely, when the elasticity of substitution is greater than one, the second effect dominates: the reduction in relative quantity exceeds the increase in relative price, so that relative expenditure on $c_{2}$ falls. In this case, the goods are gross substitutes.

Note that when the elasticity of substitution is exactly one (as in the Cobb–Douglas case), expenditure on $c_{2}$ relative to $c_{1}$ is independent of the relative prices.

Notes[edit]

References[edit]

Hicks, J. R. (1932). The Theory of Wages. Macmillan. First defined there.
Mas-Colell, Andreu; Whinston; Green (2007). Microeconomic Theory. New York, NY: Oxford University Press. ISBN 978-0195073409.
Varian, Hal (1992). Microeconomic Analysis (3rd ed.). W.W. Norton & Company. ISBN 978-0-393-95735-8.
Klump, Rainer; McAdam, Peter; Willman, Alpo (2007). «Factor Substitution and Factor-Augmenting Technical Progress in the United States: A Normalized Supply-Side System Approach». Review of Economics and Statistics. 89 (1): 183–192. doi:10.1162/rest.89.1.183. S2CID 57570638.

External links[edit]

The Elasticity of Substitution, Gonçalo L. Fonsekca, essay, The New School for Social Research.

Источник

Эластичность замены — это эластичность отношения двух ресурсов к производству (или полезность) по отношению к соотношению их предельных продуктов (или полезностей). На конкурентном рынке он измеряет процентное изменение соотношения двух используемых ресурсов в ответ на процентное изменение их цен. Это дает общее представление о кривизне изокванты, но технически не связано с геометрической кривизной. Таким образом, взаимозаменяемость между ресурсами (или товарами), т.е. насколько легко заменить одни ресурсы (или товар) на другие.

Содержание

1 История концепции
2 Определение
3 Пример
4 Экономическая интерпретация
5 См. Также
6 Примечания
7 Ссылки
8 Внешние ссылки

История концепции

Джон Хикс представил концепцию в 1932 году. Джоан Робинсон независимо открыла его в 1933 году, используя математическую формулировку, эквивалентную формуле Хикса, хотя в то время это не было реализовано.

Определение

Общее определение эластичности X относительно Y составляет EYX =% изменение X% изменение Y { displaystyle E_ {Y} ^ {X} = { frac {% { t_dv {изменение X}}} { % { t_dv {изменение в Y}}}}} ${ displaystyle E_ {Y} ^ {X} = { frac {% { t_dv {изменение в X}}} {% { t_dv {изменение в Y}}}} }$ , что сокращается до EYX = d X d YYX { displaystyle E_ {Y} ^ {X} = { frac { dX} {dY}} { frac {Y} {X}}} ${ displaystyle E_ {Y} ^ { X} = { frac {dX} {dY}} { frac {Y} {X}}}$ для бесконечно малых изменений и дифференцируемых переменных. Эластичность замещения — это изменение соотношения использования двух товаров по отношению к соотношению их предельной стоимости или цен. Чаще всего используется соотношение капитала (K) и рабочей силы (L) по отношению к соотношению их предельных продуктов MPK { displaystyle MP_ {K}} ${ displaystyle MP_ {K}}$ и MPL { displaystyle MP_ {L}} ${ displaystyle MP_ {L}}$ или стоимости аренды (r) и заработной платы (w). Другое приложение — соотношение потребительских товаров 1 и 2 по отношению к соотношению их предельных полезностей или их цен. Начнем с приложения потребления.

Пусть избыточное потребление полезности определяется как U (c 1, c 2) { displaystyle U (c_ {1}, c_ {2})}и пусть U ci = d U (c 1, c 2) / dci { displaystyle U_ {c_ {i}} = dU (c_ {1}, c_ {2}) / d {c_ {i}}} ${ displaystyle U_ {c_ {i}} = dU (c_ {1}, c_ {2}) / d {c_ {i}}}$ . Тогда эластичность замены равна:

E 21 = d ln ⁡ (c 2 / c 1) d ln ⁡ (MRS 12) = d ln ⁡ (c 2 / c 1) d ln ⁡ (U c 1 / U c 2) = d (c 2 / c 1) c 2 / c 1 d (U c 1 / U c 2) U c 1 / U c 2 = d (c 2 / c 1) c 2 / c 1 d ( p 1 / p 2) p 1 / p 2 { displaystyle E_ {21} = { frac {d ln (c_ {2} / c_ {1})} {d ln (MRS_ {12})}} = { frac {d ln (c_ {2} / c_ {1})} {d ln (U_ {c_ {1}} / U_ {c_ {2}})}} = { frac { frac {d (c_ {2} / c_ {1})} {c_ {2} / c_ {1}}} { frac {d (U_ {c_ {1}} / U_ {c_ {2}})} { U_ {c_ {1}} / U_ {c_ {2}}}}} = { frac { frac {d (c_ {2} / c_ {1})} {c_ {2} / c_ {1}} } { frac {d (p_ {1} / p_ {2})} {p_ {1} / p_ {2}}}}} $E_ {21} = frac {d ln (c_2 / c_1)} {d ln (MRS_ {12})} = frac {d ln (c_2 / c_1)} {d ln (U_ {c_1} / U_ {c_2})} = frac { frac {d (c_2 / c_1)} {c_2 / c_1}} { frac {d (U_ {c_1} / U_ {c_2})} {U_ {c_1} / U_ {c_2}}} = frac { frac { d (c_2 / c_1)} {c_2 / c_1}} { frac {d (p_1 / p_2)} {p_1 / p_2}}$

где MRS { displaystyle MRS} MRS — предельная норма замещения. Последнее равенство представляет MRS 12 = p 1 / p 2 { displaystyle MRS_ {12} = p_ {1} / p_ {2}} $MRS_ {12} = p_1 / p_2$ , которое является отношением из условия первого порядка для Задача максимизации потребительской полезности во внутреннем равновесии Эрроу – Дебре. Интуитивно мы смотрим на то, как меняется относительный выбор потребителя в отношении предметов потребления по мере изменения их относительных цен.

Также обратите внимание, что E 21 = E 12 { displaystyle E_ {21} = E_ {12}} $E_ {21} = E_ {12}$ :

E 21 = d ln ⁡ (c 2 / c 1) d ln ⁡ ( U c 1 / U c 2) = d (- ln ⁡ (c 2 / c 1)) d (- ln ⁡ (U c 1 / U c 2)) = d ln ⁡ (c 1 / c 2) d ln ⁡ (U с 2 / U с 1) = E 12 { Displaystyle E_ {21} = { гидроразрыва {d ln (c_ {2} / c_ {1})} {d ln (U_ {c_ {1 }} / U_ {c_ {2}})}} = { frac {d left (- ln (c_ {2} / c_ {1}) right)} {d left (- ln (U_ {c_ {1}} / U_ {c_ {2}}) right)}} = { frac {d ln (c_ {1} / c_ {2})} {d ln (U_ {c_ {2 }} / U_ {c_ {1}})}} = E_ {12}} ${ displaystyle E_ {21} = { frac {d ln (c_ {2} / c_ {1})} {d ln (U_ {c_ {1}} / U_ {c_ {2}})}} = { frac {d left (- ln (c_ {2} / c_ { 1}) right)} {d left (- ln (U_ {c_ {1}} / U_ {c_ {2}}) right)}} = { frac {d ln (c_ {1} / c_ {2})} {d ln (U_ {c_ {2}} / U_ {c_ {1}})}} = E_ {12}}$

Эквивалентная характеристика эластичности замещения:

E 21 = d ln ⁡ (c 2 / c 1) d ln ⁡ (MRS 12) = — d ln ⁡ (c 2 / c 1) d ln ⁡ (MRS 21) = — d ln ⁡ (c 2 / c 1) d ln ⁡ (U c 2 / U c 1) = — d (c 2 / c 1) c 2 / c 1 d (U c 2 / U c 1) U c 2 / U c 1 = — d (c 2 / c 1) c 2 / c 1 d (p 2 / п 1) п 2 / п 1 { Displaystyle E_ {21} = { frac {d ln (c_ {2} / c_ {1})} {d ln (MRS_ {12})}} = — { frac {d ln (c_ {2} / c_ {1})} {d ln (MRS_ {21})}} = — { frac {d ln (c_ {2} / c_ {1}) } {d ln (U_ {c_ {2}} / U_ {c_ {1}})}} = — { frac { frac {d (c_ {2} / c_ {1})} {c_ {2} / c_ {1}}} { frac {d (U_ {c_ {2}} / U_ {c_ {1}})} {U_ {c_ {2}} / U_ {c_ {1}}}}} = — { frac { frac {d (c_ {2} / c_ {1})} {c_ {2} / c_ {1}}} { frac {d (p_ {2} / p_ {1})} {p_ {2} / p_ {1}}}}} $E_ {21 } = frac {d ln (c_2 / c_1)} {d ln (MRS_ {12})} = - frac {d ln (c_2 / c_1)} {d ln (MRS_ {21})} = - frac {d ln (c_2 / c_1)} {d ln (U_ {c_2} / U_ {c_1})} = - frac { frac {d (c_2 / c_1)} {c_2 / c_1} } { frac {d (U_ {c_2} / U_ {c_1})} {U_ {c_2} / U_ {c_1}}} = - frac { frac {d (c_2 / c_1)} {c_2 / c_1}} { frac {d (p_2 / p_1)} {p_2 / p_1}}$

В моделях с дискретным временем эластичность замещения потребления в периодах t { displaystyle t}и t + 1 { displaystyle t + 1} t + 1 известен как эластичность межвременного замещения.

Аналогично, если производственная функция равна f (x 1, x 2) { displaystyle f (x_ {1}, x_ {2})}, то эластичность замещения равна:

σ 21 = d ln ⁡ (x 2 / x 1) d ln ⁡ MRTS 12 = d ln ⁡ (x 2 / x 1) d ln ⁡ (dfdx 1 / dfdx 2) = d (x 2 / x 1) x 2 / x 1 d (dfdx 1 / dfdx 2) dfdx 1 / dfdx 2 = — d (x 2 / x 1) x 2 / x 1 d (dfdx 2 / dfdx 1) dfdx 2 / dfdx 1 { displaystyle sigma _ {21} = { frac {d ln (x_ {2} / x_ {1})} {d ln MRTS_ {12}}} = { frac {d ln (x_ {2} / x_ {1})} {d ln ({ frac {df} {dx_ {1}}} / { frac {df} {dx_ {2}}})}} = { frac { frac {d (x_ {2} / x_ {1})} {x_ {2} / x_ {1}}} { frac {d ({ frac {df} {dx_ {1}}} / { frac {df} {dx_ {2}}})} {{ frac {df} {dx_ {1}}} / { frac {df} {dx_ {2}}}}}} = — { frac { frac {d (x_ {2} / x_ {1})} {x_ {2} / x_ {1}}} { frac {d ({ frac {df} {dx_ {2}}} / { frac {df} {dx_ {1}}})} {{ frac {df} {dx_ {2}}} / { frac {df} {dx_ {1}}}}}}} $sigma_ {21} = frac {d ln (x_2 / x_1)} {d ln MRTS_ {12}} = frac {d ln (x_2 / x_1)} {d ln ( frac {df} {dx_1} / frac {df} {dx_2})} = frac { frac {d (x_2 / x_1)} {x_2 / x_1}} { frac {d ( frac {df} { dx_1} / frac {df} {dx_2})} { frac {df} {dx_1} / frac {df} {dx_2}}} = - frac { frac {d (x_2 / x_1)} {x_2 / x_1}} { frac {d ( frac {df} {dx_2} / frac {df} {dx_1})} { frac {df} {dx_2} / frac {df} {dx_1}}}$

где MRTS { displaystyle MRTS} MRTS — предельная скорость технического замещения.

Обратная эластичность замещения: эластичность дополнительности.

Пример

Рассмотрим производственную функцию Кобба – Дугласа f (x 1, x 2) = x 1 ax 2 1 — a { displaystyle f ( x_ {1}, x_ {2}) = x_ {1} ^ {a} x_ {2} ^ {1-a}} $f (x_1, x_2) = x_1 ^ a x_2 ^ {1-a}$ .

Предельная норма технической замены составляет

MRTS 12 = a 1-ax 2 x 1 { displaystyle MRTS_ {12} = { frac {a} {1-a}} { frac {x_ {2}} {x_ {1}}}} $MRTS_ {12} = frac {a} {1-a} frac {x_2} {x_1}$

Удобно изменять обозначения. Обозначим

a 1 — ax 2 x 1 = θ { displaystyle { frac {a} {1-a}} { frac {x_ {2}} {x_ {1}}} = theta} <164.>Переписав это, мы получим

x 2 x 1 = 1 — aa θ { displaystyle { frac {x_ {2}} {x_ {1}}} = { frac {1-a} {a}} theta} $frac {x_2} {x_1} = frac {1-a} {a} theta$

Тогда эластичность замены равна

σ 21 = d ln ⁡ (x 2 x 1) d ln ⁡ MRTS 12 = d ln ⁡ (x 2 x 1) d ln ⁡ (a 1 — ax 2 Икс 1) знак равно d пер ⁡ (1 — аа θ) d пер ⁡ (θ) = d 1 — аа θ d θ θ 1 — аа θ = 1 { displaystyle sigma _ {21} = { frac {d ln ({ frac {x_ {2}} {x_ {1}}})} {d ln MRTS_ {12}}} = { frac {d ln ({ frac {x_ {2}} {x_ {1}}})} {d ln ({ frac {a} {1-a}} { frac {x_ {2}} {x_ {1}}})}} = { frac {d ln ({ frac {1-a} {a}} theta)} {d ln ( theta)}} = { frac {d { frac {1-a} {a}} theta} { d theta}} { frac { theta} {{ frac {1-a} {a}} theta}} = 1} $sigma_ {21} = frac {d ln ( frac {x_2} {x_1})} {d ln MRTS_ {12}} = frac {d ln ( frac {x_2} {x_1})} {d ln ( frac { a} {1-a} frac {x_2} {x_1})} = frac {d ln ( frac {1-a} {a} theta)} {d ln ( theta)} = frac {d frac {1-a} {a} theta} {d theta} frac { theta} { frac {1-a} {a} theta} = 1$

Экономическая интерпретация

Учитывая исходное распределение / комбинацию и конкретной замены при распределении / комбинации для исходной, тем больше величина эластичности замещения (предельная ставка эластичности замещения e относительное распределение) означает, что вероятность замены выше. У рынка всегда есть 2 стороны; здесь мы говорим о получателе, поскольку эластичность предпочтений — это эластичность получателя.

Эластичность замещения также определяет, как изменяются относительные расходы на товары или вводимые факторы при изменении относительных цен. Пусть S 21 { displaystyle S_ {21}} $S_ {21}$ обозначает расходы на c 2 { displaystyle c_ {2}} $c_ {2}$ относительно расходов на c. 1 { displaystyle c_ {1}} $c_ {1}$ . То есть:

S 21 ≡ p 2 c 2 p 1 c 1 { displaystyle S_ {21} Equiv { frac {p_ {2} c_ {2}} {p_ {1} c_ {1}}} } $S_ {21} Equiv frac {p_2 c_2} {p_1 c_1}$

При изменении относительной цены p 2 / p 1 { displaystyle p_ {2} / p_ {1}}относительные расходы изменяются согласно:

d S 21 d (p 2 / p 1) = c 2 c 1 + p 2 p 1 ⋅ d (c 2 / c 1) d (p 2 / p 1) = c 2 c 1 [1 + d (c 2 / c 1) d (п 2 / п 1) ⋅ п 2 / p 1 c 2 / c 1] = c 2 c 1 (1 — E 21) { displaystyle { frac {dS_ {21}} {d left (p_ { 2} / p_ {1} right)}} = { frac {c_ {2}} {c_ {1}}} + { frac {p_ {2}} {p_ {1}}} cdot { frac {d left (c_ {2} / c_ {1} right)} {d left (p_ {2} / p_ {1} right)}} = { frac {c_ {2}} {c_ {1}}} left [1 + { frac {d left (c_ {2} / c_ {1} right)} {d left (p_ {2} / p_ {1} right)}} cdot { frac {p_ {2} / p_ {1}} {c_ {2} / c_ {1}}} right] = { frac {c_ {2}} {c_ {1}}} left (1-E_ {21} right)} $frac { dS_ {21}} {d left (p_2 / p_1 right)} = frac {c_2} {c_1} + frac {p_2} {p_1} cdot frac {d left (c_2 / c_1 right) } {d left (p_2 / p_1 right)} = frac {c_2} {c_1} left [1 + frac {d left (c_2 / c_1 right)} {d left (p_2 / p_1 right)} cdot frac {p_2 / p_1} {c_2 / c_1} right] = frac {c_2} {c_1} left (1 - E_ {21} right)$

Таким образом, приводит ли увеличение относительной цены c 2 { displaystyle c_ {2}} $c_ {2}$ к увеличению или уменьшение относительных расходов на c 2 { displaystyle c_ {2}} $c_ {2}$ зависит от того, длительность замены меньше или больше единицы.

Интуитивно понятно, что прямым следствием повышения относительной цены c 2 { displaystyle c_ {2}} $c_ {2}$ является увеличение расходов на c 2 { displaystyle c_ {2}} $c_ {2}$ , поскольку заданное количество c 2 { displaystyle c_ {2}} $c_ {2}$ дороже. С другой стороны, если предположить, что рассматриваемые товары не являются товарами Giffen, повышение относительной цены на c 2 { displaystyle c_ {2}} $c_ {2}$ приводит к падение относительного спроса на c 2 { displaystyle c_ {2}} $c_ {2}$ , так что количество купленных c 2 { displaystyle c_ {2}} $c_ {2}$ падает, что снижает расходы на c 2 { displaystyle c_ {2}} $c_ {2}$ .

Какой из этих эффектов доминирует, зависит от величины эластичности замещения. Когда эластичность замещения меньше единицы, преобладает первый эффект: относительный спрос на c 2 { displaystyle c_ {2}} $c_ {2}$ падает, но пропорционально меньше, чем рост его относительной цены., так что относительные расходы возрастают. В этом случае товары являются валовыми дополнениями.

И наоборот, когда эластичность замещения больше единицы, преобладает второй эффект: уменьшение относительного количества превышает увеличение относительной цены, так что относительные расходы на c 2 { displaystyle c_ {2}} $c_ {2}$ падает. В этом случае товары являются брутто-заменителями.

. Обратите внимание, что, когда эластичность замещения равна единице (как в случае Кобба – Дугласа), расходы на c 2 { displaystyle c_ {2}} $c_ {2}$ относительно c 1 { displaystyle c_ {1}} $c_ {1}$ не зависит от относительных цен.

См. Также

Примечания

Ссылки

Хикс, Дж. Р. (1932). Теория заработной платы. Макмиллан. Впервые определено здесь.
Мас-Колелл, Андреу ; Уинстон; Зеленый (2007). Микроэкономическая теория. Нью-Йорк, Нью-Йорк: Издательство Оксфордского университета. ISBN 978-0195073409.
Вариан, Хэл (1992). Микроэкономический анализ (3-е изд.). W.W. Нортон и Компания. ISBN 978-0-393-95735-8.
Кламп, Райнер; Макадам, Питер; Уиллман, Альпо (2007). «Факторное замещение и технический прогресс, увеличивающий фактор в Соединенных Штатах: Нормализованный системный подход на стороне предложения». Обзор экономики и статистики. 89(1): 183–192. doi : 10.1162 / rest.89.1.183. S2CID 57570638.

Внешние ссылки

Источник

Эластичность замещения — применяемый в экономической теории показатель, характеризующий производственную функцию или функцию полезности, и показывающий на сколько процентов необходимо изменить отношение факторов производства (или соответственно, объемов различных благ) при изменении их предельной нормы замещения на 1 % (отношение предельных продуктов или предельных полезностей соответственно), чтобы объём выпуска оставался неизменным.

Формальное определение

Пусть задана функция [math]displaystyle{ Y(x_1,x_2,…,x_n) }[/math]. Это обычно либо производственная функция от факторов [math]displaystyle{ x_i }[/math], либо функция полезности от объемов потребления благ [math]displaystyle{ x_i }[/math]. Далее изложение приводится для случая производственной функции.

Обозначим [math]displaystyle{ MRTS_{ij} }[/math] — предельную норму замещения [math]displaystyle{ j }[/math]-го фактора [math]displaystyle{ i }[/math]-м фактором, а [math]displaystyle{ k_{ij} }[/math] — отношение количества этих факторов, используемых в производстве. Тогда эластичность замещения будет равна:

[math]displaystyle{ sigma_{ij}=frac {d ln k_{ij}}{d ln MRTS_{ij}}|_{Y=const}=frac {d k_{ij}/k_{ij}}{d MRTS_{ij}/MRTS_{ij}}|_{Y=const}=frac {d k_{ij}}{d MRTS_{ij}} frac {MRTS_{ij}}{k_{ij}}|_{Y=const} }[/math]

При этом можно показать, что [math]displaystyle{ sigma_{ij}=sigma_{ji} }[/math].

Можно показать, что эластичность замещения равна:

[math]displaystyle{ sigma =frac {(1+k_{ij}MRTS_{ij})Y’_j/x_i}{Y»_{jj}MRTS_{ij}+Y»_{ii}/MRTS_{ij}-2Y»_{ij}} }[/math]

В случае однородных производственных функций она существенно упрощается:

[math]displaystyle{ sigma=frac {Y’_iY’_j} {(1-q) Y’_iY’_j+q Y Y»_{ij}} }[/math]

где [math]displaystyle{ q }[/math] — степень однородности.

В частности для стандартного случая однородности первой степени (линейной однородности) формула имеет следующий простой вид:

[math]displaystyle{ sigma=frac {Y’_iY’_j} {Y cdot Y»_{ij}} }[/math]

Эластичность замещения для некоторых производственных функций

Функция Кобба — Дугласа [math]displaystyle{ Y=AK^{alpha}L^{beta} }[/math] — эластичность замещения равна [math]displaystyle{ 1 }[/math] (для доказательства достаточно учесть, что эта функция является однородной степени [math]displaystyle{ q=alpha+beta }[/math] и воспользоваться соответствующей формулой).
Функция CES — имеет произвольную (то есть не обязательно единичную, как в случае функции Кобба — Дугласа) постоянную эластичность замещения.
Производственная функция Леонтьева — нулевая эластичность замещения.
Линейная производственная функция — бесконечная эластичность замещения.

См. также

Предельная норма технического замещения
Эластичность (экономика)
Функция CES

Источники

Источник

History of the concept[edit]

Definition[edit]

Example[edit]

Economic interpretation[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Содержание

История концепции

Определение

Пример

Экономическая интерпретация

См. Также

Примечания

Ссылки

Внешние ссылки

Формальное определение

Эластичность замещения для некоторых производственных функций

См. также

Источники