Решение задач с использованием алгоритма бинарного поиска
Время на прочтение
4 мин
Количество просмотров 14K
Алгоритм бинарного (или двоичного) поиска — это один из базовых алгоритмов, который часто применяется при решении алгоритмических задач. На LeetCode на момент написания этой статьи порядка 190 задач в решении которых он используется (можно посмотреть здесь: https://leetcode.com/tag/binary-search/). Бинарный поиск разбирается во множестве статей, его идея достаточно несложная и интуитивно понятная. Однако алгоритм имеет некоторое количество «подводных камней». В этой заметке я хотел бы показать решение одной из задач с его помощью.
Для начала несколько слов о самом алгоритме. Задача, которую он решает, может быть сформулирована следующим образом: «найти в отсортированном массиве индекс элемента, значение которого соответствует заданному». Обычно массив отсортирован по возрастанию и в данной заметке мы будем предполагать, что это так и есть.
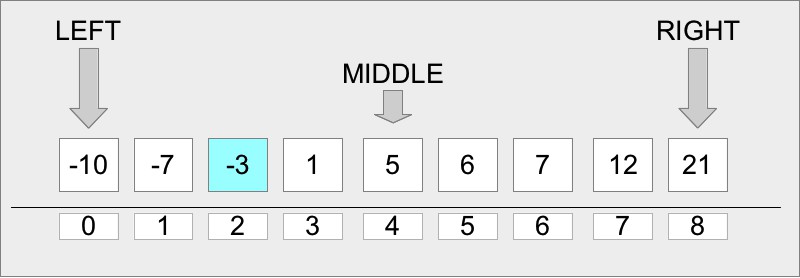
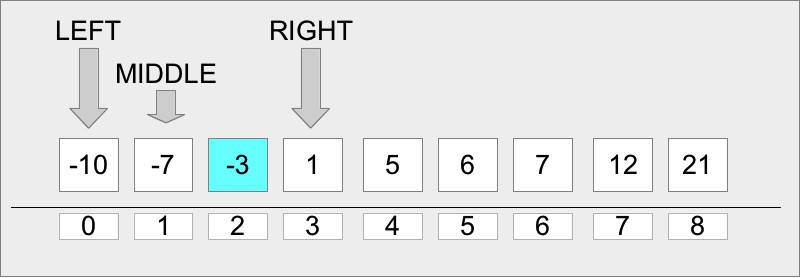
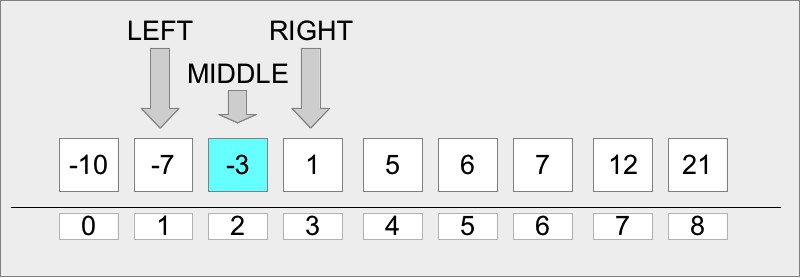
Основная идея алгоритма в том, чтобы проверить элемент в середине текущего среза массива (изначально берется весь массив). Если значение этого элемента меньше искомого, то необходимо проверить средний элемент в правой части массива, если больше, то в левой части массива. Мы будем повторять этот процесс, пока значения среднего элемента очередного среза не окажется равным искомому значению, либо больше не останется элементов (и тогда в массиве нет такого элемента). Более наглядно это видно на рисунке:
Сложность алгоритма бинарного поиска по времени выполнения O(logN) (так как мы уменьшаем срез массива на 2 на каждой итерации и проверяем только 1 элемент), и O(1) по памяти. Что касается реализации алгоритма, то обычно она выглядит следующим образом:
left, right = 0, len(array)-1
while left <= right do
middle = (left + right) / 2
if array[middle] > target then
right = middle - 1 // дальше будем проверять левую часть массива
else if array[middle] < target then
left = middle + 1 // дальше будем проверять правую часть массива
else
return middle // нашли элемент
end if
end while
return -1 // элемента нет в массивеКод на Golang можете посмотреть здесь. Есть тесты, которые включают часть corner cases. На эти случаи стоит обратить внимание и, возможно, почитать про них, например на stackoverflow (найти их описание сейчас не составляет проблем, есть много материалов как на английском, так и на русском языках).
Давайте перейдем к решению задачки с LeetCode. Возьмем для примера задачу Find Target Indices After Sorting Array. Она довольно простая, уровня easy, что позволит нам сосредоточится на одном алгоритме, а точнее его небольшой модификации. Если кратко, то суть задачи состоит в том, что нам необходимо в отсортированном массиве найти индексы всех элементов, значения которых соответствуют заданному. Есть еще одно дополнительное условие: необходимо вернуть их в порядке возрастания значений элементов массива (то есть надо сначала массив отсортировать). Таким образом, очень похоже, что нам подойдет алгоритм бинарного поиска, однако он позволяет найти индекс только одного из элементов.
Важное замечание: приведенное здесь решение задачи не является оптимальным. Оно взято просто как удобный пример. Оптимальное решение за O(N) вы можете посмотреть в этом комментарии или здесь. Далее мы говорим о сложности после сортировки, которая сама по себе O(NlogN).
Наиболее простым способом для нас будет нахождение элемента (любого) с заданным значением, затем распространение вправо и влево от него, пока значение не станет отличным с обеих сторон или мы не достигнем конца и начала массива. Однако, такой подход может привести к O(N) сложности по времени, тогда как бинарный поиск имеет сложность O(logN). Здесь может быть полезным модификация бинарного поиска, которая вернет наиболее левый элемент массива с искомым значением. Реализация алгоритма выглядит так (код на Golang можете посмотреть здесь, тесты здесь):
left, right = 0, len(array)
while left < right do
middle = (left + right) / 2
if array[middle] < target then
left = middle + 1 // дальше будем проверять правую часть массива
else
right = middle // дальше будем проверять левую часть массива
end if
end while
return leftОтлично, теперь мы сможем найти первый индекс в массиве и просто добавить все элементы начиная от него и пока не встретится элемент с отличным значением. Алгоритм будет выглядеть следующим образом (код на Golang здесь, тесты здесь):
sort(array) // сортируем массив по возрастанию ( обычно за O(NlogN) )
// бинарный поиск наиболее левого элемента
left, right = 0, len(array)
while left < right do
middle = (left + right) / 2
if array[middle] < target then
left = middle + 1 // дальше будем проверять правую часть массива
else
right = middle // дальше будем проверять левую часть массива
end if
end while
// собираем индексы элементов в результирующий массив
result = []
while left < length(array) and array[left] == target do
append(result, left)
left = left + 1
end whileКазалось бы, что все неплохо, но мы все еще можем получить сложность по времени O(N) в том случае, если все элементы массива содержат искомое значение. И, что может быть менее очевидным, мы можем потерять скорость на многократном выделении памяти и копировании при append.
Дальнейшим развитием решения может быть поиск индекса наиболее правого элемента массива с искомым значением. Это еще одна небольшая модификация бинарного поиска. Вот так выглядит сам алгоритм (код на Golang здесь, тесты здесь):
left, right = 0, len(array)
while left < right do
middle = (left + right) / 2
if array[middle] > target then
right = middle // дальше будем проверять левую часть массива
else
left = middle + 1 // дальше будем проверять правую часть массива
end if
end while
return rightТеперь мы можем найти оба (самый левый и самый правый) элемента за время O(logN) каждый. Код на golang можете посмотреть здесь и тесты.
Проверка кода на LeetCode дает результаты, представленные в таблице. Она включает в себя еще и результаты решения сортировкой и линейным поиском, которое не было рассмотрено в силу его простоты (код можно посмотреть здесь)
|
Алгоритм |
Время выполнения |
|
Сортировка и линейный поиск |
8 ms |
|
Сортировка, бинарный поиск левого элемента и линейный поиск правого элемента |
7 ms |
|
Сортировка, бинарный поиск левого и правого элементов |
5 ms |
Бенчмарки на Golang с массивом из 30 одинаковых элементов, каждый из которых равен искомому дают следующие результаты.
|
Алгоритм |
Время выполнения |
|
Сортировка и линейный поиск |
717 — 1028 ns/op |
|
Сортировка, бинарный поиск левого элемента и линейный поиск правого элемента |
943 — 1418 ns/op |
|
Сортировка, бинарный поиск левого и правого элементов |
581 — 639 ns/op |
В качестве вывода хочется отметить, что знание модификаций алгоритма бинарного поиска может помочь в решении некоторых задач. Возможно оно не настолько важно и полезно, как знание исходного алгоритма, но может позволить нам сэкономить несколько миллисекунд.
Вопросы:
· Поиск
элемента массива с заданным значением.
· Сортировка
элементов массива.
Часто при решении
некоторых задач требуется найти элемент массива со значением, равным чему-либо.
Задача: Написать
программу, которая определяет, есть ли в массиве из 100 случайных целых чисел,
на промежутке от 1 до 200, число, введённое пользователем.
Начнём написание
программы для решения задачи. Назовём нашу программу zadannoe_chislo.
Для работы программы нам потребуется массив из 100 элементов. Назовём его a.
Так как элементами массива будут целые числа на промежутке от 1 до 200, укажем
тип элементов массива byte.
Также нам понадобятся переменные для хранения номера текущего элемента — i
и для хранения числа, введённого пользователем — num.
Объявим принадлежащими к целочисленному типу byte.
Напишем логические
скобки. Тело программы будет начинаться с оператора writeln,
который будет выводить на экран сообщение о том, что это программа,
определяющая, есть ли в массиве случайных чисел число, введённое пользователем.
Теперь запишем цикл для заполнения массива случайными числами. Это будет цикл для
i, изменяющегося от 1 до 100. В нём
будет оператор присваивания i-тому
элементу массива a, суммы случайного
целого числа на промежутке от 0 до 199 и 1. После того как мы заполнили массив
случайными числами, напишем оператор write,
выводящий на экран запрос на ввод числа на промежутке от 1 до 200, а также
оператор readln для считывания
значения переменной num.
Для того чтобы
определить, есть ли введённое число в массиве a,
мы позже опишем логическую функцию, которую назовём poisk,
поэтому сейчас напишем условный оператор if,
условием которого будет значение функции poisk,
с введённым числом num
в качестве аргумента. После служебного слова then
в этом условном операторе, напишем оператор writeln,
выводящий на экран сообщение о том, что число num
есть в массиве. После слова else
также напишем оператор writeln,
который будет выводить на экран сообщение о том, что числа num нет в
массиве.
Для того чтобы
пользователь могу убедиться в том, что программа работает правильно, напишем
оператор write, выводящий
сообщение о том, что это массив, а также цикл с для i
для вывода элементов массива через пробел. На этом описание основной программы
завершено.
program zadannoe_chislo;
var
a: array [1..100] of
byte;
i, num: byte;
begin
writeln (‘Программа, определяющая, есть ли в массиве случайных чисел число,
введённое пользователем.’);
for i:=1 to 100
do
a[i]:=random (200)+1;
write (‘Введите число на промежутке [1;
200]>>> ‘);
readln (num);
if poisk (num)
then write (‘Число ‘, num, ‘ есть в
массиве.’)
else write (‘Числа ‘, num, ‘ нет в массиве.’);
end.
Заголовок,
переменные и операторный блок основной программы
Теперь рассмотрим, как же
проверить, есть ли в массиве Элемент с указанным значением. Для этого будем
проверять последовательно все элементы массива от первого к последнему, пока не
найдём нужный или же пока они не закончатся. Такой поиск элемента в массиве
называется линейным.
Напишем для нашей
программы логическую функцию, определяющую, есть ли в массиве a
заданное число. Как мы помним, она должна называться poisk.
Эта функция должна иметь один аргумент целочисленного типа byte,
назовём его t. Также функция
должна возвращать значение логического типа boolean.
Для работы функции нам потребуется дополнительная переменная, которая будет
хранить номер текущего элемента массива. Назовём её i
и укажем принадлежащей к целочисленному типу byte.
В логических скобках опишем операторный блок функции. В его начале присвоим
переменной i начальное значение – 0.
Дальше напишем цикл с постусловием. Условием окончания работы цикла будет то,
что i-тый Элемент массива a
равен t или что достигнут конец
массива и i равно 100. Тело цикла
будет содержать единственный оператор, увеличивающий значение переменной i
на 1. После завершения работы цикла нам будет достаточно проверить равен ли i-тый
элемент массива a t
и присвоить значение истинности этого высказывания переменной функции poisk.
На этом описание функции закончено.
function poisk (t: byte): boolean;
var
i: byte;
begin
i:=0;
repeat
i:=i+1;
until (a[i]=t) or (i = 100);
poisk:=a[i]=t;
end;
Функция poisk
Запустим программу на
выполнение. Введём число 75.
Программа вывела сообщение о том, что такое число есть в массиве. Просмотрев
элементы массива, мы можем убедиться, что такое число действительно в нём есть.
Снова запустим программу
и введём число 120. Программа вывела сообщение о том, что такого числа нет в
массиве. Программа работает правильно. Задача решена.
Рассмотрим функцию poisk.
Очевидно, что в лучшем случае при её выполнении будет выполнена 1 проверка, а в
худшем – 100. Это не очень много, но предположим, что у нас есть программа,
которая будет выполнять поиск тысячи или даже миллионы раз. Тогда для этого
может потребоваться много времени, но поиск в массиве можно организовать проще,
если элементы массива расположены в соответствии с некоторыми правилами,
например, по возрастанию или по убыванию своих значений.
Мы можем изменить порядок
следования элементов массива, отсортировав их. Сортировкой элементов массива
называется изменение порядка их следования в соответствии с некоторыми
правилами. По значениям элементы массива можно отсортировать разными способами.
Рассмотрим наиболее распространённые. Если в массиве не может быть равных
элементов, то его можно отсортировать по возрастанию или по убыванию.
Если же в массиве могут быть равные элементы, то его можно отсортировать по
неубыванию или по невозрастанию.
Варианты
сортировки элементов массива
Как же можно
отсортировать элементы массива, например, по возрастанию. Мы можем
последовательно проверять все пары элементов массива, расположенных рядом, то
есть первый и второй, второй и третий и так далее. Если в паре элементы
расположены не по возрастанию, то их нужно менять местами. Таким образом,
постепенно все элементы массива станут расположены по возрастанию. Такой способ
сортировки называется методом пузырька. Он был назван так потому, что
подобно пузырькам воздуха в стакане воды, элементы массива с наименьшими
значениями перемещаются в начало массива.
Итак, что же нужно
сделать чтобы отсортировать массив по возрастанию методом пузырька… Вначале предположим,
что элементы массива уже расположены по возрастанию. Дальше будем
последовательно проверять пары элементов массива. Если найдём пару, в которой
элементы расположены не по возрастанию, то мы опровергнем начальное
предположение о том, что элементы уже расположены по возрастанию. Мы поменяем
местами элементы массива в паре, и продолжим проверять его дальше. После того,
как мы проверили все пары элементов массива мы должны проверить, осталось ли
наше начальное предположение о том, что элементы массива расположены по
возрастанию не опровергнутым. Если предположение было опровергнуто – мы начнём
выполнять алгоритм сначала, в противном случае – алгоритм завершит свою работу.
Когда после завершения работы алгоритма начальное положение останется не опровергнуто
алгоритм завершит свою работу.
Для написанной нами
программы для поиска элементов массива напишем процедуру сортировки элементов
массива a но не убыванию. Назовём
её sort. Для работы
процедуры нам нужна переменная для хранения, номера текущего элемента массива –
i и переменная для хранения одного из
элементов массива, когда мы будем менять их местами – k,
а также логическая переменная – p.
Напишем программный блок процедуры. В нём будет цикл с постусловием, в качестве
условия завершения работы которого будет значение логической переменной p.
Тело цикла будет начинаться с того что мы предположим, что элементы массива уже
расположены по возрастанию. Для этого переменной p
мы присвоим значение true.
Дальше будет следовать цикл с параметром i,
изменяющимся от 1 до 99. Это будет цикл для проверки пар элементов массива. В
нём будет условный оператор, который проверяет расположены ли элементы массива
с индексами i и i
+ 1
не по неубыванию. То есть что a[i]
> a[i
+ 1].
Если это условие выполняется, мы должны поменять эти два элемента массива
местами. Для этого после слова then
в логических скобках запишем четыре оператора присваивания: переменной p
– значения false, так как мы
опровергли начальное предположение, переменной k
– значения a[i],
a[i]
– значение a[i
+ 1],
a[i
+ 1]
– значение переменной k.
Таким образом, мы опровергли начальное предположение и поменяли местами
элементы массива с индексами i
и i + 1.
На этом описание процедуры завершено.
procedure sort ();
var
p: boolean;
i, k: byte;
begin
repeat
p:=true;
for i:=1 to 99
do
if a[i]>a[i+1]
then begin
p:=false;
k:=a[i];
a[i]:=a[i+1];
a[i+1]:=k;
end;
until p;
end;
Процедура сортировки
элементов массива по неубыванию методом пузырька
В программном блоке
основной программы перед запросом на ввод числа запишем вызов процедуры sort.
Запустим программу на выполнение. Зададим число 28.
Программа вывела сообщение о том, что это число есть в массиве. Просмотрев
элементы массива, мы можем убедиться в том, что они действительно отсортированы
по невозрастанию.
Программа работает
правильно. Обратим внимание, что для того, чтобы отсортировать элементы массива
по невозрастанию достаточно изменить знак больше в условном операторе в
процедуре сортировки на противоположный знак меньше.
Теперь рассмотрим, как мы
можем организовать поиск элемента с заданным значением в массиве,
отсортированном по неубыванию. Очевидно, что элементы с наименьшим и наибольшим
значениями располагаются по краям. Для поиска элемента с заданным значением
можно использовать метод деления отрезка пополам (метод двоичной
дихотомии). Если элементы массива расположены по возрастанию, то мы можем проверить
его средний элемент. Так мы можем точно сказать где нужно искать элемент с
искомым значением. Если средний элемент массива будет меньше искомого, то
искомый элемент нужно искать после среднего, а в противном случае от первого до
среднего. Таким образом мы сократим область поиска сразу в два раза. Точно
также мы найдём средний элемент на новом промежутке поиска, сравним его с
искомым и так далее. Так будет продолжаться до тех пор, пока начальный или
конечный элемент промежутка поиска не будет равен искомому или пока промежуток
поиска не станет равен одному элементу.
В написанной нами
программе изменим функцию poisk.
В ней нам понадобится дополнительные переменные для хранения номеров первого и
последнего элемента массива на промежутке поиска, назовём их соответственно f
и l, объявим их
целочисленного типа byte.
Запишем логические скобки. Операторный блок процедуры будет начинаться с того,
что мы присвоим переменным f
и l их начальные значения,
то есть соответственно 1 и 100. Дальше мы запишем цикл с постусловием. Условием
завершения его работы будет, то что один из элементов массива с индексами f
и l равен искомому элементу t
или что промежуток поиска сузился до одного элемента, то есть f
= l.
В теле цикла будет условный оператор, который будет проверять меньше ли средний
элемент массива, с индексом равным (f
+ l) div
2,
искомого t. Если это условие
выполняется, то мы должны сократить промежуток поиска элемента. Поэтому после слова
then присвоим переменной f
значение (f
+ l) div
2 + 1. В противном случае – сократим промежуток поиска в
другом направлении и присвоим переменной l
значение (f
+ l) div
2.
После завершения работы цикла проверим, равен ли один из элементов с индексами f
и l искомому t.
И присвоим значение истинности этого высказывания переменной функции – poisk.
function poisk (t: byte): boolean;
var
f, l: byte;
begin
f:=1;
l:=100;
repeat
if a[(f+l) div 2]<t
then f:=(f+l) div 2
+ 1
else l:=(f+l)
div 2;
until (a[f]=t) or (a[l]=t)
or (f=l);
poisk:=(a[f]=t) or (a[l]=t);
end;
Функция поиска элемента с
заданным значением методом деления отрезка пополам
Запустим программу на
выполнение. Введём число 45. Программа вывела сообщение о том, что такого числа
нет в массиве.
Снова запустим программу
и введём число 190. Программа вывела сообщение о том, что это число есть в
массиве.
Программа работает
правильно задача решена.
Поиск в массиве предусмотрен во многих языках программирования, в том числе и в С. Поиск является видом обработки данных в массиве с целью определения и выявления элемента, который соответствует заданным критериям. Поиск в массиве элемента на С разделяют на 2 большие категории:
поиск в несортированном массиве;
поиск в сортированном массиве.
То есть поиск и сортировка в массиве идут тесно рядом. Сортировкой называют специальный процесс, при котором элементы в массиве переставляются по какому-либо критерию или свойству. Например, если в массиве содержатся цифровые данные, то можно осуществить сортировку по возрастанию или убыванию, — это приведет к тому, что элементы в массиве будут располагаться упорядоченно. Главная цель любой сортировки — облегчить работу с элементами массива, например облегчить поиск в массиве.
Поиск элемента в массиве на С
Поиск в массиве на С можно осуществить несколькими методами, каждый из которых отличается своими характеристиками. На сегодня существует достаточно много разнообразных алгоритмов поиска, самыми распространенными из них являются:
линейный поиск в массиве на С;
двоичный или бинарный поиск в массиве на С;
интерполирующий поиск на С.
Есть и другие методы, но, если изучить эти — их будет вполне достаточно, чтобы найти нужный элемент в массиве.
Линейный поиск элемента в массиве на С
Линейный поиск в массиве на С является самым простым алгоритмом, поэтому изучается первым. Суть его заключается в том, что необходимо будет «перебирать» все элементы массива на совпадение с заданными критериями или ключами. Самый простой не означает самый быстрый. Этот вид поиска очень затратный по времени, поэтому не рекомендуется к применению в массивах с большим количеством данных.
Пример функции линейного поиска:
int linSearch(int arr[], int requiredKey, int arrSize)
{
for (int i = 0; i < arrSize; i++)
{
if (arr[i] == requiredKey)
return i;
}
return -1;
}
Данный вид поиска подходит для поиска одиночного элемента в небольших несортированных массивах. Если массив большой, тогда лучше отсортировать его и применить один из методов, описанных ниже.
Двоичный или бинарный поиск элемента в массиве на С
Бинарный поиск в массиве на С подходит для отсортированных массивов. Он также считается довольно простым, но при этом более эффективным, чем линейный алгоритм. Алгоритм его работы основывается на делении массива «пополам» и сверки среднего значения с заданным ключом. Например:
Допустим, у вас есть отсортированный массив с простыми числами от 1 до 10: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10].
Вам необходимо найти индекс значения числа «2». «2» будет ключом поиска, поэтому на первом этапе массив поделится «пополам». Так как индексирование элементов в массиве начинается с 0, у нас получается, что 0 + 9 / 2 = 4 (0,5 отбрасывается, и индекс округляется). Под индексом 4 у нас стоит число 5, это число сравнивается с нашим ключом. 5 не равно 2 и больше него. Если бы «среднее» значение массива совпало с ключом, тогда массив бы прекратил работу.
Так как 5 больше 2, поиск значения продолжится в части массива, содержащей числа от 1 до 5, а числа от 6 до 10 «отбрасываются в сторону». Вторым шагом алгоритма будет поиск среднего значения в «укороченном» массиве: 0 + 4 / 2 = 2. Под индексом 2 у нас расположено число 3. 3 сравнивается с ключом. Алгоритм определит, что 3 не равно 2 и больше него. Значит, будет третий шаг.
На третьем шаге еще часть массива после числа 3 «отбрасывается». Алгоритм ищет среднее значение в оставшихся индексах: 0 + 2 / 2 = 1. Под индексом 1 у нас располагается число 2, это число сравнивается с нашим ключом. Алгоритм определяет, что число 2 равно нашему ключу 2, выдает нам соответствующий индекс числа и заканчивает свою работу.
Вот как все, что мы описали выше, выглядит в скрипте:
#include <iostream>
using namespace std;
int SearchingAlgorithm (int arr[], int left, int right, int keys)
{
int middle = 0;
while (1)
{
middle = (left +right) / 2;
if (keys < arr[middle])
right = middle -1;
else if (keys > arr[])
left = middle + 1;
else
return middle;
if (left > right)
return -1;
}
}
int main()
{
selocale (LC_ALL, “rus“);
const int SIZE = 10;
int array[SIZE] = {};
int keys = 0;
int index = 0;
for (int i = 0; i < SIZE; i++)
{
array[i] = i +1;
cout < < array[i] < < “ | “;
cout < < “nn Необходимо ввести числовое значение для поиска: “;
cin > > keys;
index = SearchingAlgorithm (array, 0, SIZE, keys);
if (index >= 0)
cout < < “Значение, которое вы указали, располагается с порядковым индексом: “ < < index < < “nn“;
else
cout < < “Введенное значение в массиве не обнаружено!nn“;
return 0;
}
Если запустить программу, тогда получится следующий результат:
Необходимо ввести числовое значение для поиска: 2
Значение, которое вы указали, располагается с порядковым индексом: 1
Поиск в массиве С бинарным алгоритмом хорош тем, что он работает намного быстрее, чем линейный алгоритм. Представим, что вам необходимо осуществить поиск в массиве, содержащем 1000 элементов. Линейный поиск должен будет обойти все элементы, а бинарный — около 10. Такой результат возможен, потому что при каждом определении среднего значения часть массива, где точно нет искомого значения, просто отсеивается. Например, при первом шаге в массиве с 1000 элементов 500 отсеются, при втором — еще 250 и т. д.
Самая главная проблема бинарного поиска заключается в том, что он работает только в отсортированных и упорядоченных массивах.
Интерполирующий поиск элемента в массиве С
Интерполирующий поиск пришел из математики, и он не настолько сложен, как произносится. Его смысл сводится к тому, что необходимо определять область поиска заданного значения, вычисляя подобие расстояний между искомым элементом и всей областью. Как это выглядит в коде:
#include <iostream>
using namespace std;
int main ()
{
//Определяем массив со значениями, среди которых будет проходить поиск
int OwnArray [] {2, 3, 5, 7, 8, 90, 124, 232, 1001, 1236 };
int y = 0; //определяем текущую позицию массива
int c = 0; //определяем левую границу массива, откуда будет начинаться поиск
int d = 9; //определяем правую границу массива, докуда будет продолжаться поиск
int WeSearch = 124; //определяем элемент, который ищем
bool found;
//Запускаем интерполяционный поиск в массиве С
for (found = false; (OwnArray[c] < WeSearch) && (OwnArray[d] > WeSearch) && | found;)
y = c + ((WeSearch — OwnArray[c]) * (d — c)) / (OwnArray[d] — OwnArray[c]);
if (OwnArray[y] < WeSearch)
c = y +1;
else if (OwnArray[y] > WeSearch)
d = y -1;
else
found = true;
}
//интерполяционный поиск в массиве окончен, тогда можно вывести результаты
if (OwnArray[c] == We Search)
cout < < WeSearch < < “Элемент найден“ < < c < < endl;
else if (OwnArray[d] == WeSearch)
cout < < WeSearch < < “Элемент найден“ < < d < < endl;
else
cout < < “Извините, элемент не найден“ < < endl;
return 0;
}
Простыми словами: этот метод вычисляет область, где может быть расположен искомый элемент; если в этой области нет элемента, тогда границы области в массиве сдвигаются в ту или иную сторону. Этот метод чем-то похож на бинарный алгоритм, потому что в нем также «куски» массива постепенно отсеиваются, пока искомая область не будет сужена до 1 элемента. Если и в этом случае искомый элемент не будет найден, тогда его нет в массиве.
Заключение
Поиск элемента в массиве С можно осуществить и другими алгоритмами, например, используя:
«Решето Эратосфена»;
поиск с «барьером»;
и другие алгоритмы.
Каждый из них по—своему хорош, но описанных выше алгоритмов достаточно для понимания стратегии поиска. Ведь даже их можно модифицировать по—своему, адаптируя под собственную задачу.
Пример 12.8. На складе хранятся пустые ящики для упаковки товара. Известно, что вместимость одного пакета с конфетами x кг. Какова суммарная масса пакетов с конфетами, которые можно упаковать в такие ящики, заполнив ящик целиком?
Этапы выполнения задания
I. Исходные данные: массив а, количество чисел n, число x.
II. Результат: количество ящиков — k, суммарная масса — s.
III. Алгоритм решения задачи.
1. Ввод исходных данных.
2. Инициализация счетчика и значения суммы:
k = 0; s = 0;
3. Просматривая массив, проверим, является ли текущий элемент числом, кратным x (в этом случае ящик будет заполнен целиком). Если кратен, то увеличим счетчик k на 1, а переменную s — на значение найденного элемента массива.
4. Вывод результата.
IV. Описание переменных: n, x, k — int, a – vector <int>.
Пример 12.9. Имеется список мальчиков 10 В класса и результаты их бега на 100 м. Для сдачи норматива необходимо пробежать дистанцию не более чем за 16 с. Вывести фамилии учащихся, которые не выполнили норматив по бегу. Сколько таких учащихся в классе? Исходные данные хранятся в текстовом файле input.txt. Результат вывести в текстовый файл output.txt.
Этапы выполнения задания
Исходные данные: массивы fam (фамилии учащихся) и r (результаты бега в секундах), количество учащихся n.
II. Результат: фамилии тех учащихся, которые не выполнили норматив по бегу.
III. Алгоритм решения задачи.
1. Ввод исходных данных.
2. Инициализация счетчика: k = 0;
3. Будем просматривать массив с результатами и проверять, является ли текущий элемент числом, большим 16 (норматив не сдан). Если такое значение найдено, то выведем элемент массива fam с соответствующим номером и увеличим значение счетчика на 1.
4. Вывод значения счетчика.
IV. Описание переменных:
n, k – int, r – vector <double>,
fam – vector <string>.
Пример 12.10. В двух линейных массивах x и y, заданных случайным образом, хранятся координаты точек плоскости (–200 ≤ x[i], y[i] ≤ 200). Определить, каких точек больше — лежащих внутри или снаружи области, ограниченной окружностью радиуса r, с центром в начале координат (будем считать, что точки, лежащие на окружности, лежат внутри области).
Этапы выполнения задания
I. Исходные данные: x, y — массивы чисел, r — радиус окружности, n — количество точек.
II. Результат — одно из сообщений: «внутри точек больше», «снаружи точек больше» или «точек поровну».
III. Алгоритм решения задачи.
1. Ввод исходных данных.
2. Инициализация счетчиков: k1 = 0; k2 = 0;
3. Будем просматривать все точки и для каждой проверять принадлежность области. Если x2 + y2 ≤ R2, то точка лежит внутри области, тогда увеличим значение счетчика k1 на 1, если нет, то увеличим на 1 значение счетчика k2.
4. Сравним значения k1 и k2 и выведем результат.
IV. Описание переменных: n, k1, k2 — int, x, y – vector <int>.
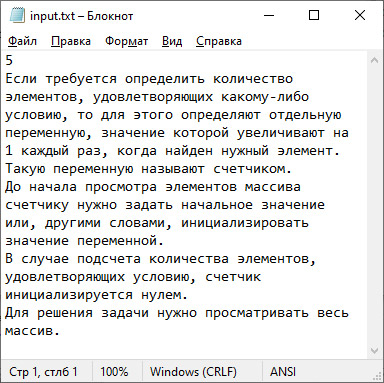
Пример 12.11. Задан одномерный массив из n целых чисел. Определить количества элементов, которые являются числами Смита. Вывести те элементы, которые являются числами Смита. (Число Смита — такое составное число, сумма цифр которого равна сумме цифр всех его простых сомножителей.) Например, числом Смита является 202 = 2 × 101, поскольку 2 + 0 + 2 = 4 и 2 + 1 + 0 + 1 = 4.
Этапы выполнения задания
I. Исходные данные: а — массив чисел, n — количество чисел в массиве.
II. Результат: числа Смита и их количество в массиве.
III. Алгоритм решения задачи.
1. Ввод исходных данных.
2. Инициализация счетчика: k = 0;
3. Будем просматривать каждый элемент массива и определять, является ли он числом Смита. Для проверки создадим функцию check, которая будет получать в качестве параметра элемент массива, а также возвращать значение true, если число является числом Смита, и false в противном случае.
3.1. Найдем сумму цифр числа.
3.2. Будем разлагать число на простые множители и для каждого множителя находить сумму цифр.
3.3. Для разложения числа на простые множители будем делить его сначала на 2 (пока делится), затем на 3. На 4 число уже делиться не будет, будем делить на 5 и т. д. Закончится разложение тогда, когда после всех делений число станет равным 1.
4. Также нам понадобится функция sum, которая для числа будет возвращать его сумму цифр.
IV. Описание переменных:
n, k – int, a – vector <int>.
Пример 12.12. Задан одномерный массив из n строк. Данные в массиве читаются из текстового файла input.txt. Каждая строка является предложением из слов, разделенных пробелами. Найти и вывести в текстовый файл output.txt те предложения, в которых нечетное количество слов. Сколько предложений вывели?
Этапы выполнения задания
I. Исходные данные: а — массив строк, n — количество строк в массиве.
II. Результат: искомые строки и их количество.
III. Алгоритм решения задачи.
1. Ввод исходных данных.
2. Инициализация счетчика: k = 0;
3. Будем просматривать каждую строку и определять, сколько в ней слов. Для проверки создадим функцию check, которая будет получать в качестве параметра элемент массива и возвращать количество слов в строке. Если количество слов является нечетным числом, то выведем строку и увеличим значение счетчика.
3.1. Перед каждым словом предложения, кроме первого, стоит пробел. Слово начинается с символа, который пробелом не является.
3.2. Добавим пробел перед первым словом, тогда количество слов будет определяться количеством сочетаний пар символов: пробел и не пробел.
IV. Описание переменных:
n, k – int, а – vector <string>.
Пример 12.8.
V. Программа:
#include <iostream>
#include <vector>
using namespace std;
int main()
{
setlocale(0,«»);
int n;
cout << «n = «;
cin >> n;
vector <int> a(n);
for (int i = 0; i < n; i++)
cin >> a[i];
int x;
cout << «масса конфет «;
cin >> x;
int s = 0, k = 0;
for (int i = 0; i < n; i++)
if (a[i] % x == 0){
k++;
s += a[i];
}
cout << «упаковали « << k;
cout << » ящиков, масса «;
cout << s << » кг» << endl;
return 0;
}
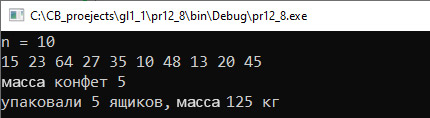
VI. Тестирование.
VII. Анализ результатов. Ящики, удовлетворяющие условию задачи, имеют массу 15, 25, 10, 20, 45.
Пример 12.9.
V. Программа:
#include <iostream>
#include <fstream>
#include <vector>
#include <string>
using namespace std;
int main()
{
ifstream fin («input.txt»);
ofstream fout («output.txt»);
int n;
fin >> n;
fin.ignore ();
vector <string> fam(n);
vector <double> r(n);
for (int i = 0; i < n; i++)
fin >> fam[i] >> r[i];
int k = 0;
for (int i = 0; i < n; i++)
if (r[i] > 16){
fout << fam[i] << endl;
k ++;
}
fout << «не сдали норматив «;
fout << k << » учащихся« << endl;
return 0;
}
VI. Тестирование.

VII. Анализ результатов. Результат Сидорова 21, а Королева 16.1, что превышает норматив.
Пример 12.10.
V. Программа:
#include <iostream>
#include <vector>
#include <ctime>
#include <cstdio>
using namespace std;
int main()
{
srand(time(NULL));
int n, r;
cout << «n = «;
cin >> n;
cout << «r = «;
cin >> r;
vector <int> x(n), y(n);
for (int i = 0; i < n; i++){
x[i] = rand() % 401 — 200;
y[i] = rand() % 401 — 200;
}
int k1 = 0, k2 = 0;
for (int i = 0; i < n; i++)
if (x[i] * x[i] + y[i] * y[i]
<= r * r)
k1++;
else
k2++;
if (k1 > k2)
cout << «vnutri»;
else
if (k1 < k2)
cout << «snarugi»;
else
cout << «porovnu»;
cout << endl;
return 0;
}
VI. Тестирование.
VII. Анализ результатов. По сообщениям, которые выдает программа, сложно судить о ее правильности. Для проверки можно вывести значения координат каждой точки в файл и при проверке ставить дополнительные пометки. Например, «+», если точка внутри, и «-», если снаружи.
Пример 12.11.
V. Программа:
#include <iostream>
#include <vector>
using namespace std;
int sum(int x)
{
int s = 0;
while (x >0){
s += x % 10;
x /= 10;
}
return s;
}
bool check(int x)
{
int s1 = sum(x);
int s2 = 0;
int d = 2;
//разложение на простые множители
while (x != 1){
while (x % d == 0){
s2 += sum(d);
x /= d;
}
d++;
}
return (s1 == s2);
}
int main()
{
int n;
cout << «n = «;
cin >> n;
vector <int> a(n);
for (int i = 0; i < n; i++)
cin >> a[i];
int k = 0;
for (int i = 0; i < n; i++)
if (check(a[i])){
k++;
cout << a[i] << » «;
}
cout << endl << «vsego « << k;
cout << » chisel Smita» << endl;
return 0;
}
VI. Тестирование.
Пример 12.12.
V. Программа:
#include <iostream>
#include <fstream>
#include <vector>
#include <string>
#include <windows.h>
using namespace std;
using namespace std::__cxx11;
int check(string x)
{
int k = 0;
x = » « + x;
int len = x.length();
for (int i = 0; i < len — 1; i++)
if (x[i] == ‘ ‘ && x[i + 1] != ‘ ‘)
k++;
return k;
}
int main()
{
SetConsoleCP(1251);
SetConsoleOutputCP(1251);
ifstream fin(«input.txt»);
ofstream fout(«output.txt»);
int n;
fin >> n;
fin.ignore();
vector <string> a(n);
for (int i = 0; i < n; i++)
getline(fin, a[i]);
int k = 0;
for (int i = 0; i < n; i++)
if (check(a[i]) % 2){
fout << a[i] << endl;
k++;
}
fout << «Всего — « << k;
fout << » строк(–а, –u)» << endl;
return 0;
}
VI. Тестирование.
-
Поиск в массиве элемента с заданным значением
Рассматриваемый
алгоритм находит только первое вхождение
элемента с заданным значением. Результат
поиска может быть как удовлетворительным,
так и не удовлетворительным, например,
при отсутствии в массиве элемента с
искомым значением. Цикл поиска искомого
элемента кодируется структурой
УНИВЕРСАЛЬНОГО ЦИКЛА ДО. Наглядный
тест:
Рассмотрим
текст готовой программы.
#include
«stdafx.h»
#include
<conio.h>
#include
<locale.h>
#define
k_Max 100 // Предельный размер массива
int
_tmain(int argc, _TCHAR* argv[])
{
//Программа
поиска заданного значения в одномерном
массиве
typedef
int Type_Elements_a; //Тип элементов массива a
typedef
Type_Elements_a Type_a[k_Max]; //Тип массива a
Type_a
a; //Сам массив a, котором идет поиск
int
k; //Текущий предельный размер
массива
int
s; //Искомое значение в массиве
int
is; //Индекс найденного элемента
массива
bool
Done; //= True, если поиск успешен
int
i; //Переменная цикла
поиска
setlocale(
LC_ALL, «russian»
); //установка русского режима
printf(«Программа
поиска заданного значения в «);
printf(«одномерном
массивеn»);
printf(«nВведите
количество элементов вводимого
массиваn»);
scanf(«%d»,&k);
//k теперь определено
printf(«n»);
//
Задание i — номера вводимого элемента
массива
for
(int i = 0; i < k; i++)
{
printf(«Введите
значение элемента номер %d) «,i);
scanf(«%d»,&a[i]);
}
printf(«nВведите
значение искомого элементаn»);
scanf(«%d»,&s);
//
Поиск значения s в массиве a */
Done
= false; //Искомый элемент пока не найден
i
= 1; //Инициализация переменной цикла
//Цикл
поиска вхождения значения в массив
do
{
if
(a[i] == s)
{
is
= i; //Запоминание индекса найденного
элемента
Done
= true; //Выработка признака — элемент найден
}
i++;
//Индекс следующего элемента i = i + 1;
}
while (!(((i > k) || (Done))));
//Вывод
на экран результатов поиска
if
(Done)
{
printf(«nВ
массиве найдено искомое значение,
равное: «);
printf(«%d»,
s);
printf(«nискомое
значение имеет номер %d»,
is);
}
else
printf(«В
массиве нет искомого значения, равного:
%d», s);
//Завершение
выполнения программы
printf(«nНажмите
любую клавишуn»);
_getch();
return
0;
}
-
Алгоритм инициализации элементов одномерного массива значениями ряда целых нечетных чисел
Далее
показан алгоритм инициализации элементов
одномерного массива значениями ряда
целых нечетных чисел a[0]
= 1, a[1] = 3, a[2]
= 5, . . . . Ряд нечетных чисел представляет
собой арифметическую прогрессию с
начальным значение 0 и шагом 2
int
k = 20; //Текущее количество
элементов массива a
//Инициализация
всех элементов массива a
значениеми
//ряда
целых нечетных чисел a[0]
= 1, a[1] = 3, a[2]
= 5,. . }
int
ix = 1.0; //{Начальное значение
арифметической прогрессии}
//Задание
i – номера инициализируемого
элемента массива
for
(int i = 0; i<k; i++)
{
//Инициализация
очередного i-го элемента
a[i]
= ix;
//Расчет
значения следущего члена арифметической
прогрессии
ix
= ix + 2; //Расчет следующего
члена
}
Обратим
внимание на то, что для инициализации
элементов одномерного массива значениями
ряда целых четных чисел a[0]=2,
a[1]=4,a[2]=6,…требуется
лишь исправить отдельные комментарии
и заменить 1 на 2 в операторе определения
начального значения арифметической
прогрессии.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #