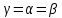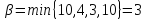Как найти элементы платежной матрицы

Рассмотрим
игру (модель конфликтной ситуации), в
которой участвуют два игрока A
и B,
имеющие прямо противоположные интересы,
поэтому выигрыш одного равен проигрышу
другого. Такая игра называется парной
игрой с нулевой суммой. Если игрок A
выигрывает a,
то игрок B
при этом выигрывает -a,
поэтому сумма выигрышей всегда равна
нулю. Процесс
игры заключается в последовательных
ходах (личных – сознательных и случайных)
противников, а
совокупность
правил, определяющих выбор варианта
действий при каждом личном ходе в
зависимости от сложившейся ситуации
называется стратегией
игрока.
При конечном числе стратегий игра будет
конечной. Пусть у игрока A
имеется m
возможных стратегий A₁,
A₂,
…, A_m,
а у игрока B
– n
возможных стратегий B₁,
B₂,
…, B_n.
Пусть также известны величины a_ij
–
выигрыши игрока A
при использовании
A_i
с
его
стороны и
B_j
со стороны противника. Тогда игра,
называемая игрой
m
× n,
может быть представлена таблицей,
называемой платежной матрицей или
просто матрицей игры.

Платежная
матрица (матрица игры)

Приведение
игры к матричной форме может само по
себе составить трудную задачу, однако
таким путем многоходовая игра фактически
сводится к одноходовой – от игрока
требуется сделать только один ход:
выбрать подходящую стратегию. Для
данного игрока среди всех стратегий
имеется оптимальная,
обеспечивающая ему максимальный выигрыш.
Задача
теории игр
– нахождение оптимальных стратегий
игроков в предположении одинаковой
«разумности» противников.

14. Нижняя и верхняя цена игры. Принцип минимакса. Решение игры в чистых стратегиях.

Каждый
игрок выбирает для себя наиболее выгодную
стратегию. При этом первый игрок стремится
выбрать такую стратегию, которая
доставляет ему максимальный выигрыш,
тогда как второй игрок выбирает стратегию,
приводящую его к минимальному проигрышу.
В этой связи вводят понятия нижней и
верхней чистой цены игры.

По
матрице игры определяются нижняя

и
верхняя

цены
игры.

Пусть
,
,
тогда

Нижней
чистой ценой игры
(максимином) называется число, определяемое
по формуле:

Верхней чистой
ценой игры (минимаксом) называется
число, определяемое по формуле:

Принцип
минимакса:

Принцип
выбора противниками стратегий,
соответствующих получению ими выигрышей

и
.

Принцип
осторожности, заставляющий игроков
придерживаться максиминной и минимаксной
стратегий соответственно, а минимаксную
стратегию и максиминную стратегию
называют общим термином «Минимаксные
стратегии»

Известно,
что минимаксные стратегии устойчивы
по отношению к информации о поведении
другой стороны только в случае, если
.
В этом случае матрица игры имеет седловую
точку, а величина

называется ценой игры.

Оптимальные
чистые стратегии
– стратегии

и
,
при которых достигается выигрыш
.
Совокупность этих стратегий – решение
игры

(Иными словами:
Целью участников любой матричной игры
является выбор наиболее выгодных
стратегий, доставляющих игроку А
максимальный выигрыш, а игроку В
минимальный проигрыш.

Определение. Чистую
стратегию Ai игрока А называют оптимальной,
если при ее применении выигрыш игрока
А не уменьшается, какими бы своими
стратегиями не пользовался игрок В.
Оптимальной для игрока В называют чистую
стратегию Bj, при использовании которой
проигрыш игрока В не увеличивается,
какие бы стратегии не применял игрок
А.)

Пример 1 —
Самая простая конечная игра
– игра
.
Ее матрица имеет вид таблицы. Если для
этой матрицы

, то игра имеет седловую точку и ее
решение – это пара чистых стратегий,
пересекающихся в седловой точке.

Пример 2 —
Найти нижнюю и верхнюю цены игры с
платежной матрицей

В
каждой строке платежной матрицы найдем
наименьший элемент и запишем его справа
от матрицы. В каждом столбце платежной
матрицы найдем наибольший элемент, и
запишем его снизу от матрицы. В
результате получим таблицу

Нижняя
цена игры

Верхняя
цена игры

,
цена
игры =3

«Теория систем и системный анализ»

И. Б. Родионов

Лекция 11: Теория игр и принятие решений

Предмет и задачи теории игр

Классическими задачами системного анализа являются игровые задачи принятия решений в условиях риска и неопределенности.

Неопределенными могут быть как цели операции, условия выполнения операции, так и сознательные действия противников или других лиц, от которых зависит успех операции.

Разработаны специальные математические методы, предназначенные для обоснования решений в условиях риска и неопределенности. В некоторых, наиболее простых случаях эти методы дают возможность фактически найти и выбрать оптимальное решение. В более
сложных случаях эти методы доставляют вспомогательный материал, позволяющий глубже разобраться в сложной ситуации и оценить каждое из возможных решений с различных точек зрения, и принять решений с учетом его возможных последствий. Одним из важных условий принятия решений в этом случае является минимизация риска.

При решении ряда практических задач исследования операций (в области экологии, обеспечения безопасности жизнедеятельности и т. д.) приходится анализировать ситуации, в которых сталкиваются две (или более) враждующие стороны, преследующие различные цели, причем результат любого мероприятия каждой из сторон зависит от того, какой образ действий выберет противник. Такие ситуации мы можно отнести к конфликтным ситуациям.

Теория игр является математической теорией конфликтных ситуаций, при помощи которой можно выработать рекомендации по рациональному образу действий участников конфликта. Чтобы сделать возможным математический анализ ситуации без учета второстепенных факторов, строят упрощенную, схематизированную модель ситуации, которая называется игрой. игра ведется по вполне определенным правилам, под которыми понимается система условий, регламентирующая возможные варианты действий игроков; объем информации каждой стороны о поведении другой; результат игры, к которому приводит каждая данная совокупность ходов.

Результат игры (выигрыш или проигрыш) вообще не всегда имеет количественное выражение, но обычно можно, хотя бы условно, выразить его числовым значением.

Ход — выбор одного из предусмотренных правилами игры действий и его осуществление. Ходы делятся на личные и случайные. Личным ходом называется сознательный выбор игроком одного из возможных вариантов действий и его осуществление. Случайным ходом называется выбор из ряда возможностей, осуществляемый не решением игрока, а каким-либомеханизмом случайного выбора (бросание монеты, выбор карты из перетасованной колоды и т. п.). Для каждого случайного хода правила игры определяют распределение вероятностей возможных исходов. Игра может состоять только их личных или только из случайных ходов, или из их комбинации. Следующим основным понятием теории игр является понятие стратегии. Стратегия — это априори принятая игроком система решений (вида «если — то»), которых он придерживается во время ведения игры, которая может быть представлена в виде алгоритма и выполняться автоматически.

Целью теории игр является выработка рекомендаций для разумного поведения игроков в конфликтной ситуации, т. е. определение «оптимальной стратегии» для каждого из них. Стратегия, оптимальная по одному показателю, необязательно будет оптимальной по другим. Сознавая эти ограничения и поэтому не придерживаясь слепо рекомендаций, полученных игровыми методами, можно все же разумно использовать математический аппарат теории игр для выработки, если не в точности оптимальной, то, во всяком случае «приемлемой» стратегии.

Игры можно классифицировать: по количеству игроков, количеству стратегий, характеру взаимодействия игроков, характеру выигрыша, количеству ходов, состоянию информации и т.д. [2, 7, 8].

В зависимости от количества игроков различают игры двух и n игроков. Первые из них наиболее изучены. Игры трех и более игроков менее исследованы из-за возникающих принципиальных трудностей и технических возможностей получения решения.

В зависимости от числа возможных стратегий игры делятся на «конечные» и «бесконечные».

Игра называется конечной, если у каждого игрока имеется только конечное число стратегий, и бесконечной, если хотя бы у одного
из игроков имеется бесконечное число стратегий.

По характеру взаимодействия игры делятся на бескоалиционные: игроки не имеют права вступать в соглашения, образовывать коалиции; коалиционные (кооперативные) — могут вступать в коалиции.

В кооперативных играх коалиции заранее определены.

По характеру выигрышей игры делятся на: игры с нулевой суммой (общий капитал всех игроков не меняется, а перераспределяется между игроками; сумма выигрышей всех игроков равна нулю) и игры с ненулевой суммой.

По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, выпуклые и др.

Матричная игра — это конечная игра двух игроков с нулевой суммой, в которой задается выигрыш игрока 1 в виде матрицы (строка матрицы соответствует номеру применяемой стратегии игрока 1, столбец — номеру применяемой стратегии игрока на пересечении строки и столбца матрицы находится выигрыш игрока 1, соответствующий применяемым стратегиям).

Для матричных игр доказано, что любая из них имеет решение и оно может быть легко найдено путем сведения игры к задаче линейного программирования.

Биматричная игра — это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец — стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице — выигрыш игрока )

Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной. Доказано, что игры этого класса имеют решения, однако не разработано практически приемлемых методов их нахождения.

Если функция выигрышей является выпуклой, то такая игра называется выпуклой. Для них разработаны приемлемые методы решения, состоящие в отыскании чистой оптимальной стратегии (определенного числа) для одного игрока и вероятностей применения чистых оптимальных стратегий другого игрока. Такая задача решается сравнительно легко.

Запись матричной игры в виде платежной матрицы

Рассмотрим конечную игру, в которой первый игрок А имеет m стратегий, а второй игрок B-n стратегий. Такая игра называется игрой m×n. Обозначим стратегии A₁, А₂, …, А_m; и В₁, В₂, …, В_n. Предположим, что каждая сторона выбрала определенную стратегию: A_i или B_j. Если игра состоит только из личных ходов, то выбор стратегий однозначно определяет исход игры — выигрыш одной из сторон a_ij. Если игра содержит кроме личных случайные ходы, то выигрыш при паре стратегий A_i и B является случайной величиной, зависящей от исходов всех случайных ходов. В этом случае естественной оценкой ожидаемого выигрыша является математическое ожидание случайного выигрыша, которое также обозначается за a_ij.

Предположим, что нам известны значения a_ij при каждой паре стратегий. Эти значения можно записать в виде прямоугольной таблицы (матрицы), строки которой соответствуют стратегиям A_i, а столбцы — стратегиям B_j.

Тогда, в общем виде матричная игра может быть записана следующей платежной матрицей:

	B1	B2	…	Bn
A1	a11	a12	…	a1n
A2	a21	a22	…	a2n
…	…	…	…	…
Am	am1	am2	…	amn

Таблица — Общий вид платежной матрицы матричной игры

где A_i — названия стратегий игрока 1, B_j — названия стратегий игрока 2, a_ij — значения выигрышей игрока 1 при выборе им i–й стратегии, а игроком 2 — j-й стратегии. Поскольку данная игра является игрой с нулевой суммой, значение выигрыша для игрока 2 является величиной, противоположенной по знаку значению выигрыша игрока 1.

Понятие о нижней и верхней цене игры. Решение игры в чистых стратегиях

Каждый из игроков стремится максимизировать свой выигрыш с учетом поведения противодействующего ему игрока. Поэтому для игрока 1 необходимо определить минимальные значения выигрышей в каждой из стратегий, а затем найти максимум из этих значений, то есть определить величину

V_н = max_i min_j a_ij

или найти минимальные значения по каждой из строк платежной матрицы, а затем определить максимальное из этих значений. Величина V_н называется максимином матрицы или нижней ценой игры. Та стратегия игрока, которая соответствует максимину V_н называется максиминной стратегией.

Очевидно, если мы будем придерживаться максиминной стратегии, то нам при любом поведении противника гарантирован выигрыш, не меньший V_н. Поэтому величина V_н — это тот гарантированный минимум, который мы можем себе обеспечить, придерживаясь своей наиболее осторожной стратегии.

Величина выигрыша игрока 1 равна, по определению матричной игры, величине проигрыша игрока Поэтому для игрока 2 необходимо определить значение

V_в = min_j max_i a_ij

Или найти максимальные значения по каждому из столбцов платежной матрицы, а затем определить минимальное из этих значений. Величина V_в называется минимаксом матрицы, верхней ценой игры или минимаксным выигрышем. Соответствующая выигрышу стратегия противника называется его минимаксной стратегией. Придерживаясь своей наиболее осторожной минимаксной стратегии, противник гарантирован, что в любом случае он проиграет не больше V_в.

В случае, если значения V_н и V_в не совпадают, при сохранении правил игры (коэффициентов a_ij ) в длительной перспективе, выбор стратегий каждым из игроков оказывается неустойчивым. Устойчивость он приобретает лишь при равенстве V_н = V_в = V. В этом случае говорят, что игра имеет решение в чистых стратегиях, а стратегии, в которых достигается V — оптимальными чистыми стратегиями. Величина V называется чистой ценой игры [8].

Например, в матрице:

	B1	B2	B3	B4	Minj
A1	17	16	15	14	14
A2	11	18	12	13	11
A3	18	11	13	12	11
Maxi	18	18	15	14

Таблица — Платежная матрица, в которой существует решение в чистых стратегиях

существует решение в чистых стратегиях. При этом для игрока 1 оптимальной чистой стратегией будет стратегия A₁, а для игрока 2 — стратегия B₄.

В матрице решения в чистых стратегиях не существует, так как нижняя цена игры достигается в стратегии A₁ и ее значение равно 12, в то время как верхняя цена игры достигается в стратегии B₄ и ее значение равно 13.

	B1	B2	B3	B4	Minj
A1	17	16	15	12	12
A2	11	18	12	13	11
A3	18	11	13	12	11
Maxi	18	18	15	13

Таблица — Платежная матрица, в которой не существует решения в чистых стратегиях

Уменьшение порядка платежной матрицы

Порядок платежной матрицы (количество строк и столбцов) может быть уменьшен за счет исключения доминируемых и дублирующих стратегий.

Стратегия K* называется доминируемой стратегией K**, если при любом варианте поведения противодействующего игрока выполняется соотношение

A_k* < A_k**,

где A_k* и A_k** — значения выигрышей при выборе игроком, соответственно, стратегий K* и K**.

В случае, если выполняется соотношение

A_k* = A_k**,

стратегия K* называется дублирующей по отношению к стратегии K**.

Например, в матрице с доминируемыми и дублирующими стратегиями стратегия A₁ является доминируемой по отношению к стратегии A₂, стратегия B₆ является доминируемой по отношению к стратегиям B₃, B₄ и B₅, а стратегия B₅ является дублирующей по отношению к стратегии B₄.

	B1	B2	B3	B4	B5	B6
A1	1	2	3	4	4	7
A2	7	6	5	4	4	8
A3	1	8	2	3	3	6
A4	8	1	3	2	2	5

Таблица — Платежная матрица с доминируемыми и дублирующими стратегиями

Данные стратегии не будут выбраны игроками, так как являются заведомо проигрышными и удаление этих стратегий из платежной матрицы не повлияет на определение нижней и верхней цены игры, описанной данной матрицей.

Множество недоминируемых стратегий, полученных после уменьшения размерности платежной матрицы, называется еще множеством Парето.

Примеры игр

1. Игра «Цыпленок»

Игра «Цыпленок» заключается в том, что игроки вступают во взаимодействие, которое ведет в нанесению серьезного вреда каждому из них, пока один из игроков не выйдет из игры. Пример использования этой игры — взаимодействие автотранспортный средств, например, ситуации, когда два автомобиля идут навстречу друг другу, и тот, который первым сворачивает в сторону, считается «слабаком» или «цыпленком». Смысл игры заключается в создании напряжения, которое бы привело к устранению игрока. Подобная ситуация часто встречается в среде подростков или агрессивно настроенных молодых людей, хотя иногда несет в себе меньший риск. Еще одно из применений этой игры — ситуация, в которой две политические партии вступают в контакт, при котором они не могут ничего выиграть, и только гордость заставляет их сохранять противостояние. Партии медлят с уступками до тех пор, пока не дойдут до финальной точки. Возникающее психологическое напряжение может привести одного из игроков к неправильной стратегии поведения: если никто из игроков не уступает, то столкновение и фатальная развязка неизбежны.

Платежная матрица игры выглядит следующей:

	Уступить	Не уступать
Уступить	0, 0	-1, +1
Не уступать	+1, -1	-100, -100

2. Игра «коршун и голубь»

Игра «коршун и голубь» является биологическим примером игры. В этой версии двое игроков, обладающих неограниченными ресурсами, выбирают одну из двух стратегий поведения. Первая («голубь») заключается в том, что игрок демонстрирует свою силу, запугивая противника, а вторая («коршун») — в том, что игрок физически атакует противника. Если оба из игроков выбирают стратегию «коршуна», они сражаются, наносф друг другу увечья. Если один из игроков выбирает стратегию «коршуна», а второй «голубя» — то первый побеждает второго. В случае, если оба игрока — «голуби», то соперники приходит к компромиссу, получая выигрыш, который оказывается меньше, чем выигрыш «коршуна», побеждающего «голубя», как это следует из платежной матрицы этой игры.

	Коршун	Голубь
Коршун	1/2*(V-C), 1/2*(V-C)	V, 0
Голубь	0, V	V/2, V/2

Здесь V — цена соглашения, C — цена конфликта, причем V<C.

В игре «коршун и голубь» есть три точки равновесия по Нэшу:

1. первый игрок выбирает «коршуна», а второй «голубя».
2. первый игрок выбирает «голубя», а второй «коршуна».
3. оба игрока выбирают смешанную стратегию, в которой «коршун» выбирается с вероятностью p, а «голубь» — с вероятностью 1-p.

3. Дилемма заключенного

«Дилемма заключенного» — одна из наиболее распространенных конфликтных ситуаций, рассматриваемая в теории игр.

Классическая «дилемма заключенного» звучит следующим образом: двое подозреваемых, A и B, находятся в разных камерах. Следователь, навещая их поодиночке, предлагает сделку следующего содержания: если один из них будет свидетельствовать против другого, а второй будет молчать, то первый заключенный будет освобожден, а второго осудят на 10 лет. Если оба будут молчать, то отсидят по 6 месяцев. Если оба предадут друг друга, то каждый получит по 2 года. Каждый из заключенных должен принять решение: предать подельника или молчать, не зная о том, какое решение принял другой. Дилемма: какое решение примут заключенные?

Платежная матрица игры:

—	Заключенный B молчит	Заключенный B предает
Заключенный A молчит	Оба осуждены на 6 месяцев	Заключенного А осуждают на 10 лет Заключенный В выходит на свободу
Заключенный A предает	Заключенный A выходит на свободу Заключенного B осуждают на 10 лет	Оба осуждены на 2 года

В данном случае, результат базируется на решении каждого из заключенных. Положение игроков осложняется тем, что они не знают о том, какое решение принял другой, и тем, что они не доверяют друг другу.

Наилучшей стратегией игроков будет кооперация, при которой оба молчат, и получают максимальный выигрыш (меньший срок), каждое другое решение будет менее выигрышным.

Проанализируем «дилемму заключенного», перейдя для наглядности к платежной матрице канонического вида:

—	Кооперация	Отказ от кооперации
Кооперация	3, 3	0, 5
Отказ от кооперации	5, 0	1, 1

Согласно этой матрице, цена взаимного отказа от кооперации (S) составляет по 1 баллу для каждого из игроков, цена за кооперацию (R) — по 3 балла, а цена соблазна предать другого (T) составляет 5 баллов. Можем записать следующее неравенство: T > R > S. При повторении игры несколько раз, выбор кооперации превосходит соблазн предать и получить максимальный выигрыш: 2 R > T + S.

Равновесие по Нэшу.

Равновесие по Нэшу — это ситуация, когда ни у одного игрока нет стимулов изменять свою стратегию при данной стратегии другого игрока (другой фирмы), позволяющая игрокам достичь компромиссного решения.

Определение равновесия по Нэшу и его существование определяется следующим образом.

Пусть (S, f) — это игра, в которой S — множество стратегий, f — множество выигрышей. Когда каждый из игроков i ∈ {1, …, n} выбирает стратегию x_i &isin S, где x = (x₁, …, x_n), тогда игрок i получает выигрыш f_i(x). Выигрыш зависит от стратегии, выбранной всеми игроками. Стратегия x* ∈ S является равновесием по Нэшу, если никакое отклонение от нее каким-то одним игроком не приносит ему прибыль, то есть, для всех i выполняется следующее неравенство:

f_i(x*) ≥ f_i(x_i, x*_-i)

Например, игра «дилемма заключенного» имеет одно равновесие по Нэшу — ситуацию, когда оба заключенных предают друг друга.

Проще всего определить равновесие по Нэшу можно по платежной матрице, особенно в случаях, когда в игре участвуют два игрока, имеющие в арсенале более двух стратегий. Так как в этом случае формальный анализ будет достаточно сложным, применяется мнемоническое правило, которое заключается в следующем: ячейка платежной матрицы представляет собой равновесие по Нэшу, если первое число, стоящее в ней, является максимальным среди всех значений, представленных в столбцах, а второе число, стоящее в ячейке — максимальное число среди всех строк.

Например, применим это правило для матрицы 3×3:

	A	B	C
A	0, 0	25, 40	5, 10
B	40, 25	0, 0	5, 15
C	10, 5	15, 5	10, 10

Точки равновесия по Нэшу: (B,A), (A,B) и (C,C). Indeed, for cell (B,A), так как 40 — максимальное значение в первом столбце, 25 максимальное значение во втором ряду. Для ячейки (A,B) 25 — это максимальное значение во втором столбце, 40 — максимальное значение во втором ряду. То же самое и для ячейки (C,C).

Рассмотрим пример игры в загрязнения (окружающей среды). Здесь объектом нашего внимания станет такой вид побочных эффектов производства, как загрязнение. Если бы фирмы никогда и никого не спрашивали о том, как им поступить, любая из них скорее предпочла бы создавать загрязнения, чем устанавливать дорогостоящие очистители. Если же какая-нибудь фирма решилась бы уменьшить вредные выбросы, то издержки, а, следовательно, и цены на ее продукцию, возросли бы, а спрос бы упал. Вполне возможно, эта фирма просто обанкротилась бы. Живущие в жестоком мире естественного отбора, фирмы скорее предпочтут оставаться в условиях равновесия по Нэшу (ячейка D), при котором не нужно расходовать средства на очистные сооружения и технологии. Ни одной фирме не удастся повысить прибыль, уменьшая загрязнение.

	Фирма 1
Фирма 2	Низкий уровень загрязнения	Высокий уровень загрязнения
Низкий уровень загрязнения	А 100,100	В -30,120
Высокий уровень загрязнения	С 120,-30	D 100,100

Таблица — Платежная матрица игры в загрязнение окружающей среды.

Вступив в экономическую игру, каждая неконтролируемая государством и максимизирующая прибыль сталелитейная фирма будет производить загрязнения воды и воздуха. Если какая-либо фирма попытается очищать свои выбросы, то тем самым она будет вынуждена повысить цены и потерпеть убытки. Некооперативное поведение установит равновесие по Нэшу в условиях высоких выбросов. Правительство может предпринять меры с тем, чтобы равновесие переместилось в ячейку А. В этом положении загрязнение будет незначительным, прибыли же останутся теми же.

Игры загрязнения — один из случаев того, как механизм действия «невидимой руки» не срабатывает. Это ситуация, когда равновесие по Нэшу неэффективно. Иногда подобные неконтролируемые игры становятся угрожающими, и здесь может вмешаться правительство. Установив систему штрафов и квот на выбросы, правительство может побудить фирмы выбрать исход А, соответствующий низкому уровню загрязнения. Фирмы зарабатывают ровно столько же, сколько и прежде, при больших выбросах, мир же становится несколько чище.

Пример решения матричной игры в чистых стратегиях

Рассмотрим пример решения матричной игры в чистых стратегиях, в условиях реальной экономики, в ситуации борьбы двух предприятий за рынок продукции региона.

Задача.

Два предприятия производят продукцию и поставляют ее на рынок региона. Они являются единственными поставщиками продукции в регион, поэтому полностью определяют рынок данной продукции в регионе.

Каждое из предприятий имеет возможность производить продукцию с применением одной из трех различных технологий. В зависимости от экологичности технологического процесса и качества продукции, произведенной по каждой технологии, предприятия могут установить цену единицы продукции на уровне 10, 6 и 2 денежных единиц соответственно. При этом предприятия имеют различные затраты на производство единицы продукции.

Технология	Цена реализации единицы продукции, д.е.	Полная себестоимость единицы продукции, д.е.
Предприятие 1	Предприятие 2
I	10	5	8
II	6	3	4
III	2	1	1

Таблица — Затраты на единицу продукции, произведенной на предприятиях региона (д.е.).

В результате маркетингового исследования рынка продукции региона была определена функция спроса на продукцию:

Y = 6 — 0.5⋅X,

где Y — количество продукции, которое приобретет население региона (тыс. ед.), а X — средняя цена продукции предприятий, д.е.

Данные о спросе на продукцию в зависимости от цен реализации приведены в таблице:

Цена реализации 1 ед. продукции, д.е.	Средняя цена реализации 1 ед. продукции, д.е.	Спрос на продукцию, тыс. ед.
Предприятие 1	Предприятие 2
10	10	10	1
10	6	8	2
10	2	6	3
6	10	8	2
6	6	6	3
6	2	4	4
2	10	6	3
2	6	4	4
2	2	2	5

Таблица — Спрос на продукцию в регионе, тыс. ед.

Значения Долей продукции предприятия 1, приобретенной населением, зависят от соотношения цен на продукцию предприятия 1 и предприятия В результате маркетингового исследования эта зависимость установлена и значения вычислены:

Цена реализации 1 ед. продукции, д.е.	Доля продукции предприятия 1, купленной населением
Предприятие 1	Предприятие 2
10	10	0,31
10	6	0,33
10	2	0,18
6	10	0,7
6	6	0,3
6	2	0,2
2	10	0,92
2	6	0,85
2	2	0,72

Таблица — Доля продукции предприятия 1, приобретаемой населением в зависимости от соотношения цен на продукцию

По условию задачи на рынке региона действует только 2 предприятия. Поэтому долю продукции второго предприятия, приобретенной населением, в зависимости от соотношения цен на продукцию можно определить как единица минус доля первого предприятия.

Стратегиями предприятий в данной задаче являются их решения относительно технологий производства продукции. Эти решения определяют себестоимость и цену реализации единицы продукции. В задаче необходимо определить:

1. Существует ли в данной задаче ситуация равновесия при выборе технологий производства продукции обоими предприятиями?
2. Существуют ли технологии, которые предприятия заведомо не будут выбирать вследствие невыгодности?
3. Сколько продукции будет реализовано в ситуации равновесия? Какое предприятие окажется в выигрышном положении?

Решение задачи

1. Определим экономический смысл коэффициентов выигрышей в платежной матрице задачи. Каждое предприятие стремится к максимизации прибыли от производства продукции. Но кроме того, в данном случае предприятия ведут борьбу за рынок продукции в регионе. При этом выигрыш одного предприятия означает проигрыш другого. Такая задача может быть сведена к матричной игре с нулевой суммой. При этом коэффициентами выигрышей будут значения разницы прибыли предприятия 1 и предприятия 2 от производства продукции. В случае, если эта разница положительна, выигрывает предприятие 1, а в случае, если она отрицательна — предприятие 2.
2. Рассчитаем коэффициенты выигрышей платежной матрицы. Для этого необходимо определить значения прибыли предприятия 1 и предприятия 2 от производства продукции.

Прибыль предприятия в данной задаче зависит:

• от цены и себестоимости продукции;
• от количества продукции, приобретаемой населением региона;
• от доли продукции, приобретенной населением у предприятия.

Таким образом, значения разницы прибыли предприятий, соответствующие коэффициентам платежной матрицы, необходимо определить по формуле:

D = p⋅(S⋅R1 — S⋅C1) — (1 — p)⋅(S⋅R2 — S⋅C2),

где D — значение разницы прибыли от производства продукции предприятия 1 и предприятия

p — доля продукции предприятия 1, приобретаемой населением региона;

S — количество продукции, приобретаемой населением региона;

R1 и R2 — цены реализации единицы продукции предприятиями 1 и

C1 и C2 — полная себестоимость единицы продукции, произведенной на предприятиях 1 и

Вычислим один из коэффициентов платежной матрицы.

Пусть, например, предприятие 1 принимает решение о производстве продукции в соответствии с технологией III, а предприятие 2 — в соответствии с технологией II. Тогда цена реализации единицы. продукции для предприятия 1 составит 2 д.е. при себестоимости единицы. продукции 1,5 д.е. Для предприятия 2 цена реализации единицы. продукции составит 6 д.е. при себестоимости 4 д.е..

Количество продукции, которое население региона приобретет при средней цене 4 д.е., равно 4 тыс. ед. (таблица 1). Доля продукции, которую население приобретет у предприятия 1, составит 0,85, а у предприятия 2 — 0,15 (табл. 1.3). Вычислим коэффициент платежной матрицы a₃₂ по формуле:

a₃₂ = 0,85⋅(4⋅2 — 4×1,5) — 0,15⋅(4⋅6 — 4⋅4) = 0,5 тыс. ед.

где i=3 — номер технологии первого предприятия, а j=2 — номер технологии второго предприятия.

Аналогично вычислим все коэффициенты платежной матрицы. В платежной матрице стратегии A₁ — A₃– представляют собой решения о технологиях производства продукции предприятием 1, стратегии B₁– B₃ — решения о технологиях производства продукции предприятием 2, коэффициенты выигрышей — разницу прибыли предприятия 1 и предприятия

	B1	B2	B3	Minj
A1	0,17	0,62	0,24	0,17
A2	0,3	-1,5	-0,8	-1
A3	0,9	0,5	0,4	0,4
Maxi	3	0,62	0,4

Таблица — Платежная матрица в игре «Борьба двух предприятий».

В данной матрице нет ни доминируемых, ни дублирующих стратегий. Это значит, что для обоих предприятий нет заведомо невыгодных технологий производства продукции. Определим минимальные элементы строк матрицы. Для предприятия 1 каждый из этих элементов имеет значение минимально гарантированного выигрыша при выборе соответствующей стратегии. Минимальные элементы матрицы по строкам имеют значения: 0,17, -1,5, 0,4.

Определим максимальные элементы столбцов матрицы. Для предприятия 2 каждый из этих элементов также имеет значение минимально гарантированного выигрыша при выборе соответствующей стратегии. Максимальные элементы матрицы по столбцам имеют значения: 3, 0,62, 0,4.

Нижняя цена игры в матрице равна 0,4. Верхняя цена игры также равна 0,4. Таким образом, нижняя и верхняя цена игры в матрице совпадают. Это значит, что имеется технология производства продукции, которая является оптимальной для обоих предприятий в условиях данной задачи. Эта технология III, которая соответствует стратегиям A₃ предприятия 1 и B₃ предприятия Стратегии A₃ и B₃ — чистые оптимальные стратегии в данной задаче.

Значение разницы прибыли предприятия 1 и предприятия 2 при выборе чистой оптимальной стратегии положительно. Это означает, что предприятие 1 выиграет в данной игре. Выигрыш предприятия 1 составит 0,4 тыс. д.е. При этом на рынке будет реализовано 5 тыс. ед. продукции (реализация равна спросу на продукцию, таблица 1).. Оба предприятия установят цену за единицу продукции в 2 д.е. При этом для первого предприятия полная себестоимость единицы продукции составит 1,5 д.е., а для второго — 1 д.е. Предприятие 1 окажется в выигрыше лишь за счет высокой доли продукции, которую приобретет у него население.

Критерии принятия решения

ЛПР определяет наиболее выгодную стратегию в зависимости от целевой установки, которую он реализует в процессе решения задачи. Результат решения задачи ЛПР определяет по одному из критериев принятия решения. Для того, чтобы прийти к однозначному и по возможности наиболее выгодному варианту решению, необходимо ввести оценочную (целевую) функцию. При этом каждой стратегии ЛПР (A_i) приписывается некоторый результат W_i, характеризующий все последствия этого решения. Из массива результатов принятия решений ЛПР выбирает элемент W, который наилучшим образом отражает мотивацию его поведения.

В зависимости от условий внешней среды и степени информативности ЛПР производится следующая классификация задач принятия решений:

• в условиях риска;
• в условиях неопределенности;
• в условиях конфликта или противодействия (активного противника).

Принятие решений в условиях риска.

1. Критерий ожидаемого значения.

Использование критерия ожидаемого значения обусловлено стремлением максимизировать ожидаемую прибыль (или минимизировать ожидаемые затраты). Использование ожидаемых величин предполагает возможность многократного решения одной и той же задачи, пока не будут получены достаточно точные расчетные формулы. Математически это выглядит так: пусть Х — случайная величина с математическим ожиданием MX и дисперсией DX. Если x₁, x₂, …, x_n — значения случайной величины (с.в.) X, то среднее арифметическое их (выборочное среднее) значений x^=(x₁+x₂+…+x_n)/n имеет дисперсию DX/n. Таким образом, когда n→∞ DX/n→∞ и X→MX.

Другими словами при достаточно большом объеме выборки разница между средним арифметическим и математическим ожиданием стремится к нулю (так называемая предельная теорема теории вероятности). Следовательно, использование критерия ожидаемое значение справедливо только в случае, когда одно и тоже решение приходится применять достаточно большое число раз. Верно и обратное: ориентация на ожидания будет приводить к неверным результатам, для решений, которые приходится принимать небольшое число раз.

Пример 1. Требуется принять решение о том, когда необходимо проводить профилактический ремонт ПЭВМ, чтобы минимизировать потери из-за неисправности. В случае если ремонт будет производится слишком часто, затраты на обслуживание будут большими при малых потерях из-за случайных поломок.

Так как невозможно предсказать заранее, когда возникнет неисправность, необходимо найти вероятность того, что ПЭВМ выйдет из строя в период времени t. В этом и состоит элемент »риска».

Математически это выглядит так: ПЭВМ ремонтируется индивидуально, если она остановилась из-за поломки. Через T интервалов времени выполняется профилактический ремонт всех n ПЭВМ. Необходимо определить оптимальное значение m, при котором минимизируются общие затраты на ремонт неисправных ПЭВМ и проведение профилактического ремонта в расчете на один интервал времени.

Пусть р_t — вероятность выхода из строя одной ПЭВМ в момент t, а n_t — случайная величина, равная числу всех вышедших из строя ПЭВМ в тот же момент. Пусть далее С₁ – затраты на ремонт неисправной ПЭВМ и С₂ — затраты на профилактический ремонт одной машины.

Применение критерия ожидаемого значения в данном случае оправдано, если ПЭВМ работают в течение большого периода времени. При этом ожидаемые затраты на один интервал составят

ОЗ = (C₁∑M(n_t)+C₁n)/T,

где M(n_t) — математическое ожидание числа вышедших из строя ПЭВМ в момент t. Так как n_t имеет биномиальное распределение с параметрами (n, p_t), то M(n_t) = np_t . Таким образом

ОЗ = n(C₁∑p_t+C₂)/T.

Необходимые условия оптимальности T^* имеют вид:

ОЗ (T^*-1) ≥ ОЗ (T^*),

ОЗ (T^*+1) ≥ ОЗ (T^*).

Следовательно, начиная с малого значения T, вычисляют ОЗ(

T), пока не будут удовлетворены необходимые условия оптимальности.

Пусть С₁ = 100; С₂ = 10; n = 50. Значенияp_t имеют вид:

T	рt	∑рt	ОЗ(Т)
1	0.05	0	50(100⋅0+10)/1=500
2	0.07	0.05	375
3	0.10	0.12	366.7
4	0.13	02	400
5	0.18	0.35	450

T^*→3, ОЗ(Т^*)→366.7

Следовательно профилактический ремонт необходимо делать через T^*=3 интервала времени.

Критерий «ожидаемое значение — дисперсия».

Критерий ожидаемого значения можно модифицировать так, что его можно будет применить и для редко повторяющихся ситуаций.

Если х — с. в. с дисперсией DX, то среднее арифметическое x^ имеет дисперсию DX/n, где n — число слагаемых в x^. Следовательно, если DX уменьшается, и вероятность того, что x^ близко к MX, увеличивается. Следовательно, целесообразно ввести критерий, в котором максимизация ожидаемого значения прибыли сочетается с минимизацией ее дисперсии.

Пример 2. Применим критерий «ожидаемое значение — дисперсия» для примера 1. Для этого необходимо найти дисперсию затрат за один интервал времени, т.е. дисперсию

з_Т=(C₁∑n_t+C₂n)/T

Т.к. n_t, t = {1, T-1} — с.в., то з_Ттакже с.в. С.в. n_tимеет биномиальное распределение с M(n_t) = np_tи D(n_t) = np_t(1–p_t). Следовательно,

D(з_Т) = D((C₁∑n_t+C₂n)/T) = (C₁/T)² D(∑n_t) =

= (C₁/T)² ∑Dn_t = (C₁/T)² ∑np_t(1-p_t) = (C₁/T)² {∑p_t — ∑p_t²},

где С₂n = const.

Из примера 1 следует, что

М(з_Т) = М(з(Т)).

Следовательно искомым критерием будет минимум выражения

М(з(Т)) + к D(з_Т).

Замечание. Константу «к» можно рассматривать как уровень не склонности к риску, т.к. «к» определяет «степень возможности» дисперсии Д(з_Т) по отношению к математическому ожиданию. Например, если предприниматель, особенно остро реагирует на большие отрицательные отклонения прибыли вниз от М(з(Т)), то он может выбрать «к» много больше 1. Это придает больший вес дисперсии и приводит к решению, уменьшающему вероятность больших потерь прибыли.

При к=1 получаем задачу

M(з(T))+D(з(T)) = n { (C₁/T+C₁²/T²)∑p_t — C₁²/T²∑p_t² + C²/T }

По данным из примера 1 можно составить следующую таблицу

T	pt	pt2	∑pt	∑pt2	М(з(Т))+D(з(Т))
1	0,05	0,0025	0	0	500.00
2	0,07	0,0049	0,05	0,0025	6312,50
3	0,10	0,0100	0,12	0,0074	6622,22
4	0,13	0,0169	0,2	0,0174	6731,25
5	0,18	0,0324	0,35	0,0343	6764,00

Из таблицы видно, что профилактический ремонт необходимо делать в течение каждого интервала Т^*=1.

3. Критерий предельного уровня

Критерий предельного уровня не дает оптимального решения, максимизирующего, например, прибыль или минимизирующего затраты. Скорее он соответствует определению приемлемого способа действий.

Пример 3. Предположим, что величина спроса x в единицу времени (интенсивность спроса) на некоторый товар задается непрерывной функцией распределения f(x). Если запасы в начальный момент невелики, в дальнейшем возможен дефицит товара. В противном случае к концу рассматриваемого периода запасы нереализованного товара могут оказаться очень большими. В обоих случаях возможны потери.

Т.к. определить потери от дефицита очень трудно, ЛПР может установить необходимый уровень запасов таким образом, чтобы величина ожидаемого дефицита не превышала A₁ единиц, а величина ожидаемых излишков не превышала A₂ единиц. Иными словами, пусть I — искомый уровень запасов. Тогда

ожидаемый дефицит = ∫(x-I)f(x)dx ≤ A₁,

ожидаемые излишки = ∫(I-x)f(x)dx ≤ A₂.

При произвольном выборе A₁ и A₂ указанные условия могут оказаться противоречивыми. В этом случае необходимо ослабить одно из ограничений, чтобы обеспечить допустимость.

Пусть, например,

f(x) = 20/x², 10≤x≤20,

f(x) = 0, x≤10 и x≥20.

Тогда

∫(x-I)f(x)dx = ∫(x-I)(20/x²)dx = 20(ln(20/I) + I/20 – 1)

∫(I-x)f(x)dx = ∫(I-x)(20/x²)dx = 20(ln(10/I) + I/10 – 1)

Применение критерия предельного уровня приводит к неравенствам

ln(I) — I/20 ≥ ln(20) – A₁/20 – 1 = 1,996 — A₁/20

ln(I) — I/10 ≥ ln(10) – A₂/20 – 1 = 1,302 — A₂/20

Предельные значения A₁ и A₂ должны быть выбраны так, что бы оба неравенства выполнялись хотя бы для одного значения I.

Например, если A₁ = 2 и A₂ = 4, неравенства принимают вид

ln(I) — I/20 ≥ 1,896

ln(I) — I/10 ≥ 1,102

Значение I должно находиться между 10 и 20, т.к. именно в этих пределах изменяется спрос. Из таблицы видно, что оба условия выполняются для I, из интервала (13,17)

I	10	11	12	13	14	15	16	17	18	19	20
ln(I) — I/20	1,8	1,84	1,88	1,91	1,94	1,96	1,97	1,98	1,99	1,99	1,99
ln(I) — I/10	1,3	19	18	16	14	11	1,17	1,13	1,09	1,04	0,99

Любое из этих значений удовлетворяет условиям задачи.

Принятие решений в условиях неопределенности

Будем предполагать, что лицу, принимающему решение не противостоит разумный противник.

Данные, необходимо для принятия решения в условии неопределенности, обычно задаются в форме матрицы, строки которой соответствуют возможным действиям, а столбцы — возможным состояниям системы.

Пусть, например, из некоторого материала требуется изготовить изделие, долговечность которого при допустимых затратах невозможно определить. Нагрузки считаются известными. Требуется решить, какие размеры должно иметь изделие из данного материала.

Варианты решения таковы:

Е₁ — выбор размеров из соображений максимальной долговечности ;

Е_m — выбор размеров из соображений минимальной долговечности ;

E_i — промежуточные решения.

Условия требующие рассмотрения таковы:

F₁ — условия, обеспечивающие максимальной долговечность;

F_n — условия, обеспечивающие min долговечность;

F_i — промежуточные условия.

Под результатом решения e_ij = е(E_i ; F_j) здесь можно понимать оценку, соответствующую варианту E_i и условиям F_j и характеризующие прибыль, полезность или надежность. Обычно мы будем называть такой результат полезностью решения.

Тогда семейство (матрица) решений ||e_ij|| имеет вид:

	F1	F2	…	Fn
E1	e11	e12	…	e1n
E2	e21	e22	…	e2n
…	…	…	…	…
Em	em1	em2	…	emn

Чтобы прийти к однозначному и по возможности наивыгоднейшему варианту решению необходимо ввести оценочную (целевую) функцию. При этом матрица решений ||e_ij|| сводится к одному столбцу. Каждому варианту E_i приписывается, т.о., некоторый результат e_ir, характеризующий, в целом, все последствия этого решения. Такой результат мы будем в дальнейшем обозначать тем же символом e_ir.

Классические критерии принятия решений

1. Минимаксный критерий.

Правило выбора решения в соответствии с минимаксным критерием (ММ-критерием) можно интерпретировать следующим образом:

матрица решений дополняется еще одним столбцом из наименьших результатов e_ir каждой строки. Необходимо выбрать те варианты в строках которых стоят наибольшее значение e_ir этого столбца.

Выбранные т.о. варианты полностью исключают риск. Это означает, что принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Это свойство позволяет считать ММ-критерий одним из фундаментальных.

Применение ММ-критерия бывает оправдано, если ситуация, в которой принимается решение следующая:

1. О возможности появления внешних состояний F_jничего не известно;
2. Приходится считаться с появлением различных внешних состояний F_j;
3. Решение реализуется только один раз;
4. Необходимо исключить какой бы то ни было риск.

2. Критерий Байеса—Лапласа.

Обозначим через q_i — вероятность появления внешнего состояния F_j.

Соответствующее правило выбора можно интерпретировать следующим образом:

матрица решений дополняется еще одним столбцом содержащим математическое ожидание значений каждой из строк. Выбираются те варианты, в строках которых стоит наибольшее значение e_ir этого столбца.

При этом предполагается, что ситуация, в которой принимается решение, характеризуется следующими обстоятельствами:

1. Вероятности появления состояния F_j известны и не зависят от времени.
2. Решение реализуется (теоретически) бесконечно много раз.
3. Для малого числа реализаций решения допускается некоторый риск.

При достаточно большом количестве реализаций среднее значение постепенно стабилизируется. Поэтому при полной (бесконечной) реализации какой-либо риск практически исключен.

Т.о. критерий Байеса-Лапласа (B-L-критерий) более оптимистичен, чем минимаксный критерий, однако он предполагает большую информированность и достаточно длительную реализацию.

3. Критерий Сэвиджа.

a_ij:= max_i(e_ij) — e_ij

e_ir:= max_i(a_ij) = max_j(max_i(e_ij) — e_ij)

Величину a_ij можно трактовать как максимальный дополнительный выигрыш, который достигается, если в состоянии F_j вместо варианта E_iвыбирать другой, оптимальный для этого внешнего состояния вариант. Величину a_ij можно интерпретировать и как потери (штрафы) возникающие в состоянии F_j при замене оптимального для него варианта на вариант E_i. В последнем случае e_ir представляет собой максимально возможные (по всем внешним состояниям F_j , j = {1,n}) потери в случае выбора варианта E_i.

Соответствующее критерию Сэвиджа правило выбора теперь трактуется так:

1. Каждый элемент матрицы решений ||e_ij|| вычитается из наибольшего результата max(e_ij) соответствующего столбца.
2. Разности a_ij образуют матрицу остатков ||e_ij||. Эта матрица пополняется столбцом наибольших разностей e_ir. Выбирают те варианты, в строках которых стоит наименьшее для этого столбца значение.

Требования, предъявляемые к ситуации, в которой принимается решение, совпадают с требованием к ММ-критерию.

4. Пример и выводы.

Из требований, предъявляемых к рассмотренным критериям становится ясно, что в следствии их жестких исходных позиций они применимы только для идеализированных практических решений. В случае, когда возможна слишком сильная идеализация, можно применять одновременно поочередно различные критерии. После этого среди нескольких вариантов ЛПР волевым методом выбирает окончательное решение. Такой подход позволяет, во-первых, лучше проникнуть во все внутренние связи проблемы принятия решений и, во-вторых, ослабляет влияние субъективного фактора.

Пример. При работе ЭВМ необходимо периодически приостанавливать обработку информации и проверять ЭВМ на наличие в ней вирусов. Приостановка в обработке информации приводит к определенным экономическим издержкам. В случае же если вирус вовремя обнаружен не будет, возможна потеря и некоторой части информации, что приведет и еще к большим убыткам.

Варианты решения таковы:

Е₁ — полная проверка;

Е₂ — минимальная проверка;

Е₃ — отказ от проверки.

ЭВМ может находиться в следующих состояниях:

F₁ — вирус отсутствует;

F₂ — вирус есть, но он не успел повредить информацию;

F₃ — есть файлы, нуждающиеся в восстановлении.

Результаты, включающие затраты на поиск вируса и его ликвидацию, а также затраты, связанные с восстановлением информации имеют вид:

	F1	F2	F3	ММ-критерий	критерий B-L
eir = minj(eij)	maxi(eir)	eir = ∑eij	maxi(eir)
E1	-20,0	-20	-25,0	-25,0	-25,0	-22,33
E2	-14,0	-23,0	-31,0	-31,0		-22,67
E3	0	-24.0	-40.0	-40.0		-21.33	-21.33

Согласно ММ-критерию следует проводить полную проверку. Критерий Байеса-Лапласа, в предположении, что все состояния машины равновероятны.

P(F_j) = q_j = 0,33,

рекомендуется отказаться от проверки. Матрица остатков для этого примера и их оценка (в тысячах) согласно критерию Сэвиджа имеет вид:

	F1	F2	F3	Критерий Сэвиджа
eir = minj(aij)	minj(eir)
E1	+20,0	0	0	+20,0
E2	+14,0	+1,0	+6,0	+14,0	+14,0
E3	0	+2,0	+15,0	+15,0

Пример специально подобран так, что каждый критерий предлагает новое решение. Неопределенность состояния, в котором проверка застает ЭВМ, превращается в неясность, какому критерию следовать.

Поскольку различные критерии связаны с различными условиями, в которых принимается решение, лучшее всего для сравнительной оценки рекомендации тех или иных критериев получить дополнительную информацию о самой ситуации. В частности, если принимаемое решение относится к сотням машин с одинаковыми параметрами, то рекомендуется применять критерий Байеса-Лапласа. Если же число машин не велико, лучше пользоваться критериями минимакса или Севиджа.

Производные критерии.

1. Критерий Гурвица.

Стараясь занять наиболее уравновешенную позицию, Гурвиц предположил оценочную функцию, которая находится где-то между точкой зрения крайнего оптимизма и крайнего пессимизма:

max_i(e_ir) = { C⋅min_j(e_ij) + (1-C)⋅max_j(e_ij) },

где С — весовой множитель.

Правило выбора согласно критерию Гурвица, формируется следующим образом:

матрица решений ||e_ij|| дополняется столбцом, содержащим среднее взвешенное наименьшего и наибольшего результатов для каждой строки. Выбираются только те варианты, в строках которых стоят наибольшие элементыe e_irэтого столбца.

При С=1 критерий Гурвица превращается в ММ-критерий. При С = 0 он превращается в критерий «азартного игрока»

max_i(e_ir) = max_i(max_j(e_ij)),

т.е. мы становимся на точку зрения азартного игрока, делающего ставку на то, что «выпадет» наивыгоднейший случай.

В технических приложениях сложно выбрать весовой множитель С, т.к. трудно найти количественную характеристику для тех долей оптимизма и пессимизма, которые присутствуют при принятии решения. Поэтому чаще всего С:=1/2.

Критерий Гурвица применяется в случае, когда:

1. о вероятностях появления состояния F_j ничего не известно;
2. с появлением состояния F_j необходимо считаться;
3. реализуется только малое количество решений;
4. допускается некоторый риск.

2. Критерий Ходжа–Лемана.

Этот критерий опирается одновременно на ММ-критерий и критерий Баеса-Лапласа. С помощью параметра n выражается степень доверия к используемому распределений вероятностей. Если доверие велико, то доминирует критерий Баеса-Лапласа, в противном случае — ММ-критерий, т.е. мы ищем

max_i(e_ir) = max_i{v⋅∑e_ij⋅q_i + (1-v) min_j(e_ir)}, 0 ≤ n ≤ 1.

Правило выбора, соответствующее критерию Ходжа-Лемана формируется следующим образом:

матрица решений ||e_ij|| дополняется столбцом, составленным из средних взвешенных (с весом v≡const) математическое ожиданиями и наименьшего результата каждой строки (*). Отбираются те варианты решений в строках которого стоит набольшее значение этого столбца.

При v = 1 критерий Ходжа-Лемана переходит в критерий Байеса-Лапласа, а при v = 0 становится минимаксным.

Выбор v субъективен т. к. Степень достоверности какой-либо функции распределения — дело темное.

Для применения критерия Ходжа-Лемана желательно, чтобы ситуация в которой принимается решение, удовлетворяла свойствам:

1. вероятности появления состояния F_j неизвестны, но некоторые предположения о распределении вероятностей возможны;
2. принятое решение теоретически допускает бесконечно много реализаций;
3. при малых числах реализации допускается некоторый риск.

3. Критерий Гермейера.

Этот критерий ориентирован на величину потерь, т.е. на отрицательные значения всех e_ij. При этом

max_i(e_ir) = max_i(min_j(e_ij)q_j).

Т.к. в хозяйственных задачах преимущественно имеют дело с ценами и затратами, условиеe e_ij<0 обычно выполняется. В случае же, когда среди величин e_ij встречаются и положительные значения, можно перейти к строго отрицательным значениям с помощью преобразования e_ij-a при подходящем образом подобранном a>0. При этом оптимальный вариант решения зависит от а.

Правило выбора согласно критерию Гермейера формулируется следующим образом:

матрица решений ||e_ij|| дополняется еще одним столбцом содержащим в каждой строке наименьшее произведение имеющегося в ней результата на вероятность соответствующего состояния F_j. Выбираются те варианты в строках которых находится наибольшее значениеe e_ij этого столбца.

В каком-то смысле критерий Гермейера обобщает ММ-критерий: в случае равномерного распределения q_j = 1/n, j={1,n}, они становятся идентичными.

Условия его применимости таковы:

1. вероятности появления состояния F_j неизвестны;
2. с появлением тех или иных состояний, отдельно или в комплексе, необходимо считаться;
3. допускается некоторый риск;
4. решение может реализоваться один или несколько раз.

Если функция распределения известна не очень надежно, а числа реализации малы, то, следуя критерию Гермейера, получают, вообще говоря, неоправданно большой риск.

4. Объединенный критерий Байеса-Лапласа и минимакса.

Стремление получить критерии, которые бы лучше приспосабливались к имеющейся ситуации, чем все до сих пор рассмотренные, привело к построению так называемых составных критериев. В качестве примера рассмотрим критерий, полученный путем объединения критериев Байеса-Лапласа и минимакса (BL(MM)-критерий).

Правило выбора для этого критерия формулируется следующим образом:

матрица решений ||e_ij|| дополняется еще тремя столбцами. В первом из них записываются математические ожидания каждой из строк, во втором — разность между опорным значением

e_i0j0 = max_i(max_j(e_ij))

и наименьшим значением

min_j(e_ij)

соответствующей строки. В третьем столбце помещаются разности между наибольшим значением

max_j(e_ij)

каждой строки и наибольшим значением max_j(e_i0j) той строки, в которой находится значение e_i0j0. Выбираются те варианты, строки которых (при соблюдении приводимых ниже соотношений между элементами второго и третьего столбцов) дают наибольшее математическое ожидание. А именно, соответствующее значение

e_i0j0 — max_j(e_ij)

из второго столбца должно быть или равно некоторому заранее заданному уровню риска E_доп. Значение же из третьего столбца должно быть больше значения из второго столбца.

Применение этого критерия обусловлено следующими признаками ситуации, в которой принимается решение:

1. вероятности появления состояний F_j неизвестны, однако имеется некоторая априорная информация в пользу какого-либо определенного распределения;
2. необходимо считаться с появлением различных состояний как по отдельности, так и в комплексе;
3. допускается ограниченный риск;
4. принятое решение реализуется один раз или многократно.

BL(MM)-критерий хорошо приспособлен для построения практических решений прежде всего в области техники и может считаться достаточно надежным. Однако заданные границы риска E_доп и, соответственно, оценок риска E_i не учитывает ни число применения решения, ни иную подобную информацию. Влияние субъективного фактора хотя и ослаблено, но не исключено полностью.

Условие

max_j(e_ij)-max_j(e_i0j)≥E_i

существенно в тех случаях, когда решение реализуется только один или малое число раз. В этих условиях недостаточно ориентироваться на риск, связанный только с невыгодными внешними состояниями и средними значениями. Из-за этого, правда, можно понести некоторые потери в удачных внешних состояниях. При большом числе реализаций это условие перестает быть таким уж важным. Оно даже допускает разумные альтернативы. При этом не известно, однако, четких количественных указаний, в каких случаях это условие следовало бы опускать.

5. Критерий произведений.

max_i(e_ir):= max_i(∏e_ij)

Правило выбора в этом случае формулируется так:

Матрица решений ||e_ij|| дополняется новым столбцом, содержащим произведения всех результатов каждой строки. Выбираются те варианты, в строках которых находятся наибольшие значения этого столбца.

Применение этого критерия обусловлено следующими обстоятельствами:

1. вероятности появления состояния F_j неизвестны;
2. с появлением каждого из состояний F_j по отдельности необходимо считаться;
3. критерий применим и при малом числе реализаций решения;
4. некоторый риск допускается.

Критерий произведений приспособлен в первую очередь для случаев, когда все e_ij положительны. Если условие положительности нарушается, то следует выполнять некоторый сдвиг e_ij+а с некоторой константой а>|min_ij(e_ij)|. Результат при этом будет, естественно зависеть от а. На практике чаще всего

а:= |min_ij(e_ij)|+1.

Если же никакая константа не может быть признана имеющей смысл, то критерий произведений не применим.

Пример.

Рассмотрим тот же пример, что и ранее (см. выше).

Построение оптимального решения для матрицы решений о проверках по критерию Гурвица имеет вид (при С=0, в 10³):

||eij||	С⋅minj(eij)	(1-С)⋅maxj(eij)	eir	maxi(eir)
-20,0	-22,0	-25,0	-12,5	-10.0	-22,5
-14,0	-23.0	-31.0	-15,5	-7.0	-22,5
0	-24.0	-40.0	-20.0	0	-20.0	-20.0

В данном примере у решения имеется поворотная точка относительно весового множителя С: до С=0,57 в качестве оптимального выбирается Е₃, а при больших значениях — Е₁.

Применение критерия Ходжа-Лемана (q=0,33, v=0, в 10³):

∑eij⋅qj	minj(eij)	v⋅∑eij⋅qj	(1-v)⋅∑eij⋅qj	eir	maxi(eir)
-22,33	-25,0	-11,17	-12,5	-23,67	-23,67
-22,67	-31,0	-11,34	-15,5	-26,84
-21,33	-40,0	-10,67	-20,0	-30,76

Критерий Ходжа-Лемана рекомендует вариант Е₁ (полная проверка) — так же как и ММ-критерий. Смена рекомендуемого варианта происходит только при v=0,94. Поэтому равномерное распределение состояний рассматриваемой машины должно распознаваться с очень высокой вероятностью, чтобы его можно было выбрать по большему математическому ожиданию. При этом число реализаций решения всегда остается произвольным.

Критерий Гермейера при q_j = 0.33 дает следующий результат (в 10³):

||eij||	||eijqj||	eir = minj(eijqj)	maxi(eir)
-20,0	-22,0	-25,0	-6,67	-7,33	-8,33	-8,33	-8,33
-14,0	-23,0	-31,.0	-4,67	-7,67	-10,33	-10,33
0	-24,0	-40,0	0	-8,0	-13,33	-13,33

В качестве оптимального выбирается вариант Е₁. Сравнение вариантов с помощью величинe e_irпоказывает, что способ действия критерия Гермейера является даже более гибким, чем у ММ-критерия.

В таблице, приведенной ниже, решение выбирается в соответствии с BL(MM)-критерием при q₁=q₂=q₃=1/2 (данные в 10³).

||eij||	∑eijqj	ei0j0 — minj(eij)	maxj(eij)	maxj(eij) — maxj(ei0j)
-20,0	-22,0	-25,0	-23,33	0	-20,0	0
-14,0	-23,0	-31,0	-22,67	+6,0	-14,0	+6,0
0	-24,0	-40,0	-21,33	+15,0	0	+20,0

Вариант Е₃ (отказ от проверки) принимается этим критерием только тогда, когда риск приближается к E_возм = 15⋅10³. В противном случае оптимальным оказывается Е₁. Во многих технических и хозяйственных задачах допустимый риск бывает намного ниже, составляя обычно только незначительный процент от общих затрат. В подобных случаях бывает особенно ценно, если неточное значение распределения вероятностей сказывается не очень сильно. Если при этом оказывается невозможным установить допустимый риск E_доп заранее, не зависимо от принимаемого решения, то помочь может вычисление ожидаемого риска E_возм. Тогда становится возможным подумать, оправдан ли подобный риск. Такое исследование обычно дается легче.

Результаты применения критерия произведения при а = 41⋅10³ и а = 200⋅10³ имеют вид:

a	||eij + a||	eir = ∏jeij	maxieir
41	+21	+19	+16	6384	6384
+27	+18	+10	4860
+41	+17	+1	697
200	+180	+178	+175	5607
+186	+177	+169	5563
+200	+176	+160	5632	5632

Условие e_ij > 0 для данной матрицы не выполнимо. Поэтому к элементам матрицы добавляется (по внешнему произволу) сначала а = 41⋅10³, а затем а = 200⋅10³.

Для а = 41⋅10³ оптимальным оказывается вариант Е₁, а для а = 200⋅10³ — вариант Е₃, так что зависимость оптимального варианта от а очевидна.

Решение матричной игры в смешанных стратегиях

Краткая теория

---

Для игры без седловой точки оптимальные стратегии игроков
находятся в области смешанных стратегий. Смешанной стратегией игрока

 называют вектор

,
компоненты которого удовлетворяют условиям

Смешанной стратегией игрока

 называют вектор

 где

 и

 – вероятности, с которыми игроки

 и

 выбирают свои чистые стратегии

 и

.
При использовании смешанных стратегий игра приобретает случайный характер,
случайной становится и величина выигрыша игрока

 (проигрыша игрока

).
Эта величина является функцией смешанных стратегий

 и

 и определяется по формуле:

Функцию

 называют платежной или функцией выигрыша.

Смешанные стратегии

 и

 называются оптимальными, если они образуют
седловую точку для платежной функции

,
то есть удовлетворяют неравенству

.
Пользуются и другим определением оптимальных смешанных стратегий; стратегии

 и

 называют оптимальными, если

Величину

 называют ценой игры.

Поиск оптимальных стратегий начинают с
упрощения платежной матрицы. Если в платежной матрице элементы

-й
строки не меньше соответствующих элементов

-й
строки, то есть

,
то говорят, что стратегия

 доминирует над стратегией

.
Аналогично, если элементы

-го
столбца не превосходят элементы

-го
столбца, то есть

,
то говорят, что стратегия

 доминирует над стратегией

.
Частным случаем доминирования является дублирование стратегий, когда

 или

.
Исключение из платежной матрицы заведомо доминируемых стратегий (ими игрокам
пользоваться заведомо невыгодно) позволяет уменьшить ее размерность, а это
упрощает решение игры. Вероятность применения доминируемых стратегий равна
нулю.

Оптимальные смешанные стратегии

 в игре с платежной матрицей

 и ценой

 остаются оптимальными и для игры с платежной
матрицей

 (где

)
и ценой

.
На этом основании платежную матрицу можно всегда преобразовать так, что ее
элементы будут целыми неотрицательными числами, а это упрощает расчеты.

Решение матричной игры сведением к
задаче линейного программирования

Пусть имеем игру размерности

  с матрицей:

Обозначим через

 оптимальные смешанные стратегии игроков

 к

.
Стратегия

 игрока

 гарантирует ему выигрыш не меньше

,
независимо от выбора стратегии

,
игроком

.
Это можно записать так:

где

.

Аналогично стратегия

 игрока

 гарантирует ему проигрыш не больше

,
независимо от выбора стратегии

,
игроком

,
т. е.:

где

.

Поскольку элементы платежной матрицы на
основании  всегда можно сделать
положительными, то и цена игры

  (оптимальные смешанные стратегии

 и

 соответственно игроков

 и

 в матричной игре  

  с ценой

 будут оптимальными и в матричной игре 

    с ценой  

,
где

).

Преобразуем системы неравенств, разделив обе части
каждого неравенства на положительное число

,
и введем новые обозначения  

; 

.
Получим:

где:

 и

где

Так как игрок А стремится максимизировать цену игры

,
то обратная величина

 будет минимизироваться, поэтому оптимальная
стратегия игрока А определится из задачи линейного программирования следующего
вида:

найти минимальное значение функции

 при 
ограничениях (1) и (2).

Оптимальная смешанная стратегия игрока

 определится решением задачи следующего вида:

найти максимальное значение функции

 при 
ограничениях (3) и (4).

Решив пару двойственных задач графическим (для
случая двух переменных) или симплексным методом, далее определим:

Поскольку задачи (1)(2) и (3)(4) образуют пару
симметричных двойственных задач линейного программирования, нет необходимости
решать обе задачи. Получив решение одной из них, достаточно воспользоваться
соответствием между переменными в канонических записях задач.

и из строки целевой функции последней
симплекс-таблицы, содержащей компоненты оптимального вектора, выписать значения
компонент оптимального вектора двойственной задачи.

При поиске оптимальных стратегий в
матричных играх размерностей

 и

 целесообразно
использовать графический метод решения ЗЛП и свойства оптимальных планов пары
двойственных задач: если в оптимальном плане задачи переменная положительна, то
соответствующее ограничение двойственной задачи ее оптимальным планом
обращается в равенство; если оптимальным планом задачи ограничение обращается в
строгое неравенство, то в оптимальном плане двойственной задачи соответствующая
переменная равна нулю.

Пример решения задачи

---

Задача

Отрасли

 и

 осуществляют капитальные вложения в четыре
объекта. С учетом особенностей вкладов и местных условий прибыль отрасли

 в зависимости от объема финансирования
выражается элементами платежной матрицы

. Для упрощения
задачи принять, что убыток отрасли

 равен прибыли отрасли

. Найти
оптимальные стратегии отраслей.

Требуется:

1)
свести исходные данные в таблицу и найти решение матричной игры в чистых
стратегиях, если оно существует (противном случае см. следующий пункт 2);

2)
упростить платежную матрицу;

3)
составить пару взаимно двойственных задач, эквивалентную данной матричной игре;

4)
найти оптимальное решение прямой задачи (для отрасли

)
симплекс-методом;

5)
используя соответствие переменных, выписать оптимальное решение двойственной
задачи (для отрасли

.

6)
используя соотношение между оптимальными решениями пары двойственных задач,
оптимальными стратегиями и ценой игры, найти решение в смешанных стратегиях;

7)
дать рекомендации по каждой отрасли.

Решение

1)
Сведем исходные данные в таблицу:

Так
как

, то седловая
точка отсутствует, и оптимальное решение следует искать в смешанных стратегиях
игроков:

 и

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

2)
Упростим платежную матрицу, отбросив стратегии, заведомо невыгодные или
дублирующие.

2-я
стратегия (2-й столбец) является невыгодной для игрока

 – элементы 2-го столбца не меньше элементов
3-го.

4-я
стратегия (4-й столбец) является невыгодной для игрока

 – элементы 4-го столбца не меньше элементов
3-го.

2-я
стратегия (2-я строка) является невыгодной для игрока

 – элементы 2-й строки не больше элементов 1-й

4-я
стратегия (4-я строка) является невыгодной для игрока

 – элементы 4-й строки не больше элементов 1-й

Получили
матрицу размером 2х2

3)  Составим пару взаимно двойственных задач, эквивалентных
данной матричной игре.

Так
как платёжная матрица содержит отрицательные числа, то лучше перейти к новой
матрице с неотрицательными элементами; для этого к элементам платёжной матрицы
достаточно добавить соответствующее положительное число, в данном случае 2.
Решение игры при этом не изменится, а цена игры увеличится на 2. Платёжная матрица примет вид:

Обозначив

  и

,

 составим две взаимно двойственные задачи
линейного программирования:

4)
Найдем оптимальное решение задачи для отрасли

 симплекс-методом.
На другой странице сайта есть задача, решенная симплекс-методом очень подробно, а в этом примере, для краткости, из расчетов приведены только симплексные таблицы.

Приведем
задачу к каноническому виду.

Заполняем
симплексную таблицу 0-й итерации.

Получаем таблицу 1-й итерации:

Получаем таблицу 2-й итерации:

В
индексной строке все члены неотрицательные, поэтому получено следующее решение
задачи линейного программирования (выписываем из столбца свободных членов):

5)
Соответствие между переменными исходной и двойственной задачи:

На
основании симплексной таблицы получено следующее решение 1-й задачи:

6)
Найдем решение игры в смешанных стратегиях.

Цена
игры:

Находим
оптимальную стратегию 

Учтем,
что 2-я и 4-я строка матрицы были отброшенные, как невыгодные для игрока

:

Находим
оптимальную стратегию 

Учтем,
что 2-й и 4-й столбец матрицы были отброшенные, как невыгодные для игрока

:

Цена
игры

7) Дадим рекомендации по каждой отрасли.

Отрасли

 необходимо вложить 37,5%  средств в 1-й объект и 62,5% средств во 3-й
объект. Во 2-й и 4-й объект капитальные вложения осуществлять невыгодно.

 Отрасли

 необходимо вложить 25%  средств в 1-й объект и 75% средств во 3-й
объект. Во 2-й и 4-й объект капитальные вложения осуществлять невыгодно.