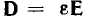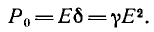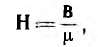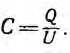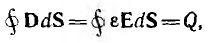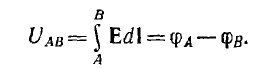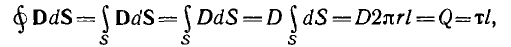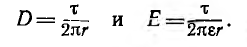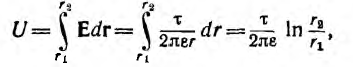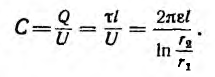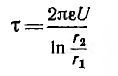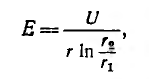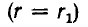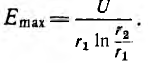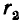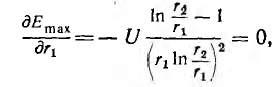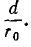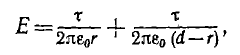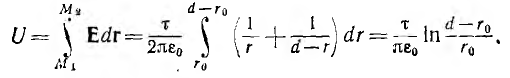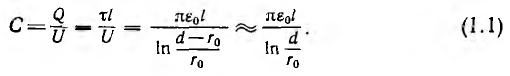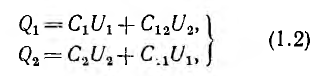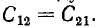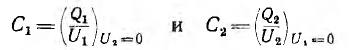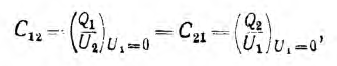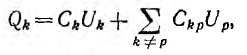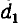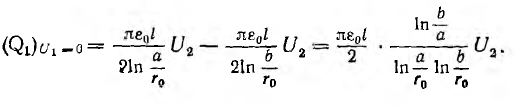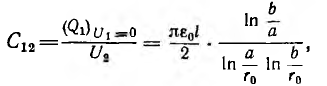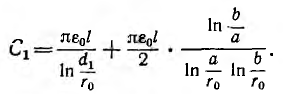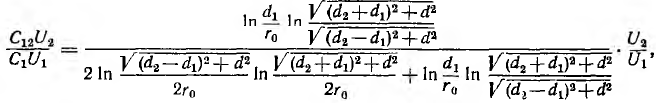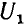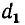ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ
Емкость одножильного и отдельных экранированных жил многожильного кабеля, включая радиочастотные кабели (рис. 2-6),
Емкость кабелей измеряют и нормируют в микрофарадах
(10–6 ф), нанофарадах (10–9 ф) и пикофарадах (10–12 ф) на 1 км или 1 м.
Емкость радиочастотных коаксиальных кабелей с многопроволочным внутренним проводником
где k3=0,98/0,99—коэффициент, учитывающий форму внешнего проводника и представляющий собой отношение емкости кабеля с внешним (Проводником в форме оплетки к емкости кабеля с.внешним проводником в форме сплошной трубы; dэ — эквивалентный диаметр, мм. Емкость одной жилы двухжильного кабеля в общей металлической оболочке и одной жилы симметричного экранированного радиочастотного кабеля (обе жилы имеют равные по величине, но противоположные по знаку потенциалы)
Если же оба провода находятся под одним и тем же потенциалом
Емкость двухжильного кабеля в общих металлической оболочке или экране может быть определена из частичных емкостей (рис. 1-14) по формуле:
где С1 — емкость между жилами А и В, соединенными с оболочкой или экраном; С12 — емкость жил А и В, соединенных вместе против оболочки и экрана; l — длина кабеля, м.
Емкость неэкранированного двухжильного (симметричного) кабеля
Рабочая емкость жилы трехжильного кабеля (рис. 2-6):
Емкость трехжильных кабелей с секторными жилами может быть приближенно определена по этим же формулам с заменой секторных жил круглыми, но с сечением, увеличенным на 50% при той же толщине изоляции.
Емкость трехжильного кабеля с поясной изоляцией в общей металлической оболочке или в экране выражается через частичные емкости между жилами и каждой жилы относительно оболочки кабеля (рис. 2-6). Вследствие симметрии жил С10=С20=С30 и С12 = C23 = C13. Емкость каждой жилы относительно двух других жил, соединенных с оболочкой (или экраном):
Емкость двух жил, соединенных вместе, относительно третьей жилы, соединенной с оболочкой (или экраном):
Емкость всех трех соединенных вместе жил относительно оболочки (или экрана):
Рабочая емкость трехжильного кабеля при трехфазном токе
Частичные емкости: между двумя жилами
между жилой и оболочкой (или экраном)
Емкостное реактивное сопротивление кабеля
где С — емкость кабеля, ф/км.
Емкость групп кабелей связи в общем виде с учетом системы скрутки и величины укрутки жил:
ψ — поправочный коэффициент, характеризующий удаление жил от заземленной оболочки или экрана (табл. 2-4), при большом удалении, ψ =1. Численные значения поправочного коэффициента ψ в зависимости от отношения диаметров жилы по изоляции (d1) к диаметру жилы (d) приведены в табл. 2–5.
Значения α и ψ для расчета рабочей емкости кабелей связи
Численные значения коэффициента ψ для парной, четверочной и двойной парной скруток
Эквивалентное значение диэлектрической проницаемости сложной (комбинированной) изоляции определяют по соотношениям объемов составных ее частей. При непрерывной и одинаковой по длине изоляции соотношение объемов можно заменить соотношением площадей поперечного сечения. Для комбинированной двухслойной изоляции
Для изоляции комбинированной в радиальном направлении
Для изоляции комбинированной в тангенциальном направлении
Значения диэлектрической проницаемости основных электроизоляционных кабельных материалов и комбинированной изоляции приведены в табл. 2–6. Величина емкости кабеля мало изменяется в зависимости от частоты (рис. 2-1).
После несложной процедуры регистрации Вы сможете пользоваться всеми сервисами и создать свой веб-сайт.
Источник
Расчёт межпроводной индуктивности и ёмкости симметричных прямых пар методами Конформных отображений и конечных элементов
Этой работой мы открываем цикл статьей, посвящённых расчёту погонных ёмкостей и индуктивностей – важнейших первичных параметров любых кабельных конструкций: для передачи информации (телефонные и телеграфные провода, витые пары, коаксиальные кабели. ), для передачи энергии (силовые кабели, воздушные линии электропередач. ) и специального назначения (триады, каротажные кабели, подводные, шахтные, нефтяные. ). Потому что именно ёмкость и индуктивность определяют скорость сигналов и волновое сопротивление линий. И, следовательно, величину и распространение напряжений и токов. А также искроопасность кабелей, используемых во взрывоопасных зонах.
Не исключено, что такое намерение может кого-то удивить, так как существует огромное количество учебной и методической литературы, а также фундаментальных монографий, посвящённых данному предмету. Как основополагающих трудов старых и заслуженных мастеров [1,2], так и современных [3,4]. И что здесь можно сказать существенно новое?
Тем не менее, неумолимый ход Времени заставляет по-новому взглянуть и на эту отрасль расчётной деятельности. Которая, казалось бы, досконально изучена и отшлифована десятилетиями труда многих и многих поколений инженеров.
21-й век начался как век информационных технологий и энергетики. Но прогресс этих отраслей невозможен без адекватного, а лучше и опережающего, развития кабельной индустрии – производства средств передачи сигналов и энергии. Этот процесс сопровождается быстрым ростом номенклатуры кабельных изделий и их компонентов, галопом цен на проводниковые и изолирующие материалы и общим ужесточением требований к качеству.
Всё вместе обусловливает ужесточение требований к точности технологических режимов и регламентов, к точности и достоверности контроля качества исходных материалов и продукции. А также значительное увеличение затрат на разработку новых изделий. Последнее не в малой степени обусловлено низкой точностью и достоверностью применяемых до сих пор методик расчёта.
Это связано с тем, что указанные методики основаны на применении формул, полученных более полувека назад для некоторых простейших геометрий проводников и изоляторов. И в практическом применении они – всего лишь приближения. Не спасают и поправочные коэффициенты для геометрий, более приближенных к реальным, но тоже достаточно простым. Так как на все случаи жизни поправок нет, и результаты таких «расчётов» (а точнее говоря, оценок) зависят от произвола или, говоря мягче, интуиции расчётчика.
Конечно, интуиция мастера, за плечами которого не один десяток лет и тысячи километров кабелей – вещь ценная. Но в условиях быстрых изменений она может и подводить. Помимо прочего, её вообще надо освободить от тупой расчётной рутины. Это тем более необходимо, что существенный прогресс в расчётном деле давно отсутствует. Чтобы убедиться в этом, достаточно сравнить упомянутые выше работы, разделённые полувеком.
Нынешнее, не очень радужное, положение – это, разумеется, не результат чьего-то недомыслия. Напротив – это итог титанического труда и мысли инженеров и учёных прошлого века, вооружённых всего лишь арифмометрами, логарифмическими линейками, номограммами и таблицами. И можно только изумляться и восхищаться их беспримерными достижениями: авиация, космос, атомная бомба, лазеры, полупроводники.
Они же вооружили нас мощными персональными компьютерами. И тем самым закрыли эпоху арифмометров и номограмм, приближённых формул и поправок к ним. Открыв дорогу новым, «абсолютным» расчётным технологиям. Которые, как представляется, должны:
1.Обеспечить расчёт проектируемого изделия из «первых принципов».
2.Исключить какие-либо приближения и поправки.
3.Обеспечить расчёт с любой, наперёд заданной, степенью точности.
Здесь, однако, требуется уточнение. Дело в том, что устройство даже простейших кабельных сборок на самом деле настолько сложно, что оно не зубам даже самым продвинутым суперкомпьютерам. И для расчётов требуются упрощения, то есть работа интуиции. А вот как раз после этого расчёт и должен отвечать указанным выше требованиям.
Существуют разные методы расчёта электрических параметров «из первых принципов»:
— с помощью вариационных процедур;
— методом конечных разностей;
— методом конечных элементов.
В первом вместо точной функции, характеризующей поле, например потенциала электрического поля U(x,y), вводят приближённую Û(x,y,a,b,c,d . ), удовлетворяющую граничным условиям, уравнению Лапласа и зависящую от ряда параметров a,b,c,d . которые подбирают с таким расчётом, чтобы обеспечить минимум энергии электрического поля
∫E 2 dω (интеграл по всему объёму ω поля).
Во втором дифференциальное уравнение заменяют системой алгебраических для конечных разностей. Где, например, производную ∂U/∂x заменяют частным ΔU/Δx.
Третий способ – как бы гибрид первых двух. Здесь объём ω покрывают сеткой небольших участков – конечных элементов, обычно в форме симплексов (на плоскости – это треугольники, в трёхмерном объёме – тетраэдры). Внутри элементов поле представляют приближением, зависящим от подгоночных параметров. Например, для двумерных задач – плоскостями, проходящими через 3 узла сетки. И подбирают параметры с таким расчётом, чтобы значения U(x,y) в узлах сетки обеспечивали минимум энергии поля, а на границах – граничные условия. Более подробно с этим методом можно ознакомиться в [5].
Разработано множество программ для решения задач с конечными элементами: ANSYS, NASTRAN, PATRAN. Но для них необходимо мощное оборудование и высокая квалификация расчётчиков. Для решения двумерных задач (а к таковым относится большинство кабельных) более пригоден пакет ELCUT [6].
Поэтому предлагаемый вниманию цикл работ мы посвящаем исследованию существующей и доступной версии ELCUT, имея в виду его перспективы в реализации указанной выше «абсолютной» расчётно-кабельной технологии.
Забегая вперёд, отметим, что, как представляется на настоящий момент, в полном объёме это реализуемо лишь для «прямых» кабельных систем, то есть таких, где можно пренебречь эффектами скрутки. Кроме того, при известном искусстве, можно получить оценки влияния скрутки на ряд параметров линий. Есть, однако, и такие «скрученные» параметры, которые в существующей версии ELCUT оценить нельзя. Хотя сам по себе его метод позволяет точно решать все эти задачи. Так что у ELCUT есть перспектива стать основным расчётным инструментом в кабельно-расчётном деле. Но, после надлежащей доработки, о чем подробнее в последующих статьях.
Если, однако, отвлечься от таких деталей, то уже первое знакомство с ELCUT убеждает в полезности этого инструмента в инженерной деятельности. Но у него есть два недостатка:
— конечный размер геометрических моделей;
— решение двумерных задач.
Первый ограничивает ELCUT при расчёте первичных параметров – погонной ёмкости и индуктивности линий с распределёнными параметрами.
Дело в том, что часть кабельной продукции оборудуют металлическими экранами, естественным образом ограждающими область электромагнитного поля в ELCUT. Но вот основная масса: телефонные линии, бытовая электропроводка, витые пары низших категорий, линии электропередач экранами не оборудованы. И в ELCUT такие задачи решают приближённо (пример – разбираемая ниже задача Lab3_Сu, приведенная в доступной для широкой общественности библиотеке демонстрационных программ).
Второе ограничивает тем, что многие практически важные кабельные объекты – структуры трёхмерные, так как при сборке сердечников кабелей их токопроводящие жилы, как правило, скручивают между собой. Равно как и сами жилы, если их свивают из нескольких (7, 19 и т.д.) проволок. И потому, на первый взгляд, применение ELCUT тут невозможно.
Тем не менее, обе эти задачи здесь могут быть решены: как точный расчёт неэкранированных кабельных конструкций, так и оценка влияния всех видов скруток.
Цель настоящей работы – показать, как без потерь точности решить (любую) «неэкранированную» задачу. А скрутки оставим для обсуждения в последующих статьях.
Индуктивность неэкранированной пары в решении задачи Lab3_Сu (http://www.tor.ru/elcut/courses/ toe/rus/lab3_r.htm).
Сначала разберём решение этой задачи, посвящённой моделированию магнитного поля бесконечной прямой симметричной двухпроводной медной линии (рис.1) по которой течёт переменный ток J = 300A. Изолятор – воздух (в отличие от рассматриваемой ниже пары с изолированными проводами). Провода толстые и близкие: a =15 мм и b = 59 мм, так что существенны скин-эффект и эффект близости.
Здесь есть две плоскости зеркальной симметрии: одна проходит через оси проводников, рассекая их, а вторая, перпендикулярная ей, – через середину расстояния между проводами. Поэтому геометрическую модель задаче строят лишь в одном квадранте. В целом линия открыта в Космос и вектор-потенциал её магнитного поля А
1/Д (Д – расстояние от линии).
По этой причине в Lab3_Сu квадрант ограничили квадратом со стороной Д =1000 мм >> a, b. На стороне квадрата, рассекающей проводники, касательная составляющая магнитного поля Нt = 0.На остальных трёх сторонах А = 0. Отметим, что на плоскости симметрии А = 0 точно, а на остальных сторонах – лишь приближённо.
На рис.2 представлена сетка конечных элементов (1925 узлов) и её фрагмент около провода. Ниже – карта полей: чёрные кривые – линии магнитного поля, цветная карта – распределение плотности тока: алый = 0.9 А/мм 2 , тёмно-синий = 0.5 А/мм 2 .
Для вычисления межпроводной индуктивности L = Ф/J в ELCUT вычислили магнитный поток между проводами Ф = 2.3402 10 -4 Вб (расчётный контур – бирюзовая линия на рис. 2). Откуда L = 0.78 МкГн/м. Точный же расчёт [7,8] даёт ёмкость и индуктивность
С = εε0π / ln[b/a + (b 2 /a 2 –1) 1/2 ] ;
L = μ0/π ln[b/a + (b 2 /a 2 – 1) 1/2 ] = 0.81843 МкГн/м (3)
то есть на 5% больше. Таков «вес» магнитного поля вне расчётного блока. Для увеличения точности необходимо последовательно увеличивать площадь квадрата (соответственно увеличивая число узлов сетки) и наблюдать за сходимостью величины L .
Межпроводная индуктивность конформно преобразованной пары.
Но в ЕLCUT эту задачу можно решить точно. С этой целью конформно отобразим исследуемую пару в коаксиальную структуру (рис.3) с радиусами a’1 = 15 мм и a’2 = 116.06 мм с помощью дробно-линейной функции [9] w = M2/(z –Р ) где w = u + iv ; z = x + iy; Р = Px + iPy – полюс. По сути, это просто замена переменных u = M2 (x –Px) /r2; v = – M2 (y –Py)/r2 , где r2 = (x–Px)2 + (y–Py)2. Проще всего её провести в полярных координатах.
Тогда решаемое в ELCUT уравнение Пуассона:
преобразуется к виду :
R 4 [ ∂ (R ∂ A/ ∂ R)/ ∂ R/R + ∂ 2 A/ ∂ φ 2 /R 2 ] /M 2 + i µ0 g ω A = – µ0 jстор (5)
где: R = [u 2 + v 2 ] 1/2 = М 2 /r
В ELCUT величину jвихр = i µ0 g ω A называют плотностью вихревых токов, jстор – плотностью сторонних токов. По физическому смыслу первый – это ток самоиндукции проводника, вызываемый переменным магнитным полем протекающего через него тока j = jвихр + jстор, а второй по величине равен постоянному току, который протекал бы через проводник при том же падении напряжения на нём (то есть при отсутствии индуктивного сопротивления).
В изоляторе g = 0 , jвихр = 0 ; jстор = 0, уравнения (5) и (4) вырождаются в уравнения Лапласа и совпадают с точностью до обозначений переменных:
∂ (r ∂ A/ ∂ r)/ ∂ r + ∂ 2 A/ ∂ φ 2 /r 2 = 0 ;
∂ (R ∂ A/ ∂ R)/ ∂ R + ∂ 2 A/ ∂ φ 2 /R 2 = 0
То есть, в изоляторах конформное преобразование не меняет вид уравнения Лапласа (отметим попутно, что дробно-линейное отображение в некотором смысле не меняет и вид уравнений Пуассона (4) и (5) [9] ). Это значит, что вместо приближённого решения безграничной задачи можно точно решить ей конформную, ограниченную экраном, в который отображаем один из проводов. В данном случае – получить точно известные индуктивность и ёмкость коаксиального кабеля:
Проверим это с помощью ELCUT, для чего вычислим поток Ф магнитного поля вокруг жилы с током. Для этого достаточно вычислить поле в узком секторе (100 на рис. 4).
Тогда получим L = Ф / J = 0.81878 мкГн/м, что всего на 0.04% больше точного. И это всего при 254 узлах сетки (0.14%, если узлов 119). Отметим попутно, что в ELCUT предусмотрен ещё более точный и быстрый способ вычисления индуктивных параметров, о чём подробнее – в одной из следующих статей.
Отображение пар в структуры, близкие к коаксиальным, полезно ещё и потому, что такие структуры имеют широкий минимум ёмкости (максимум индуктивности). На рис.5 представлены графики зависимости ёмкости от смещения жилы относительно центра экрана. Как видно, небольшое смещение осей экрана и/или провода мало влияет на ёмкость. Цифры около кривых – отношение а’2/a’1.
Отметим, что такое смещение можно рассматривать и как частный случай искажения формы провода и/или экрана. Поэтому можно ожидать, что если пару произвольных проводов отобразить в почти коаксиальную фигуру, то выражения (3’) дадут неплохое приближение к параметрам пары, точность которого можно оценить с помощью кривых на рис.5. Кроме того, практическая полезность данного наблюдения ещё и в том, что, получая точные значения параметров кабеля в среде ELCUT, расчётчик легко сравнит их с традиционными оценками, которые производят до сих пор с помощью (3’).
Емкость неэкранированной прямой симметричной пары.
В задаче Lab3_Сu в качестве изолятора рассмотрен воздух. Но в реальных конструкциях изолятор, как правило, устроен сложнее. Вычислим в качестве примера ёмкость прямой изолированной пары: радиуc проводов а =1 мм, толщина изоляции d = 0.3 мм (полиэтилен, ε1 = 2.5), так что b = 1.3 мм . Пусть полюс Р = (b 2 –a 2 ) 1/2 = 0.830662 мм и масштаб М 2 = 2 (b 2 – a 2 ) 1/2 [b ± (b 2 – a 2 ) 1/2 ] = 3.539722 мм 2 .
Тогда пара отобразится в коаксиальную структуру с радиусом жилы a1 = a = 1.000 мм, экрана a2 = a [b/a ± (b 2 /a 2 – 1) 1/2 ] 2 = 4.540 мм и центром 2.131 мм. (рис.6). Границы изоляции отобразятся в две касающиеся эксцентричные окружности с радиусами a4 = 3.131 мм (центр 1.1304 мм ) и a3 = 1.615 мм (центр 2.647 мм ).
На основании этих данных строим геометрическую модель ELCUT и вычисляем ёмкость пары C = 61.13 пФ/м с погрешностью не больше 0.1% при числе узлов
На карте полей (рис. 7) показано распределение электрического поля внутри конформного отображения пары: тонкие чёрные кривые – линии равного потенциала. Цветом обозначена величина радиальной составляющей напряжённости электрического поля E = Ur = ∂U∂r, а также второй производной Uφφ = ∂ 2 U/∂φ 2 . Эти величины полезны в исследованиях витых пар и скрученных многопроволочных жил, исследованию которых мы посвятим последующие статьи.
Картина поля вокруг пары – это (обратное) конформное отображение линий потенциала, изображённых на рис. 6. Если необходимо, можно пересчитать и отобразить другие величины и объекты. Но здесь в этом нет надобности.
Выводы
1. С помощью ELCUT можно точно вычислить параметры любой открытой системы проводников, если с помощью конформного преобразования, например, дробнолинейного, отобразить её закрытую экраном. Поэтому дополнение математического инструментария ELCUT мастером (прямых и обратных) конформных отображений хотя бы в объёме справочника [10] позволит обеспечить максимальную точность вычислений межпроводной ёмкости и индуктивности любых нескрученных кабельных конструкций.
2. В общем случае конформное отображение модифицирует вид уравнений Лапласа и Пуассона. Например, появляются коэффициенты, пропорциональные степеням радиуса R. Потому целесообразно научить ELCUT работать с произвольными координатно-зависимыми коэффициентами при производных, а также координатно-зависимыми плотностями зарядов и токов в блоках (в правых частях уравнения (4), о чём подробнее в следующей статье).
Тогда ELCUT имеет шанс стать весьма востребованным инструментом в кабельно-расчётном деле.
Литература
1. Гроднев И.И, Лакерник Р.М., Шарле Д.Л. Основы теории и производство кабелей связи. – М, Л: Госэнергоиздат,1956.
2. Кулешов В.Н. Теория кабелей связи.-М: Государственное издательство литературы по вопросам связи и радио, 1950.
3. В.Е. Власов, Ю.А.Парфёнов. Кабели цифровых сетей электросвязи. Конструирование, технологии, применение. – М: Эко-Трендз, 2005.
4. А.И.Листратенков. Теоретические основы конструирования силовых кабелей и проводов. – М: Полиграф сервис, 2006.
5. Вишняков С.В., Гордюхина Н.М. Фёдорова Е.М. CAE: Программы курсов, учебные примеры, пособия, материалы по ANSYS. 2005 http://cae.tsogu.ru/Learning/Ansys/ ansys_learning.
6. Отсюда можно скачать студенческую версию ELCUT 5.4, 2007 http://www.tor.ru/elcut/free_soft_r.htm.
7. Иоссель Ю.Я., Кочанов Э.С., Струнский М.Г. Расчет электрической емкости. – Л.: Энергоиздат, 1981
8. П.Л.Калантаров, Л.А.Цейтлин. Расчёт индуктивностей. – Л: Энергоатомиздат, 1986.
9. Более подробно это изложено в приложениях к нашим статьям, размещённым в разделе «Наука» сайта ОТИ МИФИ http://www.oti.ru .
10. Г Корн, Т Корн. Справочник по математике. – М: Наука, 1970.
Подробнее о конформном отображении можно прочитать в монографии:
К.Каратеодори Конформное отображение. – М.-Л.: ОНТИ Государственное технико-теоретическое издательство, 1934. Книгу можно скачать из библиотеки мехмата МГУ http://lib.mexmat.ru/books/1663
Достаточно подробное изложение можно найти в статьях пятитомника «Математическая Энциклопедии». – М: БСЭ, 1979.
Нашли ошибку? Выделите и нажмите Ctrl + Enter
Источник
Содержание:
Электротехника и ее теоретические основы:
Одной из основных задач техники является преобразование при родных энергетических запасов в используемые виды энергии — в механическую, тепловую, световую и т. п., что требует транспортировки энергетического сырья к месту его использования.
Электрическая энергия легко передается на большие: расстояния и с высоким коэффициентом полезного действия преобразуется в другие виды энергии. Общепринятым является преобразование природных энергетических запасов в электрическую энергию с помощью так называемых генераторов и ее передача посредством проводов к месту потребления, где в преобразователях и приемниках она преобразуется в нужный вид энергии. Беспроводная передача энергии осуществляется с помощью радиосвязи.
Преимущества генерирования, передачи, распределения и преобразования электрической энергии обеспечили широкое применение электротехники.
Новые производственные отношения в нашей стране, отсутствие частной собственности на запасы энергетического сырья, средства и орудия производства, государственное планирование являются мощным фактором развития электротехники и всеобъемлющего охвата ею всех отраслей нашего народного хозяйства, быта и культуры.
Составленный под руководством В. И. Ленина план ГОЭЛРО построения 30 электростанций общей мощностью 1,75 млн. кет был выполнен в решающих позициях за 10 лет.
В послевоенные годы электрификация СССР развивается невиданными темпами: в 1960 г. мощность электростанций составила 66,7 млн. кет, а за пятилетку 1966— 1970 гг. введены 54 млн. кет, в том числе самая мощная в мире Красноярская гидроэлектростанция (6 млн. кет) и Белоярская атомная электростанция (600 тыс. кет). В Директивах XXIV съезда КПСС по пятилетнему плану развития народного хозяйства СССР на 1971— 1975 гг. предусмотрено ввести в действие электростанции мощностью 65—67 млн. кет, в том числе 6—8 млн. кет на атомных электростанциях. Соответственно увеличилась и увеличится мощность потребителей — устройств, преобразующих электрическую энергию в другие виды.
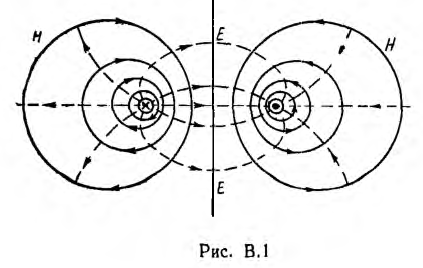
Электрическая энергия — это энергия электромагнитного поля, являющегося видом материи. Поле имеет две составляющие — электрическое и магнитное поля, что можно показать на примере линии передачи постоянного тока (рис. В. 1).
При передаче энергии провода линии, изолированные друг от друга, находятся под напряжением U. Следовательно, между проводами возникает электрическое поле, изображенное пунктиром на рис. В.1 в виде силовых линий, В проводах протекает ток 7, следовательно, в проводах и вне их создается магнитное поле, показанное сплошными линиями. На рис. В.1 видно характерное различие между электрическим и магнитным полями: силовые линии электрического поля незамкнуты, они начинаются и оканчиваются на заряженных проводах; магнитные силовые линии всегда замкнуты; они не имеют ни начала, ни конца.
Как известно из курса физики, электрическое поле в каждой точке
характеризуется вектором напряженности Е, равным силе, воздействующей на единичный положительный заряд, помещенный в эту точку, и вектором электрического смещения
Электрическое поле в проводящей среде создает ток, характеризуемый в
каждой точке поля вектором плотности тока 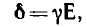
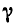
проводимость среды. Ток сопровождается появлением магнитного поля и переходом части энергии электромагнитного поля в тепло, причем мощность этого процесса в единице объема
Магнитное поле в каждой точке характеризуется вектором магнитной индукции В, величина которого равна силе, действующей на движущийся единичный положительный заряд, скорость которого равна единице, а направление В — перпендикулярно этой силе и скорости, а также вектором напряженности
где 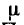
Передача, генерирование, преобразование и потребление электрической энергии, равной 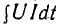
В науке об электричестве связь электрических и магнитных явлений была установлена в двадцатых годах прошлого века, когда Ампер и Эрстед доказали, что электрический ток сопровождается возникновением магнитного поля; окончательно связь электрического и магнитного полей была подтверждена Фарадеем, открывшим явление электромагнитной индукции (1831 г.).
Электротехника, зародившаяся в тридцатых годах прошлого века, вначале развивалась как техника постоянного тока. Только после создания М. О. Доливо-Добровольским системы трехфазного тока и трехфазного двигателя (1891 г.) переменный ток стал вытеснять постоянный. Передача электрической энергии стала осуществляться также трехфазным током.
Теория электромагнитного поля в законченной математической форме была создана Максвеллом в 1873 г. Подтвержденная многочисленными опытами ряда ученых, она была окончательно принята в начале нашего века.
Введенное Максвеллом представление об электромагнитных волнах, экспериментально подтвержденное работами Герца, позволило А. С. Попову в 1895 г. осуществить передачу сигнала без проводов, что послужило началом новой области электротехники — радиотехники.
Электротехника и ее теоретические основы непрерывно развиваются. Например, совершенствуются электронные, ионные и полупроводниковые приборы и аппараты, с помощью которых осуществляют прямые и обратные преобразования переменного тока в постоянный, усиление напряжения и мощности и создают электронные вычислительные машины. Увеличивается дальность и возможности проводной связи, радиотехники и телевидения, развивается электроавтоматика, в энергетике осуществляется переход к большим напряжениям (1500 кв) и мощностям генераторов (1 200 ООО кет и выше), разрабатываются и испытываются магнитогидродинамические прямые преобразователи тепловой энергии в электрическую и т. д.
Так как все электротехнические устройства основаны на использовании электромагнитного поля их систем, состоящих из заряженных тел и контуров с токами, для решения многих задач необходимо привлечение теории этого поля со сложными математическими зависимостями. Однако в большинстве устройств используются ограниченные пути электрического тока и магнитного потока — изолированные проводники малого сопротивления и магнитопроводы из материала с высокой магнитной проницаемостью, называемые электрическими и магнитными цепями. Их расчеты могут быть значительно упрощены, так как не требуют знания составляющих поля в каждой точке устройств. Теория этих цепей основана на использовании интегральных величин: напряжения 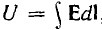
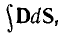
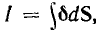
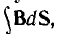
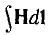
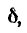
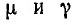
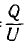
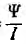
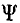
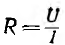
Эти величины можно называть параметрами цепей.
Если эти параметры не зависят от токов и напряжений, уравнения теории цепей, связывающие интегральные величины, будут линейными; такие цепи называют линейными.
В ряде случаев, весьма важных для современной электротехники, эти параметры являются функциями напряжений и токов; тогда уравнения и цепи становятся н нелинейными.
Осуществление грандиозных планов дальнейшей электрификации нашей страны, эксплуатация существующих и создание новых электротехнических устройств требуют от инженера-электрика глубокого понимания физических процессов и умения производить их технический расчет. Фундаментом электротехнического образования является курс теоретических основ электротехники (ТОЭ), базирующийся на сведениях, сообщенных в курсах физики, математики и механики.
Настоящее учебное пособие ТОЭ построено в соответствии с изложенным. Вначале даны параметры цепей, потом основы теории источников и приемников электрической энергии. Затем следует анализ электрических и магнитных цепей при постоянном и переменном токе — линейных и на их основе нелинейных. Курс завершается теорией постоянного и переменного электромагнитного поля.
В книге принята Международная система единиц СИ и рационализованная форма написания уравнений, предложенная Хевисайдом, в которой основные соотношения для электрического и магнитного полей имеют симметричный вид, а множители 4 π и 2 π входят лишь в те соотношения, где они соответствуют характеру симметрии — сферической (4 π) и осевой (2 π).
Параметры электрических и магнитных цепей
Электрической цепью называется совокупность устройств, состоящая из источников, преобразователей и приемников электрической энергии и соединяющих их проводов, образующих замкнутые пути для электрического тока.
Часть цепи, не содержащая источников электрической энергии, называется пассивной, а часть цепи, содержащая источники, называется активной.
Как было показано во введении на примере линии передачи, электрическая цепь характеризуется тремя параметрами: сопротивлением R, емкостью С и индуктивностью L. Этими параметрами обладают все элементы цепей, например резисторы, в которых основную роль играет их сопротивление, конденсаторы с основным параметром — емкостью, и катушки индуктивности, в которых основной является их индуктивность.
Из изложенного вo введении очевидно, что параметры линии передачи равномерно распределены по всей длине линии. Параметры распределены также в отдельных элементах цепи. Например, в катушке индуктивности сопротивление, индуктивность и емкость распределены по ее длине, так как каждый виток с током имеет сопротивление и создает магнитное поле, а отдельные витки изолированного проводника обладают друг по отношению к другу некоторой емкостью.
Этим свойством обладают все реальные электрические цепи—они являются цепями с распределенными параметрами. Так как в ряде технически важных задач не требуется знания электромагнитных процессов в каждой точке всей цепи и ее элементов, необходимо учесть только их интегральные свойства; такие цепи могут быть представлены в виде цепей с сосредоточенными параметрами, состоящих из сопротивлений, индуктивностей и емкостей. Например, катушка индуктивности может быть представлена в виде схемы с последовательным соединением сопротивления R, индуктивности L и с параллельно приключенной к ним емкостью С.
При включении цепи на постоянное напряжение в течение короткого времени от источника потребляется энергия на создание электромагнитного поля. После этого запасенная в С и L энергия сохраняет свою величину неизменной и не отражается на работе цепи, а источники доставляют энергию только на покрытие тепловых потерь в сопротивлениях. Поэтому при расчете цепей постоянного тока следует учитывать только сопротивление R.
В цепях переменного тока энергия, запасаемая в С и L, и мощность потерь в R непрерывно изменяются. Поэтому при расчете этих цепей необходимо учитывать все три параметра.
Многие электрические цепи нелинейны. Так, например, температура, а следовательно, и сопротивление проводника при прохождении по нему тока изменяются; индуктивность катушки со стальным сердечником зависит от тока, так как с величиной тока будет меняться магнитная проницаемость р, сердечника, а следовательно, и индуктивность L. Однако в большинстве случаев цепи можно рассматривать как линейные, считая параметры R, L и С постоянными.
В устройствах современной электротехники главным образом используется энергия магнитного поля, поэтому их основным параметром является индуктивность L. Для этих устройств вводится понятие магнитной цепи как совокупности тел, большей частью ферромагнитных, в которых создается магнитный поток.
При постоянном токе методы анализа магнитных цепей аналогичны методам расчета электрических цепей, содержащих лишь один параметр — сопротивление R. Его аналогом в магнитных цепях является магнитное сопротивление 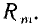
Эта глава посвящена элементарным методам расчета параметров устройств, поля которых имеют простые виды симметрии. Более сложные случаи рассматриваются в теории электромагнитного поля.
Электрическая ёмкость и ее расчет
Для электрических цепей наибольший интерес представляет система двух проводящих тел в диэлектрической среде, заряды + Q и —Q которых отличаются только знаком, являющаяся по существу конденсатором. Емкость конденсатора равна отношению его заряда Q, под которым понимается абсолютное значение разноименных зарядов, к напряжению U между обкладками:
Емкость конденсатора, определяемая размерами и формой тел и их взаимным расположением, пропорциональна диэлектрической проницаемости е среды между обкладками. Емкость измеряется Б фарадах (ф), заряд в кулонах (к), напряжение в вольтах (в).
Для расчета емкости конденсатора по заряду и напряжению необходимо предварительно рассчитать его электрическое поле, исходя из общих соотношений для электрического поля.
Связь между зарядом и вектором смещения 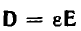
справедливой для линейных и нелинейных сред и являющейся основным соотношением для электрического поля. В правой части этого равенства стоит суммарный заряд, заключенный внутри замкнутой поверхности, в левой — поток вектора смещения. Смещение измеряется в к/м2, напряженность электрического поля — в в/м, диэлектрическая проницаемость в ф/м.
Поле в каждой точке характеризуется потенциалом 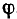
Напряжение 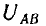
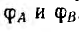
Потенциал также измеряется в вольтах.
Так как сумма напряжений по замкнутому пути равна нулю, то 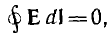
Емкость коаксиального кабеля
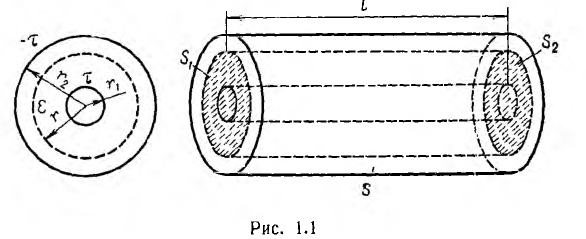
Коаксиальный кабель представляет собой два проводящих соосных
цилиндра с радиусом внутреннего цилиндра r1 внутренним радиусом
внешнего цилиндра г2, длиной цилиндров I (рис. 1.1).
Пусть внутренний цилиндр — жила кабеля — заряжен положительно и изолирован диэлектриком с проницаемостью е от оболочки — обратного провода, являющегося внешним цилиндром и несущим заряд обратного знака, а напряжение между жилой и оболочкой равно U.
При выполнении условия 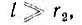
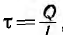
Для цилиндрической поверхности радиуса г, охватывающей заряженную жилу (на рис. 1.1 указана пунктиром), можно применить теорему Гаусса. Из- за радиального направления вектора смещения потоки через основания цилиндра 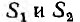
Так как при неизменном радиусе смещение D остается постоянным, то
откуда
В последние выражения не входит радиус 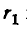
Напряжение на кабеле
откуда емкость кабеля
После подстановки из предпоследнего равенства
в выражение для напряженности поля получим
т .е . напряженность поля обратно пропорциональна радиусу, а ее максимальное значение у поверхности жилы
Исследование на минимум показывает, что наименьшее значение
максимальной напряженности при заданных напряжении и радиусе
внешней оболочки будет при
т. е. при 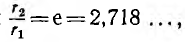
При таком соотношении радиусов кабель, очевидно, обладает наибольшей электрической прочностью.
Емкость двухпроводной линии
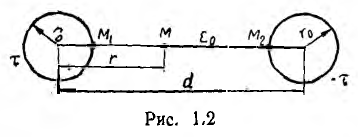
Широко используемые в электротехнике двухпроводные линии передачи представляют собой систему двух прямых параллельных проводов кругового сечения (рис. 1.2). Провода оказываются заряженными разноименно, когда линия включена на напряжение.
Так как длина проводов I велика по сравнению с расстоянием d между их осями, искажением электрического поля у концов заряженных проводов можно пренебречь. Поэтому распределение поля в пространстве остается неизменным в любой плоскости, перпендикулярной осям проводов.
Пусть двухпроводная линия подвешена настолько высоко, что влиянием земли можно пренебречь. Напряжение на линии равно U, величина заряда на единицу длины — τ, радиус проводов — 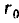
В отличие от коаксиального кабеля, где вследствие равномерного распределения заряда по поверхности жилы ее электрическая ось совпадает с геометрической, плотность зарядов на проводах линии больше на частях их поверхностей, обращенных друг к другу из-за притяжения разноименных зарядов. Поэтому расстояние между электрическими осями проводов становится тем меньше расстояния между их геометрическими осями, чем меньше отношение
Для воздушных линий 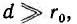
где 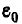
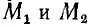
Отсюда емкость двухпроводной воздушной линии
Взаимоёмкость и ее расчёт
Для многих технических задач представляет интерес рассмотрение электрического поля, созданного системой нескольких пар разноименно заряженных тел. Заряды этих тел и напряжения связаны между собой линейными уравнениями.
В системе из двух конденсаторов (1-1′ и 2-2′ на рис. 1.3) все четыре тела связаны электрическим полем, поэтому заряд каждого из конденсаторов зависит от их напряжений 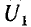
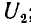
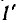
напряжением второго, совпадает по знаку с зарядом, создаваемым собственным напряжением, суммарные заряды обоих конденсаторов будут:
где 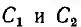
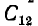
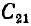
Собственные емкости конденсаторов
определяются всеми четырьмя телами системы и отличаются от емкости каждого из этих конденсаторов, определенной при отсутствии другого.
При определении ёмкости 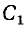
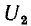
Соответственно, при определении 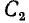
Взаимоемкость:
т. е. равна отношению заряда на обкладках накоротко замкнутого одного конденсатора, когда его заряд создается напряжением другого, к этому напряжению.
Взаимоемкость определяется конфигурацией тел, образующих конденсаторы, их взаимным расположением и пропорциональна диэлектрической проницаемости среды.
При несовпадении знаков собственных зарядов, обусловленных емкостью, и взаимных зарядов, обусловленных взаимоемкостью, знак перед вторыми членами в выражениях (1.2) будет отрицательным. Взаимоемкость также измеряется в фарадах (ф).
Для системы многих конденсаторов, соответственно, заряд Qk
конденсатора k определяется всеми напряжениями:
где 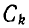
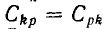
Взаимоемкость между конденсаторами k и р равна отношению заряда конденсатора k, созданного напряжением конденсатора р, к этому напряжению. При этом все конденсаторы, кроме p -того, замкнуты накоротко.
Взаимоемкость двух параллельных двухпроводных линий
Примером системы из четырех тел, рассматриваемой как совокупность двух конденсаторов, могут служить две параллельные линии, расположенные симметрично одна над другой (рис. 1.4).
Пусть радиус проводов 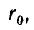
и 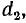
Заряды на проводах первой линии замкнутой накоротко 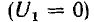
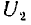
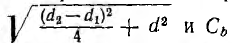
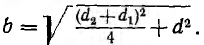
Тогда, соответственно формуле (1.1), получается
Поэтому взаимоемкость
а собственная емкость первой линии при учете второй линии равна
Такая задача представляет технический интерес, позволяя определить влияние линии передачи 2 на линию связи 1 (рис. 1.4).
Это влияние состоит в наведении на проводах линии связи заряда взаимоемкости 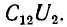
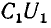
а напряжение 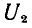
линии связи, то для уменьшения наведенного заряда необходимо увеличивать расстояние d между линиями и уменьшать расстояние
между проводами линии связи.
- Линейные н нелинейные диэлектрики и конденсаторы
- Сопротивление и его расчет
- Линейные и нелинейные резисторы
- Индуктивность и ее расчет
- Преобразование схем электрических цепей
- Установившиеся процессы в линейных электрических цепях
- Методы расчета простых электрических цепей
- Метод сигнальных графов
Провода
двухпроводной цепи можно рассматривать
как обкладки конденсатора, между которыми
расположен диэлектрик (воздух, стирофлекс,
полиэтилен и т. п.), и емкость С
находится как отношение заряда,
приходящегося на длину в 1 км,
к напряжению между проводами цепи.
Емкость
1 км
двухпроводной цепи определяется по
формуле

где
— относительная диэлектрическая
проницаемость (равная для воздуха
единице); а
—
расстояние между центрами проводов; r
—
радиус проводов, причем а
и r
должны быть в одинаковых единицах.
Для
цепей воздушных линий а>>r,
поэтому вместо отношения
обычно подставляют отношение
.
Емкость
цепи из биметаллического провода
вычисляется аналогично.
Жилы
кабельной цепи расположены близко друг
к другу и разделены слоем диэлектрика.
Толщина диэлектрика зависит как от
диаметра жил, так и от материала
диэлектрика и вида скрутки жил. Чаще
всего диэлектрик заполняет не все
пространство между жилами, а часть его;
другая же часть пространства между
жилами заполнена воздухом. В этом случае
в формулу для емкости цепи необходимо
подставлять эквивалентную величину
относительной диэлектрической
проницаемости Э,
которая определяется по величинам
относительной диэлектрической
проницаемости 1
и 2
отдельных диэлектриков и по объемам V1
и V2
, занимаемым
этими диэлектриками, по формуле
. (4.15)
Так
как относительная диэлектрическая
проницаемость воздуха равна единице и
меньше относительной диэлектрической
проницаемости любого диэлектрика, то
ясно, что эквивалентная относительная
диэлектрическая проницаемость Э
получается меньше, чем относительная
диэлектрическая проницаемость материала
диэлектрика.
Емкость между
жилами кабельной пары зависит также от
емкости жил этой пары по отношению к
соседним жилам и к свинцовой оболочке.
Емкость кабельной цепи с учетом емкости
относительно других жил и свинцовой
оболочки называют рабочей емкостью.
Так как число жил в кабеле бывает
различным и способы скрутки жил также
различны, для подсчета рабочей емкости
пары пользуются приближенными формулами
с поправочными коэффициентами. Наиболее
употребительна формула

где
а—
расстояние между центрами жил, мм;
r—
радиус жил, мм;
— поправочный
коэффициент (меньше единицы), зависящий
от способа скрутки и от расстояния жил
от заземленной оболочки;
— коэффициент
спиральности или
скрутки;
Э
— эквивалентная
относительная
диэлектрическая
проницаемость составного диэлектрика.
Емкость
коаксиальной цепи определяется по
формуле емкости цилиндрического
конденсатора
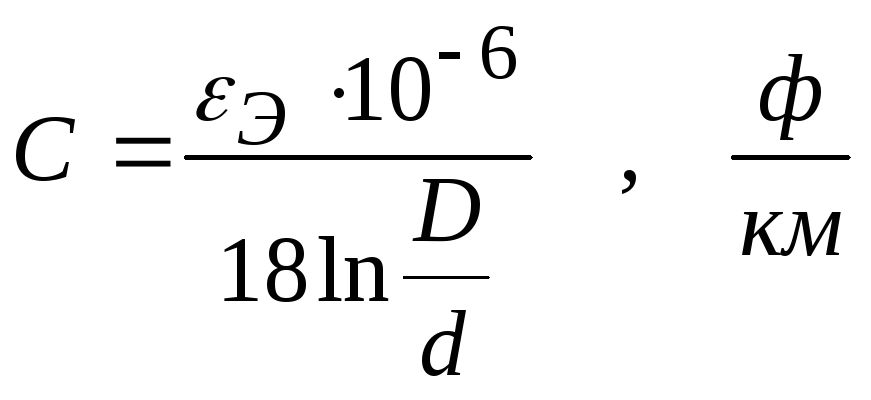
где
э
—
эквивалентная относительная диэлектрическая
проницаемость диэлектрика, служащего
для изоляции внутреннего провода цепи
от наружного.
4.4.
Проводимость изоляции цепей связи
При
передаче электрических сигналов по
цепям связи ток от одного провода к
другому или от провода к земле переходит
не только через емкость, но и через
проводимость изоляции.
Провода
воздушных линий связи изолируются друг
от друга и от земли изоляторами, а жилы
кабельных цепей изолируются друг от
друга специальной бумагой, стирофлексом,
полиэтиленом и другими изолирующими
материалами.
Любой
вид изоляции имеет конечное сопротивление,
поэтому через изоляцию происходит
утечка (ответвление) тока. Если
сопротивление изоляции на 1 км
обозначить через W0,
то величина обратная, т. е.
будет представлять гальваническую
проводимость изоляции.Go
является проводимостью изоляции цепи,
возникающей вследствие несовершенства
изоляции. Эта проводимость имеется как
при постоянном токе, так и при переменном.
Кроме этого, при переменном токе имеют
место потери в диэлектриках, пересекаемых
переменным электрическим полем.
При
прохождении переменного тока по цепи
образуется электрическое поле, которое
на воздушных линиях пересекает изоляторы,
деревянные траверсы, штыри и столбы, а
в кабелях это поле пересекает диэлектрик,
изолирующий одну жилу цепи от другой,
в результате чего происходит поляризация
диэлектрика. Явление поляризации состоит
в том, что в такт с изменениями направления
электрического поля меняют свое положение
(смещаются) диполи вещества диэлектрика.
При
поляризации диполей на преодоление
внутреннего трения расходуется часть
передаваемой по цепи энергии, которая
выделяется в виде тепла. Наличие потерь
энергии на поляризацию диполей вещества
диэлектрика приводит к увеличению тока
утечки, т.е. к появлению проводимости
диэлектрических потерь, обозначаемой
GДП.
Так
как обе рассмотренные проводимости
включены параллельно, то общая проводимость
изоляции G
на 1 км
цепи будет равна сумме двух проводимостей
. (4.18)
Проводимость
изоляции измеряется в единицах
проводимости — сименсах (сокращенно
сим).
Как и другие первичные параметры,
проводимость изоляции цепей связи
принято относить к 1 км
цепи.
При постоянном
токе, когда энергия в диэлектрике не
теряется, проводимость изоляции воздушной
цепи определяется лишь первым слагаемым
G0.
При
переменном токе к проводимости G0
прибавляется проводимость GДП,
вызванная потерями энергии в диэлектрике,
и общая проводимость изоляции определяется
по формуле 4.18.
Так
как проводимость изоляции GДП
пропорциональна частоте переменного
тока f,
то величину ее можно определять по
формуле
. (4.19)
Коэффициент
n
для цепей воздушных линий определяется
опытным путем. При расчетах принимают:
а) для сухой погоды коэффициент
n=0,05-10-9;
б) для сырой погоды n=0,25-10-9.
Таким
образом, для определения проводимости
изоляции воздушных цепей связи пользуются
формулой
, (4.20)
принимая
величину G0
равной в сухую погоду 0,0110-6
сим/км, а в сырую погоду — 0,510-6
сим/км.
Проводимость
изоляции биметаллических цепей
определяется аналогично.
Проводимость
изоляции кабельных цепей определяется
по той же формуле, но, поскольку G0
для кабельных цепей очень мала (0,000110-6
сим/км), то ею обычно пренебрегают.
Проводимость
изоляции GДП,
обусловленная потерями энергии
в диэлектрике,
вычисляется через коэффициент
диэлектрических потерь tgЭ
следующим образом.
|
Утечка |
|
|
Рис. 4.2. Угол |
На диаграмме ток
ICчерез емкость опережает напряжениеUна 90o, а токIGчерез проводимость изоляции совпадает
с напряжением по фазе. Если бы проводимость
изоляции равнялась нулю, то токIGтакже был бы равен нулю и сдвиг фаз между
напряжениемUи током
утечкиIУбыл бы равен 90oкак
у идеального конденсатора. При наличии
токаIG
сдвиг фаз междуUиIУбудет
меньше 90oна угол.
Этот уголназывается углом диэлектрических потерь
или коэффициентом диэлектрических
потерь. Поскольку ток утечки через
емкостьICопределяется по формуле
а ток утечки через проводимость изоляцииIGпо формуле,
то,
откуда проводимость изоляции цепи.
Обычно
часть объема между жилами кабельной
цепи занята изолирующим материалом, а
другая часть – воздухом или другим
диэлектриком. В этом случае величина
tg
определяется как средневзвешенная
величина tgЭ.
, (4.21)
т.е.
проводимость изоляции кабельной цепи
тем больше, чем больше частота переменного
тока ,
емкость цепи С
и коэффициент диэлектрических потерь
tgЭ.
Следовательно, для уменьшения проводимости
изоляции кабельных цепей следует
применять диэлектрики с малым коэффициентом
диэлектрических потерь. Проводимость
изоляции коаксиальной кабельной цепи
определяется по этой же формуле.
4.5. Вторичные
параметры линий связи
По известным
первичным параметрам линии могут быть
найдены вторичные параметры, к которым
относятся волновое сопротивление,
определяемое по формуле
, (4.22)
и коэффициент
распространения, определяемый по формуле
. (4.23)
Коэффициент
распространения представляет собой
комплексную величину
,
где
называется коэффициентом затухания, а
— коэффициентом фазы. Если обозначить
(4.24)
и
, (4.25)
то
, (4.26)
. (4.27)
Волновое сопротивление
линии можно выразить в виде
, (4.28)
где модуль волнового
сопротивления может быть найден по
формуле

а фазовый угол
. (4.30)
Если известна
величина напряжения Uн(токаIн) в
начале линии и найден коэффициент
затухания, то
можно определить напряжение (ток) в
любой точке линии на расстоянииlот ее начала по формулам
. (4.31)
Величина
l,входящая в
эти выражения называется волновым
затуханием линии и измеряется либо в
неперах
, (4.32)
либо в децибелах
,
(4.33)
причем 1неп = 8,68
дб, 1дб = 0,115неп.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Вся активность
Так и не нашёл более специалдизированного раздела, поэтому сюда.Может ещё остались физики на форуме ?
Есть медный кабель, скажем длиной километр. У него есть ёмкость. Какая-то. Зная её, как посчитать ёмкость этого кабеля длиной полкилометра ?
Т.е вопрос состоит в том, емкость медного кабеля изменяется линейно от длины, или нет ?
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
В оптике есть предел когда не поможет повышение мощности передатчика. И этот предел линейно зависит от длины и типа кабеля.
А в меди — не все так однозначно. Тут многое решают помехи. По одной паре можно прокачать мегабиты ADSL но если по всем парам пытаться передавать в 100-парнике — оно может совсем не заработать.
Но на вполовину меньшей длины будет скорее всего лучше. Скорость может и вырастет в 2 раза, но вот удастся ли вместить в 2 раза больше потоков в один кабель при сохранении скоростей каждого — не думаю.
И медный кабель ограничен по частоте иначе. И если оптика вот прямо тупо в N раз короче — в N раз быстрее при любых N то в меди так может не получится.
Надо действительно ждать конкретно специалиста по теории передачи по медной линии связи… Самому стало интересно…
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
Так и не нашёл более специалдизированного раздела, поэтому сюда.Может ещё остались физики на форуме ?
Есть медный кабель, скажем длиной километр. У него есть ёмкость. Какая-то. Зная её, как посчитать ёмкость этого кабеля длиной полкилометра ?
Т.е вопрос состоит в том, емкость медного кабеля изменяется линейно от длины, или нет ?
Ёмкость зависит от длины линейно.
Вот только замерить ёмкость кабеля совсем непросто. Кроме ёмкости кабель обладает сопротивлением и индуктивностью. Причём ёмкость у кабеля распределённая. То есть, то, что покажет измеритель ёмкости имеет к ёмкости кабеля отношение довольно посредственное. И разные измерители покажут разную ёмкость в зависимости от метода измерения.
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
ну для начала — емкость это площадь пластин
площадь — величина линейная и получается прямая пропорция длины кабеля
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
ну для начала — емкость это площадь пластин
площадь — величина линейная и получается прямая пропорция длины кабеля
Линейная да, только погрешности разные.
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
тут же просто геометрия — площадь
какие погрешности?
и на 500 метров 2 проводника и на 1000 метров параллельно друг другу
если речь о переменном токе и еще высокой частоты и еще форма импульса какая нить хитрая — другой разговор
собственно для какой цели интересует емкость кабеля?
все наши суждения хороши для случая, когда одной стороны лампочка и с другой батарейка и надо прикинуть сколько пикосекунд после отключения источника питания лампа будет светить от заряда между проводниками кабеля 
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
Из общих соображений:Зависимость -линейная. Теоретически все это рассчитано в установившемся режиме как задача электростатики — в любом учебнике электротехники есть общие методы и конкретные расчетные случаи. Расчетная величина довольно хорошо согласуется с практикой на большой длине. Точность измерения, естественно, будет, до известной степени, зависеть от длины, то есть, меньше какой-то длины кусок вообще мерить бесполезно.
Конкретный метод измерения- лучше всего смотреть соответствующий ГОСТ Р МЭК. Там все должно быть написано.
P.S. Есть раздел-«Монтаж телекоммуникаций, пассивные компоненты..» — туда и писать надо. Там все спецы на эту тему обитают.
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
ТОЭ, раздел «длинные линии». Мне так кажется ))
Не путайте народ, вам неправильно кажется. Длинные линии- это когда размер сопоставим с длиной волны, практически, когда размер больше 1/8 длины волны. Иначе — не при чем тут длинные линии.
Электротехника для ВУЗов, раздел Электростатика.
Из того, с чем сталкивался и считал сам- расчет потенциала в точке подвеса ОКСН на ВЛЭП. Методом электростатики через расчет емкости системы проводников.
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
Предполагаю, что исходить надо от понятия «погонная ёмкость».
А по поводу измерений «погонной ёмкости» вот что нашлось:
I. Патент «Способ измерения погонной емкости одножильного электрического провода» (ссылка)
Из описания:
1. Известен способ измерения погонной емкости одножильного провода (одиночной жилы), регламентируемый ГОСТ 27893-88 (СТ СЭВ 1101-87). Кабели связи. Методы испытаний. Москва: Изд-во стандартов, 1989, 26 с. Способ заключается в измерении емкости между жилой и водой после погружения отрезка провода в бак с водой, соединенный с землей.
…
2. Способ измерения погонной емкости одножильного электрического провода, заключающийся в создании гармонического электрического поля между участком поверхности изоляции провода и заземленной электропроводящей жилой посредством помещенного в воду трубчатого измерительного преобразователя, через который перемещают контролируемый провод, с измерительным и двумя обеспечивающими однородность электрического поля на его краях дополнительными защитными электродами, измерении при известных амплитуде и частоте приложенного к электродам гармонического напряжения силы тока, протекающего через измерительный электрод, по которой судят о значении погонной емкости, отличающийся тем, что измеряют суммарную силу тока, протекающего через все электроды измерительного преобразователя, и определяют значение погонной емкости Cп по формуле
…
То есть суть этих способов — проводник, емкость которого мы хотим измерить, является частью некого конденсатора, емкость которого известно как рассчитать (наш проводник — одна из обкладок «конденсатора»)
II. Исследование уединенной ёмкости и индуктивности прямого провода толщиной d=1 мм и длиной 1.40 м
http://electricaleather.com/d/358095/d/issledovanie-uedinennoy-emkosti-i-induktivnosti.pdf
С картинками 
Там (см. стр.3) в качестве проверки правильности измеренного значения используют расчёт по формуле Зоммерфельда. В этой формуле зависимость емкости провода от его длины — нелинейная. Только вот не знаю, можно ли применять эту формулу для длин километр или полкилометра.
P.S. Как-то невнимательно я прочитал — оказывается спрашивается про «кабель», а я про «одиночный провод» искал. Оставлю, может кому пригодится и про провод.
Изменено 19 апреля, 2017 пользователем NN—-NN
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
Предполагаю, что исходить надо от понятия «погонная ёмкость».
А по поводу измерений «погонной ёмкости» вот что нашлось:
I. Патент «Способ измерения погонной емкости одножильного электрического провода» (ссылка)
Из описания:
1. Известен способ измерения погонной емкости одножильного провода (одиночной жилы), регламентируемый ГОСТ 27893-88 (СТ СЭВ 1101-87). Кабели связи. Методы испытаний. Москва: Изд-во стандартов, 1989, 26 с. Способ заключается в измерении емкости между жилой и водой после погружения отрезка провода в бак с водой, соединенный с землей.
…
2. Способ измерения погонной емкости одножильного электрического провода, заключающийся в создании гармонического электрического поля между участком поверхности изоляции провода и заземленной электропроводящей жилой посредством помещенного в воду трубчатого измерительного преобразователя, через который перемещают контролируемый провод, с измерительным и двумя обеспечивающими однородность электрического поля на его краях дополнительными защитными электродами, измерении при известных амплитуде и частоте приложенного к электродам гармонического напряжения силы тока, протекающего через измерительный электрод, по которой судят о значении погонной емкости, отличающийся тем, что измеряют суммарную силу тока, протекающего через все электроды измерительного преобразователя, и определяют значение погонной емкости Cп по формуле
…
То есть суть этих способов — проводник, емкость которого мы хотим измерить, является частью некого конденсатора, емкость которого известно как рассчитать (наш проводник — одна из обкладок «конденсатора»)
II. Исследование уединенной ёмкости и индуктивности прямого провода толщиной d=1 мм и длиной 1.40 м
http://electricaleat…duktivnosti.pdf
С картинками

Там (см. стр.3) в качестве проверки правильности измеренного значения используют расчёт по формуле Зоммерфельда. В этой формуле зависимость емкости провода от его длины — нелинейная. Только вот не знаю, можно ли применять эту формулу для длин километр или полкилометра.
P.S. Как-то невнимательно я прочитал — оказывается спрашивается про «кабель», а я про «одиночный провод» искал. Оставлю, может кому пригодится и про провод.
Как человек, имевший дело со всякими подобными испытаниями и измерениями, посоветую:
Ищите действующий ГОСТ Р МЭК, где описан метод измерений. Если нет такового, ищите СТО какой-нибудь крупной организации, ОТУ на кабель также от крупняка, и «пляшите» от них. Одновременно посмотрите теорию этого дела в учебнике. В общем, если хочется конкретики, быстро и с наскока не получится.
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
В ГОСТ 27893-88:
3.3.1. Измерение емкости симметричных и коаксиальных пар и одиночных жил строительных длин кабелей не менее 5 м проводят на частоте 800 Гц.
Допускается проводить измерения на одной из частот в диапазоне от 10 Гц до 2000 Гц.
<далее там изложен порядок измерения>
3.3.2.
3.3.3.
3.3.4.
3.3.5.
3.3.6.
3.4. Обработка и оценка результатов измерений
3.4.1. Измеренное значение емкости (С) в нФ должно быть пересчитано на 1 км длины кабеля по формуле:
С= Сн*(1000/L),
где
Сн — измеренная емкость, нФ
L — длина измеряемого кабеля, м.
Т.е вопрос состоит в том, емкость медного кабеля изменяется линейно от длины, или нет ?
Получается (см. выше формулу из ГОСТа), что линейно.
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
Да линейно, емкость на барабане при смотке-размотке от статики иногда убивает. У нас в древние времена одного кабельщика-монтажника убило. Слабое сердце+разряд статики — и готово. Я к тому, что у кабеля есть погонная ёмкость, зависящая от длины, но при хорошей изоляции — в этой ёмкости могут просто так навестись заряды.
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
Что то все в дебри полезли. У всех , наверно паспорта или сертификаты на кабели есть, там либо ссылка на ГОСТ , ТУ или тому подобное. Далее смотришь ёмкость на единицу длины. На коаксиал практически точная удельная величина ( на один метр), на витую пару в зависимости от категории даётся диапазон, на многопарный ёмкость от фонаря, которая к тому же меняется от времени эксплуатации. Пусть Киря вопрос уточнит, ему про что и для чего надо.
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
ааа… в этом смысле емкость… (посыпал голову пеплом)
конечно же прямопропорциональна длине. Но это важно только для работы на постоянном токе и низкой частоте.
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
ааа… в этом смысле емкость… (посыпал голову пеплом)
конечно же прямопропорциональна длине. Но это важно только для работы на постоянном токе и низкой частоте.
Ты про силовые кабели пишешь, Киря вопрос задал про связные.
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
а в чем отличия?
в каком случае разные законы — связной физики и энергетической ?
что то еще может стоит иметь ввиду — вдруг речь о кабеле в звездолете и на разгоне к скорости света все электроны по инерции улетят в сторону розетки 
ТС! научно-техническому совету межгалактического форума НАГ надо однозначно и конкретно ставить условия использования!
вдруг про Нептун речь и нужно иметь ввиду эффект сверхпроводимости жил кабеля
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
Ну на вопрос ТС -ответили. Емкость кабеля- это погонная емкость.
А вот вопрос- зачем она ему нужна, он не раскрыл.
Возможные варианты многочисленны, в их числе:
1. Симметрирование НЧ кабелей связи
2. Пупинизация кабелей
3. Оценка наведенного на кабель напряжения
4. Оценка взаимного влияния кабелей
5. Оценка влияния высших интеллектов на низшие.. :-)), что уже удалось :-)).
6. Иные приложения…
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
Ну на вопрос ТС -ответили. Емкость кабеля- это погонная емкость.
А вот вопрос- зачем она ему нужна, он не раскрыл.
Ответили, спасибо.
Но здесь минимум три участника треда могли со мной мгновенно связаться напрямуюпо данному вопросу через телефон/мыло/аську/джаббер/телеграмм.Не связался никто !Т.е всех устраивает русло дискуссии.:)
Возможные варианты многочисленны, в их числе:…
6. Иные приложения…
Вот.
Вопрос задавался про связной кабель.По расчётам ЛЭП — это к vIv-у.
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
Что сказать? И по связному кабелю там может быть масса вопросов и ответ будет зависеть от того, что за вопрос.
Ваш вопрос не был сформулирован в достаточной мере.
Выяснять. что Вы имели ввиду — не собираюсь — хлеб за брюхом не ходит. Вам надо- Вы и формулируйте.
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
Я получил ответ(ы) в исчерпывающем количестве.Спасибо всем, кто морщил лобик !
Сам вопрос задал, сам выбрал формат обсуждения на форуме. Потом задаёт вопрос, а что не позвонили. Встречный вопрос, а что сам не позвонил?:))
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
Встречный вопрос, а что сам не позвонил?:))
Да я как-то не сообразил, ты же криогенщик, а значит тоже физик.Ну извини…
-
Вставить ник
- Цитата
- Ответить с цитированием
Поделиться сообщением
Ссылка на сообщение
Поделиться на других сайтах
- Назад
- 1
- 2
- Вперёд
- Страница 1 из 2
Join the conversation
You can post now and register later.
If you have an account, sign in now to post with your account.