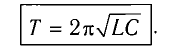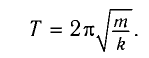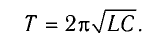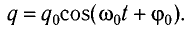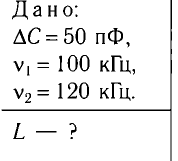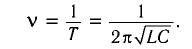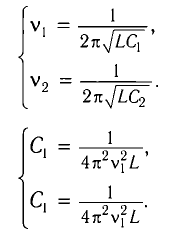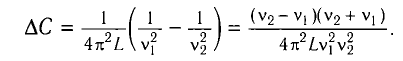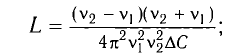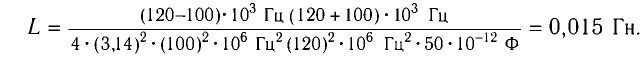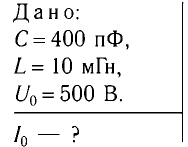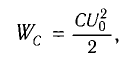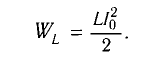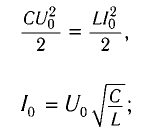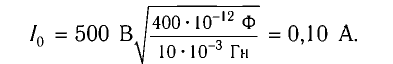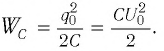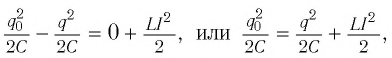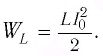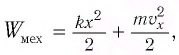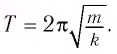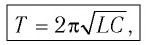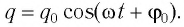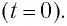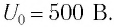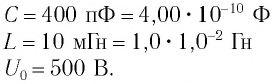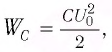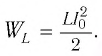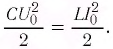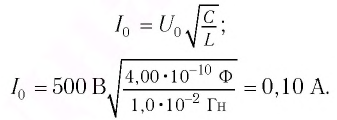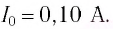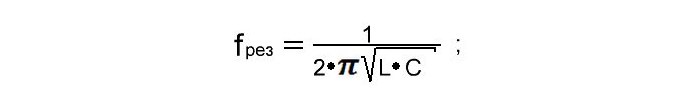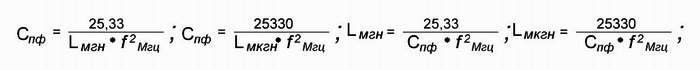Расчёт ёмкости колебательного контура
Расчёт ёмкости колебательного контура (L,C)
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания.
Колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.
Формула расчета ёмкости колебательного контура
- C = 1/(4π²F²L)
Где:
- F — Резонансная частота, Гц)
- L — Индуктивность, (Гн)
- C — Ёмкость, (Ф)
Онлайн-калькулятор для расчёта ёмкости колебательного контура
Индуктивность:
Частота:
Ёмкость:
Поделиться в соц сетях:
Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн — косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о «Использование сердечного индекса Руфье в медико-спортивном контроле». Проба Руфье — представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор — онлайн tg φ: cos φ: ± Поделиться в соц сетях:
Колебательный контур:
Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре. Правило Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.
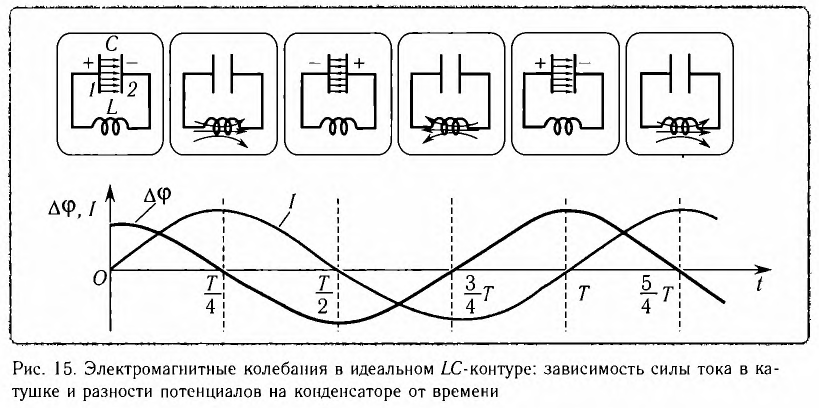
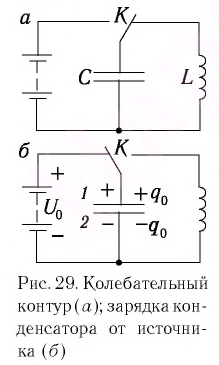
Рассмотрим электрическую цепь, содержащую конденсатор электроемкостью С и катушку (соленоид) индуктивностью L (рис. 15). Такая цепь называется идеальным колебательным контуром или LC-контуром.
В отличие от реального колебательного контура, который всегда обладает некоторым электрическим сопротивлением (R
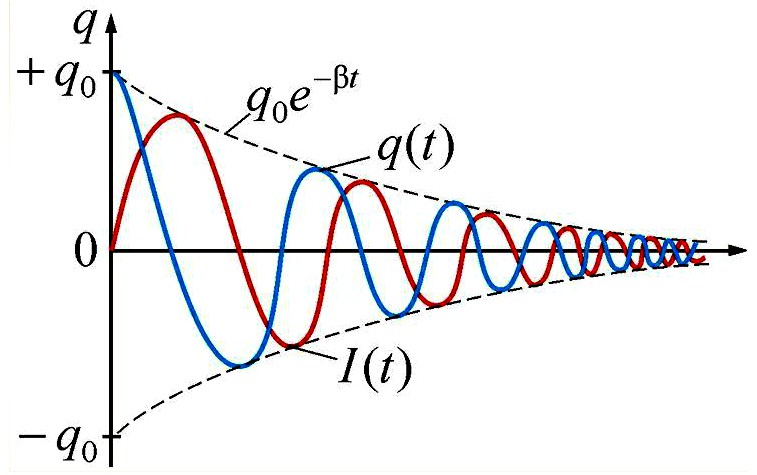
Пусть в начальный момент времени (t = 0) конденсатор С заряжен так, что на его первой обкладке находится заряд +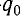

С течением времени конденсатор начнет разряжаться, и в цепи появится электрический ток, сила l(t) которого будет меняться с течением времени. Поскольку при прохождении такого электрического тока в катушке индуктивности возникнет изменяющийся во времени магнитный поток, то это вызовет появление ЭДС самоиндукции, препятствующей изменению силы тока.
Вследствие этого сила тока в колебательном контуре будет возрастать от нуля до максимального значения в течение некоторого промежутка времени, определяемого индуктивностью катушки.
В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального значения 
После разрядки конденсатора сила тока в катушке начнет убывать. Это также произойдет не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создаст индукционный ток. Он будет иметь такое же направление, как и уменьшающийся ток в цепи, и поэтому будет «поддерживать» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезарядит конденсатор до начального напряжения обратной полярности — знак заряда на каждой обкладке окажется противоположным начальному.
Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения 
Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.
Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением в катушке ЭДС самоиндукции, которая «обеспечивает» эту перезарядку. Заметим, что заряд q(t) конденсатора и сила тока I(t) в катушке достигают своих максимальных значений 

Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Период свободных электромагнитных колебаний в контуре определяется по формуле Томсона:
Получим эту формулу, используя закон сохранения энергии. Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство
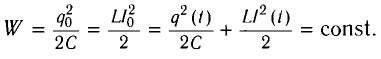
Поскольку закономерности гармонических колебаний носят универсальный характер, то можно сравнить колебания в LC-контуре с колебаниями пружинного маятника.
Для пружинного маятника полная механическая энергия в любой момент времени 2 ,
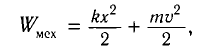
и период его колебаний
Проанализируем соотношения (1) и (2). Сравним выражения для энергии электростатического поля конденсатора 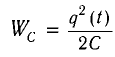
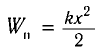
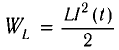
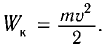
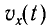
Следуя аналогии, заменим в формуле для периода колебаний пружинного маятника т на L и k на 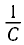
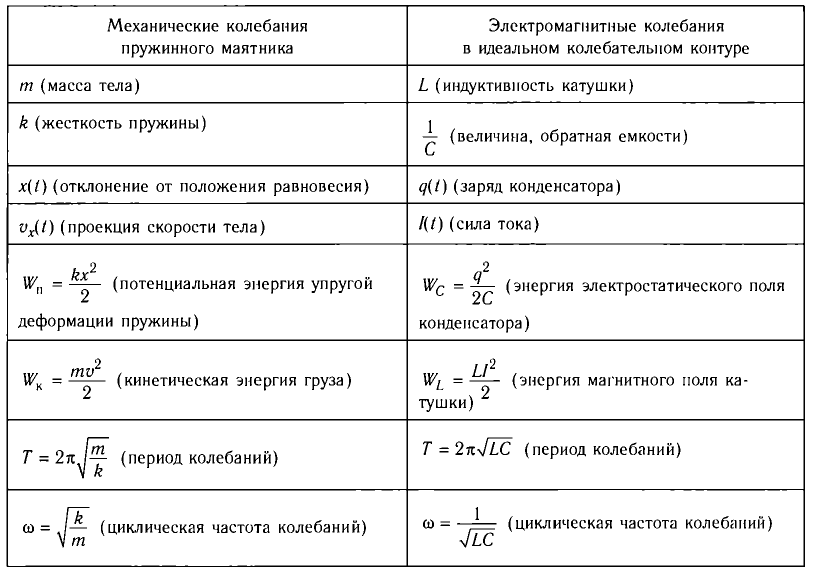
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).
Таблица 4
Сопоставление физических величин, характеризующих электромагнитные и механические колебания
Соответственно, зависимость заряда конденсатора от времени будет иметь такой же характер, как и зависимость координаты (смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону (но с другими начальными фазами) будут изменяться сила тока в цепи, напряжение на конденсаторе.
Для определения начальной фазы 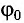
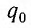
Полная энергия идеального колебательного контура (R = 0) с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется.
Как уже отмечалось, реальный колебательный контур всегда имеет некоторое сопротивление R, обусловленное сопротивлением катушки, соединительных проводов и т. д. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они «будут происходить» сколь угодно долго.
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без трения, а механическим аналогом реального колебательного контура — пружинный маятник с трением.
Пример №1
При изменении емкости конденсатора идеального LC-контура на 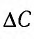
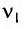
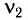
Решение
Частота колебаний в контуре
Поскольку частота колебаний в контуре увеличилась (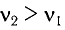
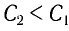
Из условия задачи получаем систему уравнений
Откуда
Вычитая из первого уравнения второе, получаем
Откуда находим
Ответ: L = 0,015 Гн.
Пример №2
Колебательный контур состоит из конденсатора емкостью С = 400пФ и катушки индуктивностью L=10 мГн. Определите амплитудное значение силы тока 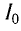
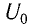
Решение
Максимальная энергия электростатического поля конденсатора
а максимальная энергия магнитного поля катушки
Так как контур идеальный (R = 0), то его полная энергия не меняется с течением времени. Кроме того, в момент, когда заряд конденсатора максимален, сила тока в катушке равна нулю, а в момент, когда заряд конденсатора равен нулю, сила тока в ней максимальна. Это позволяет утверждать, что максимальные энергии в конденсаторе и катушке равны: 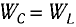
откуда
Ответ: 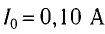
Колебательный контур и свободные электромагнитные колебания в контуре
Явление возникновения ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.
Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью 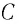
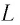
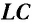
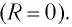
Подключив (при помощи ключа 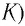
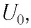
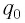
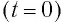
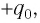
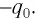
Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа 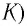
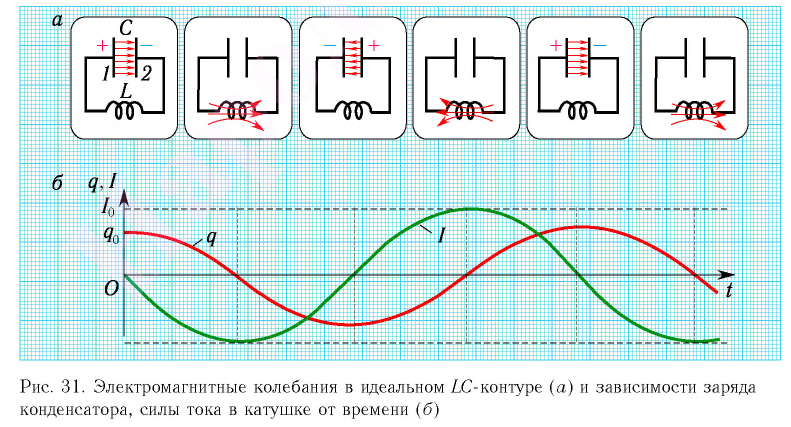
Таким образом, в контуре появится нарастающий по модулю электрический ток, сила 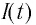
Вследствие этого модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения 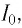
При разрядке конденсатора энергия его электростатического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):
где 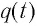
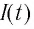
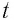
В момент полной разрядки конденсатора 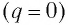
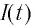
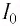
После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезаряжает конденсатор до начального напряжения 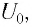
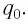
Таким образом, в идеальном 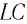
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без пополнения энергии от внешних источников.
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд 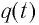
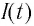
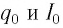
Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальным значениям заряда на каждой из обкладок), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального 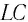
Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:
где 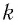
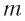
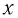
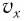
Период его колебаний:
Проанализируем соотношения (1) и (2). Видно, что энергия электростатического поля конденсатора 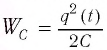
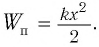
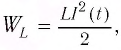
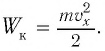
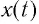
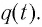
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника массу 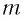
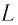
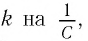
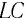
которая называется формулой Томсона.
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).

Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты (проекции смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.
Для определения начальной фазы 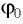
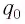
Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.
Полная энергия идеального колебательного контура 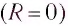
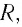
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.
Пример решения задачи:
Идеальный колебательный контур состоит из конденсатора емкостью 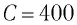
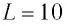
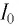
Дано:
Решение
Максимальная энергия электростатического поля конденсатора:
а максимальная энергия магнитного поля катушки:
Так как контур идеальный 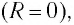
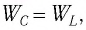
Отсюда
Ответ:
- Исследовательские методы в физике
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Распространение механических волн в средах
- Электромагнитное поле
- Опыты Фарадея в физике
- Электромагниты и их применение в физике
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
Параллельный и последовательный колебательный контур
Что такое колебательный LC-контур? Принцип работы, формулы расчёта основных
параметров. Онлайн калькулятор резонансной
частоты колебательного контура,
добротности и коэффициента затухания в зависимости от величин индуктивности,
ёмкости и сопротивления потерь
Колебательный контур – это пассивная электрическая цепь, состоящая из конденсатора и катушки индуктивности, в которой
возможно возбудить свободные электромагнитные колебания.
Если конденсатор и катушка соединены параллельно, то контур называется параллельным, при последовательном соединении элементов колебательный
контур называется последовательным.
Для начала рассмотрим параллельный колебательный контур, который в радиотехнике используется как основа частотно-избирательных цепей и встречается намного
чаще последовательного.
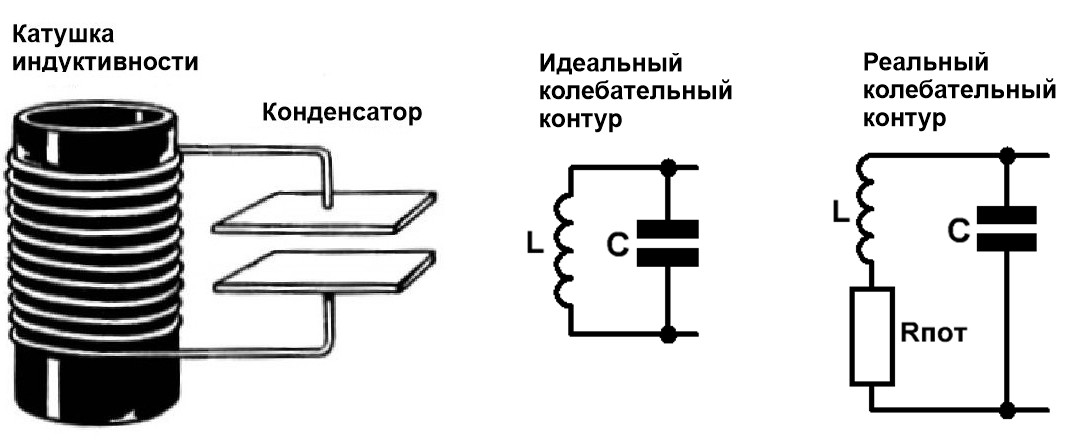
Рис.1 Параллельный колебательный контур, его изображение на схеме (идеальный
колебательный контур), реальный колебательный контур
При анализе цепи колебательного контура обычно используется реалистичная модель (Рис.1 справа), состоящая из идеальных пассивных элементов и активного
сопротивления потерь катушки – Rпот.
Сопротивление потерь катушки Rпот складывается из потерь в проводах, диэлектрике, сердечнике и экране (если он есть).
Поскольку потери в контурном конденсаторе на порядки меньше, чем потери в катушке, то его сопротивление потерь при расчётах обычно не учитывается.
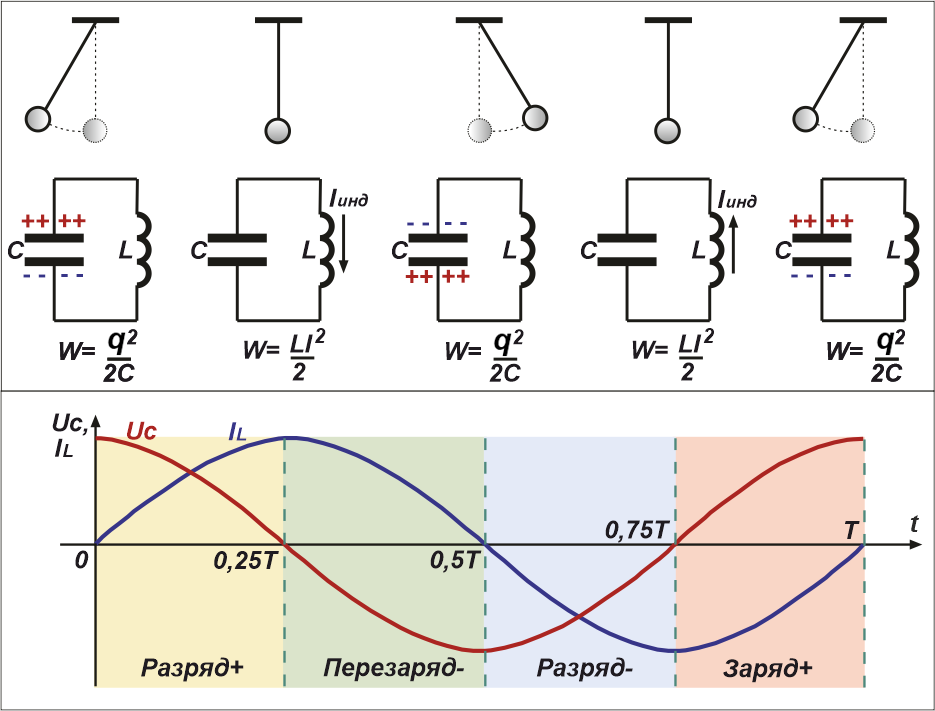
Так, за счёт чего в колебательном контуре возникают свободные колебания? Для того чтобы ответить на этот вопрос, давайте соберём простейшую схему (Рис.2)
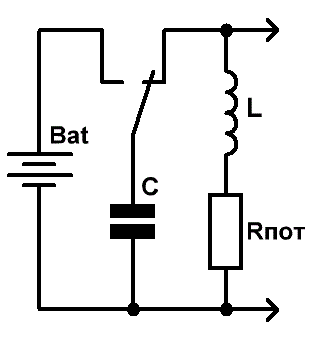
Рис.2 Колебательный процесс в параллельном колебательном контуре
Для возбуждения в контуре колебаний конденсатор следует предварительно зарядить, сообщая его обкладкам заряд
qmax от внешнего источника Bat напряжением
Umax.
После того как конденсатор будет заряжен, переводим переключатель в правое по схеме положение, отключая контур от источника, и наблюдаем возникшие в цепи затухающие
электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот (Рис.2 справа).
Из-за потерь, возникающих в элементах контура, электромагнитные колебания в цепи всегда будут затухающими. Скорость их затухания зависит от величины этих потерь,
суммарное значение которых характеризуются параметром, называемым добротностью колебательного контура Q. Численно добротность равна числу
колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в
еπ = 23,14 раз. Для желающих поподробнее познакомиться с тем, что такое добротность и как её
измерить, имеет смысл посетить страницу – ссылка на страницу.
А мы тем временем рассмотрим последовательные фазы колебаний, происходящие в контуре после зарядки конденсатора.
Рис.3 Фазы колебаний, происходящих в колебательном контуре за полный период
Электромагнитные колебания, а также описывающие их уравнения во многом подобны механическим колебаниям.
Опишем стадии колебательного процесса за полный период колебаний:
1. t = 0 – начало разрядки конденсатора (энергия электрического поля, запасённая в конденсаторе, равна
W = q2/2C ).
Через катушку начинает течь ток. При этом катушка оказывает сопротивление моментальному росту тока, поскольку в ней присутствует ЭДС
самоиндукции, препятствующая этому росту.
2. t = 0,25Т – конденсатор полностью разряжен.
Ток через катушку максимален, так как вся энергия из конденсатора перешла в энергию магнитного электрического поля катушки
W = L*I2/2.
Начиная с этого момента, эта энергия начинает опять перетекать в конденсатор, перезаряжая его потенциалом обратной полярности.
3. t = 0,5Т – конденсатор опять полностью заряжен, но потенциалом противоположной полярности. Ток через
катушку индуктивности равен нулю. Начинается фаза, описанная в п.1, но с током, текущем в обратном направлении.
4. t = 0,75Т – конденсатор вновь полностью разряжен, ток через катушку максимален и направлен
в противоположную (по отношению к п.2) сторону.
5. t = Т – всё начинается сначала, т. е. аналогично 1п.
А теперь – формулы, которые могут понадобиться при расчёте колебательного LC контура:
Период колебаний: T0 = 2π√LC ;
Частота: F0 = 1/T0 ;
Круговая (циклическая) частота: ω0 = 2π/T0 =
2πF0 ;
Максимальный заряд конденсатора: qmax = UmaxC ;
Максимальная сила тока через катушку: Imax = ωqmax .
Добротность колебательного контура:
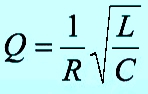
Мгновенные значения напряжения, силы тока и энергии можно рассчитать по формулам:
Заряд: q(t) = qmax cos(ωt) ;
Напряжение: U(t) = Umax cos(ωt) ;
Сила тока: I(t) = Imax sin(ωt) ;
Энергия: W(t) = I(t)2L/2 + q(t)2/(2C) .
Все приведённые формулы хороши для идеального колебательного контура, в котором нет потерь, а соответственно, и нет затухания колебаний. Для реальных же контуров
(с потерями) вводятся дополнительные параметры, характеризующие скорость затухания колебаний. Одними из таких параметров являются коэффициент затухания
β и логарифмический декремент колебаний λ.
Коэффициент затухания β – это величина, характеризующая скорость затухания колебаний и обратно
пропорциональная времени τ, по истечении которого амплитуда колебаний убывает в
е раз.
Для колебательного контура данная величина вычисляется по формуле:
β = Rпотерь /(2L).
Логарифмическим декрементом затухания λ называется величина, равная натуральному логарифму отношения
двух последовательных амплитуд, отстоящих друг от друга на период колебаний. Численно логарифмический декремент колебаний равен коэффициенту затухания,
умноженному на период колебаний:
λ = βT.
С учётом коэффициента затухания наши формулы приобретают следующий вид:
Заряд: q(t) = qmax cos(ωt) e(-βt) ;
Напряжение: U(t) = Umax cos(ωt) e(-βt) ;
Сила тока: I(t) = Imax sin(ωt) e(-βt) ;
Энергия: W(t) = I(t)2L/2 + q(t)2/(2C) ;
Период:
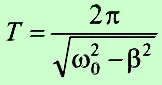
Круговая (циклическая) частота:
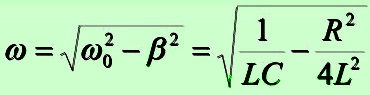
Добротность: Q = Lω/R .
При относительно высокой добротности цепи, то есть когда колебания затухают не слишком быстро и выполняется условие
β2 << ω02, круговая частота контура равна
ω ≈ ω0 ,
а формулы по расчёту резонансной частоты и добротности принимают привычный вид, приведённый выше на синем фоне.
Для проверки знаний, полученных в рамках данной статьи, приведём онлайн калькулятор для расчёта основных параметров колебательного контура.
РАСЧЁТ РЕЗОНАНСНОЙ ЧАСТОТЫ, ДОБРОТНОСТИ И КОЭФФИЦИЕНТА ЗАТУХАНИЯ КОНТУРА
Ёмкость конденсатора контура |
||
Индуктивность катушки контура L |
||
Сопротивление потерь Rпот |
||
Резонансная частота |
||
Добротность = кол-во колебаний |
||
Коэффициент затухания β (сек-1) |
Для последовательного колебательного контура резонансная частота (период и круговая частота) не зависит от сопротивления потерь, однако остальные приведённые
выше параметры описываются теми же формулами, что и для параллельного. При этом в составе частотно-избирательных цепей эти контуры ведут себя по-разному и
имеют значительно отличающиеся друг от друга передаточные характеристики. Какие это характеристики? – рассмотрим в рамках отдельной статьи.
А на следующей странице рассмотрим, как на добротность LC-контура влияют сопротивления нагрузки и источника сигнала.
Колебательный контур
Опубликовал | Дата 26 октября, 2013
Емкость и индуктивность в колебательном контуре
Радиолюбителям известна классическая формула, связывающая параметры последовательного или параллельного колебательного контура.
Где частота колебаний в герцах (Гц), L— индуктивность контура в генри (Гн) и С — емкость контура в фарадах (ф.). В современных радиотехнических устройствах используются колебании с частотами от нескольких килогерц (КГц) до 100000 мегагерц (МГц) или 100гигагерц (ГГц).
Несмотря на столь широкий диапазон частот в колебательных радиотехнических контурах, индуктивности и емкости имеют значительно меньшие величины по сравнению с теми, которые надо подставлять и формулу Томсона, а именно: индуктивности исчисляются в миллигенри (мГн), микрогенри (мкГн), а емкости — в пикофарадах (пф). Это создает неудобства при пользовании классическими формулами, так как приходится иметь дело с очень большими или, наоборот, с очень маленькими числами. Выше приведен набор производных от классической формулы, позволяющий производить быстрый расчет последовательных и параллельных колебательных контуров, применяемых в практических схемах.
Просмотров:3 353