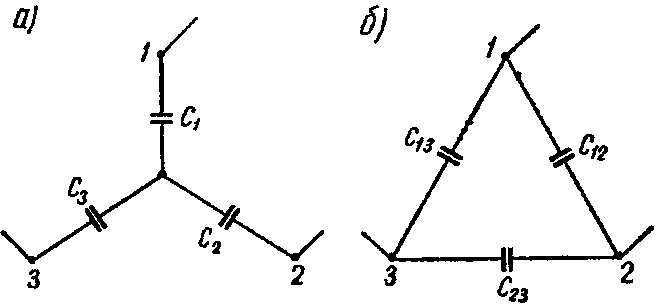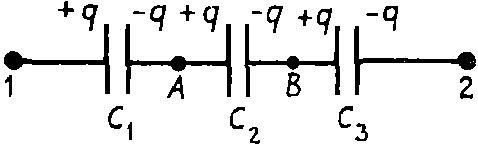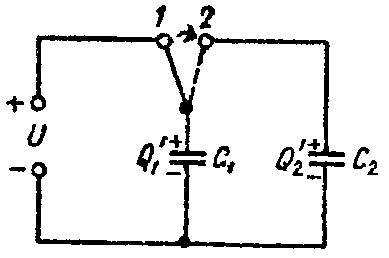Как найти емкость конденсатора по схеме

Содержание:

1. Последовательное соединение конденсаторов
2. Параллельное соединение конденсаторов
3. Смешанное соединение конденсаторов
4. Пример расчета

В данной статье приведены различные схемы соединения конденсаторов, а так же формулы их расчета с примером.

1. Последовательное соединение конденсаторов

Если условно разделить выводы каждого из конденсаторов на первый и второй выводы последовательное соединение конденсаторов будет выполняется следующим образом: второй вывод первого конденсатора соединяется с первым выводом второго конденсатора, второй вывод второго конденсатора, соединяется с первым выводом третьего и так далее. Таким образом мы получим группу (блок) последовательно соединенных конденсаторов с двумя свободными выводами — первым выводом первого конденсатора в блоке и вторым выводом последнего конденсатора, через которые данный конденсаторный блок и подключается в электрическую цепь.

Схема последовательного соединения конденсаторов будет иметь следующий вид:

Фактически последовательное соединение конденсаторов имеет следующий вид:

При данной схеме соединения заряды на конденсаторах будут одинаковы:

Q_общ=Q₁=Q₂=Q₃, 

где: Q₁, Q₂, Q₃ — соответственно заряд на первом, втором, третьем и т.д. конденсаторах

Напряжение на каждом конденсаторе при такой схеме зависит от его емкости:

U₁=Q/C₁; U₂=Q/C₂; U₃=Q/C₃, где:

• U₁, U₂, U₃ — соответственно напряжение на первом, втором, третьем конденсаторах
• C₁, C₂, C₃ — соответственно емкости первого, второго, третьего конденсаторов

При этом общее напряжение составит:

U_общ=U₁+U₂+U₃+…+U_n

Рассчитать общую емкость конденсаторов при последовательном соединении можно по следующим формулам:

• При последовательном соединении двух конденсаторов:

С_общ=(C₁*C₂)/(C₁+C₂)

• При последовательном соединении трех и более конденсаторов:

1/С_общ=1/C₁+1/C₂+1/C₃+…+1/C_n

1. Параллельное соединение конденсаторов

Если условно разделить выводы каждого из конденсаторов на первый и второй выводы параллельное соединение конденсаторов будет выполняется следующим образом: первые выводы всех конденсаторов соединяются в одну общую точку (условно — точка №1) вторые выводы всех конденсаторов соединяются в другую общую точку (условно — точка №2). В результате получается группа (блок) параллельно соединенных конденсаторов подключение которой к электрической цепи производится через условные точки №1 и №2.

Схема параллельного соединения конденсаторов будет иметь следующий вид:

Таким образом параллельное соединение конденсаторов будет иметь следующий вид:

При данной схеме напряжение на всех конденсаторах будет одинаково:

U=U₁=U₂=U₃

Заряд же на каждом из конденсаторов будет зависеть от его емкости:

Q₁=U*C₁; Q₂=U*C₂; Q₃=U*C₃

При этом общий заряд цепи будет равен сумме зарядов всех параллельно подключенных конденсаторов:

Q_общ=Q₁+Q₂+Q₃…+…Q_n.

Рассчитать общую емкость конденсаторов при параллельном соединении можно по следующей формуле:

С_общ=C₁+C₂+C₃+…+C_n

1. Смешанное соединение конденсаторов

Схема в которой присутствует две и более группы (блока) конденсаторов с различными схемами соединения называется схемой смешанного соединения конденсаторов.

Приведем пример такой схемы:

Для расчетов такие схемы условно разделяются на группы одинаково соединенных конденсаторов, после чего расчеты ведутся для каждой группы по формулам приведенным выше.

Для наглядности приведем пример расчета общей емкости данной схемы.

1. Пример расчета

Условно разделив схему на группы получим следующее:

Как видно из схемы на первом этапе мы выделили 3 группы (блока) конденсаторов, при этом конденсаторы в первой и второй группе соединены последовательно, а конденсаторы в третьей группе — параллельно.

Произведем расчет каждой группы:

• Группа 1 — последовательное соединение трех конденсаторов:

1/C_1,2,3 = 1/C₁+1/C₂+1/C₃ = 1/5+1/15+1/10=0,2+0,067+0,1 = 0,367 → C_1,2,3 = 1/0,367 = 2,72 мкФ

• Группа 2 — последовательное соединение двух конденсаторов:

С_4,5 = (C₄*C₅)/(C₄+C₅)= (20*30)/(20+30) = 600/50 = 12 мкФ

• Группа 3 — параллельное соединение трех конденсаторов:

С_6,7,8 = C₆+C₇+C₈ = 5+25+30 = 60 мкФ

В результате расчета схема упрощается:

Как видно в упрощенной схеме осталась еще одна группа из двух параллельно соединенных конденсаторов, произведем расчет ее емкости:

• Группа 4 — параллельное соединение двух групп конденсаторов:

С_1,2,3,4,5 = C_1,2,3+C_4,5 = 2,72+12 = 14,72 мкФ

В конечном итоге получаем простую схему из двух последовательно соединенных групп конденсаторов:

Теперь можно определить общую емкость схемы:

С_общ = (C_1,2,3,4,5*C_6,7,8)/(C_1,2,3,4,5+C_6,7,8) = 14,72*60/14,72+60 = 883,2/74,72 = 11,8 мкФ

---

---

Была ли Вам полезна данная статья? Или может быть у Вас остались вопросы? Пишите в комментариях!

Не нашли на сайте ответа на интересующий Вас вопрос? Задайте его на форуме! Наши специалисты обязательно Вам ответят.

↑ Наверх

Главная
→
Примеры решения задач ТОЭ
→
Расчет электрической цепи постоянного тока с конденсаторами

Расчет электрической цепи постоянного тока с конденсаторами

Расчет электрической цепи постоянного тока с конденсаторами

Основные положения и соотношения

1. Общее выражение емкости конденсатора

C= Q U .

2. Емкость плоского конденсатора

C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d ,

здесь

S — поверхность каждой пластины конденсатора;

d — расстояние между ними;

ε_a = ε_r·ε₀ — абсолютная диэлектрическая проницаемость среды;

ε_r — диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);

ε 0 = 1 4π⋅ с 2 ⋅ 10 −7 ≈8,85418782⋅ 10 −12    Ф м  – электрическая постоянная.

3. При параллельном соединении конденсаторов С₁, С₂, …, С_n эквивалентная емкость равна

C= C 1 + C 2 +…+ C n = ∑ k=1 n C k .

4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:

C= C 1 ⋅ C 2 C 1 + C 2 ,

а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:

U 1 =U⋅ C 2 C 1 + C 2 ;    U 2 =U⋅ C 1 C 1 + C 2 .

5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)

Рис. 0

осуществляется по формулам:

Y→Δ { C 12 = C 1 ⋅ C 2 ΣC ;   C 13 = C 1 ⋅ C 3 ΣC ;   C 23 = C 2 ⋅ C 3 ΣC , где          ΣC= C 1 + C 2 + C 3 , Δ→Y { C 1 = C 12 + C 13 + C 12 ⋅ C 13 C 23 ; C 2 = C 12 + C 23 + C 12 ⋅ C 23 C 13 ; C 3 = C 13 + C 23 + C 13 ⋅ C 23 C 12 .

6. Энергия электростатического поля конденсатора:

W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C .

7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:

1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:

ΣQ=Σ Q ′ .

2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:

∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k .

Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.

Решение задач на расчет электрической цепи постоянного тока с конденсаторами

Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).

Рис. 1

Решение

На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U₁₂, то на левую пластину конденсатора С₁ перейдет заряд +q, на правую пластину конденсатора С₃ заряд –q.

Вследствие электризации через влияние правая пластина конденсатора С₁ будет иметь заряд –q, а так как пластины конденсаторов С₁ и С₂ соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C₂ будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.

Найти эквивалентную емкость — это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.

Разность потенциалов U₁₂ = φ₁ — φ₂ складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов

U 12 = φ 1 − φ 2 =( φ 1 − φ A )+( φ A − φ B )+( φ B − φ 2 )= U 1A + U AB + U B2 .

Воспользовавшись формулой напряжения на конденсаторе

U= q C ,

запишем

q C = q C 1 + q C 2 + q C 3 .

Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов

1 C = 1 C 1 + 1 C 2 + 1 C 3 .

В общем случае эквивалентная емкость при последовательном соединении конденсаторов

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

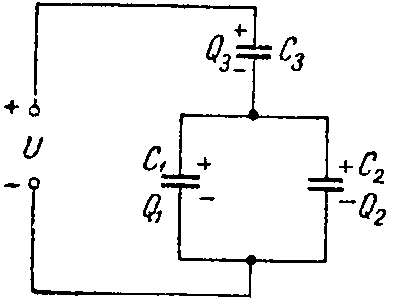
Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.

Рис. 2

Емкости конденсаторов: C₁ =50 мкФ; C₂ =150 мкФ; C₃ =300 мкФ.

Решение

Эквивалентная емкость конденсаторов C₁ и C₂, соединенных параллельно

C₁₂ = C₁ + C₂ = 200 мкФ,

эквивалентная емкость всей цепи равна

C= C 12 ⋅ C 3 C 12 + C 3 = 200⋅300 500 =120  мкФ.

Заряд на эквивалентной емкости

Q = C·U = 120·10^–6·240 = 288·10^–4 Кл.

Той же величине равен заряд Q₃ на конденсаторе C₃, т.е. Q₃ = Q = 288·10^–4 Кл; напряжение на этом конденсаторе

U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96  В.

Напряжение на конденсаторах C₁ и C₂ равно

U₁ = U₂ = U — U₃ = 240 — 96 = 144 В.

их заряды имеют следующие значения

Q₁ = C₁·U₁ = 50·10^–6·144 = 72·10^–4 Кл;

Q₂ = C₂·U₂ = 150·10^–6·144 = 216·10^–4 Кл.

Энергии электростатического поля конденсаторов равны

W 1 = Q 1 ⋅ U 1 2 = 72⋅ 10 −4 ⋅144 2 ≈0,52  Дж; W 2 = Q 2 ⋅ U 2 2 = 216⋅ 10 −4 ⋅144 2 ≈1,56  Дж; W 3 = Q 3 ⋅ U 3 2 = 288⋅ 10 −4 ⋅96 2 ≈1,38  Дж.

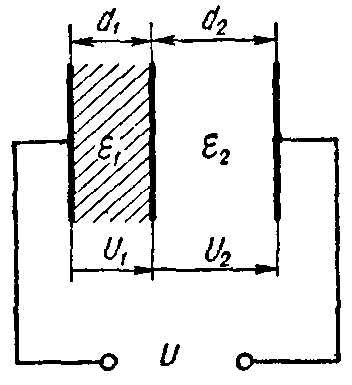
Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см², имеет диэлектрик, состоящий из слюды (ε_r1 = 6) толщиною d₁ = 0,3 мм и стекла (ε_r2 = 7) толщиною d₂ =0,4 мм.

Пробивные напряженности слюды и стекла соответственно равны E₁ = 77 кВ/мм, E₂ = 36 кВ/мм.

Рис. 3

Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.

Решение

Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов

C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .

Подставляя сюда числовые значения, предварительно заменив ε_a1 = ε_r1·ε₀ и ε_a2 = ε_r2·ε₀, получим

C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12   Ф.

Обозначим общее напряжение, подключаемое к слоистому конденсатору, через U_пр, при этом заряд конденсатора будет равен

Q = C·U_пр.

Напряжения на каждом слое будут равны

U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .

Напряженности электростатического поля в каждом слое

E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .

Здесь U’_np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U»_np — общее напряжение, при котором происходит пробой второго слоя.

Из последнего выражения находим

U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5  кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0  кВ.

Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное

27,0 кВ / 2 = 13,5 кВ.

Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d₁ = 1 см друг от друга. Площадь обкладок S = 50 см². Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.

Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d₂ = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.

Решение

Энергия заряженного плоского конденсатора равна

W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,

где С₁ — емкость до раздвижения обкладок.

Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения

Q = C₂·U₂,

где C₂ — емкость конденсатора после раздвижения обкладок, следует, что, так как C₂ = ε₀·S/d₂ стало меньше в 10 раз (d₂ увеличилось в 10 раз), то напряжение на конденсаторе U₂ увеличилось в 10 раз, т. е. U₂ = 10U.

Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d₂ будет больше первоначальной

W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .

Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.

Таким образом, надо совершить работу, равную

W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7   Дж.

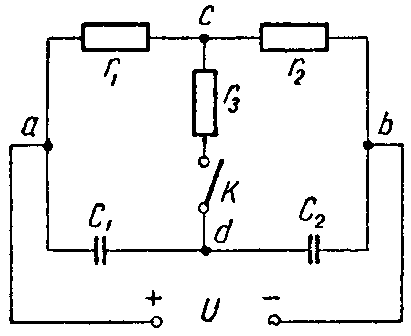
Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.

Даны: C₁ = 30 мкФ; C₂ = 20 мкФ; r₁ = 100 Ом. r₂ = 400 Ом. r₃ = 600 Ом, U = 20 В.

Решение

Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям

U 1 = C 2 C 1 + C 2 ⋅U= 20⋅ 10 −6 30⋅ 10 −6 +20⋅ 10 −6 ⋅20=8  В; U 2 =U− U 1 =20−8=12  В.

Рис. 4

Ключ К замкнут. Через сопротивления r₁ и r₂ протекает ток

I= U r 1 + r 2 = 20 500 =0,04  А,

а через сопротивление r₃ ток не протекает.

Поэтому точки c и d равнопотенциальны (φ_c = φ_d). Следовательно, напряжение между точками a и c (U_ac = φ_a — φ_c) равно напряжению между точками a и d (U_ad = φ_a — φ_d).

Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r₁

U_C1 = I·r₁ = 0,04·100 = 4 В.

Аналогично напряжение на втором конденсаторе равно

U_C2 = I·r₂ = 0,04·400 = 16 В.

Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C₁ = 5 мкФ; C₂ = 120 мкФ. Конденсатор C₂ предварительно не был заряжен.

Рис. 5

Решение

Когда рубильник находится в положении 1, то конденсатор C₁ заряжен до напряжения U и его заряд равен

Q = C₁·U = 5·10^–6·25 = 125·10^–6 Кл.

После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C₁ и C₂ (рис. 5). Обозначим эти заряды через Q’₁ и Q’₂.

На основании закона сохранения электричества имеем

Q = Q’₁ + Q’₂ = 125 10^–6 Кл. (1)

По второму закону Кирхгофа имеем

0= U C1 − U C2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,

или

Q ′ 1 5⋅ 10 −6 − Q ′ 2 120⋅ 10 −6 =0.   (2)

Решая уравнения (1) и (2), найдем

Q’₁ = 5 10^–6 Кл; Q’₂ = 120 10^–6 Кл.

Доставка свежих и аппетитных японских суши в Новороссийске — ям ям..

Напряжение на зажимах конденсаторов станет равным

U C1 = Q ′ 1 C 1 = U C2 = Q ′ 2 C 2 = 5⋅ 10 −6 5⋅ 10 −6 =1  В.

Энергия обоих конденсаторов будет равна

W= C 1 ⋅ U C1 2 2 + C 2 ⋅ U C2 2 2 =62,5⋅ 10 −6   Дж.

Подсчитаем энергию, которая была запасена в конденсаторе С₁, при его подключении к источнику электрической энергии

W нач = C 1 ⋅U 2 = 5⋅ 10 −6 ⋅ 25 2 2 =1562,5⋅ 10 −6   Дж.

Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10^–6 — 62,5·10^–6 = 1500·10^–6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C₁ в конденсатор C₂ после перевода рубильника в положение 2.

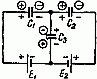
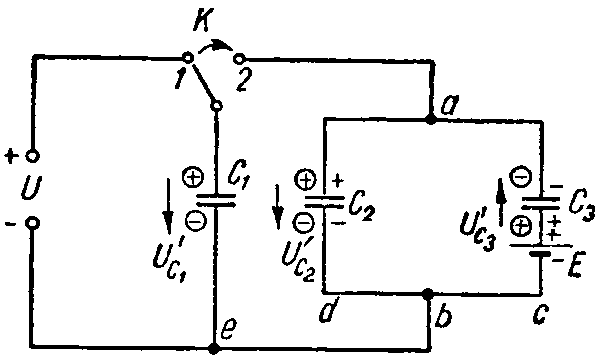
Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.

Емкости конденсаторов равны: C₁ = 10 мкФ; C₂ = 30 мкФ; C₃ = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.

Рис. 6

Решение

Рубильник находится в положении 1. Заряд конденсатора C₁ равен

Q₁ = C₁·U = 10·10^–6·30 = 0,3·10^–3 Кл.

В указанном положении рубильника конденсаторы C₂ и C₃ соединены последовательно друг с другом, поэтому их заряды равны: Q₂ = Q₃. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем

E= U C2 + U C3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,

откуда

Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅E= 30⋅ 10 −6 ⋅60⋅ 10 −6 90⋅ 10 −6 ⋅50=1⋅ 10 −3   Кл.

При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’₁, Q’₂ и Q’₃. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.

Для узла a

Q’₁ + Q’₂ — Q’₃ = Q₁ + Q₂ — Q₃. (1)

Для контура 2ebda2

0= U ′ C1 − U ′ C2 = Q ′ 1 C 1 − Q ′ 2 C 1 .

Для контура bcadb

E= U ′ C2 − U ′ C3 = Q ′ 2 C 2 + Q ′ 3 C 3 .

Уравнения (1) — (3), после подстановки числовых значений величин, примут вид

Q’₁ + Q’₂ — Q’₃ = 0,3·10^–3; (4)

3Q’₁ — Q’₂ = 0; (5)

2Q’₂ + Q’₃ = 3·10^–3. (6)

Решая совместно уравнения (4) — (6), получим

Q’₁ = 0,33·10^–3 Кл; Q’₂ = 0,99·10^–3 Кл; Q’₃ = 1,02·10^–3 Кл.

Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.

Напряжения на конденсаторах после перевода рубильника будут равны

U C1 = Q ′ 1 C 1 = 0,33⋅ 10 −3 10⋅ 10 6 =33  В; U C2 = Q ′ 2 C 2 = 0,99⋅ 10 −3 30⋅ 10 6 =33  В; U C3 = Q ′ 3 C 3 = 1,02⋅ 10 −3 60⋅ 10 6 =17  В.

Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C₁ = 5 мкФ; C₂ = 4 мкФ; C₃ = 3 мкФ; э. д. с. источников E₁ = 20 В и E₂ = 5 В.

Рис. 7

Решение

Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках

− Q 1 + Q 2 − Q 3 =0; E 1 = U C1 − U C3 = Q 1 C 1 − Q 3 C 3 ; E 2 =− U C2 − U C3 =− Q 2 C 2 − Q 3 C 3 .

Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q₁ = 50 мкКл; Q₂ = 20 мкКл; Q₃ = –30 мкКл.

Таким образом, истинная полярность зарядов на обкладках конденсаторов C₁ и C₂ соответствует выбранной, а у конденсатора C₃ — противоположна выбранной.

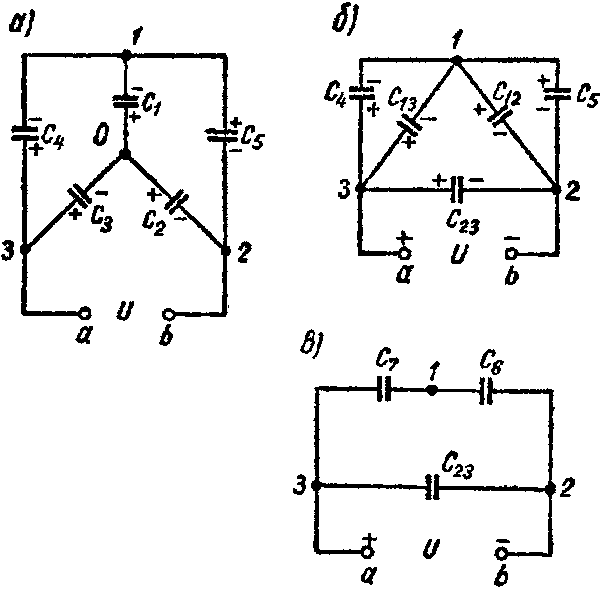
Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C₁ = 2 мкФ; C₂ = 3 мкФ; C₃ = 5 мкФ; C₄ = 1 мкФ; C₅ = 2,4 мкФ.

Рис. 8

Индивидуалка Дана (34 лет) т.8 926 650-82-63 Москва, метро Сокол.

Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.

Решение

1-й способ. Звезду емкостей C₁, C₂ и C₃ (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)

C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 =0,6  мкФ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 =1,0  мкФ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 =1,5  мкФ.

Емкости C₁₂ и C₅ оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость

C₆ = C₁₂ + C₅ = 3 мкФ.

Аналогично

C₇ = C₁₃ + C₄ = 2 мкФ.

Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется

C ab = C 23 + C 6 ⋅ C 7 C 6 + C 7 =2,7  мкФ.

Вычислим напряжение на каждом из конденсаторов.

На конденсаторе C₇ напряжение равно

U 7 = C 6 C 6 + C 7 ⋅U=6  В.

Таково же напряжение и на конденсаторах C₄ и C₁₃

U₄ = U₃₁ = 6 В.

Напряжение на конденсаторе C₆ равно

U₆ = U — U₇ = 4 В;

U₅ = U₁₂ = 4 В.

Вычислим заряды

Q₄ = C₄·U₄ = 6·10^–6 Кл;

Q₅ = C₅·U₅ = 9,6·10^–6 Кл;

Q₁₂ = C₁₂·U₁₂ = 6·10^–6 Кл;

Q₁₃ = C₁₃·U₃₁ = 2,4·10^–6 Кл.

По закону сохранения электричества для узла 1 схем 8, а и б имеем

–Q₄ — Q₁ + Q₅ = –Q₄ — Q₁₃ + Q₁₂ + Q₅,

отсюда

Q₁ = Q₁₃ — Q₁₂ = 3,6·10^–6 Кл,

а напряжение на конденсаторе, емкостью C₁ составляет

U 1 = Q 1 C 1 =1,8  В.

Далее находим напряжения и заряды на остальных конденсаторах

U₃₁ = U₁ + U₃,

отсюда

U₃ = U₃₁ — U₁ = 4,2 В;

Q₃ = C₃·U₃ = 21·10^–6 Кл,

также

U₁₂ = U₂ — U₁ = 4,2 В,

откуда

U₂ = U₁₂ + U₁ = 5,8 В;

Q₂ = C₂·U₂ = 17,4·10^–6 Кл.

Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.

2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)

для узла 1

Q₅ — Q₁ — Q₄ = 0; (1)

для узла О

Q₁ + Q₂ — Q₃ = 0; (2)

для контура О13О

Q 1 C 1 − Q 4 C 4 + Q 3 C 3 =0;  (3)

для контура О12О

Q 1 C 1 + Q 5 C 5 − Q 2 C 2 =0;  (4)

для контура a3О2b

Q 3 C 3 + Q 2 C 2 =U.  (5)

Система уравнений (1) — (5) — содержит пять неизвестных: Q₁, Q₂, Q₃, Q₄ и Q₅. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы С_ab можно найти из отношения

C ab = Q U ,

где Q = Q₃ + Q₄, или Q = Q₂ + Q₅.

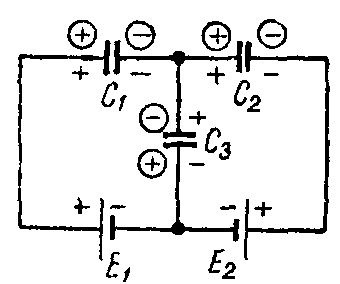
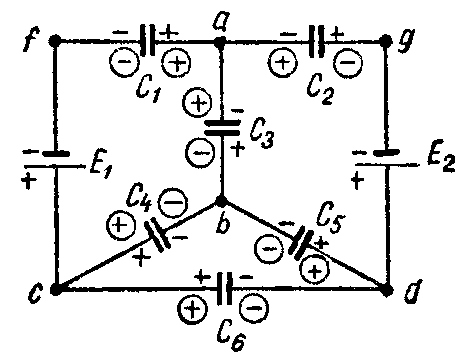
Задача 9. В схеме рис. 9 найти распределение зарядов, если E₁ = 20 В; E₂ = 7 В; C₁ = 7 мкФ; C₂ = 1 мкФ; C₃ = 3 мкФ; C₄ = 4 мкФ; C₅ = C₆ = 5 мкФ.

Рис. 9

Решение

При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:

для узла а

Q₁ + Q₂ + Q₃ = 0;

для узла b

–Q₃ — Q₄ — Q₅ = 0;

для узла c

–Q₁ + Q₄ + Q₆ = 0;

для контура afcba

E 1 = U C1 + U C4 − U C3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;

ля контура gdbag

E 2 = U C5 − U C3 + U C2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;

для контура cbdc

0= U C4 − U C5 − U C6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .

Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды

Q₁ = 35 мкКл; Q₂ = –5 мкКл; Q₃ = –30 мкКл;

Q₄ = 20 мкКл; Q₅ = 10 мкКл; Q₆ = 15 мкКл.

Таким образом, истинные знаки зарядов Q₁, Q₄, Q₅ и Q₆ соответствуют выбранным, а знаки Q₂ и Q₃ противоположны выбранным.

Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.

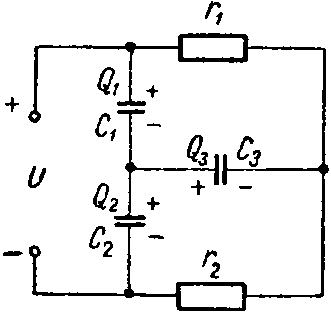
Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C₁ = 6 мкФ; C₂ = 2 мкФ; C₃ = 3 мкФ; r₁ = 500 Ом; r₂ = 400 Ом; U = 45 В.

Рис. 10

Решение

Через сопротивления протекает ток

I= U r 1 + r 2 =0,05  А.

Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:

− Q 1 + Q 2 + Q 3 =0; U= U C1 + U C2 = Q 1 C 1 + Q 2 C 2 ; I⋅ r 1 = U C1 + U C3 = Q 1 C 1 + Q 3 C 3 ,

или

Q 1 = Q 2 + Q 3 ; 45= Q 1 6⋅ 10 −6 + Q 2 2⋅ 10 −6 ; 25= Q 1 6⋅ 10 −6 + Q 3 3⋅ 10 −6 .

Решив эту систему уравнений, найдем, что

Q₁ = 90 мкКл; Q₂ = 60 мкКл; Q₃ = 30 мкКл.

---

последовательное соединение конденсаторов,
параллельное соединение конденсаторов,
Расчет цепи конденсаторов,
Конденсатор в цепи постоянного тока,
Цепи с конденсаторами

Комментарии

• • Поделиться

Как по обозначениям например ( С 11..С16..С 25 ) узнать какой именно по напряжению и ёмкости должен стоять конденсатор..?

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

• • Поделиться

Всё зависит от того,в каком месте схемы этот конденсатор стоит.

А так вопрос ни о чём.

• Цитата

Не можешь-научим! Не хочешь-не надо!P.S. А достанешь-заБАНят!

Решительный шаг вперёд-как правило результат хорошего пинка сзади.

Не тратьте силы, возьмите молоток побольше!

Ссылка на комментарий

Поделиться на другие сайты

---

• Автор

• • Поделиться

Стоят конденсаторы в усилителе мощности звука ..схема есть а вот напряжение и емкость кондеров на ней не указано ..так как я новичок даже элементарного не знаю но паять могу ..

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

ИБП MEAN WELL серии DRC-180 на DIN-рейку – новое решение для пожарно-охранных систем

Компания MEAN WELL расширила семейство DRC-40/60/100 – недорогих ИБП (UPS) 2-в-1 (ИП и контроллер заряда/разряда АКБ в одном корпусе) с креплением на DIN-рейку. Теперь доступны модели мощностью 180 Вт новой серии DRC-180.

Источник питания DRC-180 предназначен для создания систем бесперебойного питания с внешней АКБ и может использоваться в охранно-пожарных системах, системах аварийной сигнализации, контроля доступа и в других приложениях, где требуется простая, недорогая и в то же время качественная система бесперебойного питания соответствующей мощности. Подробнее>>

• • Поделиться

Так схему и нужно выложить на всеобщее обозрение.Тогда подскажем.

• Цитата

Не можешь-научим! Не хочешь-не надо!P.S. А достанешь-заБАНят!

Решительный шаг вперёд-как правило результат хорошего пинка сзади.

Не тратьте силы, возьмите молоток побольше!

Ссылка на комментарий

Поделиться на другие сайты

---

• Автор

• • Поделиться

Хорошо ..схему выложу позже так как сейчас на работе.

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

• • Поделиться

Так на самих же конденсаторах  написана и ёмкость и напряжение 

Или как ?

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

Вебинар «Мощные модульные системы питания MEAN WELL 3+N. Новинки и хиты» (22.06.2023)
Приглашаем 22 июня на вебинар, посвященный подходу компании MEAN WELL к созданию мощных управляемых систем низковольтного и высоковольтного питания и зарядных установок для промышленного, технологического, телекоммуникационного, медицинского, радиопередающего и другого оборудования, а также для систем альтернативной энергетики.
На вебинаре мы рассмотрим новинки и серийную продукцию в концепции «3+N», расскажем об этой концепции и о том, как создать из готовых модулей систему питания мощностью до 360 кВт с напряжением до 380…400 В (постоянного тока). Будут представлены ИП с рециркуляцией энергии для тестового оборудования и модули управления питанием. Подробнее>>

• Автор

• • Поделиться

3 часа назад, vas320 сказал:

Так на самих же конденсаторах  написана и ёмкость и напряжение 

Или как ?

Дело в том что усилитель я купил бу звук у него не такой качественный как должен быть …когда открыл крышку увидел что кондеры там не родные и запаяны не окуратно..вот и есть подозрение что и по емкости и напряжению не такие как в паспорте.

5 часов назад, Hambaker сказал:

Так схему и нужно выложить на всеобщее обозрение.Тогда подскажем.

вот схема Одиссей у 010

Odissey-010_Pril2.tif

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

• • Поделиться

В каком блоке эти, искомые, конденсаторы стоят?

К примеру в блоке питания конденсатор С11 имеет емкость 0,22мкф, т.к. выходное напряжение плеча блока питания 37 вольт, то конденсатор пойдет на напряжение 50 и более вольт.

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

• • Поделиться

В 09.11.2016 в 23:10, Евгений 120 сказал:

звук у него не такой качественный как должен быть

Как определялась его «качественность»? И кто сказал. что дело не в акустике/источнике звука?

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

• Автор

• • Поделиться

3 часа назад, BARS_ сказал:

Как определялась его «качественность»? И кто сказал. что дело не в акустике/источнике звука?

 У меня до этого был «амфитон 002» звук был обалденный ..в общем не сравнить . Акустика у меня  S-90 состояние идеальное так как покупались еще моим отцом в магазине..

4 часа назад, Maks сказал:

В каком блоке эти, искомые, конденсаторы стоят?

К примеру в блоке питания конденсатор С11 имеет емкость 0,22мкф, т.к. выходное напряжение плеча блока питания 37 вольт, то конденсатор пойдет на напряжение 50 и более вольт.

А как вы вичислили мкФ на конденсаторе С 11..?

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

• • Поделиться

А где написано, что одиссей должен звучать лучше? Тем более на шлаке С90 (уж не знаю, как она у вас могла звучать «обалденно»).

16 минут назад, Евгений 120 сказал:

А как вы вичислили мкФ на конденсаторе С 11.

Наверно по схеме

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

• Автор

• • Поделиться

В 11.11.2016 в 09:34, Maks сказал:

В каком блоке эти, искомые, конденсаторы стоят?

К примеру в блоке питания конденсатор С11 имеет емкость 0,22мкф, т.к. выходное напряжение плеча блока питания 37 вольт, то конденсатор пойдет на напряжение 50 и более вольт.

На мой взгляд не родные кондеры стоят во всех блоках кроме предварительного усилителя !

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

• • Поделиться

А фото «пациента» можно увидеть?

• Цитата

Интересуют акустические и электрогитары в рабочем и не рабочем состоянии, а так же комплектующие от них.

Людям, не слушающим советов, нельзя помочь ( Б.Франклин ).

Ссылка на комментарий

Поделиться на другие сайты

---

• Автор

• • Поделиться

В 11.11.2016 в 09:34, Maks сказал:

20 минут назад, SVN сказал:

А фото «пациента» можно увидеть?

19 минут назад, SVN сказал:

Вы про фото внутреностей Усилителя или его схему .? Если схему то опубликовал чуть выше.

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

• • Поделиться

В 11.11.2016 в 14:41, Евгений 120 сказал:

А как вы вичислили мкФ на конденсаторе С 11..?

На схеме написано. С11, а под ним 0,22, что означает 0,22мкф

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

• • Поделиться

Конечно внутренностей!

Ведь именно к ним у Вас претензии…

Сделайте детальные фото проблемных (по Вашему мнению) мест в монтаже так,  чтобы была видна и маркировка номинала и маркировка детали по принципиальной схеме.

• Цитата

Интересуют акустические и электрогитары в рабочем и не рабочем состоянии, а так же комплектующие от них.

Людям, не слушающим советов, нельзя помочь ( Б.Франклин ).

Ссылка на комментарий

Поделиться на другие сайты

---

• Автор

• • Поделиться

37 минут назад, SVN сказал:

Конечно внутренностей!

Ведь именно к ним у Вас претензии…

Сделайте детальные фото проблемных (по Вашему мнению) мест в монтаже так,  чтобы была видна и маркировка номинала и маркировка детали по принципиальной схеме.

Фото сделаю. Просто сегодня на работе…а вечером обязательно сделаю!

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

• • Поделиться

извиняюсь не хочу плодить темы потому спрошу здесь. Чего это на фото, вроде какая-то индуктивность.

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

• • Поделиться

Ссылка на комментарий

Поделиться на другие сайты

---

• Автор

• • Поделиться

9 часов назад, SVN сказал:

Конечно внутренностей!

Ведь именно к ним у Вас претензии…

Сделайте детальные фото проблемных (по Вашему мнению) мест в монтаже так,  чтобы была видна и маркировка номинала и маркировка детали по принципиальной схеме.

Вот сделал три фото ..плата усилителя мощности ..блока защиты..и блок питания ..но вот так сфотографировать что бы видно было маркировку не получилось, так как доступа нет.

• Цитата

Ссылка на комментарий

Поделиться на другие сайты

---

• • Поделиться

Картина примерно ясна. Если Вас смущают габариты современных электролитических конденсаторов, то не стоит на это обращать внимание. 

Главное — конденсатор должен быть заведомо исправен (ESR), и соответствовать указанному на принципиальной схеме номиналу. Рабочее напряжение конденсаторов должно быть не ниже действующего постоянного напряжения в конкретной точке схемы, а ещё лучше превышать его на 25-30%…

• Цитата

Интересуют акустические и электрогитары в рабочем и не рабочем состоянии, а так же комплектующие от них.

Людям, не слушающим советов, нельзя помочь ( Б.Франклин ).

Ссылка на комментарий

Поделиться на другие сайты

---

Соединение конденсаторов

Как правильно соединять конденсаторы?

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.

В реальности это выглядит так:

Параллельное соединение

Принципиальная схема параллельного соединения

Последовательное соединение

Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.

Как рассчитать общую ёмкость соединённых конденсаторов?

Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.

Общая ёмкость параллельно соединённых конденсаторов:

C_общ – суммарная ёмкость составного конденсатора.

Как видим, при параллельном соединении ёмкости нужно всего-навсего сложить!

Внимание! Все расчёты необходимо производить в одних единицах. Если выполняем расчёты в микрофарадах, то нужно указывать ёмкость C₁, C₂ в микрофарадах. Результат также получим в микрофарадах. Это правило стоит соблюдать, иначе ошибки не избежать!

Чтобы не допустить ошибку при переводе микрофарад в пикофарады, а нанофарад в микрофарады, необходимо знать сокращённую запись численных величин. Также в этом вам поможет таблица. В ней указаны приставки, используемые для краткой записи и множители, с помощью которых можно производить пересчёт. Подробнее об этом читайте здесь.

Ёмкость двух последовательно соединённых конденсаторов можно рассчитать по другой формуле. Она будет чуть сложнее:

Внимание! Данная формула справедлива только для двух конденсаторов! Если их больше, то потребуется другая формула. Она более запутанная, да и на деле не всегда пригождается .

Или то же самое, но более понятно:

Если вы проведёте несколько расчётов, то увидите, что при последовательном соединении результирующая ёмкость будет всегда меньше наименьшей, включённой в данную цепочку. Что это значить? А это значит, что если соединить последовательно конденсаторы ёмкостью 5, 100 и 35 пикофарад, то общая ёмкость будет меньше 5.

В том случае, если для последовательного соединения применены конденсаторы одинаковой ёмкости, эта громоздкая формула волшебным образом упрощается и принимает вид:

Здесь, вместо буквы M ставиться количество конденсаторов, а C₁ – его ёмкость.

Стоит также запомнить простое правило:

При последовательном соединении двух конденсаторов с одинаковой ёмкостью результирующая ёмкость будет в два раза меньше ёмкости каждого из них.

Таким образом, если вы последовательно соедините два конденсатора, ёмкость каждого из которых 10 нанофарад, то в результате она составит 5 нанофарад.

Не будем пускать слов по ветру, а проверим конденсатор, замерив ёмкость, и на практике подтвердим правильность показанных здесь формул.

Возьмём два плёночных конденсатора. Один на 15 нанофарад (0,015 мкф.),а другой на 10 нанофарад (0,01 мкф.) Соединим их последовательно. Теперь возьмём мультиметр Victor VC9805+ и замерим суммарную ёмкость двух конденсаторов. Вот что мы получим (см. фото).

Замер ёмкости при последовательном соединении

Ёмкость составного конденсатора составила 6 нанофарад (0,006 мкф.)

А теперь проделаем то же самое, но для параллельного соединения. Проверим результат с помощью того же тестера (см. фото).

Измерение ёмкости при параллельном соединении

Как видим, при параллельном соединении ёмкость двух конденсаторов сложилась и составляет 25 нанофарад (0,025 мкф.).

Что ещё необходимо знать, чтобы правильно соединять конденсаторы?

Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.

При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.

Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.

Для электролитических конденсаторов.

При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.

Параллельное соединение электролитов

Схема параллельного соединения

В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.

Последовательное соединение электролитов

Схема последовательного соединения

Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.

Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.

Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены

Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!

Главная » Радиоэлектроника для начинающих » Текущая страница

Также Вам будет интересно узнать:

• Научись паять! Минимальный наборчик для пайки.

• Научись паять! Подготовка и уход за паяльником.

• «Мультирозетка». Собираем многофункциональную розетку.

• Резистор. Параметры резисторов.