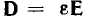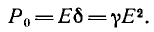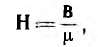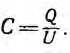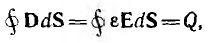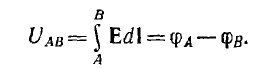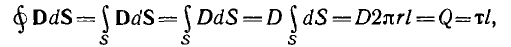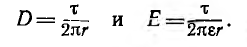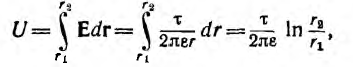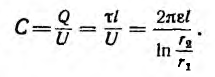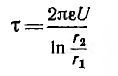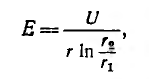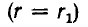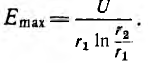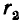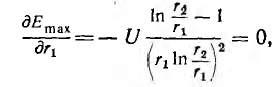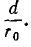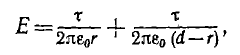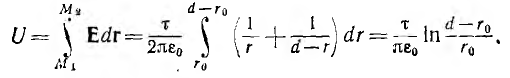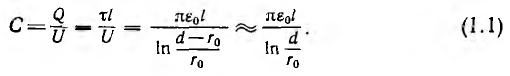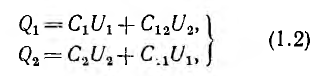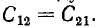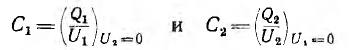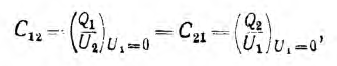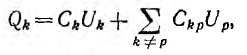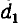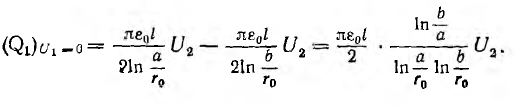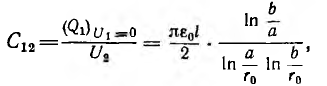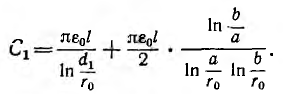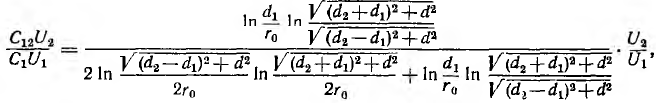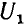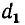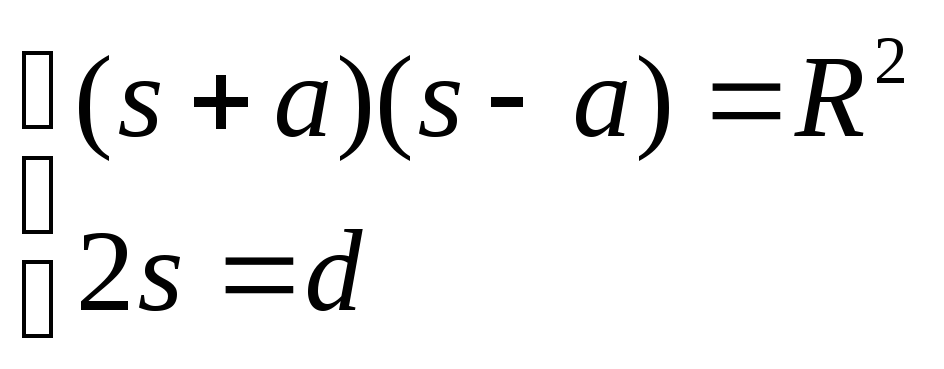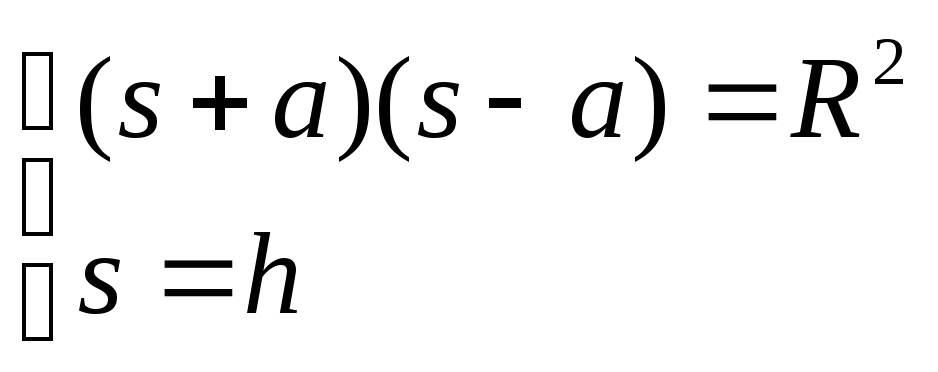Содержание:
Электротехника и ее теоретические основы:
Одной из основных задач техники является преобразование при родных энергетических запасов в используемые виды энергии — в механическую, тепловую, световую и т. п., что требует транспортировки энергетического сырья к месту его использования.
Электрическая энергия легко передается на большие: расстояния и с высоким коэффициентом полезного действия преобразуется в другие виды энергии. Общепринятым является преобразование природных энергетических запасов в электрическую энергию с помощью так называемых генераторов и ее передача посредством проводов к месту потребления, где в преобразователях и приемниках она преобразуется в нужный вид энергии. Беспроводная передача энергии осуществляется с помощью радиосвязи.
Преимущества генерирования, передачи, распределения и преобразования электрической энергии обеспечили широкое применение электротехники.
Новые производственные отношения в нашей стране, отсутствие частной собственности на запасы энергетического сырья, средства и орудия производства, государственное планирование являются мощным фактором развития электротехники и всеобъемлющего охвата ею всех отраслей нашего народного хозяйства, быта и культуры.
Составленный под руководством В. И. Ленина план ГОЭЛРО построения 30 электростанций общей мощностью 1,75 млн. кет был выполнен в решающих позициях за 10 лет.
В послевоенные годы электрификация СССР развивается невиданными темпами: в 1960 г. мощность электростанций составила 66,7 млн. кет, а за пятилетку 1966— 1970 гг. введены 54 млн. кет, в том числе самая мощная в мире Красноярская гидроэлектростанция (6 млн. кет) и Белоярская атомная электростанция (600 тыс. кет). В Директивах XXIV съезда КПСС по пятилетнему плану развития народного хозяйства СССР на 1971— 1975 гг. предусмотрено ввести в действие электростанции мощностью 65—67 млн. кет, в том числе 6—8 млн. кет на атомных электростанциях. Соответственно увеличилась и увеличится мощность потребителей — устройств, преобразующих электрическую энергию в другие виды.
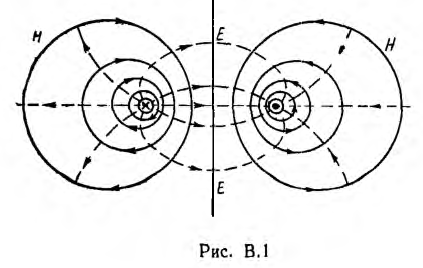
Электрическая энергия — это энергия электромагнитного поля, являющегося видом материи. Поле имеет две составляющие — электрическое и магнитное поля, что можно показать на примере линии передачи постоянного тока (рис. В. 1).
При передаче энергии провода линии, изолированные друг от друга, находятся под напряжением U. Следовательно, между проводами возникает электрическое поле, изображенное пунктиром на рис. В.1 в виде силовых линий, В проводах протекает ток 7, следовательно, в проводах и вне их создается магнитное поле, показанное сплошными линиями. На рис. В.1 видно характерное различие между электрическим и магнитным полями: силовые линии электрического поля незамкнуты, они начинаются и оканчиваются на заряженных проводах; магнитные силовые линии всегда замкнуты; они не имеют ни начала, ни конца.
Как известно из курса физики, электрическое поле в каждой точке
характеризуется вектором напряженности Е, равным силе, воздействующей на единичный положительный заряд, помещенный в эту точку, и вектором электрического смещения
Электрическое поле в проводящей среде создает ток, характеризуемый в
каждой точке поля вектором плотности тока 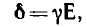
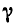
проводимость среды. Ток сопровождается появлением магнитного поля и переходом части энергии электромагнитного поля в тепло, причем мощность этого процесса в единице объема
Магнитное поле в каждой точке характеризуется вектором магнитной индукции В, величина которого равна силе, действующей на движущийся единичный положительный заряд, скорость которого равна единице, а направление В — перпендикулярно этой силе и скорости, а также вектором напряженности
где 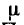
Передача, генерирование, преобразование и потребление электрической энергии, равной 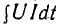
В науке об электричестве связь электрических и магнитных явлений была установлена в двадцатых годах прошлого века, когда Ампер и Эрстед доказали, что электрический ток сопровождается возникновением магнитного поля; окончательно связь электрического и магнитного полей была подтверждена Фарадеем, открывшим явление электромагнитной индукции (1831 г.).
Электротехника, зародившаяся в тридцатых годах прошлого века, вначале развивалась как техника постоянного тока. Только после создания М. О. Доливо-Добровольским системы трехфазного тока и трехфазного двигателя (1891 г.) переменный ток стал вытеснять постоянный. Передача электрической энергии стала осуществляться также трехфазным током.
Теория электромагнитного поля в законченной математической форме была создана Максвеллом в 1873 г. Подтвержденная многочисленными опытами ряда ученых, она была окончательно принята в начале нашего века.
Введенное Максвеллом представление об электромагнитных волнах, экспериментально подтвержденное работами Герца, позволило А. С. Попову в 1895 г. осуществить передачу сигнала без проводов, что послужило началом новой области электротехники — радиотехники.
Электротехника и ее теоретические основы непрерывно развиваются. Например, совершенствуются электронные, ионные и полупроводниковые приборы и аппараты, с помощью которых осуществляют прямые и обратные преобразования переменного тока в постоянный, усиление напряжения и мощности и создают электронные вычислительные машины. Увеличивается дальность и возможности проводной связи, радиотехники и телевидения, развивается электроавтоматика, в энергетике осуществляется переход к большим напряжениям (1500 кв) и мощностям генераторов (1 200 ООО кет и выше), разрабатываются и испытываются магнитогидродинамические прямые преобразователи тепловой энергии в электрическую и т. д.
Так как все электротехнические устройства основаны на использовании электромагнитного поля их систем, состоящих из заряженных тел и контуров с токами, для решения многих задач необходимо привлечение теории этого поля со сложными математическими зависимостями. Однако в большинстве устройств используются ограниченные пути электрического тока и магнитного потока — изолированные проводники малого сопротивления и магнитопроводы из материала с высокой магнитной проницаемостью, называемые электрическими и магнитными цепями. Их расчеты могут быть значительно упрощены, так как не требуют знания составляющих поля в каждой точке устройств. Теория этих цепей основана на использовании интегральных величин: напряжения 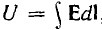
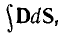
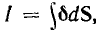
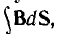
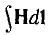
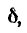
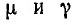
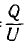
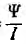
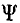
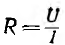
Эти величины можно называть параметрами цепей.
Если эти параметры не зависят от токов и напряжений, уравнения теории цепей, связывающие интегральные величины, будут линейными; такие цепи называют линейными.
В ряде случаев, весьма важных для современной электротехники, эти параметры являются функциями напряжений и токов; тогда уравнения и цепи становятся н нелинейными.
Осуществление грандиозных планов дальнейшей электрификации нашей страны, эксплуатация существующих и создание новых электротехнических устройств требуют от инженера-электрика глубокого понимания физических процессов и умения производить их технический расчет. Фундаментом электротехнического образования является курс теоретических основ электротехники (ТОЭ), базирующийся на сведениях, сообщенных в курсах физики, математики и механики.
Настоящее учебное пособие ТОЭ построено в соответствии с изложенным. Вначале даны параметры цепей, потом основы теории источников и приемников электрической энергии. Затем следует анализ электрических и магнитных цепей при постоянном и переменном токе — линейных и на их основе нелинейных. Курс завершается теорией постоянного и переменного электромагнитного поля.
В книге принята Международная система единиц СИ и рационализованная форма написания уравнений, предложенная Хевисайдом, в которой основные соотношения для электрического и магнитного полей имеют симметричный вид, а множители 4 π и 2 π входят лишь в те соотношения, где они соответствуют характеру симметрии — сферической (4 π) и осевой (2 π).
Параметры электрических и магнитных цепей
Электрической цепью называется совокупность устройств, состоящая из источников, преобразователей и приемников электрической энергии и соединяющих их проводов, образующих замкнутые пути для электрического тока.
Часть цепи, не содержащая источников электрической энергии, называется пассивной, а часть цепи, содержащая источники, называется активной.
Как было показано во введении на примере линии передачи, электрическая цепь характеризуется тремя параметрами: сопротивлением R, емкостью С и индуктивностью L. Этими параметрами обладают все элементы цепей, например резисторы, в которых основную роль играет их сопротивление, конденсаторы с основным параметром — емкостью, и катушки индуктивности, в которых основной является их индуктивность.
Из изложенного вo введении очевидно, что параметры линии передачи равномерно распределены по всей длине линии. Параметры распределены также в отдельных элементах цепи. Например, в катушке индуктивности сопротивление, индуктивность и емкость распределены по ее длине, так как каждый виток с током имеет сопротивление и создает магнитное поле, а отдельные витки изолированного проводника обладают друг по отношению к другу некоторой емкостью.
Этим свойством обладают все реальные электрические цепи—они являются цепями с распределенными параметрами. Так как в ряде технически важных задач не требуется знания электромагнитных процессов в каждой точке всей цепи и ее элементов, необходимо учесть только их интегральные свойства; такие цепи могут быть представлены в виде цепей с сосредоточенными параметрами, состоящих из сопротивлений, индуктивностей и емкостей. Например, катушка индуктивности может быть представлена в виде схемы с последовательным соединением сопротивления R, индуктивности L и с параллельно приключенной к ним емкостью С.
При включении цепи на постоянное напряжение в течение короткого времени от источника потребляется энергия на создание электромагнитного поля. После этого запасенная в С и L энергия сохраняет свою величину неизменной и не отражается на работе цепи, а источники доставляют энергию только на покрытие тепловых потерь в сопротивлениях. Поэтому при расчете цепей постоянного тока следует учитывать только сопротивление R.
В цепях переменного тока энергия, запасаемая в С и L, и мощность потерь в R непрерывно изменяются. Поэтому при расчете этих цепей необходимо учитывать все три параметра.
Многие электрические цепи нелинейны. Так, например, температура, а следовательно, и сопротивление проводника при прохождении по нему тока изменяются; индуктивность катушки со стальным сердечником зависит от тока, так как с величиной тока будет меняться магнитная проницаемость р, сердечника, а следовательно, и индуктивность L. Однако в большинстве случаев цепи можно рассматривать как линейные, считая параметры R, L и С постоянными.
В устройствах современной электротехники главным образом используется энергия магнитного поля, поэтому их основным параметром является индуктивность L. Для этих устройств вводится понятие магнитной цепи как совокупности тел, большей частью ферромагнитных, в которых создается магнитный поток.
При постоянном токе методы анализа магнитных цепей аналогичны методам расчета электрических цепей, содержащих лишь один параметр — сопротивление R. Его аналогом в магнитных цепях является магнитное сопротивление 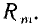
Эта глава посвящена элементарным методам расчета параметров устройств, поля которых имеют простые виды симметрии. Более сложные случаи рассматриваются в теории электромагнитного поля.
Электрическая ёмкость и ее расчет
Для электрических цепей наибольший интерес представляет система двух проводящих тел в диэлектрической среде, заряды + Q и —Q которых отличаются только знаком, являющаяся по существу конденсатором. Емкость конденсатора равна отношению его заряда Q, под которым понимается абсолютное значение разноименных зарядов, к напряжению U между обкладками:
Емкость конденсатора, определяемая размерами и формой тел и их взаимным расположением, пропорциональна диэлектрической проницаемости е среды между обкладками. Емкость измеряется Б фарадах (ф), заряд в кулонах (к), напряжение в вольтах (в).
Для расчета емкости конденсатора по заряду и напряжению необходимо предварительно рассчитать его электрическое поле, исходя из общих соотношений для электрического поля.
Связь между зарядом и вектором смещения 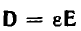
справедливой для линейных и нелинейных сред и являющейся основным соотношением для электрического поля. В правой части этого равенства стоит суммарный заряд, заключенный внутри замкнутой поверхности, в левой — поток вектора смещения. Смещение измеряется в к/м2, напряженность электрического поля — в в/м, диэлектрическая проницаемость в ф/м.
Поле в каждой точке характеризуется потенциалом 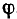
Напряжение 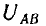
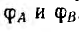
Потенциал также измеряется в вольтах.
Так как сумма напряжений по замкнутому пути равна нулю, то 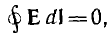
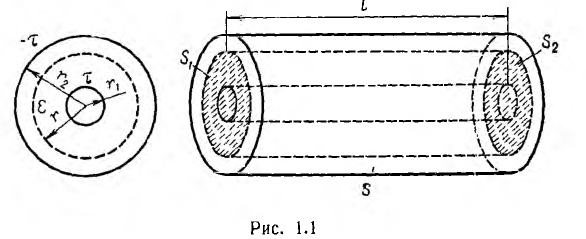
Емкость коаксиального кабеля
Коаксиальный кабель представляет собой два проводящих соосных
цилиндра с радиусом внутреннего цилиндра r1 внутренним радиусом
внешнего цилиндра г2, длиной цилиндров I (рис. 1.1).
Пусть внутренний цилиндр — жила кабеля — заряжен положительно и изолирован диэлектриком с проницаемостью е от оболочки — обратного провода, являющегося внешним цилиндром и несущим заряд обратного знака, а напряжение между жилой и оболочкой равно U.
При выполнении условия 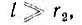
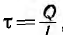
Для цилиндрической поверхности радиуса г, охватывающей заряженную жилу (на рис. 1.1 указана пунктиром), можно применить теорему Гаусса. Из- за радиального направления вектора смещения потоки через основания цилиндра 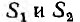
Так как при неизменном радиусе смещение D остается постоянным, то
откуда
В последние выражения не входит радиус 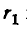
Напряжение на кабеле
откуда емкость кабеля
После подстановки из предпоследнего равенства
в выражение для напряженности поля получим
т .е . напряженность поля обратно пропорциональна радиусу, а ее максимальное значение у поверхности жилы
Исследование на минимум показывает, что наименьшее значение
максимальной напряженности при заданных напряжении и радиусе
внешней оболочки будет при
т. е. при 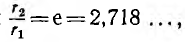
При таком соотношении радиусов кабель, очевидно, обладает наибольшей электрической прочностью.
Емкость двухпроводной линии
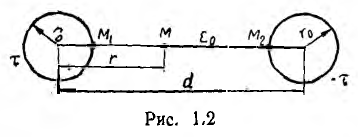
Широко используемые в электротехнике двухпроводные линии передачи представляют собой систему двух прямых параллельных проводов кругового сечения (рис. 1.2). Провода оказываются заряженными разноименно, когда линия включена на напряжение.
Так как длина проводов I велика по сравнению с расстоянием d между их осями, искажением электрического поля у концов заряженных проводов можно пренебречь. Поэтому распределение поля в пространстве остается неизменным в любой плоскости, перпендикулярной осям проводов.
Пусть двухпроводная линия подвешена настолько высоко, что влиянием земли можно пренебречь. Напряжение на линии равно U, величина заряда на единицу длины — τ, радиус проводов — 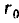
В отличие от коаксиального кабеля, где вследствие равномерного распределения заряда по поверхности жилы ее электрическая ось совпадает с геометрической, плотность зарядов на проводах линии больше на частях их поверхностей, обращенных друг к другу из-за притяжения разноименных зарядов. Поэтому расстояние между электрическими осями проводов становится тем меньше расстояния между их геометрическими осями, чем меньше отношение
Для воздушных линий 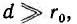
где 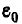
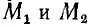
Отсюда емкость двухпроводной воздушной линии
Взаимоёмкость и ее расчёт
Для многих технических задач представляет интерес рассмотрение электрического поля, созданного системой нескольких пар разноименно заряженных тел. Заряды этих тел и напряжения связаны между собой линейными уравнениями.
В системе из двух конденсаторов (1-1′ и 2-2′ на рис. 1.3) все четыре тела связаны электрическим полем, поэтому заряд каждого из конденсаторов зависит от их напряжений 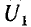
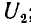
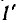
напряжением второго, совпадает по знаку с зарядом, создаваемым собственным напряжением, суммарные заряды обоих конденсаторов будут:
где 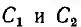
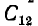
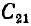
Собственные емкости конденсаторов
определяются всеми четырьмя телами системы и отличаются от емкости каждого из этих конденсаторов, определенной при отсутствии другого.
При определении ёмкости 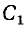
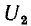
Соответственно, при определении 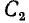
Взаимоемкость:
т. е. равна отношению заряда на обкладках накоротко замкнутого одного конденсатора, когда его заряд создается напряжением другого, к этому напряжению.
Взаимоемкость определяется конфигурацией тел, образующих конденсаторы, их взаимным расположением и пропорциональна диэлектрической проницаемости среды.
При несовпадении знаков собственных зарядов, обусловленных емкостью, и взаимных зарядов, обусловленных взаимоемкостью, знак перед вторыми членами в выражениях (1.2) будет отрицательным. Взаимоемкость также измеряется в фарадах (ф).
Для системы многих конденсаторов, соответственно, заряд Qk
конденсатора k определяется всеми напряжениями:
где 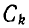
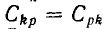
Взаимоемкость между конденсаторами k и р равна отношению заряда конденсатора k, созданного напряжением конденсатора р, к этому напряжению. При этом все конденсаторы, кроме p -того, замкнуты накоротко.
Взаимоемкость двух параллельных двухпроводных линий
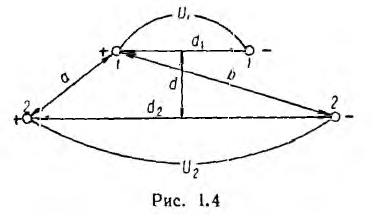
Примером системы из четырех тел, рассматриваемой как совокупность двух конденсаторов, могут служить две параллельные линии, расположенные симметрично одна над другой (рис. 1.4).
Пусть радиус проводов 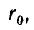
и 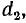
Заряды на проводах первой линии замкнутой накоротко 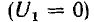
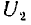
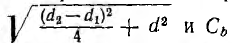
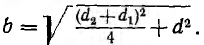
Тогда, соответственно формуле (1.1), получается
Поэтому взаимоемкость
а собственная емкость первой линии при учете второй линии равна
Такая задача представляет технический интерес, позволяя определить влияние линии передачи 2 на линию связи 1 (рис. 1.4).
Это влияние состоит в наведении на проводах линии связи заряда взаимоемкости 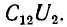
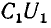
а напряжение 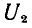
линии связи, то для уменьшения наведенного заряда необходимо увеличивать расстояние d между линиями и уменьшать расстояние
между проводами линии связи.
- Линейные н нелинейные диэлектрики и конденсаторы
- Сопротивление и его расчет
- Линейные и нелинейные резисторы
- Индуктивность и ее расчет
- Преобразование схем электрических цепей
- Установившиеся процессы в линейных электрических цепях
- Методы расчета простых электрических цепей
- Метод сигнальных графов
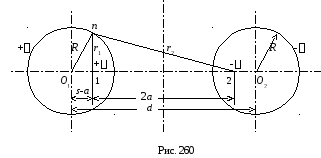
Пусть
требуется рассчитать электростатическое
поле и емкость двухпроводной линии
с заданными геометрическими размерами
(радиус проводов R,
межосевое расстояние d,
радиус R
соизмерим с расстоянием
d).
Провода линии не заземлены, к линии
приложено постоянное напряжение U
(рис. 260).
Согласно
второму следствию из теоремы единственности
заменим поверхностные заряды
проводов осевыми +
и
—,
проводящую среду
диэлектриком
так, чтобы на поверхности проводов
сохранились прежние условия, а именно:
эти поверхности должны остаться
эквипотенциальными с теми же
значениями потенциалов
=
+
и
=.
Чтобы выполнить эти условия, электрические
оси проводов должны быть смещены
относительно геометрических осей
на некоторое расстояние s
a.
Согласно
второму следствию из теоремы единственности
заменим поверхностные заряды
проводов осевыми +
и
—,
проводящую среду
диэлектриком
так, чтобы на поверхности проводов
сохранились прежние условия, а именно:
эти поверхности должны остаться
эквипотенциальными с теми же
значениями потенциалов
=
+
и
=.
Чтобы выполнить эти условия, электрические
оси проводов должны быть смещены
относительно геометрических осей
на некоторое расстояние s
a.
Положение
электрических осей определяется из
теоремы Аполония:
Таким
образом, электростатическое поле,
создаваемое двумя проводами с
поверхностными зарядами σ,
будет эквивалентным полю, которое
создается двумя разноименно заряженными
осями +
и
—,
и для его расчета можно применить
полученные ранее формулы:
Потенциал
положительного провода:
.
В
силу симметрии
,
тогда напряжение:
U
=,
где
sa
– смещение
электрической оси провода относительно
геометрической.
Из
полученного выражения вытекают расчетные
формулы:

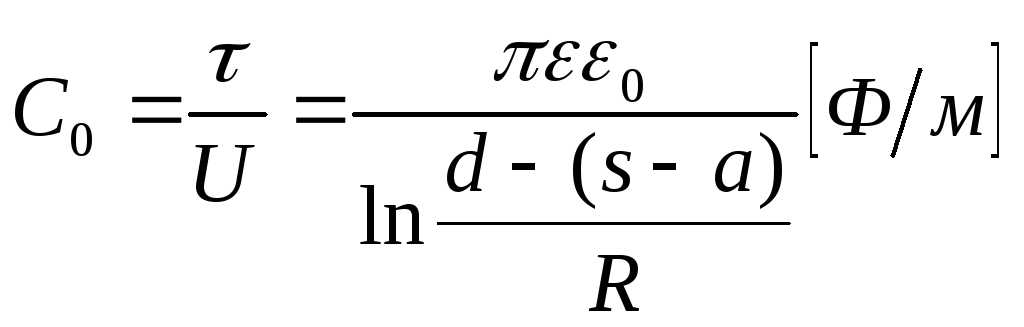
Для
воздушных линий (=1)
межосевое расстояниеd
многократно больше радиуса проводов
R.
В этом случае смещением электрических
осей можно пренебречь (sa0)
и считать, что электрические оси
проводов совпадают с геометрическими.
Для таких линий полученные выше
расчетные формулы будут иметь вид:
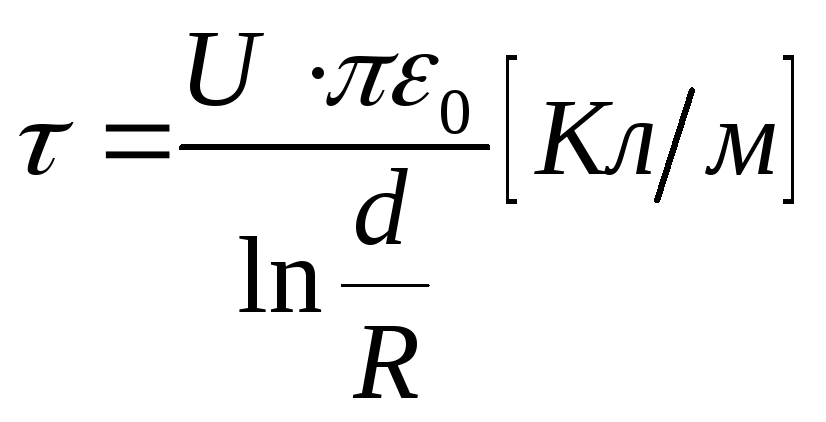
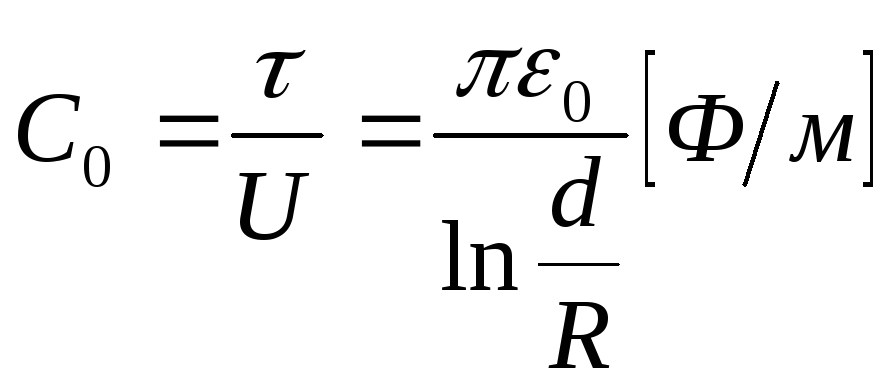
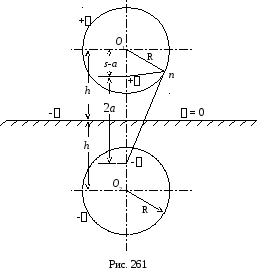
7. Электростатическое поле и емкость цилиндрического провода, расположенного над проводящей плоскостью (землей)
Пусть
требуется рассчитать электростатическое
поле и емкость цилиндрического провода,
расположенного над проводящей плоскостью
(землей). Заданны радиус провода R,
высота подвески h
(радиус R
соизмерим с высотой h).
К проводу приложено постоянное
напряжение U
(рис. 261).
Согласно
второму следствию из теоремы единственности
заменим проводящую среду диэлектриком,
а поверхностные заряды провода и земли
двумя разноименно заряженными осями
+
и
—
так, чтобы
остались неизменными прежние граничные
условия: 1) поверхность земли должна
быть эквипотенциальной с потенциалом
=
0, 2) поверхность провода должна быть
эквипотенциальной с потенциалом=U.
Чтобы выполнить эти условия, электрические
оси +
и
—
должны быть смещены относительно
геометрических осей на некоторое
расстояние sa.
Положение
электрических осей определяется из
теоремы Аполония:
Таким
образом, электростатическое поле,
создаваемое двумя проводами с
поверхностными зарядами σ,
будет эквивалентным полю, которое
создается двумя разноименно заряженными
осями +
и
—,
и для его расчета можно применить
полученные ранее формулы:
Потенциал
провода:
,
где
s—a
– смещение электрической оси провода
относительно геометрической.
Из
полученного выражения вытекают расчетные
формулы:
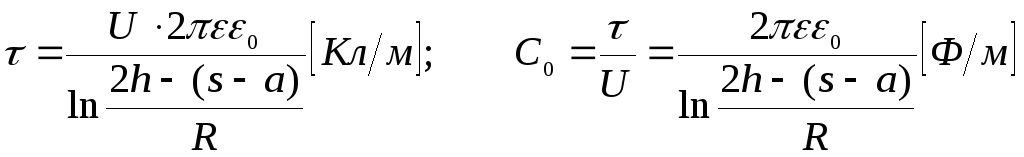
Если
высота подвеса провода намного больше
его радиуса, то смещением электрических
осей можно пренебречь (s
a0)
и считать, что электрические оси проводов
совпадают с геометрическими. В этом
случае расчетные формулы будут иметь
вид:
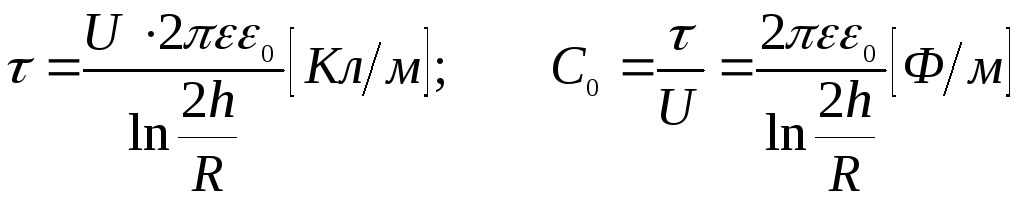
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Таблицы DPVA.ru — Инженерный Справочник
Адрес этой страницы (вложенность) в справочнике dpva.ru: 
Электроемкость. Емкость заряженного конденсатора (плоского, циллиндрического и коаксиального провода, сферического, двухпроводной линии). Энергия.
Электроемкость. Емкость заряженного конденсатора (плоского, циллиндрического и коаксиального провода, сферического, двухпроводной линии). Энергия кондесатора. Емкость конденсатора.
Емкость плоского конденсатора в системах СГС и СИ:
Емкость циллиндрического конденсатора и коаксиального кабеля в системах СГС и СИ:
Емкость сферического конденсатора в системах СГС и СИ:
Емкость конденсатора «сфера» (состоящим из одной сферы) в системе СИ:
Емкость двухпроводной линии в системах СГС и СИ:
При параллельном соединении конденсаторов с емкостями C1, C2, C3, … , Cn общая емкость:
При последовательном соединении конденсаторов общая емкость:
Энергия, сосредоточенная в заряженном конденсаторе, энергия заряженного конденсатора:
В пространстве, где имеется электрическое поле, сосредоточена энергия. Величина этой энергии в единице объема: Плотность энергии однородного поля может быть вычислена по формулам для систем СИ и СГС:
|
|
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator
Главная
→
Примеры решения задач ТОЭ
→
Электроемкость. Емкость конденсатора
Электроемкость. Емкость конденсатора
Электроемкость. Емкость конденсатора
Основные положения и соотношения
1. Закон Кулона
F= Q 1 ⋅ Q 2 4π⋅ ε a ⋅ R 2 , (1)
здесь
F — сила взаимодействия между зарядами;
Q1 и Q2 — точечные заряды;
R — расстояние между ними;
εa — абсолютная диэлектрическая проницаемость среды, равная ε0·εr;
εr — относительная диэлектрическая проницаемость;
– электрическая постоянная.
2. Напряженность электростатического поля точечного заряда Q на расстоянии R от него
E= Q 4π⋅ ε a ⋅ R 2 . (2)
Напряженность поля в любой точке между пластинами плоского конденсатора вдалеке от краев
E= U d , (3)
здесь d — расстояние между пластинами конденсатора, U — напряжение.
Напряженность поля в точке, отстоящей на расстоянии r от бесконечно длинной заряженной оси с линейной плотностью τ
E= τ 2π⋅ ε a ⋅r . (4)
Напряженность поля в точке, отстоящей на расстоянии r от оси цилиндрического конденсатора (r1 <r < r2)
E= U r⋅ln r 2 r 1 , (5)
здесь U — напряжение конденсатора, r1 и r2 — соответственно внутренний и внешний радиусы конденсатора.
Напряженность поля в точке, отстоящей на расстоянии R от центра сферического конденсатора (R1 < R < R2)
E= U⋅ R 1 ⋅ R 2 R 2 ⋅( R 2 − R 1 ) , (6)
здесь U — напряжение конденсатора, R1 и R2 — соответственно внутренний и внешний радиусы конденсатора.
3. Вектор электрического смещения
D → = ε a ⋅ E → . (7)
4. Общее выражение емкости конденсатора
C= Q U . (8)
Емкость плоского конденсатора
C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d , (9)
здесь S — поверхность каждой пластины конденсатора; d — расстояние между ними.
Скачать статью Вывод формулы емкости плоского конденсатора
Емкость цилиндрического конденсатора
C= 2π⋅ ε a ⋅l ln r 2 r 1 , (10)
здесь l — длина конденсатора, r1 и r2 — соответственно внутренний и внешний радиусы конденсатора.
Скачать статью Вывод формулы емкости коаксиального кабеля
Емкость сферического конденсатора
C= 4π⋅ ε a ⋅ R 1 ⋅ R 2 R 2 − R 1 , (11)
здесь R1 и R2 — соответственно внутренний и внешний радиусы конденсатора.
Скачать статью Вывод формулы емкости сферического конденсатора
Емкость двухпроводной линии
C= π⋅ ε a ⋅l ln[ D 2a + ( D 2a ) 2 −1 ] , (12)
здесь l — длина линии, D — расстояние между осями проводов, a — радиус проводов.
Емкость однопроводной линии
C= 2π⋅ ε a ⋅l ln[ h a + ( h a ) 2 −1 ] , (13)
здесь l — длина линии, h — высота подвеса провода над землей, a — радиус провода.
5. При параллельном соединении конденсаторов С1, С2, …, Сn эквивалентная емкость равна
C= C 1 + C 2 +…+ C n = ∑ k=1 n C k . (14)
При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы
1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k . (15)
Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет
C= C 1 ⋅ C 2 C 1 + C 2 , (16)
а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям
U 1 =U⋅ C 2 C 1 + C 2 ; U 2 =U⋅ C 1 C 1 + C 2 . (17)
6. Энергия электростатического поля конденсатора
W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C . (18)
Удельная энергия электростатического поля (на единицу объема диэлектрика) выражается следующим образом
w= dW dV = E⋅D 2 = ε a ⋅ E 2 2 . (19)
Общая величина энергии электростатического поля выражается интегралом величины удельной энергии по всему объему диэлектрика конденсатора
W= ∫ V ε a ⋅ E 2 2 dV . (20)
7. Расчет распределения зарядов в сложных цепях, содержащих источники э. д. с. и конденсаторы, производится путем составления уравнений по двум законам:
1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:
ΣQ=Σ Q ′ . (21)
2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:
∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k . (22)
Задача 1. Имеется конденсатор переменной емкости от 500 до 1500 пФ. Указать, какой добавочный конденсатор с минимальным диапазоном переменной емкости следует взять и как его включить, чтобы эквивалентная емкость изменялась от 100 до 250 пФ.
Ответ: 125 — 300 пФ, включить параллельно.
Смотрите key54.ru ремонт замка зажигания.
Задача 2. Емкость плоского конденсатора, имеющего слюдяной диэлектрик, равна 44,3 пФ. Площадь каждой пластины конденсатора составляет 25 см2, расстояние между пластинами равно 3 мм.
Чему равна относительная диэлектрическая проницаемость слюды? Принимая пробивное напряжение слюды равным 80 кВ/мм, определить, при каком максимальном напряжении может работать этот конденсатор, чтобы он имел трехкратный запас прочности.
Начертить график изменения потенциала между пластинами конденсатора.
Ответ: εr = 6; Umax = 80 кВ; график падения потенциала вычерчивается по уравнению φ = U·(1 — x/d), здесь U — потенциал положительно заряженной обкладки, принятый равным напряжению конденсатора, d — расстояние между пластинами, x — переменное расстояние до положительной обкладки конденсатора.
Задача 3. Доказать, что многопластинчатый конденсатор (рис. 1), состоящий из n одинаковых пластин, площадью S каждая, с рас стоянием между двумя соседними пластинами d, с диэлектриком, абсолютная диэлектрическая проницаемость которого ε, имеет емкость, равную
C= ε a ⋅S⋅( n−1 ) d .
Рис. 1
Подсчитать, сколько надо взять листов станиоля, каждый площадью S = 40 см2, чтобы получить многопластинчатый конденсатор емкостью 0,5 мкФ при условии, что диэлектриком является парафинированная бумага (εr = 1,8) толщиною 0,05 мм.
Ответ: 393 листа.
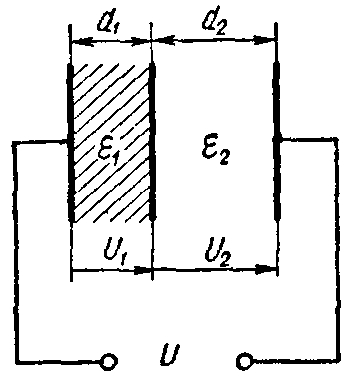
Задача 4. Плоский слоистый конденсатор (рис. 2), поверхность каждой пластины которого S = 12 см2, имеет диэлектрик, состоящий из слюды (εr1 = 6) толщиною d1 = 0,3 мм и стекла (εr2 = 7) толщиною d2 =0,4 мм.
Пробивные напряженности слюды и стекла соответственно равны E1 = 77 кВ/мм, E2 = 36 кВ/мм.
Рис. 2
Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.
Решение
Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов
C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .
Подставляя сюда числовые значения, предварительно заменив εa1 = ε0εr1 и εa2 = ε0εr2, получим
C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12 Ф.
Обозначим общее напряжение, подключаемое к слоистому конденсатору, через Uпр, при этом заряд конденсатора будет равен
Q = C·Uпр.
Напряжения на каждом слое будут равны
U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .
Напряженности электростатического поля в каждом слое
E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .
Здесь U’np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U»np — общее напряжение, при котором происходит пробой второго слоя.
Из последнего выражения находим
U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5 кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0 кВ.
Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное
27,0 кВ / 2 = 13,5 кВ.
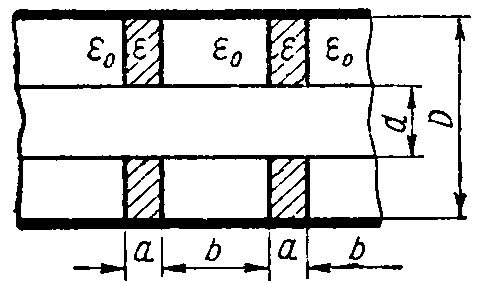
Задача 5. Вычислить емкость 1 км коаксиального кабеля типа 2,6/9,4. В этом кабеле изоляция осуществлена с помощью полиэтиленовых шайб (εr = 2,2) толщиною a = 2,2 мм, размещенных через равные промежутки b = 25 мм, остальное пространство между шайбами заполнено воздухом (рис. 3). Диаметр жилы d = 2,6 мм, внутренний диаметр наружного провода D = 9,4 мм.
Рис. 3
Указание. Емкость кабеля может быть подсчитана, исходя из того, что отдельные его участки соединены параллельно.
Ответ: 48·10–9 Ф/км = 48 нФ/км.
Задача 6. Силовой одножильный кабель с резиновой изоляцией в свинцовой оболочке марки СРГ имеет сечение жилы 25 мм2. Известно, что наибольшая напряженность электростатического поля в изоляции кабеля не должна превышать 6 кВ/мм. Определить толщину слоя резиновой изоляции, если при испытании кабеля между жилой и оболочкой включают напряжение, равное 10 кВ.
Принимая потенциал жилы кабеля равным U = 10 кВ, построить график падения потенциала в диэлектрике кабеля в зависимости от расстояния до центра кабеля.
Ответ: 2,25 мм. График строится по уравнению φ( r )= U⋅ln r 2 r ln r 2 r 1 .
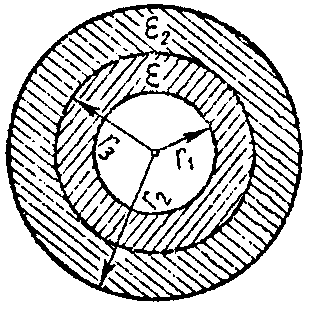
Задача 7. Цилиндрический конденсатор длиною l = 5 см имеет двухслойный диэлектрик (рис. 4).
Рис. 4
Внутренний радиус r1 = 1 см, внешний — r2 = 3 см, радиус разграничения слоев диэлектриков r3 = 1.5 см. Относительные диэлектрические проницаемости: внутреннего слоя изоляции εr1 = 2, наружного εr2 = 4.
Вычислить емкость конденсатора и начертить кривые изменения напряженностей и потенциалов в каждом из слоев, если конденсатор находится под напряжением U = 2 кВ.
Указание. При помощи теоремы Гаусса находятся напряженности электростатического поля в каждом из слоев
E 1 = τ 2π⋅ ε a1 ⋅r ; E 2 = τ 2π⋅ ε a2 ⋅r ,
где τ — линейная плотность заряда (заряд на единицу длины конденсатора). Затем вычисляется напряжение между обкладками конденсатора по формуле
U= ∫ r 1 r 3 E 1 dr + ∫ r 3 r 2 E 2 dr .
Отсюда определяется линейная плотность заряда
τ= 2π⋅U 1 ε a1 ln r 3 r 1 + 1 ε a2 ln r 2 r 3 .
Емкость конденсатора вычисляется по формуле (8). Потенциал φ1 в любой точке области первого слоя диэлектрика (r3 > r > r1) определяется из выражения
φ r 1 − φ 1 = ∫ r 1 r E 1 dr ,
а потенциал φ2 в любой точке области второго слоя (r2 > r > r3) диэлектрика вычисляется из выражения
φ r 2 − φ 2 = ∫ r 2 r E 2 dr .
В последних формулах φr1 = U — потенциал внутренней обкладки конденсатора, φr2 — потенциал на границе раздела диэлектриков. Внешняя оболочка заземлена: φ2(r2) = 0.
Ответ:
C= 2π⋅l 1 ε a1 ln r 3 r 1 + 1 ε a2 ln r 2 r 3 ; E 1 ( r )= U r⋅( ln r 3 r 1 + ε a1 ε a2 ln r 2 r 3 ) ; E 2 ( r )= U r⋅( ε a2 ε a1 ln r 3 r 1 +ln r 2 r 3 ) ; φ 1 ( r )=U⋅( 1− ln r r 1 ln r 3 r 1 + ε a1 ε a2 ln r 2 r 3 ); φ 2 ( r )= U⋅ ε a1 ε a2 ln r 2 r ln r 3 r 1 + ε a1 ε a2 ln r 2 r 3 .
Пример вывода формулы емкости двухслойного цилиндрического конденсатора при помощи теоремы Гаусса
Задача 8. Чему равен внешний радиус сферического конденсатора емкостью 20 пФ, внутренний радиус которого 2 см. а относительная Диэлектрическая проницаемость изоляции εr = 3. При каком напряжении конденсатор будет пробит, если пробивное напряжение изоляции равно 15 кВ/мм?
Ответ: 3 см, 100 кВ.
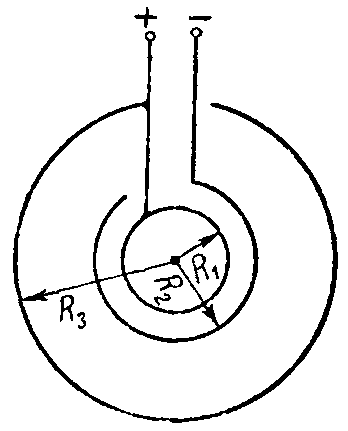
Задача 9. Найти емкость сферического конденсатора, изображенного на рис. 5.
Рис. 5
Даны радиусы R1, R2 и R3; изоляция однородная, ее абсолютная диэлектрическая проницаемость равна ε.
Указание. Данный конденсатор может быть рассмотрен как два Параллельно соединенных конденсатора.
Ответ: C= 4π⋅ ε a ⋅ R 2 2 ⋅( R 3 − R 1 ) ( R 3 − R 2 )( R 2 − R 1 ) .
Задача 10. К пластинам плоского двухслойного конденсатора приложено напряжение 3 кВ. Площадь пластины равна 5 см2. Толщины первого и второго слоев конденсатора равны соответственно 4 и 6 мм, а диэлектрические проницаемости — 6 и 1.
Построить графики изменения напряженности и потенциала между пластинами в зависимости от расстояния до положительной пластины, потенциал которой принять равным + 3 кв.
Задача 11. Имеется два одинаковых конденсатора переменной емкости. Емкость каждого конденсатора можно плавно изменять от 20 до 200 пФ.
Какие границы изменения емкости можно получить при различном соединении этих конденсаторов между собой?
Ответ: от 10 до 400 пФ.
Задача 12. Определить емкость воздушной двухпроводной линии длиной 2 км, если диаметр проводов равен 3 мм и расстояние между осями проводов составляет 30 см.
Задача 13. Определить емкость однопроводной телеграфной линии длиною 180 км, если диаметр провода равен 3 мм, а средняя высота подвеса провода над землей составляет 7 м.
Начертить кривую зависимости емкости этого провода в функции расстояния от земли.
Ответ: 1,1 мкФ.
Задача 14. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d1 = 1 см друг от друга. Площадь обкладок S = 50 см2. Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.
Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d2 = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.
Решение
Энергия заряженного плоского конденсатора равна
W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,
где С1 — емкость до раздвижения обкладок.
Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения
Q = C2·U2,
где C2 — емкость конденсатора после раздвижения обкладок, следует, что, так как C 2 = ε 0 ⋅S d 2 стало меньше в 10 раз (d2 увеличилось в 10 раз), то напряжение на конденсаторе U2 увеличилось в 10 раз, т. е. U2 = 10U.
Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d2 будет больше первоначальной
W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .
Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.
Таким образом, надо совершить работу, равную
W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7 Дж.
Задача 15. Плоский конденсатор с воздушным диэлектриком заряжается от источника электрической энергии с напряжением U.
Определить, как изменится энергия конденсатора, если после отключения его от источника энергии расстояние между обкладками увеличить вдвое.
Ответ: энергия увеличится в два раза.
Задача 16. Плоский конденсатор с диэлектриком из эбонита (εr = 2,5) в виде пластинки толщиной d = 5 см присоединен к полюсам батареи. После зарядки эбонитовая пластинка вынимается. Как нужно изменить расстояние между обкладками конденсатора, чтобы энергия конденсатора осталась без изменения?
Задачу решить в двух случаях: 1) если конденсатор остается присоединенным к батарее и 2) если конденсатор отключить от батареи.
Ответ: в обоих случаях пластины должны отстоять друг от друга на расстоянии 2 см.
Задача 17. Конденсатор емкостью C1 = 40 мкФ заряжен от сети до напряжения U1 = 220 В; другой конденсатор емкостью C2 = 10 мкФ заряжен от другой сети до напряжения U2 = 110 В.
Положительные зажимы конденсаторов после отсоединения от источников соединяются вместе:
а) Чему равна разность потенциалов между отрицательными зажимами конденсаторов?
б) Чему равны заряды до и после последующего соединения друг с другом отрицательных зажимов конденсаторов?
в) Чему равны напряжения на конденсаторах после соединения их отрицательных зажимов?
г) Чему равна энергия каждого конденсатора до. и после соединения отрицательных зажимов?
Ответ: а) 110 В, б) до соединения: Q1 = 8800 мкКл, Q2 = 1100 мкКл; после соединения: Q′1 = 7920 мкКл, Q′2 = 1980 мкКл, в) 198 В, г) до соединения: W1 = 0,97 Дж, W2 = 0,06 Дж; после соединения: W′1 = 0,784 Дж, W′2 = 0,196 Дж.
Задача 18. Три последовательно соединенных конденсатора, емкости которых 2, 10 и 15 мкФ, заряжаются от сети с напряжением 120 В. После отключения от сети конденсаторы разъединяются друг от друга без потери заряда. Если затем конденсаторы соединить параллельно, то чему будет равно напряжение на их зажимах?
Ответ: 20 В.
Список литературы
1. Бессонов Л.А. Теоретические основы электротехники. Электромагнитное поле. — М.: Гардарики, 2001.– 317 с.
2. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники: в 3-х тт.: Учебник для вузов. Том 3. –4-е изд. — СПб.: Питер, 2003. — 377 с.
3. Купалян С.Д. Теоретические основы электротехники / Под ред. Г.И. Атабекова. — М.-Л.: Госэнергоиздат, 1963. — ч. 3. Электромагнитное поле. — 112 с.
4. Теоретические основы электротехники. т. 2. Нелинейные цепи и основы теории электромагнитного поля. Под ред. П.А. Ионкина. Учебник для электротехн. вузов. Изд. 2-е, перераб. и доп. — М.: Высш. шк., 1976. — 383 с.
5. Поливанов, К.М. Теоретические основы электротехники: в 3-х ч. / К.М. Поливанов. ч. 3: Теория электромагнитного поля. — М.: Энергия, 1969. — 352 с.
6. Бессонов Л.А. Сборник задач по теоретическим основам электротехники: Учебное пособие для вузов / Бессонов Л.А., Демидова И.Г. и др.; Под ред. Л.А. Бессонова. — М., Высшая школа, 2000. — 528с.: ил.
7. Колли Я.Н. и др. Задачник по теоретическим основам электротехники (теория поля). Уч. пособие для вузов. Под ред. Поливанова К.М. — М., «Энергия», 1972.
8. Ионкин П.А. Сборник задач и упражнений по теоретическим основам электротехники: Учебное пособие. — М., Энергоиздат, 1982. — 768с.
9. Татур Т.А. Основы теории электромагнитного поля: Справочное пособие. — М.: Высш. шк., 1989 . — 270 с.

емкость конденсатора,
электроемкость,
емкость плоского конденсатора,
емкость цилиндрического конденсатора,
сферический конденсатор,
емкость двухпроводной линии,
емкость однопроводной линии,
емкость коаксиального кабеля
Поле и емкость двухпроводной линии с учетом влияния Земли
Рис. 8.
Дано: над плоской поверхностью Земли подвешены горизонтально два цилиндрических провода с параллельными осями (рис. 8).
h1 – высота подвеса 1-го провода; h2 – высота подвеса 2-го провода; R – радиусы проводов; d – расстояние между нормальными проекциями осей проводов на поверхности Земли.
По условию задачи требуется: вывести уравнения, связывающие между собой линейные плотности зарядов на проводах и потенциалы проводов. Определить параметры этих уравнений: потенциальные и емкостные коэффициенты, частичные емкости и рабочую емкость линии, если d, h1 и h2>>R.
Для решения поставленной задачи можно воспользоваться методом изображений. Распределение поля над поверхностью Земли не изменится, если Землю убрать, а под поверхностью Земли расположить на глубинах h1 и h2 провода с линейной плотностью заряда .
После такого преобразования можно считать, что в системе действует электростатическое поле двух пар параллельных разноименно заряженных осей (рис. 9).
Рис. 9.
Поскольку d, h и h >> R, смещением электрических осей относительно геометрических осей можно пренебречь.
Используя принцип наложения, выразим потенциалы проводов через линейные плотности зарядов
Из этих уравнений видно, что потенциалы проводов являются линейными комбинациями линейных плотностей зарядов
или
Коэффициентыназываются потенциальными коэффициентами единицы длины проводов.
,– это собственные потенциальные коэффициенты проводов,
, – это взаимные потенциальные коэффициенты.
Как видно, матрица симметричная, значит, для линии выполняется принцип взаимности.
Из системы уравнений (1) выразим τ1 и τ2.
Коэффициентыназываются емкостными коэффициентами на единицу длины линии и измеряются в Ф/м. Собственные потенциальные и емкостные коэффициенты всегда положительны.
Взаимные потенциальные коэффициенты положительны, а взаимные емкостные коэффициенты всегда отрицательны.
Систему уравнений (2) можно записать иначе
Коэффициенты Сij называют частичными емкостями на единицу длины.
Если провода линии не связаны с Землей и питаются от незаземленного источника ЭДС, то суммарный заряд линии равен нулю, т.е
Вычтем второе уравнение из первого и получим
Отношение линейной плотности заряда провода к напряжению называют в данном случае рабочей ёмкостью линии на единицу длины
Можно изобразить эквивалентную схему системы заряженных проводников линии (рис. 10). Рис. 10.
Анализируя эту схему, можно получить другое выражение для рабочей емкости линии
Cраб = C12 + C11C22/(C11 + C22) (4)
Можно доказать, что выражения (3) и (4) тождественны.
Ниже представлен текст вычислительного сценария расчёта потенциальных и ёмкостных коэффициентов, а также частичных ёмкостей многопроводной воздушной линии с учётом влияния земли.
% ElStatLin — Расчёт потенциальных и емкостных коэффициентов многопроводной линии.
% Смещение электрических осей относительно геометрических не учитываетсq.
% Входные параметры:
% x — горизонтальные координаты подвеса проводов;
% y — вериткальные координаты подвеса проводов;
% D — диаметры всех проводов
% Все эти переменные — строковые матрицы
% Выходные параметры:
% al — потенциальные коэффициенты проводов;
% be — ёмкостные коэффициенты проводов;
% c — частичные ёмкости проводов
eps0=8.85e-12; % Абcолютнаq диэлектрическаq проницаемость вакуума, Ф/м
rp=sqrt((repmat(x,length(x),1)-repmat(x,length(x),1).’).^2+…
(repmat(y,length(y),1)-repmat(y,length(y),1).’).^2)+diag(D/2);
rm=sqrt((repmat(x,length(x),1)-repmat(x,length(x),1).’).^2+…
(repmat(y,length(y),1)+repmat(y,length(y),1).’).^2);
al=log(rm./rp)/eps0/2/pi % Потенциальные коэффициенты, м/Ф
be=inv(al) % Ёмкостные коэффициенты, Ф/м
c=diag(sum(be))+diag(diag(be))-be % Частичные ёмкости, Ф/м