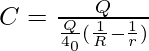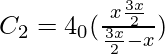Как найти емкость сфера - Исправление недочетов и поиск решений вместе с Examum.ru

A capacitor is simply an electric device that consists of two terminals that have the ability to store energy in the form of an electric charge. It can be designed by simply placing two electrical conductors at a distance from each other. The empty space between the conductors may be filled by vacuum(or air) or with an insulating material known as a dielectric. The ability of the capacitor to store charges is known as capacitance.

In a capacitor, the two terminals having opposite charges are placed at a distance from each other which allows it to generate(store) energy. The simplest design for a capacitor is a parallel plate, which consists of two metal plates with a gap between them. It should be noted that a capacitor can be of any shape or size or be made of any material until its terminals store opposite charges and thus store energy.

Capacitance of a capacitor

Consider a capacitor whose positive and negative plates hold +q and -q charge respectively. A DC voltage source is applied across it which gives it a potential difference of V across the plates. Now as we know,

Q α V

Putting a constant C in this relation.

Q=CV.

Note: The capacitance of every material is unique and its SI unit is Farad(F).

Working of a capacitor

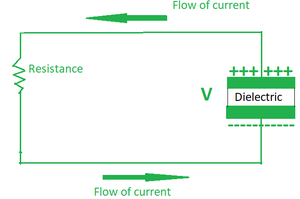
Let’s suppose that we are given the most basic form of the capacitor, which is a parallel plate capacitor. It consists of two parallel plates separated by a small distance and that gap is filled by a dielectric. Next, we are given a DC voltage source that is linked across the capacitor, where one plate is attached to the positive end (plate I) and the other plate is connected to the negative end (plate II). When the battery’s potential is applied across the capacitor, plate I become positive in relation to plate II. At steady-state, current attempts to pass through the capacitor from the positive plate to the negative plate. However, because of a gap between them with an insulating layer(dielectric), it is unable to flow.

Structure of a simple capacitor.

For some time the capacitor continues to get charged by the incoming flow of the current. But after some time it reaches a state where it holds the maximum amount of charge that it can possibly hold. This is how a capacitor stores energy The time taken to reach this state of maximum charge is called the charging time of the capacitor. Later we disconnect the voltage source from the circuit and insert a load resistor in it. Now the current starts flowing from the positively charged terminal of the capacitor to the negatively charged terminal and loses all of its energy in the process. This time period is called the discharging time of the capacitor.

Discharging of a capacitor.

Spherical Capacitor Formula

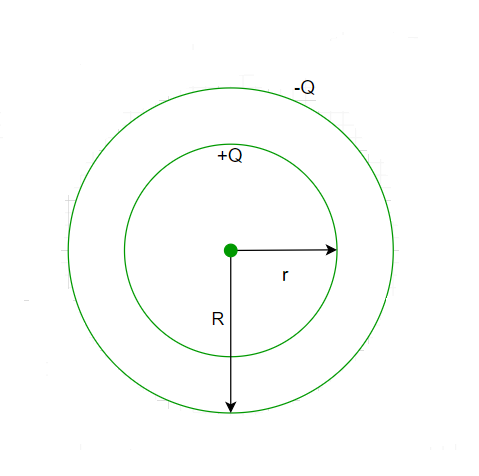
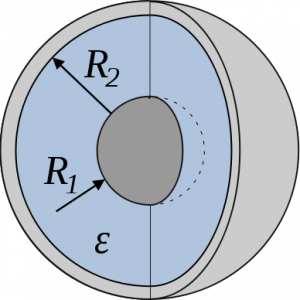
As mentioned earlier capacitance occurs when there is a separation between the two plates. So for constructing a spherical capacitor we take a hollow sphere such that the inner surface is positively charged and the outer surface of the sphere is negatively charged. The inner radius of the sphere is r and the outer radius is given by R. The distance of R-r between the two oppositely charged surfaces acts as the dielectric. Let’s assume that the inner spherical surface has a potential of V₁ and V_2.

A spherical capacitor

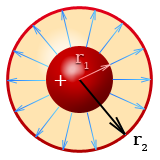
Next, the electric field generated by a charged sphere (hollow) of radius r having charge Q is given by,

E= $frac{Q}{4π∈_0r^2}$ . ⇢ (1)

Also, we know that the Electric field generated is related to the potential difference as,

E= $-frac{dV}{dr}$ . ⇢ (2)

Comparing (1) and (2),

$-frac{dV}{dr} =frac{Q}{4π∈_0r^2}$

$-dV= frac{Qdr}{4π∈_0r^2}$

Integrating on both sides within the limits V, V and r, R.

$int_{V_1}^{V_2} -dV = int_{r}^{R} frac{Q}{4π∈_0r^2}dr$

$int_{V_1}^{V_2}-dV = frac{Q}{4π∈_0} int_{r}^{R} frac{dr}{r^2}$

$-[V] |_{V_1}^{V_2} = frac{Q}{4π∈_0} frac{-r^{-2}+1}{-2+1}|_{r}^{R}$

$[V_2 -V_1] = frac{Q}{4π∈_0} [frac{1}{R}-frac{1}{R}]$

$Delta = frac{Q}{4π∈_0} [frac{1}{R}-frac{1}{R}]$ ⇢ (3)

is the change in potential as we move from inside the sphere to outside. Now the capacitance of a capacitor is given by,

$C= frac{Q}{Delta V}$ ⇢ (4)

Comparing (3) and (4),

$C = frac{Q}{frac{Q}{4π∈_0}(frac{1}{R} - frac{1}{r})}$

$C = frac{Q4π∈_0}{Q[frac{1}{R} - frac{1}{r}]}$

Simplifying further we get,

$C = 4π∈_0 (frac{rR}{r-R})$

Since capacitance can’t be negative the positive value is taken. This is the expression for the capacitance of a spherical capacitor.

Sample Questions

Question 1: A spherical capacitor has an inner radius of 7 cm and an outer radius of 10 cm. Find the capacitance of the sphere. Assume the dielectric in between to be air.

Solution:

The capacitance of the sphere is given by,

C = $4π∈_0 (frac{rR}{r-R})$

Here ∈₀ = 8.85 × 10^-12, r = 7, R = 10

C= $frac{4times3.14times8.85times10^{-12} times70times10^{-2}}{(10-7)10^{-1}}$

C = 2.593 × 10^-12F

Question 2: In the above problem find how much charge will it take for the capacitor to raise its potential from 0 to10,000 V.

Solution:

The capacitance of the spherical capacitor is C = 2.593 × 10^-12F.

The charge required can be found by using Q = CV. where V is the potential difference.

Potential difference V in this case is 1000-0 = 1000V

Therefore, Q = 3.7052 × 10^-12 × 1000

Q = 2.593 × 10^-9C

Question 3: The inner radius of a spherical capacitor is x m and its outer radius is 5/4 x m if the outer radius is increased to 3/2x m, find by what ratio its capacitance is changed.

Solution:

In this case $C_1 =4π∈_0(frac{rR}{R-r})$

= $4π∈_0(frac{xfrac{5x}{4}}{frac{5}{4}x -x})$

= 20 πε_ox F

$C_2 = 4π∈_0(frac{xfrac{3x}{2}}{frac{3x}{2}-{x}})$

= 20 πε_ox F

$frac{C_1}{C_2} =frac{ 20 π∈_0 x }{12 π∈_0x}$

$frac{C_1}{C_2} =frac{5}{3}$

So the capacitance decreases as the external radius is increased.

Question 4: A sphere has a radius of 10 cm. find the capacitance on it and also find the potential difference required to give it a charge of 10^-8 C.

Solution:

C = 4 πε_ox F

C = 4 × 3.14 × 8.85 × 10⁻¹² × 10 × 10⁻²

C = 111.156 × 10⁻¹³

C = 1.11 × 10⁻¹¹ F

Now Q = CV

Therefore $V = frac{10^{-8}}{1.11x10^{-11}}$

Hence V = 900.9 V

Question 5: The outer radius of a spherical capacitor is 10 % bigger than its inner radius. The capacitance of this capacitor is 10^-8 F. Find the value of its inner and outer radii.

Answer:

$C = 4π∈_0 (frac{rR}{r-R})$

Here r = x, R = 1.1x and C= 10^-8 F

So, $C = frac{1.1x(x)}{1.1x-x}$

$10^{-12}=4piepsilonfrac{1.1x^2}{0.1x}$

$11x =frac{10^{-12}}{4piepsilon}$

x = 0.009 m

So the inner radius is 0.09 cm and the outer radius is 0.099 cm.

Question 6: The inner and outer radii of a spherical capacitor are 5cm and 6cm. Find the energy of the capacitor if a potential difference of 1000V is applied to it.

Solution:

The capacitance of this capacitor is calculated as,

$C = 4{pi}{epsilon}{frac{6times5times10^{-2}}{(6-5)times10^{-1}}}$

C = 3.3363 × 10⁻¹² F

U = 1/2 CV²

U = 21 × 3.3363 × 10⁻¹²× (1000)²

U = 1.66815 × 10⁻⁹ J

Question 7: A spherical capacitor of inner and outer radii 8cm and 10cm has an energy of 10^-8 J . Find its Voltage.

Solution:

Lets find the capacitance first,

$C = 4piepsilonfrac{8times10times10^{-2}}{(10-8)times10^{-1}}$

C = 4.446 × 10^-9 F

U = 1/2 CV²

$V =sqrt {frac{2U}{C}}$

$V=sqrt{frac{2times{10^{-8}}}{4.446times 10^{-9}}}$

V = 2.12 V

Last Updated :
01 May, 2022

Like Article

Save Article

Источник

Электроемкость сферического конденсатора

Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.

Чтобы найти емкость сферического конденсатора, который состоит из двух
концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:
.

Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:

При малой величине зазора, то есть , а следовательно можно считать, что емкость сферического конденсатора будет равна . Площадь сферы S = 4πr² следовательно формула будет совпадать с формулой емкости плоского конденсатора .

Формулы:

Энергия конденсатора: .

Ёмкость конденсатора: .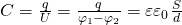

Ёмкость цилиндрического конденсатора: .

Ёмкость плоского конденсатора: .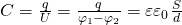

Обозначения в формулах:

C — электрическая ёмкость (ёмкость конденсатора);

g — заряд;

U — потенциал проводника (напряжение);

φ — потенциал;

ε — относительная диэлектрическая проницаемость;

— электрическая постоянная;

S — площадь одной обкладки;

d — расстояние между обкладками;

r₂— Больший радиус (от центра, до края конденсатора);

r₁ — Малый радиус (Его может и не быть — это пустота).

вернутся в раздел: электрическая ёмкость

Источник

$Large C=4pi varepsilon varepsilon _0(frac{1}{R_1} - frac{1}{R_2})^{-1}= 4pi varepsilon varepsilon _0frac{r_1r_2}{r_2-r_1}$

Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:

$Largevarphi _1-varphi _2=frac{q}{4pi varepsilon varepsilon _0}(frac{1}{r_1}-frac{1}{r_2})$

$Large C=4pi varepsilon varepsilon _0(frac{1}{R_1} - frac{1}{R_2})^{-1}= 4pi varepsilon varepsilon _0frac{r_1r_2}{r_2-r_1}$

При малой величине зазора, то есть , а следовательно можно считать, что емкость сферического конденсатора будет равна $frac{4pi r^2varepsilon varepsilon _2}{d}$ . Площадь сферы следовательно формула будет совпадать с формулой емкости плоского конденсатора $varepsilon varepsilon _0frac{S}{d}$

Так же есть:

Энергия конденсатора: $large W_p=frac{U q}{2}=frac{q^2}{2C}=frac{CU^2}{2}$

Ёмкость конденсатора : $large C=frac{q}{U}=frac{q}{varphi_1-varphi _2} =varepsilon varepsilon _0frac{S}{d}$

Ёмкость цилиндрического конденсатора : $large C=2pi varepsilon varepsilon _0frac{l}{ln(frac{R_2}{R_1})}$

Емкость плоского конденсатора : $large C=frac{q}{U}=frac{q}{varphi_1-varphi _2} =varepsilon varepsilon _0frac{S}{d}$ ;

В Формуле мы использовали :

— Электроемкость сферического конденсатора

— Относительная диэлектрическая проницаемость

$varepsilon _0 = 8.854185times 10^{-12}$ — Электрическая постоянная

— Больший радиус (от центра, до края конденсатора)

— Малый радиус (Его может и не быть — это пустота)

Источник

Емкость сферического конденсатора

Сферический конденсатор состоит из двух концентрических полых сфер. Если расстояние между сферами ∆r очень мало, так что площадь обеих сферических поверхностей практически одинакова, то можно пользоваться выражением для емкости плоского конденсатора. Полагая S = 4πr² см. площадь сферы, получаем:

[ C = 4 π ε_{0} ε frac{r^2}{∆r} ]

При большем расстоянии между поверхностями нужно учитывать различие площадей сфер.

Если

C	емкость сферического конденсатора,	фарад
r₁	радиус внутренней сферы,	метр
r₂	радиус внешней сферы,	метр
ε_a	ε_a=ε₀ε абсолютная диэлектрическая проницаемость,	Фарад/метр
ε₀	ε₀=8.85·10^-12электрическая постоянная,	Фарад/метр
ε	относительная диэлектрическая проницаемость,

то

[ C = 4 π ε_{0} ε frac{r_1 r_2}{r_2 — r_1} ]

Вычислить найти емкость сферического конденсатора по формуле (2)

Емкость сферического конденсатора	стр. 635

Источник

Конфигурация конденсатора такова, что поле, которое создается зарядами, локализовано между обкладками. В общем случае электроемкость конденсатора равна:

[C=frac{q}{{varphi }_1-{varphi }_2}=frac{q}{U}left(1right),]

где ${varphi }_1-{varphi }_2=U$ — разность потенциалов обкладок, которую называют напряжением и обозначают $U$. Емкость по определению считается положительной величиной. Она зависит только от геометрии обкладок конденсатора их взаиморасположения и диэлектрика. Форму обкладок и их расположение подбирают так, чтобы внешние поля минимально влияли на внутреннее поле конденсатора. Силовые линии поля конденсатора начинались на проводнике с положительным зарядом и заканчивались на проводнике с отрицательным зарядом. Конденсатор может быть проводником, который помещен в полость, окруженную замкнутой оболочкой.

В соответствии с конфигураций конденсаторов можно выделить три большие группы: плоские, сферические и цилиндрические (по форме обкладок). Вычисление емкости конденсатора сводится к определению $напряжения$ конденсатора при известном заряде на его обкладках.

Плоский конденсатор

Плоский конденсатор (рис.1) — это две разноименно заряженные пластины, разделенные тонким слоем диэлектрика. Формула для расчета емкости такого конденсатора представляет собой выражение:

[С=frac{varepsilon {varepsilon }_0S}{d}left(2right),]

где $S$ — площадь обкладки, $d$ — расстояние между обкладками, $varepsilon $ — диэлектрическая проницаемость вещества. Чем меньше $d$, тем больше совпадает расчётная емкость конденсатора (2), с реальной емкостью.

Рис. 1

Электроемкость плоского конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равна $d_i$, диэлектрическая проницаемость этого слоя ${varepsilon }_i$ вычисляется по формуле:

[C=frac{{varepsilon }_0S}{frac{d_1}{{varepsilon }_1}+frac{d_2}{{varepsilon }_2}+dots +frac{d_N}{{varepsilon }_N}} left(3right).]

Сферический конденсатор

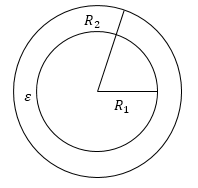
В том случае, если внутренний проводник шар или сфера, внешняя замкнутая оболочка — концентрическая ему сфера, то конденсатор является сферическим. Сферический конденсатор (рис.2) состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком. Емкость его можно рассчитать по формуле:

[C=4pi varepsilon {varepsilon }_0frac{R_1R_2}{R_2-R_1} left(4right),]

где $R_1{ и R}_2$ — радиусы обкладок.

Рис. 2

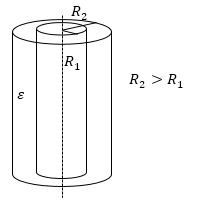
Цилиндрический конденсатор

Емкость цилиндрического конденсатора равна:

[C=frac{2pi varepsilon {varepsilon }_0l}{{ln left({R_2}/{R_1}right) }}left(5right),]

где $l$ — высота цилиндров, $R_1$ и $R_2$ — радиусы обкладок. Этот вид конденсаторов представляет собой две коаксиальных (соосных) проводящих цилиндрических поверхности (рис.3).

Рис. 3

Еще одной, но не маловажной характеристикой всех конденсаторов является пробивное напряжение ($U_{max}$)— это напряжение, при котором происходит электрический разряд через слой диэлектрика. $U_{max}$ зависит от толщины слоя и свойств диэлектрика, конфигурации конденсатора.

Помимо одиночных конденсаторов применяют их соединения. Для того чтобы увеличить емкость используют параллельное соединение конденсаторов (соединение одноименными обкладками). В этом случае результирующая емкость такого соединения может быть найдена как сумма${ С}_i$ где $С_i$ — емкость конденсатора с номером i:

[C=sumlimits^N_{i=1}{С_i} left(6right).]

Если конденсаторы соединить последовательно (обкладками с разными знаками заряда), то суммарная емкость соединения будет всегда меньше, чем минимальная емкость любого конденсатора, который входит в систему. В этом случаем для того чтобы рассчитать результирующую емкость складывают величины, обратные к емкостям отдельных конденсаторов:

[frac{1}{C}=sumlimits^N_{i=1}{{frac{1}{C_i}}_i}left(7right).]

Пример 2

Задание: Какова напряженность электростатического поля сферического конденсатора на расстоянии x=1 см=${10}^{-2}м$ от поверхности внутренней обкладки, если внутренний радиус обкладки конденсатора $R_1=$1 см${=10}^{-2}м$, внешний $R_2=$ 3 см=${3cdot 10}^{-2}м$. Напряжение на обкладках равно ${10}^3В$.

Решение:

Напряженность поля, которое создается проводящей заряженной сферой, вычисляется в соответствии с формулой:

[E=frac{1}{4pi varepsilon {varepsilon }_0}frac{q}{r^2} left(2.1right),]

где $q$ — заряд внутренней сферы (обкладки конденсатора), $r=R_1+x$ —расстояние от центра сферы.

Заряд сферы найдем из определения емкости конденсатора (С):

[q=CU left(2.2right).]

Емкость сферического конденсатора определяется как:

[C=4pi varepsilon {varepsilon }_0frac{R_1R_2}{R_2-R_1} left(2.3right),]

где $R_1{ и R}_2$ — радиусы обкладок конденсатора.

Подставим выражения (2.2) и (2.3) в (2.1), получим искомую напряженность:

[E=frac{1}{4pi varepsilon {varepsilon }_0}frac{U}{{(x+R_1)}^2}4pi varepsilon {varepsilon }_0frac{R_1R_2}{R_2-R_1}=frac{U}{{(x+R_1)}^2}frac{R_1R_2}{R_2-R_1}.]

Так как все данные в задаче уже переведены в систему СИ, проведем вычисления:

[E=frac{{10}^3}{{{(1+1)}^2cdot 10}^{-4}}cdot frac{{{10}^{-2}cdot 3cdot 10}^{-2}}{{3cdot 10}^{-2}-{10}^{-2}}=frac{3cdot {10}^{-1}}{8cdot 10^{-6}}=3,75cdot {10}^4left(frac{В}{м}right).]

Ответ: $E=3,75cdot {10}^4frac{В}{м}.$

Источник