Как найти емкость системы конденсатора

Содержание:

1. Последовательное соединение конденсаторов
2. Параллельное соединение конденсаторов
3. Смешанное соединение конденсаторов
4. Пример расчета

В данной статье приведены различные схемы соединения конденсаторов, а так же формулы их расчета с примером.

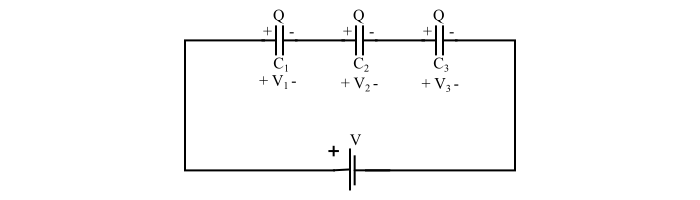
1. Последовательное соединение конденсаторов

Если условно разделить выводы каждого из конденсаторов на первый и второй выводы последовательное соединение конденсаторов будет выполняется следующим образом: второй вывод первого конденсатора соединяется с первым выводом второго конденсатора, второй вывод второго конденсатора, соединяется с первым выводом третьего и так далее. Таким образом мы получим группу (блок) последовательно соединенных конденсаторов с двумя свободными выводами — первым выводом первого конденсатора в блоке и вторым выводом последнего конденсатора, через которые данный конденсаторный блок и подключается в электрическую цепь.

Схема последовательного соединения конденсаторов будет иметь следующий вид:

Фактически последовательное соединение конденсаторов имеет следующий вид:

При данной схеме соединения заряды на конденсаторах будут одинаковы:

Q_общ=Q₁=Q₂=Q₃, 

где: Q₁, Q₂, Q₃ — соответственно заряд на первом, втором, третьем и т.д. конденсаторах

Напряжение на каждом конденсаторе при такой схеме зависит от его емкости:

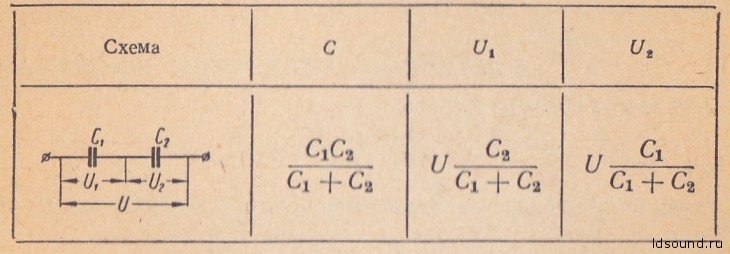
U₁=Q/C₁; U₂=Q/C₂; U₃=Q/C₃, где:

• U₁, U₂, U₃ — соответственно напряжение на первом, втором, третьем конденсаторах
• C₁, C₂, C₃ — соответственно емкости первого, второго, третьего конденсаторов

При этом общее напряжение составит:

U_общ=U₁+U₂+U₃+…+U_n

Рассчитать общую емкость конденсаторов при последовательном соединении можно по следующим формулам:

• При последовательном соединении двух конденсаторов:

С_общ=(C₁*C₂)/(C₁+C₂)

• При последовательном соединении трех и более конденсаторов:

1/С_общ=1/C₁+1/C₂+1/C₃+…+1/C_n

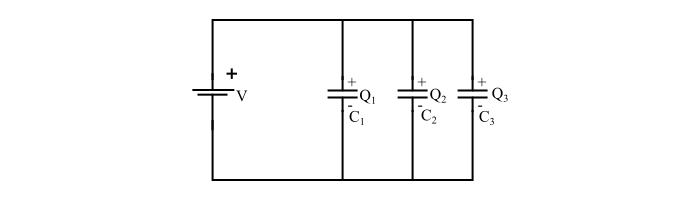
1. Параллельное соединение конденсаторов

Если условно разделить выводы каждого из конденсаторов на первый и второй выводы параллельное соединение конденсаторов будет выполняется следующим образом: первые выводы всех конденсаторов соединяются в одну общую точку (условно — точка №1) вторые выводы всех конденсаторов соединяются в другую общую точку (условно — точка №2). В результате получается группа (блок) параллельно соединенных конденсаторов подключение которой к электрической цепи производится через условные точки №1 и №2.

Схема параллельного соединения конденсаторов будет иметь следующий вид:

Таким образом параллельное соединение конденсаторов будет иметь следующий вид:

При данной схеме напряжение на всех конденсаторах будет одинаково:

U=U₁=U₂=U₃

Заряд же на каждом из конденсаторов будет зависеть от его емкости:

Q₁=U*C₁; Q₂=U*C₂; Q₃=U*C₃

При этом общий заряд цепи будет равен сумме зарядов всех параллельно подключенных конденсаторов:

Q_общ=Q₁+Q₂+Q₃…+…Q_n.

Рассчитать общую емкость конденсаторов при параллельном соединении можно по следующей формуле:

С_общ=C₁+C₂+C₃+…+C_n

1. Смешанное соединение конденсаторов

Схема в которой присутствует две и более группы (блока) конденсаторов с различными схемами соединения называется схемой смешанного соединения конденсаторов.

Приведем пример такой схемы:

Для расчетов такие схемы условно разделяются на группы одинаково соединенных конденсаторов, после чего расчеты ведутся для каждой группы по формулам приведенным выше.

Для наглядности приведем пример расчета общей емкости данной схемы.

1. Пример расчета

Условно разделив схему на группы получим следующее:

Как видно из схемы на первом этапе мы выделили 3 группы (блока) конденсаторов, при этом конденсаторы в первой и второй группе соединены последовательно, а конденсаторы в третьей группе — параллельно.

Произведем расчет каждой группы:

• Группа 1 — последовательное соединение трех конденсаторов:

1/C_1,2,3 = 1/C₁+1/C₂+1/C₃ = 1/5+1/15+1/10=0,2+0,067+0,1 = 0,367 → C_1,2,3 = 1/0,367 = 2,72 мкФ

• Группа 2 — последовательное соединение двух конденсаторов:

С_4,5 = (C₄*C₅)/(C₄+C₅)= (20*30)/(20+30) = 600/50 = 12 мкФ

• Группа 3 — параллельное соединение трех конденсаторов:

С_6,7,8 = C₆+C₇+C₈ = 5+25+30 = 60 мкФ

В результате расчета схема упрощается:

Как видно в упрощенной схеме осталась еще одна группа из двух параллельно соединенных конденсаторов, произведем расчет ее емкости:

• Группа 4 — параллельное соединение двух групп конденсаторов:

С_1,2,3,4,5 = C_1,2,3+C_4,5 = 2,72+12 = 14,72 мкФ

В конечном итоге получаем простую схему из двух последовательно соединенных групп конденсаторов:

Теперь можно определить общую емкость схемы:

С_общ = (C_1,2,3,4,5*C_6,7,8)/(C_1,2,3,4,5+C_6,7,8) = 14,72*60/14,72+60 = 883,2/74,72 = 11,8 мкФ

---

---

Была ли Вам полезна данная статья? Или может быть у Вас остались вопросы? Пишите в комментариях!

Не нашли на сайте ответа на интересующий Вас вопрос? Задайте его на форуме! Наши специалисты обязательно Вам ответят.

↑ Наверх

Элементы цепи могут быть подключены двумя способами:

1. последовательно
2. параллельно

Проиллюстрируем данные подключения на примере двух конденсаторов (рис. 1).

• последовательное соединение конденсаторов

Логическая зарядка конденсаторов происходит как показано на рис.1. Приходя из цепи, электрон останавливается на левой обкладке (пластине) конденсатора. При этом, благодаря своему электрическому полю (электризация через влияние), он выбивает другой электрон с правой обкладки, уходящий дальше в цепь (рис. 1.1). Этот образовавшийся электрон приходит на левую обкладку следующего конденсатора, соединённого последовательно. И всё повторяется снова. Таким образом, в результате «прохождения» через последовательную цепь конденсаторов «одного» электрона, мы получаем заряженную систему с одинаковыми по значению зарядами на каждом из конденсаторов (рис. 1.2).

Кроме того, напряжение на последовательно соединённой батареи конденсаторов есть сумма напряжений на каждом из элементов (аналог последовательного сопротивления проводников).

Часть задач школьной физики касается поиска общей электроёмкости участка цепи, логика такого поиска: найти такую электроёмкость, которым можно заменить цепь, чтобы параметры напряжения и заряда остались неизменными (рис. 2). Пусть заряд на обоих конденсаторах —  (помним, что они одинаковы), электроёмкости — ,  и соответствующие напряжения —  и .

Учитывая определение электроёмкости:

 (1)

Тогда:

 (2)

• где

 (3)

• где

 (4)

• где

Памятуя о том, что конденсаторы соединены последовательно, получаем:

 (5)

Тогда:

 (6)

Или в общем виде:

(7)

• где

Для цепи из двух последовательных соединений:

(8)

•  параллельное соединение конденсаторов

Параллельное подключение конденсаторов представлено на рисунке 3. При внесении электрона в систему, у него есть выбор: пойти на верхний или нижний конденсатор. При большом количестве электронов заполнение обкладок конденсатора происходит прямо пропорционально электроёмкости конденсаторов.

Опять попробуем решить задачу по поиску полной ёмкости конденсаторов (рис. 4). Помним, что при параллельном подключении напряжения на элементах одинаковы, тогда:

(9)

• где

(10)

• где

(11)

• где

С учётом того, что , получим:

(12)

Сокращаем:

(13)

Или в общем виде:

(14)

• где

Вывод: в задачах, в которых присутствует цепь, необходимо рассмотреть, какое конкретно соединение рассматривается, а потом использовать соответствующую логику рассуждений:

• для последовательного соединения
• для параллельного соединения

Практически все электрические цепи включают в себя емкостные элементы. Соединение конденсаторов между собой выполняют по схемам. Их необходимо знать как при расчетах, так и при выполнении монтажа.

Последовательное соединение

Конденсатор, а в просторечии — «ёмкость», та деталь, без которой не обходится ни одна электрическая или электронная плата. Даже в современных гаджетах он присутствует, правда, уже в измененном виде.

Вспомним, что представляет собой этот радиотехнический элемент. Это накопитель электрических зарядов и энергии, 2 проводящие пластины, между которыми расположен диэлектрик. При прикладывании к пластинам источника постоянного тока через устройство кратковременно потечет ток, и оно зарядится до напряжения источника. Его емкость используют для решения технических задач.

Само это слово произошло задолго до того, как придумали устройство. Термин появился ещё тогда, когда люди считали, что электричество — это что-то типа жидкости, и ею можно наполнить какой-нибудь сосуд. Применительно к конденсатору — он неудачен, т.к. подразумевает, что прибор может вместить только конечное количество электричества. Хотя это и не так, но термин остался неизменным.

Чем больше пластины, и меньше расстояние между ними, тем больше ёмкость конденсатора. Если его обкладки соединить с каким-либо проводником, то через этот проводник произойдет быстрый разряд.

В координатных телефонных станциях с помощью этой особенности происходит обмен сигналами между приборами. Длина импульсов, необходимых для команд, таких как: «соединение линии», «ответ абонента», «отбой», регулируется величиной ёмкости установленных в цепь конденсаторов.

Единица измерения ёмкости — 1 Фарад. Т.к. это большая величина, то пользуются микрофарадами, пикофарадами и нанофарадами, (мкФ, пФ, нФ).

На практике, выполнив последовательное соединение, можно добиться увеличения прикладываемого напряжения. В этом случае поданное напряжение получают 2 внешние обкладки собранной системы, а обкладки, находящиеся внутри, заряжаются с помощью распределения зарядов. К таким приемам прибегают, когда под рукой не оказывается нужных элементов, зато есть детали других номиналов по напряжению.

К участку, имеющему 2 последовательно соединенных конденсатора, рассчитанных на напряжение 125 В, можно подключить питание 250 В.

Если для постоянного тока, конденсатор является препятствием за счет своего диэлектрического промежутка, то с переменным — все иначе. Для токов разных частот, подобно катушкам и резисторам, сопротивление конденсатора будет меняться. Токи высокой частоты он пропускает хорошо, а для их собратьев низкой частоты создает барьер.

У радиолюбителей есть способ — через емкость 220-500 пФ к радиоприемнику подключают вместо антенны сеть освещения напряжением 220 В. Ток с частотой 50 Гц он отфильтрует, а токи высокой частоты пропустит. Это сопротивление конденсаторов легко рассчитать по формуле для емкостного сопротивления:RC =1/6*f*C.

Где:

• Rc — емкостное сопротивление, Ом;
• f — частота тока, Гц;
• C — емкость данного конденсатора, Ф;
• 6 — округленное до целой части число 2π.

Но не только прикладываемое напряжение к цепи можно изменить, пользуясь подобной схемой включения. Так добиваются изменений емкостей при последовательных соединениях. Для легкости запоминания придумали подсказку, что общее значение емкости, полученное при выборе подобной схемы, получается всегда меньше меньшей из двух, включенных в цепочку.

Если так соединить 2 детали одинаковой ёмкости, то их общее значение будет вдвое меньше каждой из них. Расчеты последовательных соединений конденсатора можно выполнить по приведенной ниже формуле:

Собщ = С1*С2/С1+С2,

Пусть С1=110 пФ, а С2=220 пФ, тогда Собщ = 110×220/110+220 = 73 пФ.

Не стоит забывать про простоту и удобство монтажа, а также обеспечение качественной работы собранного устройства или оборудования. В последовательных соединениях у емкостей должен быть 1 производитель. А если детали всей цепочки будут одной партии выпуска, то проблем с эксплуатацией созданной цепи не будет.

Параллельное соединение

Накопители электрического заряда постоянной емкости, различают:

• керамические;
• бумажные;
• слюдяные;
• металлобумажные;
• электролитические конденсаторы.

Их делят на 2 группы: низковольтные и высоковольтные. Применяют их в фильтрах выпрямителей, для связи между низкочастотными участками цепей, в блоках питания различных устройств и т.д.

Конденсаторы переменной ёмкости тоже существуют. Они нашли свое предназначение в настраиваемых колебательных контурах теле- и радиоприемников. Емкость регулируется за счет изменения положения пластин относительно друг друга.

Рассмотрим соединение конденсаторов, когда их выводы соединятся попарно. Подобное включение подходит для 2 или более элементов, рассчитанных на одно и то же напряжение. Номинальное напряжение, которое указано на корпусе детали, превышать нельзя. В противном случае произойдет пробой диэлектрика, и элемент выйдет из строя. Но в цепь, где присутствует напряжение меньше номинального, конденсатор включать можно.

Параллельным включением конденсаторов можно добиться увеличения общей ёмкости. В некоторых устройствах необходимо обеспечить большое накопление электрического заряда. Существующих номиналов не хватает, приходится выполнять параллели и использовать то, что есть под рукой. Определить общую величину полученного соединения просто. Для этого нужно просто сложить величины всех используемых элементов.

Для вычисления емкостей конденсаторов формула имеет вид:

Собщ = С1+С2, где С1 и С2 — емкость соответствующих элементов.

Если С1=20 пФ, а С2=30 пФ, то Собщ = 50 пФ. Деталей в в параллели может быть n-ое количество.

На практике такое соединение находит применение в специальных устройствах, используемых в энергетических системах, и на подстанциях. Их монтируют, зная, как соединить конденсаторы для увеличения емкости, в целые блоки из батарей.

Для того чтобы поддерживать равновесие реактивной мощности как в энергоснабжающих установках, так и в установках энергопотребителей, существует необходимость включать в работу компенсирующие устройства реактивной мощности (УКРМ). Для снижения потерь и регулировки напряжения в сетях при расчетах устройства необходимо знать величины реактивных сопротивлений конденсаторов, используемых в установке.

Случается, что возникает необходимость вычислить по формуле напряжение на конденсаторах. В этом случае будем исходить из того, что С=q/U, т.е. отношение заряда к напряжению. И если величина заряда — q, а ёмкость — C, можем получим искомое число, подставляя значения. Она имеет вид:

U=q/C.

Смешанное соединение

При расчете цепи, представляющей собой совокупность рассмотренных выше комбинаций, поступают так. Сначала ищем в сложной цепи конденсаторы, которые соединены между собой либо параллельно, либо последовательно. Заменив их эквивалентным элементом, получим более простую схему. Потом в новой схеме с участками цепи проводим те же манипуляции. Упрощаем до тех пор, пока не останется только параллельное или последовательное соединение. Их рассчитывать мы уже научились в этой статье.

Параллельно-последовательное соединение применимо для увеличения емкости, батареи или для того, чтобы приложенное напряжение не превышало рабочего напряжения конденсатора.

Capacitance — Definition

The ability of a capacitor to store charge is known as its capacitance. In other word, the capacitance can also be defined as the property of a material by virtue of it opposes the any change in voltage applied across it.

Capacitance: Formula

Experimentally, it has been found that, the charge Q stored in a capacitor is directly proportional to the voltage across it, i.e.

$$Qpropto:V$$

$$Q=CV$$

Where, C is a constant and is called as capacitance of the capacitor.

$$Rightarrow:C=frac{Q}{V}$$

Thus, the capacitance (C) of a capacitor can also be defined as the ratio of the charge on the either plate to the voltage across it.

Unit of Capacitance

We have seen that,

$$C=frac{Q}{V}=frac{Coulomb}{Volt}=Farad$$

The SI unit of capacitance is coulomb/volt which is also known as farad and denoted by F.

Equivalent Capacitance

Case 1 – When capacitors are connected in series

By referring the circuit, we can write,

$$V=V_{1}+V_{2}+V_{3}=(frac{Q}{C_{1}}+frac{Q}{C_{2}}+frac{Q}{C_{3}})=Q(frac{1}{C_{1}}+frac{1}{C_{2}}+frac{1}{C_{3}})$$

$$Rightarrow:frac{V}{Q}=(frac{1}{C_{1}}+frac{1}{C_{2}}+frac{1}{C_{3}})$$

$$Rightarrowfrac{1}{C_{r}}=frac{1}{C_{1}}+frac{1}{C_{2}}+frac{1}{C_{3}}$$

From this equation, the total equivalent capacitance of series connected capacitors can be determined.

Case 2 – When capacitors are connected in parallel

By referring the circuit, it can be written,

$$Q=Q_{1}+Q_{2}+Q_{3}=C_{1}V+C_{2}V+C_{3}V=V(C_{1}+C_{2}+C_{3})$$

$$Rightarrow:frac{Q}{V}=(C_{1}+C_{2}+C_{3})$$

$$Rightarrow:C_{r}=C_{1}+C_{2}+C_{3}$$

The above equation gives the total capacitance of parallel connected capacitors.

Capacitance of a Parallel Plate Capacitor

Case 1 – With uniform dielectric medium

Consider a parallel plate capacitor consisting of two plates, each of surface area A. The plates are separated by a distance d. Air is present in between the plates as the dielectric medium.

Therefore, the capacitance of a parallel plate capacitor is,

• Directly proportional to the surface area (A) of each plate.

• Inversely proportional to the distance (d) between the plates.

Thus,

$$Capacitance,Cpropto:frac{A}{d}$$

$$Rightarrow:C=varepsilon_{0}frac{A}{d}$$

Where, ε₀ is the constant of proportionality and is known as absolute permittivity of vacuum or air and its value is equal to 8.854 × 10^{−12 F/m .}

If there is a uniform dielectric material is placed between the plates of the capacitor, then capacitance of the capacitor becomes,

$$C=varepsilon_{0}varepsilon_{r}frac{A}{d}$$

Where, ε_r  is the relative permittivity of the dielectric material.

Case 2 – With composite dielectric medium

Consider the space between the plates of the capacitor is occupied by three dielectric materials of thickness d₁, d₂ and d₃ and the relative permittivity ε_r1, ε_r2 and ε_r3 respectively. Then, the capacitance of individual section is given as,

$$C_{1}=varepsilon_{0}varepsilon_{r1}frac{A}{d_{1}}:;:C_{2}=varepsilon_{0}varepsilon_{r2}frac{A}{d_{2}}:and:C_{3}=varepsilon_{0}varepsilon_{r3}frac{A}{d_{3}}$$

As from the figure, the three capacitances are appearing as they are connected in series, so

$$frac{1}{C}=frac{1}{C_{1}}+frac{1}{C_{2}}+frac{1}{C_{3}}=frac{1}{(varepsilon_{0}varepsilon_{r1}frac{A}{d_{1}})}+frac{1}{(varepsilon_{0}varepsilon_{r2}frac{A}{d_{2}})}+frac{1}{(varepsilon_{0}varepsilon_{r3}frac{A}{d_{3}})}$$

$$Rightarrowfrac{1}{C}=frac{d_{1}}{varepsilon_{0}varepsilon_{r1}A}+frac{d_{2}}{varepsilon_{0}varepsilon_{r2}A}+frac{d_{3}}{varepsilon_{0}varepsilon_{r3}A}=frac{1}{varepsilon_{0}A}(frac{d_{1}}{varepsilon_{r1}}+frac{d_{2}}{varepsilon_{r2}}+frac{d_{3}}{varepsilon_{r3}})$$

$$C=frac{varepsilon_{0}A}{(frac{d_{1}}{varepsilon_{r1}}+frac{d_{2}}{varepsilon_{r2}}+frac{d_{3}}{varepsilon_{r3}})}$$

$$In:general,C=frac{varepsilon_{0}A}{sum(frac{d}{varepsilon_{r}})}$$

Capacitance of Multiplate Capacitor

In order to obtain larger capacitance value, multiplate construction is employed. In this construction, the capacitor is built of alternate metal plates and thin sheets of dielectric. The odd numbered of plates are connected together to form one terminal A and even numbered plates are connected together to form the second terminal B.

Refer the figure of a multiplate (in this case 7 plates) capacitor, which is equivalent to 6 capacitors in parallel. Therefore, the total capacitance will be 6 times the capacitance of a single capacitor. If there are n plates, then (n – 1) capacitors will be in parallel. Therefore,

$$Capacitance:of:n-plate:capacitor=(n-1)frac{varepsilon_{0}varepsilon_{r}A}{d}$$

Where,

• A is the area of each plate,

• d is the distance between any two adjacent plates.

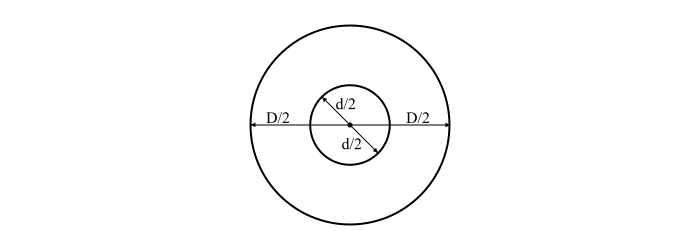
Capacitance of a Cylindrical Capacitor

A cylindrical capacitor (e.g. a cable) consists of two coaxial cylinders separated by a dielectric medium.

By referring the figure, the capacitance per unit length of cylindrical capacitor is given by,

$$C=frac{2pi:varepsilon_{0}varepsilon_{r}}{log_{e}(frac{D}{d})}:F/m$$

If the length of cable (cylindrical capacitor) is l meters, then the capacitance of the cable is

$$C=frac{2pi:varepsilon_{0}varepsilon_{r}l}{log_{e}(frac{D}{d})}:Farad$$

Электрическая емкость конденсатора:

C=q/U (к/в),

где q – заряд на обкладках конденсатора, к;

U – напряжение на обкладках, в.

Кулон на вольт называется фарадой.

1 ф=10⁶ мкф; 1 мкф=10⁶ пф (мкмкф); 1 пф=0,9 см.

Емкость плоского конденсатора:

C=(0,88ɛˏS)/a,

где С – емкость, пф;

S – площадь обкладок конденсатора, см²;

ɛˏ – относительная диэлектрическая проницаемость диэлектрика, находящегося между обкладками конденсатора;

а – расстояние между обкладками, мм.

Емкость плоского конденсатора, состоящего из n параллельно соединенных обкладок:

C=(0,88ɛˏS(n-1))/a.

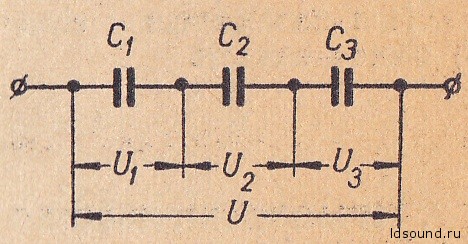
Последовательное соединение конденсаторов (рис. 1).

Общее напряжение равно сумме напряжений на отдельных конденсаторах:

U=U₁+U₂+U₃.

Напряжение на конденсаторах обратно пропорциональны их емкостя:

U₁:U₂:U₃=(1/С₁):(1/С₂):(1/С₃).

Такое распределение напряжений наблюдалось бы только при отсутствии проводимости у конденсаторов. Если же сопротивления между обкладками (сопротивления утечки) конечны по величине, то напряжения постоянного тока на конденсаторах будут пропорциональны их сопротивлениям утечки. Поэтому при последовательном включении конденсаторов их шунтируют внешними сопротивлениями, чтобы напряжения на них определялись величинами этих сопротивлений, а не случайными значениями сопротивлений утечки.

Общая емкость определяется по формуле:

1/С = (1/С₁) + (1/С₂) + (1/С₃)

и будет меньше емкости наименьшего конденсатора данной цепи.

Формулы для расчета последовательного соединения двух конденсаторов в табл. 1:

Последовательное соединение двух конденсаторов

Общую емкость двух последовательно соедененных конденсаторов можно определить и по номограмме (рис. 2), но вместо R₁ и R₂ необходимо брать С₁ и С₂ в одинаковых единицах (мкф, пф и т.д.).

Рис. 2. Номограмма для определения общего сопротивления двух параллельно соединенных сопротивлений.

При последовательном соединении n конденсаторов одинаковой емкости С₁ общая емкость

С= С₁/n.

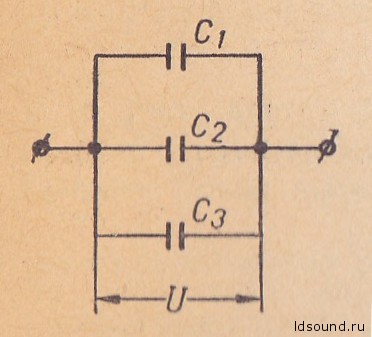
Параллельное соединение конденсаторов (рис. 3).

Напряжения на каждом конденсаторе одинаковы и равны U.

Общая емкость С равна сумме емкостей параллельно соединенных конденсаторов:

С=С₁+С₂+С₃.

При параллельном соединении n конденсаторов одинаковой емкости С₁ общая емкость:

С= С₁n.