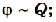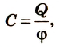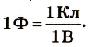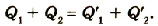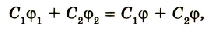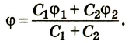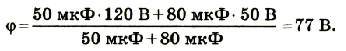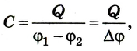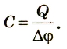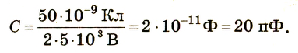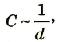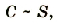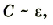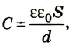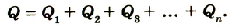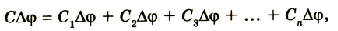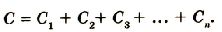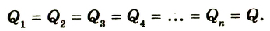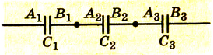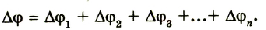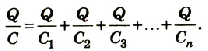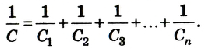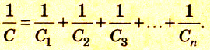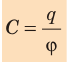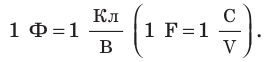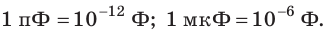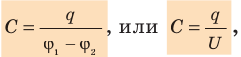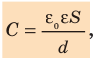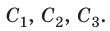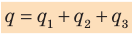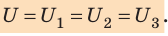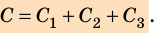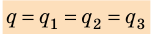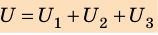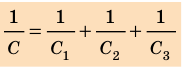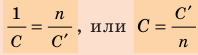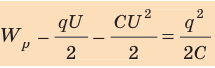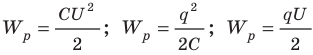|
Один метр кубический является единицей объема. Чтобы найти объем какого-то предмета, имеющего КУБИЧЕСКУЮ форму (например, параллелепипед), нужно его длину (в метрах) умножить на ширину (тоже в метрах) и умножить на высоту (опять в метрах). Логично, не правда ли, что метр, умноженный сам на себя три раза превращается в метр кубический! Если требуется посчитать объем предмета НЕ КУБИЧЕСКОЙ формы (например, шар, призма, конус), то для вычисления их объема есть специальные формулы. Если они вам нужны, то советую посмотреть учебник по геометрии. автор вопроса выбрал этот ответ лучшим Ксарфакс 5 лет назад Думаю, всем понятно, что формула расчёта объёма в кубических метрах для каждой геометрической фигуры будет разной. Поэтому нужно произвести все необходимые измерения, а затем воспользоваться соответствующей формулой. Если фигура имеет неправильную формулу, то разбиваем её на несколько стандартных фигур, а затем складываем их объёмы между собой. Нужно помнить, что все измерения проводятся именно в метрах. Например, если высота объекта 70 см, то её нужно перевести в метры: 70 см = 0,7 м. Самый простейший пример — объём помещения Для того, чтобы посчитать объём, нужно воспользоваться формулой нахождения объёма прямоугольного параллелепипеда. V = abc. a — длина, b — ширина, c — высота. Таким образом, измеряем длину / ширину / высоту комнаты, а затем перемножаем эти значения между собой. Если вы знаете площадь, то посчитать объём ещё проще — достаточно измерить высоту и умножить это значение на данное значение. Например, длина комнаты = 6 м, ширина = 5 м, высота = 2,5 м. V = 6 * 5 * 2,5 = 75 м³. Nelli4ka 5 лет назад Для примера возьмем прямоугольник и параллелепипед. Прямоугольник лежит на плоскости, и мы можем найти либо его периметр (т.е. длину всех сторон данной фигуры), либо его площадь, которая будет выражаться, скажем, в сантиметрах или метрах квадратных. Параллелепипед — фигура трехмерного пространства, у нее есть помимо ширины и длины еще и высота. Когда значения высоты, длины и ширины умножаются друг на друга, находится объем трехмерной фигуры, которая уже будет выражаться не в квадратных, а в кубических сантиметрах, метрах и т.д., но для каждого некубического случая существует своя индивидуальная формула. Galina7v7 7 лет назад Если ваш вопрос трактовать так: «как посчитать объём 1 метра кубического , то V = 1м * 1 м = 1м = 1 м ^3 (1 метр кубический ) , и это единица измерения объёма в системе СИ. Если вас интересует тело в форме параллелепипеда ,где все соседние ребра перпендикулярны друг другу , то объём такого тела определяется путём произведения : длина *ширина * высота. ОБЪЁМ ТЕЛА = ДЛИНА (м) х ШИРИНА (м) х ВЫСОТА (м)Для того,чтобы получить объём в м^3 нужно все 3 параметра тоже выразить в метрах. Zolotynka 5 лет назад В метрах кубических можно высчитать объем предмета, который представляет собой форму куба. Для этого следует воспользоваться формулой: длина*ширина*высота. ** Данная формула имеет важное практическое значение. Рассмотрим на примере: Предположим, нам нужно рассчитать, расход бетона для того, чтобы сделать пол в сарае, размер которого: ширина 2.0 м, длина 2.0 м, а желаемая толщина бетона — 100 мм. Формула для расчета объема бетона в м3 будет выглядеть следующими образом: 2,0 × 2,0 × 0,1 = 0.4m3 Математика обязательный предмет в школьной программе, но знания уходят, забываются формулы, как проводить вычисления уже не каждый вспомнит, остается в голове то, что используется нами ежедневно, и на работе требуется все время, поэтому формула расчета кубического метра может придти в голову не сразу, и придется искать эту информацию, для тех, кому нужно — длину умножить на ширину и умножить на высоту. Kerbal Space Program 6 лет назад Крайне просто. Для этого достаточно брать длины и расстояния в метрах: будь то длина, высота и ширина или же радиус, при вычислении объема круга или цилиндра. Например, имеем: Параллелепипед длиной 1245 см, шириной 3 см и высотой 25 см. Эти длины переведем в метры и получим:
Считаем теперь объем: V=1,245*0,03*0,25=0,00933 метра кубических. moreljuba 5 лет назад Посчитать объём в метрах кубических вы вполне спокойно можете. Для это вам необходимо иметь представление о значениях для таких величин как высота, ширина (толщина) и длина. Переводите в метры и перемножаете эти три составляющие и получаете в результате объём в метрах кубических. FantomeRU 5 лет назад Чтобы вычислить объем необходимо умножить длину на ширину и на высоту. При этом, чтобы искомый результат был в кубических метрах, сначала нужно все стороны данного предмета выразить в метрах и только потом перемножать. vksvovko 6 лет назад Один из распространенных способов найти объем предмета неправильной формы — это налить воду в измерительный сосут и опустить туда предмет. далее смотрим сколько он вытеснил воды и легко подсчитываем объем в м3. EvgeniyAlekseevich 7 лет назад Высоту, выраженную в м3, умножить на длину и умножить на ширину. Знаете ответ? |
From Wikipedia, the free encyclopedia
Body capacitance is the physical property of the human body that it acts as a capacitor. Like any other electrically conductive object, a human body can store electric charge if insulated. The actual amount of capacitance varies with the surroundings; it would be low when standing on top of a pole with nothing nearby, but high when leaning against an insulated, but grounded large metal surface, such as a household refrigerator, or a metal wall in a factory.
Properties[edit]
Synthetic fabrics and friction can charge a human body to about 3 kV. Low potentials may not have any notable effect, but some electronic devices can be damaged by modest voltages of 100 volts. Electronics factories are very careful to prevent people from becoming charged up. A whole branch of the electronics industry deals with preventing static charge build-up and protecting products against electrostatic discharge.
Notably, a combination of footwear with some sole materials, low humidity, and a dry carpet (synthetic fiber in particular) can cause footsteps to charge a person’s body capacitance to as much as a few tens of kilovolts with respect to the earth. The human and surroundings then constitute a highly charged capacitor. A close approach to any conductive object connected to earth (ground) can create a shock, even a visible spark.
Body capacitance was a significant nuisance when tuning the earliest radios; touching a tuning knob would couple the body capacitance into the tuning circuit, slightly changing its resonant frequency. However, body capacitance is very useful in the Theremin, a musical instrument in which it causes slight frequency shifts of the instrument’s internal oscillators. One of them changes pitch, and the other causes loudness (volume) to change smoothly between silence and full amount.
Capacitance of a human body in normal surroundings is typically in the tens to low hundreds of picofarads, which is small by typical electronic standards. While humans are much larger than typical electronic components, they are also mostly separated by significant distance from other conductive objects. Although the occasional static shock can be startling and even unpleasant, the amount of stored energy is relatively low, and won’t harm a healthy person.
The Human Body Model for capacitance, as defined by the Electrostatic Discharge Association (ESDA) is a 100pF capacitor in series with a 1.5kΩ resistor.[1]
Touch sensors[edit]
The body capacitance can be used to operate pushbutton switches such as for elevators or faucets. Certain voltage tester probes rely on body capacitance.
A capacitive touch sensor responds to close approach (but not force of touch) of a part of a human body, usually a fingertip. The capacitance between the device itself and the fingertip is sensed. Capacitive touch screens don’t require applying any force to their surfaces, which makes them easier to use and design in some respects. Furthermore, because of body capacitance, people act as good antennas, and some small televisions use people to enhance reception.[citation needed]
See also[edit]
- Triboelectric series
- Triboelectric effect
- Touch-sensitive lamp
References[edit]
- ^ ESD Association (2010). Fundamentals of Electrostatic Discharge. Part Five—Device Sensitivity and Testing (PDF). Rome, NY. Retrieved 13 April 2023.
External links[edit]
- Downloadable electrostatic BEM modules in MATLAB for self-capacitance of a human body and relevant human body meshes
Электрическая емкость
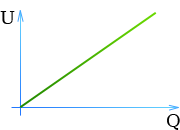
Если сообщать телу электрический заряд, то его потенциал относительно какой-либо точки (например, Земли) будет возрастать пропорционально заряду: U ~ Q.
Коэффициент пропорциональности между зарядом и потенциалом называется электрической емкостью тела.
Емкость характеризует способность тела накапливать заряды.
Электрическая емкость C есть отношение сообщенного заряда Q
к возникающему в результате этого потенциалу U.
Единица СИ электрической емкости:
[ [C] = frac{Кл}{В} = фарад enspace (Ф) ]
Если
| С | электрическая емкость тела, | фарад |
|---|---|---|
| Q | подведенный заряд, | Кулон |
| U | потенциал, | Вольт |
то
[ C = frac{Q}{U} ]
Соотношение между единицами электрической емкости
1 Ф = 106 микрофарад (мкФ) = 1012 пикофарад (пФ)
Вычислить найти электрическую емкость по формуле (2)
| Q (Кулон) | U (Вольт) |
Вычислить
нажмите кнопку для расчета
Электрическая емкость, подтемы
- Конденсатор
- Плоский конденсатор
- Емкость плоского конденсатора
- Сферический конденсатор
- Емкость сферического конденсатора
- Емкость шара
- Плоский конденсатор
- Соединение конденсаторов
- Параллельное соединение конденсаторов, Емкость параллельно соединенных конденсаторов
- Последовательное соединение конденсаторов, Емкость последовательно соединенных конденсаторов
Электрическая емкость |
стр. 630 |
|---|
Содержание книги
Предыдующая страница
§16. Превращение энергии в электрических и магнитных явлениях
В многочисленных электротехнических устройствах происходят постоянные переходы энергии из одной формы в другую. В данном параграфе мы рассмотрим некоторые примеры таких превращений и покажем, что во многих случаях эти переходы связаны с преобразованиями электрических и магнитных полей. Начнем обсуждение этих проблем с устройств, способных накапливать электрический заряд, сохранять его и создаваемое ими электрическое поле в течение длительного промежутка времени.
16.1 Электроемкость.
16.1.1 Электроемкость уединенного проводника.
Любое тело способно накапливать электрический заряд. На первый взгляд, кажется, что любому телу можно сообщить сколь угодно большой заряд. Однако существует ряд причин, которые ограничивают величину максимального заряда. С ростом электрического заряда возрастает напряженность поля, создаваемого телом. Если тело находится в воздухе или другой среде, то может начаться электрический разряд, посредством которого заряд начнет стекать с тела. Даже если рассматриваемое тело находится в вакууме, то электростатическое взаимодействие заряженных частиц внутри вещества приведет к испусканию, эмиссии частиц (чаще всего электронов), что тоже приведет к уменьшению заряда тела. Поэтому необходимо ввести некоторую характеристику тела, описывающую его возможность накапливать электрический заряд. Такой характеристикой является электроемкость тела C : отношение заряда тела к его потенциалу
(~C = frac{Q}{varphi}) . (1)
В этом определении необходимо оговорить, относительно какой точки определяется потенциал. Как правило, для уединенного тела его потенциал отсчитывается относительно бесконечности. Можно дать и несколько иное определение, свободное от указанной неопределенности значения потенциала: электроемкость тела равна заряду, который необходимо сообщить телу, чтобы увеличить его потенциал на единицу
(~C = frac{Delta Q}{Delta varphi}) . (2)
Вспомним другую «емкость»: теплоемкость тела равна количеству теплоты, которое необходимо сообщить телу, чтобы увеличить его температуру на один градус (~C = frac{Delta Q}{Delta t^circ}). Как видите, определение электроемкости полностью аналогично.
Можно дать аналогичное определение емкости сосуда: объем жидкости, который необходимо влить в сосуд, чтобы увеличит высоту его уровня на единицу, то придется признать, что емкость цилиндрического сосуда равна площади его дна (~C = frac{Delta V}{Delta h}). В этом примере аналогом электрического заряда является объем жидкости, налитой в сосуд, аналогом изменения потенциала – изменение уровня жидкости.
Электроемкость является размерной физической величиной. В системе единиц СИ единицей электроемкости является фарад[1] (сокращенно Ф). Емкостью в 1 фарад обладает тело, потенциал которого возрастает на 1 вольт при увеличении его заряда на 1 кулон. Один фарад очень большая емкость, поэтому чаще используются дольные единицы: микрофарад (мкФ, 1 мкФ = 10-6 Ф), нанофарад (нФ, 1 нФ = 10-9 Ф), пикофарад (пФ, 1 пФ = 10-12 Ф).
Для расчета электроемкости следует задать электрический заряд тела и рассчитать его потенциал, после чего вычислить их отношение. Так потенциал тела всегда пропорционален его заряду, то емкость тела не зависит от его заряда, а полностью определяется его размерами, формой и диэлектрическими свойствами среды, в которой находится тело.
Для примера найдем электрическую емкость уединенного шара радиуса R, находящегося в вакууме. Если заряд шара равен Q, то его потенциал (относительно бесконечности) равен
(~varphi = frac{Q}{4 pi varepsilon_0 R}) .
Следовательно, электрическая емкость шара равна
(~C = frac{Q}{varphi} = 4 pi varepsilon_0 R) . (3)
Так электрическая емкость земного шара (R ≈ 6350 км) равна С ≈ 7·10-4 Ф — действительно 1 фарад очень большая емкость.
Если поместить шар в бесконечную среду из однородного диэлектрика с проницаемостью ε, то напряженность поля уменьшится в ε раз, потенциал шара также уменьшится, поэтому его емкость возрастет в ε раз:
(~C = 4 pi varepsilon_0 varepsilon R) . (4)
16.1.2 Конденсаторы.
Мы показали, что уединенные тела малопригодны как накопители электрического заряда. Еще в середине XVIII века было изобретено устройство, способное накапливать и длительное время сохранять большие электрические заряды – конденсатор.
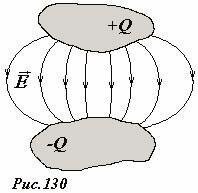
Конденсатор представляет собой два проводника (которые называются обкладками), разделенными диэлектриком (Рис. 130). Как правило, на обкладки подают разноименные электрические заряды, равные по величине. В этом случае электрическое поле практически полностью локализуется в пространстве между обкладками. Емкостью конденсатора называется отношение заряда одной из обкладок к разности потенциалов между обкладками
(~C = frac{Delta Q}{Delta varphi}) . (5)
В этом определении фигурирует разность потенциалов, которая не зависит от выбора нулевого уровня потенциала, поэтому нет необходимости в дополнительных оговорках. Часто зарядом конденсатора называют заряд одной из его обкладок (ясно, что полный заряд конденсатора на двух обкладках равен нулю), вместо разности потенциалов между обкладками чаще говорят о напряжении конденсатора U, которое, конечно, равно разности потенциалов U = Δϕ, так в пространстве между обкладками не действуют сторонние силы.
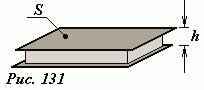
Простейший конденсатор состоит из двух проводящих параллельных пластин, разделенных слоем диэлектрика, причем расстояние между пластинами значительно меньше их размеров – такой конденсатор называется плоским (Рис. 131). Найдем емкость такого конденсатора. Будем считать, что на обкладки конденсатора (проводящие пластины) поданы разноименные электрические заряды, модули которых равны Q. Если площадь каждой пластины равна S , то поверхностная плотность заряда на них равна (~sigma = frac{Q}{S}). Эти заряды создают в пространстве между пластинами электрическое поле напряженности (~E = frac{sigma}{varepsilon varepsilon_0} = frac{Q}{varepsilon varepsilon_0 S}), где ε — диэлектрическая проницаемость вещества между пластинами. Разность потенциалов между обкладками конденсатора равна (~Delta varphi = Eh = frac{Qh}{varepsilon varepsilon_0 S}). По определению емкость плоского конденсатора рассчитывается по формуле
(~C = frac{Q}{Delta varphi} = frac{varepsilon varepsilon_0 S}{h}) . (6)
Таким образом, емкость конденсатора пропорциональна проницаемости диэлектрика, площади пластин и обратно пропорциональна расстоянию между ними. Если расстояние между пластинами сделать малым, а площади пластин большими, то такой конденсатор может иметь большую емкость (даже превосходящую емкость земного шара).
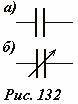
Конденсаторы широко используются не только для накопления электрического заряда, но и в цепях переменного электрического тока (эти вопросы мы рассмотрим позднее). На электрических схемах конденсаторы изображаются в виде двух параллельных отрезков (Рис. 132).
Промышленностью выпускаются конденсаторы различных типов, которые различаются своей конструкцией. Емкости промышленно выпускаемых конденсаторов изменяются в широких пределах от нескольких пикофарад, до единиц фарад. Часто пластины таких конденсаторов изготавливают из тонкой металлической фольги, которую скручивают в рулоны и помещают в корпус. В качестве диэлектрика используется воздух (в этом случае с высокой точностью можно считать ε = 1), слюда, сухая бумага, и другие материалы.
Большой электрической емкостью обладают электролитические конденсаторы. Одной обкладкой такого конденсатора служит тонкая полоска фольги большой площади, покрытая слоем окисла (который играет роль диэлектрика), второй обкладкой является раствор электролита. Так как толщина оксидного слоя может быть малой (порядка нескольких микрон), то емкость такого конденсатора весьма велика. При использовании таких конденсаторов следует внимательно следить за полярностью их включения в электрическую цепь, так как при ошибочном подключении оксидный слой быстро разрушается, что приводит к выходу конденсатора из строя.
Широко используются также конденсаторы переменной емкости, в котором наборы пластин могут двигаться друг относительно друга, при этом изменяется площадь их перекрытия, вследствие чего изменяется и емкость конденсатора. На схемах переменные конденсаторы отмечаются стрелкой (Рис. 132б).
16.1.3 Соединение конденсаторов.
Установим правила для расчета электроемкости системы конденсаторов, подобно правилам расчета сопротивлений соединенных резисторов.
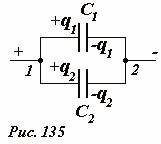
При параллельном соединении конденсаторов (Рис. 135) емкости которых равны C1 и C2 напряжения на обоих конденсаторах одинаковы и равны разности потенциалов между точками соединения U1 = U2 = Δϕ, что является следствием потенциальности электростатического поля. Суммарный заряд конденсатора равен сумме зарядов конденсаторов q = q1 + q2.
По определению емкость такого составного конденсатора равна отношению его суммарного заряда к напряжению, следовательно,
(~C = frac{q_1 + q_2}{U} = frac{q_1}{U} + frac{q_2}{U} = C_1 + C_2) . (1)
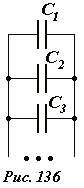
Это правило легко обобщается: общая емкость системы параллельно соединенных конденсаторов (Рис. 136) равна сумме емкостей всех конденсаторов
(~C_o = C_1 + C_2 + C_3 + ldots = sum_k C_k) . (2)
В частном случае плоских конденсаторов с одинаковыми расстояниями между пластинами установленное правило утверждает, что суммарная площадь пластин равна сумме площадей отдельных обкладок
(~S_o = S_1 + S_2 + S_3 + ldots) .
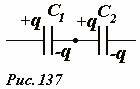
При последовательном соединении конденсаторов (Рис. 137) суммарное напряжение на батарее конденсаторов равно сумме напряжений на отдельных конденсаторах
(~U_o = U_1 + U_2) . (3)
Электрические заряды на всех конденсаторах одинаковы
(~q_o = q_1 = q_2) .
Для доказательства этого утверждения достаточно рассмотреть две соединенных внутренних обкладки, которые изолированы от внешних источников – их суммарный заряд остается равным нулю. Поэтому если на обкладке первого конденсатора индуцируется заряд − q, то на соединенной с ней обкладке второго конденсатора возникнет такой же по модулю заряд противоположного знака.
Выразим напряжения на конденсаторах через их заряды и емкости (~U = frac{q}{C}) и подставим их в уравнение (3)
(~frac{q_o}{C_o} = frac{q_1}{C_1} + frac{q_2}{C_2}) ,
принимая во внимание равенство всех зарядов, получим правило расчета емкости последовательно соединенных конденсаторов (Рис. 138):
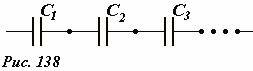
величина обратная емкости батареи последовательно соединенных конденсаторов равна сумме величин, обратных емкости каждого конденсатора,
(~frac{1}{C_o} = frac{1}{C_1} + frac{1}{C_2} + frac{1}{C_3} + ldots = sum_k frac{1}{C_k}) . (4)
Для плоских конденсаторов с одинаковыми площадями пластин это правило утверждает, что суммарное расстояние между пластинами равно сумме этих расстояний всех конденсаторов.
Интересно отметить, что правила расчетов емкости батареи конденсаторов противоположны правилам расчета сопротивлений соединений резисторов: при последовательном соединении складываются сопротивления; при параллельном – складываются величины обратные сопротивлениям (проводимости), а для конденсаторов наоборот: при параллельном соединении складываются емкости, а при последовательном – складываются обратные величины.
Примечания
- ↑ Названа в честь выдающегося английского физика Майкла Фарадея.
Следующая страница
Содержание:
Электроемкость:
Сообщая телу определенный заряд, мы изменяем его потенциал. Это изменение непосредственно связано со значением заряда, сообщаемого телу.
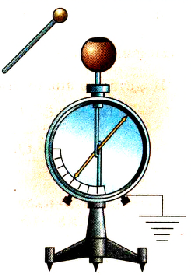
Для исследования зависимости потенциала тела от его заряда проведем опыт с электрометром, корпус которого соединен с поверхностью Земли. ‘Гикая система может измерять потенциал тела относительно Земли. Укрепим на стержне этого электрометра пустотелый металлический шар и будем сообщать ему заряд с помощью маленького металлического шарика на изоляционной ручке. Если коснуться заряженным шариком внутренней поверхности металлического шара, то весь его заряд перейдет на шар, а стрелка электрометра покажет увеличение потенциала шара. Последовательно повторяя опыт с переносом заряда на большой шар, заметим, что каждый раз его потенциал увеличивается (рис. 1.28).
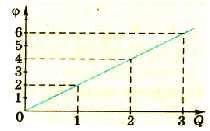
Применяя более точные способы измерения заряда и потенциала, можно установить, что потенциал возрастает пропорционально возрастанию заряда. Потенциал пропорционален заряду шара. Результаты одного из таких опытов отражены на графике (рис 1.29).
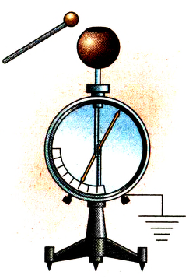
Если ни стержне электрометра укрепим шар большего (меньшего) диаметра и продолжим опыты (рис. 1.31), то увидим, что скорость зарядки изменилась, соответственно уменьшилась (увеличилась).
Процесс электризации шара большего диаметра отображен графиком на рисунке 1.32.
Сопоставив графики, которые иллюстрируют процессы зарядки шаров различных диаметров (рис. 1.30 и 1.32), увидим, что графики имеют различный наклон относительно горизонтальной оси. Это свидетельствует о том, что при одинаковых значениях заряда шары разных диаметров будут иметь разные потенциалы. Оказывается, что на князь между зарядом и потенциалом шара существенно влияют геометрические размеры шаров.
Рис. 130. Электризация шара большего диаметра
Потенциал металлического шара пропорционален его заряду; коэффициент пропорциональности для различных шаров разный.
Анализируя результаты опытов и соответствующие графики, можно сделать выводы:
- потенциал каждого шара пропорционален его заряду:
- для тел различных размеров коэффициент пропорциональности разный.
Установлено, что этот коэффициент для каждого тела имеет вполне определенное значение, что отражает способность тела накапливать электрический заряд. Физическая величина, равная отношению электрического заряда, сообщенного телу, к его потенциалу, называется электроемкостью тела.
где C — электроемкость проводника; Q — заряд; φ — потенциал.
Для измерения электроемкости в физике применяют единицу, которую называют фарад (Ф).
Тело имеет электроемкость в 1 фарад, если при изменении его заряда на 1 кулон потенциал изменяется па 1 вольт:
Электроемкость 1 фарад имеют тела, у которых при изменении заряда на 1 кулон потенциал изменяется на 1 вольт.
- 1Ф — довольно большое значение электроемкости. Например, электроемкость Земли, имеющей радиус 6400 км, составляет всего 7 ∙ 104 Ф. Поэтому на практике используют единицу электроемкости, кратную фараду:
- 1 микрофарад = 1 мкФ = 10-5 Ф.
- 1 пикофарад = 1 пФ = 10-12 Ф.
Пример:
Два шара, электроемкости которых 50 мкф и 80 мкФ, а потенциалы 120 В и 50 В соответственно, соединяют проводом. Найти потенциал шаров после соединения.
|
Дано: |
Решение |
| φ-? |
После соединения шаров произойдет перераспределение зарядов между ними так, что их потенциалы станут одинаковыми. Согласно закону сохранения электрических зарядов
Отсюда
или
Подставив значения физических величин и произведя расчеты, получим:
Ответ: после соединения шары будут иметь потенциал 77 В.
Конденсатор
Чтобы экспериментально определить электроемкость проводника, как и его потенциал, нужно создать условия, исключающие влияние всех окружающих тел, которые, влияя па тело, изменяют его потенциал и электроемкость.
Это утверждение можно проверить опытом.
Укрепим на стержне электрометра металлический шар и сообщим ему определенный заряд. Стрелка прибора отклонится от положения равновесия и покажет определенное значение потенциала относительно земли.
Поднесем к шару металлическую пластину, соединенную проводником с землей (рис. 1.32).
Pиc. 132. Заземленная металлическая пластина влияет на электроемкость шара
Показания стрелки электрометра уменьшатся. Поскольку заряд шара в опыте не изменялся, то уменьшение потенциала свидетельствует об увеличении электроемкости шара. Изменение потенциала и соответственно электроемкости шара будет наблюдаться и в случае изменения расстояния между шаром и пластиной.
Таким образом, определяя электроемкость тела, необходимо учитывать также наличие окружающих тел. Поскольку на практике это сделать трудно, то применяют систему из двух или более проводников произвольной формы, разделенных диэлектриком. В этом случае электрические свойства такой системы проводников и диэлектрика не зависят от окружающих тел. Такую систему называют конденсатором. Простейшим для изучения и расчетов является конденсатор из двух металлических пластин, разделенных диэлектриком.
Электроемкость конденсатора, в отличие от обособленного тела, определяется по разности потенциалов между пластинами:
где Q — заряд одной пластины; (φl— φ2) и ∆φ — разность потенциалов между пластинами.
Слово конденсатор обозначает накопитель. В электричестве понимают как «накопитель электрических зарядов».
Пример:
Какую электроемкость имеет конденсатор, если на его обкладках накапливается заряд 50 нКл при разности потенциалов 2,5 кВ?
|
Дано: |
Решение |
| С-? |
Подставим значения физических величин:
Ответ: электроемкость данного конденсатора 20 пФ.
Первый конденсатор был создан в 1745 г. голландским ученым Питером ван Мушенбруком, профессором Лейденского университета. Проводя опыты по электризации различных тел, он опустил проводник от кондуктора электрической машины в стеклянный графин с водой (рис. 1.33).
 |
Питер ван Мушенбрук (1692-1781) — голландский физик; работы посвящены электричеству, теплоте, оптике; изобрел первый конденсатор — лейденскую банку и провел опыты с ней. |
Pиc. 133. Из истории открытия простейшего конденсатора лейденской банки
Случайно коснувшись пальцем этого проводника, ученый ощутил сильный электрический удар. В дальнейшем жидкость заменили металлическими проводниками, укрепленными на внутренней и внешней поверхностях банки. Такой конденсатор назвали лейденской банкой. В таком первозданном виде она использовалась в лабораториях более 200 лет.
Более совершенные конденсаторы применяются в современной электротехнике и радиоэлектронике. Их можно найти в преобразователях напряжения (адаптерах), питающих постоянным электрическим током электронные приборы, в радиоприемниках и радиопередатчиках как поставные части колебательных контуров. Они применяются практически во всех функциональных узлах электронной аппаратуры. В фотовспышках конденсаторы накапливают большие заряды, необходимые для действия вспышки.
В электротехнике конденсаторы обеспечивают необходимый режим работы электродвигателей, автоматических и релейных приборов, линий электропередач и т. п.
Во многих широкодиапазонных радиоприемниках конденсаторы переменной емкости (рис. 1.34) позволяют плавно изменять собственную частоту колебательного контура н процессе поиска передачи определенной радиостанции.
Рис. 134. Конденсатор переменной емкости с воздушным диэлектриком
Весьма распространены конденсаторы варикапы, электроемкость которых можно изменять электрическим способом. Конструктивно они весьма схожи с полупроводниковыми диодами.
Конденсаторы могут быть плоскими, трубчатыми, дисковыми. В качестве диэлектрика в них используют парафинированную бумагу, слюду, воздух, пластмассы, керамику (рис. 1.35).
Рис. 1.35. Различные типы конденсаторов
Искусственно созданные диэлектрические материалы позволяют создавать конденсаторы больших емкостей при небольших размерах.
Электроемкость плоского конденсатора
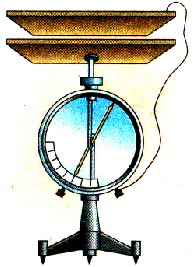
Плоским конденсатором обычно называют систему плоских проводящих пластин — обкладок, разделенных диэлектриком. Благодаря простоте конструкции такого конденсатора легко рассчитывать его емкость и получать значения, подтверждаемые опытами. Для этого достаточно знать его геометрические параметры и электрические свойства диэлектрика между его пластинами. Зависимость электроемкости плоского конденсатора от указанных параметров можно исследовать в школьной лаборатории.
Создадим плоский конденсатор из двух плоских пластин. Для этого одну пластину укрепим на стержне электрометра, я другую — па изоляционной подставке, присоединив ее проводником к корпусу электрометра (рис. 1.36.). В такой системе электрометр будет измерять разность потенциалов между пластинами, образующими плоский конденсатор.
Pиc. 136. Плоский конденсатор, присоединенный к электрометру
Проводя исследования, нужно помнить, что при постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
При постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
Сообщим пластинам некоторый заряд и отметим показания стрелки прибора. Когда начнем сближать пластины, уменьшая расстояние между ними, показания стрелки начнут уменьшаться. Это будет свидетельством того, что при уменьшении расстояния между пластинами электроемкость конденсатора будет увеличиваться. При увеличении расстояния между пластинами показания стрелки будут увеличиваться, что свидетельствует об уменьшении электроемкости.
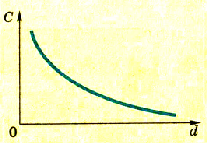
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
где d — расстояние между обкладками.
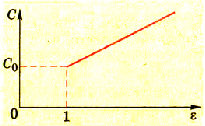
Эту, зависимость можно изобразить на графике как обратно пропорциональную зависимость (рис. 1.37).
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
Pиc. 137. График зависимости электроемкости и плоского конденсатора от расстояния между пластинами
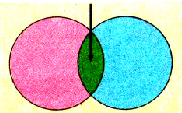
Будем смещать одну пластину относительно другой в параллельных плоскостях, не изменяя расстояния между ними. При атом площадь перекрытия между пластинами будет изменяться (рис. 1.38). Изменение разности потенциалов, отмеченное электрометром, засвидетельствует изменение электроемкости.
Pиc. 138. При расчетах электроемкости плоского конденсатора учитывают площадь перекрытия пластин
Увеличение площади перекрытия приведет к увеличению электроемкости, при уменьшении — наоборот.
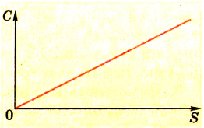
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
где S — площадь пластин, которые перекрываются.
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
Эту зависимость можно изобразить графиком прямой пропорциональной зависимости (рис. 1.39).
Pиc. 139. График зависимости электроемкости плоского конденсатора от площади его пластин
Возвратив пластины в первоначальное положение, внесем в пространство между обкладками пластину из диэлектрика. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увеличении электроемкости. Если внести пластину из другого диэлектрика (другая диэлектрическая проницаемость), то изменение электроемкости будет другим.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика между обкладками.
где ε — диэлектрическая проницаемость диэлектрика.
Эта зависимость изображена графиком на рисунке 1.40.
Рис. 1.40. График зависимости электроемкости плоского конденсатора от диэлектрической проницаемости диэлектрика
Результаты описанных выше исследований можно обобщить формулой электроемкости плоского конденсатора
где ε — относительная диэлектрическая проницаемость диэлектрика; ε0— электрическая постоянная; d — расстояние между пластинами; S — площадь пластины.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика.
Соединение конденсаторов в батареи
Для получения необходимых значений электроемкости конденсаторы соединяют в батареи. На практике встречается параллельное, последовательное и смешанное соединение конденсаторов.
При параллельном соединении конденсаторов все обкладки соединяются в две группы, в каждую из которых входит по одной обкладке каждого конденсатора. На рисунке 1.41 приведена схема такого соединения. При таком соединении каждая группа обкладок имеет одинаковый потенциал.
Pиc 1.41. Схема параллельного соединения конденсаторов
Если батарею параллельно соединенных конденсаторов зарядить, то между обкладками каждого конденсатора будет одинаковая разность потенциалов. Общий заряд батареи будет равен сумме зарядов каждого из конденсаторов, входящих в батарею:
Если учесть, что 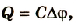
или
Электроемкость батареи параллельно соединенных конденсаторов равна сумме электроемкостей всех конденсаторов.
При последовательном соединении конденсаторов соединяются между собой только две пластины разных конденсаторов. Если в каждом конденсаторе пластины обозначить буквами А и В, то при последовательном соединении пластина B1 будет соединена с пластиной A2, пластина B2 -с пластиной А3 и т. д. (рис. 1.43).
Если цепочку последовательно соединенных конденсаторов присоединить к источнику тока, то об-
кладка A1 и обкладка B1 будут иметь одинаковые по значению заряды +Q и -Q. Благодаря этому все обкладки внутри цепочки будут иметь такие же, но попарно противоположные по знаку заряды:
Pиc. 1.42. Последовательное соединение конденсаторов
Вместе с тем общая разность потенциалов на концах цепочки будет равна сумме разностей потенциалов на каждом конденсаторе:
Учитывая, что 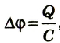
Разделим левую и правую части равенства на Q:
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно с
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.
При последовательном соединении конденсаторов разной электроемкости C1, C2, C3, … Сn общая электроемкость С будет меньше электроемкости самого меньшего конденсатора.
Если C1 < C7 < C9 < … < Cn, то C < C1.
Электроемкость
То, что деньги хранят в банках, знает даже первоклассник. А вот где хранят заряды? И зачем вообще хранить заряды?
Что такое электроемкость
Электроемкость характеризует способность проводника или системы проводников накапливать электрический заряд. Различают электроемкость уединенного проводника и электроемкость системы проводников (например, конденсатора). Уединенным называют проводник, расположенный вдали от других тел так, что они не оказывают на этот проводник никакого влияния.
Электроемкость уединенного проводника (C) — физическая величина, характеризующая способность проводника накапливать заряд и равная отношению электрического заряда q проводника к его потенциалу М:
Единица электроемкости в Си — фарад: [C] = 1 Ф (названа в честь М. Фарадея).
1 Ф — это электроемкость такого проводника, потенциал которого равен 1 В при сообщении ему заряда 1 Кл;
1 Ф — очень большая единица емкости, поэтому используют дольные единицы:
Что такое конденсатор
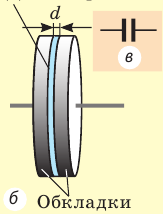
Конденсатор — устройство, представляющее собой систему из двух проводящих обкладок, разделенных тонким слоем диэлектрика (рис. 44.1).
Рис. 44.1. Школьный воздушный конденсатор: а — вид; б — устройство; в — обозначение на схемах
Обкладкам конденсатора передают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов: разноименные заряды притягиваются, а значит, располагаются на внутренних поверхностях обкладок.
Обычно для зарядки конденсатора обе его обкладки соединяют с полюсами батареи аккумуляторов: на обкладках появляются равные по модулю, но противоположные по знаку заряды. Результат не изменится, если соединить с полюсом батареи только одну обкладку, заземлив вторую: вследствие электростатической индукции на заземленной обкладке тоже появится заряд, равный по модулю заряду на другой обкладке, но имеющий противоположный знак.
Зарядом конденсатора называют модуль заряда одной из обкладок. Отношение заряда q данного конденсатора к разности потенциалов (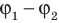
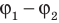
где U — напряжение между обкладками: 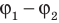
Как показывают исследования, емкость конденсатора увеличится, если увеличить площадь поверхности обкладок или приблизить обкладки друг к другу. На емкость конденсатора влияет также диэлектрик: чем больше его диэлектрическая проницаемость, тем большую емкость имеет конденсатор.
Конденсатор, состоящий из двух параллельных металлических пластин (обкладок), разделенных слоем диэлектрика, называют плоским (см. рис. 44.1). Электроемкость плоского конденсатора вычисляют по формуле:
где 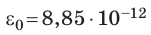
Поле между пластинами плоского конденсатора однородно, поэтому напряженность Е поля связана с напряжением U на конденсаторе формулой U=Ed.
Как рассчитывают электроемкость батареи конденсаторов
Конденсаторы характеризуются емкостью и максимальным рабочим напряжением Umax. Если напряжение, поданное на конденсатор, значительно превысит Umax, произойдет пробой — между обкладками возникнет искра, которая разрушит изоляцию.
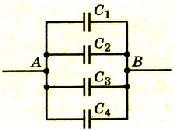
Чтобы получить необходимую электроемкость при определенном рабочем напряжении, конденсаторы соединяют в батареи, применяя параллельное, последовательное и смешанное соединения. Рассмотрим батарею из трех конденсаторов электроемкостями
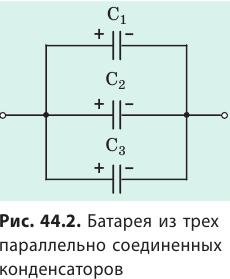
При параллельном соединении конденсаторов положительно заряженные обкладки всех конденсаторов соединяют в один узел, а отрицательно заряженные — в другой узел (рис. 44.2). В таком случае общий заряд q батареи конденсаторов равен алгебраической сумме зарядов отдельных конденсаторов:
Соединенные в один узел обкладки представляют собой один проводник, поэтому потенциалы обкладок, а следовательно, и разность потенциалов (напряжение) между обкладками всех конденсаторов одинаковы:
Таким образом, при параллельном соединении конденсаторов допустимое рабочее напряжение батареи определяется рабочим напряжением одного конденсатора.
Поскольку 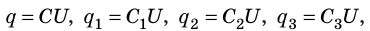
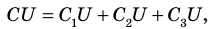
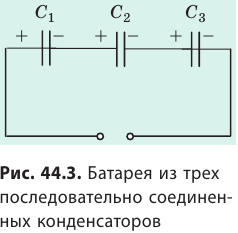
При последовательном соединении конденсаторы соединяют друг с другом разноименно заряженными обкладками (рис. 44.3). В этом случае заряды всех конденсаторов будут одинаковы и равны заряду батареи:
Напряжение на батарее последовательно соединенных конденсаторов равно сумме напряжений на отдельных конденсаторах:
Таким образом, допустимое рабочее напряжение батареи последовательно соединенных конденсаторов больше допустимого рабочего напряжения отдельного конденсатора. Электроемкость батареи последовательно соединенных конденсаторов вычисляют по формуле:
При последовательном соединении конденсаторов емкость батареи меньше, чем емкость конденсатора с минимальной емкостью.
Приведенные соотношения можно обобщить для любого количества конденсаторов.
Обратите внимание!
- Если батарея содержит n параллельно соединенных конденсаторов электроемкостью C′ каждый, то: C=nC′
- Если батарея содержит n последовательно соединенных конденсаторов электроемкостью C′ каждый, то:
Энергия заряженного конденсатора
Заряженный конденсатор, как и любая другая система заряженных тел, обладает энергией.
Убедимся в этом с помощью простого эксперимента. Присоединим к обкладкам заряженного конденсатора лампочку. Замкнем ключ — лампочка загорится. Теперь измерим напряжение на обкладках конденсатора — оно равно нулю, то есть конденсатор разрядился, а это означает, что заряженный конденсатор обладал энергией, которая частично превратилась в энергию света.
Вычислим энергию заряженного до напряжения 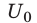
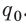
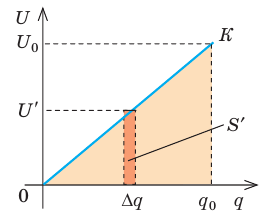
При разрядке конденсатора напряжение U на его обкладках изменяется прямо пропорционально заряду q конденсатора: 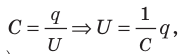
Рис. 44.4. К определению работы, которую совершает электрическое поле заряженного конденсатора при его разрядке
Мысленно разделим весь заряд конденсатора на маленькие «порции» Dq и будем считать, что при потере каждой такой «порции» напряжение на конденсаторе не изменяется. Таким образом получим ряд полос. Площадь S′ каждой полосы равна произведению двух ее сторон: 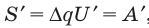
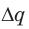
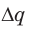
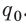
Следовательно,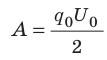
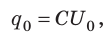
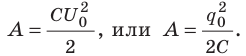
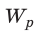
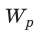
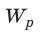
Для чего нужны конденсаторы
В современной технике сложно найти отрасль, где не применялись бы конденсаторы. Без них не обходятся радио и телеаппаратура (настройка колебательных контуров), радиолокационная и лазерная техника (получение мощных импульсов), телефония и телеграфия (разделение цепей переменного и постоянного токов, тушение искр в контактах), электроизмерительная техника (создание образцов емкости). И это далеко не полный перечень.
В современной электроэнергетике конденсаторы тоже имеют широкое применение: они присутствуют в конструкциях люминесцентных светильников, электросварочных аппаратов, устройств защиты от перенапряжений. Конденсаторы применяют и в других, не электротехнических, областях техники и промышленности (в медицине, фототехнике и т. д.).
Разнообразие областей применения обусловливает большое разнообразие конденсаторов. Наряду с миниатюрными конденсаторами, имеющими массу меньше грамма, а размеры порядка нескольких миллиметров, существуют конденсаторы массой несколько тонн и высотой больше человеческого роста. Емкость современных конденсаторов может составлять от долей, а рабочее напряжение может быть в пределах от нескольких вольт до нескольких сотен киловольт. Конденсаторы можно классифицировать по следующим признакам и свойствам:
- по назначению — постоянной и переменной емкости;
- по форме обкладок — плоские, сферические, цилиндрические и др.;
- по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и др.
Выводы:
- Энергию заряженного конденсатора можно вычислить по формулам:
- Конденсаторы классифицируют по назначению (постоянной и переменной емкости); по форме обкладок (плоские, сферические, цилиндрические и др.); по типу диэлектрика (воздушные, бумажные, слюдяные, керамические, электролитические и др.).
- Полупроводники
- Потенциал электрического поля
- Постоянный электрический ток
- Законы постоянного тока
- Принцип суперпозиции электрических полей
- Проводники в электрическом поле
- Диэлектрики в электрическом поле
- Закон Кулона