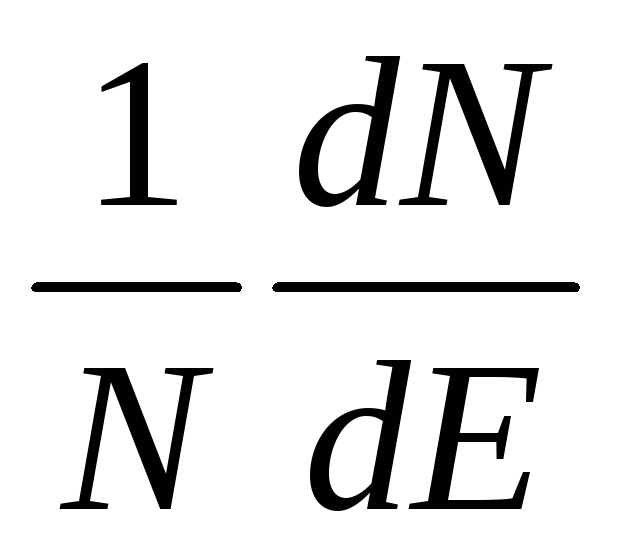
система переходит на более низкий энергетический уровень. Изменение потенциальной энергии системы вдоль пути реакции (или вдоль координаты реакции х) представляют в виде энергетической диаграммы.
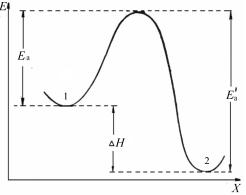
На рис. 7 изображена энергетическая диаграмма элементарной экзотермической реакции А +ВС [АВС]= → АВ +С. Кривая показывает, как изменяется потенциальная энергия системы в процессе реакции. Эта кривая энергетически описывает весь путь реакции, т. е. совокупность наиболее вероятных состояний системы. На вершине энергетического барьера система находится в переходном состоянии или в состоянии активированного комплекса, а высота барьера определяет энергию активации Eа прямой реакции.
Рис. 7. Изменение потенциальной энергии системы при протекании элементарной химической реакции (x — координата реакции; H — изменение энтальпии)
В соответствии с уравнением Аррениуса, чем меньше энергия активации, тем больше константа скорости реакции и тем больше скорость химической реакции.
Рассмотрим методы расчета энергии активации. Для расчета
энергии активации используют уравнение Аррениуса.
1. Графический метод. Запишем уравнение Аррениуса (см. (41)) в логарифмической форме:
22
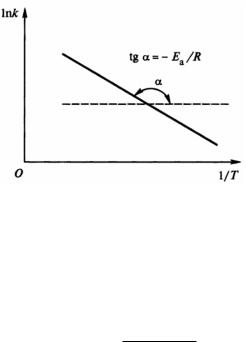
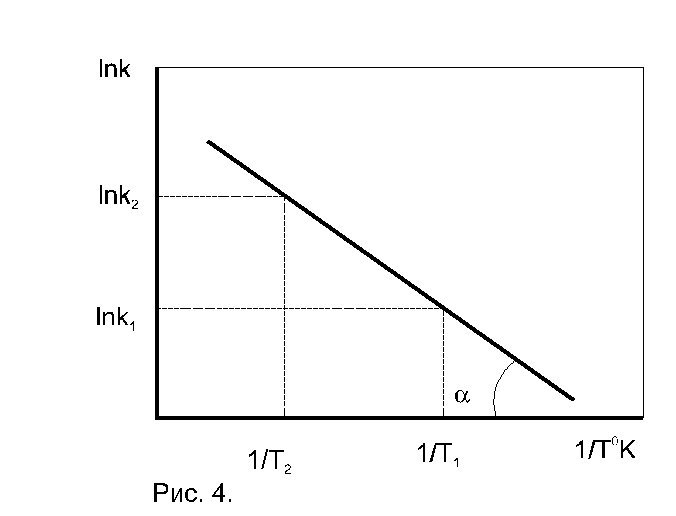
удобной для графического определения энергии активации. Энергию активации можно найти по значениям константы скорости реакции, измеренным при нескольких значениях температуры. При этом экспериментальные данные представляют в координатах Аррениуса (lnk; 1/T). Тангенс угла наклона полученной прямой линии равен (−Eа/R) (рис. 8).
Рис. 8. Графическое определение энергии активации
2. Аналитический метод. Уравнение Аррениуса (см. (41)) можно представить в дифференциальной форме:
|
dlnk |
= |
Ea |
. |
(44) |
|
dT |
||||
|
RT2 |
Тогда, интегрируя уравнение (44) в пределах от T1 до T2, получаем
|
ln(k2/k1) = |
Ea(T2 −T1) |
. |
(45) |
||
|
RT2T1 |
|||||
|
Из уравнения (45) следует: |
|||||
|
Ea = |
RT1T2 ln(k2/k1) |
. |
(46) |
||
|
T2 −T1 |
Таким образом, энергию активации можно рассчитать аналитически по формуле (46), если известны константы скорости реакции при двух значениях температуры T1 и T2. Однако такой
23
Содержание
- Расчет энергии активации
- Методы определения энергии активации:
- Лекция 4 теория соударений
- Методы расчета энергии активации химической реакции
- Расчет энергии активации
Расчет энергии активации
Энергию активации можно рассчитать по экспериментальным данным графическим или аналитическим способами, используя уравнение Аррениуса
,
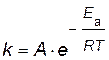
представив его в логарифмическом виде
 . |
(4.14) |
Графический способ. По экспериментальным значениям константы скорости реакции при различных температурах строят график зависимости lnk=f ( 
) (рис. 4.5).
Рис. 4.5. Зависимость константы скорости реакции от температуры
По тангенсу угла наклона прямой к оси абсцисс вычисляют энергию активации
.
Аналитический способ. Если предположить, что для выбранной реакции величины А и Еа постоянны в небольших пределах температур от Т1 до Т2, то:
;
.
В результате вычитания первого уравнения из второго получим
 . |
(4.15) |
 . |
(4.16) |
Под символом логарифма находится отношение констант скоростей реакции при двух температурах, поэтому константы можно заменить любыми пропорциональными им величинами при тех же температурах. Например, вместо констант скоростей можно подставить скорости реакции, если исходные концентрации реагирующих веществ при измерении скоростей в обоих опытах были одинаковы и скорость изменилась только под влиянием изменения температуры. Тогда получим следующие выражения:
Источник
Методы определения энергии активации:
По экспериментальным значениям константы скорости реакции: Графический метод (рис. 4):
(41)
(42)
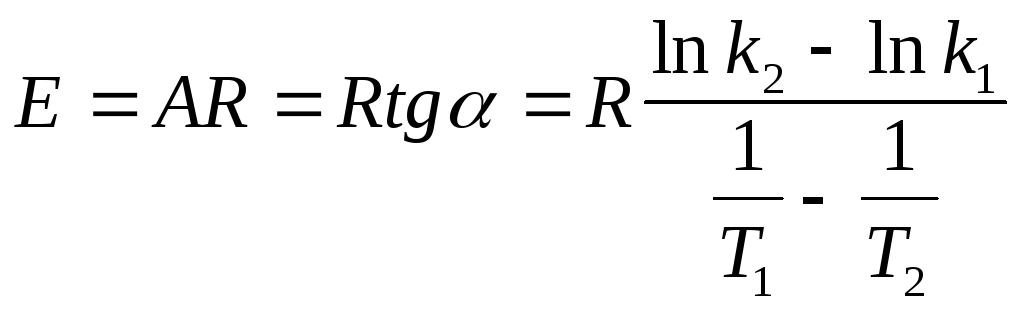
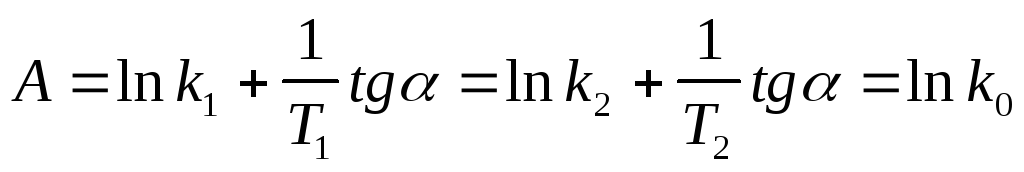
где k0 = k при Т =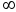 
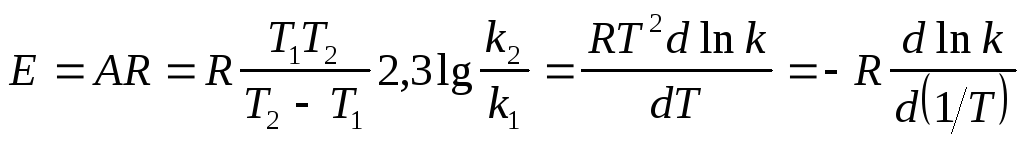
(экстраполяция).
(43)
Относительный температурный коэффициент константы скорости реакции:
(44)
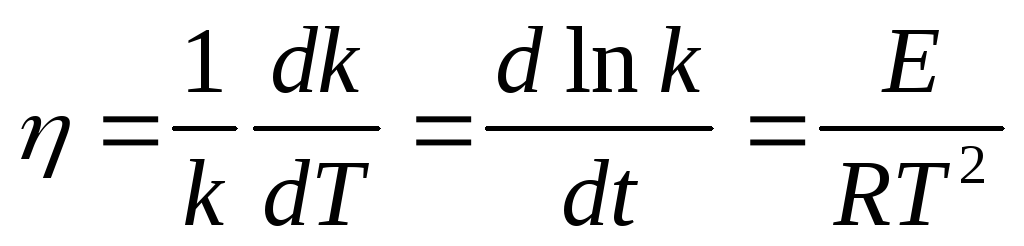
Коэффициент зависит от температуры и поэтому пригоден лишь для сравнительной оценки и ориентировочных расчетов в небольших интервалах температур.
Было сделано много попыток рассчитать теоретически энергию активации. Выдвинуты две основные теории: теория соударений и теория активированного комплекса.
Лекция 4 теория соударений
В 1918г. Льюис предположил, что для протекания реакции А + В = АВ должны столкнуться две молекулы А и В. Поэтому, зная число столкновений, можно, казалось бы, рассчитать скорость химической реакции. Однако если сравнить расчетное число соударяющихся молекул с числом реагирующих молекул, которое определяется экспериментально, то обнаруживаются два противоречия. Во-первых, число соударений примерно в 10 17 раз больше числа реагирующих молекул, т.е. из каждых 10 17 соударений только одно соударение является эффективным в осуществлении реакции. Во-вторых, в то время как при повышении температуры на 10 0 С число бинарных столкновений увеличивается примерно на 2%, скорость химической реакции возрастает на 200-300%.
Эти противоречия были разрешены при допущении, что реакция происходила только в том случае, если соударяющиеся молекулы обладали некоторой избыточной энергией; все остальные соударения неэффективны и не приводят к химической реакции, т.е. скорость реакции равна общему числу соударений, умноженному на долю эффективных соударений. Это допущение опиралось на изучение: 1) распределения скоростей реагирующих молекул и 2) влияния температуры.
Закон распределения скоростей. Все молекулы газа движутся с различными скоростями из-за частых соударений. Между молекулами постепенно происходит взаимообмен количеством движения и, следовательно, их скорости изменяются: одни молекулы увеличивают свою скорость, другие – уменьшают. Математический закон, которому подчиняется распределение скоростей и энергий, был найден Максвеллом и Больцманом в 1860г. Согласно этому закону, доля N/N молекул, обладающих большими скоростями, чем средняя скорость и , или кинетической энергией, превышающей величину ½ mи 2 , составляет:
( )
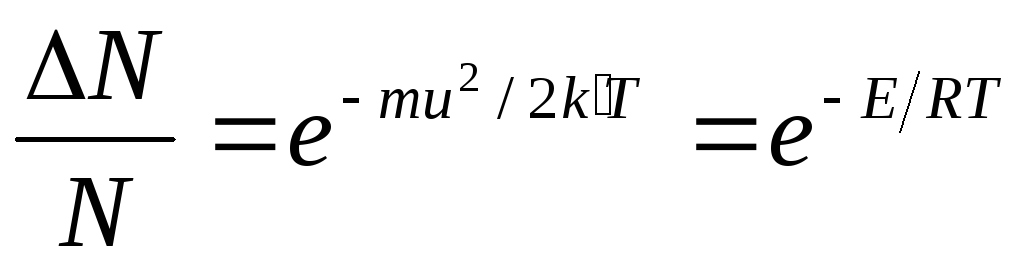
где k’ – константа Больцмана; u — средняя квадратичная скорость, см/с.
В дифференциальной форме это уравнение имеет вид:
, (45)
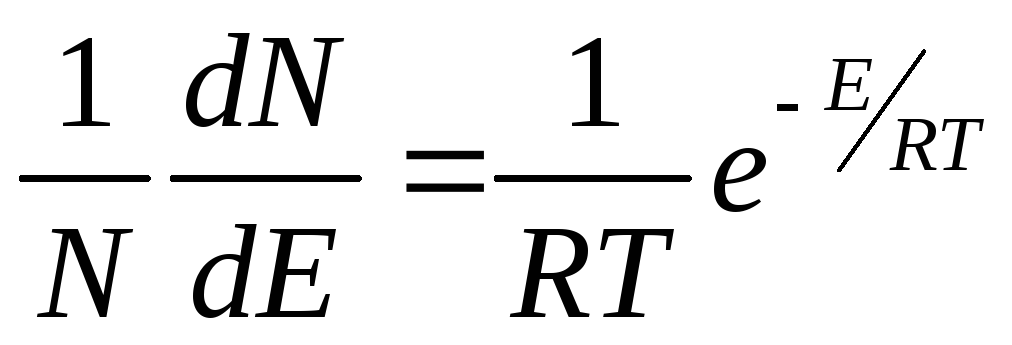
где R — универсальная газовая постоянная, эрг; Т — температура газа, К.
На рисунке 3 представлен график, построенный по уравнению (45). Доля молекул, энергия которых лежит в пределах определенного интервала, изображается площадью столбика, ограниченного кривой и соответствующими ординатами.
Рисунок 3. Распределение энергии по Максвеллу-Больцману.
В результате соударений всегда имеется несколько молекул с энергиями, намного превосходящими среднее значение. Таким образом, возможны столкновения между молекулами, имеющими высокую энергию активации, необходимую для реакции, но число таких соударений будет составлять очень небольшую долю от общего числа столкновений, происходящих в газе. Это объясняет тот факт, что лишь небольшая часть соударений приводит к реакции.
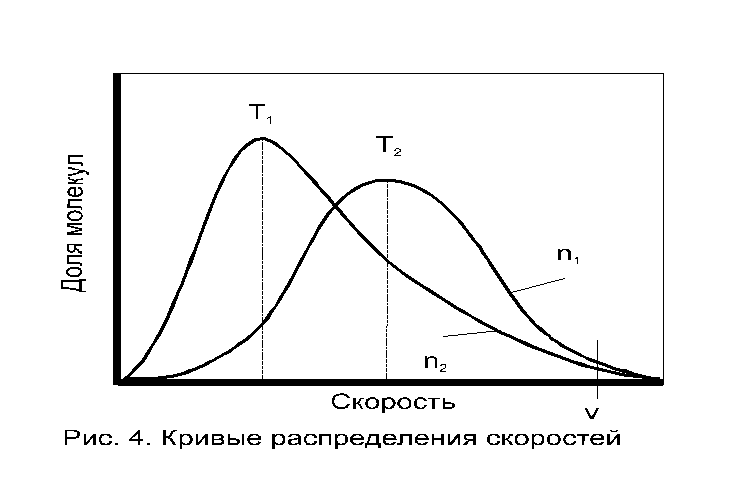
Влияние температуры на распределение скорости (см. Рис. 5.). С ростом температуры наблюдается смещение максимума в сторону более высокой скорости; происходит резкое увеличение числа молекул, имеющих скорости намного выше средней [при скорости имеется число (доля) молекул n1, при температуре Т1, которое увеличивается до n2 при температуре Т2, T2 > T1]. Общее число молекул, имеющих скорости, равные или большие определенного значения определяются площадью под кривой. Но именно небольшая доля молекул n1 и n2 при температурах Т1 и Т2 в конце кривых распределения, обладающих максимальными энергиями и скоростями в сечениях и будет определять эффективную долю столкновений, приводящих к их взаимодействию.
Экспоненциальный фактор в уравнении Максвелла учитывает изменение формы кривой при повышении температуры. Если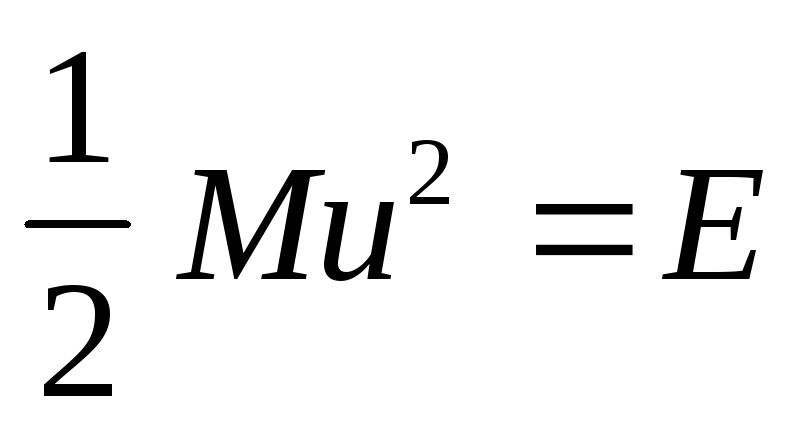 
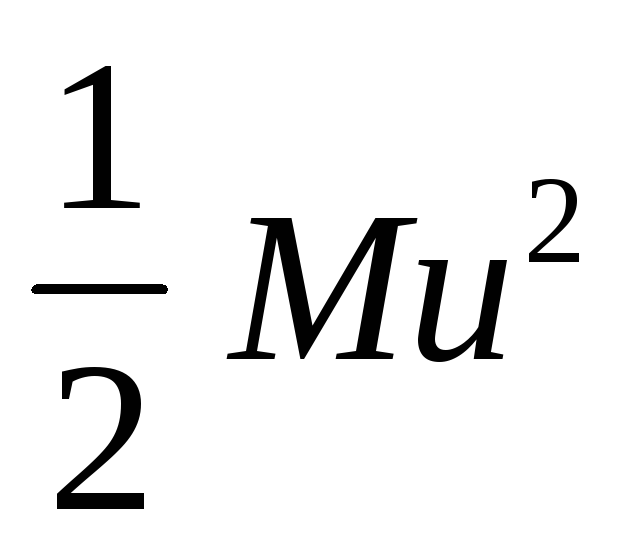
, где М – молекулярный вес, то член
будет представлять собой кинетическую энергию 1 моля молекул, каждая из которых имеет одну и ту же скоростьu . Член exp(-E/RT) называется фактором Больцмана. Этот фактор заметно увеличивается с увеличением температуры. Хотя общее число столкновений незначительно изменяется с ростом температуры, доля эффективных столкновений сильно повышается. Таким образом, отмеченное влияние температуры на скорость реакции может быть объяснено тем, что в газах (или растворах) имеются молекулы со всеми значениями скоростей и кинетических энергий. Число молекул с энергией, равной или большей, определенного значения Е, составляет приблизительно exp(-E/RT) часть от общего числа молекул. Так, например, повышение абсолютной температуры газа вдвое (например от 1000 К до 2000 К) приводит к увеличению средней кинетической энергии молекул в 2 раза, но доля молекул, обладающих энергией свыше 80 кДж/моль возрастает в 150 раз.
Источник
Методы расчета энергии активации химической реакции
Энергия активации – избыточная энергия, которой должны обладать частицы для вступления в химическую реакцию. Энергия активации является постоянной величиной для данной химической реакции и практически не зависит от температуры.
Чем больше активных молекул принимают участие в химической реакции, тем больше скорость реакции. Увеличение скорости реакции при повышении температуры обусловлено ростом доли активных молекул и числа столкновений между ними. Для определения величины энергии активации используют уравнение Аррениуса в интегральной и дифференциальной формах. Расчет энергии активации можно вести графическим и аналитическим способом.
Графический способ: Энергию активации графическим способом можно найти, если прологарифмировать уравнение Аррениуса:
Аналитический способ:
Энергию активации химической реакции можно вычислить по значениям констант скоростей при двух различных температурах по уравнению:
Отсюда, уравнение для расчета энергии активации имеет вид:
Теоретический вывод уравнения Аррениуса сделан для элементарных реакций, но опыт показывает, что подавляющее большинство сложных реакций также подчиняются этому уравнению.
Дата добавления: 2015-01-30 ; просмотров: 125 | Нарушение авторских прав
Источник
Расчет энергии активации
Энергию активации можно рассчитать по экспериментальным данным графическим или аналитическим способами, используя уравнение Аррениуса
,
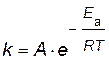
представив его в логарифмическом виде
 . |
(4.14) |
Графический способ. По экспериментальным значениям константы скорости реакции при различных температурах строят график зависимости lnk=f ( 
) (рис. 4.5).
Рис. 4.5. Зависимость константы скорости реакции от температуры
По тангенсу угла наклона прямой к оси абсцисс вычисляют энергию активации
.
Аналитический способ. Если предположить, что для выбранной реакции величины А и Еа постоянны в небольших пределах температур от Т1 до Т2, то:
;
.
В результате вычитания первого уравнения из второго получим
 . |
(4.15) |
 . |
(4.16) |
Под символом логарифма находится отношение констант скоростей реакции при двух температурах, поэтому константы можно заменить любыми пропорциональными им величинами при тех же температурах. Например, вместо констант скоростей можно подставить скорости реакции, если исходные концентрации реагирующих веществ при измерении скоростей в обоих опытах были одинаковы и скорость изменилась только под влиянием изменения температуры. Тогда получим следующие выражения:
Источник
Энергия активации – это количество энергии, которое необходимо подать для протекания химической реакции. В приведенном ниже примере задачи показано, как определить энергию активации реакции по константам скорости реакции при различных температурах.
Содержание
- Проблема энергии активации
- Решение
- Как использовать график для определения энергии активации
- Кто обнаружил энергию активации?
Проблема энергии активации
Наблюдалась реакция второго порядка. Константа скорости реакции при трех градусах Цельсия составила 8,9 x 10 -3 л/моль и 7,1 x 10 -2 л/моль при 35 градусах. Цельсия. Какова энергия активации этой реакции?
Решение
Энергию активации можно определить с помощью уравнения:
ln (k 2 /k 1 ) = E a /R x (1/T 1 – 1/T 2 )
, где
E a = энергия активации реакция в Дж/моль
R = постоянная идеального газа = 8,3145 Дж/К · моль
T 1 и T 2 = абсолютные температуры (в Кельвинах)
k 1 и k 2 = константы скорости реакции при T 1 и T 2
Шаг 1: преобразование температуры из градусов Цельсия до Кельвина
T = градусы Цельсия + 273,15
T 1 = 3 + 273,15
T 1 = 276,15 К
T 2 = 35 + 273,15
T 2 = 308,15 Кельвина
Шаг 2 – Найдите E a
ln (k 2 /k 1 ) = E a /R x (1/T 1 – 1/T 2 )
ln (7,1 x 10 -2 /8,9 x 10 -3 ) = E a /8,3145 Дж/К · моль x (1/276,15 K – 1/308,15 K)
ln (7,98) = E a / 8,3145 Дж/К · моль x 3,76 x 10 -4 K -1
2,077 = E a (4,52 x 10 -5 моль/Дж)
E a = 4,59 x 10 4 Дж/моль
или в кДж/моль (разделить на 1000)
E a = 45,9 кДж/моль
Ответ: Энергия активации этой реакции составляет 4,59 x 10 4 Дж/моль или 45,9 кДж/моль.
Как использовать график для определения энергии активации
Другой способ вычислить энергию активации реакции – построить график ln k ( константа скорости) в зависимости от 1/T (величина, обратная температуре в Кельвинах). График будет образовывать прямую линию, выраженную уравнением:
m = – E a /R
где m – наклон линии, Ea – энергия активации, а R – постоянная идеального газа, равная 8,314 Дж/моль-К. Если вы измеряли температуру в градусах Цельсия или Фаренгейта, не забудьте преобразовать их в градусы Кельвина, прежде чем рассчитывать 1/T и строить график..
Если бы вы построили график зависимости энергии реакции от координаты реакции, разница между энергией реагентов и продуктов была бы ΔH , в то время как избыточная энергия (часть кривой выше, чем у продуктов) будет энергией активации.
Имейте в виду, в то время как скорость большинства реакций увеличивается В зависимости от температуры в некоторых случаях скорость реакции уменьшается с увеличением температуры. Эти реакции имеют отрицательную энергию активации. Итак, хотя вы должны ожидать, что энергия активации будет положительным числом, имейте в виду, что она также может быть отрицательной.
Кто обнаружил энергию активации?
Шведский ученый Сванте Аррениус предложил термин «энергия активации» в 1880 году для определения минимальной энергии, необходимой для набора химических реагентов для взаимодействия и образования продуктов. На диаграмме энергия активации изображена как высота энергетического барьера между двумя точками минимума потенциальной энергии. Точки минимума – это энергии стабильных реагентов и продуктов.
Даже экзотермические реакции, такие как горение свечи, требуют ввода энергии. В случае возгорания горящая спичка или сильный жар запускают реакцию. Оттуда тепло, выделяющееся в результате реакции, обеспечивает энергию, чтобы сделать ее самоподдерживающейся.
Download Article
Step-by-step examples for calculating activation energy with the Arrhenius equation
Download Article
- What is activation energy?
- Sample Problem (Type 1)
- Sample Problem (Type 2)
- More Examples
- How do I find activation energy from a graph?
|
|
|
|
For a chemical reaction to happen—for instance, for logs on a fire to ignite—a certain energy threshold must be reached. Calculating activation energy requires some advanced math skills, but we’ll walk you through the process using common test question types. So, if your own “activation energy” to get your homework done is flagging, don’t worry—we’re here to help!
Things You Should Know
- Use the Arrhenius equation as your starting point for calculating activation energy: k = Ae^(-E_a/RT).
- Rearrange the equation to E_a = -R * T * ln(k/A) if you’re given one temperature reading and the pre-exponential factor.
- Adjust the equation to E_a = R * ln(k_1/k_2) / (1/T_2 — 1/T_1) if you’re given two temperature readings and two rate constant amounts.
-
It’s the minimum amount of energy required to begin a chemical reaction. It is, you might say, the energy “barrier” that needs to be broken through, or the energy “hump” that needs to be passed over, in order for the reactants’ existing bonds to break and begin forming new bonds. If this minimum threshold isn’t met, the reaction won’t happen.[1]
- Swedish scientist Svante Arrhenius pioneered the concept of activation energy and, in 1889, came up with an equation to calculate it. This is now known as the “Arrhenius equation:»
- k = Ae^(-E_a/RT)
- Swedish scientist Svante Arrhenius pioneered the concept of activation energy and, in 1889, came up with an equation to calculate it. This is now known as the “Arrhenius equation:»
Advertisement
-
1
If the rate constant is 21 M^(-1)s^(-1) at 234 K and the pre-exponential factor is 31 M^(-1)s^(-1), what is the activation energy? This type of question provides you with the pre-exponential factor (or frequency factor), which means you can calculate the activation energy at a single temperature value. (The other common type of activation energy question provides you with two temperature values, but not the pre-exponential factor.)[2]
- The pre-exponential factor is a temperature-dependent representation of the frequency of molecular collisions.
-
2
Rearrange the Arrhenius equation to solve for E_a. In the Arrhenius equation [k = Ae^(-E_a/RT)], E_a represents the activation energy, k is the rate constant, A is the pre-exponential factor, R is the ideal gas constant (8.3145), T is the temperature (in Kelvins), and e is the exponential constant (2.718). You can rearrange the equation to solve for the activation energy as follows:[3]
- k = Ae^(-E_a/RT)
- ln(k) = -E_a/R * 1/T + ln(A)
- E_a = -R * T * ln(k/A)
-
3
Input the given data into the rearranged equation. The question gave you the temperature (234 K), the rate constant (21), and the pre-exponential factor (31), so plug these into the correct spots:[4]
- E_a = -R * T * ln(k/A)
- E_a = -8.3145 * 234 * ln(21/31)
-
4
Solve the equation. Grab a scientific calculator (or an online version) and use it to determine the activation energy (given in J/mol, or, in some cases, kJ/mol, which is just J/mol divided by 1000).[5]
- E_a = -1945.6 * ln(0.38946)
- E_a = -1945.6 * -0.38946
- E_a = 757.7 J/mol (0.7577 kJ/mol)
Advertisement
-
1
What is the activation energy of a reaction if the rate constant is 33 M^(-1)s^(-1) at 298 K and 45 M^(-1)s^(-1) at 675 K? This form of question omits the pre-exponential factor but provides two temperature readings (and two rate constants). You’ll still get the answer by using the Arrhenius equation—just rearranged differently.[6]
- As a refresher, the original Arrhenius equation is k = Ae^(-E_a/RT).
-
2
Use the equation form for multiple temperatures and constants. Without going into extensive detail here, let’s just say that the original Arrhenius equation can be rearranged into the following form: ln(k_1/k_2) = -E_a/R * (1/T_2 — 1/T_1). (Remember that k represents the rate constant, T the temperature, R the ideal gas constant, and E_a the activation energy.) This can be further rearranged to solve for the activation energy:[7]
- E_a = R * ln(k_1/k_2) / (1/T_2 — 1/T_1)
-
3
Plug in the given data. The first given rate constant and temperature are k_1 and T_1, while the second are k_2 and T_2:[8]
- E_a = R * ln(k_1/k_2) / (1/T_2 — 1/T_1)
- E_a = 8.3145 * ln(33/45) / (1/675 — 1/298)
-
4
Solve for E_a to get the result in J/mol. If you’re asked to provide the answer in kJ/mol, simply divide by 1000.[9]
- E_a = 8.3145 * ln(33/45) / (1/675 — 1/298)
- E_a = 8.3145 * ln(0.73333) / (0.0014814 — 0.0033557)
- E_a = 8.3145 * -0.31016 / -0.0018743
- E_a = 1375.9 J/mol
Advertisement
-
1
If the rate constant is 45 M^(-1)s^(-1) at 333 K and the pre-exponential factor is 78 M^(-1)s^(-1), what is the activation energy?
- k = Ae^(-E_a/RT)
- ln(k) = -E_a/R * 1/T + ln(A)
- E_a = -R * T * ln(k/A)
- E_a = -8.3145 * 333 * ln(45/78)
- E_a = -2768.7 * ln(0.57692)
- E_a = -2768.7 * -0.55005
- E_a = 1522.92 J/mol
-
2
If the rate constant is 32 M^(-1)s^(-1) at 517 K and the pre-exponential factor is 95 M^(-1)s^(-1), what is the activation energy?
- k = Ae^(-E_a/RT)
- ln(k) = -E_a/R * 1/T + ln(A)
- E_a = -R * T * ln(k/A)
- E_a = -8.3145 * 517 * ln(32/95)
- E_a = -4298.6 * ln(0.33684)
- E_a = -4298.6 * -1.0881
- E_a = 4677.3 J/mol
-
3
What is the activation energy of a reaction if the rate constant is 19 M^(-1)s^(-1) at 222 K and 78 M^(-1)s^(-1) at 451 K?
- k = Ae^(-E_a/RT)
- ln(k_1/k_2) = -E_a/R * (1/T_2 — 1/T_1)
- E_a = R * ln(k_1/k_2) / (1/T_2 — 1/T_1)
- E_a = 8.3145 * ln(19/78) / (1/451 — 1/222)
- E_a = 8.3145 * ln(.24359) / (0.0022173 — 0.0045045)
- E_a = 8.3145 * -1.4122 / -0.0022872
- E_a = 5133.7 J/mol
Advertisement
-
Find the slope and use the formula E_a = -R * m. Activation energy produces a straight line on a graph with ln(k) on the y (vertical) axis and 1/T on the x (horizontal) axis. Another rearranging of the Arrhenius equation (with m representing the slope of the line) gives you -E_a / R = m and thus E_a = -R * m. Here’s a quick rundown of the process:[10]
- Calculate the slope (m) using the slope equation m = (y_2 — y_1) / (x_2 — x_1). To do this calculation, find the y and x coordinates at two separate points along the line.
- Plug the slope into E_a = -R * m, with R representing the ideal gas constant (8.3145). So, in a simple example, let’s say m = -2/3:
- E_a = -8.3145 * -2/3 → E_a = 5.543 J/mol
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
References
About This Article
Thanks to all authors for creating a page that has been read 2,359 times.
If you buy through links on our site, we may earn a commission.