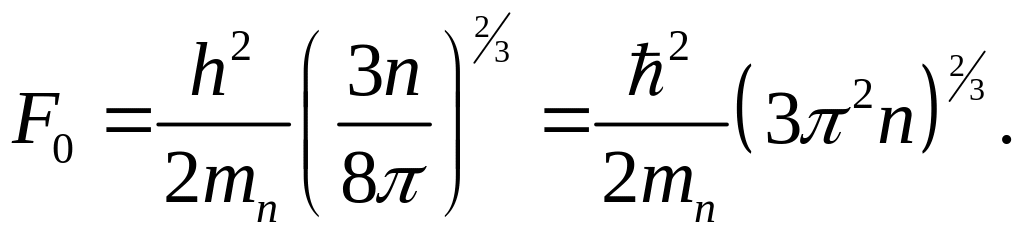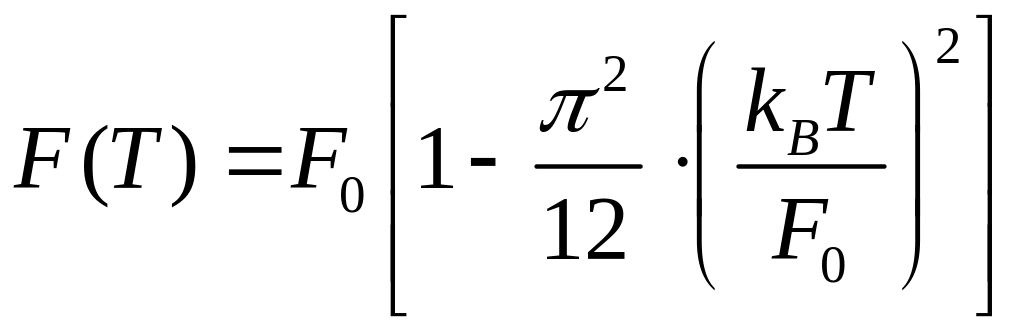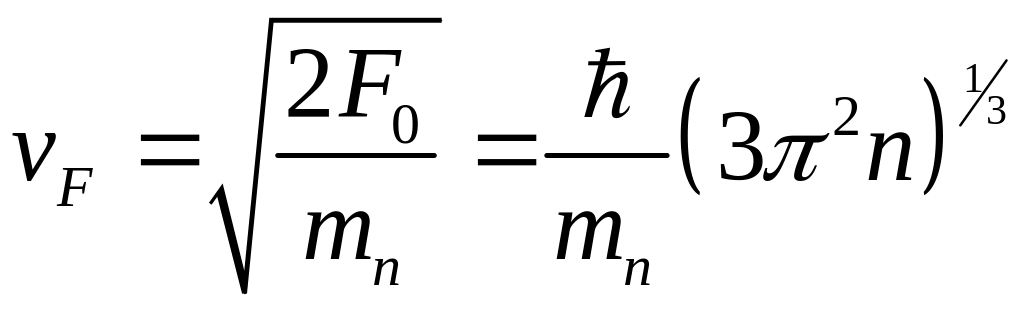Как найти энергию ферми в металле - Исправление недочетов и поиск решений вместе с Examum.ru

Энергия Ферми и концентрация электронов в металле

Электронный газ металла, находящийся
в основном состоянии при абсолютном
нуле, заполняет в

—
пространстве все состояния внутри
некоторой сферы, которая называется
поверхностью Ферми. Энергия, соответствующая
этой поверхности, называется энергией
Ферми и представляет максимальную
энергию, что могут иметь электроны при
абсолютном нуле температур. Таким
образом, поверхность Ферми отделяет в

—
пространстве занятые состояния от
свободных.

Определим величину энергии Ферми

через
концентрацию электронов

Для этого проинтегрируем (4.76) по всем
возможными значениями энергии и учтем,
что при

функция

равняется единице для всех

и нулю для всех

(4.78)

Отсюда
энергия Ферми при

равна

(4.79)

Для отличной от абсолютного нуля
температуры энергия Ферми будет являться
функцией температуры

.
(4.80)

Поскольку в металлах при любой температуре,
то положение уровня Ферми в металлах
определяется лишь концентрацией
свободных электронов и практически не
изменяется с температурой.

Скорость электронов на поверхности
Ферми и температура Ферми определяются
через энергию Ферми

и

.
(4.81)

Оценим величину энергии Ферми для
типичного металла, считая концентрацию
электронов

м^-3,

эВ.

Среднюю энергию электронов можно
определить через энергию Ферми

(4.82)

Следовательно, средняя энергия электронов
по порядку величины совпадает с энергией
Ферми. Такой энергией молекулы
классического газа обладали бы при
температуре в несколько десятков тысяч
градусов. Это свидетельствует о том,
что электронный газ в металлах находится
в особом, вырожденном состоянии. Его
энергия практически не зависит от
температуры.

В том случае, когда фермиевская функция
распределения переходит в максвелловскую,
вырождение с электронного газа снимается.
Это возможно при выполнении условия

(4.83)

Выразим это условие через параметры
электронного газа. Для этого проинтегрируем
(4.76) с учетом (4.83)

Отсюда условие снятия вырождения с
электронного газа может быть представлено
в виде

(4.84)

Обратное неравенство означает, что
электронный газ находится в вырожденном
состоянии.

Если приравнять левую часть неравенства
(4.84) единице, можно определить температуру
снятия вырождения:

(4.85)

Оценивая величину этой температуры для
концентрации электронов

м^-3,
получим

К.

Таким образом, электронный газ в металлах
всегда находится в вырожденном состоянии.

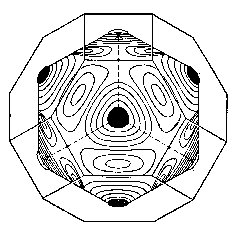
В заключение заметим, что поверхность
Ферми является сферической только в
приближении свободных электронов. Для
реальных металлов, когда закон дисперсии
носит сложный характер, вид поверхности
Ферми может быть весьма экзотическим
(рис. 4.18).


Рис.4.18. Поверхность Ферми для реальных металлов

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
08.05.20151.69 Mб584.doc
#
#
#
#
#
#
#
#

Источник

From Wikipedia, the free encyclopedia

The Fermi energy is a concept in quantum mechanics usually referring to the energy difference between the highest and lowest occupied single-particle states in a quantum system of non-interacting fermions at absolute zero temperature.
In a Fermi gas, the lowest occupied state is taken to have zero kinetic energy, whereas in a metal, the lowest occupied state is typically taken to mean the bottom of the conduction band.

The term «Fermi energy» is often used to refer to a different yet closely related concept, the Fermi level (also called electrochemical potential).^{[note 1]}
There are a few key differences between the Fermi level and Fermi energy, at least as they are used in this article:

The Fermi energy is only defined at absolute zero, while the Fermi level is defined for any temperature.
The Fermi energy is an energy difference (usually corresponding to a kinetic energy), whereas the Fermi level is a total energy level including kinetic energy and potential energy.
The Fermi energy can only be defined for non-interacting fermions (where the potential energy or band edge is a static, well defined quantity), whereas the Fermi level remains well defined even in complex interacting systems, at thermodynamic equilibrium.

Since the Fermi level in a metal at absolute zero is the energy of the highest occupied single particle state,
then the Fermi energy in a metal is the energy difference between the Fermi level and lowest occupied single-particle state, at zero-temperature.

Context[edit]

In quantum mechanics, a group of particles known as fermions (for example, electrons, protons and neutrons) obey the Pauli exclusion principle. This states that two fermions cannot occupy the same quantum state. Since an idealized non-interacting Fermi gas can be analyzed in terms of single-particle stationary states, we can thus say that two fermions cannot occupy the same stationary state. These stationary states will typically be distinct in energy. To find the ground state of the whole system, we start with an empty system, and add particles one at a time, consecutively filling up the unoccupied stationary states with the lowest energy. When all the particles have been put in, the Fermi energy is the kinetic energy of the highest occupied state.

As a consequence, even if we have extracted all possible energy from a Fermi gas by cooling it to near absolute zero temperature, the fermions are still moving around at a high speed. The fastest ones are moving at a velocity corresponding to a kinetic energy equal to the Fermi energy. This speed is known as the Fermi velocity. Only when the temperature exceeds the related Fermi temperature, do the particles begin to move significantly faster than at absolute zero.

The Fermi energy is an important concept in the solid state physics of metals and superconductors. It is also a very important quantity in the physics of quantum liquids like low temperature helium (both normal and superfluid ³He), and it is quite important to nuclear physics and to understanding the stability of white dwarf stars against gravitational collapse.

Formula and typical values[edit]

The Fermi energy for a non-interacting ensemble of identical spin-1⁄2 fermions in a three-dimensional (non-relativistic) system is given by^[1]

${displaystyle E_{text{F}}={frac {hbar ^{2}}{2m_{0}}}left({frac {3pi ^{2}N}{V}}right)^{2/3},}$

where N is the number of particles, m₀ the rest mass of each fermion, V the volume of the system, and hbar the reduced Planck constant.

Metals[edit]

Under the free electron model, the electrons in a metal can be considered to form a Fermi gas. The number density N/V of conduction electrons in metals ranges between approximately 10²⁸ and 10²⁹ electrons/m³, which is also the typical density of atoms in ordinary solid matter. This number density produces a Fermi energy of the order of 2 to 10 electronvolts.^[2]

White dwarfs[edit]

Stars known as white dwarfs have mass comparable to the Sun, but have about a hundredth of its radius. The high densities mean that the electrons are no longer bound to single nuclei and instead form a degenerate electron gas. Their Fermi energy is about 0.3 MeV.

Nucleus[edit]

Another typical example is that of the nucleons in the nucleus of an atom. The radius of the nucleus admits deviations, so a typical value for the Fermi energy is usually given as 38 MeV.

[edit]

Using this definition of above for the Fermi energy, various related quantities can be useful.

The Fermi temperature is defined as

${displaystyle T_{text{F}}={frac {E_{text{F}}}{k_{text{B}}}},}$

where $k_{text{B}}$ is the Boltzmann constant, and $E_{{text{F}}}$ the Fermi energy. The Fermi temperature can be thought of as the temperature at which thermal effects are comparable to quantum effects associated with Fermi statistics.^[3] The Fermi temperature for a metal is a couple of orders of magnitude above room temperature.

Other quantities defined in this context are Fermi momentum

${displaystyle p_{text{F}}={sqrt {2m_{0}E_{text{F}}}}}$

and Fermi velocity

${displaystyle v_{text{F}}={frac {p_{text{F}}}{m_{0}}}.}$

These quantities are respectively the momentum and group velocity of a fermion at the Fermi surface.

The Fermi momentum can also be described as

${displaystyle p_{text{F}}=hbar k_{text{F}},}$

where ${displaystyle k_{text{F}}}$ , called the Fermi wavevector, is the radius of the Fermi sphere.^[4]

These quantities may not be well-defined in cases where the Fermi surface is non-spherical.

Notes[edit]

^ The use of the term «Fermi energy» as synonymous with Fermi level (a.k.a. electrochemical potential) is widespread in semiconductor physics. For example: Electronics (fundamentals And Applications) by D. Chattopadhyay, Semiconductor Physics and Applications by Balkanski and Wallis.

References[edit]

^ Kittel, Charles (1986). «Ch. 6: Free electron gas». Introduction to Solid State Physics. Wiley.
^ Nave, Rod. «Fermi Energies, Fermi Temperatures, and Fermi Velocities». HyperPhysics. Retrieved 2018-03-21.
^ Torre, Charles (2015-04-21). «PHYS 3700: Introduction to Quantum Statistical Thermodynamics» (PDF). Utah State University. Retrieved 2018-03-21.
^ Ashcroft, Neil W.; Mermin, N. David (1976). Solid State Physics. Holt, Rinehart and Winston. ISBN 978-0-03-083993-1.

Further reading[edit]

Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN 978-0-7167-1088-2.

Источник

Студентам

Знакомимся ближе

Разделы

Уровень Ферми

Фе́рми-эне́ргия — значение энергии, ниже которой при температуре абсолютного нуля Т=0 К, все энергетические состояния системы частиц, подчиняющихся Ферми — Дирака статистике, заняты, а выше — свободны. Уровень Ферми — некоторый условный уровень, соответствующий энергии Ферми системы фермионов; в частности электронов твердого тела, играет роль химического потенциала для незаряженных частиц. Статистический смысл уровня Ферми — при любой температуре его заселенность равна 1/2.

Положение уровня Ферми является одной из основных характеристик состояния электронов (электронного газа) в твердом теле. В квантовой теории вероятность заполнения энергетических состояний электронами, определяется функцией Ферми F(E):

F(E) =1/(e^(E-E^F^)/kT+1), где

Е — энергия уровня, вероятность заполнения которого определяется,

E_F — энергия характеристического уровня, относительно которого кривая вероятности симметрична;

Т — абсолютная температура;

При абсолютном нуле из вида функции следует, что

F(E) = 1 при Е _F;

F(E) = 0 при Е >E_F.

То есть все состояния, лежащие ниже уровня Ферми, полностью заняты электронами, а выше него свободны.

Энергия Ферми E_F — максимальное значение энергии, которое может иметь электрон при температуре абсолютного нуля. Энергия Ферми совпадает со значениями химического потенциала газа фермионов при Т =0 К, то есть уровень Ферми для электронов играет роль уровня химического потенциала для незаряженных частиц. Соответствующий ей потенциал j_F = E_F/е называют электрохимическим потенциалом.

Таким образом, уровнем Ферми или энергией Ферми в металлах является энергия, которую может иметь электрон при температуре абсолютного нуля. При нагревании металла происходит возбуждение некоторых электронов, находящихся вблизи уровня Ферми (за счет тепловой энергии, величина которой порядка kT). Но при любой температуре для уровня с энергией, соответствующей уровню Ферми, вероятность заполнения равна 1/2. Все уровни, расположенные ниже уровня Ферми, с вероятностью больше 1/2 заполнены электронами, а все уровни, лежащие выше уровня Ферми, с вероятностью больше1/2 свободны от электронов.

Для электронного газа в металлах при Т = 0 величина энергии Ферми однозначно определяется концентрацией электронов и ее можно выразить через число n частиц электронного газа в единице объема: зависимость энергии Ферми от концентрации электронов нелинейная.

С ростом температуры (а также уменьшением концентрации электронов) уровень Ферми смещается по шкале энергий влево, но его заселенность остается равной 1/2. В реальных условиях изменение E_Fсувеличением температуры мало. Например, для Ag, имеющего при Т=0 значение E_F равное 5,5 эВ, изменение энергии Ферми при температуре плавления составляет всего около 0,03% от исходного значения.

В полупроводниках при очень низких температурах уровень Ферми лежит посередине между дном зоны проводимости и потолком валентной зоны. (Для донорных полупроводников — полупроводников n-типа проводимости — уровень Ферми лежит посередине между дном зоны проводимости и донорным уровнем). С повышением температуры вероятность заполнения донорных состояний уменьшается, и уровень Ферми перемещается вниз. При высоких температурах полупроводник по свойствам близок к собственному, и уровень Ферми устремляется к середине запрещенной зоны. Аналогичные закономерности проявляются и полупроводниках р-типа проводимости.

Существование энергии Ферми является следствием Принципа Паули. Величина энергии Ферми существенно зависит от свойств системы. Понятие об энергии Ферми используется в физике твердого тела, в ядерной физике, в астрофизике и т. д.

Вероятность нахождения электрона на том или ином энергетическом уровне при температуре Т определяется функцией Ферми – Дирака:

где W_F – энергетический уровень, называемый уровнем Ферми.

При Т=0°К вероятность занятия электронами уровней W > W_F равна нулю:

а уровней W < W_F единице:

Энергия для перахода в зону проводимости берется от тепловых колебаний. Поэтому при Т=0°К свободных электронов в полупроводнике нет (ни один уровень в ЗП не занят электроном), все электроны находятся на орбитах (в ВЗ), следовательно, энергетические ЗП соответствуют условию W > W_F, а энергетические уровни ВЗ – условию W < W_F. Это говорит о том, что уровень Ферми W_F расположен ниже «дна» ЗП W_П и выше «потолка» ВЗ W_В, т.е. в ЗЗ. На рис. 3 приведены кривые функции Ферми – Дирака.

При Т=0°К фуекция f_n(W) имеет ступенчатый характер. Вероятность занятия электронами уровней в ЗП = 0, а в ВЗ = 1.

При Т > 0°К появляется небольшая вероятность занятия электронами уровней в ЗП, а вероятность занятия уровней в ВЗ соответственно снижается.

Из формулы Ферми – Дирака видно, что при температуре, отличной от абсолютного нуля (Т>0), уровень Ферми – это такой энергетический уровень W = W_F, формальная вероятность заполнения которого электроном равна 0,5 (т.к. е° = 1).

Формальное потому, что уровень Ферми находится в запрещенной зоне и фактически не может быть занят электроном. Таким образом, конкретный смысл имеют только те участники кривой распределения f_n(W), которые расположены в ЗП и в ВЗ.

Кривая распределения Ферми – Дирака всегда симметрична относительно уровня Ферми. Из этого, в частности, следует, что в собственном полупроводнике уровень Ферми расположен посередине ЗЗ. При повышении температуры от нуля появляется определенная вероятность занятия электронами энергетических уровней в ЗП. Но при этом на такую же величину снижается вероятность нахождения электронов в ВЗ. Нетрудно видеть, что при симметричном размещении кривой распределения f_n(W) относительно уровня Ферми это возможно только в случае, если уровень Ферми будет находиться посередине ЗЗ.

Источники:

1.http://megabook.ru/article/%D0%A4%D0%B5%D1%80%D0%BC%D0%B8-%D1%8D%D0%BD%D0%B5%D1%80%D0%B3%D0%B8%D1%8F

2. http://studopedia.ru/5_119018_uroven-fermi.html

Источник

Энергия Ферми и концентрация электронов в металле

Context[edit]

Formula and typical values[edit]

Metals[edit]

White dwarfs[edit]

Nucleus[edit]

[edit]

See also[edit]

Notes[edit]

References[edit]

Further reading[edit]

Студентам

Знакомимся ближе

Разделы

Уровень Ферми