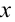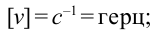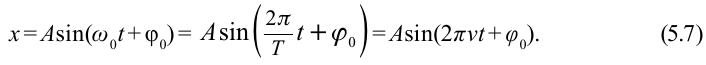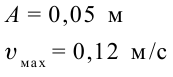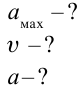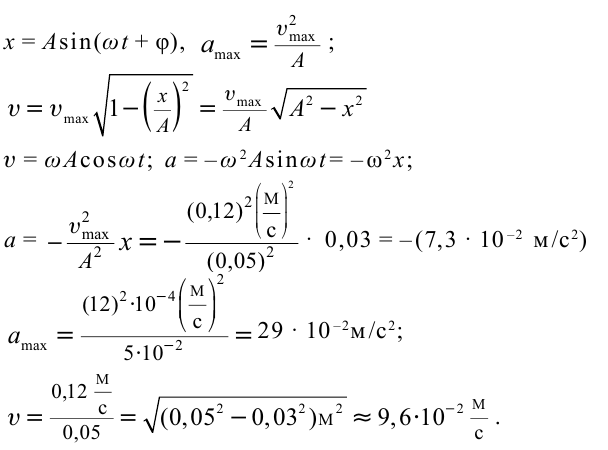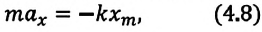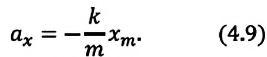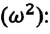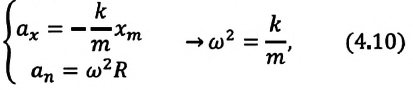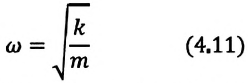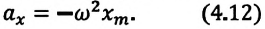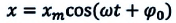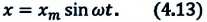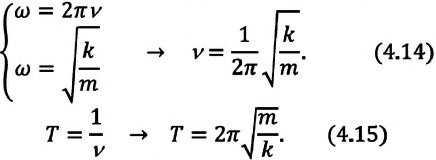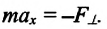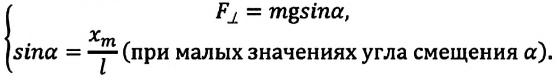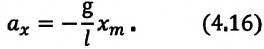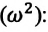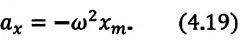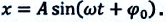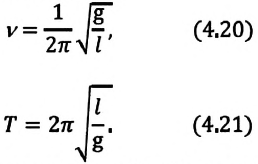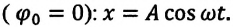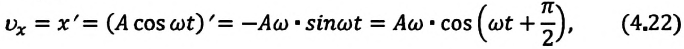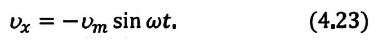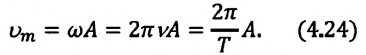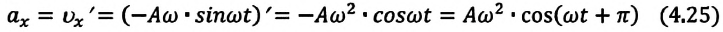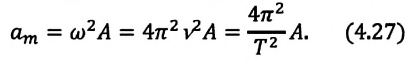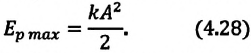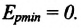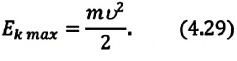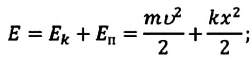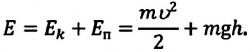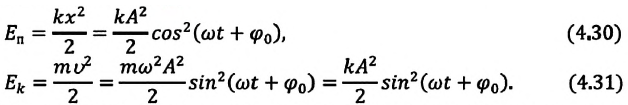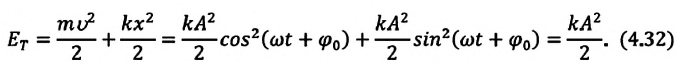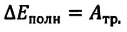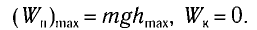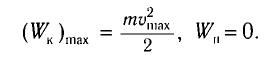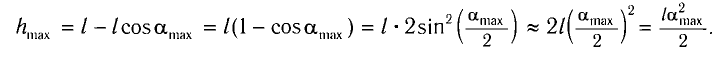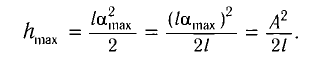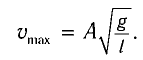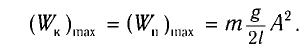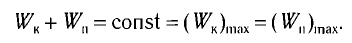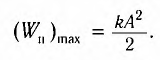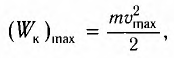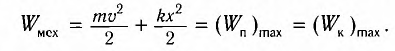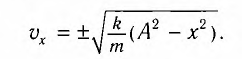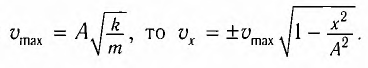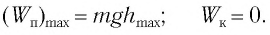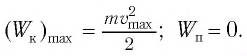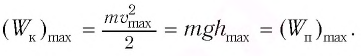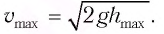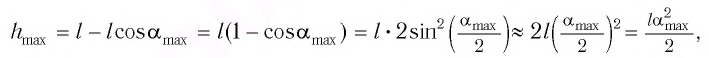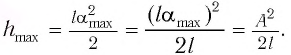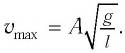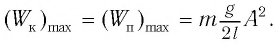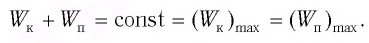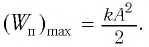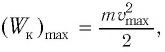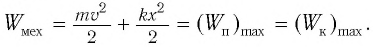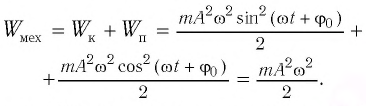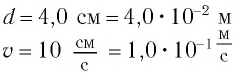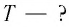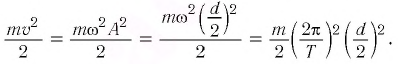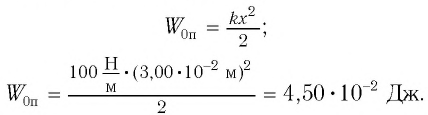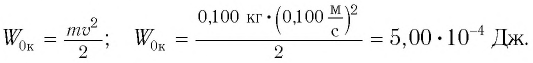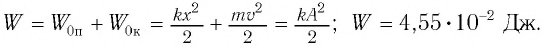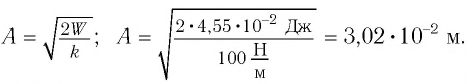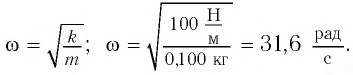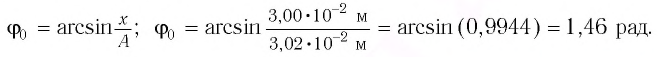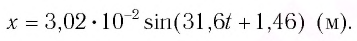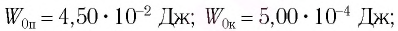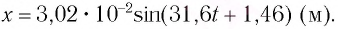Выясним,
как изменяется со временем кинетическая
Еk
и потенциальная Еп
энергия гармонического колебания.
Кинетическая энергия равна:
,
(4)
где
k
= m 02.
Потенциальную
энергию находим из формулы потенциальной
энергии для упругой деформации и
используя (3):
EП.
(5)
Складывая
(4) и (5), с учетом соотношения
,
получим:
E = EK
+ EП
=
.
(6)
Таким
образом, полная энергия гармонического
колебания остается постоянной в
отсутствие сил трения, во время
колебательного процесса кинетическая
энергия переходит в потенциальную и
наоборот.
38.Разложение колебаний в гармонический спектр. Применение гармонического анализа для обработки диагностических данных. (часть1).
Возможны
случаи, когда тело участвует одновременно
в нескольких колебаниях, происходящих
вдоль одного и того же или вдоль различных
направлений.
Рассмотрим
сложение двух гармонических колебаний
одинакового направления, одинаковой
частоты и с одинаковыми амплитудами,
но с разными начальными фазами 01
и 02
. Смещение
x
колеблющегося
тела будет суммой смещений
x1
и x2:
x
= x1
+ x2
= Acos(0t
+ 01)
+ Acos(0t
+ 02).
Используя
известную из тригонометрии формулу для
суммы косинусов двух углов,
имеем:
Aрез
,
то есть получается гармоническое
колебание той же частоты с начальной
фазой
и амплитудой Aрез.
Как
видно, амплитуда Aрез
результирующего
колебания зависит от разности фаз
складываемых колебаний.
Рассмотрим
два крайних случая:
А)
Колебания происходят в фазе, то есть
01
= 02,
тогда
и
,
поэтому Aрез
= 2A.
Если
амплитуды не равны,
Aрез
= A1
+ A2.
Б)
Колебания происходят в противофазе, то
есть 01
= 02
,
тогда
.
Следовательно, и Aрез
= 0.
Если амплитуды не равны, например, A1
> A2
, то
Aрез
= A1
— A2.Таким
образом, при сложении двух одинаково
направленных гармонических колебаний
одного периода и с равными амплитудами
получается гармоническое колебание
того же периода с амплитудой, которая
в зависимости от соотношения фаз
складываемых колебаний может изменяться
от удвоенного значения, если колебания
происходят в фазе, до нуля, если они
находятся в противофазе.При сложении
гармонических колебаний с разными
частотами результирующее колебание не
будет гармоническим, а будет являться
сложным колебанием
Сложное
колебание и его гармонический спектр.
Согласно
теореме Фурье, любое сложное колебание
может быть представлено как сумма
простых (гармонических) колебаний
(гармоник), периоды или частоты которых
кратны основному периоду или частоте
сложного колебания.
Совокупность
простых колебаний, на которые можно
разложить данное сложное колебание,
называется его гармоническим спектром.
В
гармоническом спектре сложного колебания
указываются частоты и амплитуды всех
составляющих его простых колебаний.
Обычно спектр изображается в виде
графика, на горизонтальной оси которого
откладываются частоты; затем для каждой
из частот простых колебаний имеющихся
в спектре, строится ордината, соответствующая
амплитуде этого колебания. Если
гармонический спектр сложного колебания
содержит только небольшое число простых
колебаний и график его состоит из
отдельных ординат, то такой спектр
называется линейчатым
(рис.
5.).
Соседние файлы в предмете Биофизика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Энергия гармонических колебаний, теория и онлайн калькуляторы
Энергия гармонических колебаний
Рассмотрим превращения энергии, которые происходят при гармонических колебаниях в консервативной системе на примере пружинного маятника.
Потенциальная энергия гармонических колебаний
В процессе механических колебаниях груза на пружине периодически кинетическая энергия ($E_k$) движущегося груза переходит в потенциальную энергию ($E_p$) колебательной системы, состоящей из потенциальной энергии упругодеформированной пружины и потенциальной энергии груза в поле тяжести Земли. Потенциальная энергия пружины при упругой деформации равна:
[E_{p1}=frac{k{left(x+x_0right)}^2}{2}left(1right),]
где $left(x+x_0right)$ — удлинение пружины; $k$ — жесткость пружины.
Потенциальную энергию груза в поле тяжести ($E_{p2}$) найдем как:
[E_{p2}=-mg x+Cleft(2right),]
где $m$ — масса груза, прикрепленного к пружине.
Постоянную $C,$ будем выбирать так, чтобы в положении равновесия полная потенциальная энергия колебательной системы равнялась:
[frac{kx^2_0}{2}+C=0to C=-frac{kx^2_0}{2} left(3right).]
Тогда потенциальная энергия представлена выражением:
[E_p=E_{p1}+E_{p2}=frac{k{left(x+x_0right)}^2}{2}-mg x-frac{kx^2_0}{2}=frac{kx^2}{2}left(4right).]
Кинетическая энергия пружинного маятника
Кинетическая энергия рассматриваемой колебательной системы состоит из энергии движения груза. Используя уравнение смещения груза пружинного маятника при гармонических колебаниях, происходящих по оси X:
[x=A{cos left({omega }_0t+varphi right)(5) }]
найдем уравнение изменения кинетической энергии груза. Для этого найдем скорость движения груза как:
[v=frac{dx}{dt}=-A{omega }_0{sin left({omega }_0t+varphi right)left(6right). }]
В таком случае кинетическая энергия равна:
[E_k=frac{m}{2}A^2{{omega }_0}^2{{sin}^2 left({omega }_0t+varphi right)left(7right). }]
Полная механическая энергия консервативной колебательной системы
Так как пружинный маятник мы считаем консервативной системой, то механическая энергия ее постоянна:
[E=E_k+E_p=const left(8right).]
Проверим справедливость выражения (8),) непосредственным суммированием правых частей выражений (4) и (7): (учитывая (5))
[E=frac{m}{2}A^2{{omega }_0}^2{{sin}^2 left({omega }_0t+varphi right)+ }{frac{kx^2}{2} =frac{m}{2}A^2frac{k}{m}{{sin}^2 left({omega }_0t+varphi right)+frac{k}{2}A^2 }{cos}^2left({omega }_0t+varphi right)=frac{k}{2}A^2=frac{1}{2}m{omega }^2_0A^2(9) },]
где ${{omega }_0}^2=frac{k}{m}$. Формула (9) показывает, что постоянная полная энергия колебательной системы равна потенциальной ее энергии в точках максимального отклонения от положения равновесия (при $x=pm A$). Энергия $E$ равна кинетической энергии при прохождении грузом положения равновесия, скорость груза равна:
[v_x=pm {omega }_0Aleft(10right).]
В ходе взаимных превращений потенциальная и кинетическая энергии гармонически колеблются с одинаковой амплитудой, равной $frac{E}{2}$ в противофазе друг с другом, частота их колебаний равна $2{omega }_0$.
[{E_k =frac{E}{2}left[1-{cos 2({omega }_0t+varphi ) }right]left(11right). }]
[E_p=frac{E}{2}left[1+{cos 2({omega }_0t+varphi ) }right]left(12right).]
Примеры задач на энергию гармонических колебаний
Пример 1
Задание. Что собой представляет фазовая траектория пружинного маятника, при рассмотрении его как гармонического осциллятора?
Решение. Уравнение фазовой траектории — это уравнение закона сохранения энергии:
[frac{kx^2}{2}+frac{mv^2_x}{2}=E=const left(1.1right).]
Разделим обе части выражения (1.1) на $E$ получим:
[frac{x^2}{2{E}/{k}}+frac{v^2_x}{2{E}/{m}}=1left(1.2right).]
Выражение (1.2) — это уравнение эллипса, полуоси которого равны $sqrt{2{E}/{k}}$ и $sqrt{2{E}/{m}}$.
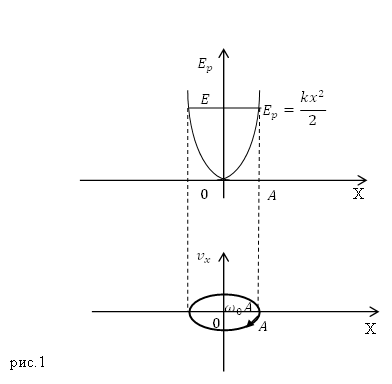
Фазовую траекторию часто сопоставляют с графиком потенциальной энергии осциллятора. При этом в верхней части рисунка (рис.1) изображают график потенциальной энергии ($E_p(x)$), в нижней части изображают фазовую траекторию, которая соответствует колебаниям со значением полной энергии равной E, указанной на верхнем графике.
Пример 2
Задание. Материальная точка, имеющая массу $m=5cdot {10}^{-2}кг,$ совершает колебания в соответствии с законом: $xleft(tright)={cos (frac{3pi }{2}t)(м) }$. Какова полная энергия этой точки?
Решение. Полная энергия в консервативной колебательной системе величина постоянная и найти ее можно в соответствии с выражением:
[E=frac{1}{2}m{omega }^2_0A^2 left(2.1right).]
Рассматривая уравнение колебаний точки, данное в условии задачи:
[xleft(tright)={cos (frac{3pi }{2}t)(м) },]
имеем: $A=1 м; {omega }_0=frac{3pi }{2}$. Вычислим искомую энергию:
[E=frac{1}{2}cdot 5cdot {10}^{-2}cdot {left(frac{3pi }{2}right)}^21^2approx 0,56 left(Джright).]
Ответ. $E=0,56$ Дж
Читать дальше: гидравлический пресс.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Алексей Алексеевич Ивахно
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Колебания — это самая общая форма движения динамических систем около положения равновесия. При малых отклонениях от положения равновесия колебания обычно являются гармоническими. В этом заключается их особенная значимость.
Уравнение вида:
$frac{d^2x}{dt^2}+omega^2x=0 (1),$
где $omega^2$ — циклическая частота колебаний; $x$ -расстояние положения равновесия
называют уравнением механических гармонических колебания. Колебания происходят вдоль оси $X$.
Решением уравнения (1) можно считать функции:
$x=Asin (omega t+varphi)$ или
$x=Acos (omega t+varphi_1)$,
где $A$ — амплитуда колебаний.
Систему, которая реализует данные малые колебания, называют линейным или гармоническим осциллятором. Примером гармонического осциллятора может служить
- малое тело, подвешенное на упругую пружину (Пружинный маятник);
- физический маятник (Тело, которое совершает колебания относительно точки (или оси, проходящей через точку тела), не являющейся его центром масс);
- математический маятник; (Малое тело, совершающее колебания на длинном, нерастяжимом, невесомом подвесе).
Определение 1
Собственными называют колебания системы под воздействием только внутренних сил при отсутствии внешних воздействий.
В полной механической энергии гармонического осциллятора выделяют:
- потенциальную энергию;
- и кинетическую энергию.
Потенциальная энергия
Говорить о потенциальной энергии можно только, если действующие силы потенциальны. Если колебательные движения между двумя точками являются одномерным, то автоматически обеспечивается условие потенциальности и всякую силу, зависящую только от координат, можно считать потенциальной.
Если рассматривается линейный осциллятор, то обычно считают, что потенциальная энергия точки равна нулю в положении равновесия. Считая, что осциллятор заставляет совершать колебания сила упругости;
$F=-kx(2)$
и зная, как связана потенциальная энергия и потенциальная сила, (для одномерного случая: $F=-frac{dU}{dx}$), потенциальную энергию линейного осциллятора определим как:
«Энергия гармонических колебаний» 👇
$U(x)=frac{kx^2}{2}=frac{momega^2x^2}{2}=frac{mA^2omega_0^2}{2}cos^2 (omega t+varphi)= frac{mA^2omega_0^2}{4}(1+cos 2(omega t +varphi)) (3).$
Из формулы (3) видно, что потенциальная энергия при колебаниях изменяется с течением времени, так как изменяется $x$. Частота колебаний потенциальной энергии $2omega$.
Кинетическая энергия.
Кинетическая энергия тела – это энергия движения, она зависит от скорости перемещения материальной точки, задается выражением:
$E_k=frac{mv^2}{2}=frac{mdot{x}^2}{2}=frac{mA^2omega_0^2}{2}sin^2 (omega t+varphi) =frac{mA^2omega_0^2}{4}(1-cos 2(omega t +varphi)) (4).$
Кинетическая энергия является переменной во времени физической величиной. Колебания ее происходят с частотой $2omega$ (эта частота в два раза больше, чем частота колебаний $x$)
Закон сохранения энергии при гармонических колебаниях
Как было отмечено, кинетическая энергия и потенциальная энергия являются переменными во времени величинами, однако, их сумма у гармонического осциллятора, выполняющего свободные колебания, не изменяется:
$frac{mdot{x}^2}{2}+frac{momega^2x^2}{2}=frac{momega^2A^2}{2}=const$.
Полная энергия системы ($E$) не изменяется, поскольку при гармонических колебаниях выполняется закон сохранения механической энергии, так как сила упругости является консервативной.
Закон сохранения энергии позволяет сделать два существенных вывода
Вывод первый. Наибольшая кинетическая энергия осциллятора равна его наибольшей энергии потенциальной энергии.
Данный вывод очевиден, так как потенциальная энергия осциллятора максимальна при смещении точки выполняющей колебания на максимально возможное расстояние, при этом скорость, а соответственно и кинетическая энергия осциллятора равна нулю.
Наибольшую кинетическую энергию колебательная система имеет тогда, когда она проходит положение равновесия ($x=0$), то есть потенциальная энергия равна нулю.
$frac{mV^2}{2}=frac{momega^2A^2}{2}(5),$
где $V$ — максимальная скорость.
Вывод второй. Средняя кинетическая энергия осциллятора равна его средней потенциальной энергии.
Средняя кинетическая энергия.
Пусть параметр $f$ функция времени, тогда средняя ее величина на отрезке времени от $t_1$ до $t_2$ равна:
$f_{sr}=frac{1}{t_2-t_1}int_1^2f(t)dt (6),$
где пределы интегрирования обозначают 1 — время $t_1$; 2 — $t_2$.
Если функцию $f(t)$ изобразить на графике (рис.1), то ее среднее значение будет соответствовать высоте прямоугольника, площадь которого ограничивают функция $f$ и ось $t$ на заданном отрезке времени.
Замечание 1
Площадь под осью $t$ считают отрицательной.
Рисунок 1. График. Автор24 — интернет-биржа студенческих работ
Запишем закон движения осциллятора как:
$x(t)=Acos (omega t+varphi) (7)$,
его скорость равна:
$dot{x}=-Aomegasin (omega t+varphi) (8).$
Выражение для потенциальной энергии представим как:
$U(t) = frac{omega^2A^2}{2}cos^2 (omega t+varphi) (9)$.
Кинетическую энергию представит выражение:
$E_k=frac{omega^2A^2}{2}sin^2 (omega t+varphi) $
Отрезком времени, на котором будем брать среднее, станет период колебаний, вернее одного колебания. Нахождение средних значений кинетической и потенциальной энергии сводят к поиску средних от $cos^2 (omega t+varphi)$ и $sin^2 (omega t+varphi)$:
$(sin^2 (omega t+varphi))_{sr}=frac{1}{T}int_0^T cos^2 (omega t+varphi)dt=frac{1}{T}int_0^Tfrac{1}{2}(1-cos 2(omega t+varphi)dt)=frac{1}{2},$
где $T$ — период колебаний; $omega T=2pi.$
По аналогии получаем:
$sin^2 (omega t+varphi)_sr=frac{1}{2}.$
В результате имеем:
-
средняя по времени потенциальная энергия гармонического колебания за один период равна:
$U_{sr}=frac{momega^2A^2}{4}(10),$
-
средняя по времени кинетическая энергия составила:
$E_{k,sr}=frac{momega^2A^2}{4}(11)$.
Сравнивая (10) и (11) мы видим, что:
$U_{sr}= E_{k,sr}=frac {1}{2}E$,
где $E$ — полная механическая энергия гармонических колебаний.
то есть средняя по времени кинетическая энергия осциллятора равна средней по времени потенциальной энергии.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Введём энергию колебания.
Колебательная система движется со скоростью , тогда его кинетическая энергия должна быть равна:
(1)
- где
Вспомним зависимость скорости от времени при гармоническом колебании:
(2)
- где
Подставим (2) в (1) при условии (для упрощения):
=
(3)
Тогда максимальная кинетическая энергия данной системы:
(4)
т.к. максимальное значение .
С другой стороны для пружинного маятника можем записать потенциальную энергию деформации:
(5)
- где
Вспомним зависимость координаты от времени при гармоническом колебании:
(6)
Подставим (5) в (4) при условии (для упрощения):
=
(7)
Тогда максимальная потенциальная энергия данной системы:
(8)
т.к. максимальное значение .
Вывод: задачи школьной физики чаще всего связаны именно с максимальным значением энергии колебания. Её можно рассчитать и как кинетическую энергию в положении равновесия (4), и как потенциальную энергию в точке максимального отклонения (8).
Содержание:
Гармонические колебания:
Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием.
Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением (
Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня.
Коэффициент упругости пружины – 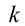
Если груз, который находится в равновесии, потянем вправо на расстояние 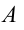
сторону равновесного состояния.
С течением времени смещение груза уменьшается относительно 
Для определения закономерности изменения в течение времени системы, которая периодически совершает колебания, заполним воронку песком, подвесим на веревке, подложим бумагу под систему и раскачаем воронку. В ходе колебания начинаем равномерно вытягивать бумагу из-под системы. В результате мы увидим, что следы песка на бумаге образуют синусоиду. Из этого можно сделать следующий вывод: смещение периодически колеблющегося тела по истечении времени изменяется по закону синусов и косинусов. При этом самое большое значение смещения равняется амплитуде (
здесь: 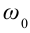
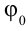
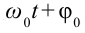
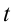
Из математики известно, что 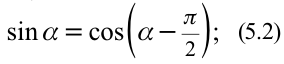
Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями.
Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений.
Основные параметры гармонических колебаний
a) период колебания 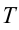

б) частота колебания 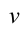
Единица
c) циклическая частота 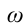
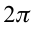
С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме.
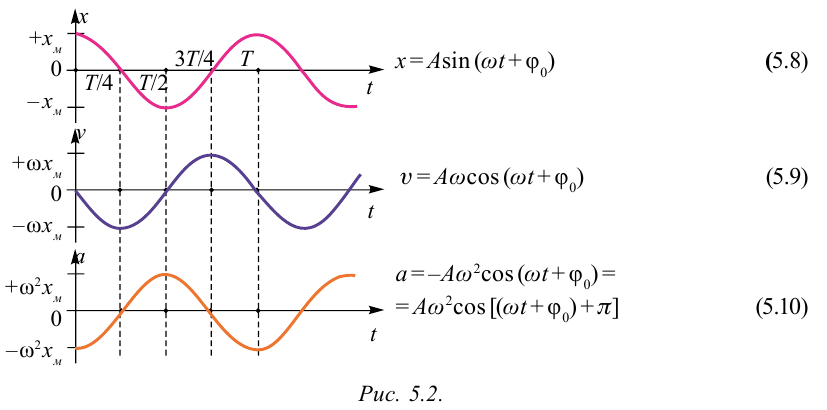
Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются.
Это подтверждается следующими графиками и уравнениями:
Пример решения задачи:
Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.
Дано:
Найти:
Формула и решение:
Гармонические колебания пружинного маятника
В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний.
Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.
Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:
Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.
Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.
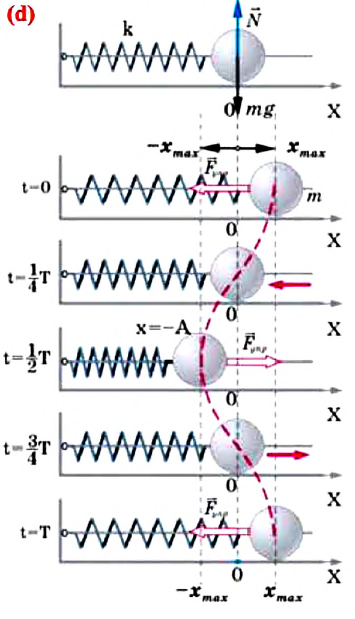
С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).
В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения 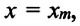
или
Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.
Где 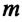
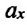
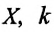
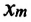
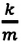
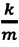
или
Таким образом, уравнение движения пружинного маятника можно записать и так:
Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой 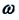
Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.
Здесь 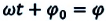
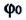
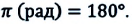
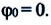

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.
Гармонические колебания математического маятника
До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.
Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника.
Математический маятник — это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити.
Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b).
Сила тяжести 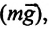
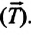
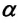
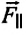
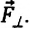
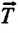
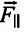
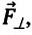
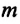
Приняв во внимание, что:
Для уравнения движения математического маятника получим:
Где 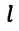
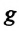
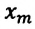
Для данной колебательной системы отношение 

или
Таким образом, уравнение движения математического маятника можно записать и так:
Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция:
Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями.
Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника:
Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке.
Скорость и ускорение при гармонических колебаниях
Вы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания.
При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю
Так как скорость является первой производной смещения (координат) по времени, то:
или
Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на 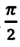
Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний:
Так как ускорение является первой производной скорости по времени, то получим:
или
Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на 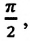
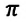
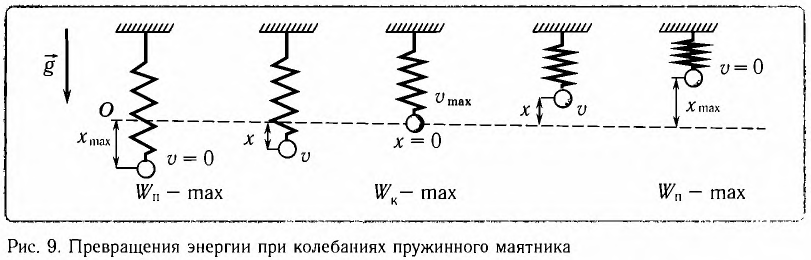
Превращения энергии при гармонических колебаниях
Теоретический материал
Потенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга.
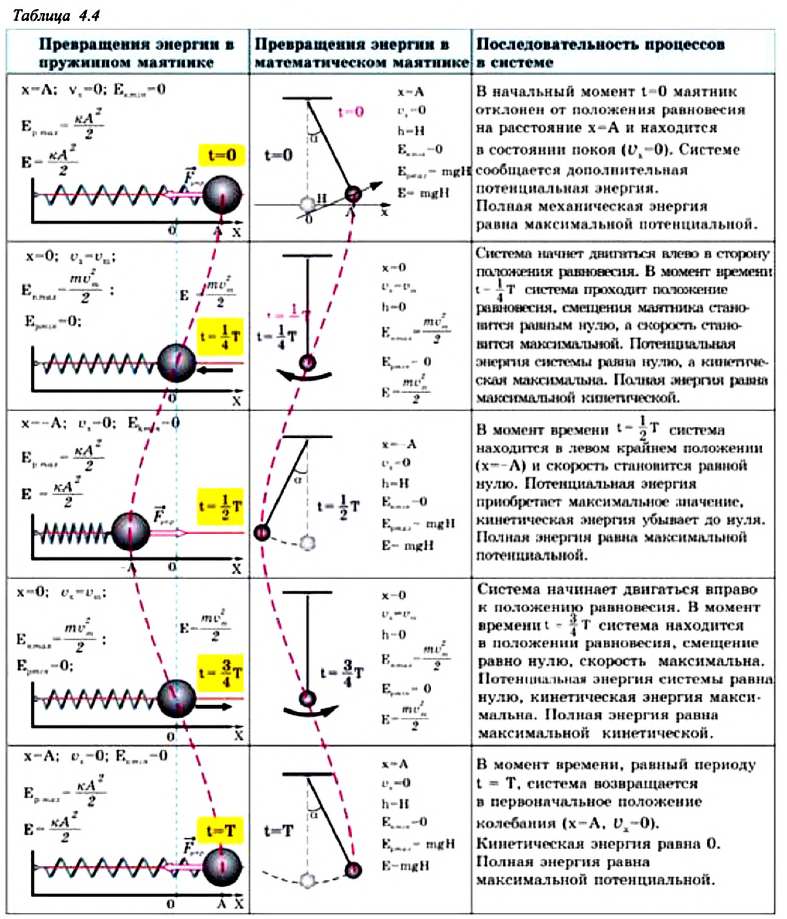
В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения 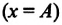
Если же маятник находится в точке равновесия, потенциальная энергия минимальна:
Кинетическая энергия системы, наоборот, в точке возвращения минимальна 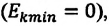
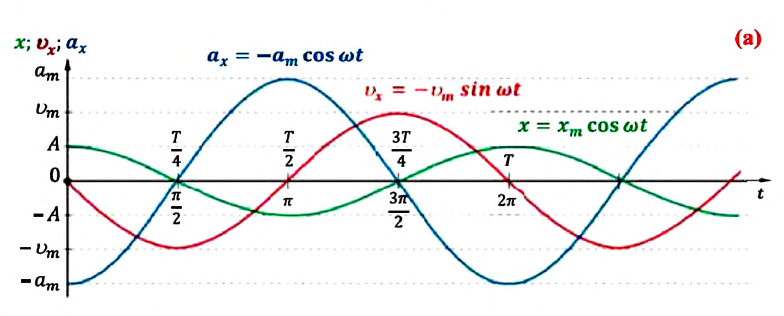
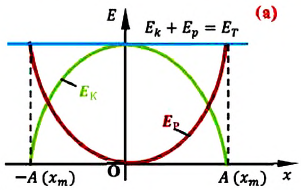
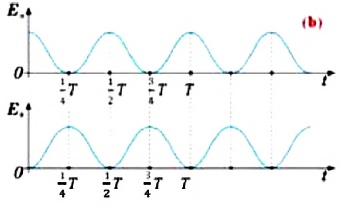
На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения.
Полная механическая энергия замкнутой колебательной системы в произвольный момент времени 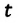
a) для пружинного маятника:
b) для математического маятника:
Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b):
Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону:
• Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний.
Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают:
Превращения энергии при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.
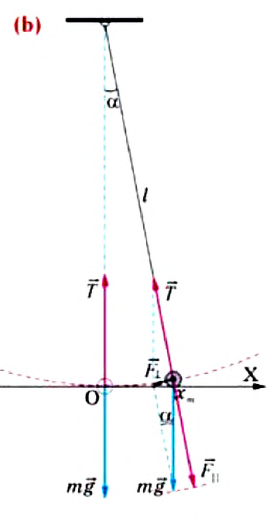
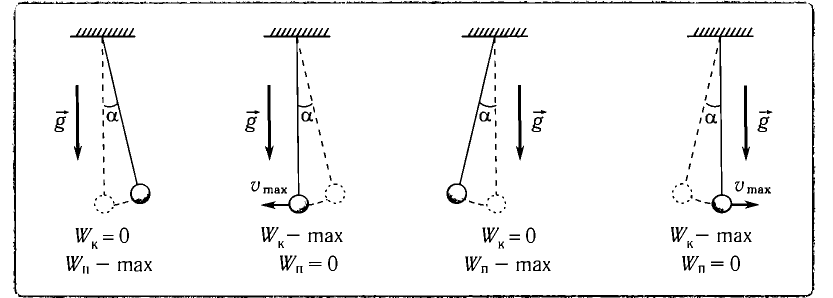
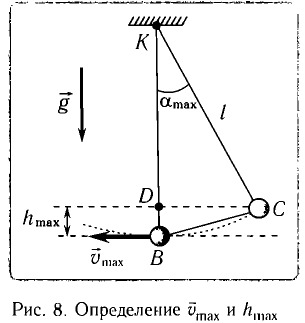
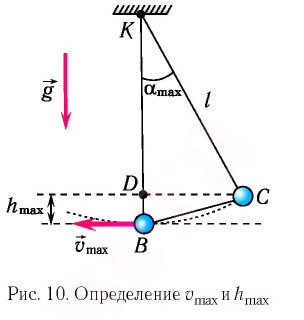
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:
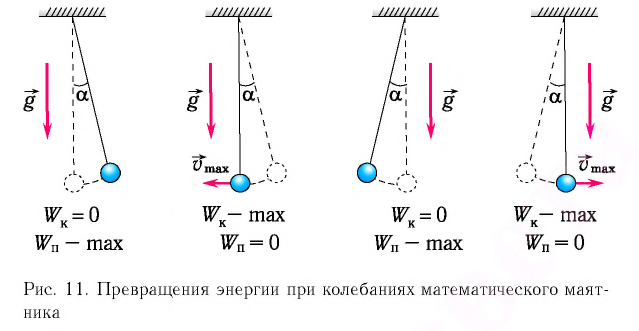
Рис. 7. Превращения энергии при колебаниях математического маятника
Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:
Из закона сохранения механической энергии следует (рис. 8), что
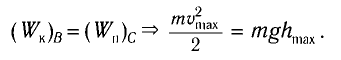
Отсюда найдем модуль максимальной скорости маятника:
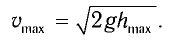
Высоту 
Если колебания малые, то 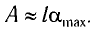
Отсюда
Подставив выражение для 
Подставляя выражения для 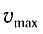

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.
В любом промежуточном положении
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение 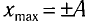
Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза:
где 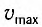
В промежуточных точках полная механическая энергия
Отсюда можно вывести выражение для модуля скорости 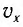
координатой х:
Так как
Энергия при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
При отклонении маятника на угол 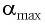
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю 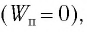
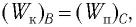
Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии:
Отсюда найдем модуль максимальной скорости маятника:
Высоту 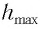
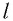
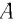
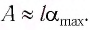
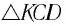
или
Подставив выражение (3) для 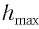
Подставляя выражения (3) для 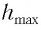
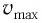
Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении
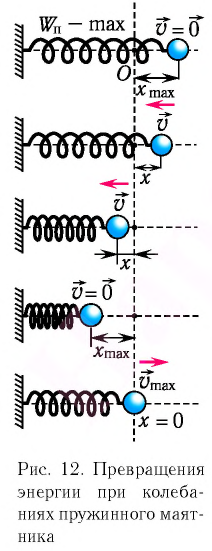
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12).
В крайних положениях, когда 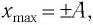
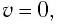
Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда 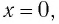
где 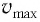
В положениях между крайними точками полная энергия
С учетом выражений для координаты 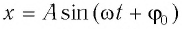
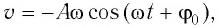
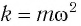
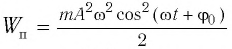
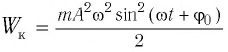
Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная:
Таким образом, начальное смещение 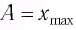
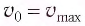
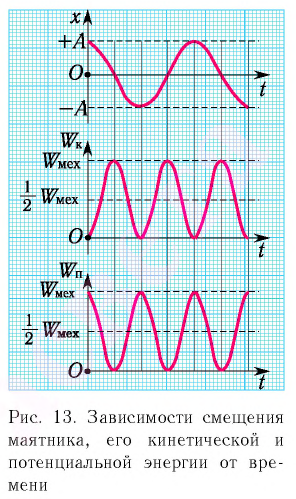
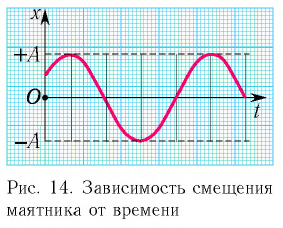
Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13).
Пример №1
Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние 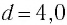
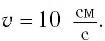
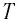
Дано:
Решение
По закону сохранения механической энергии
Отсюда:
Ответ:
Пример №2
Груз массой 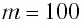
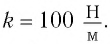
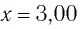
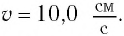
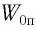
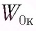
Дано:
Решение Потенциальная энергия груза:
Кинетическая энергия груза:
Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний:
Отсюда
Циклическая частота:
В начальный момент времени 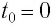
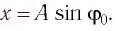
Тогда закон гармонических колебаний имеет вид (рис. 14):
Ответ:
- Вынужденные колебания в физике
- Электромагнитные колебания
- Свободные и вынужденные колебания в физике
- Вынужденные электромагнитные колебания
- Закон Архимеда
- Движение жидкостей
- Уравнение Бернулли
- Механические колебания и волны в физике