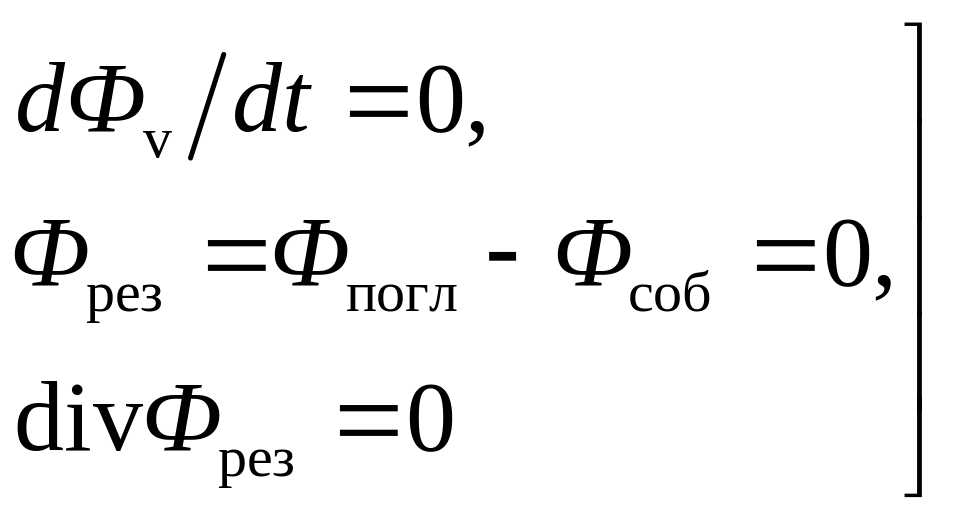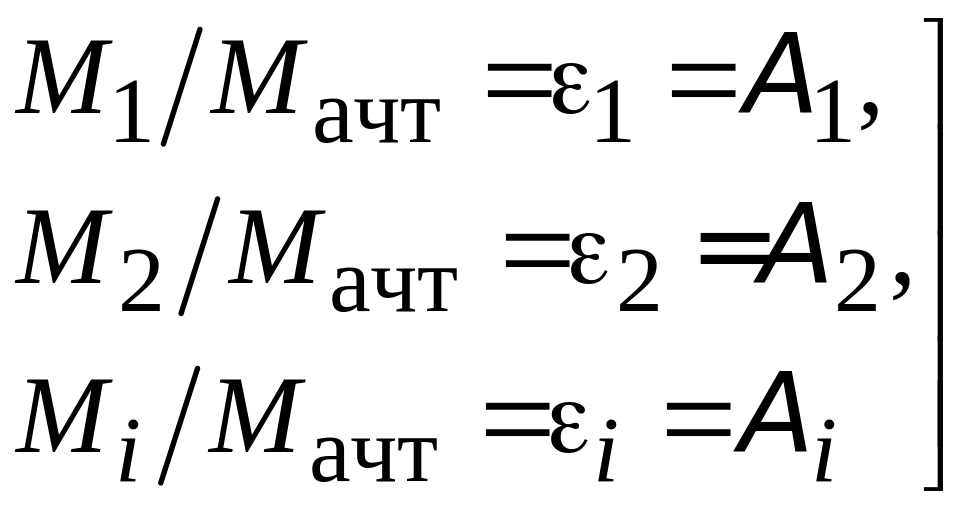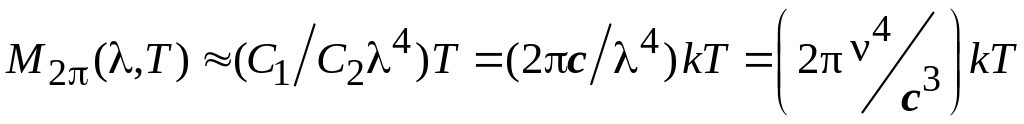характеризующие
излучение, и единицы их измерения
Энергия излучения
– это количественная мера различных
превращений материи, и, в частности,
той, которая называется излучением.
Энергия –
это количество излученной, поглощенной,
отраженной, пропущенной или рассеянной
энергии. Единицами
измерения энергии являются:
1 Дж = 1 Кл·1 В; 1 эВ = 1 е·1 В = 1,6·10—19
Дж.
Мощность (поток)
излучения
— это энергия излучения
,
излученная, поглощенная, отраженная,
пропущенная или рассеянная за интервал
времени
,
значительно превосходящий период
колебаний световой волны, т. е.
.
Единицей измерения
мощности (потока) излучения является 1
Вт = 1 Дж/с.
Угловая плотность
потока излучения (сила излучения)
– это поток излучения
точечного
источника,
распространяющийся в данном направлении
в малом телесном угле
,
т. е.
. (1.1)
Сила излучения
измеряется в Вт/ср.
Точечным источником
называют источник излучения, поперечные
размеры которого во много раз меньше
по сравнению с расстоянием до объекта
облучения.
Телесный угол –
это область пространства, ограниченная
конической поверхностью с центром в
точке расположения источника, которая
опирается на элемент сферической
поверхности
с произвольным радиусом
,
т. е.
.
Единицей измерения телесного угла
является 1 стерадиан, так, что при
=
,
= 1 ср. В частном случае для кругового
конуса с половинным углом
при вершине
и
.
(1.2)
Излучательность
– это поток
излучения, который испускается во всех
направлениях (например, в полусферу)
единичной излучающей площадкой
протяженного источника излучения (не
являющегося точечным); при
ср эту величину называют полусферической
излучательностью
,
[Вт/м2].
(1.3)
Облученность
– это поток излучения, падающий на
единицу площади независимо от направления
его распространения (иначе — поверхностная
плотность падающего потока), т. е.
,
[Вт/м2].
Энергетическая
яркость
— это отношение потока излучения
,
распространяющегося в заданном
направлении
в пределах телесного угла
,
к площади проекции
элемента излучающей площади
на плоскость, перпендикулярную направлению
лучей, т. е.
[Вт/м2
ср]. (1.4)
1.3. Основные законы равновесного теплового излучения
Тепловое излучение
является результатом превращения
энергии микрочастиц вещества (электронов,
ионов, атомов, молекул) в энергию их
возбуждения и затем в энергию
электромагнитного излучения. Из теплового
излучения исключаются такие процессы
излучения, которые обусловлены не
температурой тела, а связаны с какими-либо
его изменениями (ионизацией, поляризацией,
химическими реакциями, фазовыми
превращениями) либо сопровождаются
неравновесными процессами излучения
(люминесценцией, тормозным, рекомбинационным
или вынужденным когерентным излучением),
либо, наконец, перераспределением
энергии излучения в пространстве
(интерференцией волн).
Физическим носителем
равновесного
теплового излучения
является абсолютно черное тело (АЧТ),
модель которого, строго говоря,
представляет собой вакуумированную
замкнутую полость (часто в виде сферы),
ограниченную непрозрачными изотермическими
стенками, теплоизолированными от
окружающей среды. При необходимости
вывода излучения наружу полость
снабжается отверстием малой площади
(
— площадь внутренней поверхности
полости), которое не нарушает равновесия
в полости и позволяет считать, что
отверстие АЧТ полностью поглощает все
падающее внутрь него излучение независимо
от направления его распространения,
поляризации и спектрального состава,
т.е. характеризуется полусферическим
коэффициентом поглощения равным единице
При установлении
в полости АЧТ состояния термодинамического
равновесия (ТДР) совокупность любых
находящихся внутри полости тел, элементов
ее собственных стенок и объемной
плотности энергии излучения является
равновесной
системой. В
равновесной системе (полости) в
соответствии с принципом
детального равновесия
излучение может оставаться макроскопически
неизменным во времени, если каждому
происходящему в полости элементарному
микропроцессу соответствует обратно
направленный микропроцесс той же
вероятности. Состояние ТДР соответствует
выполнению условий
,
(1.5)
которые утверждают
неизменность объемной плотности мощности
равновесного излучения во времени и в
пространстве и отсутствие результирущего
теплообмена в любой точке полости.
Внутри полости акты излучения и поглощения
статистически независимы, равновероятны
и уравновешены.
Из формул (1.5) и
принципа детального
равновесия вытекает
обязательность таких конкретных свойств
поля равновесного излучения:
,
которое свидетельствует о равновероятности
элементарных актов излучения любого
направления,
т.е. о выполнении закона Ламберта,
устанавливающего изотропность
равновесного излучения;
,
которое соответствует изотермичности
объема и любых поверхностей в полости,
включая и ее стенки.
Заметим, что
успешность создания совершенной модели
АЧТ зависит от степени соблюдения
указанных условий.
К основным законам
равновесного излучения относятся:
1. Закон
Ламберта (закон косинуса) (1760 г.).
Многолетний опыт показывает, что
поверхность многих естественных и
искусственных объектов или толстые
слои дисперсных сред (такие как земная
поверхность, песок, шероховатая
поверхность графита, бумага, мел, облака,
атмосфера и др.) характеризуются угловой
зависимостью силы излучения, близкой
к закону косинуса, т.е.
где
сила излучения в направлении нормали
к поверхности.
Для таких объектов
энергетическую яркость (см. формулу
(1.4)) можно представить в виде
,
который показывает,
что энергетическая яркость этих объектов,
называемых ламбертовскими,
при отклонении
направления излучения от нормали к
излучающей поверхности остается
постоянной.
Объединяя формулы
(1.1), (1.2) и (1.4), представим элементарный
поток излучения
ламбертовского
источника
в элемент телесного угла
в направлении
относительно нормали к поверхности
выражением
Интегрируя последнее
выражение по углу
в пределах полупространства (
),
получим
и в соответствии
с (1.3) запишем
=
.
(1.6)
Выражение (1.7)
устанавливает зависимость между
полусферической излучательностью и
энергетической яркостью равнояркого
(т.е. ламбертовского)
источника излучения.
По аналогии с
результатом (1.6) интегрированием
в пределах телесных углов
ср можно получить полезную в энергетических
расчетах угловую зависимость
излучательности ламбертовских источников
в виде
.
Заметим, что закон
Ламберта строго соблюдается только для
АЧТ.
2. Закон Кирхгофа
(~1860 г.). Закон
Кирхгофа является результатом детального
анализа излучательного энергообмена
системы произвольно излучающих и
поглощающих тел, расположенных в
замкнутой непрозрачной изотермической
полости, изолированной от внешней среды.
Пусть в замкнутой полости находятся
два непрозрачных тела в состоянии
температурного равновесия, которые
имеют излучательности
и
и коэффициенты поглощения
и
.
Полагая, что тело 1 посылает в направлении
тела 2 собственную мощность
и
отраженную мощность
,
а тело 2 в направлении тела 1 – соответственно
мощности
и
,
запишем их энергетический (тепловой)
баланс уравнением
=
=
=
,
из которого следует, что
,
(1.7)
т.е. тела,
находящиеся в состоянии ТДР, испускают
потоки излучения пропорциональные их
коэффициентам поглощения.
Положив, что одно из этих тел, например
тело 1, является абсолютно черным, т. е.
характеризуется излучательностью
и
=1,
из (1.7) получим формулу
,
(1.8)
которая является
другим, равноценным формуле (1.7), выражением
закона Кирхгофа, показывающим, что
отношение
излучательности любого тела к его
коэффициенту поглощения при данной
температуре в равновесном состоянии
не зависит от природы тела и равно
универсальной
функции
– излучательности АЧТ при данной
температуре.
Преобразовав равенства (1.9), запишем их
в виде уравнений
,
(1.9)
в которых отношения
вида
по определению являются коэффициентами
излучения
любого тела в равновесном состоянии.
Из уравнений (1.9) видно, что в равновесном
состоянии для любого тела при данной
температуре справедливо тождество
,
которое является еще одним (равноценным
с указанными ранее) выражением закона
Кирхгофа2.
3. Закон Планка
(1900 г.).
Универсальная функция
(см. 1.8), впервые постулированная Кирхгофом
(1859 г.), была получена М. Планком (спустя
более 40 лет) путем отказа от важнейшего
в классической термодинамике принципа
равного распределения энергии по
степеням свободы и использования
гипотезы квантования энергии излучения
[1.3., С. 18] в виде
,
(1.10)
где
;
;
,
константы, выраженные через
постоянную
Планка,
,
постоянную
Больцмана;
— длина волны излучения.
При условии
1
универсальная функция Планка (1.10)
переходит в известную формулу
Вина
,
(1.11)
которая была
получена (~1896 г.) на основе классической
электродинамики и максвелловского
распределения скоростей микрочастиц
и с отклонением менее 1 % воспроизводит
функцию Планка в коротковолновой области
спектра излучения АЧТ. Из выражений
(1.10) и (1.11) следует известный закон
смещения
Вина,
определяющий положение максимума
спектральной плотности излучательности
АЧТ по шкале длин волн и имеющий вид
мкм·К.
В другом предельном
случае при соблюдении условия
,
раскладывая в формуле (1.10) третий
множитель в ряд по степеням
и ограничиваясь двумя первыми членами,
получим
и запишем (1.10) в виде
,
(1.12)
т.е. формулу
Рэлея – Джинса,
которая была получена экспериментально
Рэлеем (1894 г.), теоретически обоснована
Джинсом (1906 г.) и удовлетворительно
совпадает с функцией Планка в длинноволновой
области спектра.
4. Закон
Стефана-Больцмана
(экспериментально установлен Стефаном
(1879 г.) и теоретически обоснован Больцманом
(1884 г.)) определяет зависимость интегральной
полусферической излучательности АЧТ
от его температуры, т. е. является
интегралом функции Планка по длине
волны (или другому спектральному
аргументу), который выражается формулой
,
(1.13)
где
Вт/(см2К4)
называется
постоянной Стефана-Больцмана. Формула
(1.13) показывает, что интегральная
полусферическая излучательность АЧТ
пропорциональна четвертой степени
абсолютной температуры T
тела.
Завершая рассмотрение
законов равновесного теплового излучения,
напомним, что в конце 19 века формула
Релея-Джинса (1.12) привела физиков к
представлению о так называемом кризисе
классической физики (иначе
– «ультрафиолетовой
катастрофе»
и даже о тепловой
смерти Вселенной).
Наглядным основанием
для таких выводов можно признать кривую
1
на рис. 1.1,
рассчитанную по формуле (1.12) и стремящуюся
к бесконечно большим значениям
спектральной плотности излучательности
АЧТ в коротковолновой (высокочастотной
(
))
области спектра. Анализ отношения
в формуле (1.12) показывает, что она
измеряется в единицах
и представляет собой число
степеней свободы (колебаний), приходящихся
на единицу объема в единицу времени.
Поскольку в классической физике средняя
энергия, приходящаяся при данной
температуре на одну степень свободы
есть постоянная величина
,
то естественно, что при постоянной
температуре излучателя и уменьшении
длины волны (или увеличении частоты
колебаний) спектральная плотность
излучательности должна была стремиться
к бесконечности.
Обратившись к
функции Планка (1.10), используем формулы
, определяющие постоянные
и
и, заменив
на
,
запишем функцию Планка в виде
,
(1.10′)
из которой следует,
что первый множитель (в круглых скобках),
как и в формуле Релея-Джинса (1.12), является
числом степеней свободы в единице объема
за единицу времени, а множитель (в
квадратных скобках) представляет собой
среднюю энергию, которая приходится на
одну степень свободы и изменяется в
зависимости от длины волны или частоты
излучения. Сравнение формул Релея-Джинса
(1.12) и Планка в виде (1.10′), показывает, что
результаты рассмотрения проблемы
равновесного излучения Джинсом (на
основе классической термодинамики) и
Планком (на основе квантовой гипотезы)
не отличаются числом степеней свободы
на единицу объема, но принципиально
различаются средней энергией, приходящейся
на одну степень свободы.
Таким образом,
использование квантовой гипотезы Планка
позволило не только избежать
«ультрафиолетовой катастрофы», но и
получить расчетный спектр излучения
АЧТ, точно совпадающий с экспериментом.
Идея квантования
энергии, введенная М. Планком в решение
проблемы равновесного излучения, как
оказалось со временем, далеко вышла за
рамки этой задачи, но скоро приобрела
фундаментальное значение в физике,
знаменуя собой начало новой — квантовой
физики.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кванты, Энергия кванта, формула
Согласно Планку, любое излучение (в том числе и свет) состоит из отдельных квантов. Вследствие этого энергия излучения всегда равна энергии целого числа квантов. Однако энергия отдельного кванта зависит от частоты.
Если
| E | энергия кванта, или квант энергии, | Дж |
|---|---|---|
| ν | частота излучения, | Гц |
| h | постоянная Планка (квант действия), | Дж × с |
постоянная Планка (квант действия)
[ h = 6,626176 × 10^{-34} ]
то энергия кванта определяется формулой:
[ E = hν ]
Вычислить, найти энергию кванта по формуле (2)
Кванты, Энергия кванта |
стр. 727 |
|---|
VI. Квантовая физика
Тестирование онлайн
Формула Планка
14 декабря 1900 г. Макс Карл Эрнст Людвиг Планк в докладе на заседании Берлинского физического общества выдвинул революционную гипотезу, что излучение света веществом происходит не непрерывно, а порциями, квантами.
Согласно гипотезе Планка наименьшая порция энергии, которую несет излучение, определяется по формуле (формула Планка):

Фотон
Развивая идею Планка, Эйнштейн предложил корпускулярную теорию света, предположив, что свет не только излучается, но распространяется и поглощается отдельными порциями. По теории Эйнштейна, монохроматическая электромагнитная волна представляет собой поток частиц — квантов или фотонов. Каждый фотон всегда движется со скоростью света и несет квант энергии. При взаимодействии с веществом фотон передает свою энергию одному или нескольким электронам, после чего фотона больше не существует.
Фотон — это удивительная частица, которая обладает энергией, импульсом, но не обладает массой! Фотон «обречен» всегда летать со скоростью света.
Свойства фотона:
1) Не имеет состояния покоя.
2) Безмассовая частица (m=0).
3) Электрически нейтрален (q=0).
4) Скорость его движения равна скорости света во всех инерциальных системах отсчета.
5) Энергия фотона пропорциональна частоте соответствующего электромагнитного излучения (формула Планка).
6) Энергия фотона может быть выражена через длину волны:

7) Модуль импульса фотона равен отношению его энергии к скорости:
To use your Google Account on a browser (like Chrome or Safari), turn on cookies if you haven’t already.
Important: If you get a message that cookies are turned off, you need to turn them on to use your account.
In Chrome
- On your computer, open Chrome.
- At the top right, click More
Settings.
- Under «Privacy and security,» click Site settings.
- Click Cookies and site data.
- From here, you can:
- Turn on cookies: Next to «Blocked,» turn on the switch.
- Turn off cookies: Turn off Allow all cookies.
Learn how to change more cookie settings in Chrome.
In other browsers
For instructions, check the support website for your browser.
Why cookies are helpful
Cookies are files created by sites you visit. They make your online experience easier by saving browsing information. With cookies, sites can:
- Keep you signed in
- Remember your site preferences
- Give you locally relevant content
We use cookies to improve our services. To learn more, read our Privacy Policy.
Fix problems
If you can’t use your Google Account and get a message that cookies are turned off:
- Follow the steps above to turn on cookies.
- Try signing in again.
If you still get the error message, here are some possible solutions. Try each one, then try signing in.
- Open a new browser window.
- Clear your browser’s cache and cookies. Learn how to clear cache and cookies.
- Browse in private. Learn how to browse privately in Chrome.
- Change your browser’s privacy settings. Learn how to change privacy settings.
Was this helpful?
How can we improve it?
Фотон
Фотон — это частица света или квант света; частица с которой можно делать расчёты.
Фотоны всегда находятся в движении и в вакууме движутся с постоянной скоростью 2,998 x 10^8 м/с (это называется скоростью света и обозначается буквой c).
В марте 1905 года Эйнштейн создал квантовую теорию света, это была идея о том, что свет существует в виде крошечных частиц, которые он назвал фотонами.
Позже в том же году была расширена специальная теория относительности, в которой Эйнштейн доказал, что энергия (E) и материя (масса – m) связаны, и это соотношение стало самым знаменитым в физике: E=mc²; (напомним: c — скорость света).
Формулы фотона
Эти формулы являются наиболее важными.
Формула энергии кванта/фотона (формула Планка или Энергия кванта)
Энергия — это постоянная Планка, умноженная на частоту колебаний
E = h×v
Где:
- E — энергия фотона/кванта (в Дж – джоуль),
- h = 6,6.10^(–34) (постоянная Планка, в Дж.с – джоуль в секунду),
- ν — частота колебаний света (в Гц – герц).
Масса фотона
m = hv/c² = h/cλ
Где:
- m — масса фотона (в кг),
- h = 6,6.10^(–34) (постоянная Планка, в Дж.с – джоуль в секунду),
- ν — частота колебаний света (в Гц – герц),
- c = 3.10^8 (это скорость света в м/с),
- λ — длина световой волны (в метрах).
Примечание:
Фотоны всегда движутся со скоростью света. В состоянии покоя фотоны не существуют (т.е. можно сказать, что масса покоя равна нулю).
Формула массы фотона (m = h/cλ) была выведена из формулы эквивалентности массы и энергии (E = mc²), при этом было использовано также равенство с энергией Кванта (E = h×v).
Импульс фотона
p = hv/c = h/λ
Где:
- p — импульс фотона (в Н•с – ньютон-секунда),
- h = 6,6.10^(–34) (постоянная Планка, в Дж.с – джоуль в секунду),
- ν — частота колебаний света (в Гц – герц),
- c = 3.10^8 (это скорость света в м/с),
- λ — длина световой волны (в метрах).
Длина волны света, период и частота
Это ещё одно соотношение, которое может быть полезным в расчётах.
λ = cT = c/v
Где:
- λ — длина световой волны (в метрах),
- c = 3.10^8 (это скорость света в м/с),
- T — период световых колебаний (в секундах),
- ν — частота колебаний света (в Гц – герц).
Пример решения задачи с данными формулами
Определите энергию фотонов красного (λк = 0,76 мкм) света.
Известно:
λк = 0,76 мкм = 0,76 × 10^(–6) м
Решение:
Формула энергии фотонов: E = h×v
Где:
h — постоянная Планка,
v — частота света; из равенства λ = c/v выходит, что v = с/λ.
Таким образом, составляем равенство:
E = h × (с/λ) = hc / λ
Вспоминаем другие данные:
c = 3.10^8 (это скорость света в м/с)
h = 6,6.10^(–34) (постоянная Планка, в Дж.с – джоуль в секунду)
E = hc / λ = ((6,6.10^(–34) Дж.с) × (3.10^8 м/с)) / (0,76 × 10^(–6) м) = 2,6 × 10^(–19) Дж
Фотон является волной?
Фотон является одновременно частицей и волной. Согласно квантовой теории света Эйнштейна, энергия фотонов (E) равняется их частоте колебаний (v), умноженной на постоянную Планка (h); т.е. эта формула выглядит так: E = h×v.
Так он доказал, что:
- свет — это поток фотонов,
- энергия этих фотонов — это высота их частоты колебаний,
- интенсивность света соответствует количеству фотонов.
Таким образом, учёный объяснил, что поток фотонов действует и как волна, и как частица.
Узнайте также про:
- Нейтрино
- Теорию относительности
- Магнитную индукцию
- Полимер
- Теорию струн