Как найти энергию магнитного поля катушки индуктивности - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание:

Расчет индуктивности
Определение энергии магнитного поля катушки индуктивности

Определение 1

Рассмотрим проводящий контур. Если проходящий по контуру ток будет меняться во времени, то в том же контуре возникнет электродвижущая сила. Такое явление называется самоиндукция.

Самоиндукция возникает за счёт взаимосвязи переменных электрического и магнитного полей. Если по контуру идёт переменный ток, то он создаёт переменное магнитное поле. Оно в свою очередь обуславливает изменение потока вектора магнитной индукции через поверхность, ограниченную контуром. Изменяющийся поток, согласно закону электромагнитной индукции вызывает появление ЭДС (электродвижущей силы)

При этом, магнитный поток контура Φ находится в прямой зависимости от величины тока. Выполняется соотношение: Φ=LI.

Определение 2

Коэффициент самоиндукции (L), также называемый индуктивностью контура или катушки, является коэффициентом пропорциональности в формуле Φ=LI. Физический смысл величины в том, что она является мерой электрической инерции катушки (контура).

В международной системе СИ, индуктивность измеряется в Генри (Гн). Контур обладает индуктивностью в 1 Генри, если при росте, либо снижении электротока на 1 Ампер за 1 секунду, создаётся ЭДС индукции величиной в 1 Вольт. Верна запись: $ 1Гн = 1Вбcdot 1А$.

Расчет индуктивности

Пример 1

Чтобы лучше понять, что такое индуктивность, рассмотрим пример вычисления данного параметра для катушки, имеющей N витков. Обладающей площадью поперечного сечения S и длина которой составляет l. В этом случае возьмём такую катушку цилиндрической формы, длина которой во много раз больше диаметра. Запишем магнитную индукцию:

$ B = μ_0 nI $

I — ток в катушке;

$ n = N/e $ — величина, характеризующая количество витков, соответствующее единице длины катушки.

Запишем выражение для магнитного потока проходящего через N витков:

$ Φ = B cdot S cdot N = (μ_0 n^2 cdot S)/l $

Запишем выражение для индуктивности:

$ L = μ_0 cdot n^2 S cdot l = $,

$ V = Scdot l $ – объем катушки с магнитным полем.

Наше решение является оценочным и не рассматривает целый ряд нюансов, таких, как, например, краевые эффекты. Однако оно остаётся полностью верным в определённых граничных условиях — так, влиянием краевых эффектов можно пренебречь, если длина катушки в несколько раз больше её диаметра.

Несмотря на ограничения, данный пример хорошо иллюстрирует принцип возникновения ЭДС самоиндукции. Также видно, что от типа вещества которым заполнена катушка, точнее от его магнитной проницаемости μ, зависит индуктивность. Она будет тем больше по модулю, чем больше μ. Индуктивность катушки имеющей сердечник будет в μ раз больше, чем у такой же катушки, но без сердечника:

$ L_μ = μ cdot L = μ_0 cdot μ cdot n ^2 cdot V $

Определение 3

Также мера инерции электрического контура (катушки), то есть способность сопротивляться изменению (повышению, понижению, возникновению) электрического тока в нём, характеризуется через ЭДС самоиндукции. Параметр зависит от характеристик вещества проводника. Записывает следующим образом:

$delta _{инд}=delta_L = -frac{triangle Ф}{triangle t} = -L frac{triangle I}{triangle t} $

ЭДС самоиндукции имеет зависимость не только от скорости приращения или убывания магнитного потока, но и от того как быстро происходит изменение тока, протекающего в проводящем контуре.

В случае подключения катушки, созданное ею магнитное поле играет роль накопителя энергии. Проверить это утверждение не трудно, достаточно включить в схему параллельно катушке лампу. При отключении схемы от питания, лампа ненадолго зажжётся — это убывающее магнитное поле создало ЭДС, сгенерировало непродолжительный электрический ток.

В целом же энергия запасаемая катушкой и вовсе никуда не исчезает. Согласно закону сохранения энергии она превращается во внутреннюю энергию, вызывая нагрев. Пусть R сопротивление системы, а Δt время передачи тепловой энергии, тогда верно следующее выражение:

$triangle Q = I^{2}Rtriangle t$

Для электротока:

$I=frac{delta_L}{R} = — frac{L}{R}frac{triangle I}{ triangle t}$

Изменение тепла $ triangle Q $:

$triangle Q = − L ⋅ I ⋅ triangle I = − Φ ( I ) triangle I $

Очевидно, что изменение тока $ triangle I < 0 $;

При передаче энергии происходит уменьшение электротока от $I_0$ до нулевого значения. Интегрируя по электротоку получим выражение для тепловой энергии, которая выделится при отключении катушки от питания:

$ Q = frac {L I_0^2}{2} $

Определение энергии магнитного поля катушки индуктивности

Зависимость магнитного потока Φ от электротока I, то получим прямую, направленную под углом из центра координат. Попробуем с помощью такого графика определить энергию магнитного поля. Здесь вся, выделившаяся в виде тепла, энергия будет представлена в виде площади прямоугольного треугольника, катетами которого станут значения потока и элетротока. Тогда используя выражение

Φ=LI

получим для энергии $ W_м $ магнитного поля катушки, имеющей индуктивность L, проходящий ток I, следующее выражение:

$ W_м = frac {Φ I} {2} = frac {L I^2}{2} = frac {Φ^2} (2 L) $

Применим здесь выведенное в первом примере выражение и получим формулу:

$ W_м = frac {μ_0 μ n^2 I^2}{2} V = frac {B^2} {2 μ_0 μ} V $, где

$ L_μ $ — самоиндукция;

В — индукция магнитного поля;

I — величина силы тока;

V — объем соленоида.

Формула наглядно показывает характер распределения энергии магнитного поля. Он не сосредоточена в витках или в сердечнике — она равномерно распределена по всему объёму соленоида.

Определение 4

Введём понятие плотность энергии. Данный параметр актуален для магнитного поля и характеризует способность электромагнитного элемента накапливать энергию. Плотность показывает количество энергии сосредоточенное в одной единице объёма. Вычисляется как:

$W_м = frac{B^2}{ 2 μ_0 ⋅ μ} $

Согласно исследованиям Максвелла, формула верно описывает физическую величину применительно к любым магнитным полям.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Источник

Магнитное поле, связанное с электрическим током, характеризуется определенной энергией.

Если через проводник или катушку проходит ток, то часть электроэнергии расходуется на преодоление сопротивления проводника и превращается в тепло, а часть образует магнитное поле, в котором накапливается некоторая часть энергии, превращается в потенциальную энергию.

Определение магнитной энергии

Магнитная энергия и электростатическая потенциальная энергия связаны уравнениями Максвелла. Потенциальная энергия магнитного момента mm в магнитном поле BB определяется как механическая работа магнитной силы (фактически магнитного момента) на повторное выравнивание вектора магнитного дипольного момента и равна:

E=−m⋅BE = — m cdot B

в то время как энергия, запасенная в катушке индуктивности (с индуктивностью LL) при прохождении через нее тока II, определяется как:

E=1/2LI2E = 1/2 LI^2

Это выражение лежит в основе сверхпроводящего накопления магнитной энергии.

Энергия также хранится в магнитном поле. Энергия на единицу объема в области пространства проницаемости μ0μ0, содержащей магнитное поле BB, равна:

U=B2/2μ0U = B^2/2μ_0

В более широком смысле, если мы предположим, что среда является парамагнитной или диамагнитной и существует линейное определяющее уравнение, связывающее BB, то можно показать, что магнитное поле хранит энергию

E=12∫HBdV,E=frac{1}{2}int{HBdV},

где интеграл оценивается по всей области, где существует магнитное поле.

Аналогично энергию магнитного поля тока можно определить также через работу тока против ЭДС самоиндукции, которая выполняется при замыкании цепи.

Сравнивая выражение энергии магнитного поля через индукцию и силу тока с формулой для определения кинетической энергии, делаем вывод, что индуктивность в электромагнитных явлениях играет такую же роль, как масса в механических явлениях, и является мерой инертности электрической цепи.

Энергия магнитного поля соленоида

Индуктивность контура

Физическая величина, определяемая удвоенной энергией магнитного поля, сформированного единичным током в этом контуре.

Определим энергию магнитного поля соленоида, индуктивность которого LL:

L=μμ0n02VL=mu {{mu }_{0}}n_{0}^{2}V

Wm=12μμ0n02I2V{{W}_{m}}=frac{1}{2}mu {{mu }_{0}}n_{0}^{2}{{I}^{2}}V.

Индукция магнитного поля внутри соленоида:

B=μμ0n0IB=mu {{mu }_{0}}{{n}_{0}}I

откуда

I=Bμμ0n0I=frac{B}{mu {{mu }_{0}}{{n}_{0}}}

Из данных формул получаем

Wm=12B2Vμμ0,{{W}_{m}}=frac{1}{2}frac{{{B}^{2}}V}{mu {{mu }_{0}}},

где VV –объем соленоида.

Поскольку поле соленоида однородно и почти полностью локализовано в его объеме, можно определить плотность энергии магнитного поля, то есть энергию, рассчитанную на единицу объема поля:

wm=WmV=12B2μμ0=BH2=μμ0H22{{w}_{m}}=frac{{{W}_{m}}}{V}=frac{1}{2}frac{{{B}^{2}}}{mu {{mu }_{0}}}=frac{BH}{2}=frac{mu {{mu }_{0}}{{H}^{2}}}{2}

Плотность энергии магнитного поля как характеристику поля относят к любой точке поля, в которых заданы векторы BB или HH.

Зная энергию магнитного поля, можно по теории относительности найти подходящую массу поля:

m=Wmc2m=frac{{{W}_{m}}}{{{c}^{2}}}

Итак, как электрическое, так и магнитное поля имеют не только энергию, но и массу. Эти поля так же материальны, как и вещества.

Тест по теме «Энергия магнитного поля»

Источник

Явление самоиндукции заключается в возникновении индукционного тока (тока самоиндукции) в катушке при изменении силы тока в ней.

В опыте, демонстрирующем самоиндукцию при размыкании цепи, лампа, перед тем как погаснуть, ярко вспыхивает.

Появление мощного тока самоиндукции при размыкании цепи свидетельствует о том, что магнитное поле тока в катушке обладает энергией. Работа по созданию индукционного тока определяется уменьшением энергии магнитного поля. В свою очередь, энергия магнитного поля копится за счёт источника тока при совершении работы по преодолению тока самоиндукции, препятствующего увеличению тока в цепи.

Экспериментально выведена формула энергии магнитного поля катушки с током:

где (L) — индуктивность катушки (Гн), (I) — сила тока в катушке (А).

Энергия магнитного поля равна половине произведения индуктивности катушки на квадрат силы тока в ней.

Источник

Если
в контуре с индуктивностью L
течёт ток I,
то в момент размыкания цепи возникает
индукционный ток и им совершается
работа. Эта работа совершается за счёт
энергии исчезнувшего при размыкании
цепи магнитного поля. На основании
закона сохранения и превращения энергию
магнитного поля превращается главным
образом в энергию электрического поля,
за счёт которой происходит нагревание
проводников. Работа может быть определена
из соотношения

dA=ε_смIdt

Так
как
,
то

dA=-LIdI

Уменьшение
энергии магнитного поля равно работе
тока, поэтому

(16.18)

Формула
справедлива для любого контура и
показывает, что энергия магнитного поля
зависит от индуктивности контура и силы
тока, протекающего по нему.

Рассчитаем
энергию однородного магнитного поля
длинного соленоида, индуктивность
которого определяется по формуле L
= μμ₀n²V.
B
этом случае формула энергии примет вид

Учитывая,
что напряжённость поля внутри бесконечно
длинного соленоида Н=In,
получаем

(16.19)

Выразим
энергию через индукцию магнитного поля
B=
μμ₀H:

(16.20)

Или

(16.21)

Вследствие
того, что магнитное поле соленоида
однородно и локализовано внутри
соленоида, энергия распределена по
объёму соленоида с постоянной плотностью

(16.22)

Учитывая
последние три формулы, получаем

Учитывая
правило Ленца, можно заметить, что
явление самоиндукции аналогично
проявлению инертности тел в механике.
Так, вследствие инертности тело не
мгновенно приобретает определённую
скорость, а постепенно. Так же постепенно
происходит и его торможение. То же самое,
как мы видели, происходит и с силой тока
при самоиндукции. Эту аналогию можно
провести и дальше.

эти
уравнения эквивалентны.

т.е.
m
~L
, υ~I

Эквивалентны
и формулы

Примеры решения задач

Пример.
В магнитном поле, изменяющемся по закону
B=B₀cosωt
(B₀=5мТл,

ω=5с^-1),
помещён круговой проволочный виток
радиусом r=30см,
причём нормаль к витку образует с
направлением поля угол α=30º. Определите
ЭДС индукции, возникающую в витке в
момент времени t=10с.

Дано:
B=B₀cosωt;
B₀=5мТл=5∙10^-3
Тл;
ω=5с^-1;
r=30см=0,3
м;
α=30º; t=10 с.

Найти:
ε_i.

Решение:
Согласно
закону Фарадея,

,
(1)

Где
магнитный поток, сцепленный с витком
при произвольном его расположении
относительно магнитного поля.

Ф=BScosα.

По
условию задачи B=B₀cosωt,
а площадь кольца S=πr²,
поэтому

Ф=πr²
B₀cosωt∙cosα.
(2)

Подставив
выражение (2) в формулу (1) и продифференцировав,
получаем искомую ЭДС индукции в заданный
момент времени:

Ответ:
ε_i=4,69
мВ.

Пример
В
соленоиде длиной ℓ=50см и диаметром
d=6см
сила тока равномерно увеличивается на
0,3А за одну секунду. Определите число
витков соленоида, если сила индукционного
тока в кольце радиусом 3,1 см из медной
проволоки (ρ=17нОм∙м), надетом на катушку,
I_к=0,3
А.

Дано:
ℓ=50см=0,5
м; d=6см=0,06м;
;r_к=3,1см=3.1∙10^-2м;
ρ=17нОм∙м=17∙10^-9
Ом∙м; I_к=0,3
А.

Найти:
N.

Решение.
При изменении силы тока в соленоиде
возникает ЭДС самоиндукции

(1)

где
—
индуктивность соленоида. Подставив это
выражение в (1)

с
учётом

ЭДС
индукции, возникающая в одном кольце,
в N
раз меньше, чем найденное значение ЭДС
самоиндукции в соленоиде, состоящем из
N
витков, т.е.

.
(2)

Согласно
закону Ома, сила индукционного тока в
кольце

,
(3)

где
—
сопротивление кольца. Поскольку ℓ_к=πd,
а S_к=πr_к²,
выражение (3) примет вид

Подставив
в эту формулу выражение (2), найдём искомое
число витков соленоид

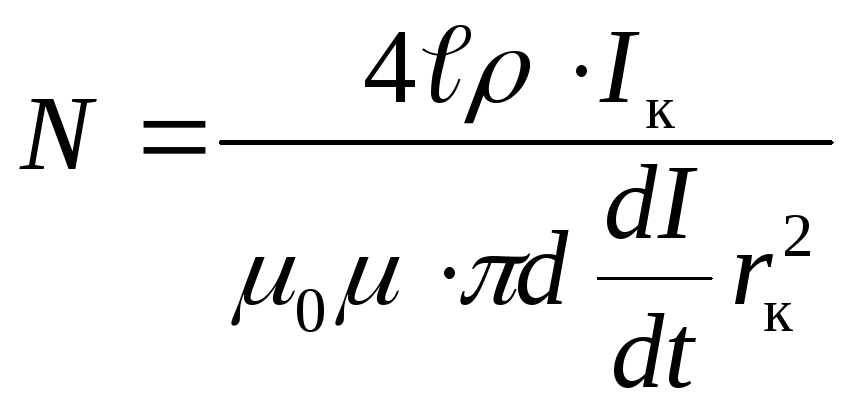
Ответ:
N=150

Пример
В
однородном магнитном поле подвижная
сторона (её длина ℓ=20см) прямоугольной
рамки (см. рисунок) перемещается
перпендикулярно линиям магнитной
индукции со скоростью υ=5 м/с. Определите
индукцию В магнитного поля, если
возникающая в рамке ЭДС индукции ε_i=0,2
В.

Дано:
ℓ=20см=0,2
м; υ=5 м/с; ε_i=0,2
В.

Найти:
B.

Р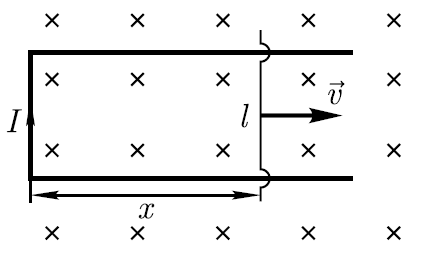ешение.
При движении в магнитном поле подвижной
стороны рамки поток Ф вектора магнитной
индукции сквозь рамку возрастает, что,
согласно закону Фарадея,

,
(1)

приводит
к возникновению ЭДС индукции.

Поток
вектора магнитной индукции, сцепленный
с рамкой,

Ф=Bℓx.
(2)

Подставив
выражение (2) в формулу (1) и учитывая, что
B
и ℓ — величины постоянные, получаем

откуда
искомая индукция магнитного поля

Ответ:
В=0,2 Тл.

Пример
В
однородном магнитном поле с индукцией
В=0,2 Тл равномерно вращается катушка,
содержащая N=600
витков, с частотой n=6
с^-1.
Площадь
S
поперечного сечения катушка 100см².
Ось вращения перпендикулярна оси катушки
и направлению магнитного поля. Определите
максимальную ЭДС индукции вращающейся
катушки.

Дано:
В=0,2
Тл; N=600;
n=6
с^-1;
S=100см²=10^-2м².

Найти:
(ε_i)_max.

Решение.
Согласно закону Фарадея,

где
Ф – полный магнитный поток, сцеплённый
со всеми витками катушки. При произвольном
расположении катушки относительно
магнитного поля

Ф=NBScosωt,
(1)

где
круговая частота ω=2πn.
Подставив ω в (1), получим

Ф=NBScos2πnt.

Тогда

ε_i=-NBS2πn(-sin2πnt)=2πnNBSsin2πnt,

ε_i=(
ε_i)_maxпри
sin2πnt=1, поэтому

(ε_i)_max=2πnNBS

Ответ:
(ε_i)_max=45,2
В.

Пример
Однослойная
длинная катушка содержит N=300
витков, плотно прилегающих друг к другу.
Определите индуктивность катушки, если
диаметр проволоки d=0,7
мм (изоляция ничтожной толщины) и она
намотана на картонный цилиндр радиусом
r=1
см. .

Дано:
N=300;
d=0,7
мм=7∙10^-4
м; r=1
см=10^-2м.

Найти:
L.

Решение.
Индуктивность катушки

(1)

где
Ф – полный магнитный поток, сцепленный
со всеми витками катушки; I
— сила тока в катушке.

Учитывая,
что полный магнитный поток

Ф=NBS

(N-число
витков катушки; В – магнитная индукция;
S
– площадь поперечного сечения катушки);
магнитная индукция в катушке без
сердечника

(μ₀
– магнитная постоянная; ℓ- длина
катушки), длина катушки

ℓ=Nd

(d-диаметр
проволоки; витки вплотную прилегают
друг к другу), площадь поперечного
сечения катушки

S=πr²,

Получим
осле подстановки записанных выражений
в формулу (1) искомую индуктивность
катушки:

Ответ:
L=1,69
мГн.

Пример
Первичная
обмотка понижающего трансформатора с
коэффициентом трансформации k=0,1
включена в сеть с источником переменного
напряжения с ЭДС ε₁=220
В. Пренебрегая потерями энергии в
первичной обмотке, определите напряжение
U₂
на зажимах вторичной обмотки, если её
сопротивление R₂=5
Ом и сила тока в ней I₂=2А.

Дано:
k=0,1;
ε₁=220
В; R₂=5
Ом; I₂=2А.

Найти:
U₂.

Решение.
В первичной обмотке под действием
переменной ЭДС ε₁
возникает переменный ток I₁,
создающий в сердечнике трансформатора
переменногый магнитный поток Ф, который
пронизывает вторичную обмотку. Согласно
закону Ома, для первичной обмотки

где
R₁
– сопротивление первичной обмотки.
Падение напряжения I₁R₁
при быстропеременных полях мало по
сравнению с ε₁
и ε₂.
Тогда можем записать:

(1)

ЭДС
взаимной индукции, возникающая во
вторичной обмотке,

(2)

Из
выражений (1) и (2) получаем

где
—
коэффициент трансформации, а знак «-»
показывает, что ЭДС в первичной и
вторичной обмотках противоположны по
фазе. Следовательно, ЭДС во вторичной
обмотке

ε₂=k
ε₂.

Напряжение
на зажимах вторичной обмотки

U₂=
ε₂-I₂R₂=
kε₁-I₂R₂.

Ответ:
U₂=12
В.

Пример
Соленоид
без сердечника с однослойной обмоткой
из проволоки диаметром d=0,4
мм имеет длину ℓ=0.5 м и поперечное сечение
S=60см².
За какое время при напряжении U=10
В и силе тока I=1,5
А в обмотке выделится количество теплоты,
равное энергии поля внутри соленоида?
Поле считать однородным.

Дано:
d=0,4
мм=0,4∙10^-4
м; ℓ=0,5 м; S=60см²=6∙10^-3
м²;
I=1,5А;
U=10В;
Q=W.

Найти:
t.

Решение.
При прохождении тока I
при напряжении U
в обмотке за время t
выделяется теплота

Q=IUt.
(1)

Энергия
поля внутри соленоида

(2)

где
(N
– общее число витков соленоида). Если
витки вплотную прилегают друг к другу,
то ℓ=Nd,
откуда
.
Подставив выражение для В иN
в
(2), получаем

.
(3)

Согласно
условию задачи, Q=W.
Приравняв выражение (1) и (3),найдём искомое
время:

Ответ:
t
=1,77 мс.

Пример
Катушка
без сердечника длиной ℓ=50 см содержит
N=200
витков. По катушке течёт ток I=1А.
Определите объёмную плотность энергии
магнитного поля внутри катушки..

Дано:
ℓ=50
см=0,5
м;
N=200; I=1 А.

Найти:
ω.

Решение.
Объёмная плотность энергии магнитного
поля (энергия единицы объёма)

,
(1)

где
—
энергия магнитного поля (L
— индуктивность катушки); V=Sℓ-
объём катушки (S
— площадь катушки; ℓ- длина катушки).

Магнитная
индукция поля внутри соленоида с
сердечником с магнитной проницаемостью
μ равна

Полный
магнитный поток, сцепленный со всеми
витками соленоида,

Учитывая,
что Ф=LI,
получаем формулу для индуктивности
соленоида:

(2)

Подставив
выражение (2) в формулу (1) с учётом того,
что
,
найдём искомую объёмную плотность
энергии магнитного поля внутри катушки:

Вопрос 1. Что такое энергия магнитного поля?

Ответ. Магнитное поле обладает энергией. Эта физическая величина показывает, какую работу ток в проводнике (катушке индуктивности) затрачивает на создание данного магнитного поля. Энергия магнитного поля тока вычисляется по формуле:

W=LI22

Вопрос 2. Что такое объемная плотность энергии магнитного поля?

Ответ. Объемная плотность энергии магнитного поля определяет энергию поля в единице объема. Формула, выведенная Максвеллом для объемной плотности энергии магнитного поля соленоида:

w= B2μ0μ

Вопрос 3. От чего зависит энергия магнитного поля?

Ответ. Энергия магнитного поля прямо пропорциональна индуктивности.

Вопрос 4. Что такое индуктивность?

Ответ. Индуктивность – физическая величина, коэффициент пропорциональности между силой тока в контуре и магнитным потоком через контур, создаваемым данным током.

Индуктивность также называют коэффициентом самоиндукции, она характеризует магнитные свойства электрической цепи (контура, катушки и т.д.)

Вопрос 5. Как можно переписать формулу для энергии магнитного поля?

Ответ. Формула может быть записана в виде:

W=LI22=ФI2=Ф22L

Нужна помощь в решении задач или любых других заданий по учебе? Профессиональный сервис для студентов всегда готов поспособствовать с их решением.

Источник