Как найти энергию основного состояния атома

и энергии
нулевых колебаний осциллятора

Некоторые задачи
квантовой механики могут быть решены
или поняты на качественном уровне, если
использовать различные комбинации
законов классической физики и соотношения
неопределенностей Гейзенберга.

Пример 1. Оценим
энергию основного состояния атома
водорода.

Основным
состоянием атома водорода является
состояние с наименьшей энергией (1 –
энергетический уровень).

Полная механическая
энергия атома водорода равна сумме
кинетической энергии вращающегося
электрона вокруг ядра и потенциальной
энергии взаимодействия электрона с
ядром, т. е.

W
= W_к
+ W_р,

где
W_к
=
p²/(2m)
– кинетическая энергия вращающегося
электрона вокруг ядра;

W_р
=
–q_e²/(4₀r)
– потенциальная энергия взаимодействия
электрона с ядром.

При
допущении неопределенности положения
электрона в пределах радиуса его орбиты,
т. е. r

r
и неопределенность импульса в пределах
самого импульса, т. е. р

р.

Тогда на
основании соотношений неопределенностей
Гейзенберга имеем

r

р

h
/(4)

или
по порядку величины р 
h
/2
r.

Если
возьмем равенство

р
= h
/(2r)

и
подставим в формулу кинетической
энергии, то полная энергия атома водорода

W
= h²/(4²m
r²)
– q_e²/(4₀r).

Теперь
перейдем к условию минимума, т. к. нас
интересует состояние с наименьшей
энергией:

dW/dr
= – h²/(4²m
r³)
+ q_e²/(4₀r²)
= 0.

Корень
этого уравнения, соответствующий
минимуму полной энергии W,
равен

r₁
= ₀h²
/ (m
q_e²).

В
квантовой механике, полученное значение
r₁
называют
радиусом первой боровской орбиты.

После вычисления получим r1  510 11 м. Для энергии основного состояния атома водорода получим

W₁
= –
m
q_e⁴
/ (8²₀²h²).

W₁
= –
13,6 эВ

или

W₁
= –
2,176 10
^18Дж.

Пример 2. Энергия
нулевых колебаний одномерного

гармонического
осциллятора.

В
качестве одномерного гармонического
осциллятора рассмотрим колебания груза
на пружине (пружинный маятник), который
характеризуется потенциальной энергией

W_р
=
k
x²
/
2,

представляющий
собой, параболическую потенциальную
яму.

Для
оценки минимально возможной полной
энергии осциллятора применим соотношения
неопределенностей Гейзенберга.

Полная
механическая энергия данного осциллятора

W
= W_к
+ W_р,

где
W_к
=
p_х²
/
(2m)
– кинетическая энергия осциллятора;
W_р
=
k
x²
/
2.

Следовательно,

W
= p_х²
/
(2m)
+ k
x²
/
2.

Согласно
классической механике минимум полной
энергии W
= 0 соответствует х
= 0 и р_х
=
0, т. е. пружинный маятник неподвижен.

При
рассмотрении квантового случая должны
учесть, что одновременно точные значения
координаты (х)
и проекции импульса на ось х (р_х)
указать
невозможно.

Согласно, принципа
неопределенностей Гейзенберга, имеем

х

р_х

h
/(4).

Если
положим, что х

х ; р_х

р_х
или
по порядку величины х 
р_х

h
/ (2),
т. е. р_х

h
/(2x).

При
переходе к равенству р_х
= h
/(2x)
для полной энергии осциллятора будем
иметь

W
= h²
/(8²mx²)
+ k
x²
/
2.

Перейдем
к условию минимума энергии:

dW
/dx
= – h²
/(4²mx³)
+ k
x
= 0.

Корень
этого уравнения запишем в виде

.

Тогда
минимальное значение полной энергии
рассматриваемого квантового осциллятора

W₀
= h
/(2).

или

W₀
= h,

где

– собственная
круговая частота осциллятора; 
= 2.

Данная
оценка отличается от точного значения
только численным множителем 1/2.

Полная
энергия квантового осциллятора
называется энергией нулевых колебаний
гармонического осциллятора.

Энергия — основное состояние — атом

Cтраница 1

Энергия основного состояния атома обычно принимается равной нулю. Если желательно показать тонкую структуру, отдельные фрагменты диаграммы можно увеличить.
 [1]

Энергия основного состояния атома водорода заслуживает подробного обсуждения. Основываясь на законах классической механики, следует ожидать, что электрон проводит как можно больше времени в окрестности ядра, поскольку при этом его потенциальная энергия минимальна. Идеальным положением электрона с этой точки зрения является контакт с ядром. На самом же деле в основном состоянии атома водорода электрон, находящийся на ls — орбитали, хотя и распределен в области, близкой к ядру, вовсе не ограничен этой областью. Что отталкивает электрон от ядра. Классический ответ гласит: Причиной отталкивания является угловой момент электрона и сопутствующая центробежная сила. Это предположение и было положено в основу модели Бора. Однако, поскольку с s — орбиталью не связан никакой угловой момент, такое объяснение нельзя считать приемлемым.
 [2]

Определите энергию основного состояния атома, образованного из электрона и позитрона, которые связаны между собой силами кулоновского притяжения.
 [3]

Дж-моль — 1 выше энергии основного состояния атома углерода.
 [4]

Ридберга, равная fi о — энергия основного состояния атома.
 [5]

Ридбергом называется единица энергии, равная энергии основного состояния атома водорода, взятой с обратным знаком.
 [6]

Полученное выражение ( 3) представляет приближенное значение энергии основного состояния атома водорода, находящегося в слабом электрическом поле.
 [7]

Для того чтобы проиллюстрировать использование таких уравнений, вычислим энергию основного состояния атома водорода.
 [8]

Здесь Ev — энергия, соответствующая потолку валентной зоны, а Еа — энергия основного состояния акцепторного атома.
 [10]

Указанная ошибка несколько больше ( хотя имеет тот же порядок величины) соответствующей ошибки в энергии основного состояния атома гелия.
 [11]

Вариационные методы, развитые в работах Ритца, Хиллерааса и других, были с успехом использованы для нахождения энергий основных состояний атомов.
 [12]

А, Е ( МА) и Е ( Мв) — энергии электронных конфигураций А и В, усредненные с весом по всем мульти-плетам, возникающим для этих конфигураций, и взятые относительно энергии основного состояния атома. Усреднение по мульти-плетам, очевидно, следует проводить в соответствии с количеством микросостояний, принадлежащих данному мультиплету.
 [13]

Пусть оба атома находятся в основных состояниях. Полная энергия системы не будет равна удвоенной энергии основного состояния атома водорода. К), которая зависит от расстояния R. Только в случае очень большого К эта энергия будет равна нулю.
 [15]

Страницы:  

   1

   2

Решая совместно уравнения
(2),
(5), (9), получим выражение для полной
энергии электрона в атоме водорода:

(10)

Уравнение (10) определяет разрешенные
значения энергии электрона в атоме
водорода. Число n
принимает целые значения n =
1,2,3, …¥ .
Таким образом, энергия электрона в атоме
водорода может иметь не любые значения,
а только дискретный набор значений,
определяемых числом n,
или, как говорят, энергия электрона квантуется.

Подставляя значения

массы и
заряда электрона, постоянных 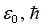в
уравнение (10) и выражая энергию в электронвольтах
(эВ) (1эВ = 1,6^.10^-19
Дж), получим
формулу

(11)

Энергия основного состояния
(при n
= 1), равна E₁=
— 13,6 эВ. На рис. 1
приведена диаграмма энергетических
уровней электрона в атоме водорода, на
которой горизонтальными прямыми
отмечены разрешенные значения энергии.
Все состояния с величиной n= 1 … ¥ являются
связанными. При увеличении числа n
энергетические уровни сближаются все
больше и больше. При n ® ¥ E ®
0.
Энергетические состояния с энергией E ³
0
соответствуют тому, что электрон
становится свободным (не связанным с
ядром).

Диаграмма
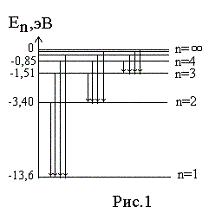
энергетических уровней (рис.1) позволяет
дать несколько важных определений.

Энергия возбуждения Е_воз
– это энергия, которую необходимо
сообщить электрону, чтобы он из
основного состояния (n = 1)
перешел в возбужденное. Например, Е_воз
= 10,2 эВ – энергия, необходимая для
перехода электрона в состояние,
соответствующее n =
2 (первое возбужденное состояние).

Энергия ионизации Е_ион
– энергия, необходимая для отрыва
электрона, находящегося в основном
состоянии (n
= 1), от ядра, т.е. для перевода электрона
на уровень с n = ¥ .
Для атома водорода энергия ионизации
равна 13,6 эВ.

Согласно постулату Бора, при
переходе электрона из одного состояния (с
большей энергией) в другое (с меньшей
энергией) испускается фотон, частота
которого определяется формулой (8).
Учитывая выражение (10) для энергии
электрона в атоме, получим выражение для
частот испускаемых фотонов:

(12)

или, соответственно, для длин
волн испускаемых фотонов:

(13)

где Ry =
1,0974^.10⁷
м^–1
– так называемая постоянная Ридберга.

Таким образом, модель атома Н.Бора
объясняет дискретный (линейчатый)
характер спектра испускания атома
водорода.

Спектральные
серии атома водорода

На диаграмме энергетических уровней (рис.1)
показаны возможные переходы электрона с
верхних уровней на нижние. При каждом
таком переходе излучается фотон с
частотой, определяемой формулой (12), или

длиной волны, определяемой формулой (13).
Переходы электрона с различных верхних
уровней на определенный нижний образуют
так называемые спектральные серии
атома водорода. Так, все переходы из
состояний с n
= 2, 3, 4, … в
состояние с n
= 1 образуют так называемую серию
Лаймана (ультрафиолетовое излучение).
Все длины волн этой серии лежат в
ультрафиолетовой области шкалы
электромагнитных волн. Переходы из
состояний с n
= 3, 4, 5, … в состояние с n
= 2 образуют серию Бальмера (видимый
свет). Переходы из состояний с n
= 4, 5, 6, … в состояние с n
= 3 образуют серию Пашена (инфракрасное
излучение). Длины волн всех остальных
серий (переходы на уровни с n
= 4, 5, и т.д.) лежат в инфракрасной области
спектра электромагнитного излучения.