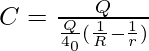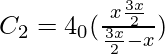Как найти энергию сферического конденсатора - Исправление недочетов и поиск решений вместе с Examum.ru

Задание:

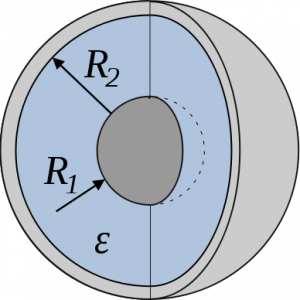
Определить энергию электрического поля воздушного сферического конденсатора, если радиус внутренней сферы R₁, радиус внешней сферы R₂, и внутренняя сфера имеет заряд q.

Решение:

Источник

Электроемкость сферического конденсатора

Электроемкость сферического конденсатора — характеристика плоского конденсатора, мера его способности накапливать электрический заряд.

Чтобы найти емкость сферического конденсатора, который состоит из двух
концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:
.

Подставим данное выражение в формулу электроемкости конденсатора и получим емкость конденсатора для сферического тела:

При малой величине зазора, то есть , а следовательно можно считать, что емкость сферического конденсатора будет равна . Площадь сферы S = 4πr² следовательно формула будет совпадать с формулой емкости плоского конденсатора .

Формулы:

Энергия конденсатора: .

Ёмкость конденсатора: .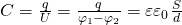

Ёмкость цилиндрического конденсатора: .

Ёмкость плоского конденсатора: .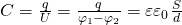

Обозначения в формулах:

C — электрическая ёмкость (ёмкость конденсатора);

g — заряд;

U — потенциал проводника (напряжение);

φ — потенциал;

ε — относительная диэлектрическая проницаемость;

— электрическая постоянная;

S — площадь одной обкладки;

d — расстояние между обкладками;

r₂— Больший радиус (от центра, до края конденсатора);

r₁ — Малый радиус (Его может и не быть — это пустота).

вернутся в раздел: электрическая ёмкость

Источник

Энергия заряженного конденсатора. Калькулятор онлайн для плоского, цилиндрического и сферического конденсаторов.

Онлайн калькулятор вычисления энергии электростатического поля заряженного конденсатора, позволит найти энергию заряженного плоского, цилиндрического и сферического конденсаторов.
Калькулятор произведет вычисление и даст подробное решение. Единицы измерения, могут включать любые приставки Си. Калькулятор автоматически переведет
одни единицы в другие.

Калькулятор вычислит:
Энергию заряженного плоского конденсатора.
Энергию заряженного цилиндрического конденсатора.
Энергию заряженного сферического конденсатора.

Так же для вычисления энергии электростатического поля заряженного (любого) конденсатора, можно воспользоваться
калькулятором вычисления энергии заряженного конденсатора.

Энергия заряженного плоского конденсатора

Плоский конденсатор представляет собой две параллельные проводящие пластины, разделенные диэлектриком, расположенные на малом расстоянии друг от друга.

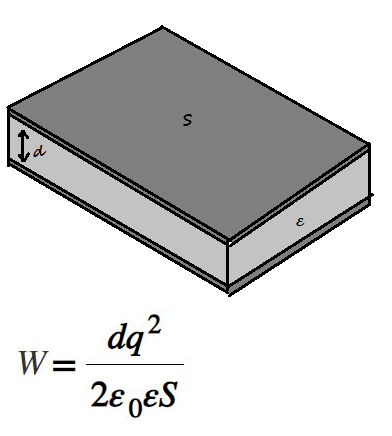
Энергия заряженного плоского конденсатора определяется формулой, где

q — электрический заряд на одной из обкладок
ε₀ – электрическая постоянная, ε₀ = 8.85418781762039 × 10^-12
ε – диэлектрическая проницаемость диэлектрика
S — площадь пластины
d — расстояние между пластинами

Единицей измерения энергии — Джоуль (Дж, J).

Диэлектрическая проницаемость ε =
Расстояние между пластинами d =
Заряд q =
Площадь пластины S =
Единица измерения энергии W

Энергия заряженного цилиндрического конденсатора

Цилиндрический конденсатор представляет собой конденсатор, обкладками, которого являются два цилиндра, внутренний с радиусом R₁ и внешний с радиусом R₂. Между обкладками находится диэлектрик с диэлектрической проницаемостью ε.

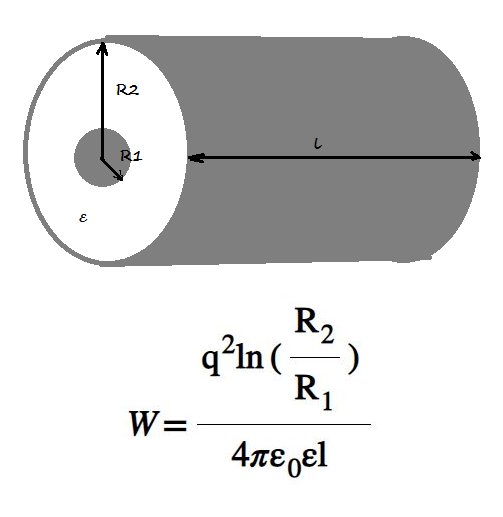
Энергия заряженного цилиндрического конденсатора определяется формулой, где

q — заряд
π – число Пи (3.14)
ε₀ – электрическая постоянная, ε₀ = 8.85418781762039 × 10^-12
ε – диэлектрическая проницаемость диэлектрика
l – длина цилиндра
ln – натуральный логарифм
R₁ – радиус внутренней обкладки
R₂ – радиус внешней обкладки

Единицей измерения энергии — Джоуль (Дж, J).

Диэлектрическая проницаемость ε =
Заряд q =
Радиус R1 =
Радиус R2 =
Длина l =
Единица измерения энергии W

Энергия заряженного сферического конденсатора

Сферический конденсатор представляет собой конденсатор, обкладками которого являются две концентрические сферы, радиусами R₁ и R₂, между которыми расположен диэлектрик, с диэлектрической проницаемостью ε.

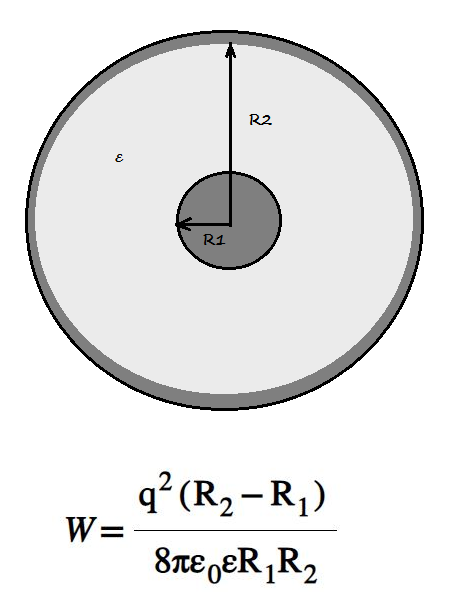
Энергия заряженного сферического конденсатора определяется формулой, где

q — заряд
π – число Пи (3.14)
ε₀ – электрическая постоянная, ε₀ = 8.85418781762039 × 10^-12
ε – диэлектрическая проницаемость диэлектрика
R₁ – радиус внутренней обкладки
R₂ – радиус внешней обкладки

Единицей измерения энергии — Джоуль (Дж, J).

Диэлектрическая проницаемость ε =
Заряд q =
Радиус R1 =
Радиус R2 =
Единица измерения энергии W

Вам могут также быть полезны следующие сервисы

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажер по математике

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Источник

A capacitor is simply an electric device that consists of two terminals that have the ability to store energy in the form of an electric charge. It can be designed by simply placing two electrical conductors at a distance from each other. The empty space between the conductors may be filled by vacuum(or air) or with an insulating material known as a dielectric. The ability of the capacitor to store charges is known as capacitance.

In a capacitor, the two terminals having opposite charges are placed at a distance from each other which allows it to generate(store) energy. The simplest design for a capacitor is a parallel plate, which consists of two metal plates with a gap between them. It should be noted that a capacitor can be of any shape or size or be made of any material until its terminals store opposite charges and thus store energy.

Capacitance of a capacitor

Consider a capacitor whose positive and negative plates hold +q and -q charge respectively. A DC voltage source is applied across it which gives it a potential difference of V across the plates. Now as we know,

Q α V

Putting a constant C in this relation.

Q=CV.

Note: The capacitance of every material is unique and its SI unit is Farad(F).

Working of a capacitor

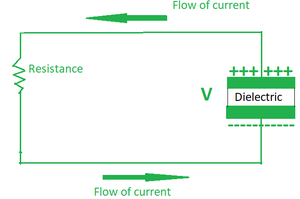
Let’s suppose that we are given the most basic form of the capacitor, which is a parallel plate capacitor. It consists of two parallel plates separated by a small distance and that gap is filled by a dielectric. Next, we are given a DC voltage source that is linked across the capacitor, where one plate is attached to the positive end (plate I) and the other plate is connected to the negative end (plate II). When the battery’s potential is applied across the capacitor, plate I become positive in relation to plate II. At steady-state, current attempts to pass through the capacitor from the positive plate to the negative plate. However, because of a gap between them with an insulating layer(dielectric), it is unable to flow.

Structure of a simple capacitor.

For some time the capacitor continues to get charged by the incoming flow of the current. But after some time it reaches a state where it holds the maximum amount of charge that it can possibly hold. This is how a capacitor stores energy The time taken to reach this state of maximum charge is called the charging time of the capacitor. Later we disconnect the voltage source from the circuit and insert a load resistor in it. Now the current starts flowing from the positively charged terminal of the capacitor to the negatively charged terminal and loses all of its energy in the process. This time period is called the discharging time of the capacitor.

Discharging of a capacitor.

Spherical Capacitor Formula

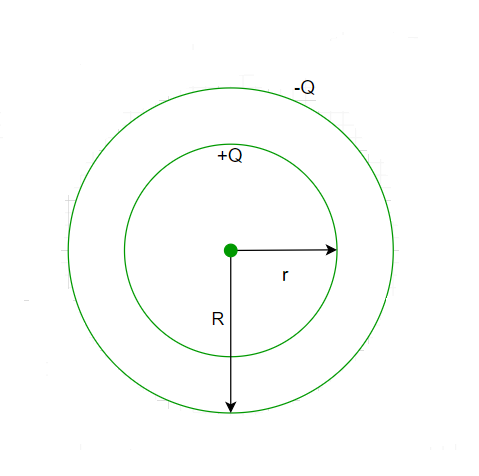
As mentioned earlier capacitance occurs when there is a separation between the two plates. So for constructing a spherical capacitor we take a hollow sphere such that the inner surface is positively charged and the outer surface of the sphere is negatively charged. The inner radius of the sphere is r and the outer radius is given by R. The distance of R-r between the two oppositely charged surfaces acts as the dielectric. Let’s assume that the inner spherical surface has a potential of V₁ and V_2.

A spherical capacitor

Next, the electric field generated by a charged sphere (hollow) of radius r having charge Q is given by,

E= $frac{Q}{4π∈_0r^2}$ . ⇢ (1)

Also, we know that the Electric field generated is related to the potential difference as,

E= $-frac{dV}{dr}$ . ⇢ (2)

Comparing (1) and (2),

$-frac{dV}{dr} =frac{Q}{4π∈_0r^2}$

$-dV= frac{Qdr}{4π∈_0r^2}$

Integrating on both sides within the limits V, V and r, R.

$int_{V_1}^{V_2} -dV = int_{r}^{R} frac{Q}{4π∈_0r^2}dr$

$int_{V_1}^{V_2}-dV = frac{Q}{4π∈_0} int_{r}^{R} frac{dr}{r^2}$

$-[V] |_{V_1}^{V_2} = frac{Q}{4π∈_0} frac{-r^{-2}+1}{-2+1}|_{r}^{R}$

$[V_2 -V_1] = frac{Q}{4π∈_0} [frac{1}{R}-frac{1}{R}]$

$Delta = frac{Q}{4π∈_0} [frac{1}{R}-frac{1}{R}]$ ⇢ (3)

is the change in potential as we move from inside the sphere to outside. Now the capacitance of a capacitor is given by,

$C= frac{Q}{Delta V}$ ⇢ (4)

Comparing (3) and (4),

$C = frac{Q}{frac{Q}{4π∈_0}(frac{1}{R} - frac{1}{r})}$

$C = frac{Q4π∈_0}{Q[frac{1}{R} - frac{1}{r}]}$

Simplifying further we get,

$C = 4π∈_0 (frac{rR}{r-R})$

Since capacitance can’t be negative the positive value is taken. This is the expression for the capacitance of a spherical capacitor.

Sample Questions

Question 1: A spherical capacitor has an inner radius of 7 cm and an outer radius of 10 cm. Find the capacitance of the sphere. Assume the dielectric in between to be air.

Solution:

The capacitance of the sphere is given by,

C = $4π∈_0 (frac{rR}{r-R})$

Here ∈₀ = 8.85 × 10^-12, r = 7, R = 10

C= $frac{4times3.14times8.85times10^{-12} times70times10^{-2}}{(10-7)10^{-1}}$

C = 2.593 × 10^-12F

Question 2: In the above problem find how much charge will it take for the capacitor to raise its potential from 0 to10,000 V.

Solution:

The capacitance of the spherical capacitor is C = 2.593 × 10^-12F.

The charge required can be found by using Q = CV. where V is the potential difference.

Potential difference V in this case is 1000-0 = 1000V

Therefore, Q = 3.7052 × 10^-12 × 1000

Q = 2.593 × 10^-9C

Question 3: The inner radius of a spherical capacitor is x m and its outer radius is 5/4 x m if the outer radius is increased to 3/2x m, find by what ratio its capacitance is changed.

Solution:

In this case $C_1 =4π∈_0(frac{rR}{R-r})$

= $4π∈_0(frac{xfrac{5x}{4}}{frac{5}{4}x -x})$

= 20 πε_ox F

$C_2 = 4π∈_0(frac{xfrac{3x}{2}}{frac{3x}{2}-{x}})$

= 20 πε_ox F

$frac{C_1}{C_2} =frac{ 20 π∈_0 x }{12 π∈_0x}$

$frac{C_1}{C_2} =frac{5}{3}$

So the capacitance decreases as the external radius is increased.

Question 4: A sphere has a radius of 10 cm. find the capacitance on it and also find the potential difference required to give it a charge of 10^-8 C.

Solution:

C = 4 πε_ox F

C = 4 × 3.14 × 8.85 × 10⁻¹² × 10 × 10⁻²

C = 111.156 × 10⁻¹³

C = 1.11 × 10⁻¹¹ F

Now Q = CV

Therefore $V = frac{10^{-8}}{1.11x10^{-11}}$

Hence V = 900.9 V

Question 5: The outer radius of a spherical capacitor is 10 % bigger than its inner radius. The capacitance of this capacitor is 10^-8 F. Find the value of its inner and outer radii.

Answer:

$C = 4π∈_0 (frac{rR}{r-R})$

Here r = x, R = 1.1x and C= 10^-8 F

So, $C = frac{1.1x(x)}{1.1x-x}$

$10^{-12}=4piepsilonfrac{1.1x^2}{0.1x}$

$11x =frac{10^{-12}}{4piepsilon}$

x = 0.009 m

So the inner radius is 0.09 cm and the outer radius is 0.099 cm.

Question 6: The inner and outer radii of a spherical capacitor are 5cm and 6cm. Find the energy of the capacitor if a potential difference of 1000V is applied to it.

Solution:

The capacitance of this capacitor is calculated as,

$C = 4{pi}{epsilon}{frac{6times5times10^{-2}}{(6-5)times10^{-1}}}$

C = 3.3363 × 10⁻¹² F

U = 1/2 CV²

U = 21 × 3.3363 × 10⁻¹²× (1000)²

U = 1.66815 × 10⁻⁹ J

Question 7: A spherical capacitor of inner and outer radii 8cm and 10cm has an energy of 10^-8 J . Find its Voltage.

Solution:

Lets find the capacitance first,

$C = 4piepsilonfrac{8times10times10^{-2}}{(10-8)times10^{-1}}$

C = 4.446 × 10^-9 F

U = 1/2 CV²

$V =sqrt {frac{2U}{C}}$

$V=sqrt{frac{2times{10^{-8}}}{4.446times 10^{-9}}}$

V = 2.12 V

Last Updated :
01 May, 2022

Like Article

Save Article

Источник

$Large C=4pi varepsilon varepsilon _0(frac{1}{R_1} - frac{1}{R_2})^{-1}= 4pi varepsilon varepsilon _0frac{r_1r_2}{r_2-r_1}$

Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r1 и r2 (r2 > r1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов будет выглядеть так:

$Largevarphi _1-varphi _2=frac{q}{4pi varepsilon varepsilon _0}(frac{1}{r_1}-frac{1}{r_2})$

$Large C=4pi varepsilon varepsilon _0(frac{1}{R_1} - frac{1}{R_2})^{-1}= 4pi varepsilon varepsilon _0frac{r_1r_2}{r_2-r_1}$

При малой величине зазора, то есть , а следовательно можно считать, что емкость сферического конденсатора будет равна $frac{4pi r^2varepsilon varepsilon _2}{d}$ . Площадь сферы следовательно формула будет совпадать с формулой емкости плоского конденсатора $varepsilon varepsilon _0frac{S}{d}$