Как найти энергию системы колебаний

Энергия колебательной системы

Сергей Сергеевич Соев

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Понятие колебательной системы

Физика колебаний актуальна в разных сферах нашей повседневной жизни, например, в изготовлении телефонов и двигателей.

Определение 1

Колебания — это движение или изменение состояния, обладающее той или иной степенью повторяемости во времени. Совершать их может качающийся маятник или брусок, подвешенный вертикально на пружине.

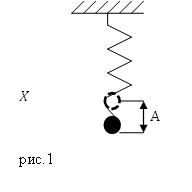
В качестве колеблющейся системы рассмотрим пружинный маятник. В пружинном маятнике колебания совершаются под действием сил упругости в пределах упругости тела (пружины).

Рисунок 1. Пружинный маятник. Автор24 — интернет-биржа студенческих работ

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Жирная стрелочка — это $overrightarrow{F}_{уп}$.

Из рисунка можем сделать вывод, что: $F_{упр.x}=-kx$, где $k$ — это жёсткость пружины, а $x$ — смещение от положения равновесия.

Энергия колебательной системы

Преобразование энергии при колебаниях пружинного маятника: энергия упругой деформации превращается в кинетическую энергию: $E_{пmax}=E_{кmax}$. То есть:

$frac{kx^2_{max}}{2}=frac{mv^2_{max}}{2}=frac{kx^2}{2}+frac{mv^2}{2}$, где

• $ k$ — это жёсткость пружины;
• $x_{max}$ — максимальное значение колеблющейся величины;
• $m$ — масса груза;
• $v_{max}$ — максимальная сокрость движения груза.

Решим простую задачу.

Пример 1

Задача. Дан груз с массой 511 г. Он совершает колебательное движение на пружине жёсткостью 361 Н/м. Амплитуда колебаний 26 см. Найти полную механическую энергию колебаний груза. Трением пренебречь.

Решение.

По условию $m=511 г, k=361 Н/м, x_m = 26 см$ Нужно найти $E_{мех}$.

Переведём единицы измерения в СИ. $m=511 г = 0,511 кг; x_m = 26 см=0,26 м$.

Закон сохранения энергии: $E_{мех}=E_{пmax}$.

По определению: $E_{пmax}=frac{kx^2_{max}}{2}$.

Подставляем значения:

$E_{мех}=E_{пmax}=frac{361cdot 0,26^2}{2}approx 12,2 $.

Ответ: $E_{мех}approx 12,2$ Дж..

Таким образом, мы рассмотрели на простом примере энергию колебательной системы, при этом дав понятие колебательной системе.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 23.04.2023

Полная энергия колебаний, теория и онлайн калькуляторы

Полная энергия колебаний

Энергия колебаний пружинного маятника

Рассмотрим превращения энергии, которые происходят при гармонических колебаниях в консервативной системе на примере пружинного маятника. Так как пружинный маятник мы считаем консервативной системой, то механическая энергия ее постоянна:

[E=E_k+E_p=const left(1right).]

Проверим справедливость выражения (1),) непосредственным суммированием выражений для кинетической и потенциальной энергии рассматриваемого маятника.

Уравнение колебаний маятника запишем в виде:

[x=A{cos left({omega }_0t+varphi right)(2) },]

где $x$ — смещение груза маятника по оси X. В таком случае изменение кинетической энергии груза, совершающего колебания на напружине равна:

[E_k=frac{m}{2}A^2{{omega }_0}^2{{sin}^2 left({omega }_0t+varphi right)left(3right). }]

Потенциальна энергия пружинного маятника равна: потенциальной энергии упругодеформированной пружины и потенциальной энергии груза в поле тяжести Земли:

[E_p=frac{kx^2}{2}=frac{k}{2}A^2{{cos}^2 left(щ_0t+цright) }left(4right).]

Суммируем правые части выражений (3) и (4), получим:

[E=frac{m}{2}A^2{щ_0}^2{{sin}^2 left(щ_0t+цright)+ }frac{k}{2}A^2{{cos}^2 left(щ_0t+цright) }=frac{k}{2}A^2=frac{1}{2}m{omega }^2_0A^2left(5right).]

где ${{omega }_0}^2=frac{k}{m}$.

Из формулы (5) мы видим, что неизменная суммарная энергия колебательной системы равна потенциальной ее энергии в точках максимального отклонения от положения равновесия (при $x=pm A$). Энергия $E$ равна кинетической энергии при прохождении грузом положения равновесия, скорость груза равна:

[v_x=pm {omega }_0Aleft(6right).]

В ходе взаимных превращений потенциальная и кинетическая энергии гармонически колеблются с одинаковой амплитудой, равной $frac{E}{2}$ находятся в противофазе друг с другом, частота их колебаний равна $2{omega }_0$.

[{E_k =frac{E}{2}left[1-{cos 2({omega }_0t+varphi ) }right]left(7right). }]

[E_p=frac{E}{2}left[1+{cos 2({omega }_0t+varphi ) }right]left(8right).]

И так, выражения (7) и (8) показывают, что кинетическая и потенциальная энергии колебательной системы совершают гармонические колебания вокруг их общего значения $frac{E}{2}$ с удвоенной частотой 2${omega }_0$, тогда как полная энергия системы остается постоянной. Она связана с амплитудой колебаний как:

[E=frac{k}{2}A^2.]

Энергия колебательных систем с одной степенью свободы

Все, что сказано для пружинного маятника можно применить , для любых механических колебаний систем с одной степенью свободы. Мгновенное положение такой системы можно определить, используя один параметр, который называют обобщенной координатой ($q$), например, угла поворота или смещения по оси координат. При этом величина $dot{q}=frac{dq}{dt}$ называется обобщённой скоростью.

Потенциальная энергия в таких обозначениях примет вид:

[E_p=frac{alpha q^2}{2}left(9right),]

кинетическая энергия:

[E_p=frac{beta {dot{q}}^2}{2}left(10right),]

где $alpha , beta $ — параметры системы. Полная энергия системы в нашем случае равна:

[E=frac{alpha q^2}{2}+frac{beta {dot{q}}^2}{2}=const left(11right),]

обобщенная координата совершает гармонические колебания с частотой:

[{omega }_0=sqrt{frac{alpha }{beta }}left(12right).]

Примеры задач на полную энергию колебаний

Читать дальше: понятие силы.

1. Колебания.

2. Механические
   колебания.

3. Превращения
   энергии при механических колебаниях.

4. Период колебаний.

5. Частота колебаний.

6. Циклическая
   частота колебаний.

7. Амплитуда
   механических колебаний.

8. Гармонические
   колебания.

9. Фаза гармонического
   колебания.

10. Аналитическое
    представление колебаний.

11. Графическое
    представление колебаний.

12. Скорость точки в
    гармоническом колебании.

13. Ускорение точки
    в гармоническом колебании.

14. Динамика
    гармонического колебания.

15. Период колебаний
    пружинного маятника.

16. Математический
    маятник. Квазиупругая сила.

17. Колебания тела,
    плавающего на поверхности жидкости.

18. Колебания однородной
    жидкости в U
    – образной трубке.

19. Колебания тела в
    сферической чаше.

20. Энергия гармонического
    колебания.

21. Затухающие
    колебания.

22. Вынужденные
    колебания.

23. Резонанс.

24. Свободные колебания.
    Собственная частота.

25. Автоколебания.

1. Колебания.
Колебаниями
вообще называют периодические изменения
состояния системы, при которых периодически
изменяются значения различных физических
величин, характеризуют данную систему.
Например, периодические изменения
давления и плотности воздуха, напряжения
и силы электрического тока есть колебания
этих величин.

Математически
периодичность означает, что, если

— есть периодическая функция времени с
периодом Т,
то при любом t
выполняется
равенство

2. Механические
колебания
– движения тела, которые точно или почти
точно повторяются через равные интервалы
времени.

Механические
колебания возникают в системах, имеющих
положение устойчивого равновесия.
Согласно с принципом минимума потенциальной
энергии, в положении устойчивого
равновесия потенциальная энергия
системы минимальна. Когда тело выводят
из положения устойчивого равновесия,
его потенциальная энергия возрастает.
При этом возникает сила, направленная
к положению равновесия (возвращающая
сила), и чем дальше от положения равновесия
отклоняется тело, тем больше его
потенциальная энергия и тем больше
модуль возвращающей силы. Например, при
отклонении пружинного маятника от
положения равновесия, роль возвращающей
силы играет сила упругости, модуль
которой изменяется пропорционально
отклонению

,
где х
отклонение маятника от положения
равновесия. Потенциальная энергия
пружинного маятника изменяется
пропорционально квадрату смещения

.

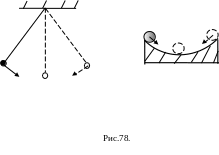
Аналогично возникают
колебания нитяного маятника и шарика,
движущегося по дну сферической чаши
радиуса R,
который можно рассматривать как нитяной
маятник с длиной нити равной радиусу
чаши (Рис.78).

3.Превращения
энергии при механических колебаниях.
Если отсутствуют силы трения, то полная
механическая энергия тела, совершающего
колебательное движение, остаётся
постоянной. В процессе колебаний
происходят периодические взаимные
превращения потенциальной и кинетической
энергии тела. Проведем рассуждения на
примере колебаний нитяного маятника .
Для упрощения рассуждений примем
потенциальную энергию маятника в
положении равновесия равной нулю. В
крайнем отклонённом положении
потенциальная энергия маятника
максимальна, а кинетическая энергия
равна нулю, т.к. в этом положении маятник
находится в покое. При движении к
положению равновесия высота маятника
над поверхностью Земли уменьшается,
уменьшается и потенциальная энергия,
при этом возрастают его скорость и
кинетическая энергия. В положении
равновесия потенциальная энергия равна
нулю, а кинетическая энергия максимальна.
Продолжая движение по инерции, маятник
проходит положение равновесия. После
прохождения положения равновесия
кинетическая энергия маятника убывает,
но возрастает его потенциальная энергия.
Когда произойдёт остановка маятника,
его кинетическая энергия станет равной
нулю, а потенциальная энергия достигнет
максимума и всё повторится в обратном
порядке.

По закону сохранения
энергии потенциальная энергия маятника
в крайнем отклоненном положении равна
его кинетической в момент прохождения
положения равновесия.

В процессе колебаний
в любой момент времени полная механическая
энергия маятника равна его потенциальной
в крайнем отклонённом положении или
кинетической энергии в момент прохождения
положения равновесия

где

высота
маятника в крайнем отклоненном положении,

скорость
в момент прохождения положения
равновесия.

4. Период
колебания
– минимальный интервал времени , через
который происходит повторение движения,
или интервал времени, в течение которого
происходит одно полное колебание. Период
(Т)
измеряется в секундах.

5. Частота
колебании
—

определяет число полных колебаний,
совершаемых за одну секунду. Частота и
период связаны соотношением

,

.

Частота измеряется
в герцах (Гц). Один герц – одно полное
колебание совершаемое за одну секунду

6. Циклическая
частота или круговая частота


определяет число полных колебаний,
свершаемых за

секунд

.

Частота – величина
положительная

,

.

7. Амплитуда
механических колебаний
– максимальное отклонение тела от
положения равновесия. В общем случае
колебаний амплитуда есть максимальное
значение, которое принимает периодически
изменяющаяся физическая величина.

8. Гармонические
колебания
– колебания, в которых колеблющаяся
величина изменяется по закону синуса
или косинуса (по гармоническому закону):

Здесь

амплитуда
колебаний,

циклическая
частота.

9
.
Фаза
гармонического колебания –
величина

,
стоящая под
знаком синуса или косинуса. Фаза
определяет значение колеблющейся
величины в данный момент времени,

начальная
фаза, т.е. в момент начала отсчёта времени

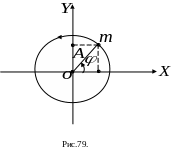
Простейшим
примером гармонических колебаний
является колебание проекции на оси
координат точки m
движущейся равномерно по окружности

радиуса А
в плоскости XOY,
центр которой совпадает с началом
координат (рис. 79)

Для простоты
положим

,
т.е.

тогда

Многие известные
колебательные системы можно лишь
приближенно считать гармоническими
лишь приближенно при очень малых
отклонениях. Главным условием
гармонического колебания является
постоянство циклической частоты и
амплитуды. Например, при колебаниях
нитяного маятника, угол отклонения от
вертикали изменяется неравномерно,
т.е. циклическая частота

не постоянна. Если отклонения очень
малы, то движение маятника происходит
очень медленно и неравномерностью
движения можно пренебречь, полагая

.
Чем медленнее движение, тем меньше
сопротивление среды, те меньше потери
энергии и меньше изменения амплитуды.

Итак, малые колебания
можно приближенно считать гармоническими.

1
0.
Аналитическое
представление колебаний
– запись колеблющейся величины в виде
функции

,
выражающей зависимость величины от
времени.

11. Графическое
представление колебаний – представление
колебаний
в виде графика функции

в координатных осях OX
и t
.

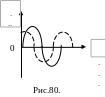
Например, аналитически
гармоническое колебания записывается
в виде

,
а его графическое представление
изображается синусоидой — сплошная
линия на Рис.80.

12.
Скорость точки при гармоническом
колебании
– получим, дифференцируя по времени
функцию х(t)

,
где

амплитуда скорости, пропорциональна
циклической частоте и амплитуде смещения.

Итак, скорость V
по синусоидальному закону с таким же
периодом T,
что и смещение
х
в пределах

.
Фаза скорости

опережает фазу смещения на

.
Это значит, что скорость максимальна,
когда точка проходит положение равновесия

,
а при максимальных смещениях точки

её скорость равна нулю . График скорости
представлен пунктирной линией на рис
Рис.80

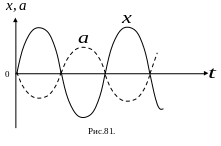
13. Ускорение
точки при гармонических колебаниях
получим,
дифференцируя скорость по времени или
дифференцируя смещение х
дважды по времени :

,

где

— амплитуда ускорения пропорциональная
амплитуде смещения и квадрату циклической
частоты.

У
скорение
точки при гармонических колебаниях
изменяется по синусоидальному закону
с тем же периодом Т,
что и смещение в пределах

Фаза ускорения опережает фазу смещения
на

.
Ускорение равно нулю в момент прохождения
точкой положения равновесия, На Рис.81
график ускорения изображен пунктирной
линией, сплошная линия изображает
график смещения.

Учитывая, что

ускорение запишем в виде

,

т.е. ускорение в
гармоническом колебании пропорционально
смещению и всегда направлено к положению
равновесия ( против смещения). Удаляясь
от положения равновесия точка движется
ускоренно, приближаясь к положению
равновесия точка движется ускоренно.

14. Динамика
гармонического колебания.
Умножив ускорение точки, совершающей
гармоническое колебание, на её массу
получим согласно второму закону Ньютона
силу, действующую на точку

Обозначим

Теперь запишем силу, действующую на
точку

.

Из последнего равенства
следует, что гармонические колебания
вызываются силой пропорциональной
смещению и направленной против смещения,
т.е. к положению равновесия.

15. Период
колебаний пружинного маятника. Пружинный
маятник совершает колебания под
действием силы упругости

.

Сила пропорциональная
смещению и направленная к положению
равновесия вызывает гармонические
колебания точки. Поэтому колебания
пружинного маятника гармонические.
Коэффициент жесткости равен

.

Помня, что

получим период свободных колебаний
пружинного маятника

.

Частота пружинного
маятника равна

.

1
5.
Математический
маятник –
материальная точка, подвешенная на
бесконечно тонкой, невесомой, нерастяжимой
нити, совершающая колебания в вертикальной
плоскости, под действием силы тяжести.

Груз, подвешенный
на нити, размеры которого пренебрежимо
малы по сравнению с длиной нити , можно
приближенно считать математическим
маятником. Часто такой маятник называют
нитяным маятником.

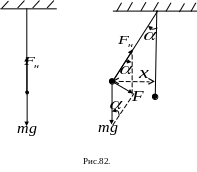
Рассмотрим малые
колебания математического маятника
длиной l.
В положении равновесия сила тяжести
уравновешена силой натяжения нити,
т.е.

.

Если отклонить
маятник на малый угол

,
то сила тяжести и сила натяжения,
направленные под углом друг к другу, в
сумме дают равнодействующую силу

,которая
направлена к положению равновесия. На
Рис.82 отклонение маятника от вертикали
равно

.

Угол

настолько мал, что циклическую частоту,
т.е. угловую скорость вращения нити
можно считать постоянной. Поэтому

и смещение маятника запишем в виде

.

Таким образом,
малые колебания математического маятника
есть гармонические колебания. Из Рис.
82 следует, что сила

,
но

,
следовательно

,

где m,
g,
и l
постоянные величины. Обозначим

и получим модуль возвращающей силы в
виде

.
Если учесть, что сила

всегда направлена к положению равновесия,
т.е. против смещения, то её выражение
запишем в виде

.

Итак, сила, вызывающая
колебания математического маятника
пропорциональна смещению и направлена
против смещения, как при колебаниях
пружинного маятника, т.е характер этой
силы такой же как и силы упругой. Но по
природе упругая сила есть сила
электромагнитная. Сила же вызывающая
колебания математического маятника по
своей природе есть сила гравитационная
– неэлектромагнитная поэтому её называют
квазиупругой
силой. Любая сила, которая действует
как сила упругая, по природе не является
электромагнитной, называется квазиупругой
силой. Это позволяет нам записать
выражение периода колебаний математического
маятника в виде

.

Из этого равенства
следует, что период колебаний
математического маятника не зависит
от массы маятника, но зависит от его
длины и ускорения свободного падения.
Зная период колебаний математического
маятника и его длину, можно определить
ускорение свободного падения в любой
точке на поверхности Земли.

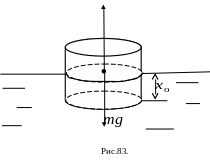
17. Колебания
тела, плавающего на поверхности жидкости.
Для простоты
рассмотрим тело массы m
в форме цилиндра с площадью основания
S.
Тело плавает
частично погрузившись в жидкость,
плотность которой

(Рис.
83).

Пусть в положении
равновесия глубина погружения

.
При этом равнодействующая силы Архимеда

и силы тяжести

равна нулю

.

Если изменить
глубину погружения на х
то сила Архимеда станет равной

и модуль равнодействующей силы F
станет отличен от нуля

Учитывая, что

получим

.

Обозначая

,
модуль силы F
в виде

.

Если глубина
погружения увеличивается, т.е. тело
смещается вниз, сила Архимеда становится
больше силы тяжести и равнодействующая
F
направлена вверх, т.е. против смещения.
Если же глубина погружения уменьшается
, т.е. смещается вверх от положения
равновесия, сила Архимеда становится
меньше силы тяжести и равнодействующая
F
направлена вниз, т.е. против смещения.

Итак, сила F
всегда направлена против смещения и
её модуль пропорционален смещению

.

Э
та
сила квазиупругая и она вызывает
гармонические колебания тела, плавающего
на поверхности жидкости. Период этих
колебаний вычисляется по общей для
гармонических колебаний формуле

.

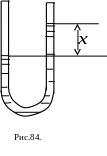
18. Колебания
однородной жидкости в U-трубке.
Пусть однородная жидкость массы m,
плотность которой

налита
в U
– образную трубку, площадь сечения
которой S
(Рис.84) В состоянии равновесия высоты
столбов в обоих коленах трубки одинаковы,
по закону сообщающихся сосудов для
однородной жидкости.

Если жидкость
вывести из состояния равновесия, то
высоты столбов жидкости в коленах будут
периодически изменяться, т.е. жидкость
в трубке будет совершать колебан
ия.

Пусть в некоторый
момент времени высота столба жидкости
в правом колене на х
больше . чем в левом. Это значит, что на
жидкость в трубке действует сил тяжести
жидкости в столбе высотой х,

,
где

— объём столба жидкости высотой x.
Произведение

величина постоянная, следовательно

.

Таким образом,
модуль силы F
пропорционален разности высот столбов
жидкости в коленах, т.е. пропорционален
смещению жидкости в трубке. Направление
этой силы всегда противоположно смещению,
т.е.

.

Следовательно
эта сила вызывает гармонические колебания
жидкости в трубке. Период этих колебаний
запишем по правилу для гармонических
колебаний

.

19. Колебания
тела в сферической чаше.
Пусть тело скользит без трения в
сферической чаше радиуса R
(Рис. 78). При малых отклонениях от положения
равновесия колебания этого тела можно
рассматривать как гармонические
колебания математического маятника,
длина которого равна R,
с периодом равным

.

20. Энергия
гармонического колебания.
В качестве примера рассмотрим колебания
пружинного маятника. При смещении х
его потенциальная энергия равна

.
В
этот же момент его кинетическая энергия
равна

.

Учитывая, что

получим
полную механическую энергию маятника

.

Или подставив

,

.

Эта формула
позволяет вычислить полную механическую
энергию любой системы, совершающей
гармонические колебания.

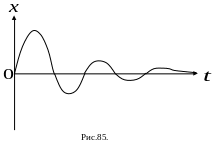
21. Затухающие
колебания.
Механические колебания происходят в
средах, оказывающих сопротивление
движению. Поэтому энергия колебательного
движения расходуется на работу по
преодолению сил трения.

Е
сли
силы трения не очень велики, то амплитуда
колебаний постепенно уменьшается и
колебания прекратятся. График затухающего
колебания представлен на Рис. 85. Это
периодическое движение, амплитуда
которого постепенно уменьшается.

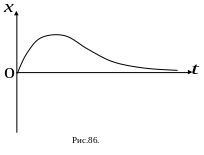
Если сила трения
очень велика, то затухающие колебания
не происходят. Тело , выведенное из
положения равновесия какими-либо силами,
после прекращения действия этих сил
возвращается в положение равновесия и
останавливается. Такое движение
называется апериодическим (непериодическим).
График апериодического движения
представлен на Рис.86.

2
2.
Вынужденные
колебания
– незатухающие колебания системы,
которые вызываются внешними периодически
меняющимися с течением времени силами
( вынуждающие силы).

Если вынуждающая
сила изменяется по гармоническому
закону

,

где

амплитуда
вынуждающей силы,

её
циклическая частота, то в системе могут
установиться вынужденные гармонические
колебания с циклической частотой равной
частоте вынуждающей силы

.

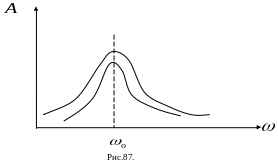
23. Резонанс
– резкое возрастание амплитуды
вынужденных колебаний при совпадении
частоты вынуждающей силы с частотой
свободных колебаний системы

.
Если колебание происходит в среде,
оказывающей сопротивление, то график
зависимости амплитуды вынужденных
колебаний от частоты вынуждающей силы
выглядит так как на Рис.87

Вынуждающая сила,
частота которой совпадает с частотой
свободных колебаний системы, даже при
очень малых амплитудах вынуждающей
силы может вызвать колебания с очень
большой амплитудой.

24. Свободные
колебания. Собственная частота системы.
Свободными колебаниями называют
колебания системы, происходящие под
действием её внутренних сил. Для
пружинного маятника внутренней силой
является сила упругости. Для математического
маятника, который состоит из самого
маятника и Земли, внутренней силой
является сила тяжести. Для тела, плавающего
на поверхности жидкости, внутренней
силой является сила Архимеда.

25. Автоколебания
– незатухающие
колебания, происходящие в среде, за счет
источника энергии не обладающего
колебательными свойствами, компенсирующего
потери энергии на преодоление сил
трения. Автоколебательные системы
получают равные порции энергии через
равные интервалы времени например,
через один период. Примером автоколебательной
системы являются часы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #