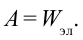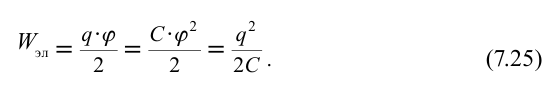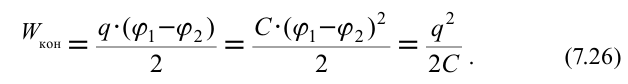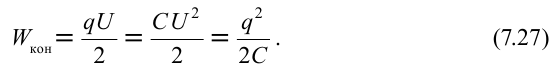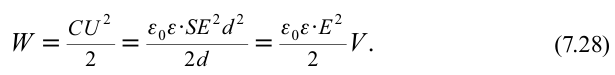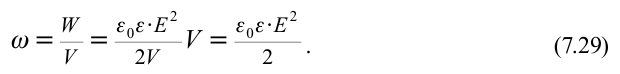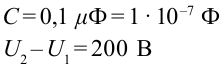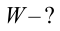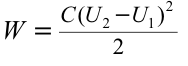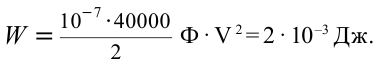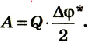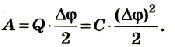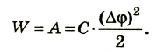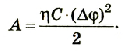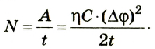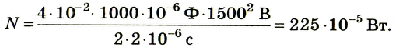Однородным электрическим полем называют такое электрическое поле, вектор напряжённости которого не зависит от точки пространства ((vec{r(t)} =const)), где (vec{r(t)}) — радиус-вектор исследуемой точки.
Потенциальные и непотенциальные силы в электродинамике
Все силы можно разделить на потенциальные и непотенциальные.
Работа потенциальной силы зависит только от начального и конечного положения тела и от формы траектории не зависит. Сила Кулона является потенциальной.
Потенциальность кулоновских сил позволяет говорить о потенциальной энергии заряда в поле электрических сил. По определению потенциальной энергии полагается, что изменение потенциальной энергии при его переносе из точки (А) в точку (Б) в любом электрическом поле — это работа кулоновских сил при перемещении заряда между этими точками, взятая со знаком минус:
(A=-(E_Б-E_А)). ((1))
Энергия системы заряженных тел
Вокруг заряженного тела появляется электрическое поле, которое оказывает действие на другие заряды. Таким образом, система, состоящая из какого-либо набора заряженных тел, обладает потенциальной энергией, которую обычно называют кулоновской или электрической.
Изменение потенциальной энергии заряда в однородном электрическом поле
Рассмотрим изменение потенциальной энергии положительного заряда (q), если переместить его в однородном электрическом поле из точки (А) в точку (Б) по красной траектории (рис. (1)).
Рис. (1). Перемещение заряда в однородном поле
Она изменяется так же, как если бы заряд перемещался по прямой (чёрной) траектории, поскольку работа потенциальной силы зависит только от начальной и конечной точки траектории.
Сила, действующая на него, постоянна:
(vec{F}=q vec{E}). ((2))
Если ввести радиус-векторы начала и конца этой траектории (vec{r}_А) и (vec{r}_Б) соответственно, то перемещение этого заряда:
(vec{r}=(vec{r}_Б — vec{r}_А)). ((3))
Работу кулоновской силы можно записать как скалярное произведение силы на перемещение:
(A=vec{F}cdot {r}=q vec{E} (vec{r}_Б — vec{r}_А) ). ((4))
Выбрав за ноль потенциальной энергии начальную точку ((vec{r}_А)), перепишем формулу ((1)) в виде:
(A=-E_Б). ((5))
Из формулы ((4)) получим, что потенциальная энергия заряда, который расположен в точке с радиус-вектором (vec{r}_Б=vec{r}) в однородном электрическом поле, равна скалярному произведению радиус-вектора на вектор напряжённости электрического поля:
(E= -A=-q vec{E} cdot vec{r} ), ((6))
что в координатном виде может быть записано как:
(E=-q (E_x x+E_у y+E_z z).) ((7))
Энергия взаимодействия точечных зарядов
Для того чтобы найти энергию взаимодействия точечных зарядов, рассмотрим систему из двух положительных зарядов (q_1) и (q_2). Положим, что заряд (q_1) неподвижен.
Рассмотрим, какую работу совершит электрическое поле, которое создано зарядом (q_1), при перемещении заряда (q_2) из точки (А) в точку (Б) по красной траектории (рис. (2)).
Рис. (2). Перемещение заряда в поле точечного заряда
Как и в случае однородного электрического поля, вместо красной траектории будем рассматривать чёрную траекторию, где из точки (А) в точку (С) заряд перемещается вдоль линии, соединяющей эти два заряда, а из точки (С) в точку (Б) — по дуге окружности, центром которой является первый заряд.
В таком случае работа электрического поля на дуге (СБ) будет нулевой:
(A=vec{F} cdot vec{r}=|F|cdot |r|cos(pi/2)=0,) ((8))
поскольку сила Кулона всегда перпендикулярна перемещению. На участке (АС) сила Кулона сонаправлена с перемещением, а по модулю:
( F(r)=frac{k q_1q_2}{r^2}), ((9))
поэтому работу электрического поля можно рассчитать как:
(A=F(r_A)r+F(r_A+Delta r)Delta r+F(r_A+2Delta r) Delta r+F(r_A+3Delta r) Delta r+ldots +)
(+F(r_C-2Delta r) Delta r+ F(r_C-Delta r) r=sum limits_{r=r_A}^{r_C}F(r)Delta r=sum limits_{r=r_A}^{r_C} frac{k q_1 q_2}{r^2} cdot Delta r.) ((10))
В пределе, когда (Delta r) мало, эта сумма равна:
(A=-frac{k q_1 q_2}{r}). ((11))
Сравнивая формулы ((1)) и ((11)), получаем, что потенциальная энергия взаимодействия точечных зарядов:
(E=frac{k q_1q_2}{r}.) ((12))
Энергия системы (n) точечных зарядов
Если рассматривать систему, состоящую из (n) точечных зарядов, то её потенциальная энергия:
( E=frac{1}{2} sum limits_{i neq j} frac{k q_i q_j}{r_{i,j}}=frac{1}{2} left(frac{k q_1 q_2}{r_{12}}+frac{k q_2 q_1}{r_{21}}+frac{k q_2 q_3}{r_{23}}+frac{k q_3 q_2}{r_{32}}+ldots right),) ((13))
где (r_{i,j}) — это расстояние между (i)-м и (j)-м точечными зарядами, а множитель (frac{1}{2}) появляется из-за того, что в сумме дважды учитывается потенциальная энергия взаимодействия (i)-го и (j)-го точечных зарядов.
Свойство линий напряжённости электрического поля
Поскольку сила Кулона потенциальна, то, если перемещать заряд по любому замкнутому контуру, работа силы Кулона равна нулю.
Отсюда вытекает, что линия напряжённости электростатического поля не замкнута.
Докажем это от противного: предположим, что линия электрического поля замкнута (рис. (3)).
Рис. (3). Замкнутая линия электрического поля
Но тогда при перемещении положительного заряда по замкнутой линии электрического поля работа электрического поля будет равна:
(A=sum vec{F} cdot vec{r}). ((14))
Каждый член этой суммы положителен, поскольку сила всегда сонаправлена с перемещением (рис. (3)).
Мы пришли к противоречию. Следовательно, линии электрического поля не замкнуты.
Источники:
Рис. 1. Перемещение заряда в однородном поле. © ЯКласс.
Рис. 2. Перемещение заряда в поле точечного заряда. © ЯКласс.
Рис. 3. Замкнутая линия электрического поля. © ЯКласс.
Работа
сил электрического поля, созданного
зарядом
,
по перемещению зарядаиз точки 1 в точку 2 равна:

Работа сил
консервативного поля равна убыли
потенциальной энергии:
,
тогда
потенциальная энергия заряда
в поле заряда
равна:
.
Значение
константы выбирается таким, чтобы при
удалении заряда на бесконечность (то
есть при
)
потенциальная энергия обратилась бы в
ноль, поэтому
.
Ясно,
что разные пробные заряды
и
в одной и той же точке поля будут обладать
разной потенциальной энергиейи
.
Однако отношениедля всех пробных зарядов будет одинаково.
Величина
называется
потенциалом электрического поля и
является его энергетической характеристикой.
Потенциал поля точечного заряда равен
.
Если
поле создается системой
точечных зарядов, то
,
где
— расстояние от заряда
до начального положения заряда
,
— расстояние от заряда
до конечного положения заряда
(заряд
перемещается силами поля).
Тогда
потенциальная энергия зарядав поле системы зарядов:
,
а
потенциал
-
потенциал поля,
создаваемого системой зарядов, равен
алгебраической сумме потенциалов,
создаваемых каждым из зарядов в
отдельности.
Зная
потенциал, можно найти потенциальную
энергию заряда
в электрическом поле:
.
Работа поля над
зарядом:
—
работа равна убыли потенциала, умноженной
на заряд.
Если заряд удаляется
из точки на бесконечность, то работа
сил поля равна
следовательно,
потенциал численно равен отношению
работы, которую совершают силы поля над
положительным зарядом при удалении его
из данной точки на бесконечность, к
величине этого заряда. Потенциал
измеряется в вольтах:
.
1.5.Связь между напряженностью и потенциалом
Электрическое
поле можно описывать либо с помощью
векторной величины
(силовая характеристика), либо с помощью
скаляра(энергетическая характеристика). Сила
связана, как известно, с потенциальной
энергией:
,
где
— оператор Набла,
.
Для
заряженной частицы в электрическом
поле:
,
,
тогда,
,
тогда— связь напряженности и потенциала, или
,
или,
или—
проекция
вектора
на произвольное направление
равна скорости убывания потенциала
вдоль направления
,или
.
Так
как градиент потенциала направлен в
сторону его возрастания, а численная
величина градиента является мерой
быстроты этого возрастания, то можно
сказать, что напряженность электрического
поля есть мера быстроты спадания
потенциала, или, просто, что она равна
спаду потенциала.
Вернемся к
определению работы поля:
,
,
отсюда циркуляция вектора
на
участке 1=2
равна
.
Интеграл можно брать по любой линии,
соединяющей точки 1 и 2, так как работа
не зависит от пути.
Для
обхода по замкнутому контуру:
и
— пришли к теореме о циркуляции вектора
напряженности электростатического
поля.
1.6. Эквипотенциальные поверхности
Воображаемая
поверхность, все точки которой имеют
одинаковый потенциал, называется
эквипотенциальной поверхностью:
— уравнение
эквипотенциальной поверхности.
При
перемещении по эквипотенциальной
поверхности на отрезок
потенциал не изменяется
.
Таким образом, касательная к поверхности
составляющая вектораравна нулю. Тогда вектор
направлен по нормали к эквипотенциальной
поверхности в каждой ее точке, а линии
напряженности в каждой точке перпендикулярны
к эквипотенциальным поверхностям.
эквипотенциальные поверхности построить
таким образом, чтобы разность потенциалов
для двух соседних поверхностей была
одна и та же, то по густоте эквипотенциальных
поверхностей можно судить о напряженности
поля. Действительно, чем гуще
эквипотенциальные поверхности, тем
больше,
тем больше.
Для
однородного поля эквипотенциальные
поверхности представляют собой систему
равноотстоящих друг от друга плоскостей,
перпендикулярных к направлению поля.
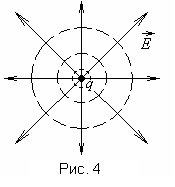
Рассмотрим
эквипотенциальную поверхность точечного
заряда. Потенциал точечного заряда
(рис.1.4)
.
Таким
образом, эквипотенциальная поверхность
этого заряда будет сферой радиуса
с центром в точке заряда. Силовые же
линии, как мы установилиранее,
расходятся радиально от заряда если он
,
или сходятся к заряду, если он “-”. То
есть векторперпендикулярен эквипотенциальным
поверхностям.
Соседние файлы в папке 2. Электромагнетизм
- #
- #
- #
- #
- #
Содержание:
Энергия электрического поля:
Для зарядки проводника выполняется работа по преодолению силы отталкивания между зарядами. За счет этой работы проводник получает энергию. Полученная энергия заряженного тела количественно равна работе, выполненной при его зарядке, т.е.
Среднее значение потенциала тела равно среднему арифметическому его начальных и конечных значений, т.е.
Поставляя значении 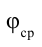
Значит, работа, выполненная при зарядке тела, равняется половине произведения его заряда на потенциал. При зарядке тела его потенциал плавно, т.е. линейно изменяется согласно формуле 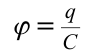
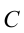
Согласно соотношению 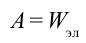
Если заряженное тело является конденсатором, то при расчете энергии (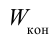
Исходя из этого, формулу определения электрической энергии конденсатора можно записать в виде:
Энергия заряженного тела сосредоточена в электрическом поле, созданном вокруг него, величина энергии зависит от объема пространства, занимаемого полем и напряженности поля.
Рассмотрим частный случай плоского заряженного конденсатора.
Электрическое поле, созданное зарядами обкладок плоского конденсатора, сосредоточено в среде между его обкладками. Объем пространства можно вычислить по формуле 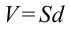
Учитывая емкость заряженного плоского конденсатора 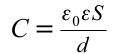
Энергия заряженного плоского конденсатора прямо пропорциональна квадрату напряженности созданного им поля и объему пространства, занимаемого этим полем. Энергия, приходящаяся на удельную единицу поля, называется объемной плотностью энергии. То есть:
Каждый конденсатор имеет свойство накапливать в себе не только заряд, но и энергию. Энергия, полученная конденсатором, сосредоточена в среде между его обкладками. Эту энергию невозможно хранить длительное время. Конденсатор с течением времени передает полученный заряд в окружающую среду, т.е. разряжается.
При разрядке конденсатора через цепь с маленьким электрическим сопротивлением энергия передается практически мгновенно.
Образец решения задачи:
Емкость плоского воздушного конденсатора равна 0,1 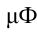
Дано:
Найти:
Формула:
Решение:
Ответ: 2 мДж.
Основные понятия, правила и законы:
| Закон сохранения зарядов | Алгебраическая сумма зарядов всех тел внутри любой закрытой системы не меняется, т.е.: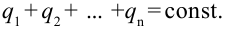 |
| Силовые линии электрического поля |
Линии, показывающие направления силы, действующие со стороны поля на положительный заряд, введенный в электрическое поле. Силовые линии электрического поля, образованного положительным зарядом, направлены от заряда, а в случае отрицательного заряда – направлены к нему. |
| Напряженность электрического поля |
Напряженность электрического поля – векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы 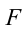 , действующей на , действующей нанеподвижный заряд, помещенный в данную точку поля, к величине этого заряда 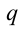 : :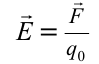 |
| Напряженность поля, создаваемого точечным зарядом 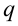 на расстоянии на расстоянии 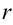 . . |
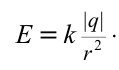 |
| Принцип суперпозиции электрического поля. |
Напряженность электростатического поля, создаваемого в данной точке системой зарядов, равна векторной сумме напряженностей полей, создаваемых в этой точке каждым зарядом в отдельности: 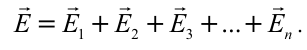 |
| Напряженность электрического поля в точках внутри заряженного шара (сферы) и за его пределами |
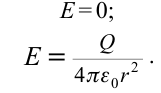 |
| Поляризация диэлектрика. |
Деформация электронной оболочки атомов (молекул) диэлектрика под воздействием электрического поля, в результате чего центры положительных и отрицательных зарядов атома не накладываются друг на друга. |
| Диэлектрическая восприимчивость. |
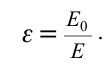 |
| Напряженность поля в точке на расстоянии 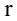 от точечного заряда, от точечного заряда,расположенного внутри диэлектрика. |
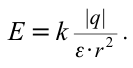 |
Потенциальная энергия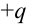 заряда, находящегося заряда, находящегосяна расстоянии 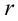 от неподвижного положительного от неподвижного положительногозаряда 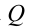 |
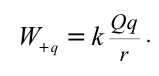 |
| Потенциал точечного заряда 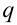 . . |
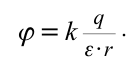 |
| Электрическое напряжение. |
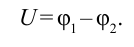 |
| Консервативная сила. | Сила, работа которой не зависит от траектории перемещения. |
| Объемная плотность энергии. |
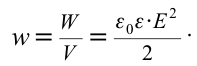 |
Энергия электрического поля
В заряженном конденсаторе обкладки имеют разноименные .заряды и взаимодействуют благодаря наличию электрического поля. О телах, которые взаимодействуют, говорят, что они имеют энергию. Таким образом можно утверждать, что заряженный конденсатор имеет энергию.
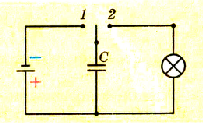
Наличие энергии в заряженном конденсаторе можно подтвердить опытами. Для этого возьмем конденсатор довольно большой емкости, источник тока, лампочку и составим цепь, показанную на рисунке 1.44. Сначала переведем переключатель в положение 1, зарядив таким образом конденсатор от источника тока.
Pиc. 1.44. Схема цепь, в которой лампочка вспыхивает за счет энергии заряженного конденсатора
Если после этого перевести переключатель в положение 2, то увидим кратковременную вспышку света вследствие накала нити лампочки.
Наблюдаемое явление можно объяснить тем, что заряженный конденсатор имел энергию, благодаря которой была выполнена работа по накалу спирали лампочки.
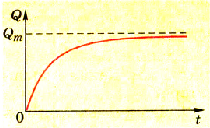
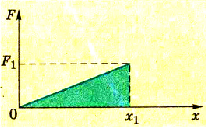
Согласно закону сохранения энергии работа, выполненная при разрядке конденсатора, равна работе, выполненной при его зарядке. Расчет этой работы и соответственно потенциальной энергии заряженного конденсатора должен учитывать особенности процесса зарядки конденсатора. Зависимость заряда Q от времени зарядки t показана на графике (рис. 1.45).
Pиc. 1.45. Изменение заряда конденсатора при его зарядке
Поскольку заряд конденсатора изменяется не пропорционально времени, вести расчет на основании формулы A = QEd нельзя, ведь напряженность поля также все время изменяется. Вместе с тем разность потенциалов между обкладками при зарядке линейно изменяется от нуля до определенного максимального значения (рис. 1.46).
Рис. 1.46. К расчету работы электрического поля в конденсаторе
Поэтому работа, которая выполняется при зарядке конденсатора, равна:
Если учесть, что 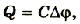
Таким образом, энергия электрического поля в конденсаторе равна:
Приняв во внимание, что 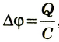
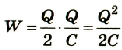
Задача:
Импульсную контактную сварку медной проволоки совершают при помощи разряда конденсатора электроемкостью 1000 мкФ при разности потенциалов между обкладками 1500 В. Какова средняя мощность импульсного разряда, если его дли тельность 2 мкс и КПД установки равен 4 %?
|
Дано: |
Решение |
| N — ? |
Средняя полезная мощность определяется с учетом времени выполнения работы:
Подставив значения физических величин, получим:
Ответ: полезная мощность, которую развивает сварочная установка, равна 225 ∙ 10-5 Вт.
Влияние электрического поля на живые организмы
Многие люди понятие электричества и электрического поля связывают только с электризацией различных тел, мощными электрическими машинами, средствами электроники и т. п. Вместе с тем электрические явления происходят и в живой природе. И это не только электризация шерсти кошки или собаки, когда их гладят рукой, но и более сложные формы, связанные с их жизнедеятельностью. В природе существуют живые организмы, способные генерировать электричество и использовать его для охоты, защиты и ориентирования в пространстве.
Одним из таких живых существ является электрический угорь (рис. 1.47). Он может генерировать разность потенциалов между отдельными частями своего тела до 360 В. Разряды, которые создает эта рыба, живые существа ощущают на расстоянии до 20 см.
Рис. 1.47 Электрический угорь
Свойства электрического угря использовали древние врачи для лечения подагры, мигрени, эпилепсии и т. п.
Аналогичные свойства и у электрического ската-торпедо (рис. 1.48). Он может на протяжении 15 с генерировать до 150 разрядов за секунду по 80 В каждый.
Pиc. 1.48 Электрический скат
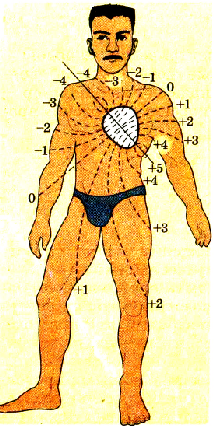
Электрические явления играют существенную роль и в физиологии человека. Одним из мощных генераторов человека является сердце. На рисунке 1.49 показаны о к ни потенциальные поверхности тела человека при активной работе сердца.
Рис. 1.49. Эквипотенциальные растений.
Хотя эти потенциалы сравнительно невелики — несколько милливольт, но их используют для диагностирования болезней сердца. Записывая эти потенциалы, специальные аппараты создают кардиограммы, по которым врач определяет состояние человека.
В физиотерапевтических кабинетах используют лечебный метод -фарадизацию, когда человека подвергают действию электрического поля и таким образом лечат некоторые болезни.
Исследования ученых показали, что под действием электрического поля улучшаются свойства семян растений. Растения, выращенные поверхности человека из таких семян, существенно улучшают спою урожайность. Даже трава растет интенсивнее под линиями электропередач, где существует сильное электрическое поле.
Если человека определенным образом изолировать от действия электрического поля «Земли, то его состояние существенно ухудшается. Некоторые люди чувствуют себя не комфортно в цельнометаллических вагонах, самолетах, автомобилях, где электрическое поле Земли экранируется металлическими корпусами транспортных средств.
- Электрическое поле заряженных неподвижных тел
- Напряженность электрического поля
- Принцип суперпозиции электрических полей
- Проводники в электрическом поле
- Электрическое поле заряженного шара
- Электрические явления в физике
- Потенциал поля точечного заряда в физике
- Работа электрического поля при перемещении заряда в физике
Энергия электрического поля
Содержание:
- Что такое энергия электрического поля
- Энергия заряженного конденсатора
- Как рассчитать энергию электрического поля через напряженность, формула
- Объемная плотность электрической энергии
Что такое энергия электрического поля
Электрическое поле — одна из двух компонент электромагнитного поля, представляющая собой векторное поле, существующее вокруг тел или частиц, обладающих электрическим зарядом, а также возникающее при изменении магнитного поля.
Энергия электрического поля — энергия проводника, обладающего зарядом, которая равна работе, затраченной, чтобы зарядить этот проводник.
Физик Майкл Фарадей сделал следующие выводы об электрическом поле:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Каждый заряд формирует вокруг себя электрическое поле определенной мощности.
- Электрическое поле воздействует на другой заряд с определенной силой.
Электрическое поле обладает рядом свойств:
- поле материально;
- источником является заряд;
- обнаружить поле можно, исходя из действия на заряд;
- поле распределяется непрерывно в пространстве;
- при удалении от заряда поле слабеет.
Тело, обладающее зарядом, действует на другие тела, притягивая и отталкивая их. По отношению к заряженному объекту другие тела поворачиваются и перемещаются. Для любого электрического поля характерен запас энергии. В случае исчезновения электрического поля его электроэнергия трансформируется обратно в работу.
Энергия заряженного конденсатора
Конденсатор — двухполюсник с постоянным или переменным значением емкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Емкость конденсатора измеряется в фарадах.
Компоненты конденсаторов в виде проводников обозначают обкладками. Наиболее простым примером конденсатора является совокупность двух плоских пластин. Данные элементы способны проводить электрический ток и расположены параллельно относительно друг друга. Пластины удалены на небольшое по сравнению с их габаритами расстояние и отделены диэлектрическим материалом.
В плоском конденсаторе можно наблюдать электрическое поле:
- Основное — в области между пластин.
- Слабое или поле рассеяния — около краев пластин и во внешней среде.
Опытным путем было доказано, что конденсатор, обладая электрическим полем, вмещает определенный запас энергии. Для ее расчета необходимо найти сумму работы внешних сил, необходимых для питания конденсатора. Такой процесс является последовательным переносом минимальных порций заряда Δq > 0 с одном пластины на другую.
Один элемент при этом будет постепенно приобретать положительный заряд, а другой — заряжаться отрицательно. Транспортировка заряда осуществляется при условии, что пластины уже обладают неким зарядом q. Разность потенциалов между ними будет определена по формуле:
(U=frac{q}{C})
В процессе переноса некоторого заряда Δq вешние силы совершают работу, которая определяется следующим уравнением:
(Delta A=UDelta q=frac{qDelta q}{C})
Энергию We конденсатора, емкость которого составляет С, а заряд равен Q, можно рассчитать с помощью интегрирования предыдущей формулы в пределах от 0 до Q:
(W_{e}=A=frac{Q^{2}}{2C})
Следует учитывать следующее условие:
(Q=CU)
Тогда энергия заряженного конденсатора будет переписана в другом эквивалентном уравнении:
(W_{e}=A=frac{Q^{2}}{2C}=frac{CU^{2}}{2}=frac{QU}{2})
Электрическая энергия (We) будет рассматриваться в качестве потенциальной энергии, которая находится в запасе заряженного конденсатора. Для расчета электрической энергии справедливо применять формулу, с помощью которой определяют потенциальную энергию деформированной пружины ((Ер)):
(E_{p}=frac{kx^{2}}{2}=frac{F^{2}}{2k}=frac{Fx}{2})
Где k является жесткостью пружины, (х) — деформацией, а (F = kx) равно внешней силе.
Исходя из современных представлений, электрическую энергию можно наблюдать в области между пластинами конденсатора, то есть в пространстве с электрическим полем. Отсюда появилось название энергии электрического поля.
Как рассчитать энергию электрического поля через напряженность, формула
В качестве примера можно рассмотреть плоский конденсатор. Его однородное электрическое поле в этом случае будет обладать напряженностью. Данная величина определяется по формуле:
(E=frac{U}{d})
Емкость конденсатора будет рассчитываться таким образом:
(C=frac{varepsilon _{0}varepsilon S}{d})
Исходя из приведенных равенств, энергия электрического поля будет равна:
(W_{e}=frac{CU^{2}}{2}=frac{varepsilon _{0}varepsilon SE^{2}d^{2}}{2d}=frac{varepsilon _{0}varepsilon E^{2}}{2}V)
Где V = Sd является объемом пространства между пластинами конденсатора, который вмещает электрическое поле.
Объемная плотность электрической энергии
Расчет физической величины We выглядит следующим образом:
(W_{e}=frac{varepsilon _{0}varepsilon E^{2}}{2}V)
Таким образом, (We) представляет собой электрическую или потенциальную энергию единицы объема пространства, в котором сформировано электрическое поле. Данная величина — объемная плотность электрической энергии. Для того чтобы найти энергию поля, созданного путем распределения электрически заряженных частиц в пространстве, необходимо интегрировать объемную плотность по всему объему, для которого характерно наличие электрического поля.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Электрический заряд
q — заряд
n — число частиц
e — заряд электрона
Найти
- q
- n
- e
Известно, что:
=
Вычислить ‘q‘
Закон Кулона
F — сила
k — коэффициент пропорциональности
q1, q2 — заряды
r — расстояние
Найти
- F
- k
- q1
- q2
- r
Известно, что:
=
Вычислить ‘F‘
Постоянная Кулона
k — коэффициент пропорциональности
ε_0 — электрическая постоянная
Найти
- k
- π
- ε_0
Известно, что:
=
Вычислить ‘k‘
Относительная диэлектрическая проницаемость
ε — диэлектрическая постоянная (проницаемость)
F_вак — сила в вакууме
F_окр — сила в окружающей среде
Найти
- ε
- F_вак
- F_окр
Известно, что:
=
Вычислить ‘ε‘
Электрическое поле
E — электрическое поле
F — сила
q — заряд
Найти
- E
- F
- q
Известно, что:
=
Вычислить ‘E‘
Электрическое поле точечного заряда в вакууме
E — электрическое поле
k — коэффициент пропорциональности
q_0 — заряд
r — расстояние
Найти
- E
- k
- q_0
- r
Известно, что:
=
Вычислить ‘E‘
Электрическое поле точечного заряда в окружающей среде
E — электрическое поле
k — коэффициент пропорциональности
q — заряд
ε — диэлектрическая постоянная (проницаемость)
r — расстояние
Найти
- E_окр
- k
- q_0
- ε
- r
Известно, что:
=
Вычислить ‘E_окр‘
Электрическое поле вне заряженной сферы
E — электрическое поле
k — коэффициент пропорциональности
σ — плотность поверхностного заряда
R — радиус
r — расстояние
Найти
- E
- k
- σ4
- π
- R
- r
Известно, что:
=
Вычислить ‘E‘
Электрическое поле вне заряженной сферы
E — электрическое поле
k — коэффициент пропорциональности
q — заряд
r — расстояние
Найти
- E
- k
- q
- r
Известно, что:
=
Вычислить ‘E‘
Электрическое поле бесконечной заряженной плоскости
E — электрическое поле
k — коэффициент пропорциональности
σ — плотность поверхностного заряда
Найти
- E
- k2
- π
- σ
Известно, что:
=
Вычислить ‘E‘
Электрическое поле бесконечной заряженной плоскости
E — электрическое поле
σ — плотность поверхностного заряда
ε_0 — электрическая постоянная
Найти
- E
- σ
- ε_0
Известно, что:
=
Вычислить ‘E‘
Электрическое поле конденсатора
E — электрическое поле
k — коэффициент пропорциональности
σ — плотность поверхностного заряда
Найти
- E
- k
- π
- σ
Известно, что:
=
Вычислить ‘E‘
Работа в электрическом поле
A — работа
F — сила
Δd — расстояние
Найти
- A
- F
- Δ_d
Известно, что:
=
Вычислить ‘A‘
Потенциальная энергия системы двух точечных зарядов
W — потенциальная энергия
k — коэффициент пропорциональности
q0, q — заряды
ε — диэлектрическая постоянная (проницаемость)
r — расстояние
Найти
- W
- k
- q0
- q
- ε
- r
Известно, что:
=
Вычислить ‘W‘
Работа в электрическом поле — разность потенциальных энергий
A — работа
W1 — начальная потенциальная энергия
W2 — конечная потенциальная энергия
Найти
- A
- W1
- W2
Известно, что:
=
Вычислить ‘A‘
Потенциал электростатического поля
φ — потенциал
W — потенциальная энергия
q — заряд
Найти
- φ
- W
- q
Известно, что:
=
Вычислить ‘φ‘
Напряжение — разность потенциалов
U — напряжение
φ1 — начальный потенциал
φ2 — конечный потенциал
Найти
- U
- φ1
- φ2
Известно, что:
=
Вычислить ‘U‘
Работа переноса заряда
A — работа
q — заряд
U — напряжение
Найти
- A
- q
- U
Известно, что:
=
Вычислить ‘A‘
Потенциал электростатического поля вокруг точечного заряда
φ — потенциал
k — коэффициент пропорциональности
q_0 — заряд
ε — диэлектрическая постоянная (проницаемость)
r — расстояние
Найти
- φ
- k
- q0
- ε
- r
Известно, что:
=
Вычислить ‘φ‘
Напряжённость электростатического поля
E — электрическое поле
U — напряжение
Δd — расстояние
Найти
- E
- U
- Δ_d
Известно, что:
=
Вычислить ‘E‘
Результирующее электрическое поле
E — результирующее электрическое поле
E0 — внешнее электрическое поле
E1 — внутреннее электрическое поле
Найти
- E
- E0
- E1
Известно, что:
=
Вычислить ‘E‘
Электрический момент
p — электрический момент
q — заряд
l — расстояние
Найти
- p
- q
- l
Известно, что:
=
Вычислить ‘p‘
Электрическая ёмкость
C — электрическая ёмкость
q — заряд
φ — потенциал
Найти
- C
- q
- φ
Известно, что:
=
Вычислить ‘C‘
Электрическая ёмкость шара
C — электрическая ёмкость
ε — диэлектрическая постоянная (проницаемость)
R — радиус
k — коэффициент пропорциональности
Найти
- C
- ε
- R
- k
Известно, что:
=
Вычислить ‘C‘
Электрическая ёмкость двух проводников
C — электрическая ёмкость
q — заряд
U — напряжение
Найти
- C
- q
- U
Известно, что:
=
Вычислить ‘C‘
Электрическая ёмкость плоского конденсатора
C — электрическая ёмкость
ε — диэлектрическая постоянная (проницаемость)
ε0 — электрическая постоянная
S — площадь
d — расстояние между плас
Найти
- C
- ε
- ε0
- S
- d
Известно, что:
=
Вычислить ‘C‘
Электрическая ёмкость сферического конденсатора
C — электрическая ёмкость
ε — диэлектрическая постоянная (проницаемость)
ε0 — электрическая постоянная
R1 — радиус внутренней сферы
R2 — радиу
Найти
- C
- π
- ε
- ε0
- R1
- R2
Известно, что:
=
Вычислить ‘C‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
q — заряд
E1 — напряженность электрического поля, создаваемого пластиной конденсатора
d — расстояние между пластин
Найти
- W
- q
- E1
- d
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
q — заряд
E — электрическое поле
d — расстояние между пластинами
Найти
- W
- q
- E
- d
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
q — заряд
U — напряжение
Найти
- W
- q
- U
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
C — электрическая ёмкость
U — напряжение
Найти
- W
- C
- U
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
q — заряд
C — электрическая ёмкость
Найти
- W
- q
- C
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
ε — диэлектрическая постоянная (проницаемость)
ε0 — электрическая постоянная
E — электрическое поле
V — объём
Найти
- W
- ε
- ε0
- E
- V
Известно, что:
=
Вычислить ‘W‘
Потенциальная энергия заряженного плоского конденсатора
W — потенциальная энергия
ε — диэлектрическая постоянная (проницаемость)
ε0 — электрическая постоянная
E — электрическое поле
S — площадь
d —
Найти
- W
- ε
- ε0
- E
- S
- d
Известно, что:
=
Вычислить ‘W‘
Плотность энергии электрического поля
ω_p — плотность энергии электрического поля
W — потенциальная энергия
V — объём
Найти
- ω_p
- W
- V
Известно, что:
=
Вычислить ‘ω_p‘
Плотность энергии электрического поля
ω_p — плотность энергии электрического поля
ε0 — электрическая постоянная
ε — диэлектрическая постоянная (проницаемость)
E — электрическое п
Найти
- ω_p
- ε0
- ε
- E
Известно, что:
=
Вычислить ‘ω_p‘