Как найти энтропию случайной величины

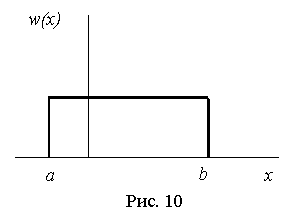
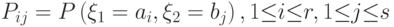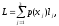5.2 Элементы теории информации

Кратко перечислим основные понятия, более подробное изложение можно найти в [1], [2], [3].

5.2.1 Энтропия

Количественной мерой неопределенности служит энтропия. Пусть задана дискретная случайная величина , принимающая значения с вероятностями соответственно.

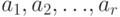
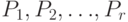
Определение 5.10 Энтропия случайной величины определяется равенством:

где .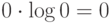

Свойства энтропии:

1. 
2. 
3. .

Пример 5.3 [3] Пусть имеется три источника сообщений, которые порождают буквы и , иными словами, есть три случайные величины , принимающие значения и :

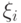
Вычисления дают: , бит, бит.

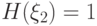
И мы видим, что неопределенность этих случайных величин разная.

Пусть двумерная случайная величина задана распределением

Определение 5.11 Энтропия двумерной случайной величины задаётся формулой:

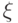
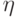
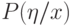
Пусть имеются дискретные случайные величины и , заданные вероятностными распределениями , . Для них можно вычислить совместное распределение и условные распределения , для любых фиксированных значений , .

Определение 5.12 Условная энтропия задаётся формулой:

Определение 5.13 Условной энтропией двух вероятностных распределений называется усредненная (по всем величина :

Мы ежедневно работаем с информацией из разных источников. При этом каждый из нас имеет некоторые интуитивные представления о том, что означает, что один источник является для нас более информативным, чем другой. Однако далеко не всегда понятно, как это правильно определить формально. Не всегда большое количество текста означает большое количество информации. Например, среди СМИ распространена практика, когда короткое сообщение из ленты информационного агентства переписывают в большую новость, но при этом не добавляют никакой «новой информации». Или другой пример: рассмотрим текстовый файл с романом Л.Н. Толстого «Война и мир» в кодировке UTF-8. Его размер — 3.2 Мб. Сколько информации содержится в этом файле? Изменится ли это количество, если файл перекодировать в другую кодировку? А если заархивировать? Сколько информации вы получите, если прочитаете этот файл? А если прочитаете его второй раз?

По мотивам открытой лекции для Computer Science центра рассказываю о том, как можно математически подойти к определению понятия «количество информации».

В классической статье А.Н. Колмогорова «Три подхода к определению понятия количества информации» (1965) рассматривают три способа это сделать:

• комбинаторный (информация по Хартли),

• вероятностный (энтропия Шеннона),

• алгоритмический (колмогоровская сложность).

Мы будем следовать этому плану.

Комбинаторный подход: информация по Хартли

Мы начнём самого простого и естественного подхода, предложенного Хартли в 1928 году.

Пусть задано некоторое конечное множество . Количеством информации в будем называть .

Можно интерпретировать это определение следующим образом: нам нужно битов для описания элемента из .

Почему мы используем биты? Можно использовать и другие единицы измерения, например, триты или байты, но тогда нужно изменить основание логарифма на 3 или 256, соответственно. В дальшейшем все логарифмы будут по основанию 2.

Этого определения уже достаточно для того, чтобы измерить количество информации в некотором сообщении. Пусть про стало известно, что . Теперь нам достаточно битов для описания , таким образом нам сообщили битов информации.

Пример

Загадано целое число от до . Нам сообщили, что делится на . Сколько информации нам сообщили?

Воспользуемся рассуждением выше.

(Тот факт, что некоторое сообщение может содержать нецелое количество битов, может показаться немного неожиданным.)

Можно ещё сказать, что сообщение, уменшающее пространство поиска в раз приносит битов информации. В данном примере пространство поиска уменьшилось в 1000/166 раз.

Интересно, что одного этого определения уже достаточно для того, чтобы решать довольно нетривиальные задачи.

Применение: цена информации

Загадано целое число от до . Разрешается задавать любые вопросы на ДА/НЕТ. Если ответ на вопрос «ДА», то мы должны заплатить рубль, если ответ «НЕТ» — два рубля. Сколько нужно заплатить для отгадывания числа ?

Любой вопрос можно сформулировать как вопрос о принадлежности некоторому множеству, поэтому мы будем считать, что все вопросы имеют вид «?» для некоторого множества .

Каким образом нужно задавать вопросы? Нам бы хотелось, чтобы вне зависимости от ответа цена за бит информации была постоянной. Другими словами, в случае ответа «НЕТ» и заплатив два рубля мы должны узнать в два больше информации, чем при ответе «ДА». Давайте запишем это формально.

Потребуем, чтобы

Пусть , тогда . Подставляем и получаем, что

Это эквивалентно квадратному уравнению Положительный корень этого уравнения . Таким образом, при любом ответе мы заплатим рублей за бит информации, а в сумме мы заплатим примернорублей (с точностью до округления).

Осталось понять, как выбирать такие множества . Будем выбирать в качестве непрерывные отрезки прямой. Пусть нам известно, что принадлежит отрезку (изначально это отрезок ). В следующего множества возмём отрезок , где. Тогда за каждый заплаченный рубль текущий отрезок будет уменьшаться в раз. Когда длина отрезка станет меньше единицы, мы однозначно определим . Поэтому цена отгадывания не будет превосходить

Приведённое рассуждение доказывает только верхнюю оценку. Можно доказать и нижнюю оценку: для любого способа задавать вопросы будет такое число , для отгадывания которого придётся заплатить не менее рублей.

Вероятностный подход: энтропия Шеннона

Вероятностный подход, предложенный Клодом Шенноном в 1948 году, обобщает определение Хартли на случай, когда не все элементы множества являются равнозначными. Вместо множества в этом подходе мы будем рассматривать вероятностное распределение на множестве и оценивать среднее по распределению количество информации, которое содержит случайная величина.

Пусть задана случайная величина , принимающая различных значений с вероятностями . Энтропия Шеннона случайной величины определяется как

(По непрерывности тут нужно доопределить .)

Энтропия Шеннона оценивает среднее количество информации (математическое ожидание), которое содержится в значениях случайной величины.

При первом взгляде на это определение, может показаться совершенно непонятно откуда оно берётся. Шеннон подошёл к этой задаче чисто математически: сформулировал требования к функции и доказал, что это единственная функция, удовлетворяющая сформулированным требованиям.

Я попробую объяснить происхождение этой формулы как обобщение информации по Хартли. Нам бы хотелось, чтобы это определение согласовывалось с определением Хартли, т.е. должны выполняться следующие «граничные условия»:

Будем искать в виде математического ожидания количества информации, которую мы получаем от каждого возможного значения .

Как оценить, сколько информации содержится в событии ? Пусть — всё пространство элементарных исходов. Тогда событие соответствует множеству элементарных исходов меры . Если произошло событие , то размер множества согласованных с этим событием элементарных исходов уменьшается с до , т.е. событие сообщает нам битов информации. Тут мы пользуемся тем, что количество информации в сообщении, которое уменьшает размер пространство поиска в раз приносит битов информации.

Примеры

Свойства энтропии Шеннона

Для случайной величины , принимающей значений с вероятностями , выполняются следующие соотношения.

• .

• распределение вырождено.

• .

• распределение равномерно.

Чем распределение ближе к равномерному, тем больше энтропия Шеннона.

Энтропия пары

Понятие энтропии Шеннона можно обобщить для пары случайных величин. Аналогично это обощается для тройки, четвёрки и т.д.

Пусть совместно распределённые случайные величины и принимают значения и , соответственно. Энтропия пары случайных величин и определяется следующим соотношением:

Примеры

Рассмотрим эксперимент с выбрасыванием двух игральных кубиков — синего и красного.

Свойства энтропии Шеннона пары случайных величин

Для энтропии пары выполняются следующие свойства.

Условная энтропия Шеннона

Теперь давайте научимся вычислять условную энтропию одной случайной величины относительно другой.

Условная энтропия относительно определяется следующим соотношением:

Примеры

Рассмотрим снова примеры про два игральных кубика.

Свойства условной энтропии

Условная энтропия обладает следующими свойствами

Взаимная информация

Ещё одна информационная величина, которую мы введём в этом разделе — это взаимная информация двух случайных величин.

Информация в о величине (взаимная информация случайных величин и ) определяется следующим соотношением

Примеры

И снова обратимся к примерам с двумя игральными кубиками.

Свойства взаимной информации

Выполняются следующие соотношения.

• . Т.е. определение взаимной информации симметрично и его можно переписать так:

• Или так: .

• и .

• .

• .

Все информационные величины, которые мы определили к этому моменту можно проиллюстрировать при помощи кругов Эйлера.

Мы пойдём дальше и рассмотрим информационную величину, зависящую от трёх случайных величин.

Пусть , и совместно распределены. Информация в о при условии определяется следующим соотношением:

Свойства такие же как и обычной взаимной информации, нужно только добавить соответствующее условие ко всем членам.

Всё, что мы успели определить можно удобно проиллюстрировать при помощи трёх кругов Эйлера.

Из этой иллюстрации можно вывести все определения и соотношения на информационные величины.

Мы не будем продолжать дальше и рассматривать четыре случайные величины по трём причинам. Во-первых, рисовать четыре круга Эйлера со всеми возможными областями — это непросто. Во-вторых, для двух и трёх случайных величин почти все возможные соотношения можно вывести из кругов Эйлера, а для четырёх случайных величин это уже не так. И в третьих, уже для трёх случайных величин возникают неприятные эффекты, демонстрирующие, что дальше будет хуже.

Рассмотрим треугольник в пересечении всех трёх кругов , и . Этот треугольник соответствуют взаимной информации трёх случайных величин . Проблема с этой информационной величиной заключается в том, что ей не удаётся придать какой-то «физический» смысл. Более того, в отличие от всех остальных величин на картинке может быть отрицательной!

Рассмотрим пример трёх случайных величин равномерно распределённых на . Пусть и будут независимы, а . Легко проверить, что . При этом . В то же время . Получается следующая картинка.

Мы знаем, что . При этом . Получается, что , а , т.е. для таких случайных величин.

Применение энтропии Шеннона: кодирование

В этом разделе мы обсудим, как энтропия Шеннона возникает в теории кодирования. Будем рассматривать коды, которые кодируют каждый символ по отдельности.

Пусть задан алфавит . Код — это отображение из в . Код называется однозначно декодируемым, если любое сообщение, полученное применением к символам некоторого текста, декодируется однозначно.

Код называется префиксным (prefix-free), если нет двух символов и таких, что является префиксом .

Префиксные коды являются однозначно декодируемыми. Действительно, при декодировании префиксного кода легко понять, где находятся границы кодов отдельных символов.

Теорема [Шеннон]. Для любого однозначно декодируемого кода существует префиксный код с теми же длинами кодов символов.

Таким образом для изучения однозначно декодируемых кодов достаточно рассматривать только префиксные коды.

Задача об оптимальном кодировании.
Дан текст . Нужно найти такой код , что

Пусть . Обозначим через частоту, с которой символ встречается в . Тогда выражение выше можно переписать как

Следующая теорема могла встречаться вам в курсе алгоритмов.

Теорема [Хаффман]. Код Хаффмана, построенный по , является оптимальным префиксным кодом.

Алгоритм Хаффмана по набору частот эффективно строит оптимальный код для задачи оптимального кодирования.

Связь с энтропией

Имеют место две следующие оценки.

Теорема [Шеннон]. Для любого однозначно декодируемого кода выполняется

Теорема [Шеннон]. Для любых значений существует префиксный код , такой что

Рассмотрим случайную величину , равномерно распределённую на символах текста . Получим, что . Таким образом, эти две теоремы задают оценку на среднюю длину кода символа при оптимальном кодировании, т.е. и для кодирования Хаффмана.

Следовательно, длину кода Хаффмана текста можно оценить, как

Применение энтропии Шеннона: шифрования с закрытым ключом

Рассмотрим простейшую схему шифрования с закрытым ключом. Шифрование сообщения с ключом шифрования выполняется при помощи алгоритма шифрования . В результате получается шифрограмма . Зная получатель шифрограммы восстанавливает исходное сообщение : .

Мы будем анализировать эту схему с помощью аппарата энтропии Шеннона. Пусть и являются случайными величинами. Противник не знает и , но знает , которая так же является случайной величиной.

Для совершенной схемы шифрования (perfect secrecy) выполняются следующие соотношения:

1. , т.е. шифрограмма однозначно определяется по ключу и сообщению.

2. , т.е. исходное сообщение однозначно восстанавливается по шифрограмме и ключу.

3. , т.е. в отсутствие ключа из шифрограммы нельзя получить никакой информации о пересылаемом сообщении.

Теорема [Шеннон]. , даже если условие нарушается (т.е. алгоритм использует случайные биты).

Эта теорема утверждает, что для совершенной схемы шифрования длина ключа должна быть не менее длины сообщения. Другими словами, если вы хотите зашифровать и передать своему знакомому файл размера 1Гб, то для этого вы заранее должны встретиться и обменяться закрытым ключом размера не менее 1Гб. И конечно, этот ключ можно использовать только однажды. Таким образом, самая оптимальная совершенная схема шифрования — это «одноразовый блокнот», в котором длина ключа совпадает с длиной сообщения.

Если же вы используете ключ, который короче пересылаемого сообщения, то шифрограмма раскрывает некоторую информацию о зашифрованном сообщении. Причём количество этой информации можно оценить, как разницу между энтропией сообщения и энтропией ключа. Если вы используете пароль из 10 символов при пересылке файла размера 1Гб, то вы разглашаете примерно 1Гб – 10 байт.

Это всё звучит очень печально, но не всё так плохо. Мы ведь никак не учитываем вычислительную мощь противника, т.е. мы не ограничиваем количество времени, которое противнику потребуется на выделение этой информации.

Современная криптография строится на предположении об ограниченности вычислительных возможностей противника. Тут есть свои проблемы, а именно отсутствие математического доказательства криптографической стойкости (все доказательства строятся на различных предположениях), так что может оказаться, что вся эта криптография бесполезна (подробнее можно почитать в статье о мирах Рассела Импальяццо, которая переведена на хабре), но это уже совсем другая история.

Доказательство. Нарисуем картинку для трёх случайных величин и отметим то, что нам известно.

• .

• , следовательно , а значит .

• (по свойству взаимной информации), следовательно , а значит .

• . Таким образом,

В доказательстве мы действительно не воспользовались тем, что .

Алгоритмический подход: колмогоровская сложность

Подход Шеннона хорош для случайных величин, но если мы попробуем применить его к текстам, то выходит, что количество информации в тексте зависит только от частот символов, но не зависит от их порядка. При таком подходе получается, что в «Войне и мире» и в тексте, который получается сортировкой всех знаков в «Войне и мире», содержится одинаковое количество информации. Колмогоров предложил подход, позволяющий измерять количество информации в конкретных объектах (строках), а не в случайных величинах.

Внимание. До этого момента я старался следить за математической строгостью формулировок. Для того, чтобы двигаться дальше в том же ключе, мне потребовалось бы предположить, что читатель неплохо знаком с математической логикой и теорией вычислимости. Я пойду более простым путём и просто буду махать руками, заметая под ковёр некоторые подробности. Однако, все утверждения и рассуждения дальше можно математически строго сформулировать и доказать.

Нам потребуется зафиксировать способ описания битовой строки. Чтобы не углубляться в рассуждения про машины Тьюринга, мы будем описывать строки на языках программирования. Нужно только сделать оговорку, что программы на этих языках будут запускаться на компьютере с неограниченным объёмом оперативной памяти (иначе мы получили бы более слабую вычислительную модель, чем машина Тьюринга).

Сложностью строки относительно языка программирования называется длина кратчайшей программы, которая выводит .

Таким образом сложность «Войны и мира» относительноя языка Python — это длина кратчайшей программы на Python, которая печатает текст «Войны и мира». Естественным образом сложность отсортированной версии «Войны и мира» относительно языка Python получится значительно меньше, т.к. её можно предварительно закодировать при помощи RLE.

Сравнение языков программирования

Дальше нам потребуется научиться любимой забаве всех программистов — сравнению языков программирования.

Будем говорить, что язык не хуже языка программирования и обозначать , если существует константа такая, что для для всех выполняется

Исходя из этого определения получается, что язык Python не хуже (!) этого вашего Haskell! И я это докажу. В качестве константы мы возьмём длину реализации интепретатора Haskell на Python. Таким образом, любая программа на Haskell переделывается в программу на Python просто дописыванием к ней интерпретатора Haskell на Python.

Соломонов и Колмогоров пошли дальше и доказали существования оптимального языка программирования.

Теорема [Соломонова-Колмогорова]. Существует способ описания (язык программирования) такой, что для любого другого способа описания выполняется .

И да, некоторые уже наверное догадались, что  — это JavaScript. Или любой другой Тьюринг полный язык программирования.

Это приводит нас к следующему определению, предложенному Колмогоровым в 1965 году.

Колмогоровской сложностью строки будем называть её сложность относительно оптимального способа описания и будем обозначать .

Важно понимать, что при разных выборах оптимального языка программирования колмогоровская сложность будет отличаться, но только на константу. Для любых двух оптимальных языков программирования и выполняется и , т.е. существует такая константа , что Это объясняет, почему в этой науке аддитивные константы принято игнорировать.

При этом для конкретной строки и конкретного выбора колмогоровская сложность определена однозначно.

Свойства колмогоровской сложности

Начнём с простых свойств. Колмогоровская сложность обладает следующими свойствами.

Первое свойство выполняется потому, что мы всегда можем зашить строку в саму программу. Второе свойство верно, т.к. из программы, выводящей строку , легко сделать программу, которая выводит эту строку дважды.

Примеры

Несжимаемые строки

Важнейшее свойство колмогоровской сложности заключается в существовании сложных (несжимаемых строк). Проверьте себя и попробуйте объяснить, почему не бывает идеальных архиваторов, которые умели бы сжимать любые файлы хотя бы на 1 байт, и при этом позволяли бы однозначно разархивировать результат.

В терминах колмогоровской сложности это можно сформулировать так.

Вопрос. Существует ли такая длина строки , что для любой строки колмогоровская сложность меньше ?

Следующая теорема даёт отрицательный ответ на этот вопрос.

Теорема. Для любого существует такой, что .

Доказательство. Битовых строк длины всего . Число строк сложности меньше не превосходит число программ длины меньше , т.е. таких программ не больше чем

Таким образом, для какой-то строки гарантированно не хватит программы.

Верна и более сильная теорема.

Теорема. Существует такое, что для слов длины верно

Другими словами, почти все строки длины имеют почти максимальную сложность.

Колмогоровская сложность: вычислимость

В этом разделе мы поговорим про вычислимость колмогоровской сложности. Я не буду давать формально определение вычислимости, а буду опираться на интуитивные предствления читателей.

Теорема. Не существует программы, которая по двоичной записи числа выводит строку , такую что .

Эта теорема говорит о том, что не существует программы-генератора, которая умела бы генерировать сложные строки по запросу.

Доказательство. Проведём доказетельство от противного. Пусть такая программа существует и . Тогда с одной стороны сложность не меньше , а с другой стороны мы можем описать при помощи битов и кода программы.

Это приводит нас к противоречию, т.к. при достаточно больших значениях неизбежно станет больше, чем .

Как следствие мы получаем невычислимость колмогоровской сложности.

Следствие. Отображение не является вычислимым.

Опять же, предположим, что это нет так и существует программа , которая по строку вычисляет её колмогоровскую сложность. Тогда на основе программы можно реализовать программу из теоремы выше: она будет перебирать все строки длины не более и находить лексикографически первую, для которой сложность будет не меньше . А мы уже доказали, что такой программы не существует.

Связь с энтропией Шеннона

Теорема. Пусть длины содержит единиц и нулей, тогда

Я надеюсь, что вы уже узнали энтропию Шеннона для случайной величины с двумя значениями с вероятностями и .

Для колмогоровской сложности можно проделать весь путь, который мы проделали для энтропии Шеннона: определить условную колмогоровскую сложность, сложность пары строк, взаимную информацию и условную взаимную информацию и т.д. При этом формулы будут повторять формулы для энтропии Шеннона с точностью до . Однако это тема для отдельной статьи.

Применение колмогоровской сложности: бесконечность множества простых чисел

Начнём с довольно игрушечного применения. С помощью колмогоровской сложности мы докажем следующую теорему, знакомую нам со школы.

Теорема. Простых чисел бесконечно много.

Очевидно, что для доказательства этой теоремы никакая колмогоровская сложность не нужна. Однако на этом примере я смогу продемонстрировать основные идеи применения колмогоровской сложности в более сложных ситуациях.

Доказательство. Проведём доказательство от обратного. Пусть существует всего простых чисел: . Тогда любое натуральное раскладывается на степени простых:

т.е. определяется набором степеней . Каждое , т.е. задаётся битами. Поэтому любое можно задать при помощи битов (помним, что — это константа).

Теперь воспользуемся теоремой о существовании несжимаемых строк. Как следствие, мы можем заключить, что существуют -битовые числа сложности не менее (можно взять сложную строку и приписать в начало единицу). Получается, что сложное число можно задать при помощи небольшого числа битов.

Противоречие.

Применение колмогоровской сложности: алгоритмическая случайность

Колмогоровская сложность позволяет решить следующую проблему из классической теории вероятностей.

Пусть в лаборатории живёт обезьянка, которую научили печатать на печатной машинке так, что каждую кнопку она нажимает с одинаковой вероятность. Вам предлагается посмотреть на лист печатного текста и сказать, верите ли вы, что его напечатала эта обезьянка. Вы смотрите на лист и видите, что это первая страница «Гамлета» Шекспира. Поверите ли вы? Очевидно, что нет. Хорошо, а если это не Шекспир, а, скажем, текст детектива Дарьи Донцовой? Скорей всего тоже не поверите. А если просто какой-то набор русских слов? Опять же, очень сомневаюсь, что вы поверите.

Внимание, вопрос. А как объяснить, почему вы не верите? Давайте для простоты считать, что на странице помещается 2000 знаков и всего на машинке есть 80 знаков. Вы можете резонно заметить, что вероятность того, что обезьянка случайным образом породила текст «Гамлета» порядка , что астрономически мало. Это верно.

Теперь предположим, что вам показали текст, который вас устроил (он с вашей точки зрения будет похож на «случайный»). Но ведь вероятность его появления тоже будет порядка . Как же вы определяете, что один текст выглядит «случайным», а другой — не выглядит?

Колмогоровская сложность позволяет дать формальный ответ на этот вопрос. Если у текста отстутствует короткое описание (т.е. в нём нет каких-то закономерностей, которые можно было бы использовать для сжатия), то такую строку можно назвать случайной. И как мы увидели выше почти все строки имеют большую колмогоровскую сложность. Поэтому, когда вы видите строку с закономерностями, т.е. маленькой колмогоровской сложности, то это соответствует очень редкому событию. В противоположность наблюдению строки без закономерностей. Вероятность увидеть строку без закономерностей близка к 1.

Это обобщается на случай бесконечных последовательностей. Пусть . Как определить понятие случайной последовательности?

(неформальное определение)
Последовательность случайна по Мартину–Лёфу, если каждый её префикс является несжимаемым.

Оказывается, что это очень хорошее определение случайных последовательностей, т.к. оно обладает ожидаемыми свойствами.

Свойства случайных последовательностей

• Почти все последовательности являются случайными по Мартину–Лёфу, а мера неслучайных равна .

• Всякая случайная по Мартину-Лёфу последовательность невычислима.

• Если случайная по Мартин-Лёфу, то

Заключение

Если вам интересно изучить эту тему подробнее, то я рекомендую обратиться к следующим источникам.

• Верещагин Н.К., Щепин Е.В. Информация, кодирование и предсказание. МЦНМО. (нет в свободном доступе, но pdf продаётся за копейки)

• В.А. Успенский, А.Х. Шень, Н.К. Верещагин. Колмогоровская сложность и алгоритмическая случайность.

• Курс «Введение в теорию информации» А.Е. Ромащенко в Computer Science клубе.

Если вам интересны подобные материалы, подписывайтесь в соцсетях на CS клуб и CS центр, а так же на наши каналы на youtube: CS клуб, CS центр.

Пусть
имеется отрезок случайной функции
X(t)
дискретной по времени и амплитуде, и он
полностью определяется по­следовательностью
отсчетов Х¹…Хⁿ,
взятых
в моменты времени
t₁,…,t_n.
Тогда энтропия отрезка этой случайной
функции длиною в n
отсчетов
(m-ичных
символов) равна

(2.4.1)

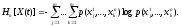
Для
стационарных случайных последовательностей
ис­пользуют более удобную характеристику,
называемую эн­тропией случайной
последовательности

(2.4.2.)

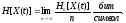
Эта
величина имеет смысл средней энтропии,
приходящейся на один отсчет (символ) в
реализациях бесконечно большой длины.

Энтропия
случайной последовательности удовлетворяет
следующим неравенствам:

1.H[X(t)]
H₁[X(t)],


(2.4.3)

где
H₁[X(t)]
—
энтропия
одного из отсчетов. Энтропия случайной
последовательности достигает наиболь­шего
значения (знак равенства в (2.4.3)) только
тогда, ког­да отдельные отсчеты функции
X(t)
(т. е. случайные величи­ны Х¹,...,Хⁿ)
статистически независимы (см. формулу
(2.2.4)).

2.
H₁[X(t)]
H_1
max
,




(2.4.4)

где
H_1
max
— максимальное
значение энтропии одного символа.
Энтропия случайной последовательности
максимальна, когда все возможные значения
символов равновероятны (см. формулу
(2.2.3)). В итоге получаем

H[X(t)]
log m.


(2.4.5)

Можно
найти и среднюю условную энтропию
стационарной случайной последовательности
X(t).
Она вычисляется при условии, что известно
значение другой дискретной случайной
последовательности
Y(t),
также стационарной и стационарно
связанной с
X(t):

(2.4.6)

где

(2.4.7)

Среднее
количество информации, содержащейся в
отрезке последовательности
Y(t)
относительно отрезка
X(t),
равно

I_n[X(t);Y(t)]=H_n[X(t)]-
H_n[X(t)/
Y(t)].

а
средняя информация, приходящаяся на
один отсчет (символ)

I[X(t);Y(t)]=H[X(t)]-
H[X(t)/ Y(t)].
(2.4.8)

Возможен
и другой способ вычисления средней
энтропии (условной и безусловной)
дискретной стационарной случайной
последовательности, приводящий к тем
же результатам. Энтропия последовательности
X(t)
равна

(2.4.9)

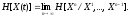
и
определяет среднее количество
дополнительной информации переносимой
одним символом в реализациях бесконеч­ной
длины.

Средняя
условная энтропия последовательности
X(t)
вычисляется по формуле

(2.4
10)

Решение
типовых примеров

Пример
2.4.1.Сообщение
Х
есть стационарная после­довательность
независимых символов, имеющих ряд
распре­деления

xj	x1	x2	x3
p(xj)	0,2	0,1	0,7

Сигнал
Y
является последовательностью двоичных
символов, связанных с сообщением ‘по
следующему правилу:

x₁00,
x₂00,
x₃1.

Определить:

а)средние
безусловную и условную энтропии,
приходящиеся на 1 символ сообщения;

б)средние
безусловную и условную энтропии,
приходя­щиеся на 1 символ сигнала;

в)среднюю
взаимную информацию в расчете на 1 символ
сообщения.

Решение.

Символы
в последовательности на выходе ис­точника
независимы, поэтому из (2.4.3)

H[X(t)]=H₁[X(t)]=Н(Х)=
-0,2log
0,2-0,1log
0,1-0,7log0,7=1,157
бит/симв.

Обозначив
y₁=00,
у₂=1,
вычислим условные и безусловные
вероятности сигнала:

p(y₁/x₁)=
p(y₁/x₂)=1,
p(y₁/x₃)=0,

p(y₂/x₁)=
p(y₂/x₂)=0,
p(y₂/x₃)=1,

p(y₁)=
p(y₁/x₁)p(x₁)+p(y₁/x₂)p(x₂)+p(y₁/x₃)p(x₃)=0,2+0,1=0,3,

p(y₂)=0,7.

Энтропия
случайной величины Y
равна

H(Y)=0,31ogO,3-0,71og
0,7=0,881 бит,

а
условная энтропия
H(Y/X)
= 0, так как сигнал однозначно определяется
сообщением.

Взаимная
информация

I(X;Y)
= H(Y)-H(Y/X) =
0,881 бит.

Условная
энтропия сообщения

H(X/Y)=H(X)-I(X;Y)
= 1,157—0,881=0,276
бит.

Итак,
получаем, что условная энтропия сообщения
равна 0,276
бит/симв,
а взаимная информация в расчете на 1
символ сообщения равна 0,881 бит/симв.

Среднее
количество символов сигнала, приходящихся
на 1 символ сообщения, равно

где
l_j
—
длина
кодового слова, соответствующего
x_j,

L
= 0,22+0,12+0,71
= 1,3 симв.

Энтропия
последовательности
Y(t)
равна

H[Y(t)]=
H[Y]/L=0,881/1,3=0,68 бит/симв.,

а
условная энтропия равна нулю.

Пример
2.4.2.
Вычислить энтропию однородной
нераз­ложимой марковской
последовательности, заданной матрицей
вероятностей перехода p(X^k/X^k-1)
от
символа
X^k-1
к
сим­волу
X^k

Xk	Xk-1
	x1	x2	x3
x1	0,2	0,3	0,6
x2	0,4	0,5	0,1
x3	0,4	0,2	0,3

Решение.
Однородность последовательности
проявляет­ся в том,
что при
k
безусловная вероятность
p_j
того,
что k-й
символ примет значение
x_j,
не
зависит от
k
и от значения первого символа и связана
с вероятностями переходов p_rj
=
p(x_j
^k/
x_r
^k-1
)
уравнением

Записываем
это уравнение для каждого
j
и получаем систему

p₁=
p₁
p₁₁
+
p₂
p₂₁
+
p₃
p₃₁;

p₂=
p₁
p₁₂
+
p₂
p₂₂
+
p₃
p₃₂;

p₃=
p₁
p₁₃
+
p₂
p₂₃
+
p₃
p₃₃.

Подставляем
численные значения вероятностей
переходов и получаем

-0,8p₁
+
0,3р₂
+ 0,6р₃
= 0,

0,4р₁—0,5р₂+0,1р₃
= 0,

0,4p₁
+0,2р₂—0,7р₃
=
0.

Определитель
этой системы равен нулю, поэтому
p_j
опре­деляется с точностью до постоянного
множителя. Выбираем его так, чтобы
выполнялось условие нормировки

p₁
+
p₂
+
p₃=1,

и
получим
p₁
=
0.36,
p₂
=
0.34,

p₃=
0.30.

Энтропия
последовательности
H[X(t)]
по смыслу есть средняя дополнительная
(условная) информация, приноси­мая
средним символом последовательности,
поэтому для марковской последоваательности
ее можно вычислить по формуле
(2.4.9)

ЗАДАЧИ

2.4.1.Периодически,
один раз в 5 с, бросают игральную кость,
и результат каждого бросания передают
при помощи трехразрядного двоичного
числа. Найти:

а)
энтропию шестиричной последовательности
на входе;

б)энтропию
двоичной последовательности на выходе;

в)среднюю
информацию, содержащуюся в отрезке
выходного сигнала для длительностью 1
мин.

2.4.2.Известно,
что энтропия, приходящаяся на 1 букву
русского текста, составляет приблизительно
1.2 бит. Каково минимальное среднее
количество десятичных символов,
необходимо для передачи информации,
содержащейся в телеграмме из 100 букв ?

2.4.3.Периодически
проводятся тиражи лотереи. В каждом
тираже участвует 1024 билета, но выигрывает
из них один. Результат каждого тиража
передается при помощи 10-раз­рядного
двоичного числа. Из-за наличия помех
возможны искажения символов с вероятностью
0,001. Ошибки в отдель­ных символах
независимы. Найти:

а)энтропию
исходной 1024-ичной последовательности;

б)энтропию
двоичной последовательности на входе;

в)энтропию
двоичной последовательности на выходе;

г)энтропию
выходной 1024-ичной последовательности;

д)среднее
количество передаваемой информации в
расчете на двоичный символ входной
последовательности.

2.4.4.В
условиях задачи 2.4.3 для повышения
помехоустойчивости каждый двоичный
символ передается трехкратно. В месте
приема из каждых трех символов формируется
один, причем решение выносится простым
“большинством голосов”. Найти:

а)энтропию
двоичной последовательности на выход;

б)среднее
количество информации в расчете на
передаваемый двоичный символ.

2.4.5.В
некотором районе состояние погоды
зависит только от того, что было накануне.
При ежедневной регистрации погоды
различают лишь два состояния:
x₁
ясно
и x₂
пе­ременно. Вероятности переходов
равны

p(x₁/
x₁)=0.9,
p(x₂/
x₁)=0.1,
p(x₂/
x₂)=0.3,
p(x₁/
x₂)=0.7.

Вычислить
энтропию последовательности сообщений
о состоянии погоды.

2.4.6.Найти
энтропию последовательности на выходе
троичного Марковского источника, если
вероятности всех переходов равны 1/3.

1. Буквы
   в последовательности на выходе источника
   выбираются из алфавита А, В, С и образуют
   марковскую последовательность.
   Совместные вероятности всевозможных
   пар букв заданы в табл. 2.4.2.

Таблица
2.4.2

Xk	Xk+1
	A	B	C
A	0,2	0,05	0,15
B	0,15	0,05	0,1
C	0,05	0,2	0,05

Вычислить
энтропию последовательности.

2.4.8.
Троичная марковская последовательность
задана матрицей

вероятностей
переходов P
от X^k
(строка) к X^k+1
(столбец)

Вычислить:

а)энтропию
одного символа;

б)энтропию
последовательности и избыточность.

2.4.9.
На кольцевой трассе расположено 10
станций. По трассе в направлении часовой
стрелки курсирует автобус, де­лая
остановки на каждой станции. Исключение
составляет только станция № 1, с которой
с вероятностью 0,8 автобус мо­жет
вернуться на предыдущую станцию. С
каждой станции водитель посылает
сообщение о направлении дальнейшего
движения. Найти среднюю информацию,
содержащуюся в одном сообщении, и
избыточность.

1. На
   водохранилище имеются 3 контрольные
   отмет­ки. Сброс воды из водохранилища
   производится периодиче­ски один раз
   в год, а в промежутках между этими
   момента­ми оно заполняется. Поступление
   воды поднимает уровень на одну отметку
   с вероятностью 0,7 и с вероятностью 0,3
   со­храняет его неизменным. Величины
   поступлений в различ­ные годы
   независимы. Если уровень воды достигает
   отметки № 3, то после сброса он
   понижается
   до отметки № 1; в ос­тальных случаях
   сброс не производится. Найти среднее
   коли­чество информации, содержащейся
   в сообщениях об уровне воды.

Соседние файлы в папке ТИИС

• #
• #
• #
• #
• #
• #
• #

Понятие энтропии

Случайные события могут быть описаны с использованием понятия «вероятность». Соотношения теории вероятностей позволяют найти (вычислить) вероятности как одиночных случайных событий, так и сложных опытов, объединяющих несколько независимых или связанных между собой событий. Однако описать случайные события можно не только в терминах вероятностей.

То, что событие случайно, означает отсутствие полной уверенности в его наступлении, что, в свою очередь, создает неопределенность в исходах опытов, связанных с данным событием. Безусловно, степень неопределенности различна для разных ситуаций.

Например, если опыт состоит в определении возраста случайно выбранного студента 1-го курса дневного отделения вуза, то с большой долей уверенности можно утверждать, что он окажется менее 30 лет; хотя по положению на дневном отделении могут обучаться лица в возрасте до 35 лет, чаще всего очно учатся выпускники школ ближайших нескольких выпусков. Гораздо меньшую определенность имеет аналогичный опыт, если проверяется, будет ли возраст произвольно выбранного студента меньше 18 лет. Для практики важно иметь возможность произвести численную оценку неопределенности разных опытов. Попробуем ввести такую количественную меру неопределенности.

Начнем с простой ситуации, когда опыт имеет %%n%% равновероятных исходов. Очевидно, что неопределенность каждого из них зависит от n, т.е.

Мера неопределенности является функцией числа исходов %%f(n)%%.

Можно указать некоторые свойства этой функции:

1. %%f(1) = 0%%, поскольку при %%n = 1%% исход опыта не является случайным и, следовательно, неопределенность отсутствует;
2. %%f(n)%% возрастает с ростом %%n%%, поскольку чем больше число возможных исходов, тем более затруднительным становится предсказание результата опыта.

* Для обозначения опытов со случайными исходами будем использовать греческие буквы (%%α%%, %%β%% и т.д.), а для обозначения отдельных исходов опытов (событий) — латинские заглавные (%%А%%, %%В%% и т.д.).

Для определения явного вида функции %%f(n)%% рассмотрим два независимых опыта %%α%% и %%β*%% с количествами равновероятных исходов, соответственно %%n_α%% и %%n_β%%. Пусть имеет место сложный опыт, который состоит в одновременном выполнении опытов α и β; число возможных его исходов равно %%nα cdot nβ%%, причем, все они равновероятны. Очевидно, неопределенность исхода такого сложного опыта %%α ^ β%% будет больше неопределенности опыта %%α%%, поскольку к ней добавляется неопределенность %%β%%; мера неопределенности сложного опыта равна %%f(n_α cdot n_β)%%. С другой стороны, меры неопределенности отдельных %%α%% и %%β%% составляют, соответственно, %%f(n_α)%% и %%f(n_β)%%. В первом случае (сложный опыт) проявляется общая (суммарная) неопределенность совместных событий, во втором — неопределенность каждого из событий в отдельности. Однако из независимости %%α%% и %%β%% следует, что в сложном опыте они никак не могут повлиять друг на друга и, в частности, %%α%% не может оказать воздействия на неопределенность %%β%%, и наоборот. Следовательно, мера суммарной неопределенности должна быть равна сумме мер неопределенности каждого из опытов, т.е. мера неопределенности аддитивна:

$$f(n_α cdot n_β)=f(n_α)+f(n_β)

Теперь задумаемся о том, каким может быть явный вид функции %%f(n)%%, чтобы он удовлетворял свойствам (1) и (2) и соотношению (2.1)? Легко увидеть, что такому набору свойств удовлетворяет функция %%log(n)%%, причем можно доказать, что она единственная из всех существующих классов функций. Таким образом:

За меру неопределенности опыта с n равновероятными исходами можно принять число %%log(n)%%.

Следует заметить, что выбор основания логарифма в данном случае значения не имеет, поскольку в силу известной формулы преобразования логарифма от одного основания к другому.

$$log_b n=log_b аcdot log_a n $$

переход к другому основанию состоит во введении одинакового для обеих частей выражения (2.1) постоянного множителя %%log_b а%%, что равносильно изменению масштаба (т.е. размера единицы) измерения неопределенности. Поскольку это так, имеется возможность выбрать удобное (из каких-то дополнительных соображений) основание логарифма. Таким удобным основанием оказывается 2, поскольку в этом случае за единицу измерения принимается неопределенность, содержащаяся в опыте, имеющем лишь два равновероятных исхода, которые можно обозначить, например, ИСТИНА (True) и ЛОЖЬ (False) и использовать для анализа таких событий аппарат математической логики.

Единица измерения неопределенности при двух возможных равновероятных исходах опыта называется бит.

Название бит происходит от английского binary digit, что в дословном переводе означает «двоичный разряд» или «двоичная единица».

Таким образом, нами установлен явный вид функции, описывающей меру неопределенности опыта, имеющего %%n%% равновероятных исходов:

Эта величина получила название энтропия. В дальнейшем будем обозначать ее Н .

Вновь рассмотрим опыт с %%n%% равновероятными исходами. Поскольку каждый исход случаен, он вносит свой вклад в неопределенность всего опыта, но так как все %%n%% исходов равнозначны, разумно допустить, что и их неопределенности одинаковы. Из свойства аддитивности неопределенности, а также того, что согласно (2.2) общая неопределенность равна %%log_2 n%%, следует, что неопределенность, вносимая одним исходом составляет

$$fraclog_2 n = — fraclog_2 frac = -p cdot log_2 p $$

где %%р =frac%% — вероятность любого из отдельных исходов.

Таким образом, неопределенность, вносимая каждым из равновероятных исходов, равна:

$$H=-p cdot log_2 p

Теперь попробуем обобщить формулу (2.3) на ситуацию, когда исходы опытов неравновероятны, например, %%p(A_1)%% и %%p(A_2)%%. Тогда:

$$H_1=-p(А_1) cdot log_2 р(А_1)$$ $$H_2=-p(А_2) cdot log_2 р(А_2)$$

$$H=H_1+H_2=-p(А_1) cdot log_2 р(А_1)-p(А_2) cdot log_2 р(А_2)$$

Обобщая это выражение на ситуацию, когда опыт %%α%% имеет %%n%% неравновероятных исходов %%А_1, А_2. А_n%%, получим:

Введенная таким образом величина, как уже было сказано, называется энтропией опыта. Используя формулу для среднего значения дискретных случайных величин, можно записать:

$$H(α)leqslant -log_2 p(A^α)$$

%%А^α%% — обозначает исходы, возможные в опыте α.

Энтропия является мерой неопределенности опыта, в котором проявляются случайные события, и равна средней неопределенности всех возможных его исходов.

Для практики формула (2.4) важна тем, что позволяет сравнить неопределенности различных опытов со случайными исходами.

Пример 2.1. Имеются два ящика, в каждом из которых по 12 шаров. В первом -3 белых, 3 черных и 6 красных; во втором — каждого цвета по 4. Опыты состоят в вытаскивании по одному шару из каждого ящика. Что можно сказать относительно неопределенностей исходов этих опытов?

Согласно (2.4) находим энтропии обоих опытов:

%%Н_β > Н_α%%, т.е. неопределенность результата в опыте β выше и, следовательно, предсказать его можно с меньшей долей уверенности, чем результат α.

Как определяется энтропия дискретных случайных величин

Установив, что случайные процессы являются адекватной моделью сигналов, мы получаем возможность воспользоваться результатами и мощным аппаратом теории случайных процессов. Это не означает, что теория вероятностей и теория случайных процессов дают готовые ответы на все вопросы о сигналах: подход с новых позиций выдвигает такие вопросы, которые просто не возникали. Так и родилась теория информации, специально рассматривающая сигнальную специфику случайных процессов. При этом были построены принципиально новые понятия и получены новые, неожиданные результаты, имеющие характер научных открытий.

Понятие неопределенности

Первым специфическим понятием теории информации является понятие неопределенности случайного объекта, для которого удалось ввести количественную меру, названную энтропией. Начнем с простейшего примера — со случайного события. Пусть, например, некоторое событие может произойти с вероятностью 0,99 и не произойти с вероятностью 0,01, а другое событие имеет вероятности соответственно 0,5 и 0,5. Очевидно, что в первом случае результатом опыта «почти наверняка» является наступление события, во втором же случае неопределенность исхода так велика, что от прогноза разумнее воздержаться.

Для характеристики размытости распределения широко используется второй центральный момент (дисперсия) или доверительный интервал. Однако эти величины имеют смысл лишь для случайных числовых величин и не могут применяться к случайным объектам, состояния которых различаются качественно. Следовательно, мера неопределенности, связанной с распределением, должна быть некоторой его числовой характеристикой, функционалом от распределения, никак не связанным с тем, в какой шкале измеряются реализации случайного объекта.

Энтропия и ее свойства

Примем (пока без обоснования) в качестве меры неопределенности случайного объекта А с конечным множеством возможных состояний А1. Аn с соответствующими вероятностями P₁,P₂. P_n величину

которую и называют энтропией случайного объекта А (или распределения . Убедимся, что этот функционал обладает свойствами, которые вполне естественны для меры неопределенности.

1. Н(p₁. p_n)=0 в том и только в том случае, когда какое-нибудь одно из

   i > равно единице (а остальные — нули). Это соответствует случаю, когда исход опыта может быть предсказан с полной достоверностью, т.е. когда отсутствует всякая неопределенность. Во всех других случаях энтропия положительна. Это свойство проверяется непосредственно.

2. Н(p₁. p_n) достигает наибольшего значения при p₁=. p_n=1/n т.е. в случае максимальной неопределенности. Действительно, вариация Н по p_i при условии ∑p_i = 1 дает p_i = const = 1/n.
3. Если А и В — независимые случайные объекты, то H(A∩B) = H(

   iq_k>) = H(

   i>) + H(k>) = H(A) + H(B). Это свойство проверяется непосредственно.

4. Если А и В — зависимые случайные объекты, то H(A∩B) = H(A) + H(B/A) = H(B) + H(A/B), где условная энтропия H(А/В) определяется как математическое ожидание энтропии условного распределения. Это свойство проверяется непосредственно.
5. Имеет место неравенство Н(А) > Н(А/В), что согласуется с интуитивным предположением о том, что знание состояния объекта В может только уменьшить неопределенность объекта А, а если они независимы, то оставит ее неизменной.

Как видим, свойства функционала Н позволяют использовать его в качестве меры неопределенности.

Дифференциальная энтропия

Обобщение столь полезной меры неопределенности на непрерывные случайные величины наталкивается на ряд сложностей, которые, однако, преодолимы. Прямая аналогия

не приводит к нужному результату: плотность p(x) является размерной величиной (размерность плотности p(x) обратно пропорциональна x а логарифм размерной величины не имеет смысла. Однако положение можно исправить, умножив p(x) под знаком логарифма на величину К, имеющую туже размерность, что и величина х:

Теперь величину К можно принять равной единице измерения х, что приводит к функционалу

который получил название «дифференциальной энтропии». Это аналог энтропии дискретной величины, но аналог условный, относительный: ведь единица измерения произвольна. Запись (3) означает, что мы как бы сравниваем неопределенность случайной величины, имеющей плотность p(x), с неопределенностью случайной величины, равномерно распределенной в единичном интервале. Поэтому величина h(X) в отличие от Н(Х) может быть не только положительной. Кроме того, h(X) изменяется при нелинейных преобразованиях шкалы х, что в дискретном случае не играет роли. Остальные свойства h(X) аналогичны свойствам Н(Х), что делает дифференциальную энтропию очень полезной мерой.

Пусть, например, задача состоит в том, чтобы, зная лишь некоторые ограничения на случайную величину (типа моментов, пределов области возможных значений и т.п.), задать для дальнейшего (каких-то расчетов или моделирования) конкретное распределение. Один из подходов к решению этой задачи дает «принцип максимума энтропии»: из всех распределений, отвечающих данным ограничениям, следует выбирать то, которое обладает максимальной дифференциальной энтропией. Смысл этого критерия состоит в том, что, выбирая максимальное по энтропии распределение, мы гарантируем наибольшую неопределенность, связанную с ним, т.е. имеем дело с наихудшим случаем при данных условиях.

Фундаментальное свойство энтропии случайного процесса

Особое значение энтропия приобретает в связи с тем, что она связана с очень глубокими, фундаментальными свойствами случайных процессов. Покажем это на примере процесса с дискретным временем и дискретным конечным множеством возможных состояний.

Назовем каждое такое состояние «символом», множество возможных состояний — «алфавитом», их число m — «объемом алфавита». Число возможных последовательностей длины n, очевидно, равно mn. Появление конкретной последовательности можно рассматривать как реализацию одного из mn возможных событий. Зная вероятности символов и условные вероятности появление следующего символа, если известен предыдущий (в случае их зависимости), можно вычислить вероятность P(C) для каждой последовательности С. Тогда энтропия множества , по определению, равна

На множестве можно задать любую числовую функцию f_n(C), которая, очевидно, является случайной величиной. Определим f_n(C) c помощью соотношения f_n(C) = -[1/n]⋅logP(C).

Математическое ожидание этой функции

Это соотношение является одним из проявлений более общего свойства дискретных эргодических процессов. Оказывается, что не только математическое ожидание величины f_n(C) при n стремящемся к бесконечности имеет своим пределом H, но и сама эта величина f_n(C) стремится к H при n стремящемся к бесконечности. Другими словами, как бы малы ни были e > 0 и s > 0, при достаточно большом n справедливо неравенство

т.е. близость f_n(C) к H при больших n является почти достоверным событием.

Для большей наглядности сформулированное фундаментальное свойство случайных процессов обычно излагают следующим образом. Для любых заданных e > 0 и s > 0 можно найти такое no, что реализация любой длины n > no распадаются на два класса:

1. группа реализаций, вероятность P(C) которых удовлетворяет неравенству |[1/n]⋅log(P(C))+H| < ε
2. группа реализаций, вероятности которых этому неравенству не удовлетворяют.

Cуммарные вероятности этих групп равны соответственно 1-s и s, то первая группа называется «высоковероятной», а вторая — «маловероятной».

Это свойство эргодических процессов приводит к ряду важных следствий, из которых три заслуживают особого внимания.

1. независимо от того, каковы вероятности символов и каковы статистические связи между ними, все реализации высоковероятной группы приблизительно равновероятны. Это следствие, в частности, означает, что при известной вероятности P(C) одной из реализаций высоковероятной группы можно оценить число N₁ реализаций в этой группе: N₁ = 1 / P(C).
2. Энтропия H_n с высокой точностью равна логарифму числа реализаций в высоковероятной группе: H_n = n * H = log N₁
3. При больших n высоковероятная группа обычно охватывает лишь ничтожную долю всех возможных реализаций (за исключением случая равновероятных и независимых символов, когда все реализации равновероятны и и H = log m).

Действительно, из соотношения (9) имеем

Число N всех возможных реализаций есть

Доля реализаций высоковероятной группы в общем числе реализаций выражается формулой

и при H < logm эта доля неограниченно убывает с ростом n. Например, если a = 2, n = 100, H = 2,75, m = 8, то

т.е. к высоковероятной группе относится лишь одна тридцати миллионная доля всех реализаций!

Строгое доказательство фундаментального свойства эргодических процессов здесь не приводится. Однако следует отметить, что в простейшем случае независимости символов это свойство является следствием закона больших чисел. Действительно, закон больших чисел утверждает, что с вероятностью, близкой к 1, в длиной реализации i-й символ, имеющий вероятность p_i встретится примерно np_i раз. Следовательно вероятность реализации высоковероятной группы есть

что и доказывает справедливость фундаментального свойства в этом случае.

Подведем итог

Связав понятие неопределенности дискретной величины с распределением вероятности по возможным состояниям и потребовав некоторых естественных свойств от количественной меры неопределенности, мы приходим к выводу, что такой мерой может служить только функционал (1), названный энтропией. С некоторыми трудностями энтропийный подход удалось обобщить на непрерывные случайные величины (введением дифференциальной энтропии) и на дискретные случайные процессы.

Количество информации

В основе всей теории информации лежит открытие, что «информация допускает количественную оценку». В простейшей форме эта идея была выдвинута еще в 1928г. Хартли, но завершенный и общий вид придал ее Шэннон в 1948г. Не останавливаясь на том, как развивалось и обобщалось понятие количества информации, дадим сразу ее современное толкование.

Количество информации как мера снятой неопределенности

Процесс получения информации можно интерпретировать как «изменение неопределенности в результате приема сигнала». Проиллюстрируем эту идею на примере достаточно простого случая, когда передача сигнала происходит при следующих условиях:

1. полезный (передаваемый) сигнал является последовательностью статистически независимых символов с вероятностями p(x_i),i = 1,m ;
2. принимаемый сигнал является последовательностью символов Y_k того же алфавита;
3. если шумы (искажения) отсутствуют, то принимаемый сигнал совпадает с отправленным Y_k=X_k ;
4. если шум имеется, то его действие приводит к тому, что данный символ либо остается прежним (i-м), либо подменен любым другим (k-м) с вероятностью p(y_k/x_i) ;
5. искажение данного символа является событием статистически независимым от того, что произошло с предыдущим символом.

Итак, до получения очередного символа ситуация характеризуется неопределенностью того, какой символ будет отправлен, т.е. априорной энтропией Н(Х). После получения символа y_k неопределенность относительно того, какой символ был отправлен, меняется: в случае отсутствия шума она вообще исчезает (апостериорная энтропия равна нулю, поскольку точно известно, что был передан символ y_k=x_i), а при наличии шума мы не можем быть уверены, что принятый символ и есть переданный, т.е. возникает неопределенность, характеризуемая апостериорной энтропией H(X/y_k)=H(

i/y_k)>)>0.

В среднем после получения очередного символа энтропия H(X/Y)=M_yk)>

Определим теперь количество информации как меру снятой неопределенности: числовое значение количества информации о некотором объекте равно разности априорной и апостериорной энтропии этого объекта, т.е. I(X,Y) = H(X)-H(X/Y). (1)

Используя свойство 2 энтропии, легко получить, что I(X,Y) = H(Y) — H(Y/X) (2)

В явной форме равенство (1) запишется так:

а для равенства (2) имеем:

Количество информации как мера соответствия случайных процессов

Представленным формулам легко придать полную симметричность: умножив и разделив логарифмируемое выражение в (3) на p(y_k), а в (4) на p(x_i) сразу получим, что

Эту симметрию можно интерпретировать так: «количество информации в объекте Х об объекте Y равно количеству информации в объекте Y об объекте Х. Таким образом, количество информации является не характеристикой одного из объектов, а характеристикой их связи, соответствия между их состояниями. Подчеркивая это, можно сформулировать еще одно определение: «среднее количество информации, вычисляемое по формуле (5), есть мера соответствия двух случайных объектов».

Это определение позволяет прояснить связь понятий информации и количества информации. Информация есть отражение одного объекта другим, проявляющееся в соответствии их состояний. Один объект может быть отражен с помощью нескольких других, часто какими-то лучше, чем остальными. Среднее количество информации и есть числовая характеристика степени отражения, степени соответствия. Подчеркнем, что при таком описании как отражаемый, так и отражающий объекты выступают совершенно равноправно. С одной стороны, это подчеркивает обоюдность отражения: каждый из них содержит информацию друг о друге. Это представляется естественным, поскольку отражение есть результат взаимодействия, т.е. взаимного, обоюдного изменения состояний. С другой стороны, фактически одно явление (или объект) всегда выступает как причина, другой — как следствие; это никак не учитывается при введенном количественном описании информации.

Формула (5) обобщается на непрерывные случайные величины, если в отношении (1) и (2) вместо Н подставить дифференциальную энтропию h; при этом исчезает зависимость от стандарта К и, значит, количество информации в непрерывном случае является столь же безотносительным к единицам измерения, как и в дискретном:

где р(x), p(y) и p(x,y) — соответствующие плотности вероятностей.

Свойства количества информации

Отметим некоторые важные свойства количества информации.

1. Количество информации в случайном объекте Х относительно объекта Y равно количеству информации в Y относительно Х: I(X,Y) = I(Y,X)
2. Количество информации неотрицательно: I(X,Y) > 0. Это можно доказать по-разному. Например, варьированием p(x,y) при фиксированных p(x) и p(y) можно показать, что минимум I, равный нулю, достигается при p(x,y) = p(x) p(y).
3. Для дискретных Х справедливо равенство I(X,X) = H(X).
4. Преобразование y (.) одной случайной величины не может увеличить содержание в ней информации о другой, связанной с ней, величине: I[y (X),Y] < I(X,Y) (9)
5. Для независимых пар величин количество информации аддитивно: I(i,Y_i>) = ∑ I(X_i,Y_i)

Единицы измерения энтропии и количества информации

Рассмотрим теперь вопрос о единицах измерения количества информации и энтропии. Из определений I и H следует их безразмерность, а из линейности их связи — одинаковость их единиц. Поэтому будем для определенности говорить об энтропии. Начнем с дискретного случая. За единицу энтропии примем неопределенность случайного объекта, такого, что

Легко установить, что для однозначного определения единицы измерения энтропии необходимо конкретизировать число m состояний объекта и основание логарифма. Возьмем для определенности наименьшее число возможных состояний, при котором объект еще остается случайным, т.е. m=2, и в качестве основания логарифма также возьмем число 2. Тогда из равенства

вытекает, что p₁=p₂=1/2. Следовательно, единицей неопределенности служит энтропия объекта с двумя равновероятными состояниями. Эта единица получила название «бит». Бросание монеты дает количество информации в один бит. Другая единица «нит» получается, если использовать натуральные логарифмы. Обычно она употребляется для непрерывных величин.

Количество информации в индивидуальных событиях

Остановимся еще на одном важном моменте. До сих пор речь шла о среднем количестве информации, приходящемся на пару состояний (x_i,y_k) объектов X и Y. Эта характеристика естественна для рассмотрения особенностей стационарно функционирующих систем, когда в процессе функционирования принимают участие все возможные пары (x_i,y_k). Однако в ряде практических случаев оказывается необходимым рассмотреть информационное описание конкретной пары состояний, оценить содержание информации в конкретной реализации сигнала. Тот факт, что некоторые сигналы несут информации намного больше, чем другие, виден на примере того, как отбираются новости средствами массовой информации (о рождении шестерых близнецов сообщают практически все газеты мира, а о рождении двойни не пишут).

Допуская существование количественной меры информации (x_i,y_k), в конкретной паре (x_i,y_k) естественно потребовать, чтобы индивидуальное и среднее количество информации удовлетворяли соотношению

Хотя равенство имеет место не только при равенстве всех слагаемых, сравнение формул (5) и, например, (4) наталкивает на мысль, что мерой индивидуальной информации в дискретном случае может служить величина

называемая «информационной плотностью». Свойства этих величин согласуются с интуитивными представлениями и, кроме того, доказана единственность меры, обладающей указанными свойствами. Полезность введения понятия индивидуального количества информации проиллюстрируем на следующем примере.

Пример

Пусть по выборке (т.е. совокупности наблюдений x=x1. xn требуется отдать предпочтение одной из конкурирующих гипотез (H или H₁), если известны распределения наблюдений при каждой из них, т.е. p(x/H₀) и p(x/H₁). Как обработать выборку? Из теории известно, что никакая обработка не может увеличить количество информации, содержащегося в выборке x (см. формулу (9). Следовательно, выборке x следует поставить в соответствие число, содержащее всю полезную информацию, т.е. обработать выборку без потерь. Возникает мысль о том, чтобы вычислить индивидуальное количество информации в выборке x о каждой из гипотез и сравнить их:

Какой из гипотез теперь отдать предпочтение зависит теперь от величины 7d 0i и от того, какой порог сравнения мы назначим. Оказывается, что мы получили статистическую процедуру, оптимальность которой специально доказывается в математической статистике, — именно к этому сводится содержание фундаментальной леммы Неймана-Пирсона. Данный пример иллюстрирует эвристическую силу теоретико-информационных представлений.

Подведем итог

Для системного анализа теория информации имеет двоякое значение. Во-первых, ее конкретные методы позволяют провести ряд количественных исследований информационных потоков в изучаемой или проектируемой системе. Однако более важным является эвристическое значение основных понятий теории информации — неопределенности, энтропии, количество информации, избыточности, пропускной способности и пр. Их использование столь же важно для понимания системных процессов, как и использование понятий, связанных с временными, энергетическими процессами. Системный анализ неизбежно выходит на исследование ресурсов, которые потребуются для решения анализируемой проблемы. Информационные ресурсы играют далеко не последнюю роль наряду с остальными ресурсами — материальными, энергетическими, временными, кадровыми.

Необходимые сведения о случайных величинах

Кратко перечислим основные понятия, более подробное изложение можно найти в [1], [2], [3].

5.2.1 Энтропия

Количественной мерой неопределенности служит энтропия. Пусть задана дискретная случайная величина , принимающая значения определяется равенством:

.

1. 
2. 
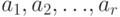
3. и , иными словами, есть три случайные величины и :

   и , заданные вероятностными распределениями , . Для них можно вычислить совместное распределение и условные распределения , для любых фиксированных значений , .

   Определение 5.12 Условная энтропия задаётся формулой:

   величина :

   

Энтропия дискретного случайного сигнала определяется выражением (2). Для непрерывной случайной величины воспользуемся этим же выражением, заменив вероятность p(x) на w(x)dx.

В результате получим

.

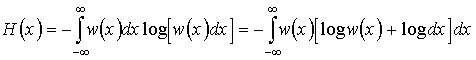
Но логарифм бесконечно малой величины (dx) равен минус бесконечности, в результате чего получаем

.

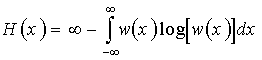
Таким образом, энтропия непрерывной случайной величины бесконечно велика. Но так как в последнем выражении первое слагаемое (¥) от величины x или от w(x) не зависит, при определении энтропии непрерывной величины это слагаемое отбрасывают, учитывая только второе слагаемое (некоторую “добавку” к бесконечности). Эта добавочная энтропия, определяемая формулой

(31)

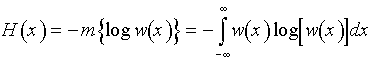
-называется дифференциальной энтропией непрерывной случайной величины.

В дальнейшем слово “дифференциальная” в определении энтропии будем иногда опускать.

Как и для дискретных сообщений, существуют следующие разновидности дифференциальной энтропии непрерывной величины.

1. Условная энтропия случайной величины y относительно случайной величины x.

, или

. (32)

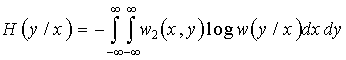
2. Совместная энтропия двух непрерывных случайных величин равна

, или . (33)

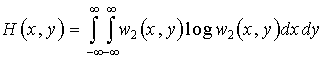
Для независимых x и y H(x,y)=H(x)+H(y).

Для совместной дифференциальной энтропии непрерывной случайной величины справедливы соотношения (17) и (18).

3. Взаимная информация I(x,y), содержащаяся в двух непрерывных сигналах x и y, определяется формулой (16).

Для независимых x и y взаимная информация I(x,y)=0.

4. Если случайная величина ограничена в объёме V=b-a, то её дифференциальная энтропия максимальна при равномерном закона распределения этой величины (рис. 10).

. (34)

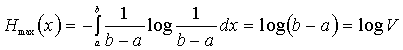
Так как эта величина зависит только от разности (b-a), а не от абсолютных величин b и a, следовательно, Hmax(x) не зависит от математического ожидания случайной величины x.

5. Если случайная величина не ограничена в объёме (т.е. может изменяться в пределах от -¥ до +¥), а ограничена только по мощности, то дифференциальная энтропия максимальна в случае гауссовского закона распределения этой величины. Определим этот максимум.

В соответствии с (31)

;

.

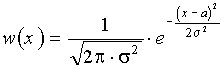
Отсюда

.

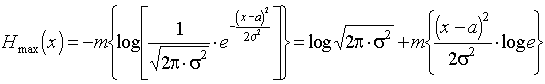
Но математическое ожидание m{(x-a2)}=s2, отсюда получаем

,

или окончательно

. (35)

Cледовательно, энтропия зависит только от мощности s2.

Эта очень важная формула будет использоваться позднее для определения пропускной способности непрерывного канала связи.

Заметим, что, как и ранее, Hmax(x) не зависит от математического ожидания a случайной величины x. Это важное свойство энтропии. Оно объясняется тем, что математическое ожидание является не случайной величиной.

Вопросы

1. Как определяется дифференциальная энтропия непрерывной случайной величины? Разновидности энтропии непрерывной случайной величины.
2. Чему равна максимальная дифференциальная энтропия, если случайная величина ограничена в объёме, при каком законе распределения она максимальна?
3. Чему равна максимальная дифференциальная энтропия, если случайная величина не ограничена в объёме?
4. Как влияет математическое ожидание случайной величины на её энтропию?