Как найти энтропию в термодинамике

Энтропия? Это просто!

Время на прочтение
7 мин

Количество просмотров 407K

Этот пост является вольным переводом ответа, который Mark Eichenlaub дал на вопрос What’s an intuitive way to understand entropy?, заданный на сайте Quora

Энтропия. Пожалуй, это одно из самых сложных для понимания понятий, с которым вы можете встретиться в курсе физики, по крайней мере если говорить о физике классической. Мало кто из выпускников физических факультетов может объяснить, что это такое. Большинство проблем с пониманием энтропии, однако, можно снять, если понять одну вещь. Энтропия качественно отличается от других термодинамических величин: таких как давление, объём или внутренняя энергия, потому что является свойством не системы, а того, как мы эту систему рассматриваем. К сожалению в курсе термодинамики её обычно рассматривают наравне с другими термодинамическими функциями, что усугубляет непонимание.
энтропия

Так что же такое энтропия?

Если в двух словах, то

Энтропия — это то, как много информации вам не известно о системе

Например, если вы спросите меня, где я живу, и я отвечу: в России, то моя энтропия для вас будет высока, всё-таки Россия большая страна. Если же я назову вам свой почтовый индекс: 603081, то моя энтропия для вас понизится, поскольку вы получите больше информации.
почтовый индекс
Почтовый индекс содержит шесть цифр, то есть я дал вам шесть символов информации. Энтропия вашего знания обо мне понизилась приблизительно на 6 символов. (На самом деле, не совсем, потому что некоторые индексы отвечают большему количеству адресов, а некоторые — меньшему, но мы этим пренебрежём).
игральные кости
Или рассмотрим другой пример. Пусть у меня есть десять игральных костей (шестигранных), и выбросив их, я вам сообщаю, что их сумма равна 30. Зная только это, вы не можете сказать, какие конкретно цифры на каждой из костей — вам не хватает информации. Эти конкретные цифры на костях в статистической физике называют микросостояниями, а общую сумму (30 в нашем случае) — макросостоянием. Существует 2 930 455 микросостояний, которые отвечают сумме равной 30. Так что энтропия этого макросостояния равна приблизительно 6,5 символам (половинка появляется из-за того, что при нумерации микросостояний по порядку в седьмом разряде вам доступны не все цифры, а только 0, 1 и 2).

А что если бы я вам сказал, что сумма равна 59? Для этого макросостояния существует всего 10 возможных микросостояний, так что его энтропия равна всего лишь одному символу. Как видите, разные макросостояния имеют разные энтропии.

Пусть теперь я вам скажу, что сумма первых пяти костей 13, а сумма остальных пяти — 17, так что общая сумма снова 30. У вас, однако, в этом случае имеется больше информации, поэтому энтропия системы для вас должна упасть. И, действительно, 13 на пяти костях можно получить 420-ю разными способами, а 17 — 780-ю, то есть полное число микросостояний составит всего лишь 420х780 = 327 600. Энтропия такой системы приблизительно на один символ меньше, чем в первом примере.

Мы измеряем энтропию как количество символов, необходимых для записи числа микросостояний. Математически это количество определяется как логарифм, поэтому обозначив энтропию символом S, а число микросостояний символом Ω, мы можем записать:

S = log Ω

Это есть ничто иное как формула Больцмана (с точностью до множителя k, который зависит от выбранных единиц измерения) для энтропии. Если макросостоянию отвечают одно микросостояние, его энтропия по этой формуле равна нулю. Если у вас есть две системы, то полная энтропия равна сумме энтропий каждой из этих систем, потому что log(AB) = log A + log B.
больцман
Из приведённого выше описания становится понятно, почему не следует думать об энтропии как о собственном свойстве системы. У системы есть опеделённые внутренняя энергия, импульс, заряд, но у неё нет определённой энтропии: энтропия десяти костей зависит от того, известна вам только их полная сумма, или также и частные суммы пятёрок костей.

Другими словами, энтропия — это то, как мы описываем систему. И это делает её сильно отличной от других величин, с которыми принято работать в физике.

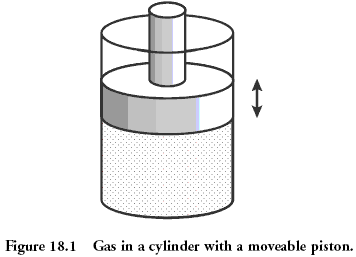
Физический пример: газ под поршнем

Классической системой, которую рассматривают в физике, является газ, находящийся в сосуде под поршнем. Микросостояние газа — это положение и импульс (скорость) каждой его молекулы. Это эквивалентно тому, что вы знаете значение, выпавшее на каждой кости в рассмотренном раньше примере. Макросостояние газа описывается такими величинами как давление, плотность, объём, химический состав. Это как сумма значений, выпавших на костях.
газ в сосуде под поршнем
Величины, описывающие макросостояние, могут быть связаны друг с другом через так называемое «уравнение состояния». Именно наличие этой связи позволяет, не зная микросостояний, предсказывать, что будет с нашей системой, если начать её нагревать или перемещать поршень. Для идеального газа уравнение состояния имеет простой вид:

p = ρT

хотя вы, скорее всего, лучше знакомы с уравнением Клапейрона — Менделеева pV = νRT — это то же самое уравнение, только с добавлением пары констант, чтобы вас запутать. Чем больше микросостояний отвечают данному макросостоянию, то есть чем больше частиц входят в состав нашей системы, тем лучше уравнение состояния её описывают. Для газа характерные значения числа частиц равны числу Авогадро, то есть составляют порядка 1023.

Величины типа давления, температуры и плотности называются усреднёнными, поскольку являются усреднённым проявлением постоянно сменяющих друг друга микросостояний, отвечающих данному макросостоянию (или, вернее, близким к нему макросостояниям). Чтобы узнать в каком микросостоянии находится система, нам надо очень много информации — мы должны знать положение и скорость каждой частицы. Количество этой информации и называется энтропией.

Как меняется энтропия с изменением макросостояния? Это легко понять. Например, если мы немного нагреем газ, то скорость его частиц возрастёт, следовательно, возрастёт и степень нашего незнания об этой скорости, то есть энтропия вырастет. Или, если мы увеличим объём газа, отведя поршень, увеличится степень нашего незнания положения частиц, и энтропия также вырастет.

Твёрдые тела и потенциальная энергия

Если мы рассмотрим вместо газа какое-нибудь твёрдое тело, особенно с упорядоченной структурой, как в кристаллах, например, кусок металла, то его энтропия будет невелика. Почему? Потому что зная положение одного атома в такой структуре, вы знаете и положение всех остальных (они же выстроены в правильную кристаллическую структуру), скорости же атомов невелики, потому что они не могут улететь далеко от своего положения и лишь немного колеблются вокруг положения равновесия.
кристаллическая стурктура
Если кусок металла находится в поле тяготения (например, поднят над поверхностью Земли), то потенциальная энергия каждого атома в металле приблизительно равна потенциальной энергии других атомов, и связанная с этой энергией энтропия низка. Это отличает потенциальную энергию от кинетической, которая для теплового движения может сильно меняться от атома к атому.

Если кусок металла, поднятый на некоторую высоту, отпустить, то его потенциальная энергия будет переходить в кинетическую энергию, но энтропия возрастать практически не будет, потому что все атомы будут двигаться приблизительно одинаково. Но когда кусок упадёт на землю, во время удара атомы металла получат случайное направление движения, и энтропия резко увеличится. Кинетическая энергия направленного движения перейдёт в кинетическую энергию теплового движения. Перед ударом мы приблизительно знали, как движется каждый атом, теперь мы эту информацию потеряли.

Понимаем второй закон термодинамики

Второй закон термодинамики утверждает, что энтропия (замкнутой системы) никогда не уменьшается. Мы теперь можем понять, почему: потому что невозможно внезапно получить больше информации о микросостояниях. Как только вы потеряли некую информацию о микросостоянии (как во время удара куска металла об землю), вы не можете вернуть её назад.
нельзя просто так взять и объяснить второй закон термодинамики
Давайте вернёмся обратно к игральным костям. Вспомним, что макросостояние с суммой 59 имеет очень низкую энтропию, но и получить его не так-то просто. Если бросать кости раз за разом, то будут выпадать те суммы (макросостояния), которым отвечает большее количество микросостояний, то есть будут реализовываться макросостояния с большой энтропией. Самой большой энтропией обладает сумма 35, и именно она и будет выпадать чаще других. Именно об этом и говорит второй закон термодинамики. Любое случайное (неконтролируемое) взаимодействие приводит к росту энтропии, по крайней мере до тех пор, пока она не достигнет своего максимума.

Перемешивание газов

И ещё один пример, чтобы закрепить сказанное. Пусть у нас имеется контейнер, в котором находятся два газа, разделённых расположенной посередине контейнера перегородкой. Назовём молекулы одного газа синими, а другого — красными.

Если открыть перегородку, газы начнут перемешиваться, потому что число микросостояний, в которых газы перемешаны, намного больше, чем микросостояний, в которых они разделены, и все микросостояния, естественно, равновероятны. Когда мы открыли перегородку, для каждой молекулы мы потеряли информацию о том, с какой стороны перегородки она теперь находится. Если молекул было N, то утеряно N бит информации (биты и символы, в данном контексте, это, фактически, одно и тоже, и отличаются только неким постоянным множителем).

Разбираемся с демоном Максвелла

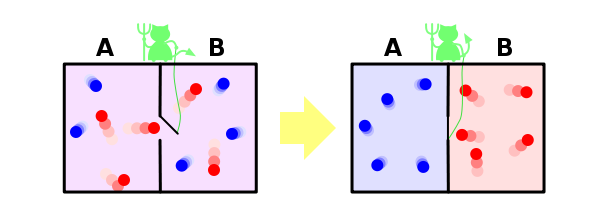
Ну и напоследок рассмотрим решение в рамках нашей парадигмы знаменитого парадокса демона Максвелла. Напомню, что он заключается в следующем. Пусть у нас есть перемешанные газы из синих и красных молекул. Поставим обратно перегородку, проделав в ней небольшое отверстие, в которое посадим воображаемого демона. Его задача — пропускать слева направо только красных, и справа налево только синих. Очевидно, что через некоторое время газы снова будут разделены: все синие молекулы окажутся слева от перегородки, а все красные — справа.
демон максвелла
Получается, что наш демон понизил энтропию системы. С демоном ничего не случилось, то есть его энтропия не изменилась, а система у нас была закрытой. Получается, что мы нашли пример, когда второй закон термодинамики не выполняется! Как такое оказалось возможно?

Решается этот парадокс, однако, очень просто. Ведь энтропия — это свойство не системы, а нашего знания об этой системе. Мы с вами знаем о системе мало, поэтому нам и кажется, что её энтропия уменьшается. Но наш демон знает о системе очень много — чтобы разделять молекулы, он должен знать положение и скорость каждой из них (по крайней мере на подлёте к нему). Если он знает о молекулах всё, то с его точки зрения энтропия системы, фактически, равна нулю — у него просто нет недостающей информации о ней. В этом случае энтропия системы как была равна нулю, так и осталась равной нулю, и второй закон термодинамики нигде не нарушился.

Но даже если демон не знает всей информации о микросостоянии системы, ему, как минимум, надо знать цвет подлетающей к нему молекулы, чтобы понять, пропускать её или нет. И если общее число молекул равно N, то демон должен обладать N бит информации о системе — но именно столько информации мы и потеряли, когда открыли перегородку. То есть количество потерянной информации в точности равно количеству информации, которую необходимо получить о системе, чтобы вернуть её в исходное состояние — и это звучит вполне логично, и опять же не противоречит второму закону термодинамики.

Источник
Термодинамические величины
Thermodynamics navigation image
Статья является частью серии «Термодинамика».
Энтропия
Количество теплоты
Термодинамическая работа
Химический потенциал
См. также: Термодинамические потенциалы.
Разделы термодинамики
Начала термодинамики
Уравнение состояния
Термодинамические величины
Термодинамические потенциалы
Термодинамические циклы
Фазовые переходы
править

Термодинами́ческая энтропи́я S, часто просто именуемая энтропия, в химии и термодинамике является функцией состояния термодинамической системы; её существование постулируется вторым началом термодинамики.

Термодинамическое определение энтропии

Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение изменения общего количества тепла ΔQ к величине абсолютной температуры T:

{displaystyle Delta S={frac {Delta Q}{T}}.}

Рудольф Клаузиус дал величине S имя «энтропия», происходящее от греческого слова τρoπή, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию.

Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольного квазистатического процесса выглядит так:

{displaystyle dS={frac {delta Q}{T}}},

где {displaystyle dS} — приращение (дифференциал) энтропии, а {displaystyle delta Q} — бесконечно малое приращение количества теплоты.

Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия).

Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому {displaystyle delta Q} считать полным дифференциалом нельзя.

Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.

Статистическое определение энтропии: принцип Больцмана

В 1877 году Людвиг Больцман нашёл, что энтропия системы может относиться к количеству возможных «микросостояний» (микроскопических состояний), согласующихся с их термодинамическими свойствами. Рассмотрим, например, идеальный газ в сосуде. Микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома. Связность предъявляет к нам требования рассматривать только те микросостояния, для которых:
(I) месторасположения всех частей расположены в рамках сосуда,
(II) для получения общей энергии газа кинетические энергии атомов суммируются.
Больцман постулировал, что:

{displaystyle S=k(ln Omega ),!,}

где константу k=1,38•10–23 Дж/К мы знаем теперь как постоянную Больцмана, а Ω является числом микросостояний, которые возможны в имеющемся макроскопическом состоянии (статистический вес состояния). Этот постулат, известный как принцип Больцмана, может быть оценен как начало статистической механики, которая описывает термодинамические системы, используя статистическое поведение составляющих их компонентов. Принцип Больцмана связывает микроскопические свойства системы (Ω) с одним из её термодинамических свойств (S).

Согласно определению Больцмана, энтропия является просто функцией состояния. Так как Ω может быть только натуральным числом (1,2,3,…), то энтропия Больцмана должна быть положительной — исходя из свойств логарифма.

Понимание энтропии как меры беспорядка

Существует мнение, что мы можем смотреть на Ω и как на меру беспорядка в системе. В определённом смысле это может быть оправдано, потому что мы думаем об «упорядоченных» системах как о системах, имеющих очень малую возможность конфигурирования, а о «беспорядочных» системах, как об имеющих очень много возможных состояний. Собственно, это просто переформулированное определение энтропии как числа микросостояний на данное макросостояние.

Рассмотрим, например, распределение молекул идеального газа. В случае идеального газа наиболее вероятным состоянием, соответствующим максимуму энтропии, будет равномерное распределение молекул. При этом реализуется и максимальный «беспорядок», т.к. при этом будут максимальные возможности конфигурирования.

Границы применимости понимания энтропии как меры беспорядка

Подобное определение беспорядка термодинамической системы как количества возможностей конфигурирования системы фактически дословно соответствует определению энтропии как числа микросостояний на данное макросостояние. Проблемы начинаются в двух случаях:

  • когда начинают смешивать различные понимания беспорядка, и энтропия становится мерой беспорядка вообще;
  • когда понятие энтропии применяется для систем, не являющихся термодинамическими.

В обоих этих случаях применение понятия термодинамической энтропии совершенно неправомерно[1].

Рассмотрим оба пункта более подробно.

Рассмотрим пример термодинамической системы — распределение молекул в поле тяготения. В этом случае наиболее вероятным распределением молекул будет распределение согласно барометрической формуле Больцмана. Другой пример — учёт электромагнитных сил взаимодействия между ионами. В этом случае наиболее вероятным состоянием, соответствующим максимуму энтропии, будет упорядоченное кристаллическое состояние, а совсем не «хаос». (Термин «хаос» здесь понимается в смысле беспорядка — в наивном смысле. К хаосу в математическом смысле как сильно неустойчивой нелинейной системе это не имеет отношения, конечно.)

Рассмотрим случай с кристаллической решёткой более подробно. Кристаллическая решётка может быть и в равновесном, и в неравновесном состоянии, как и любая термодинамическая система. Скажем, возьмём следующую модель — совокупность взаимодействующих осцилляторов. Рассмотрим некоторое неравновесное состояние: все осцилляторы имеют
одинаковое отклонение от положения равновесия. С течением времени эта система перейдёт в состояние ТД равновесия, в котором отклонения (в каждый момент времени) будут подчинены некоторому распределению типа Максвелла (только это распределение будет для отклонений, и оно будет зависеть от типа взаимодействия осцилляторов). В таком случае максимум энтропии будет действительно реализовывать максимум возможностей конфигурирования, т.е. — беспорядок согласно вышеуказанному определению. Но данный «беспорядок» вовсе не соответствует «беспорядку» в каком-либо другом понимании, например, информационному. Такая же ситуация возникает и в примере с кристаллизацией переохлаждённой жидкости, в которой образование структур из «хаотичной» жидкости идёт параллельно с увеличением энтропии.

Это неверное понимание энтропии появилось во время развития теории информации, в связи с парадоксом термодинамики, связанным с мысленным экспериментом т.н. «демона Максвелла». Суть парадокса заключалась в том, что рассматривалось два сосуда с разными температурами, соединённых узкой трубкой с затворками, которыми управлял т.н. «демон». «Демон» мог измерять скорость отдельных летящих молекул, и т.о. избирательно пропускать более быстрые в сосуд с высокой температурой, а более медленные — в сосуд с низкой. Из этого мысленного эксперимента вытекало кажущееся противоречие со вторым началом термодинамики.

Парадокс может быть разрешён при помощи теории информации. Для измерения скорости молекулы «демон» должен был бы получить информацию о её скорости. Но всякое получение информации — материальный процесс, сопровождающийся возрастанием энтропии. Количественный анализ, проведённый, например, в [2] показал, что приращение энтропии при измерении превосходит по абсолютной величине уменьшение энтропии, вызванное перераспрелением молекул «демоном».

Однако многие учёные стали отождествлять информацию с «отрицательной энтропией» ввиду совпадения выражений для этих понятий. Начало этому заблуждению положил Н. Винер [3] (стр. 23). На самом деле энтропия не является мерой дезорганизации, мерой беспорядка и хаоса, а информация совсем не является мерой упорядоченности, организованности, порядка.

Рассмотрим второй случай неверного применения понятия энтропии.

Рассмотрим, например, набор 10 монет, каждая из которых может находиться либо в состоянии «орёл», либо в состоянии «решка». Наиболее «упорядоченным» макроскопическим состоянием будет являться или 10 «орлов», или 10 «решек»; для каждого результата в каждом случае имеется только одна возможная конфигурация. И наоборот, наиболее «неупорядоченное» состояние содержит 5 «орлов» и 5 «решек», и здесь 10C5 = 252 способов для получения этого результата (см. комбинаторика.)

Безусловно, этот пример также некорректен, т.к. система монет не является термодинамической системой, и поэтому термодинамическая энтропия системы в обоих случаях (как бы ни были перевёрнуты монеты) окажется, конечно, одинаковой. Т.о., разбросанные по комнате стулья не имеют отношения к термодинамической энтропии, хотя и могут иметь отношение к энтропии информационной.

Впрочем, это легко подтвердить на практике: замкнутая система 10 монет, перевёрнутых орлами вверх, самопроизвольно не перейдёт в систему хаотично перевёрнутых монет.

Энтропия в открытых системах

В силу второго начала термодинамики, энтропия {displaystyle S_{i}} замкнутой системы не может уменьшаться» (закон неубывания энтропии). Математически это можно записать так: {displaystyle dS_{i}geq 0}, индекс {displaystyle i} обозначает так называемую внутреннюю энтропию, соответствующую замкнутой системе. В открытой системе возможны потоки тепла как из системы, так и внутрь неё. В случае наличия потока тепла в систему приходит количество тепла {displaystyle delta Q_{1}} при температуре {displaystyle T_{1}} и уходит количество тепла {displaystyle delta Q_{2}} при температуре {displaystyle T_{2}}. Приращение энтропии, связанное с данными тепловыми потоками, равно:

{displaystyle dS_{o}={frac {delta Q_{1}}{T_{1}}}-{frac {delta Q_{2}}{T_{2}}}.}

В стационарных системах обычно {displaystyle delta Q_{1}=delta Q_{2}}, {displaystyle T_{1}>T_{2}}, так что {displaystyle dS_{o}<0}. Поскольку здесь изменение энтропии отрицательно, то часто употребляют выражение «приток негэнтропии», вместо оттока энтропии из системы. Негэнтропия определяется таким образом как обратная величина энтропии.
Суммарное изменение энтропии открытой системы будет равно:

{displaystyle dS=dS_{i}+dS_{o}.}

Если всё время {displaystyle dS>0}, то рост внутренней энтропии не компенсируется притоком внешней негэнтропии, система движется к ближайшему состоянию равновесия. Если {displaystyle dS=0}, то мы имеем стационарный процесс с неизменной общей энтропией. В этом случае в системе осуществляется некоторая внутренняя работа с генерацией внутренней энтропии, которая преобразует, например, температуру {displaystyle T_{1}} внешнего потока тепла в температуру {displaystyle T_{2}} уходящего из системы потока тепла.

Измерение энтропии

В реальных экспериментах очень трудно измерить энтропию системы. Техники измерения базируются на термодинамическом определении энтропии и требуют экстремально аккуратной калориметрии.

Для упрощения мы будем исследовать механическую систему, термодинамические состояния которой будут определены через её объем V и давление P. Для измерения энтропии определенного состояния мы должны сперва измерить теплоёмкость при постоянных объёме и давлении (обозначенную CV и CP соответственно), для успешного набора состояний между первоначальным состоянием и требуемым. Тепловые ёмкости связаны с энтропией S и с температурой T согласно формуле:

{displaystyle C_{X}=Tleft({frac {partial S}{partial T}}right)_{X}}

где нижний индекс X относится к постоянным объёму и давлению. Мы можем проинтегрировать для получения изменения энтропии:

{displaystyle Delta S=int {frac {C_{X}}{T}}dT}

Таким образом, мы можем получить значение энтропии любого состояния (P,V) по отношению к первоначальному состоянию (P0,V0). Точная формула зависит от нашего выбора промежуточных состояний. Для примера, если первоначальное состояние имеет такое же давление, как и конечное состояние, то

{displaystyle S(P,V)=S(P,V_{0})+int _{T(P,V_{0})}^{T(P,V)}{frac {C_{P}(P,V(T,P))}{T}}dT}

В добавление, если путь между первым и последним состояниями лежит сквозь любой фазовый переход первого рода, скрытая теплота, ассоциированная с переходом, должна также учитываться.

Энтропия первоначального состояния должна быть определена независимо. В идеальном варианте выбирается первоначальное состояние как состояние при экстремально высокой температуре, при которой система существует в виде газа. Энтропия в этом состоянии подобна энтропии классического идеального газа плюс взнос от молекулярных вращений и колебаний, которые могут быть определены спектроскопически.

Построение графика изменения энтропии

Основная статья: адиабатический процесс

Следующее уравнение может быть использовано для построения графика изменения энтропии на диаграмме P-V:

{displaystyle S=nR ln(1+P^{C_{V} over R}V^{C_{P} over R})}

Здесь два замечания: (1) это не определение энтропии (но выведено из него), (2) предполагается, что CV и CP постоянные, что на самом деле не так.

См. также

  • Термодинамика чёрных дыр
  • Тепловая смерть
  • Демон Максвелла
  • Термодинамические потенциалы
  • Стрела времени
  • Информационная энтропия
  • Негэнтропия
  • Энергетическое определение энтропии
  • Список статей по энтропии

Литература

  • Fermi, E., Thermodynamics, Prentice Hall (1937)
  • Reif, F., Fundamentals of statistical and thermal physics, McGraw-Hill (1965)
  • Шамбадаль П. Развитие и приложение понятия энтропии. – М.: Наука, 1967. – 280 с.
  • Волькенштейн М.В. Энтропия и информация. – М.: Наука, 1986. – 192 с.
  1. ↑ http://www.entropysite.com/
  2. ↑ Бриллюэн Л. Наука и теория информации. — М., 1960.
  3. ↑ Винер Н. Кибернетика. — М.: Советское радио, 1958.

Ссылки

  • Термодинамическая энтропия
  • Entropy and chaos (англ.)
  • Роль Термодинамики в современном мире. Второе начало термодинамики
  • Статья «Эволюция как сопротивление энтропии»
  1. Википедия Энтропия (в термодинамике) адрес
  2. Викисловарь — адрес
  3. Викицитатник — адрес
  4. Викиучебник — адрес
  5. Викитека — адрес
  6. Викиновости — адрес
  7. Викиверситет — адрес
  8. Викигид — адрес

Выделить Энтропия (в термодинамике) и найти в:

  1. Вокруг света (в термодинамике) адрес
  2. Академик (в термодинамике)/ru/ru/ адрес
  3. Астронет адрес
  4. Элементы (в термодинамике)+&search адрес
  5. Научная Россия (в термодинамике)&mode=2&sort=2 адрес
  6. Кругосвет (в термодинамике)&results_per_page=10 адрес
  7. Научная Сеть
  8. Традиция — адрес
  9. Циклопедия — адрес
  10. Викизнание — (в термодинамике) адрес
  1. Google
  2. Bing
  3. Yahoo
  4. Яндекс
  5. Mail.ru
  6. Рамблер
  7. Нигма.РФ
  8. Спутник
  9. Google Scholar
  10. Апорт
  11. Онлайн-переводчик
  12. Архив Интернета
  13. Научно-популярные фильмы на Яндексе
  14. Документальные фильмы
  1. Список ru-вики
  2. Вики-сайты на русском языке
  3. Список крупных русскоязычных википроектов
  4. Каталог wiki-сайтов
  5. Русскоязычные wiki-проекты
  6. Викизнание:Каталог wiki-сайтов
  7. Научно-популярные сайты в Интернете
  8. Лучшие научные сайты на нашем портале
  9. Лучшие научно-популярные сайты
  10. Каталог научно-познавательных сайтов
  11. НАУКА В РУНЕТЕ: каталог научных и научно-популярных сайтов
  • Страница 0 — краткая статья
  • Страница 1 — энциклопедическая статья
  • Разное — на страницах: 2 , 3 , 4 , 5
  • Прошу вносить вашу информацию в «Энтропия (в термодинамике) 1», чтобы сохранить ее

Комментарии читателей:

Источник

From Wikipedia, the free encyclopedia

In classical thermodynamics, entropy (from Greek τρoπή (tropḗ) ‘transformation’) is a property of a thermodynamic system that expresses the direction or outcome of spontaneous changes in the system. The term was introduced by Rudolf Clausius in the mid-19th century to explain the relationship of the internal energy that is available or unavailable for transformations in form of heat and work. Entropy predicts that certain processes are irreversible or impossible, despite not violating the conservation of energy.[1] The definition of entropy is central to the establishment of the second law of thermodynamics, which states that the entropy of isolated systems cannot decrease with time, as they always tend to arrive at a state of thermodynamic equilibrium, where the entropy is highest. Entropy is therefore also considered to be a measure of disorder in the system.

Ludwig Boltzmann explained the entropy as a measure of the number of possible microscopic configurations Ω of the individual atoms and molecules of the system (microstates) which correspond to the macroscopic state (macrostate) of the system. He showed that the thermodynamic entropy is k ln Ω, where the factor k has since been known as the Boltzmann constant.

Concept[edit]

Figure 1. A thermodynamic model system

Differences in pressure, density, and temperature of a thermodynamic system tend to equalize over time. For example, in a room containing a glass of melting ice, the difference in temperature between the warm room and the cold glass of ice and water is equalized by energy flowing as heat from the room to the cooler ice and water mixture. Over time, the temperature of the glass and its contents and the temperature of the room achieve a balance. The entropy of the room has decreased. However, the entropy of the glass of ice and water has increased more than the entropy of the room has decreased. In an isolated system, such as the room and ice water taken together, the dispersal of energy from warmer to cooler regions always results in a net increase in entropy. Thus, when the system of the room and ice water system has reached thermal equilibrium, the entropy change from the initial state is at its maximum. The entropy of the thermodynamic system is a measure of the progress of the equalization.

Many irreversible processes result in an increase of entropy. One of them is mixing of two or more different substances, occasioned by bringing them together by removing a wall that separates them, keeping the temperature and pressure constant. The mixing is accompanied by the entropy of mixing. In the important case of mixing of ideal gases, the combined system does not change its internal energy by work or heat transfer; the entropy increase is then entirely due to the spreading of the different substances into their new common volume.[2]

From a macroscopic perspective, in classical thermodynamics, the entropy is a state function of a thermodynamic system: that is, a property depending only on the current state of the system, independent of how that state came to be achieved. Entropy is a key ingredient of the Second law of thermodynamics, which has important consequences e.g. for the performance of heat engines, refrigerators, and heat pumps.

Definition[edit]

According to the Clausius equality, for a closed homogeneous system, in which only reversible processes take place,

oint frac{delta Q}{T}=0.

With T being the uniform temperature of the closed system and delta Q the incremental reversible transfer of heat energy into that system.

That means the line integral {textstyle int _{L}{frac {delta Q}{T}}} is path-independent.

A state function S, called entropy, may be defined which satisfies

mathrm{d}S = frac{delta Q}{T}.

Entropy measurement[edit]

The thermodynamic state of a uniform closed system is determined by its temperature T and pressure P. A change in entropy can be written as

{displaystyle mathrm {d} S=left({frac {partial S}{partial T}}right)_{P}mathrm {d} T+left({frac {partial S}{partial P}}right)_{T}mathrm {d} P.}

The first contribution depends on the heat capacity at constant pressure CP through

{displaystyle left({frac {partial S}{partial T}}right)_{P}={frac {C_{P}}{T}}.}

This is the result of the definition of the heat capacity by δQ = CP dT and T dS = δQ. The second term may be rewritten with one of the Maxwell relations

{displaystyle left({frac {partial S}{partial P}}right)_{T}=-left({frac {partial V}{partial T}}right)_{P}}

and the definition of the volumetric thermal-expansion coefficient

{displaystyle alpha _{V}={frac {1}{V}}left({frac {partial V}{partial T}}right)_{P}}

so that

mathrm{d}S=frac {C_P}{T}mathrm{d}T-alpha_V Vmathrm{d}P.

With this expression the entropy S at arbitrary P and T can be related to the entropy S0 at some reference state at P0 and T0 according to

S(P,T)=S(P_0,T_0)+int_{T_0}^T frac {C_P(P_0,T^prime)}{T^prime}mathrm{d}T^prime-int_{P_0}^P alpha_V(P^prime ,T) V(P^prime ,T)mathrm{d}P^prime.

In classical thermodynamics, the entropy of the reference state can be put equal to zero at any convenient temperature and pressure. For example, for pure substances, one can take the entropy of the solid at the melting point at 1 bar equal to zero. From a more fundamental point of view, the third law of thermodynamics suggests that there is a preference to take S = 0 at T = 0 (absolute zero) for perfectly ordered materials such as crystals.

S(P, T) is determined by followed a specific path in the P-T diagram: integration over T at constant pressure P0, so that dP = 0, and in the second integral one integrates over P at constant temperature T, so that dT = 0. As the entropy is a function of state the result is independent of the path.

The above relation shows that the determination of the entropy requires knowledge of the heat capacity and the equation of state (which is the relation between P,V, and T of the substance involved). Normally these are complicated functions and numerical integration is needed. In simple cases it is possible to get analytical expressions for the entropy. In the case of an ideal gas, the heat capacity is constant and the ideal gas law PV = nRT gives that αVV = V/T = nR/p, with n the number of moles and R the molar ideal-gas constant. So, the molar entropy of an ideal gas is given by

S_m(P,T)=S_m(P_0,T_0)+C_P ln frac {T}{T_0}-Rlnfrac{P}{P_0}.

In this expression CP now is the molar heat capacity.

The entropy of inhomogeneous systems is the sum of the entropies of the various subsystems. The laws of thermodynamics hold rigorously for inhomogeneous systems even though they may be far from internal equilibrium. The only condition is that the thermodynamic parameters of the composing subsystems are (reasonably) well-defined.

Temperature-entropy diagrams[edit]

Fig.2 Temperature–entropy diagram of nitrogen. The red curve at the left is the melting curve. The red dome represents the two-phase region with the low-entropy side the saturated liquid and the high-entropy side the saturated gas. The black curves give the TS relation along isobars. The pressures are indicated in bar. The blue curves are isenthalps (curves of constant enthalpy). The values are indicated in blue in kJ/kg.

Entropy values of important substances may be obtained from reference works or with commercial software in tabular form or as diagrams. One of the most common diagrams is the temperature-entropy diagram (TS-diagram). For example, Fig.2 shows the TS-diagram of nitrogen,[3] depicting the melting curve and saturated liquid and vapor values with isobars and isenthalps.

Entropy change in irreversible transformations[edit]

We now consider inhomogeneous systems in which internal transformations (processes) can take place. If we calculate the entropy S1 before and S2 after such an internal process the Second Law of Thermodynamics demands that S2 ≥ S1 where the equality sign holds if the process is reversible. The difference Si = S2 − S1 is the entropy production due to the irreversible process. The Second law demands that the entropy of an isolated system cannot decrease.

Suppose a system is thermally and mechanically isolated from the environment (isolated system). For example, consider an insulating rigid box divided by a movable partition into two volumes, each filled with gas. If the pressure of one gas is higher, it will expand by moving the partition, thus performing work on the other gas. Also, if the gases are at different temperatures, heat can flow from one gas to the other provided the partition allows heat conduction. Our above result indicates that the entropy of the system as a whole will increase during these processes. There exists a maximum amount of entropy the system may possess under the circumstances. This entropy corresponds to a state of stable equilibrium, since a transformation to any other equilibrium state would cause the entropy to decrease, which is forbidden. Once the system reaches this maximum-entropy state, no part of the system can perform work on any other part. It is in this sense that entropy is a measure of the energy in a system that cannot be used to do work.

An irreversible process degrades the performance of a thermodynamic system, designed to do work or produce cooling, and results in entropy production. The entropy generation during a reversible process is zero. Thus entropy production is a measure of the irreversibility and may be used to compare engineering processes and machines.

Thermal machines[edit]

Figure 3: Heat engine diagram. The system, discussed in the text, is indicated by the dotted rectangle. It contains the two reservoirs and the heat engine. The arrows define the positive directions of the flows of heat and work.

Clausius’ identification of S as a significant quantity was motivated by the study of reversible and irreversible thermodynamic transformations. A heat engine is a thermodynamic system that can undergo a sequence of transformations which ultimately return it to its original state. Such a sequence is called a cyclic process, or simply a cycle. During some transformations, the engine may exchange energy with its environment. The net result of a cycle is

  1. mechanical work done by the system (which can be positive or negative, the latter meaning that work is done on the engine),
  2. heat transferred from one part of the environment to another. In the steady state, by the conservation of energy, the net energy lost by the environment is equal to the work done by the engine.

If every transformation in the cycle is reversible, the cycle is reversible, and it can be run in reverse, so that the heat transfers occur in the opposite directions and the amount of work done switches sign.

Heat engines[edit]

Consider a heat engine working between two temperatures TH and Ta. With Ta we have ambient temperature in mind, but, in principle it may also be some other low temperature. The heat engine is in thermal contact with two heat reservoirs which are supposed to have a very large heat capacity so that their temperatures do not change significantly if heat QH is removed from the hot reservoir and Qa is added to the lower reservoir. Under normal operation TH > Ta and QH, Qa, and W are all positive.

As our thermodynamical system we take a big system which includes the engine and the two reservoirs. It is indicated in Fig.3 by the dotted rectangle. It is inhomogeneous, closed (no exchange of matter with its surroundings), and adiabatic (no exchange of heat with its surroundings). It is not isolated since per cycle a certain amount of work W is produced by the system given by the first law of thermodynamics

{displaystyle W=Q_{H}-Q_{a}.}

We used the fact that the engine itself is periodic, so its internal energy has not changed after one cycle. The same is true for its entropy, so the entropy increase S2 − S1 of our system after one cycle is given by the reduction of entropy of the hot source and the increase of the cold sink. The entropy increase of the total system S2 — S1 is equal to the entropy production Si due to irreversible processes in the engine so

{displaystyle S_{i}=-{frac {Q_{H}}{T_{H}}}+{frac {Q_{a}}{T_{a}}}.}

The Second law demands that Si ≥ 0. Eliminating Qa from the two relations gives

{displaystyle W=left(1-{frac {T_{a}}{T_{H}}}right)Q_{H}-T_{a}S_{i}.}

The first term is the maximum possible work for a heat engine, given by a reversible engine, as one operating along a Carnot cycle. Finally

{displaystyle W=W_{text{max}}-T_{a}S_{i}.}

This equation tells us that the production of work is reduced by the generation of entropy. The term TaSi gives the lost work, or dissipated energy, by the machine.

Correspondingly, the amount of heat, discarded to the cold sink, is increased by the entropy generation

{displaystyle Q_{a}={frac {T_{a}}{T_{H}}}Q_{H}+T_{a}S_{i}=Q_{a,{text{min}}}+T_{a}S_{i}.}

These important relations can also be obtained without the inclusion of the heat reservoirs. See the article on entropy production.

Refrigerators[edit]

The same principle can be applied to a refrigerator working between a low temperature TL and ambient temperature. The schematic drawing is exactly the same as Fig.3 with TH replaced by TL, QH by QL, and the sign of W reversed. In this case the entropy production is

{displaystyle S_{i}={frac {Q_{a}}{T_{a}}}-{frac {Q_{L}}{T_{L}}}}

and the work needed to extract heat QL from the cold source is

{displaystyle W=Q_{L}left({frac {T_{a}}{T_{L}}}-1right)+T_{a}S_{i}.}

The first term is the minimum required work, which corresponds to a reversible refrigerator, so we have

{displaystyle W=W_{text{min}}+T_{a}S_{i}}

i.e., the refrigerator compressor has to perform extra work to compensate for the dissipated energy due to irreversible processes which lead to entropy production.

See also[edit]

  • Entropy
  • Enthalpy
  • Entropy production
  • Fundamental thermodynamic relation
  • Thermodynamic free energy
  • History of entropy
  • Entropy (statistical views)

References[edit]

  1. ^ Lieb, E. H.; Yngvason, J. (1999). «The Physics and Mathematics of the Second Law of Thermodynamics». Physics Reports. 310 (1): 1–96. arXiv:cond-mat/9708200. Bibcode:1999PhR…310….1L. doi:10.1016/S0370-1573(98)00082-9. S2CID 119620408.
  2. ^ Notes for a «Conversation About Entropy»
  3. ^ Figure composed with data obtained with RefProp, NIST Standard Reference Database 23

Further reading[edit]

  • E.A. Guggenheim Thermodynamics, an advanced treatment for chemists and physicists North-Holland Publishing Company, Amsterdam, 1959.
  • C. Kittel and H. Kroemer Thermal Physics W.H. Freeman and Company, New York, 1980.
  • Goldstein, Martin, and Inge F., 1993. The Refrigerator and the Universe. Harvard Univ. Press. A gentle introduction at a lower level than this entry.
Источник
Автор статьи

Екатерина Владимировна Мосина

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Понятие энтропии ввел Р. Клаузиус в 1865 г.

Энтропия – функция состояния

Для того чтобы выяснить в чем состоит физический смысл энтропии, рассмотрим изотермический процесс и приведенное количество теплоты в этом процессе на очень малом участке этого процесса -$frac{delta Q}{T}$, где $delta Q$ – количество теплоты, которое получает тело, $T$ – температура тела.

Приведенное количество теплоты, которое сообщается телу в любом обратимом круговом процессе:

$oint {frac{delta Q}{T}=0left( 1 right).}$

Равенство нулю левой части выражения (1), который берут по замкнутому контуру, означает, что отношение δQ/T – это полный дифференциал некоторой функции состояния системы, которая не зависит от формы пути перехода системы из начального состояния в конечное.

Введем следующее обозначение:

$frac{delta Q}{T}=dSleft( 2 right)$.

Определение 1

Энтропией ($S$) называют функцию состояния, дифференциал которой равен приведенному количеству тепла на малом участке термодинамического процесса, которое передано системе в этом процессе.

Для обратимых процессов изменение энтропии равно нулю:

$Delta S=0left( 3 right)$.

Если выполняется необратимый процесс, то энтропия системы увеличивается:

$Delta S$>$0, left( 4 right)$.

Все реальные процессы являются необратимыми, поэтому в реальности энтропия изолированной системы способна только расти. Она становится максимальной в состоянии термодинамического равновесия.

Замечание 1

Формулы (3) и (4) выполняются только в том случае, если система замкнута. В том случае, если термодинамическая система может обмениваться теплом с внешней средой, то поведение энтропии может быть любым.

«Энтропия простыми словами с формулами» 👇

Неравенство Клаузиуса

Выражения (3) и (4) объединяются в неравенство, которое называется неравенством Клаузиуса:

$Delta Sge left( 5 right)$.

Неравенство Клаузиуса означает, что для замкнутой системы энтропия способна увеличиваться (если процесс необратим), или не изменяется (процесс обратим).

Неравенство Клаузиуса является математической записью второго начала термодинамики.

Знак изменения энтропии указывает направление течения процесса в обратимом процессе.

Во всех ординарных термодинамических системах при стремлении температуры к бесконечности, внутренняя энергия системы безгранично растет. Абсолютная температура при равновесных процессах может только большей нуля, следовательно, если система подвергается нагреву, то:

$dS$>$0.$

При уменьшении температуры системы имеем:

$dS$

Изменение энтропии в равновесном процессе

Допустим, что термодинамическая система совершает равновесный переход из состояния 1 в состояние 2, тогда изменение энтропии найдем как:

$Delta S=S_{2}-S_{1}=intlimits_1^2 {frac{delta Q}{T}=intlimits_1^2{frac{dU+delta A}{T}left( 6 right),} }$

где $dU$ – изменение внутренней энергии в рассматриваемом процессе; $delta A$ – работа, выполняемая в этом процессе.

Выражение (6) способно определить энтропию с точностью до аддитивной константы. Это означает то, что физическим смыслом обладает не энтропия, а ее разность.

$S=intlimits_{обр} {frac{delta Q}{T}+const, left( 7 right).}$

Свойства энтропии

Замечание 2

Энтропия – аддитивная величина. Это означает, что энтропию системы можно найти как сумму энтропий тел, которые эту систему образуют.

Свойство аддитивности имеют:

  • масса;
  • внутренняя энергия;
  • количество теплоты.

Аддитивными не являются:

  • объем,
  • температура,
  • давление.

Определение 2

Термодинамический процесс, в котором энтропия остается постоянной, называется изоэнтропийным процессом.

Так, при обратимом адиабатном процессе мы имеем:

$delta Q=0to S=const.$

Энтропия однородной термодинамической системы – это функция пары независимых параметров, характеризующих ее состояние, например, $ p,V$ или $ T,V$ при $ m=const$.

В этой связи можно записать, что:

$left( V,T right)=intlimits_0^T {C_{V}frac{dT}{T}+S_{01, }left( 8right).}$

или

$Sleft( p,T right)=intlimits_0^T {C_{p}frac{dT}{T}+S_{02, }left( 9right),}$

где $intlimits_0^T {C_{V}frac{dT}{T},}$ – находят для обратимого изобарного процесса; $intlimits_0^T {C_{p}frac{dT}{T}}$ – вычисляют для обратимого изохорного процесса, при изменении температуры от 0К до $T$; $C_V$ – теплоемкость изохорного процесса; $C_p$ – теплоемкость при изобарном процессе; $S_{01 }=S(V,0)$ ; $S_{02 }=S(p,0).$

Статистический смысл энтропии

Допустим, что энтропия в обратимом процессе претерпевает изменения под воздействием внешних условий, которые оказывают влияние на систему. Механизм действия этих условий на энтропию можно сформулировать так:

  1. Внешние условия определяют микросостояния, которые доступны системе, а также их количество.
  2. В рамках доступных для системы микросостояний, она приходит в состояние равновесия.
  3. Энтропия получает соответствующее значение. Получается, что величина энтропии идет за изменением внешних условий, принимая наибольшую величину, совместимую с внешними условиями.

Глубокий смысл энтропии раскрывается в статистической физике. Энтропия связана с термодинамической вероятностью состояния системы.

Определение 3

Термодинамическая вероятность ($W$) – количество способов, реализации данного состояния термодинамической системы. Или иначе, это число микросостояний, реализующих данное макросостояние.

Термодинамическая вероятность всегда больше или равна единице.

Энтропия системы и термодинамическая вероятность связаны между собой формулой Больцмана:

$S=k ln⁡(W) (10),$

где $k$ – постоянная Больцмана.

  1. Формула (10) означает, что энтропия определена натуральным логарифмом количества микросостояний, которые реализуют рассматриваемое макросостояние.
  2. Согласно формуле Больцмана, энтропия – это мера вероятности состояния термодинамической системы.
  3. Говорят, что энтропия – мера беспорядка системы. Это статистическая интерпретация энтропии. Большее количество микросостояний, которое осуществляет макросостояние, соответствует большей энтропии.
  4. Если система находится в состоянии термодинамического равновесия, что соответствует наиболее вероятному состоянию системы, количество микросостояний наибольшее, энтропия в этом случае максимальна.
  5. Поскольку при необратимых процессах энтропия увеличивается, при статистическом толковании это значит, процессы в замкнутой системе проходят в направлении роста количества микросостояний. Это означает, что процессы идут от менее вероятных к более вероятным, до достижения вероятностью максимальной величины.

Замечание 3

Все статистические законы справедливы для систем, которые составлены из огромного количества частиц. Но эти законы могут нарушаться с небольшим числом частиц. Для систем с малым количеством частиц возможны флуктуации, это значит, что энтропия и термодинамическая вероятность состояний замкнутой системы на некотором временном отрезке могут убывать, а не расти или не изменяться.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Однако первое начало термодинамики не дает никаких указаний относительно направления, в котором могут происходить процессы в природе. Также одного первого начала недостаточно для объяснения принципа действия тепловой машины. Необходим еще один принцип, позволяющий судить о направлении процессов, которые могут происходить в действительности.

Все процессы в термодинамике можно разделить на обратимые и необратимые.

Обратимый процесс можно провести как в прямом, так и в обратном направлениях, причем после проведения прямого и обратного процесса система и окружающиетелавозвращаютсявисходноесостояние. Анеобратимый – нельзя.

Если внутренние параметры системы в состоянии равновесия однозначно определяются внешними условиями, то любой квазистатический процесс будет обратимым. Однако в реальности таких идеализированных процессов не бывает, и все природные процессы необратимы.

Круговым процессом или циклом будем называть процесс, в результате которого система, пройдя через ряд состояний, каждый раз возвращается в исходное. Если цикл можно провести как в прямом, так и в обратном направлени-

ях, то он обратимый.

Рассмотрим произвольный цикл, состоящий из двух процессов 1A2 и 2B1, изображенный на рис. 9.1. Найдем работу в этом цикле и его коэффициент полезного действия (КПД).

Работу можно найти двумя способами. Первый способ – по определению:

V2

V1

V2

A = A12 + A21 = ∫PA (V )dV + ∫PB (V )dV = ∫PA (V )dV

V1

V2

V1

P

2

То есть работу можно найти как площадь фигуры,

ограниченной линиями процессов цикла в координатах

A

P-V. Иногда это удобно.

B

Второй способ – из первого начала термодинами-

1

ки для каждого процесса:

0 V1

V2 V

Q12 = U2 – U1 + A12,

Q21 = U1 – U2 + A21.

Рис. 9.1

Сложим левые и правые части этих выражений:

Q12 + Q21 = A12 + A21 = A.

Таким образом, работу в цикле можно найти как сумму всех теплот, полученных и отданных системой в каждом процессе цикла. Для нашего цикла

Q12 > 0, Q21 < 0.

Теперь найдем КПД цикла, то есть отношение работы, совершенной системой в цикле к полному количеству теплоты, полученному системой в этом цикле. Для данного случая

η =

A

=

Q12 + Q21

.

Q

Q

12

12

58

Итак, для нахождения КПД любого цикла надо алгебраическую сумму всех теплот, полученных и отданных в каждом процессе цикла (с учетом знаков), разделить на сумму всех полученных (положительных) теплот:

η =

Qвсех

.

(9.1)

Q+

9.1. Две формулировки второго начала термодинамики. Цикл Карно

Второе начало (закон) термодинамики сформулировали независимо друг от друга немецкий физик Р. Клаузиус и английский физик В. Томсон (получивший за научные заслуги титул лорда Кельвина) в 1850-1851 гг.

Второе начало термодинамики (формулировка Клаузиуса): в природных процессах «теплота не может самопроизвольно переходить от тела менее нагретого к телу более нагретому». Под теплотой здесь понимается внутренняя энергия.

Второе начало термодинамики (формулировка Томсона1): невозможен круговой процесс, единственным результатом которого было бы производство работы за счет уменьшения внутренней энергии теплового резервуара. Под тепловым резервуаром понимают тело или систему тел, обладающую запасом внутренней энергии.

Этот закон утверждает, что невозможно построить вечный двигатель, то есть машину, которая совершала бы работу только за счет охлаждения одного источника тепла без передачи тепла более холодному телу. Другими словами, невозможно все тепло, взятое у нагревателя Q1, перевести в полезную работу А, неизбежно будут тепловые потери Q2, то есть тепло, отданное холодильнику.

нагреватель

нагреватель

Q1>0

Q1<0

А=Q1+Q2>0

А=Q1+Q2<0

рабочее тело

рабочее тело,

например, газ

например, газ

Q2<0

Q2>0

холодильник

холодильник

а)

б)

Рис. 9.2

Упрощенный принцип работы тепловой машины изображен на схеме рис.

9.2, а). КПД такой машины определяется из (9.1) следующим образом:

η =

A

=

Q1 + Q2

=

Q1 −| Q2 |

<1.

(9.1)′

Q

Q

Q

1

1

1

Итак, согласно второму началу термодинамики «по Томсону» КПД любой тепловой машины всегда меньше 100%. Так, КПД дизельных двигателей,

1 Следует отметить, что обе формулировки второго начала эквивалентны. Этот факт имеет строгое доказательство.

59

где рабочим телом является смесь воздуха и паров дизельного топлива, порядка 40%; у карбюраторных двигателей с рабочим телом из воздуха и паров бензина он не превышает 30%. То есть в механическую работу превращается менее половины всей тепловой энергии, выделяющейся при сгорании топлива.

Холодильная машина работает по обратному циклу: отбирает теплоту Q2 у менее нагретого тела и передает теплоту Q1 более нагретому телу, рис. 9.2, б). Самопроизвольно такой процесс невозможен (не позволяет второе начало термодинамики «по Клаузиусу»), поэтому холодильная машина требует внешней работы. Так, в бытовых холодильниках периодически работает двигатель, осуществляющий циркуляцию по трубкам фреона (рабочее тело) – легкоиспаряющейся жидкости. Испарение сопровождается понижением температуры трубок. Понятие КПД холодильной машины физического смысла не имеет, так как работа затрачивается, а не производится. Когда все же ошибочно говорят о таком

КПД, то имеют ввиду КПД прямого цикла, а не обратного.

В технике для оценки эффективности какой-либо

P

1

новой тепловой машины используется идеальная тепло-

вая машина, работающая по циклу Карно. Это обрати-

T1

2

мый цикл, состоящий из двух изотерм (1-2, 3-4) и двух

4

адиабат (2-3, 4-1), рис. 9.3. В изотермическом процессе

T2

3

1-2, проводимом при температуре Т1, газ получает от

0

V

нагревателя тепло Q1 = Q12. В изотермическом процессе

Рис. 9.3

3-4, проводимом при температуре Т2 < Т1, газ отдает хо-

лодильнику тепло Q2 = Q34. В адиабатических процессах

газ не отдает и не получает тепла.

Найдем КПД цикла Карно по формуле (9.1). Для этого сначала определим

количество теплоты в каждом процессе цикла.

1-2 – изотермическое расширение при температуре T1 от объема V1 до V2:

Q

= A

= RT ln

V2

> 0 , так как V2 > V1.

12

12

1

V1

2-3 – адиабатическое расширение от объема V2 до V3:

Q23 = 0;

γ−1

T V γ−1 = T V γ−1;

V

2

T

=

2

.

(9.2)

1

2

2

3

V

T

3

1

3-4 − изотермическое сжатие при температуре T2 от объема V3 до V4:

Q

= A

= RT

ln

V4

= −RT ln

V3

< 0 , так как V3 > V4.

34

34

2

V3

2

V4

4-1 – адиабатическое сжатие от объема V4 до V1:

Q41 = 0;

γ−1

T V γ−1 = T V γ−1;

V

T

1

=

2

.

(9.3)

2

4

1

1

V

4

T

1

Из (9.2) и (9.3) следует

V2

=

V1

, откуда

V2

=

V3

. Тогда из (9.1) КПД цикла

V

V

V

V

4

3

4

1

60

Qвсех

Q

+ Q

T ln

V2

−T ln

V3

V

T

−T

1

2

V

η

к

=

=

12

34

=

1

4

=

1

2

.

Q+

Q

V2

T1 ln

T

12

1

V1

Итак, КПД цикла Карно зависит только от температур нагревателя T1 и

холодильника T2:

T1 −T2

ηк

=

.

(9.4)

T1

Почему тепловую машину, работающую по циклу Карно, называют идеальной? Потому, что КПД тепловой машины, работающей по любому другому циклу, всегда меньше КПД идеальной машины с теми же температурами нагревателя и холодильника. Другими словами, если у тепловой машины температуры нагревателя и холодильника соответственно T1 и T2, ее КПД η никогда не будет больше КПД цикла Карно ηк, определяемого формулой (9.4). Это утверждение имеет в термодинамике строгое доказательство в виде теоремы Карно.

Таким образом, «машина Карно» – это некий теоретический идеал, к которому нужно стремиться на практике. Разрабатывая тепловую машину, зная температуры нагревателя и холодильника, по формуле (9.4) можно оценить максимально возможный КПД этой машины. И иметь в виду, что в реальности он будет, конечно, меньше.

Теорему Карно можно представить в математическом виде

η ≤ ηк;

Q1 + Q2

≤

T1 −T2

;

T

Q

1

1

Q1

+

Q2

≤ 0 .

(9.5)

T

T

1

2

Величину Q/T называют приведенной теплотой.

9.2. Неравенство Клаузиуса. Энтропия

Полученное нами из теоремы Карно неравенство (9.5) называется неравенством Клаузиуса для цикла, в котором температуры нагревателя T1 и холодильника T2 поддерживаются постоянными. Обобщим неравенство на случай, когда эти температуры могут меняться в цикле.

Разобьем цикл (рис. 9.4) на n очень маленьких циклов, похожих на циклы Карно (процессы при постоянной температуре могут быть необратимыми). Это

всегда можно сделать, так как адиабаты не дают вклада

P

в теплопередачу. Возьмем цикл с номером i, «зажатый»

2

между температурами T1i и T2i. Для такого цикла нера-

T1i

A

венство Клаузиуса (9.5) имеет вид

i

Q1i

+

Q2i ≤ 0 ,

1

B

T2i

T

T

1i

2i

где Q1i и Q2i – очень маленькие количества теплоты,

0 V1

V2 V

полученная и отданная в i-м цикле.

Рис. 9.4

61

Суммируя для всех циклов, получим

n

n

∑ TQ1i

+

∑ TQ2i

≤ 0 .

(9.6)

=

1i

1A2

=

2i

2B1

i 1

i 1

Это неравенство Клаузиуса в общем виде: для любого цикла сумма приведенных теплот не может быть больше нуля, а для обратимого равна нулю.

Рассмотрим два случая: первый, когда цикл, изображенный на рис. 9.4, обратимый, второй – необратимый.

Если цикл обратимый, то выполняется равенство (9.6), а обе суммы мож-

но заменить контурными интегралами:

∫ δTQ + ∫ δTQ = 0 ;

∫ δTQ − ∫ δTQ = 0 ;

∫ δTQ = ∫ δTQ .

1A2

2B1

1A2

1B2

1A2

1B2

Таким образом, для обратимого процесса приведенная теплота не зависит от пути перехода из состояния 1 в состояние 2, а зависит только от начального и конечного состояния системы, то есть является функцией состояния системы.

Клаузиус назвал эту функцию состояния термодинамической системы энтропия S. Изменение энтропии при равновесном (квазистатическом) переходе термодинамической системы из состояния 1 в состояние 2 определяется любым из указанных выше интегралов

S = S2 − S1 = ∫

δQ

.

(9.7)

T

1→2

Энтропию еще называют приведенной теплотой и измеряют в Дж/К.

С помощью этой формулы можно найти изменение энтропии для всех рассмотренных нами процессов с идеальным газом. Например, в равновесном адиабатическом процессе энтропия не меняется, так как δQ = 0.

Перейдем ко второму случаю, когда цикл, показанный на рис. 9.4, необратимый. Пусть при этом процесс 1A2 необратимый, а процесс 2B1 обратимый. Тогда в неравенстве Клаузиуса (9.6) первую сумму заменить интегралом нельзя, а вторую можно:

n

TQ1i

∫ δTQ ≤ 0 .

∑

+

=

1i

1A2

2B1

i 1

Используя определение энтропии (9.7), получим

n

S2 − S1 ≥

∑ TQ1i

.

=

1i

1A2

i 1

Если система адиабатически изолированная (замкнутая), то Q1i = 0 для любого i, поэтому

S2 – S1 ≥ 0.

Отсюда следует третья формулировка второго начала термодинамики. Второе начало термодинамики «через энтропию»: энтропия замкнутой

системы при протекании необратимых процессов возрастает. Энтропия системы, находящейся в равновесном состоянии максимальна и постоянна.

62

Для выяснения физического смысла энтропии рассмотрим пример. Пусть в теплоизолированном сосуде вращается маленький пропеллер. Под действием силы сопротивления воздуха он останавливается. Кинетическая энергия переходит в тепло, и температура системы (пропеллер + воздух) повышается от T1 до T2 при постоянном объеме. При этом изменение энтропии воздуха

Sв = ∫

δQ

T2 dT

= νCV ln

T

> 0.

T

= νCV ∫

T

T

2

1→2

T1

1

Изменение энтропии пропеллера

δQ

T2 dT

T

Sп = ∫

T

= mc∫ T

= mcln

2

> 0 .

T

1→2

T1

1

Итак, полная энергия замкнутой системы не изменилась, а энтропия возросла. То есть энергия, не изменяясь количественно, изменилась качественно: механическая энергия упорядоченного движения пропеллера перешла в тепловую энергию хаотического движения молекул. Произошло снижение качества энергии, беспорядок в системе увеличился. Поэтому энтропию можно считать степенью упорядоченности системы: чем больше беспорядок, тем она больше. Итак, в соответствии с законом возрастания энтропии в замкнутой системе при протекании необратимых процессов растет беспорядок.

Вглобальном масштабе происходит то же самое. Поскольку все процессы

внашей Вселенной необратимы, а сама Вселенная – система замкнутая, то энтропия в ней возрастает. Это значит, что беспорядок во Вселенной постепенно нарастает. Если что-то упорядочивается (например, замерзает вода), то общий беспорядок все же увеличивается (при замерзании выделяется тепло, увеличивающее энтропию системы «вода + окружающая среда» в целом). Поэтому Вселенная не могла существовать вечно, иначе в настоящее время не было бы никаких упорядоченных структур.

Заканчивая разговор об энтропии, отметим, что при приближении к абсолютному нулю энтропия системы также стремится к нулю независимо от того, какие значения принимают при этом все параметры, характеризующие состояние системы. Этот закон называют третьим началом термодинамики или теп-

ловой теоремой Нернста.

Вопросы к лекции 9

1.Какие процессы называют обратимыми и необратимыми? Приведите примеры необратимых процессов в природе.

2.Что такое цикл? Как найти работу и КПД цикла?

3.Сформулируйте второе начало термодинамики (две формулировки).

4.Как второе начало объясняет принцип действия тепловой машины?

5.Как найти КПД тепловой машины? Почему невозможен вечный двигатель?

6.Для чего нужна идеальная (теоретическая) машина Карно, которую невозможно сделать практически?

7.Выведите неравенство Клаузиуса в общем виде и рассмотрите частные случаи.

8.Дайте определение энтропии и поясните ее физический смысл.

9.В чем сущность закона возрастания энтропии? Приведите примеры.

63

Соседние файлы в предмете Физика

  • #
  • #
  • #
  • #
  • #
  • #
Источник

Понравилась статья? Поделить с друзьями:
  • Найти как правильно пишутся слова
  • Некрасивые передние зубы как исправить
  • Волосы при осветлении рыжие как исправить
  • Как составить рекуррентную формулу для интеграла
  • Ведьмак 3 как найти золтана в новиграде