Видеоурок 1: Емкость конденсатора — Физика в опытах и экспериментах
Видеоурок 2: Емкость плоского конденсатора. Классификация конденсаторов
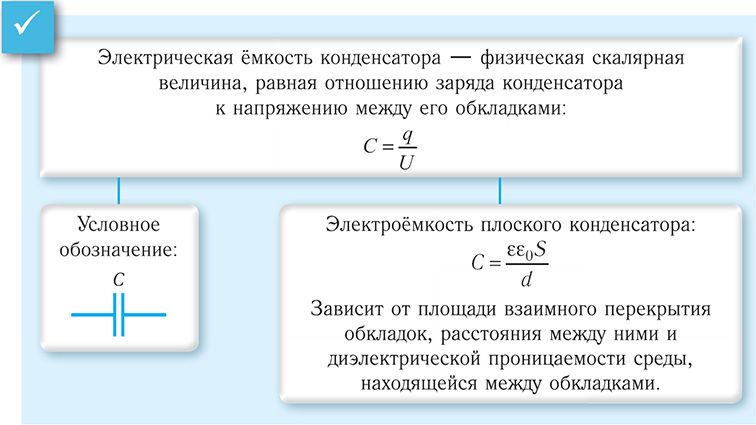
Лекция: Конденсатор. Электроёмкость конденсатора. Электроёмкость плоского конденсатора
Для определения понятия конденсатора, необходимо воспользоваться всеми знаниями по поводу проводников и диэлектриков, поскольку и те, и другие одновременно используются для изготовления конденсаторов.

Во время изучения понятия конденсаторов будем использовать термин «уединенный конденсатор». Он значит, что данное проводящее тело находится вне поля действия других тел. Рассмотрим проводник, у которого имеется какой-то определенный потенциал «фи». Данный потенциал является пропорциональным к величине заряда проводника. Данный коэффициент принято обозначать 1/С. В данном случае величина, что находится в знаменателе, является электрической ёмкостью имеющегося проводника.
Если рассматривать некоторый объемный шар в виде проводника, то его ёмкость можно определить по следующей формуле:
Эпсилон нулевое — это электрическая постоянная.
Судя из данной формулы, можно сделать вывод, что емкость сферического проводника зависит исключительно от внешнего диэлектрика, а также от радиуса сферы, то есть её размера. То есть, чем больше сфера, тем больше её емкость. Иными словами можно сказать, что ёмкость — это некая тара, которая вмещает в себя величину заряда.
Итак,
Ёмкость — это некая ФВ, позволяющая определить величину заряда, необходимую для изменения потенциала проводника на 1 В.
Ёмкость измеряется в фарадах (Ф).
Самым главным для нас сферическим проводником является Земля. Посчитать её емкость достаточно просто. Если принять радиус за 6400 км, а окружающую диэлектрическую среду мы знаем — это воздух, то получим:

Самым простым примером для исследования конденсаторов являются плоские конденсаторы. Структура плоского конденсатора достаточно проста. Он состоит из двух металлических плоскостей (обкладок), которые параллельно расположены друг к другу, и располагаются на некотором расстоянии. Между данными пластинами имеется диэлектрик.
Самым простым примером плоского конденсатора является тот, у которого в виде диэлектрика воздух, то есть Ɛ = 1.
Обе обкладки имеют противоположный заряд -q, +q. Схематически конденсатор изображают следующим образом:
Следует отметить, что поле в конденсаторе показывается линиями, выходящими из положительно заряженной пластины, и входящими в отрицательно заряженную пластину.
Для определения его ёмкости следует воспользоваться следующей формулой:
Как уже говорилось раньше, ёмкость зависит исключительно от геометрических размеров конденсатора, а также от диэлектрика между пластинами.
Содержание
- 1 Как определить емкость конденсатора формула?
- 2 Как зависит емкость конденсатора от расстояния между пластинами?
- 3 Как рассчитать емкость конденсатора при последовательном соединении?
- 4 Что такое электрическая емкость конденсатора?
- 5 Как определить емкость плоского конденсатора?
- 6 Как найти заряд q?
- 7 Как зависит емкость конденсатора от диэлектрика?
- 8 Как изменяется емкость конденсатора при наличии диэлектрика между его обкладками?
- 9 Как определить энергию конденсатора?
- 10 Как изменится емкость конденсатора при последовательном и параллельном соединениях?
- 11 Какие физические величины сохраняются при последовательном соединении конденсаторов?
- 12 Как можно увеличить общую емкость конденсаторов?
- 13 Что характеризует электрическая емкость конденсатора?
- 14 Что показывает электроемкость?
Как определить емкость конденсатора формула?
Общая формула для определения емкости конденсатора с диэлектрической проницаемостью ε (эпсилон) имеет вид: C=ε∙S/(4∙π∙d)∙1,11, пФ. Эта формула удобна для расчетов небольших переменных конденсаторов для радиоприемников.
Как зависит емкость конденсатора от расстояния между пластинами?
Она зависит от площади перекрытия пластин и расстояния между ними, а также от свойств используемого диэлектрика. Чем больше площадь перекрытия пластин (S) и чем меньше расстояние между ними (d), тем больше емкость конденсатора (С): Поделитесь: ← 3.
Как рассчитать емкость конденсатора при последовательном соединении?
Общая емкость равнозначного (эквивалентного) конденсатора C = Q / U = Q / (U1 + U2 + U3), т. е. при последовательном соединении конденсаторов величина, обратная общей емкости, равна сумме обратных величин емкостей отдельных конденсаторов.
Что такое электрическая емкость конденсатора?
Коэффициент пропорциональности С называется электрической ёмкостью, электроёмкостью или просто ёмкостью конденсатора. Электрической ёмкостью конденсатора называется физическая величина, которая численно равна отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.
Как определить емкость плоского конденсатора?
Ёмкость плоского конденсатора находиться по формуле: Где ε0=8,854187817·10 −12 Ф/м — электрическая постоянная, ε — диэлектрическая проницаемость диэлектрика расположенного между обкладками конденсатора, S — площадь обкладки конденсатора, d — расстояние между обкладками.
Как найти заряд q?
Формула нахождения заряда
В соответствии с ней, нужно перемножить силу тока на время его прохождения по проводнику. Количество заряда можно узнать через формулу +-ne, где n служит целым числом, а е равно значению = -1,6*10^-19 Кулон. Обратите внимание!
Как зависит емкость конденсатора от диэлектрика?
По сути — от толщины диэлектрика между заряженными обкладками, если речь идет о конденсаторе. … Тогда мы можем с уверенностью сказать, что емкость конденсатора C зависит от площади перекрытия обкладок A, от расстояния между ними d и от диэлектрической проницаемости диэлектрика e.
Как изменяется емкость конденсатора при наличии диэлектрика между его обкладками?
Ёмкость конденсатора увеличивается с уменьшением диэлектрической проницаемости материала из которого изготовлен диэлектрик между его обкладками.
Как определить энергию конденсатора?
Энергия конденсатора пропорциональна его электроемкости и квадрату напряжения между пластинами. Вся эта энергия сосредоточена в электрическом поле. Энергия поля пропорциональна квадрату напряженности поля.
Как изменится емкость конденсатора при последовательном и параллельном соединениях?
Последовательное и параллельное соединение конденсаторов применяют в зависимости от поставленной цели. При последовательном соединении конденсаторов уменьшается общая емкость и увеличивается общее напряжение конденсаторов. А общее напряжение будет равняться сумме напряжений всех конденсаторов.
Какие физические величины сохраняются при последовательном соединении конденсаторов?
Последовательное соединение конденсаторов
заряды одинаковы, складываются величины, обратные емкости.
Как можно увеличить общую емкость конденсаторов?
Для увеличения ёмкости конденсаторы соединяются параллельно. Для увеличения сопротивления резисторы соединяются последовательно. Вода через трубу с двумя валенками течёт хуже, чем через трубу с одним валенком.
Что характеризует электрическая емкость конденсатора?
2. Что характеризует электроёмкость конденсатора? Электроёмкость характеризует свойство конденсатора накапливать электрические заряды.
Что показывает электроемкость?
И существует некоторая величина, которая показывает способность тела накапливать электрический заряд. … Электроемкость (емкость) – величина, равная отношению заряда переданного проводнику к потенциалу этого проводника. Здесь: – емкость; – переданный заряд; – потенциал, до которого зарядился проводник.
Содержание:
- Плоские конденсаторы
- Конденсатор сферического типа
- Конденсатор цилиндрического типа
- Расчёт емкостных батарей, соединений конденсаторов
Определение 1
Конденсатором называют любые два проводника, разделённые диэлектрическим слоем. Такие проводники должны обладать зарядами одинаковыми по величине, но противоположными по знаку.
Возникающее электрическое поле будет полностью расположено внутри, между проводниками. По этой причине на электрическую ёмкость конденсатора не влияет его внешнее окружение. А на разность потенциалов между пластинами не влияет величина заряда.
Выражение для электроёмкости выглядит так:
$ C=frac{q}{phi_1-phi_2} = frac{q}{U} $
Величины $ {phi_1-phi_2=U}$ определяют разность потенциалов, которая также носит название «напряжение» и обозначается «U». Как следует из определения, ёмкость — положительная величина. Её размер определяется габаритами пластин конденсатора, их взаимным расположением, типом диэлектрика. Форма пластин, конструкция конденсатора создаются таким образом, чтобы максимально снизить влияние на внутреннее поле со стороны любых внешних сил или полей. Электрическое поле конденсатора начинается на обкладке с зарядом «+» и заканчивается на обкладке со знаком «-». Ёмкость конденсаторов измеряют так же, как и ёмкость проводников, в международной системе СИ для этого используют Фарады (Ф). Один Фарад — ёмкость конденсатора, где при заряде 1 Кельвин, разность потенциалов 1 Вольт.
Существуют три основных типа конденсаторов: плоские, сферические, цилиндрические. Вычислить ёмкость можно, если найти напряжение на обкладках и определить величину заряда.
Плоские конденсаторы
Определение 2
Плоский конденсатор — элемент состоящий из двух или нескольких плоских пластин, расположенных друг напротив друга, имеющих одинаковый по величине, но разный по знаку заряд. Чтобы не возникало воздушного разряда, пластины разделяют слоем диэлектрика.
Для вычисления ёмкости плоского конденсатора используется выражение:
$C=frac{epsilonepsilon_0 S}{d}$.
Здесь S — площадь пластин, чем она больше, тем выше ёмкость. Величина зазора между пластинами — d. Чем меньше d, тем больше ёмкость. Диэлектрическая проницаемость — ε. Она также оказывает значительное влияние на величину ёмкости.
Пример 1
Возьмём конденсатор состоящий из двух пластин, между которыми воздух, и определим его ёмкость. Затем поместим между пластинами диэлектрик, параметр ε которого выше, чем у воздуха. Измерения показывают, что ёмкость конденсатора увеличивается существенно, прямо пропорционально повышению диэлектрической проницаемости.
Чаще всего, при создании плоских конденсаторов делают не две пластины, а «пакет» обкладок в несколько слоёв. Электрическая ёмкость такого элемента, имеющего n слоёв, вычисляется с учётом толщины каждого i-го слоя $d_i$, а также диэлектрической проницаемости каждого слоя $ε_i$.
Конденсатор сферического типа
Определение 3
Сферический конденсатор отличается формой обкладок, у него они представляют собой сферы. И внешняя, и внутренняя — обе оболочки выполнены в виде сфер.
В отличии от плоского конденсатора, в сферическом площадь поверхности разнозаряженных пластин отличается. И формула для вычисления ёмкости элемента изменится:
$ C = 4piepsilonepsilon_0frac{R_1 R_2}{R_2-R_1} $,
где $ R_1 $ и $ R_2 $ являются радиусами обкладок.
Конденсатор цилиндрического типа
Отдельная формула используется для вычисления параметров конденсатора цилиндрической формы:
$ C = 2piepsilonepsilon_0 frac{l}{ln{frac{R_2}{R_1}}} $.
В уравнении использованы следующие параметры: l — высота, $R_1 и R_2$ – радиусы пластин. Конденсатор цилиндрического вида выполнен в виде вложенных друг в друга соосных цилиндрических пластин. Они выполнены из проводящего материала, а между ними находится диэлектрик.
Определение 4
Параметр, характеризующий конденсаторы — пробивное напряжение. Эта характеристика показывает минимальную величину напряжения, при которой произойдёт «пробой» диэлектрика. То есть сквозь толщу материала пройдёт сквозной электрический разряд, закорачивающий заряженные пластины.
Значение $U_max$ зависит как от характеристик диэлектрического вещества, его толщины, так и от формы конденсатора.
Расчёт емкостных батарей, соединений конденсаторов
Конденсаторы могут применяться как сами по себе – отдельно по видам, так и в виде групп элементов, соединённых параллельно или последовательно. Комбинирование конденсаторов в электроцепи позволяет с помощью стандартизированных деталей получать любые необходимые значения ёмкостей. При параллельном соединении емкость увеличивается. Если у нас имеется несколько конденсаторов, где $C_i$ — емкость i-го конденсатора, то можно записать для всей системы:
$ C=sum_{i=1}^NC_i $
Когда конденсаторы соединяют последовательно, то результирующая ёмкость будет меньше, чем ёмкость самого маленького конденсатора в системе. Итоговая ёмкость — сумма величин обратных емкости каждого из конденсаторов.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример 2
Покажем на простом примере, как рассчитать емкость плоского конденсатора, если известны площадь его пластин, величина промежутка между ними и тип вещества, заполняющего пространство. Площадь S=1 см2, зазор d=1 мм. Промежуток между пластинами заполнен вакуумом. При таких начальных условиях рассчёт ёмкости будет вестись по формуле:
$C=frac{epsilonepsilon_0 S}{d}$
Выпишем параметры, которые заданы в условии:
ε=1, $ ε_ 0=8,85⋅10^{-12} frac{Ф}{м}$; S=1см2=10 −4 м2; d=1 мм=10 − 3 м.
Применяя их в формуле, получаем выражение следующего вида:
$ С = frac{8,85cdot10^{-12}cdot10^{-4}}{10^{-13}} $
Результат:
$Сapprox 0,9 пФ$
Пример 3
Для конденсатора со сферическими пластинами произведём вычисление напряжённости поля. Величина промежутка между обкладками x = 1 см = 10-2 м. Радиусы обкладок заданы следующим образом: внутренний R1=1 см=10-2 м, внешний R2=3 см=3·10-2 м. Величина напряжения U=103 В.
Заряженные обкладки создают электростатическое поле. Его напряжённость не трудно вычислить, воспользовавшись формулой:
$ E = frac{1}{4piepsilonepsilon_0 r^2} cdotfrac{q}{r^{2}} $,
Удалённость от центра r вычисляем как R1+x.
Заряд внутренней сферической пластины, q, определяем через известные напряжение и ёмкость конденсатора:
q=CU.
Для емкости сферического конденсатора берём формулу:
$ С = 4piepsilonepsilon_0cdotfrac{R_1R_2}{R_2-R_1} $,
где $R_1$ и $R_2$ — радиусы пластин.
Подставим выражение емкости в формулу для напряженности:
$E=frac{1}{4piepsilonepsilon_0 r^2}cdot4piepsilonepsilon_0frac{R_1R_2}{R_2-R_1}$
$=frac{U}{(x+R_1)^2}cdotfrac{R_1R_2}{R_2-R_1}$
Подставляя числовые значения, в результате получим $E=3,45cdot10^4 frac{В}{м}$
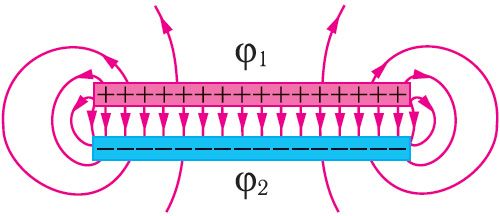
Электроёмкость плоского конденсатора. Если обкладками конденсатора являются две одинаковые параллельные друг другу пластины, то конденсатор называют плоским. Электростатическое поле заряженного плоского конденсатора в основном сосредоточено между его обкладками и является практически однородным. Вблизи краёв пластин однородность поля нарушается, однако этим часто пренебрегают, когда расстояние между пластинами значительно меньше их размеров (рис. 121).
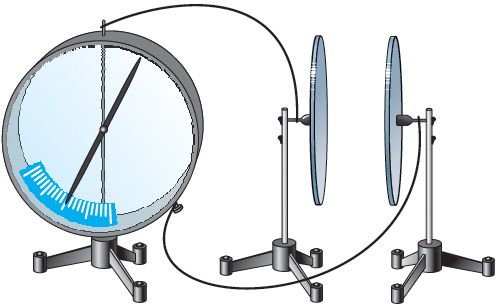
Чтобы установить, от чего зависит электроёмкость плоского конденсатора, проведём несколько опытов. В качестве обкладок конденсатора используем две металлические пластины, расположенные в воздухе на некотором расстоянии параллельно друг другу. Соединим стержень электрометра с одной из пластин, а его корпус с другой (рис. 122). Зарядим конденсатор, подключив его к источнику тока на некоторый промежуток времени. Когда между пластинами конденсатора возникнет напряжение (стрелка электрометра отклонится), отключим его от источника тока.
Если перемещать пластины относительно друг друга, уменьшая площадь их взаимного перекрытия при неизменном расстоянии между ними, то показания электрометра при этом увеличиваются, хотя сообщённый пластинам при зарядке конденсатора заряд не изменяется. Так как напряжение между пластинами увеличивается при уменьшении площади перекрытия пластин конденсатора, то его электроёмкость должна уменьшаться ().
Увеличивая расстояние между пластинами конденсатора, не меняя площади их перекрытия, будем наблюдать возрастание показаний электрометра, т. е. увеличение напряжения между пластинами конденсатора, что возможно при уменьшении его электроёмкости. Значит, чем больше расстояние между пластинами конденсатора, тем меньше его электроёмкость ().
Если между обкладками конденсатора поместить пластину из диэлектрика, например из стекла, то показания электрометра уменьшатся. Напряжение между обкладками в этом случае уменьшается, следовательно, электроёмкость конденсатора увеличивается ().
В СИ коэффициентом пропорциональности между электроёмкостью конденсатора и определяющими её величинами (S, d, ε) является электрическая постоянная .
Результаты экспериментов позволяют записать формулу для определения электроёмкости плоского конденсатора:
где S — площадь одной из обкладок конденсатора (площадь взаимного перекрытия обкладок конденсатора); d — расстояние между обкладками; ε — диэлектрическая проницаемость среды, находящейся между его обкладками.
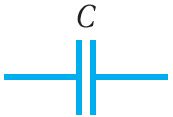
Условное изображение конденсатора постоянной электроёмкости на электрических схемах представлено на рисунке 123.
От теории к практике
1. Один из двух уединённых проводящих шаров сплошной, а второй — имеет внутри полость. Если диаметры шаров одинаковые, то какой из них имеет большую электроёмкость?
2. Расстояние между обкладками плоского воздушного конденсатора уменьшили в два раза. Если при этом заряд конденсатора остался прежним, то изменились ли напряжение между его обкладками и напряжённость поля? Если изменились, то как?
Интересно знать
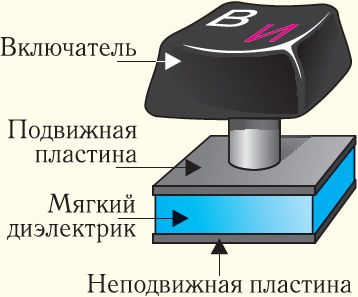
Зависимость электроёмкости конденсатора от расстояния между его обкладками используют в схемах кодирования клавиатуры персонального компьютера. Под каждой клавишей находится конденсатор, электроёмкость которого изменяется при нажатии на клавишу. Микросхема, подключённая к каждой клавише, при изменении электроёмкости выдаёт кодированный сигнал, соответствующий данной букве (рис. 124).
1. Что представляет собой конденсатор? Каково его назначение?
2. Какой процесс называют зарядкой конденсатора? Разрядкой конденсатора?
3. Что понимают под зарядом конденсатора?
4. Какую физическую величину называют электроёмкостью конденсатора? В каких единицах её измеряют?
5. От чего зависит электроёмкость плоского конденсатора?
6. Плоский воздушный конденсатор присоединён к источнику постоянного тока. Изменятся ли заряд конденсатора и напряжение на нём, если пространство между обкладками конденсатора заполнить диэлектриком?
Заряды взаимодействуют друг с другом в различных средах с различной силой, определяемой законом Кулона. Свойства этих сред определяет величина, называемая диэлектрической проницаемостью.
Содержание
- 1 Что такое диэлектрическая проницаемость
- 2 Природа диэлектрической проницаемости
- 3 Диэлектрическая проницаемость различных веществ
- 4 Диэлектрическая проницаемость и ёмкость конденсатора
- 5 Диэлектрическая проницаемость и потери в диэлектрике
- 6 Зависимость диэлектрической проницаемости от сторонних факторов
Что такое диэлектрическая проницаемость
Согласно закону Кулона, два точечных неподвижных заряда q1 и q2 в вакууме взаимодействуют между собой с силой, заданной формулой Fкл=((1/4)*π* ε0)*(|q1|*|q2|/r2), где:
- Fкл – сила Кулона, Н;
- q1, q2 – модули зарядов, Кл;
- r – расстояние между зарядами, м;
- ε0 – электрическая постоянная, 8,85*10-12 Ф/м (Фарад на метр).
Если взаимодействие происходит не в вакууме, в формулу входит ещё одна величина, определяющая влияние вещества на силу Кулона, и запись закона Кулона выглядит так:
F=((1/4)*π* ε0* ε)*(|q1|*|q2|/r2).
Эта величина обозначается греческой буквой ε (эпсилон), она безразмерна (не имеет единицы измерения). Диэлектрическая проницаемость является коэффициентом ослабления взаимодействия зарядов в веществе.
Часто в физике диэлектрическая проницаемость используется совместно с электрической постоянной, в этом случае удобно ввести понятие абсолютной диэлектрической проницаемости. Она обозначается εa и равна εa= ε0* ε. В этом случае абсолютная проницаемость имеет размерность Ф/м. Обычную проницаемость ε также называют относительной, чтобы отличить ее от εa.
Природа диэлектрической проницаемости
В основе природы диэлектрической проницаемости лежит явление поляризации под действием электрического поля. Большинство веществ в целом электрически нейтральны, хотя и содержат заряженные частицы. Эти частицы расположены в массе вещества хаотично и их электрические поля в среднем нейтрализуют друг друга.
В диэлектриках находятся, в основном связанные заряды (их называют диполями). Эти диполи условно представляют собой связки из двух разноименных частиц, которые по толщине диэлектрика ориентированы спонтанно и в среднем создают нулевую напряженность электрического поля. Под действием внешнего поля диполи стремятся сориентироваться согласно приложенной силе. В результате создается дополнительное электрическое поле. Сходные явления происходят и в неполярных диэлектриках.
В проводниках процессы похожие, только там имеются свободные заряды, которые под действием внешнего поля разделяются и также создают собственное электрическое поле. Это поле направлено навстречу внешнему, экранирует заряды и снижает силу их взаимодействия. Чем больше способность вещества к поляризации, тем выше ε.
Диэлектрическая проницаемость различных веществ
Разные вещества имеют различную диэлектрическую проницаемость. Значение ε для некоторых из них приведено в таблице 1. Очевидно, что эти значения больше единицы, поэтому взаимодействие зарядов, по сравнению с вакуумом, всегда уменьшается. Также надо заметить, что для воздуха ε немногим более единицы, поэтому взаимодействие зарядов в воздухе практически не отличается от взаимодействия в вакууме.
Таблица 1. Значения электрической проницаемости для различных веществ.
Диэлектрическая проницаемость и ёмкость конденсатора
Знание величины ε на практике важно, например, при создании электрических конденсаторов. Их ёмкость зависит от геометрических размеров обкладок, расстояния между ними и диэлектрической проницаемости диэлектрика.
Если надо получить конденсатор повышенной ёмкости, то увеличение площади обкладок ведет к увеличению габаритов. На уменьшение расстояния между электродами также имеются практические ограничения. В этом случае может помочь применение изолятора с увеличенной диэлектрической проницаемостью. Если применить материал с более высоким ε, можно кратно уменьшить размер обкладок или увеличить расстояние между ними без потерь электрической ёмкости.
В отдельную категорию выделяют вещества, называемые сегнетоэлектриками, у которых при определенных условиях возникает спонтанная поляризация. В рассматриваемой области для них характерны два момента:
- большие значения диэлектрической проницаемости (характерные значения — от сотен до нескольких тысяч);
- возможность управлять величиной диэлектрической проницаемости путем изменения внешнего электрического поля.
Эти свойства используются для изготовления конденсаторов большой ёмкости (за счёт увеличенных значение диэлектрической проницаемости изолятора) с небольшими массогабаритными показателями.
Такие устройства работают только в низкочастотных цепях переменного тока – при увеличении частоты их диэлектрическая проницаемость падает. Другое применение сегнетоэлектриков – конденсаторы переменной ёмкости, чьи характеристики меняются под действием приложенного электрического поля с изменяющимися параметрами.
Диэлектрическая проницаемость и потери в диэлектрике
Также от значения диэлектрической проницаемости зависят потери в диэлектрике – это та часть энергии, которая теряется в диэлектрике на его нагрев. Для описания этих потерь обычно применяется параметр tg δ – тангенс угла диэлектрических потерь. Он характеризует мощность диэлектрических потерь в конденсаторе, у которого диэлектрик изготовлен из материала с имеющимся tg δ. А удельная мощность потерь для каждого вещества определяется формулой p=E2*ώ*ε0*ε*tg δ, где:
- p – удельная мощность потерь, Вт;
- ώ=2*π*f – круговая частота электрического поля;
- E – напряженность электрического поля, В/м.
Очевидно, что чем выше диэлектрическая проницаемость, тем выше потери в диэлектрике при прочих равных условиях.
Зависимость диэлектрической проницаемости от сторонних факторов
Следует заметить, что значение диэлектрической проницаемости зависит от частоты электрического поля (в данном случае – от частоты напряжения, приложенного к обкладкам). С ростом частоты значение ε у многих веществ падает. Этот эффект ярко выражен для полярных диэлектриков. Объяснить это явление можно тем, что заряды (диполи) перестают успевать следовать за полем. У веществ, для которых характерна ионная или электронная поляризация, зависимость диэлектрической проницаемости от частоты мала.
Поэтому так важен подбор материалов для выполнения диэлектрика конденсатора. То, что работает на низких частотах, не обязательно позволит получить качественную изоляцию на высоких. Чаще всего на ВЧ в качестве изолятора применяют неполярные диэлектрики.
Также диэлектрическая проницаемость зависит от температуры, причем у разных веществ по-разному. У неполярных диэлектриков она падает с ростом температуры. В этом случае для конденсаторов, выполненных с применением такого изолятора, говорят об отрицательном температурном коэффициенте ёмкости (ТКЕ) – ёмкость с ростом температуры падает вслед за ε. У других веществ проницаемость с ростом температуры увеличивается, и можно получить конденсаторы с положительным ТКЕ. Включив в пару конденсаторы с противоположными ТКЕ, можно получить термостабильную ёмкость.
Понимание сущности и знание значения диэлектрической проницаемости различных веществ важно для практических целей. А возможность управлять уровнем диэлектрической проницаемости даёт дополнительные технические перспективы.