Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.
Обозначение угловой скорости: ω (омега).
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.
С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:
Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.
Быстрота изменения угла φ (перемещения плоскости П из положения П1 в положение П2) – это и есть угловая скорость:
Приняв вектор k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:
- если задан угол поворота φ за единицу времени:
- если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
Размерности угловой скорости:
- Количество оборотов за единицу времени [об/мин], [c-1].
- Угол поворота за единицу времени [рад/с].
Определение угловой скорости
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.
Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.
Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.
Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.
Другие примеры решения задач >
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Обозначение: ε (Эпсилон)
Единицы измерения углового ускорения: [рад/с2], [с-2]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
Расчет углового ускорения
Пример: По заданному значению касательной составляющей полного ускорения aτ точки B, расположенной на расстоянии r от центра вращения колеса.
Требуется определить величину и направление углового ускорения колеса ε, если aτ = 10 м/с2, r = 50 см.
Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.
Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
ω = 1,5 с-1 = 9,42 рад/с.
Смотрите также:
- Примеры расчета угловой скорости и ускорения
- Скорости и ускорения точек вращающегося тела
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Движение по окружности
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → — радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
iSopromat.ru
Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела:
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.
Обозначение: ω (омега).
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
- если известно количество оборотов n за единицу времени t:
- если задан угол поворота φ за единицу времени:
- Количество оборотов за единицу времени [об/мин], [c -1 ].
- Угол поворота за единицу времени [рад/с].
Быстрота изменения угла φ (перемещения из положения П1 в положение П2) – это и есть угловая скорость:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
Приняв k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Единицы измерения углового ускорения: [рад/с 2 ], [с -2 ]
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
-
равномерное вращение ( ω — const)
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
http://zaochnik.com/spravochnik/fizika/kinematika/dvizhenie-po-okruzhnosti/
Если
источник выдает независимые отсчеты
сигнала Х(t)
в дискретные моменты времени со скоростью
,
где интервал дискретизации
(
– полоса частот сигнала X(t)),
то эпсилон-производительность источника
(эпсилон-энтропия, приходящаяся на
единицу времени)
(4.11)
Если
время непрерывное, то
(4.12)
Максимальное
значение эпсилон-производительность
источника имеет, когда сигнал X(t)
является гауссовским (4.19):
(4.13)
(4.14)
За
время Т
существования
сигнала максимальный объем V
информации,
выданной источником, составит
(4.15)
Объем
сигнала – это максимальное количество
информации, которое сигнал может
переносить.
4.6. Дифференциальная энтропия
Источники
информации, множество возможных состояний
которых составляют континуум, называют
непрерывными.
Во
многих случаях они преобразуются в
дискретные посредством использования
устройств дискретизации и квантования.
Вместе с тем существует немало и таких
систем, в которых информация передаётся
и преобразуется непосредственно в форме
непрерывных сигналов. Примерами могут
служить системы телеизмерений с частотным
разделением сигналов.
Основные
информационные характеристики источников
непрерывных сообщений следующие:
энтропия, условная энтропия,
эпсилон-энтропия, эпсилон-производительность,
избыточность, объём информации.
Формулу
для энтропии источника непрерывных
сообщений получают путем предельного
перехода из формулы для энтропии
дискретного источника. С этой целью
разобьём диапазон изменения непрерывной
случайной величины Х,
характеризующейся плотностью распределения
вероятностей W(X),
на конечное число m
малых
интервалов шириной Δx.
При
реализации любого значения х,
принадлежащего интервалу [xi,
xi+Δx],
будем считать, что реализовалось значение
xi
дискретной
случайной величины Х.
Поскольку Δx
мало,
то вероятность
реализации
значениях
из
интервала [xi,
xi+Δx],
равна
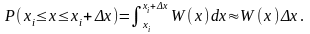
Тогда
энтропия дискретной случайной величины
X
может
быть записана в виде
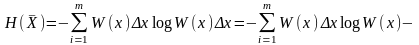
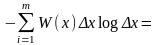

так
как
.
По
мере уменьшения
все больше приближается к вероятности
P(xi),
равной нулю, а свойства дискретной
величины
–
к свойствам непрерывной случайной
величины Х.
В
результате предельного перехода при
получено
(4.16)
Первый
член выражения (4.16) зависит только от
закона распределения непрерывной
случайной величины Х
и
имеет такую же структуру, как энтропия
дискретного источника. Второй член
стремится
к бесконечности, это полностью
соответствует интуитивному представлению
о том, что неопределенность выбора из
бесконечно большого числа возможных
состояний (значений) бесконечно велика.
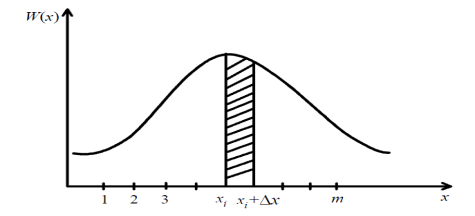
Рис.
4.6. Зависимость плотности распределения
вероятностей случайной величины
Чтобы
избавить теорию от бесконечности,
имеется единственная возможность –
ввести относительную меру неопределенности
исследуемой непрерывной случайной
величины Х
по
отношению к заданной Х0
. В качестве заданной величины Х0
возьмем непрерывную случайную величину,
равномерно распределенную на интервале
с шириной
.
Тогда её плотность вероятности W(X0)
=
1/е,
а энтропия
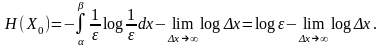
Положив
для простоты записи
=
1, составим разность
(4.17)
которая
показывает, насколько неопределенность
непрерывной случайной величины Х
с
законом распределения W(X)
больше [
]
или
меньше
неопределенности
случайной величины, распределенной
равномерно на интервале
=
1. Поэтому величину
(4.18)
называют
относительной дифференциальной энтропией
или просто дифференциальной энтропией
непрерывного источника информации
(непрерывного распределения случайной
величины Х).
В отличие от энтропии источников
дискретных сообщений
может
принимать положительные, отрицательные
и нулевые значения. Величиной
можно
характеризовать информационные свойства
источников непрерывных сообщений.
Аналогично,
используя операции квантования и
предельного перехода, найдем выражение
для условной энтропии непрерывного
источника сообщений.
(4.19)
Обозначим
первый член через

(4.20)
Эта
величина конечна и называется относительной
дифференциальной условной энтропией,
или просто дифференциальной условной
энтропией непрерывного источника. Она
характеризует неопределенность выбора
непрерывной случайной величины Х
при
условии, что известны результаты
реализации значений другой статистически
связанной с ней непрерывной случайной
величины Y,
и по сравнению со средней неопределенностью
выбора случайной величины Х0,
изменяющейся в диапазоне, равном единице,
и имеющей равномерное распределение
вероятностей.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Download Article
Download Article
Maxwell’s Equations, along with describing how the electric field 

Steps
-
1
Begin with Maxwell’s Equations in vacuum. In vacuum, charge density
and current density
-
2
Take the curl of both sides of Faraday’s Law.
- Note that partial derivatives commute with each other, given well-behaved functions.
Advertisement
-
3
Substitute the Ampere-Maxwell Law.
-
4
Rewrite the wave equation in one dimension.
-
5
-
6
Substitute these equations back into the wave equation. Note that the
expressions cancel out.
-
7
Arrive at the answer.
- The expression on the right happens to equal the speed of light. In fact, light does not only travel at the speed of electromagnetic waves, it is an electromagnetic wave.
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Thanks for submitting a tip for review!
About This Article
Thanks to all authors for creating a page that has been read 49,591 times.
Reader Success Stories
-
«This shows that a E-M wave travels at c, later it was stated by James Clerk Maxwell light is a E-M wave if and only…» more
















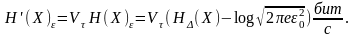

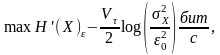

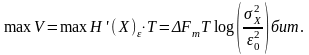
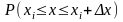


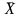
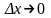







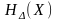
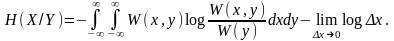





![{begin{aligned}-E_{0}left({frac {2pi }{lambda }}right)^{{2}}&=mu _{0}epsilon _{0}left[-E_{0}left({frac {2pi v}{lambda }}right)^{{2}}right]\1&=mu _{0}epsilon _{0}v^{{2}}end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd84ac7ce14d7f6c53b1b00e08dc2bdbcc37e495)
