Как найти эпсилон в физике формула

Содержание:

При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с  точностью до сантиметра, размеры дома, стадиона – с точностью до метра.

Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.

При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.

Пример:

Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).

Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением 
шкалы линейки совпадает второй край стола  (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)

Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.  

Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения 
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: .  То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой  (эпсилон): 

     (5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения –  плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 0,5) мм — Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.

На точность измерения влияет много факторов, в частности:

1. При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
2. Не вполне ровно установили рулетку.
3. Наша рулетка является копией эталона и может несколько отличаться от оригинала.

Все это необходимо учитывать при проведении измерений.

Итоги:

• Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
• Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора. 
• Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:   и указывает на качество измерения. Ее можно выразить в процентах.

Измерительные приборы

Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.

Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.

Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.

Как определяют единицы длины и времени

В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.

Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).

Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.

Можно ли расстояние измерять годами

Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!

Что надо знать об измерительных приборах

Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?

Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.

Как определить цену деления шкалы? Для этого необходимо:

1. выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
2. подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
3. вычесть из большего значения меньшее (4 см — 3 см = 1 см) и результат разделить на число делений.

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2: 

А какими линейкой и мензуркой можно измерить точнее?

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.

Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше  Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы ), мензуркой 2 — с точностью до 1 мл (сравните с ценой деления ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.

Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.

Главные выводы:

1. Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
2. Цена деления шкалы равна значению наименьшего деления шкалы.
3. Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.

Для любознательных:

В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.

• Заказать решение задач по физике

Пример решения задачи

Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:

1) Цена деления нижней шкалы:

Цена деления средней шкалы: 

Цена деления верхней шкалы:

2) Определенный но нижней шкале с точностью до 10° определенный по средней шкале с точностью до 5° определенный по верхней шкале с точностью до 1°

Электрическая постоянная (ранее также носила название диэлектрической постоянной) — физическая константа, скалярная величина, входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона, при записи их в рационализованной форме, соответствующей Международной системе единиц (СИ) [1] .

Иногда, используя устаревшую терминологию, называют электрической (или диэлектрической) проницаемостью вакуума [2] . Измеряется в фарадах, делённых на метр.

Содержание

Определение [ править | править код ]

По определению в СИ электрическая постоянная ε 0 <displaystyle varepsilon _<0>> связана со скоростью света c <displaystyle c> и магнитной постоянной μ 0 <displaystyle mu _<0>> соотношением [1]

ε 0 = 1 μ 0 c 2 . <displaystyle varepsilon _<0>=<frac <1><mu _<0>c^<2>>>.>

Численное значение [ править | править код ]

В Международной системе единиц [ править | править код ]

До изменения СИ 2018—2019 годов [ править | править код ]

Поскольку в СИ для магнитной постоянной было справедливо точное равенство μ 0 = 4 π × 10 − 7 <displaystyle mu _<0>=4pi imes 10^<-7> > Гн/м, то для электрической постоянной выполнялось соотношение

ε 0 = 1 4 π c 2 ⋅ 10 7 <displaystyle varepsilon _<0>=<frac <1><4pi c^<2>>>cdot 10^<7>> м/Гн, [3]

также являвшееся точным.

Учитывая, что скорости света в СИ приписано точное значение, по определению равное 299 792 458 м/с , из последнего соотношения следует численное значение ε 0 <displaystyle varepsilon _<0>> в СИ:

ε 0 = 1 4 π ⋅ 299792458 2 × 10 − 7 <displaystyle varepsilon _<0>=<frac <1><4pi cdot 299792458^<2> imes 10^<-7>>>> Ф/м ≈ 8,85418781762039 · 10 −12 Ф·м −1 .

Или, выражая то же через основные единицы СИ,

ε ≈ 8,85418781762039 · 10 −12 м −3 ·кг −1 ·с 4 ·А 2 .

После изменений СИ 2018—2019 годов [ править | править код ]

С 2019 года вступили в силу изменения в СИ, включающие, в частности, переопределение ампера на основе фиксации численного значения элементарного заряда. Это привело к тому, что значение электрической постоянной стало экспериментально определяемой величиной, хотя численно её значение осталось прежним с высокой точностью. Значение электрической постоянной, рекомендованное CODATA [4] :

ε = 8,8541878128(13)· 10 −12 м −3 ·кг −1 ·с 4 ·А 2 , или Ф·м −1 .

В системе СГС [ править | править код ]

В системе СГС электрическая постоянная как коэффициент, связывающий напряжённость и индукцию электрического поля в вакууме, также может быть введена. При этом в различных вариантах системы СГС электрическая постоянная имеет разную размерность и значение. Конкретно, Гауссова система единиц и система СГСЭ построены так, что электрическая постоянная безразмерна и равна 1, а в системе СГСМ она равна ε = 1/c 2 ≈ 1,11265005605362 · 10 −21 с 2 ·см −2 .

Некоторые уравнения электродинамики в СИ [ править | править код ]

В материальных уравнениях, в вакууме, через электрическую постоянную связаны вектор электрической индукции D <displaystyle mathbf > и вектор напряжённости электрического поля E <displaystyle mathbf > :

D = ε 0 E . <displaystyle mathbf =varepsilon _<0> mathbf .>

Она также входит в запись закона Кулона (тоже в вакууме):

F 12 = 1 4 π ε 0 ⋅ q 1 q 2 r 12 2 r 12 r 12 . <displaystyle mathbf _<12>=<frac <1><4pi varepsilon _<0>>>cdot <frac <1>q_<2>><12>^<2>>> <frac <mathbf _<12>><12>>>.>

При использовании СИ произведение электрической постоянной на относительную диэлектрическую проницаемость называют абсолютной диэлектрической проницаемостью.

Комментировать

12 679 просмотров

Adblock
detector

(Древне)греческий алфавит
Αα	Альфа	Νν	Ню
Ββ	Бета	Ξξ	Кси
Γγ	Гамма	Οο	Омикрон
Δδ	Дельта	Ππ	Пи
Εε	Эпсилон	Ρρ	Ро
Ζζ	Дзета	Σσς	Сигма
Ηη	Эта	Ττ	Тау
Θθ	Тета	Υυ	Ипсилон
Ιι	Йота	Φφ	Фи
Κκ	Каппа	Χχ	Хи
Λλ	Лямбда	Ψψ	Пси
Μμ	Мю	Ωω	Омега
История
Архаические локальные варианты[en] Ϝϝ · Ͷͷ · Ͱͱ · Ϻϻ · Ϙϙ · Ͳͳ
Диакритики[en] · Лигатуры (ϛ, ϗ)
Цифры Ϛϛ (6) · Ϟϟ (90) · Ϡϡ (900)
В других языках
Арнаутский: Ϳϳ Бактрийский: Ϸϸ Коптский
Похожие темы
Научные символы[en]
Ε , ε (название: э́псилон, греч. έψιλον ) — 5-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 5. Происходит от финикийской буквы — хе. От буквы «эпсилон» произошли латинская E и кириллические Е, Ё, Є и Э. Название «эпсилон» (греч. Ε ψιλόν — «е простое») было введено для того, чтобы отличать эту букву от созвучного сочетания αι. Использование Заглавная буква эпсилон не используется как символ, поскольку пишется так же, как и заглавная латинская буква E. В различных дисциплинах при помощи строчной буквы ε обозначаются: в математическом анализе — положительное сколь угодно малое вещественное число; см. примеры в статье Предел последовательности; в алгебре — предельное порядковое число последовательности ω , ω ω , ω ω ω , … ,omega ^>,dots >. в теории множеств — отношение принадлежности элемента множеству (такое обозначение является устаревшим, сейчас для той же цели используется символ ∈); в тензорном исчислении — символ Леви-Чивиты; в теории автоматов — эпсилон-переход; в физике — угловое ускорение; коэффициент экстинкции оптического поглощения; проводимость среды; электронный захват; относительное удлинение; диэлектрическая проницаемость среды; энергия активации; ЭДС; ε — электрическая постоянная; тензор деформации. в астрономии — пятая (как правило) по яркостизвезда в созвездии; в программировании — точность численного типа данных (наименьшее положительное значение eps, для которого будет соблюдаться неравенство 1 + eps > 1); в информатике — пустая строка; в фонетике — неогубленный гласный переднего ряда средне-нижнего подъёма; в теории метаболического контроля — эластичность фермента; в железнодорожных дисциплинах — коэффициент съёма.
Современный греческий алфавит	Альфа (Α α) Бета / Вита (Β β) Гамма (Γ γ) Дельта (Δ δ) Эпсилон (Ε ε) Дзета / Зита (Ζ ζ) Эта / Ита (Η η) Тета / Фита (Θ θ) Йота (Ι ι) Каппа (Κ κ) Лямбда (Λ λ) Мю / Ми (Μ μ) Ню / Ни (Ν ν) Кси (Ξ ξ) Омикрон (Ο ο) Пи (Π π) Ро (Ρ ρ) Сигма (Σ σ ς) Тау / Таф (Τ τ) Ипсилон (Υ υ) Фи (Φ φ) Хи (Χ χ) Пси (Ψ ψ) Омега (Ω ω) Дигамма (Ϝ ϝ) Дигамма памфилийская (Ͷ ͷ) Хета (Ͱ ͱ) Сан (Ϻ ϻ) Коппа архаичная (Ϙ ϙ) Коппа современная (Ϟ ϟ) Сампи архаичная (Ͳ ͳ) Сампи современная (Ϡ ϡ)
Буквы для других языков	Йот (Ϳ ϳ) Шо (Ϸ ϸ) Стигма (Ϛ ϛ) Кай / Кэ (Ϗ ϗ)
Фонетические буквы
Буквы для арнаутского диалекта
Альтернативные и устаревшие формы
Диакритические знаки	Что такое Wiki.sc Вики является главным информационным ресурсом в интернете. Она открыта для любого пользователя. Вики это библиотека, которая является общественной и многоязычной. Основа этой страницы находится в Википедии. Текст доступен по лицензии CC BY-SA 3.0 Unported License. Эпсилон зависит от вида материала, его значение ищут в таблице. Er = Cx/C0 Если нужно, могу сказать, где можно увидеть таблицу Другие вопросы из категории не более чем на. находящемуся в воздухе заряда 2*10^-7 Кл его потенциал оказался равным 18 Кб. определите радиус шара Читайте также Энергетическая характеристика электрического поля. 4.Чему равна работа сил электрического поля при перемещении заряда перпендикулярно силовым линиям поля? 5. Как связана работа с потенциалами начальной и конечной точек траектории? 6. Как называют поверхности равного потенциала? 7. Как называют разность потенциалов между двумя точками поля? 8. Как направлен вектор напряженности эл.поля относительно эквипотенциальной поверхности? 9. Как связаны напряжение и напряженность электростатического поля? 10. Чему равен потенциал поля точечного заряда (формула)? 3) увеличивается или уменьшается в зависимости от изменения объема 4) не изменяется Каково давление сжатия воздуха массой 12 кгв баллоне объемом 20 лпри 17оС? Каково давление азота плотностью 2,8 кг/м3, если его температура в сосуде равна 400 К? Какова молярная масса газа массой 0,017 г, находящегося в сосуде объемом 10 л под давлением 2.105Па и температурой 400К? Какое количество газа содержится в сосуде объемом 8,31 м3 под давлением 105Па и температуре 100К? Найдите среднюю кинетическую энергию поступательного движения молекул идеального газа при нормальных условиях. Какова среднеквадратичная скорость молекул массой 3.10-26 кг каждая, если они создают давление 105 Па и их концентрация равна 10 25м-3? 1) 10-3 м/с 2) 6.102м/с 3) 103м/с 4) 106 м/с Чему равна молярная газовая постоянная R, если плотность насыщенного водяного пара при 100оС и нормальном давлении равна 0,59 кг/м3? 1) 8,31 Дж/моль.К 2) 8,21 Дж/моль.К 3) 8,41 Дж/моль.К 4) 8,51 Дж/моль.К Какова температура газа по Цельсию, если по Кельвину она равна 273К? 2)Чему равна жесткость пружины, если скрепленное с ней тело массой 30 г совершает за 1 мин 300 колебаний? 3) Маятник, который на Земле совершал свободные колебания с частотой 0,5 Гц, был доставлен космонавтами на Луну. С какой частотой маятник будет колебаться на поверхности Луны, где ускорение свободного падения в 6 раз меньше, чем на Земле? прошу помогите решить эти задачи, при многом буду благодарен 2)чему равен импульс во время столкновения с землей 3)с какой высоты упал шар 4) чему равна полная механич энергия 2)Тело массой 6 кг движется со скоростью 2м/с.Чему равна кинетическая энергия тела? “>

Электрический заряд

Закон Кулона

Постоянная Кулона

Относительная диэлектрическая проницаемость

Электрическое поле

Электрическое поле точечного заряда в вакууме

Электрическое поле точечного заряда в окружающей среде

Электрическое поле вне заряженной сферы

Электрическое поле вне заряженной сферы

Электрическое поле бесконечной заряженной плоскости

Электрическое поле бесконечной заряженной плоскости

Электрическое поле конденсатора

Работа в электрическом поле

Потенциальная энергия системы двух точечных зарядов

Работа в электрическом поле — разность потенциальных энергий

Потенциал электростатического поля

Напряжение — разность потенциалов

Работа переноса заряда

Потенциал электростатического поля вокруг точечного заряда

Напряжённость электростатического поля

Результирующее электрическое поле

Электрический момент

Электрическая ёмкость

Электрическая ёмкость шара

Электрическая ёмкость двух проводников

Электрическая ёмкость плоского конденсатора

Электрическая ёмкость сферического конденсатора

Потенциальная энергия заряженного плоского конденсатора

Потенциальная энергия заряженного плоского конденсатора

Потенциальная энергия заряженного плоского конденсатора

Потенциальная энергия заряженного плоского конденсатора

Потенциальная энергия заряженного плоского конденсатора

Потенциальная энергия заряженного плоского конденсатора

Потенциальная энергия заряженного плоского конденсатора

Плотность энергии электрического поля

Плотность энергии электрического поля

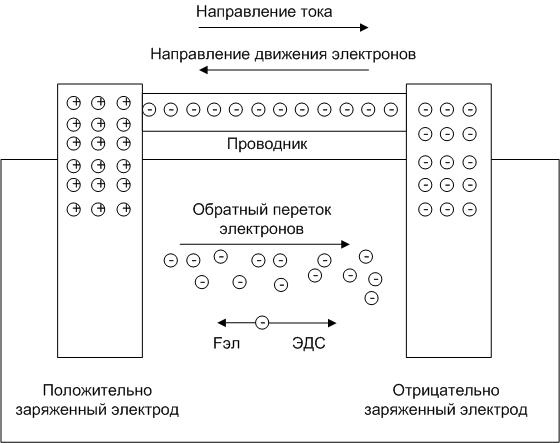
Чтобы в какой-либо среде (металле, растворе, ионизированном газе и т.п.) протекал электрический ток в течение продолжительного времени, недостаточно наличия свободных носителей заряда и электрического поля. Еще потребуется сила, которая будет разделять заряды в направлении, противоположном направлению электрического поля.

Понятие ЭДС и единица измерения

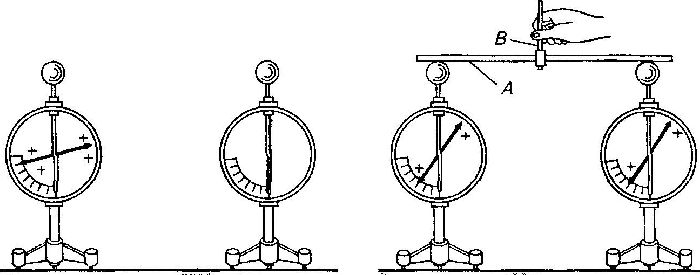
Если имеется заряженный предмет и соединить его с электрически нейтральным (или противоположно заряженным предметом), некоторое время в цепи будет существовать ток. Как только все свободные электроны перейдут от одного тела к другому, и заряды уравняются, ток прекратится.

Это можно увидеть на примере школьного опыта с двумя электроскопами. Один из них заряжен (например, положительно), а другой заряда не имеет. Если их соединить металлическим стержнем, то заряды перейдут от одного прибора к другому. Количество зарядов уравновесится, потенциалы электроскопов станут равными, электрическое поле прекратит действие на электроны, и ток перестанет течь.

Чтобы ток продолжался, надо носители зарядов из второго электроскопа перенести обратно в первый. Для этого нужна сторонняя сила, действующая против направления электрического поля. Такая сила называется ЭДС. Расшифровка этого сокращения – электродвижущая сила.

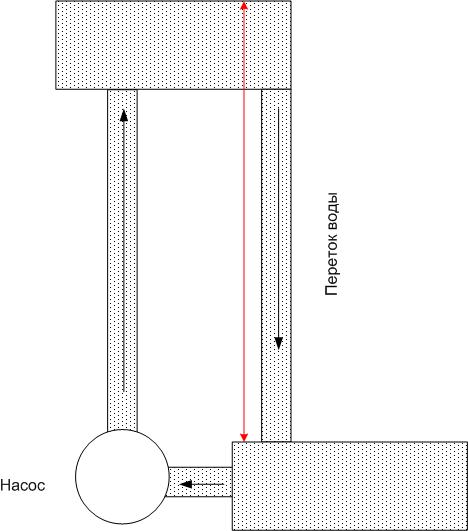
Можно провести аналогию с водой. Если есть два бассейна, один из которых находится выше другого, то вода может перетекать из верхнего водоема в нижний. Но как только запас воды закончится, переток прекратится. Чтобы он продолжался, надо воду из нижнего бассейна перекачивать обратно в верхний (например, с помощью насоса).

ЭДС обозначается греческой буквой ε (эпсилон), а иногда E. Измеряется ЭДС, как и напряжение, в вольтах (1 В). Понятие электродвижущей силы является не очень удачным – сила не измеряется в вольтах. Но этот термин укоренился и широко применяется.

Из-за сходства единиц измерения часто происходит путаница ЭДС и напряжения. Эти термины регулярно подменяются друг с другом. В некоторых случаях действительно принципиальной разницы нет, но в целом эти понятия различны.

В видео простыми словами объясняется чем отличаются ЭДС и напряжение

Где и как образуется электродвижущая сила

Электродвижущая сила образуется в источнике питания. Это необходимое условие существования разности потенциалов на выходных клеммах такого источника. Образовываться ЭДС может по-разному, в зависимости от устройства источника.

Виды ЭДС

Электродвижущая сила может быть различной природы (но всегда неэлектрической). В зависимости от типа источника питания ЭДС может быть:

• фотоэлектрического характера – возникает в полупроводниковых переходах при облучении видимым светом или ультрафиолетом (на этом эффекте основана работа солнечных батарей);
• электрохимической природы – всем известные гальванические элементы и аккумуляторы;
• термоэлектрической ЭДС – возникает при разности температур между холодным и горячим спаем металлов (термопары для генерации электроэнергии и измерения температуры);
• пьезоэлектрической природы (возникает при деформации некоторых материалов) – применяется в пьезозажигалках;
• ЭДС электромагнитного характера – генераторы электростанций, автомобилей и т.п.

В технике встречаются и некоторые другие виды ЭДС, но реже.

Законы и формулы

Электродвижущая сила совершает работу по переносу заряда, а движущийся заряд представляет собой электрический ток/ Этот ток равен I=qt, где q – заряд, перенесенный полем за время t. За это время поле совершает работу A=ε*q= ε*I*t.

Можно определить ЭДС, как отношение работы по переносу заряда к величине этого заряда:

ε=A/q=A/(I*t)

ЭДС аккумуляторной батареи

ЭДС аккумуляторной батареи определяется типом электрохимических реакций, протекающих внутри элемента. Для различных технологий батарей наибольшая электродвижущая сила составит:

1. Свинцово-кислотные элементы – 2,17 вольта.
2. Никель-кадмиевые батареи – 1,37 вольта.
3. Никель-металлогидридные элементы – 1,37 вольта.
4. Щелочные аккумуляторы – 1,45 вольта.
5. Литий-ионные элементы – 4,2 вольта.

Электродвижущая сила химических источников тока не зависит от размеров и площади пластин. Чтобы повысить выходное напряжение, единичные аккумуляторы соединяют в батареи последовательно.

ЭДС индукции

Основной источник получения электроэнергии на Земле – генераторы постоянного и переменного тока. Их принцип действия основан на создании ЭДС индукции.

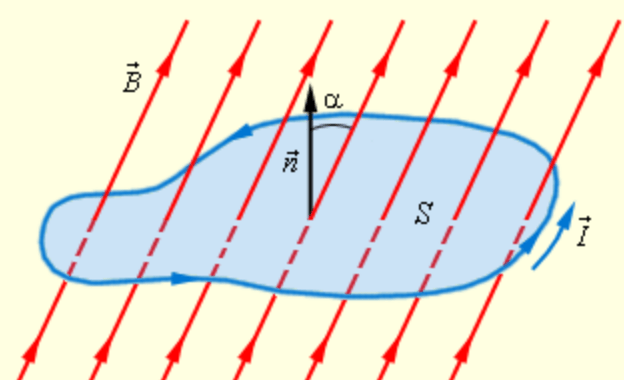
Если замкнутый контур находится в магнитном поле, и его пронизывает магнитный поток Ф, и этот поток изменяется во времени (по направлению или по величине), то в контуре возникает ЭДС. Ее величина равна:

ε=∆Ф/∆t, где Ф – магнитный поток, а t – время его изменения.

В свою очередь магнитный поток зависит от величины магнитной индукции и площади поверхности, охватываемой контуром. Следовательно, чтобы увеличить ЭДС, надо усиливать магнитное поле (повышением тока возбуждения), или увеличивать площадь витка (при разработке или изготовлении генератора), или заставить магнитный поток изменяться быстрее (например, увеличивая скорость вращения ротора генератора). Каждый путь имеет определенные технические ограничения, поэтому в генераторах делают большое количество витков, соединяя их последовательно. При этом электродвижущие силы всех контуров складываются.

Внутреннее сопротивление источника ЭДС

Пусть имеется источник тока — например, аккумулятор — с напряжением на разомкнутых клеммах (в отсутствие нагрузки) 12 вольт. Если его нагрузить на сопротивление в 5 Ом, напряжение на клеммах упадет (например, до 11,5 вольт). Если нагрузить аккумулятор на сопротивление 1 Ом, на его выходных терминалах напряжение снизится до 9,86 вольт.

Это явление легко объяснить, если ввести понятие внутреннего сопротивления источника питания. При разделении зарядов они движутся к соответствующим полюсам, но при этом взаимодействуют с кристаллической решеткой вещества, с ионами электролитов и отдают часть своей энергии. Движение носителей заряда замедляется, ток уменьшается, его ограничивает внутреннее сопротивление источника.

Это сопротивление включается последовательно с нагрузкой, и часть выходного напряжения падает на нем. Чем меньше сопротивление нагрузки, тем больше ток, тем больше потеря напряжения на внутреннем сопротивлении источника.

Внутреннее сопротивление определяется его конструкцией и типом ЭДС. Например, в аккумуляторе внутреннее сопротивление зависит от электрохимических реакций, протекающих в источнике тока.

Для анализа электрических цепей внутреннее сопротивление рисуется на схеме в виде резистора, подключенного внутри источника параллельно его выходным клеммам. На самом деле, конечно, никакого резистора там нет, но это удобно для рассмотрения процессов, протекающих в цепи.

Для наглядности рекомендуем видео-урок.

Закон Ома для полной цепи

Один из фундаментальных законов электротехники – закон Ома для участка цепи. Согласно ему, ток на участке цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению.

Ток в полной цепи, в которую кроме нагрузки входит еще и источник, определяется величиной ЭДС, приложенной к внутреннему сопротивлению r и сопротивлению внешней нагрузки R, включенными последовательно. Общее значение сопротивления равно r+R. Следовательно, ток определяется соотношением I=ε/(R+r).

Как найти мощность ЭДС

Идеальный источник имеет нулевое внутреннее сопротивление. В нем напряжение под нагрузкой не уменьшается и всегда равно ЭДС. На практике таких источников не бывает.

Согласно закону Ома для полной цепи, формула ЭДС источника выглядит, как ε=I*R+I*r (в таком виде формулируется второй закон Кирхгофа). В этом выражении:

• I*R=Uвнеш – напряжение на внешней нагрузке;
• i*r=Uвнутр – падение напряжения на внутреннем сопротивлении источника.

Если источник идеален, то r=0 и вся ЭДС прикладывается к нагрузке. Чем выше r и выше ток, тем меньше напряжения достается потребителю, тем меньшая мощность выделяется на нем. Отсюда очевидно, что с ростом внутреннего сопротивления r, при равном токе, снижается напряжение на внешней нагрузке.

Внутреннее сопротивление источника можно рассчитать по результатам измерений напряжения на терминалах источника ЭДС по итогам двух замеров. Для этого надо воспользоваться законом Ома для полной цепи. Так, в рассмотренном примере, в первом случае падение напряжения на резисторе в 5 Ом составляет 11,5 вольт. Тогда можно найти ток в цепи по формуле:

I=U/R=11,5/5=2,3 А.

Выражение для ЭДС примет вид:

ε= 2,3*5+2,3*r=11,5+2,3*r.

Для второго замера на сопротивлении 1 Ом ток составит:

I=U/R=9,86/1=9,86 ампер

Следовательно,

ε= 9,86 *1+9,86 *r=9,86 +9,86 *r.

Левые части уравнений равны, тогда можно приравнять правые:

11,5+2,3*r=9,86 +9,86 *r

Путем несложных вычислений получается, что r=0,217 Ом. Если источник имеет меньшее внутреннее сопротивление, то при подключении той же нагрузки на ней будет большее напряжение. Напряжение на разомкнутых клеммах (на холостом ходу) в отсутствие ток будет примерно равно значению величины ЭДС. Таким образом, чем меньше внутреннее сопротивление, тем большее напряжение способен выдавать источник в нагрузку и тем больше мощность ЭДС.

Если же идеальный источник тока замкнуть накоротко, ток короткого замыкания будет бесконечным, так как R=r=0. На самом деле этого не происходит – в реальном источнике ток КЗ при R=0 ограничивается внутренним сопротивлением r.

Электродвижущая сила является одним из основополагающих понятий в физике. Ее суть и значение надо четко осознавать, в противном случае дальнейшее освоение электротехники будет затруднено.