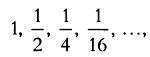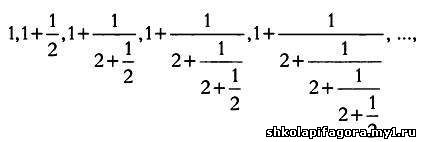Как найти эпсилон в математике

Let $0<varepsilon<1$ be a small number; then we have $$(c+varepsilon)^2=c^2+2varepsilon c+varepsilon^2le c^2+4varepsilon+varepsilon=c^2+5varepsilon$$ since $cle2$ and $varepsilon^2levarepsilon$. Since $c^2<2$, we see that we can choose an $0<varepsilon<1$ such that $c^2+5varepsilon<2$, thus $(c+varepsilon)^2<2$.

We can prove (by Archimedean property) that

Lemma 1. For any positive number $x>0$ there exists
a positive integer $N$ such that $x>1/N>0$.

Now, we want an $varepsilon$ such that $c^2+5varepsilon<2$, i.e., an $varepsilon$ such that $varepsilon<(2-c^2)/5$, which exists by Lemma 1.

In your case, since $0<(2-c^2)/(c+2)$, there is a $N$ such that $1/N<(2-c^2)/(c+2)$. Now, we can define $varepsilon:=1/N$.

The key is, supposing that there is such $varepsilon$, find some relation between $(x+varepsilon)^2$ and $x^2+Kvarepsilon$. Suppose $x^n<y$. There is many relations:

• First (Binomial formula): $$sum_{k=0}^nbinom{n}{k}x^{n-k}varepsilon^k.$$ Then use the expansion to obtain $(x+varepsilon)^nle x^n+x^{n-1}varepsilon+dotsb<y$.
• Second: $$(x+varepsilon)^nle x^n+varepsilon((x+1)^n-x^n).$$
  Then you can find $varepsilon$ such that $(x+varepsilon)^n<x$, just take a $varepsilon$ such that $$0<varepsilon<minleft{frac{x-x^n}{(x+1)^n-x^n},1right},$$
  which surely exists.
• Third: $$(x+varepsilon)^nle x^n+kvarepsilon$$
  for some $kinBbb R$. Then you obtain $(x+varepsilon)^nle x^n+kvarepsilon<y$, as desired.

All formulae are proved by induction on $m$.

A way to obtain this type of relations is see the behavior when $n$ increase.
For instance, let $x,y>0$ be rational numbers, and let $nge1$ be a integer number. We want to find some relation of the form $(x+varepsilon)^nle x^n+Kvarepsilon$ for some $varepsilon$ between $0$ and $1$.

Note that $varepsilon^nlevarepsilon$ for every $n$. Also, note that $varepsilon$ always exists by Archimedean property.

Using some algebra, we can expand $(x+varepsilon)^n$ when $n=1,2,3,4,5,dots$
$$begin{align}(x+varepsilon)^2&=x^2+2xvarepsilon+varepsilon^2\&le x^2+2xvarepsilon+varepsilon\&=x^2+varepsilon(2x+1)\\(x+varepsilon)^3&=x^3+3x^2varepsilon+3xvarepsilon^2+varepsilon^3\&le x^3+3x^2varepsilon+3xvarepsilon+varepsilon\&=x^3+varepsilon(3x^2+3x+1)\\(x+varepsilon)^4&=x^4+4x^3varepsilon+6x^2varepsilon^2+4xvarepsilon^3+varepsilon^4\&le x^4+4x^3varepsilon+6x^2varepsilon+4xvarepsilon+varepsilon\&=x^4+varepsilon(4x^3+6x^2+4x+1)\&;;vdotsend{align}$$

So we have
$$begin{align}(x+varepsilon)^2&le x^2+varepsilon(2x+1)\(x+varepsilon)^3&le x^3+varepsilon(3x^2+3x+1)\(x+varepsilon)^4&le x^4+varepsilon(4x^3+6x^2+4x+1)\(x+varepsilon)^5&le x^5+varepsilon(5x^4+10x^3+10x^2+5x+1)\(x+varepsilon)^6&le x^6+varepsilon(6x^5+15x^4+20x^3+15x^2+6x+1)\&;;vdotsend{align}$$

Now, suppose that $xle1$; so $x^nle 1$ for every $n$. Thus
$$begin{align}(x+varepsilon)^2&le x^2+3varepsilon\(x+varepsilon)^3&le x^3+7varepsilon\(x+varepsilon)^4&le x^4+15varepsilon\(x+varepsilon)^5&le x^4+31varepsilon\(x+varepsilon)^6&le x^4+63varepsilon\&;;vdots\end{align}$$

Clearly, the relation from this is $$(x+varepsilon)^nle x^n+(2^n-1)varepsilon.$$ (We can prove this by induction.)

Similarly, suppose $x>1$; so $x^nge x$ for every $n$. We can prove the relation $(x+varepsilon)^nle x^n+(2^n-1)x^{n-1}varepsilon.$

But, if we don’t want divide in cases, we can prove the relation $$(x+varepsilon)^nle x^n+n(2^n-1)(1+x)^nvarepsilon.$$
(To see this relation, try to prove the above relations and think how avoid the cases when some $k$ ensures the relation $(x+k)^nge x+k$.)

Тип трансфинитных чисел

В математике эпсилон числа — это набор трансфинитных чисел, определяющим свойством которых является то, что они являются фиксированными точками на экспоненциальной карте . Следовательно, они недостижимы из 0 с помощью конечной серии приложений выбранного экспоненциального отображения и «более слабых» операций, таких как сложение и умножение. Исходные числа эпсилон были введены Георгом Кантором в контексте порядковой арифметики ; это порядковые числа ε, которые удовлетворяют уравнению

ε = ω ε, { displaystyle varepsilon = omega ^ { varepsilon}, ,}

в котором ω это наименьший бесконечный порядковый номер.

Наименьший такой порядковый номер — ε0(произносится как эпсилон ноль или эпсилон ноль ), который можно рассматривать как «предел», полученный с помощью трансфинита. рекурсия из последовательности меньших предельных ординалов:

ε 0 = ω ω ω ⋅ ⋅ ⋅ = sup {ω, ω ω, ω ω ω, ω ω ω ω,…} { displaystyle varepsilon _ { 0} = omega ^ { omega ^ { omega ^ { cdot ^ { cdot ^ { cdot}}}}} = sup { omega, omega ^ { omega}, omega ^ { omega ^ { omega}}, omega ^ { omega ^ { omega ^ { omega}}}, dots }}

Более крупные порядковые фиксированные точки экспоненциальной карты индексируются порядковыми нижними индексами, в результате в ε 1, ε 2,…, ε ω, ε ω + 1,…, ε ε 0,…, ε ε 1,…, ε ε ε ⋅ ⋅ ⋅,… { displaystyle varepsilon _ {1 }, varepsilon _ {2}, ldots, varepsilon _ { omega}, varepsilon _ { omega +1}, ldots, varepsilon _ { varepsilon _ {0}}, ldots, varepsilon _ { varepsilon _ {1}}, ldots, varepsilon _ { varepsilon _ { varepsilon _ { cdot _ { cdot _ { cdot}}}}}, ldots}. Порядковый номер ε 0 по-прежнему счетный, как и любое число эпсилон, индекс которого является счетным (существуют несчетные порядковые числа и несчетные числа эпсилон, индекс которых является несчетным порядковым номером).

Наименьшее эпсилон-число ε 0 встречается во многих доказательствах индукции, потому что для многих целей трансфинитная индукция требуется только до ε 0 (как в доказательстве непротиворечивости Генцена и доказательстве теоремы Гудстейна ). Его использование Генценом для доказательства непротиворечивости арифметики Пеано, наряду со второй теоремой Гёделя о неполноте, показывает, что арифметика Пеано не может доказать обоснованность этого порядка (на самом деле это наименьший порядковый номер с этим свойством, и как таковой в теории доказательств порядковый анализ используется как мера силы теории арифметики Пеано).

Многие большие эпсилон-числа могут быть определены с помощью функции Веблена.

Более общий класс эпсилон-чисел был идентифицирован Джоном Хортоном Конвеем и Дональдом Кнутом в системе сюрреалистических чисел, состоящей из всех сюрреалей, которые являются неподвижными точками базового ω экспоненциального отображения x → ω.

Hessenberg (1906) ошибка harvtxt: нет цели: CITEREFHessenberg1906 (help ) определил гамма-числа (см. аддитивно неразложимый порядковый номер ) как числа γ>0, такие что α + γ = γ всякий раз, когда α <γ, and delta numbers (see аддитивно неразложимый порядковый номер # Мультипликативно неразложимый ), чтобы быть числами δ>1 такими, что αδ = δ всякий раз, когда 0 <α<δ, and epsilon numbers to be numbers ε>2 такие, что α = ε всякий раз, когда 1 <α<ε. His gamma numbers are those of the form ω, and his delta numbers are those of the form ω.

Содержание

• 1 Порядковые числа ε
• 2 Представление ε 0 { displaystyle varepsilon _ {0}}корневыми деревьями
• 3 иерархия Веблена
• 4 Сюрреалистические числа ε
• 5 См. Также
• 6 Ссылки

Порядковые числа ε

Стандартное определение порядкового возведения в степень с основанием α:

Из этого определения следует, что для любого фиксированного порядкового номера α>1 отображение β ↦ α β { displ aystyle beta mapsto alpha ^ { beta}}— это нормальная функция, поэтому она имеет произвольно большие фиксированные точки с помощью fixed- точечная лемма для нормальных функций. Когда α = ω { displaystyle alpha = omega}, эти фиксированные точки являются в точности порядковыми эпсилон-числами. Наименьшее из них, ε₀, является верхней гранью последовательности

0, ω 0 = 1, ω 1 = ω, ω ω, ω ω ω,…, ω ↑↑ k,… { displaystyle 0, omega ^ {0} = 1, omega ^ {1} = omega, omega ^ { omega}, omega ^ { omega ^ { omega}}, ldots, omega uparrow uparrow k, ldots}

, в котором каждый элемент является изображением своего предшественника при отображении β ↦ ω β { displaystyle beta mapsto omega ^ { beta}}. (Общий термин дается с использованием обозначения стрелки Кнута вверх ; оператор ↑↑ { displaystyle uparrow uparrow}эквивалентен тетрации.) Так же, как ω определяется как верхняя грань {ω} для натуральных чисел k, наименьшее порядковое эпсилон-число ε₀ может также обозначаться ω ↑↑ ω { displaystyle omega uparrow uparrow omega}; это обозначение гораздо реже, чем ε₀.

Следующее эпсилон-число после ε 0 { displaystyle varepsilon _ {0}}равно

ε 1 = sup {ε 0 + 1, ω ε 0 + 1, ω ω ε 0 + 1, ω ω ω ε 0 + 1,…}, { displaystyle varepsilon _ {1} = sup { varepsilon _ {0} +1, omega ^ { varepsilon _ {0} +1}, omega ^ { omega ^ { varepsilon _ {0} +1}}, omega ^ { omega ^ { omega ^ { varepsilon _ {0} +1}}}, dots },}

, в котором последовательность снова строится путем повторения возведения в степень по основанию ω, но вместо этого начинается с ε 0 + 1 { displaystyle varepsilon _ {0} +1}из в 0. Обратите внимание

ω ε 0 + 1 = ω ε 0 ⋅ ω 1 знак равно ε 0 ⋅ ω, { displaystyle omega ^ { varepsilon _ {0} +1} = omega ^ { varepsilon _ {0}} cdot omega ^ {1} = varepsilon _ {0} cdot omega ,,}

ω ω ε 0 + 1 = ω (ε 0 ⋅ ω) = (ω ε 0) ω знак равно ε 0 ω, { Displaystyle omega ^ { omega ^ { varepsilon _ {0} +1}} = omega ^ {( varepsilon _ {0} cdot omega)} = {( omega ^ { varepsilon _ {0}})} ^ { omega} = varepsilon _ {0} ^ { omega} ,,}

ω ω ω ε 0 + 1 = ω ε 0 ω = ω ε 0 1 + ω = ω (ε 0 ⋅ ε 0 ω) = (ω ε 0) ε 0 ω = ε 0 ε 0 ω. { displaystyle omega ^ { omega ^ { omega ^ { varepsilon _ {0} +1}}} = omega ^ {{ varepsilon _ {0}} ^ { omega}} = omega ^ { { varepsilon _ {0}} ^ {1+ omega}} = omega ^ {( varepsilon _ {0} cdot { varepsilon _ {0}} ^ { omega})} = {( omega ^ { varepsilon _ {0}})} ^ {{ varepsilon _ {0}} ^ { omega}} = { varepsilon _ {0}} ^ {{ varepsilon _ {0}} ^ { omega }} ,.}

Другая последовательность с тем же супремумом, ε 1 { displaystyle varepsilon _ {1}}, получается путем начала с 0 и возведения в степень с основанием ε₀ вместо этого:

ε 1 = sup {0, 1, ε 0, ε 0 ε 0, ε 0 ε 0 ε 0,…}, { displaystyle varepsilon _ {1} = sup {0,1, varepsilon _ {0}, { varepsilon _ {0}} ^ { varepsilon _ {0}}, { varepsilon _ {0}} ^ {{ varepsilon _ {0}} ^ { varepsilon _ {0 }}}, ldots },}

Эпсилон-число ε α + 1 { displaystyle varepsilon _ { alpha +1}}, индексируемое любым последующим порядковым номером α + 1 строится аналогично, путем возведения в степень по основанию ω, начиная с ε α + 1 { displaystyle varepsilon _ { alpha} +1}(или по основанию ε α { displaystyle varepsilon _ { alpha}}возведение в степень, начиная с 0).

ε α + 1 = sup {ε α + 1, ω ε α + 1, ω ω ε α + 1,…} = sup {0, 1, ε α, ε α ε α, ε α ε α ε α,…} { displaystyle varepsilon _ { alpha +1} = sup { varepsilon _ { alpha} +1, omega ^ { varepsilon _ { alpha} +1}, omega ^ { omega ^ { varepsilon _ { alpha} +1}}, dots } = sup {0,1, varepsilon _ { alpha}, varepsilon _ { alpha} ^ { varepsilon _ { alpha}}, varepsilon _ { alpha} ^ { varepsilon _ { alpha} ^ { varepsilon _ { alpha}}}, dots }}

Эпсилон-число с индексом предельный ординал α строится иначе. Число ε α { displaystyle varepsilon _ { alpha}}— это верхняя грань набора чисел эпсилон {ε β, β < α } {displaystyle {varepsilon _{beta },beta <alpha }}. Первое такое число — ε ω { displaystyle varepsilon _ { omega}}. Независимо от того, является ли индекс α предельным порядковым номером, ε α { displaystyle varepsilon _ { alpha}}является фиксированной точкой не только возведения в степень по основанию ω, но также и по основе возведения в степень γ для все порядковые числа 1 < γ < ε α {displaystyle 1<gamma <varepsilon _{alpha }}.

Поскольку эпсилон-числа являются неограниченным подклассом порядковых чисел, они пронумерованы с использованием самих порядковых чисел. Для любого порядкового номера α { displaystyle alpha}, ε α { displaystyle varepsilon _ { alpha}}— наименьшее число эпсилон (фиксированная точка экспоненциальной карты), а не уже в наборе {ε β, β < α } {displaystyle {varepsilon _{beta },beta <alpha }}. Может показаться, что это неконструктивный эквивалент конструктивного определения с использованием повторного возведения в степень; но эти два определения одинаково неконструктивны на этапах, индексированных предельными ординалами, которые представляют трансфинитную рекурсию более высокого порядка, чем взятие верхней грани экспоненциального ряда.

Следующие факты об эпсилон-числах очень просто доказать:

ε ω = sup {ε 0, ε 1, ε 2,…} { displaystyle varepsilon _ { omega} = sup { varepsilon _ {0}, varepsilon _ {1}, varepsilon _ {2}, ldots }}

— эпсилон-число. Таким образом, отображение α ↦ ε α { displaystyle alpha mapsto varepsilon _ { alpha}}является нормальной функцией.

• начальный порядковый номер любой несчетный кардинал является эпсилонным числом.

α ≥ 1 ⇒ ε ω α = ω α. { displaystyle alpha geq 1 Rightarrow varepsilon _ { omega _ { alpha}} = omega _ { alpha} ,.}

Представление ε 0 { displaystyle varepsilon _ {0}}по корневым деревьям

Любое эпсилон-число ε имеет нормальную форму Кантора ε = ω ε { displaystyle varepsilon = omega ^ { varepsilon}}, что означает, что нормальная форма Кантора не очень полезна для чисел эпсилон. Однако ординалы меньше ε 0 могут быть с пользой описаны с помощью их нормальных форм Кантора, что приводит к представлению ε 0 как упорядоченного набора всех конечных корневых деревья следующим образом. Любой порядковый номер α < ε 0 {displaystyle alpha <varepsilon _{0}}имеет нормальную форму Кантора α = ω β 1 + ω β 2 + ⋯ + ω β k { displaystyle alpha = omega ^ { beta _ {1}} + omega ^ { beta _ {2}} + cdots + omega ^ { beta _ {k}}}где k — натуральное число, а β 1,…, β k { displaystyle beta _ {1}, ldots, beta _ {k}}— порядковые числа с α>β 1 ≥ ⋯ ≥ β k { displaystyle alpha> beta _ {1} geq cdots geq beta _ {k}}, однозначно определяется α { displaystyle alpha}. ординалы β 1,…, β k { displaystyle beta _ {1}, ldots, beta _ {k}}, в свою очередь, имеют аналогичную нормальную форму Кантора. Мы получаем конечное корневое дерево, представляющее α, путем соединения корней деревьев, представляющих β 1,…, β k { displaystyle beta _ {1}, ldots, beta _ {k}}с новый корень (это приводит к тому, что th Число 0 представлено одним корнем, а число 1 = ω 0 { displaystyle 1 = omega ^ {0}}представлено деревом, содержащим корень и один лист.) Порядок на множестве конечных корневых деревьев определяется рекурсивно: сначала мы упорядочиваем поддеревья, соединенные с корнем, в порядке убывания, а затем используем лексикографический порядок для этих упорядоченных последовательностей поддеревьев. Таким образом, множество всех конечных корневых деревьев становится хорошо упорядоченным множеством, которое по порядку изоморфно ε 0.

иерархии Веблена

Неподвижные точки «эпсилон-отображения» Икс ↦ ε Икс { Displaystyle x mapsto varepsilon _ {x}}образуют нормальную функцию, фиксированные точки которой образуют нормальную функцию, чья…; это известно как иерархия Веблена (функции Веблена с базой φ 0 (α) = ω). В обозначениях иерархии Веблена эпсилон-отображение — это φ 1, а его неподвижные точки пронумерованы как φ 2.

. Продолжая в том же духе, можно определить отображения φ α для прогрессивно увеличивающиеся ординалы α (включая, посредством этой разреженной формы трансфинитной рекурсии, предельные ординалы), с постепенно увеличивающимися наименьшими фиксированными точками φ α + 1 (0). Наименьший порядковый номер, недоступный из 0 с помощью этой процедуры — i. е., наименьший порядковый номер α, для которого φ α (0) = α, или, что то же самое, первая фиксированная точка карты α ↦ φ α (0) { displaystyle alpha mapsto varphi _ { alpha} (0)}— это порядковый номер Фефермана – Шютте Γ0. В теории множеств, где можно доказать существование такого ординала, имеется отображение Γ, в котором перечислены неподвижные точки Γ 0, Γ 1, Γ 2,… из α ↦ φ α (0) { displaystyle alpha mapsto varphi _ { alpha} (0)}; это все еще числа эпсилон, поскольку они лежат в образе φ β для каждого β ≤ Γ 0, включая карту φ 1, которая перечисляет эпсилон числа.

Сюрреалистические ε-числа

В On Numbers and Games классическое изложение сюрреалистических чисел, Джон Хортон Конвей предоставил ряд примеров концептов, которые имели естественные расширения от ординалов до сюрреалов. Одной из таких функций является ω { displaystyle omega}-map n ↦ ω n { displaystyle n mapsto omega ^ {n}}; это отображение естественным образом обобщается, чтобы включить все сюрреалистические числа в его область, что, в свою очередь, обеспечивает естественное обобщение нормальной формы Кантора для сюрреалистических чисел.

Естественно считать любую фиксированную точку этой расширенной карты эпсилон-числом, независимо от того, является ли это строго порядковым числом. Некоторые примеры неординальных эпсилон-чисел:

ε — 1 = {0, 1, ω, ω ω,… ∣ ε 0 — 1, ω ε 0 — 1,…} { displaystyle varepsilon _ {- 1 } = {0,1, omega, omega ^ { omega}, ldots mid varepsilon _ {0} -1, omega ^ { varepsilon _ {0} -1}, ldots } }

и

ε 1 2 = {ε 0 + 1, ω ε 0 + 1,… ∣ ε 1 — 1, ω ε 1 — 1,…}. { displaystyle varepsilon _ { frac {1} {2}} = { varepsilon _ {0} +1, omega ^ { varepsilon _ {0} +1}, ldots mid varepsilon _ { 1} -1, omega ^ { varepsilon _ {1} -1}, ldots }.}

Существует естественный способ определить ε n { displaystyle varepsilon _ {n}}для каждого сюрреалистического числа n, и карта сохраняет порядок. Конвей продолжает определять более широкий класс «неприводимых» сюрреалистических чисел, который включает числа эпсилон как особенно интересный подкласс.

См. Также

• Порядковая арифметика
• Крупный счетный порядковый номер

Ссылки

• J.H. Конвей, О числах и играх (1976) Academic Press ISBN 0-12-186350-6
• Раздел XIV.20 из Серпинский, Вацлав (1965), Кардинальные и порядковые числа (2-е изд.), PWN — Polish Scientific Publishers

Когда
говорят об эпсилонах или о языке эпсилон-дельта, речь идет вовсе не о
секретных кодах Министерства обороны, а о сложном математическом
аппарате, который напрямую связан с понятием предела. Первое определение
понятию предела сформулировал Бернард Больцано (1781–1848), не
получивший, к сожалению, при жизни должного признания. Первым, кто
использовал это понятие на практике, был Огюстен Луи Коши (1789–1857),
однако окончательное строгое определение предела дал Карл Вейерштрасс.
Определение предела на языке эпсилон-дельта является чрезвычайно точным в
той части, которая касается делимости на бесконечное множество частей.
Хотя это определение очень сложно понять тому, кто не владеет некоторыми
математическими знаниями, оно тем не менее долгое время использовалось в
учебниках для средней школы. Мы не хотим сказать, что старшеклассники
недостаточно умны, чтобы понять его, но не стоит ожидать, что все поймут
его с одинаковой легкостью. Во многих учебниках оно приводится мелким
шрифтом, и преподаватели обходят его молчанием.

Карл Вейерштрасс на литографии 1895 года. Этот немецкий математик был первым, кто использовал на практике язык эпсилон-дельта.

* * *

* * *

Попробуем сделать понятие предела более ясным, несколько упростив его.

По
сути оно имеет много общего с понятием накопления. Представим, что
перед входом в помещение образовалась очередь. Можно заметить, что люди
постепенно становятся ближе ко входу и друг к другу. Это совершенно
естественно: изначально, когда в очереди немного людей, они стараются
сохранять комфортное расстояние между собой, но по мере того как число
людей растет, расстояние между ними уменьшается. Интересно, что мы
говорим о двух разных расстояниях, которые, однако, тесно связаны между
собой: о расстоянии между началом очереди и входом и о расстоянии между
людьми в очереди, которое по мере того как мы приближаемся к концу,
увеличивается. Это логично, так как те, кто становится в очередь,
стараются сохранять комфортное расстояние между собой, но по мере того
как очередь движется вперед, люди чувствуют давление тех, кто находится
позади. Можно сказать, что люди скапливаются у входа.

Можно
определить степень скопления людей с помощью параметра, который будет
описывать, например, изменение расстояния между людьми в очереди по мере
приближения к ее началу. Как правило, этот параметр будет постепенно
уменьшаться.

В
очереди, например у входа в кинотеатр, люди собираются у дверей, где
расстояние между ними будет минимальным. По мере отдаления от входа
расстояние между людьми увеличивается.

Степень
скопления людей можно определить, выбрав в качестве единицы измерения
конкретное расстояние, например 50 см. Если в 50 см от входа находятся
люди, это будет соответствовать определенной степени скопления. В
зависимости от величины этой единицы измерения число людей будет
изменяться. Аналогично можно измерить степень скопления людей, оценив
расстояние между ними.

Здесь
возникает первый интересный вопрос: когда мы видим скопление людей,
логично предположить, что они собрались по какой-то причине, то есть это
скопление возникает вокруг определенного места, где происходит что-то
важное. Когда мы видим на дороге скопление муравьев, то сразу же
понимаем, что где-то поблизости находится еда или вход в муравейник. Еще
один пример — скопление машин на автомагистрали, которое служит
признаком того, что поблизости находится пункт оплаты проезда или
произошла авария. Эти примеры помогут нам понять одно из самых
интересных открытий в истории математики. Оно касается существования
определенных чисел, которые в течение веков скрывались в мире бесконечно
малых.

В
предыдущих примерах речь шла о дискретных множествах. Рассмотрим
непрерывные величины, так как они допускают возможность бесконечного
деления.

Оставим
скопления людей и автомашин и рассмотрим возможные множества точек на
прямой. Допустим, что дана последовательность точек а₁, a₂, а₃, а_n…,
которые обладают одним свойством: соседние члены последовательности
располагаются все ближе и ближе друг к другу. Очевидно, что они
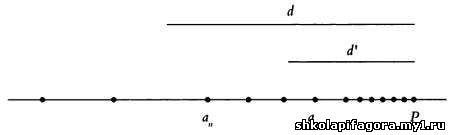
скапливаются вокруг некоторой точки — обозначим ее Р. Допустим, что выбранной нами основной мерой длины является отрезок длиной d. Если мы поместим один конец этого отрезка в точку Р, то увидим, что некоторые точки последовательности окажутся внутри этого отрезка длиной d.

Более того, мы сможем найти точку а_n, после которой все точки будут располагаться внутри отрезка d. Если мы уменьшим длину отрезка и сделаем ее равной d’ < d, то все точки, начиная с более удаленной, а_m, будут располагаться внутри этого нового отрезка. Именно такое значение имеет эпсилон в математическом анализе.

Мы можем гарантировать, что для любой величины d всегда найдется такое n, начиная с которого все элементы последовательности будут находиться внутри отрезка d. В этом случае говорят, что последовательность сходится в точке Р. Это означает следующее: во-первых, эта последовательность бесконечна, во-вторых, расстояние между точкой Р и произвольным членом последовательности может быть сколь угодно малым.

Когда
мы работаем с дискретными множествами, все изложенное выше практически
неприменимо. Рассмотрим последовательность чисел 100, 50, 25, 12, 6, 3, 1
(можно представить эту последовательность как очередь из семи чисел у
входа, которым, например, является ноль). Очевидно, что разница между
произвольным членом последовательности и нулем постепенно уменьшается,
равно как и разница между двумя соседними членами последовательности.
Например, между 100 и 50 находится 49 чисел, между 6 и 3 — всего два.
Тем не менее нельзя сказать, что члены последовательности скапливаются в
окрестности точки 0. Очевидно, что если мы возьмем отрезок длиной 1/2 и
поместим один из его концов в точку 0, на этом отрезке не будет
находиться ни один член последовательности. А если мы рассмотрим
последовательность

то вблизи нуля всегда будет находиться какой-либо ее член, сколь бы малым ни было расстояние до нуля.

На
языке математики эти расстояния называются окрестностями. Окрестность
подобна скобкам, в которые заключена точка Р. Основная идея заключается в
том, что сколь малыми ни были бы эти скобки (то есть радиус
окрестности), в них всегда будут находиться элементы последовательности.
В языке эпсилон-дельта основную роль играет соотношение между двумя
числами: шириной скобок (радиусом окрестности, который обычно
обозначают ε — эпсилон) и числом n, определяющим элемент а_n,
начиная с которого все элементы последовательности будут располагаться
внутри заданной окрестности. На языке математики это звучит так: «Для
любого эпсилон существует n, такое что…»

Именно
так определяется понятие бесконечного деления, очень близкое к понятию
предела. Когда в одном из парадоксов Зенона интервал делится пополам
бесконечное число раз, мы формируем последовательность, подобную
описанной в предыдущем примере. Теперь мы можем воспользоваться строгим
определением перехода к пределу и подтвердить, что последним членом
последовательности будет 0. Это не помогает разрешить парадокс, так как
ситуация, по сути, не изменилась: точки образуют бесконечную
последовательность и скапливаются вблизи нуля, и мы считаем, что
существует последняя точка последовательности, 0, но в действительности 0
не является членом этой последовательности. Это утверждение не является
оправданным, но четко определено на языке математики. Как говорил
Бертран Рассел, «математика может быть определена как доктрина, в
которой мы никогда не знаем ни о чем говорим, ни того, верно ли то, что
мы говорим».

В
действительности Коши в своем определении предела использовал не точки,
которые скапливаются вокруг некоторой данной точки, а точки, которые
скапливаются рядом друг с другом. Иными словами, скопление точек,
которое рассматривал Коши, подобно скоплениям автомобилей на разных
участках дороги, вызванным множеством аварий в разных местах. Ситуация
значительно осложняется тем, что если мы рассматриваем исключительно
рациональные числа, то прямая, на которой они располагаются, не будет
заполнена — на ней останутся промежутки. Например: дана
последовательность точек (теперь мы связываем точки на прямой с
рациональными числами), которые скапливаются все плотнее и плотнее. Эту
ситуацию можно четко определить на языке математики, что сделал Коши.
Однако проблема заключается в том, что эти точки могут скапливаться
вокруг пустого места на прямой, точнее вокруг точки, которой не
соответствует никакое рациональное число.

Так происходит, например, в случае с последовательностью

о
которой мы говорили в главе 2 и которая сходится к числу √2, а оно не
является рациональным. Разумеется, мы можем построить прямоугольный
треугольник, гипотенуза которого будет равна √2, но так мы определим это
число геометрически, а во времена Коши математики пытались дать
определение числам чисто арифметическими или аналитическими методами.
Рациональные числа, по сути, вообще не были определены как числа, пока
Дедекинд и, позднее, Кантор не сформулировали для них точной дефиниции.
Последний сделал не только это, но и устранил промежутки на числовой
прямой, которых в действительности существует бесконечное множество, так
как иррациональных чисел, равно как и рациональных, бесконечно много.

Однако
Кантор заслуживает отдельной главы, ведь он не только заполнил числовую
прямую, устранив эти промежутки, но и первый встретился с
бесконечностью лицом к лицу.