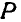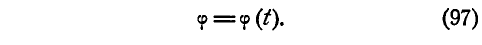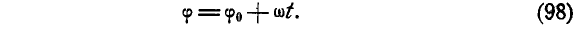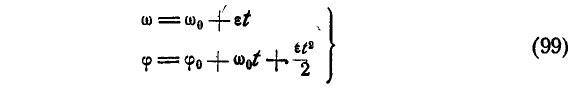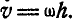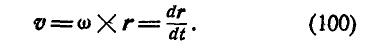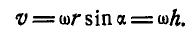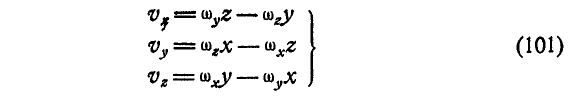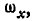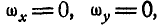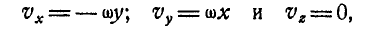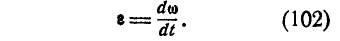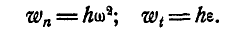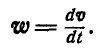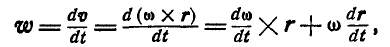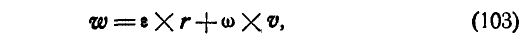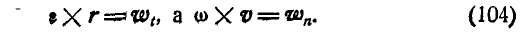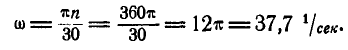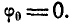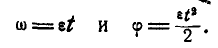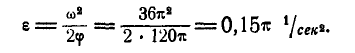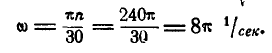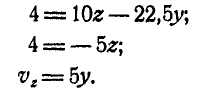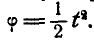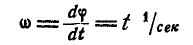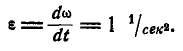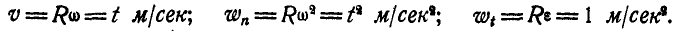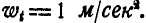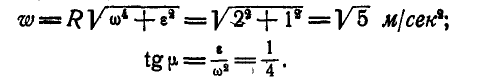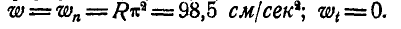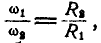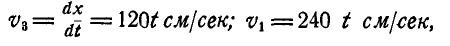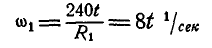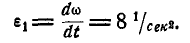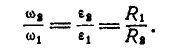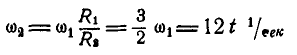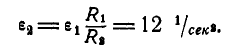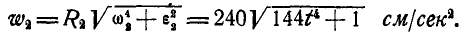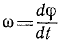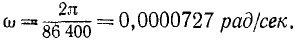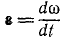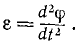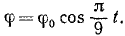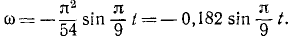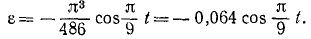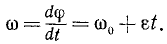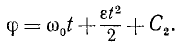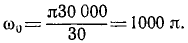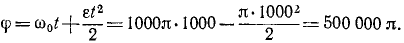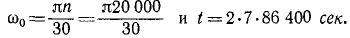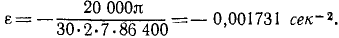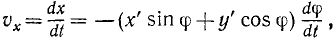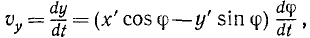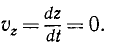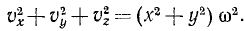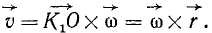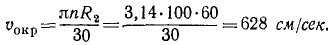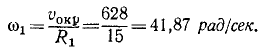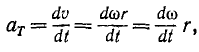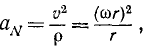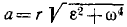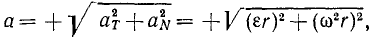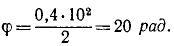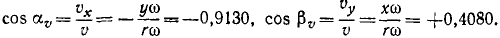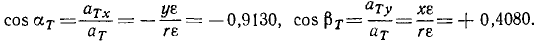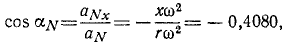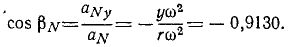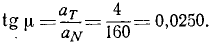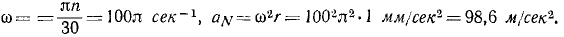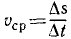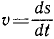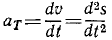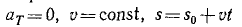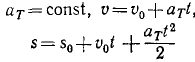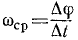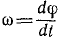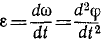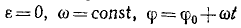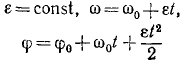Как найти эпсилон в теоретической механике

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

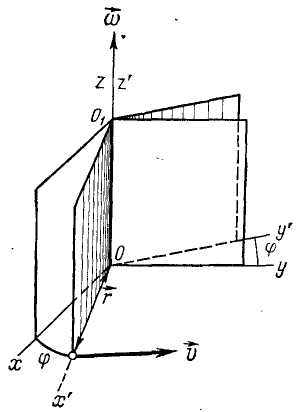
Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

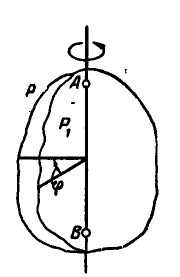
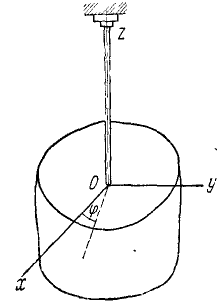
Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

1. если известно количество оборотов n за единицу времени t:
   
2. если задан угол поворота φ за единицу времени:
   
3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
   

Размерности угловой скорости:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Определение угловой скорости

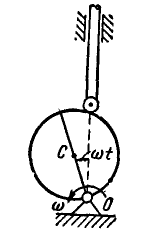
Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

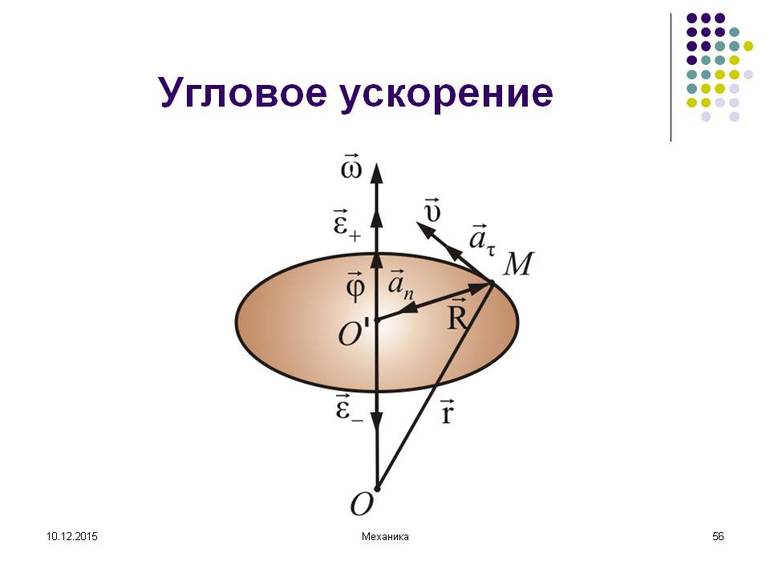
Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

• Примеры расчета угловой скорости и ускорения
• Скорости и ускорения точек вращающегося тела

Поступательным
называется движение, при котором любая
прямая, проведенная в теле, перемещается
параллельно самой себе. Т.к. при
поступательном движении траектории,
скорости и ускорения всех точек тела
совпадают, то для описания движения
тела достаточно рассмотреть движение
любой его точки.

Кинематика вращательного движения твердого тела.

Вращательным
называется движение, при котором все
точки тела движутся по окружностям,
центры которых лежат на одной прямой –
оси вращения.

1.
Характеристики
вращательного движения.

а) Угловая
скорость
.

Быстрота вращения
характеризуется угловой скоростью
«омега», которая равна производной от
угла поворота телапо времени

, (16)

— угол поворота
тела за малое время
.

При равномерном
вращении его быстроту также описывают
частотой оборотов
и периодом вращения.
Частота оборотовравна числу оборотов, сделанных за
единицу времени,

, (17)

— число оборотов
за время
.
Т.к. за один оборот тело поворачивается
на угол, равный 2,
тои

. (18)

Период вращения
— это время, за которое тело совершает
один оборот. Т.к.

,

то

. (19)

рад/с
,об/с
,с
.

Рис.3.

б) Угловое
ускорение
.

Угловое ускорение
«эпсилон» равно производной от угловой
скоростипо времени,

, (20)

—
изменение угловой скорости за время
..

Векторы
инаправлены по оси вращения тела; вектор
угловой скоростинаправлен в сторону хода правого винта
при вращении винта в направлении вращения
тела (рис.3). При ускоренном вращении
тела направления векторовисовпадают, при замедленном – противоположны.

2.
Связь линейных
и угловых характеристик.

Если точка тела
отстоит от оси вращения на расстоянии
,
то за времяона проходит путь

.

Скорость точки
,
или

. (21)

При вращении тела
тангенциальное ускорение его точки
,
или

. (22)

Нормальное ускорение
точки тела
,
или

. (23)

Полное ускорение,
как указывалось ранее, определяют по
формуле

.

3. Формулы равноускоренного вращения.

Если угловое
ускорение
постоянно, то

(24)

и

, (25)

и
– угловая скорость и угол поворота
тела в начальный момент,

и
– в момент времени.
При ускоренном вращении в уравнениях
(24) — (25) выбирается знак «+», а при
замедленном – знак «-».

Динамика. Законы ньютона.

1. Законы Ньютона.

В основе классической
механики лежат законы Ньютона.

1-й закон: если
сумма сил, действующих на тело, равна
нулю (),
то тело или покоится, или движется
прямолинейно и равномерно.

2-й закон: произведение
массы
тела на его ускорениеравно сумме сил, действующих на тело,

. (26)

3-й закон: с
какой силой первое тело действует на
второе, с такой же по величине и обратной
по направлению силой второе тело
действует на первое.

Системы отсчета,
в которых справедливы законы Ньютона,
называются инерциальными.

Силы в механике.

1. Гравитационная
   сила.

Две точечные массы

и,
расположенные на расстояниидруг от друга, притягиваются с силой

, (27)

=6,67·10^-11
м³/(кг·с²)
– гравитационная постоянная. Уравнение
(27) представляет собой закон всемирного
тяготения.

1. Сила тяжести.

Силой тяжести тела
массой
называется сила притяжения его к Земле

, (28)

–ускорение свободного
падения.

Вследствие суточного
вращения Земли и несферичности ее формы
величина
различается от 9,78 м/с²
на экваторе до 9,83 м/с²
на полюсах. В среднем на поверхности
Земли

=9,8
м/с²
,

и
— масса и радиус Земли.

На высоте
над поверхностью Земли

. (29)

1. Вес тела.

Вес представляет
собой силу, с которой тело действует на
горизонтальную опору или на подвес.

По величине вес и
сила тяжести совпадают только в том
случае, если опора неподвижна. Например,
вес тела, находящегося в движущемся
вверх с ускорением лифте, превышает его
силу тяжести.

1. Сила трения.

При скольжении
тела действующая на него сила трения

, (30)

— коэффициент
трения,
— сила реакции опоры (рис. 4 ).

Рис.4.

1. Сила упругости.
   

Сила упругости,
действующая на тело со стороны
деформированной (сжатой или растянутой)
пружины, равна по величине

,
(31)

—
коэффициент упругости (жесткость)
пружины,
— величина деформации пружины.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

Вращение твердого тела вокруг неподвижной оси:

Вращением тела вокруг неподвижной оси называется такое его движение, при котором две точки тела, например А и В, неподвижны (рис. 162). Прямая, проходящая через указанные две неподвижные точки, называется осью вращения. Если мысленно провести через тело две полуплоскости — неподвижную

Рис. 162.

При вращении тела угол поворота его 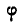изменяется с течением времени, а поэтому он является функцией времени:

Уравнение (97) называется уравнением вращения; зная его, можно для любого момента t найти угол 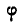, а следовательно, и положение вращающегося тела.

Величины угловой скорости и углового ускорения тела, вращающегося вокруг неподвижной оси, определяются по формулам (87) и (90).

Если 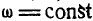, то такое вращение тела называется равномерным и уравнение вращения его (97) напишется аналогично уравнению (71) расстояний точки, движущейся равномерно:

Поэтому такое уравнение по аналогии с равномерным движением точки называется уравнением равномерного вращения.

Точно так же, если 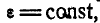то вращение тела называется равнопеременным.

Уравнения равнопеременного вращения тела могут быть выведены аналогично уравнениям (82) и (83) равнопеременного движения точки путем замены линейных характеристик угловыми и записаны в виде:

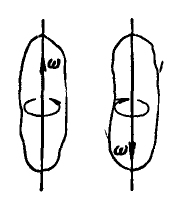
Условимся угловую скорость вращающегося тела изображать вектором, отложенным по оси вращения в такую сторону, чтобы, смотря с конца этого вектора, вращение тела происходило в направлении, противоположном движению часовой стрелки (рис. 163).

Рис. 163.

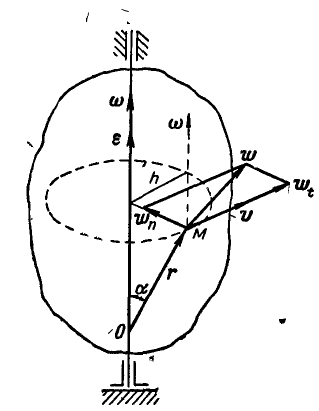
При вращении тела вокруг неподвижной оси (рис. 164) любая точка его М, отстоящая на расстоянии h от оси вращения, описывает окружность радиуса h и имеет линейную скорость, определяемую формулой (89):

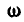
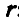
Если провести из любой точки О оси радиус-вектор в точку М, то вектор линейной скорости точки М может быть представлен также в виде векторного произведения на  :

В самом деле, раскрывая векторное произведение, получим величину скорости, определяемую формулой (89):

Вектор же скорости направлен перпендикулярно к плоскости векторов на в такую сторон, чтобы обход контура параллелограмма, построенного на на , задаваемый первым вектором , стоящим в векторном произведении, происходил против часовой стрелки, что согласуется с определением векторного, произведения двух векторов.

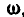
Рис. 164.                                                             Рис. 165.

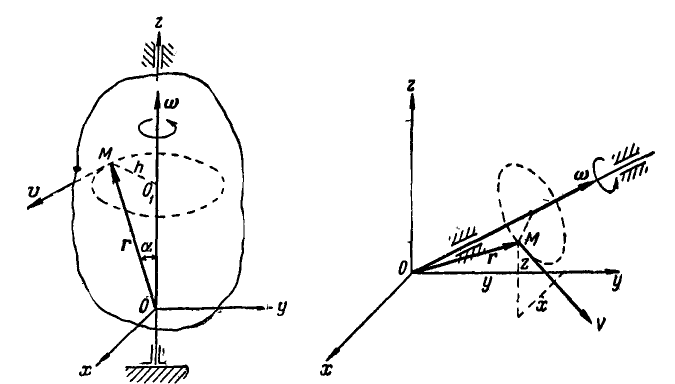
В самом общем случае, когда ось вращения тела составляет любые углы с координатными осями (рис. 165), проекции скорости точки М могут быть найдены по формулам проекций векторного произведения двух векторов (11):

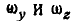
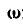
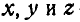
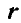
Равенства (101) называются формулами Эйлера. Здесь  — проекции ; а —проекции на координатные оси.

Если ось вращения вертикальна (рис. 164), то 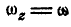и формулы Эйлера принимают вид:

что было получено нами раньше (88). Мы уже знаем, что величина углового ускорения 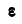определяется по формуле (90).

Рис. 166.

Введем в рассмотрение вектор углового ускорения е, под которым мы будем понимать векторную величину:

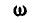
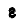
Так как имеет постоянное направление, то вектор всегда совпадает с осью вращения.

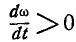
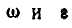
При векторы — одного направления;

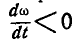
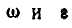
при векторы — противоположных направлений.

Нормальное и касательное ускорения любой точки М вращающегося тела (рис. 166) Moryт быть найдены по формулам (91):

Дадим векторное обобщение этим величинам. В самом общем случае вектор ускорения может быть найден по формуле (79):

Принимая во внимание формулы (100) и (102), имеем:

или

где

Действительно, в силу определения векторного произведения, находим:

Это приводит нас к формулам (91). Направления же 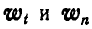соответствуют правилу откладывания векторов, полученных по правилам векторного произведения (рис. 166).

Задача №1

Маховик делает 360 об/мин. Найти его угловую скорость .    ,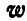

Решение. В нашем случае 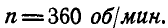По формуле (94) находим:

Задача №2

Маховик начинает вращаться равноускоренно из состояния покоя. Сделав с момента начала движения 60 оборотов, маховик имеет угловую скорость, равную 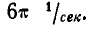Определить угловое ускорение маховика.

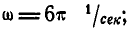
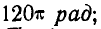
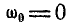
Решение. По условию задачи    и 

По формулам (99) получаем:

Подставляя значение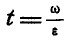 , найденное из первого уравнения, во второе, находим:

Задача №3

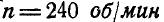
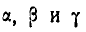
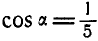
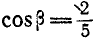
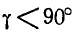
Тело делает вокруг оси, составляющей углы с координатными осями; при этом ,  и.

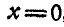
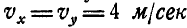
Найти такую точку тела, расположенную в плоскости , проекции скорости которой суть: .

Решение. Угловая скорость:

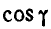
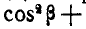
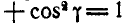
Для определения имеем известное соотношение: , откуда:

Найдем теперь проекции угловой скорости на координатные оси:

По формулам Эйлера (101) имеем:

или

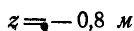
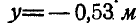
Из первых двух уравнений находим, что и , а поэтому искомая точка будет:

Задача №4

Маховик радиусом R = 1 м вращается вокруг неподвижной оси, проходящей через его центр перпендикулярно к плоскости чертежа, согласно уравнению

Найти скорость и ускорение точки М обода маховика по прошествии 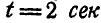после начала его движения. Для всех точек маховика, расположенных вдоль радиуса ОМ, изобразить графически скорости и ускорения.

Решение. Найдем сначала по формулам (87) и (90) угловую скорость и угловое ускорение маховика:

и 

Далее, линейная скорость, нормальное и касательное ускорения’ точки М в момент t найдутся по формулам (89) и (91):

При 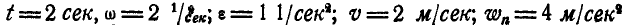и

Величина и направление ускорения точки М определятся по формулам (92) и (93):

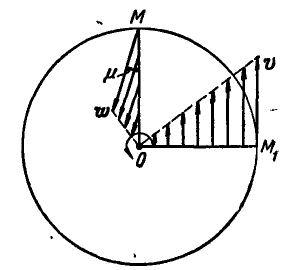
Так как величины линейных скоростей и ускорений точек, расположенных на одном из радиусов’маховика, например ОМ, зависят от величины самого радиуса, входящего в формулы (89) и (92) в первой степени, то отсюда следует, что концы векторов скоростей и ускорений точек одного радиуса будут расположены на прямой (рис. 167). Для удобства выполнения чертежа на радиусе ОМ дано изображение ускорений точек прямой ОМ, а на радиусе 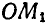— изображение скоростей.

Рис. 167.

Задача №5

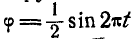
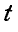
Диск, прикрепленный к вертикальной проволоке, совершает крутильные колебания вокруг оси проволоки так, что угол закручивания его меняется по закону: , где  выражается в секундах.

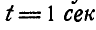
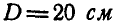
Найти нормальное, касательное и полное ускорения какой-либо точки М на ободе диска в момент , если диаметр диска (рис. 168).

Рис. 168.

Указание: находим сначала угловую скорость и угловое ускорение диска по формулам (87) и (90), а затем ускорение точки М по формулам (91) и (92).

Ответ.

Рис. 169.

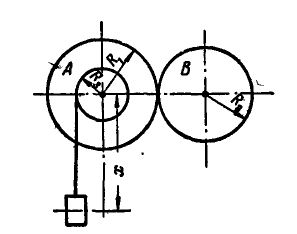
Задача №6

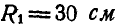
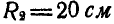
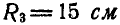
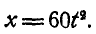
Зубчатое колесо А радиусом находится во внешнем зацеплении с колесом В радиусом (рис. 169). На выступ радиусом колеса А намотана нить, к концу которой подвешен груз. Движение груза в сантиметрах и секундах выражается уравнением: Найти угловую скорость и угловое ускорение колеса В, а также полное ускорение точки на ободе этого колеса.

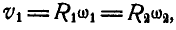
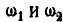
Решение. В общей точке касания колеса А и В имеют одинаковую линейную скорость, равную где  — угловые скорости колес А и В. Отсюда следует, что

т. е. отношение угловых .скоростей колес обратно пропорционально их радиусам.

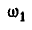
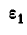
Найдем теперь угловую скорость , и угловое ускорение колеса А:

откуда

и

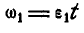
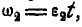
Вращение колес А и В равноускоренное, а поэтому и откуда

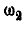
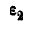
Отсюда угловая скорость  и угловое ускорение колеса В:

и

Ускорение какой-либо точки обода колеса В находим по формуле (92):

Рис. 170.

Вращение твердого тела вокруг неподвижной оси

Вращением вокруг неподвижной оси называют движение твердого тела, при котором его точки описывают окружности с центрами на одной и той же неподвижной прямой, перпендикулярной к их плоскостям

Вращательное движение

Как было показано, для определения движения твердого тела достаточно определить движение трех его точек, не лежащих на одной прямой. Пусть во- время движения тела две его точки О и O₁ остаются неподвижными.

Тогда движение тела можно определить движением третьей точки К, принадлежащей телу и не лежащей на одной прямой с точками О и O₁. Выберем эту точку произвольно и, соединив все три точки прямолинейными отрезками, получим треугольник OO₁K-Так как точки О и O₁ неподвижны, то неподвижна и сторона OO₁ треугольника OO₁K, и движение точки К, а также и всего тела определится поворотом плоскости треугольника OO₁K вокруг прямой OO₁. Точку К мы выбрали произвольно, следовательно, поворачивается вокруг прямой OO1 любая плоскость, проведенная в теле через эту прямую. Такое движение тела называют вращательным движением, или, коротко, вращением, а неподвижную прямую OO₁, вокруг которой вращается тело, называют осью вращения.

Ось вращения может проходить и за пределами тела. Так, например, Луна, двигаясь вокруг Земли, повернута к ней всегда одной стороной. Движение Луны по отношению к Земле можно назвать вращением. Ось вращения проходит за пределами Луны через центры круговых траекторий ее точек.

Если движение тела определять по движению его точек, то вращение вокруг оси можно определить как движение твердого тела, при котором все точки тела описывают окружности с центрами на одной и той же неподвижной прямой, перпендикулярной к плоскостям этих окружностей, а ось вращения можно определить как неподвижную прямую, на которой расположены центры окружностей, описываемых точками вращающегося тела.

Вращательное движение твердого тела определено, если задан как функция времени угол, на который поворачивается плоскость, проходящая через ось вращения и какую-нибудь точку вращающегося тела: φ=φ(t)

Уравнение вращательного движения. Построим основную систему координат xcyz, направив ось Oz по оси вращения тела (рис. 101). Эта система неподвижная и не связана с вращающимся телом. Построим теперь другую, подвижную, систему координат x’0y’z’, направив ось Oz’ также по оси OO₁ вращения тела, а ось Ox’ — на какую-либо точку K₁ тела. Эта система координат неизменно связана с телом и поворачивается вместе с ним относительно основной системы xOyz. Угол φ на который поворачивается плоскость, проходящая через ось вращения и какую-нибудь точку вращающегося тела, называют углом поворота и обозначают буквой φ. Так, если в начальное мгновение оси Ox’ и Ox (см. рис. 101) совпадали, то углом поворота мы назовем двугранный угол между неподвижной плоскостью xθz и подвижной плоскостью x’Oz’ или равный ему линейный угол x’Ox’.

Рис. 101

Угол φ можно рассматривать как угловую координату тела, потому что он определяет положение всего вращающегося тела. Измеряется угол φ в радианах.

Будем считать угол φ положительным, если он отсчитан от положительной оси Ox к положительной оси Оу, т. е. против вращения часовой стрелки, если смотреть с положительного направления оси Oz. При отсчете в противоположную сторону будем считать угол отрицательном.

Чтобы определить вращение тела, надо знать угол поворота как некоторую непрерывную однозначную функцию времени:

φ=φ(t)    (82)

Уравнение (82) является уравнением вращательного движения твердого тела вокруг неподвижной оси.
Всякая плоскость OO₁K, проведенная через ось вращения и какую-либо точку К тела, поворачивается за данное время на такой же угол φ, на который за это же время повернулась плоскость x’Oz’. Это следует из условия неизменяемости твердого тела.

Угловая скорость выражается первой производной от угла поворота по времени:

Угловая скорость. Угол поворота характеризует вращение тела только с геометрической стороны. Чтобы охарактеризовать вращение тела не только в пространстве, но и во времени, возьмем отношение изменения ∆φ угла поворота ко времени Δt, в течение которого это изменение происходило, называемое средней угловой скоростью тела:

                      (83′)

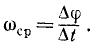
Пределом отношения (83′) при Δt, стремящимся к нулю, является первая производная от угла поворота по времени. Она характеризует изменение угла поворота в данное мгновение, т. е. характеризует вращение тела не только по отношению к окружающему пространству, но и во времени. Эта величина принята за пространственно-временную меру вращения твердого тела вокруг оси и ее называют угловой скоростью тела:

                      (83)

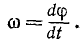
Знак производной (83) указывает, в какую сторону поворачивается тело вокруг оси Oz: если производная (83) положительна, то наблюдатель, смотрящий с положительной стороны оси Oz, видит тело вращающимся против часовой стрелки, т. е. справа налево — от положительного направления оси Ox к положительному направлению оси Оу: при отрицательной производной (83) вращение тела происходит в обратном направлении.

Размерность угловой скорости равна размерности угла поворота, деленной на размерность времени. Но угол поворота является отвлеченной величиной, и размерность его—единица. Следовательно, размерность угловой скорости обратна размерности времени.

[ω]=T^-1.

Чаще всего время измеряют в секундах, тогда единица угловой скорости ceκ^-1.

Равномерное вращение иногда характеризуют числом п оборотов, совершаемых телом за единицу времени (обычно за минуту).

Найдем соотношение между угловой скоростью ω, выраженной в радианах в секунду, и числом оборотов в минуту. Если тело делает n оборотов в минуту, то оно поворачивается за каждую минуту на 2πn радианов, а за секунду—в 60 раз меньше, следовательно,

                      (84)

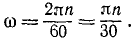
Формулу (84) широко применяют в технической механике. Приближенно можно считать

   (84′)

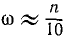
В формулах (84) и (84′) n выражеyо в оборотах за минуту, a ω — в радианах за секунду, как их большей частью и выражают. Однако для очень медленно вращающихся тел число оборотов удобнее считать не за минуту, а за другие единицы времени. Так, Земля вращается вокруг своей оси, делая 1 оборот в сутки. Было бы неудобно считать, что Земля делает 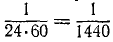 оборота в минуту. Угловую скорость Земли следует подсчитывать не по формуле (84), а из тех соображений, что Земля делает один оборот (2π радианов) за сутки, а в сутках 86400 сек, следовательно,

Самые медленные вращения встречаются в звездном мире. Так< например, период обращения Солнца вокруг центра Галактики (Млечного пути) составляет 190 миллионов лет.

Наибольшая угловая скорость, полученная в технике, соответствует миллионам оборотов в минуту. C такой скоростью вращаются гироскопы Гюгенара —маленькие роторы, подвешенные без подшипников в магнитном поле.

За одно и то же время все части твердого тела поворачиваются вокруг оси на один и тот же угол. Следовательно, угловая скорость является общей мерой вращения для всего тела, и в каждое мгновение тело, вращающееся вокруг оси, имеет только одну угловую скорость.

Для тех случаев, когда тело совершает сложное движение, например вращается вокруг оси в то время, как эта ось поворачивается, удобно изображать угловую скорость вектором, направленным вдоль оси вращения. Величина и положение вектора показывают величину угловой скорости и положение оси вращения. Но вектор угловой скорости, как и вектор момента силы относительно точки, отличается от прочих известных нашим читателям векторов (скорость точки, ускорение точки, радиус-вектор, сила и др.) тем, что, изображая его стрелкой соответствующей длины, отложенной вдоль оси вращения, надо (вполне произвольно) условиться относительно направления стрелки. В нашем курсе мы всюду пользуемся правой системой координат, поэтому установим и для вектора угловой скорости правило правого винта, т. е. будем направлять вектор угловой скорости вдоль оси вращения к той ее стороне, с которой вращение тела представляется происходящим против вращения часовой стрелки. Так, например, вектор угловой скорости земного шара, вращающегося с запада на восток, мы направим к северному полюсу: глядя с северного полюса, мы увидели бы Землю вращающейся против часовой стрелки.

Угловое ускорение выражается первой производной от угловой скорости по времени:

Угловое ускорение. Изменение угловой скорости происходит с течением Времени и, вообще говоря, бывает различным в разные моменты времени. Пространственно-временную меру, характеризующую изменение угловой скорости тела в данное мгновение, называют угловым ускорением тела.

Поскольку угловая скорость — векторная величина, вектором Должно быть и угловое ускорение. Но при вращении тела вокруг Неподвижной оси мы обычно рассматриваем угловую скорость как скаляр, и потому здесь нас могут интересовать только величина и знак углового ускорения.

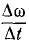
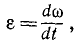
Пусть величина угловой скорости изменилась на ∆ω в течение промежутка времени Δt. Предел отношения при Δt, стремящемся к нулю, выражает угловое ускорение тела и обозначается греческой буквой ε (эпсилон):

               (85)

или, принимая во внимание равенство (83),

Следовательно, угловое ускорение выражается первой производной «от угловой скорости по времени, или, что то же, второй производной от угла поворота по времени. Эта величина характеризует быстроту изменения угловой скорости тела, вращающегося вокруг неподвижной оси.

Размерность углового ускорения равна размерности угла поворота, деленной на квадрат размерности времени, т. е. равна единице, деленной на квадрат времени.

[ω]=T^-2.

Чаще всего время измеряется в секундах, тогда единица углового ускорения ceκ^-2, или по записи, рекомендованной ГОСТом, pa∂/ceκ².

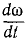
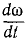
Если с течением времени абсолютная величина угловой скорости тела увеличивается, то производная  имеет тот же знак, что и ω, и вращение тела ускоренное. Если же величина угловой скорости с течением времени уменьшается, то производная  и угловая скорость имеют различные знаки — вращение тела замедленное. Каждое из этих вращений, и ускоренное и замедленное, называют переменным вращением.

Задача №7

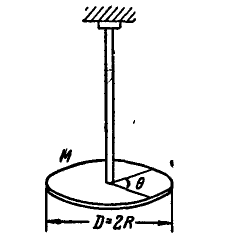
Унифиляр (тело, подвешенное на вертикальном стержне) (рис. 102) закрутили на угол 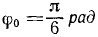от равновесного положения и затем (в мгновение t = 0) предоставили самому себе, и он стал вращаться согласно уравнению

Рис. 102

Определить угловую скорость (в ρa∂/ceκ.) и угловое ускорение (в рад/сек) через каждые 3 сек от начала движения.

Решение. Дифференцируя уравнение движения, получим выражение угловой скорости унифиляра:

Дифференцируя вторично найдем, угловое ускорение унифиляра:

Чтобы определить угол поворота, угловую скорость и угловое ускорение в заданные мгновения, надо в уравнение движения тела и в полученные соотношения подставить t = 3, 6, 9, … и т. д. секунд. Анализируя полученные данные относительно ω и ε, убедимся, что унифиляр совершает крутильные колебания с периодом 18 сек.

• Заказать решение задач по теоретической механике

Равномерное и равнопеременное вращения

Если угловая скорость ω постоянна, то производная 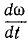= 0, и вращение равномерное. Таким образом, при равномерном вращении тела угловое ускорение равно нулю, угловая скорость постоянна, а угол поворота изменяется пропорционально времени:

ε = 0, ω = const, φ = φ₀+ωt,  (86)

где φ₀-начальное значение угла.

Формулы (86) справедливы только для равномерного вращения тела и неприменимы при других движениях.

Из различных переменных вращений тела в задачах наиболее часто встречается равнопеременное вращение. Равнопеременным вращением называют такое вращение твердого тела вокруг оси, πph котором угловое ускорение остается постоянным:

ε = const.

Интегрируя это уравнение, находим

ω = εt + C₁.

Постоянную интегрирования C₁ находим из начальных данных. В начальное мгновение (при t=0) величина угловой скорости была ω₀. Подставляя эти частные значения аргумента t и функции ω, находим постоянную C₁:

C₁ = ω₀.

Таким образом,

Интегрируя это равенство, получаем

Постоянную C₂ находим из начальных данных. Если при начале вращения тело было повернуто на некоторый угол φ₀, то, подставляя φ₀ вместо φ и 0 вместо t, найдем C₂ = φ₀. Для равнопеременного вращения тела имеем:
      (87)

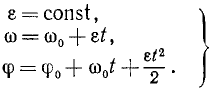
Формулы (87) справедливы только для равнопеременного вращения твердого тела и неприменимы при других движениях.

Задача №8

Барабан суперцентрифуги делает при установившемся движении 30000 об/мин, а после прекращения подачи энергии (на выбеге) вращается равнозамедленно с угловым ускорением ε=π1∕ceκ². Определить время выбега (время до остановки) и угол поворота барабана за это время.

Решение. В мгновение прекращения подачи энергии угловая скорость барабана была

C этого мгновения барабан вращается равнозамедленно по (87):

ω= 1000π—πt.

В мгновение остановки барабана угловая скорость его равна нулю. Подставляя это значение угловой скорости, находим время выбега.

t = 1000 сек = 16 мин 40 сек.

За это время барабан повернется на угол

Чтобы по углу поворота определить число оборотов, надо поделить этот угол (выраженный в радианах) yа 2π—число радианов в одном обороте.

Ответ. t = 16 мин 40 сек, φ = 250 000 об.

Задача №9

В инерционном аккумуляторе Уфимцева (1918 г.) для ветроэлектрических станций стальной диск вращается в глубоком вакууме, делая 20 000 об/мин. Предоставленный самому себе, он продолжает вращаться в течение двух недель. Определить е диска, считая вращение равнозамедленным.

Решение. Определим начальную угловую скорость диска н время (2 нед.) до остановки в секундах:

Ответ получим, разделив ω₀ на t.

Ответ. 

Траектории, скорости и ускорения точек вращающегося тела

Точки вращающегося тела, расположенные на одной прямой, параллельной оси вращения, совершают одинаковые движения

Траектории точек вращающегося тела

Вращением тела называют движение, при котором точки тела описывают окружности с центром на оси вращения. Следовательно, по самому определению вращательного движения траектории точек тела—окружности.

Если тело мысленно пересечь какой-либо плоскостью, перпендикулярной оси вращения, то в этой плоскости будут находиться круговые траектории всех расположенных в ней точек тела. Очевидно, что движения точек тела, лежащих на ном в какой-либо из точек к этой плоскости, совершенно одинаковы, а потому и движение точек всего тела может быть полностью охарактеризовано движением точек, лежащих в этой плоскости.

Сохраним и в этом параграфе расположение осей координат (см. рис. 101), при котором оси Oz и Oz’ неподвижной и подвижной систем совпадают с осью вращения тела, а плоскость x’0y’ находится в плоскости хОу.

Возьмем в этом теле какую-либо точку К (рис. 103), координаты которой относительно подвижной системы обозначимx’,y’ и г’. Эти координаты точки К во время вращения тела не меняются, так как оси подвижной системы координат неизменно связаны с телом и вращаются вместе с ним. Координаты той же точки в основной системе обозначим х, у и z.

Координаты х и у точки К связаны с координатами х’ и у’ той же точки формулами, известными из аналитической геометрии и понятными из чертежа (рис. 103):

х = х’ cos φ—y’ sin φ,    (88′)

y = x’ sin φ +y’ os φ.     (88″)

Если тело вращается, то с течением времени меняется угол φ, являющийся некоторой функцией (71) от времени t, а следовательно, меняются и координаты х и у точки К в основной системе отсчета. Координата же z при направлении оси Oz вдоль оси вращения не изменяется и остается равной z’:

z = z’.    (88″‘)

Аналогично можно определить подвижные координаты по неподвижным и углу φ:

х’ = х cos φ у sin φ; y’ = y cos φ—x sinφ; z’ = z.

Скорость точки тела, вращающегося вокруг оси, равна произведению угловой скорости тела на расстояние точки от оси: υ= ωr

Скорости точек вращающегося тела. Для получения проекций скорости на неподвижные оси координат продифференцируем по времени равенства (88), рассматривая φ как функцию времени. Будем иметь

Но согласно (88) выражение, стоящее в скобках в первом из этих равенств, есть у, а во втором х, а потому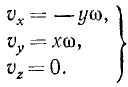      (89)

Возводя эти равенства в квадрат и складывая, найдем

Но в левой части мы имеем квадрат полной скорости точки, а в скобках правой части — квадрат расстояния точки от оси. Мы получили одну из главнейших формул кинематики:
υ = ωr     (90)

— величина скорости точки вращающегося тела равна произведению угловой скорости тела на расстояние точки от оси вращения.

Таким образом, для определения скорости точки вращающегося тела нет необходимости знать ее координаты, надо знать лишь расстояние точки от оси вращения и угловую скорость тела.

Можно определить угловую скорость тела по скорости какой-либо из его точек и по расстоянию этой точки от оси вращения:

      (91)

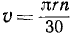
По этим формулам можно определить скорость любой точки вращающегося тела, независимо от того, какую форму имеет тело и находится точка на поверхности или внутри тела. Скорость точки тела, вращающегося вокруг оси, называют вращательной скоростью точки. Она направлена перпендикулярно к плоскости, проходящей через точку и ось вращения, против хода часовой стрелки или по ходу часовой стрелки в зависимости от знака производной (83).

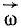
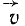
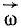
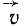
Если же смотреть на тело с той стороны оси вращения, куда мы направили вектор угловой скорости, то вектор вращательной скорости всякой точки тела направлен против хода часов. Такое же направление (против хода часов) имеет вектор , если смотреть на него с конца вектора вращательной скорости .

Следовательно, вектор вращательной скорости точки и по величине и по направлению можно рассматривать как момент вектора угловой скорости тела относительно этой точки. Его можно представить в виде векторного произведения аналогично тому, как это сделано в статике с моментом силы относительно точки.

Вращательную скорость точек, лежащих на поверхности цилиндра (шкива, барабана, махового колеса, вала и т. п.), вращающегося вокруг своей оси, называют окружной скоростью тела. Окружная скорость равна произведению ω на радиус R тела:

υ_{oκp =} ωR.

Задача №10

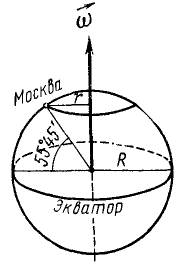
Определить вращательную скорость точек земной поверхности на экваторе и на широте Москвы (55°45′) при вращении Земли вокруг оси (рис. 104). Средний радиус Земли 6371 км и cos 55^o45′ = 0,5628.

Рис. 104

Решение. Вращаясь вокруг своей оси, Земля совершает один оборот (2π рад) за сутки (86 400 сек), и угловая скорость Земли ω=727∙10^-7 pa∂/ceκ. Умножая угловую скорость на радиус Земли, выраженный в метрах (6371 ∙ 10³), найдем вращательную скорость точек Земли на экваторе:

υ= ωR=727 •  6371 • 10^-4 = 463 м/сек.

Для определения вращательной скорости точек в Москве надо умножить ω Земли на расстояние г от Москвы до земной оси:

Она направлена против вращения часовой стрелки, если смотреть с северного полюса.

Задача №11

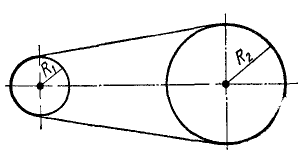
Шкив динамомашины R₁= 15 см (рис. 105) вращается посредством бесконечного ремня от паровой машины со шкивом R₂ — 60 см, делающим 100 об/мин. Определить угловую скорость ω₁ шкива динамомашины.

Рис. 105

Решение. Определим окружную скорость шкива паровой машины:

Такова же величина скорости частиц ремня, а следовательно, и окружная  скорость шкива динамомашины. Его угловая скорость

Ответ. ω₁=41,87 рад/сек, n = 400 об/мин.

Касательное ускорение точки вращающегося тела равно произведению углового ускорения тела на расстояние точки от оси вращения тела: α_r=e_r

Ускорение точек вращающегося тела

Если в выражении касательного (69) и нормального (74) ускорений вместо скорости v мы подставим выражение (90) вращательной скорости, то получим касательное и нормальное ускорения точки тела, вращающегося вокруг неподвижной оси.

Касательное ускорение

или 

a_τ = ε_r.      (92)  

Касательное ускорение точки вращающегося тела равно произведению углового ускорения тела на расстояние точки от оси вращения.

Центростремительное ускорение точки вращающегося тела равно произведению квадрата угловой скорости тела на расстояние точки от оси вращения тела:
αN=ω²r

Каждая точка вращающегося тела описывает окружность, а потому радиус кривизны р траектории точки равен расстоянию этой точки от оси вращения тела. Имеем

или 

αN=ω²r

Нормальное ускорение точки вращающегося тела обычно называют центростремительным ускорением. Оно равно произведению квадрата угловой скорости на расстояние точки от оси вращения тела.

Величина полного ускорения точки тела, вращающегося вокруг оси, выражается формулой

Зная касательное и центростремительное ускорения, определим по формуле (75) величину полного ускорения этой точки:

или

 .      (94)  

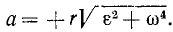
Иногда бывает необходимо определить проекции ускорения точки вращающегося тела на неподвижные оси координат. Для этого продифференцируем равенства (89) по времени, учитывая, что при вращении тела меняется не только его угловая скорость, но и координаты х и у его точек:

a_x =—уε—υ_yω, a_y = xε+υ_λω, α_z = 0.

Подставляя вместо υ_x и υ_y их значения (89), найдем проекции ускорения точки вращающегося тела на неподвижные оси:

 .      (95)  

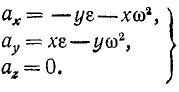
Возводя в квадрат и складывая, найдем

a² = (x² + y²) (ε² + ω⁴),

или, так как x²+y² = r², получаем уже знакомую нам формулу (94). Следовательно,

a_Tх=—yε; α_Ty = xε; a_Nх= — xω²; a_Ny=-yω².       (95′)

Задача №12

Тело вращается вокруг оси Oz без начальной угловой скорости и с постоянным угловым ускорением ε = 0,4 рад/сек². Определить для t = 10 сек: 1) координаты точки К тела, если при t = 0 координаты точки К были: х = +10, y=0, z-0∙, 2) ее вращательную скорость; 3) направляющие косинусы вращательной скорости; 4) касательное и центростремительное ускорения той же точки; 5) направляющие косинусы касательного и центростремительного ускорений; 6) угол, составляемый векторами полного и центростремительного ускорений.

Решение. Тело вращается равноускоренно; по (87) найдем угловое ускорение, угловую скорость и угол поборота тела для заданного мгновения: ε = 0,4 ρaд/ceκ²; ω = 0,4 • 10 = 4 ρaд/ceκ;

Тело повернулось за 10 сек на 20 рад. Переведем радианы в градусы:

a_r = 1145^о54’56»,

за вычетом полных оборотов определим угол αr, составляемый радиусом-вектором с осью Ox (рис. 106):

20 рад = 65^о54’56»,

По тригонометрическим таблицам находим: cos a_r = 0,4080, sin a_r = 0,9130. Приняв во внимание, что расстояние точки К от оси вращения тела равно 10 см, найдем координаты точки К в мгновение t=10 сек:

х=10 cos a_r = +4,080 см,

y = 10 sin a_r = +9,130 см.

Величину вращательной скорости определим по (90):

υ = ωr = 4 • 10 = 40 см/ceκ.

Чтобы определить направляющие косинусы вращательной скорости, найдем сначала по (89) ее проекции на оси координат:
υ_x= — yω = — 36,52 см/сек,

υ_y= +xω = + 16,32 см/сек

по затем по (62) — направляющие косинусы:

Определим по (92) величину касательного ускорения:

a_τ=ε_r = 0,4 ∙10 = 4 см/ceκ²

и по (95′) — проекции касательного ускорения на оси х и у:

a_Tx = — yε=—3,652 см/сек², a_Ty = xε =+1,632 см/сек².

Разделив проекции на модуль касательного ускорения, найдем направляющие косинусы касательного ускорения:

Мы видим, что направляющие косинусы касательного ускорения тождественны с направляющими косинусами скорости.

Напомним, что знак направляющего косинуса определяется знаком числителя. Если ω и ε имеют одинаковые знаки (как в данной задаче), то тело вращается ускоренно и направление касательных ускорений его точек совпадает с направлением их скоростей, если же знаки ω и ε различны, то вращение замедленное и векторы касательных ускорений и скоростей точек направлены в противоположные стороны.

Величину центростремительного ускорения определим по (93);

a_N=ω²r = 4²∙10 = 160 см/сек²

и по (95′) —его проекции на оси координат: 

a_Nx=—xω²= —65,280 см/сек²,

a_Ny = — yω² = —146,080 см/сек².

Проекции нормального ускорения точки на оси координат имеют знаки, обратные знаку соответствующей координаты точки. В самом деле, ayx отрицательна, если абсцисса х положительна, и положительна, если х отрицательна (аналогично и ayy). Следовательно, центростремительное ускорение всегда направлено к началу координат, т. е. к центру круговой траектории точки.

Разделив проекции центростремительного ускорения на его модуль, найдем направляющие косинусы центростремительного ускорения:

Так как касательное ускорение перпендикулярно к центростремительному, то (по условию перпендикулярности, известному из аналитической геометрии) сумма произведений соответствующих направляющих косинусов должна равняться нулю. Действительно,

cos a_T cos a_N + cos β_T cos β_N = ( — 0,9130) ( —0,4080) + ( + 0,4080) ( — 0,9130) =0.

Определим теперь тангенс угла между направлением полного и нормального ускорений:

Пользуясь таблицами тригонометрических функций, определим, что угол равен l^o26’0″.

Ответ. 1) х = + 4,080 см, у = + 9,130 см; 2) υ = 40 см/сек, 3)cos a_υ=—0,9130, cos β_υ = +0.4080; 4) a_T = 4 см/сек1, a_N= 160 см/сек²; 5) cos a_T=—0,9130, cos β_T= +0,4080, cos a_N = — 0,4080, cos β_N=—0,9130; 6) угол равен l^o26’0″.

Задача №13

При сборке ротора молотковой дробилки была допущена неточность, в результате которой центр тяжести ротора отстоит от оси вращения на расстоянии 1 мм. Определить центростремительное ускорение центра тяжести ротора, если n = 3000 об/мин.

Решение. По формулам (84) и (93) имеем

Ответ. a_N=98,6 м/сек² ≈ 10g.

Зависимости между углом поворота, угловой скоростью, угловым ускорением и временем аналогичны зависимостям между расстоянием, скоростью, касательным ускорением и временем

Аналогия формул

Формулы кинематики вращательного движения аналогичны соответствующим формулам кинематики точки и могут быть из них получены, если заменить расстояние s углом поворота φ, скорость υ— угловой скоростью ω и касательное ускорение α_T-угловым ускорением ε. Это правило является мнемоническим, оно непригодно для вывода формул, но может облегчить их запоминание. Ниже приведен ряд формул, получающихся одна из другой такой заменой.

Движение точки	Вращение точки
Уравнение движения по траектории s=s(t) Средняя скорость точки Величина скорости точки Величина касательного ускорения Равномерное движение точки Равнопеременное движение	Уравнение вращения вокруг оси φ=φ(t) Средняя угловая скорость тела Величина угловой скорости тела Величина углового ускорения Равномерное вращение тела Равнопеременное вращение

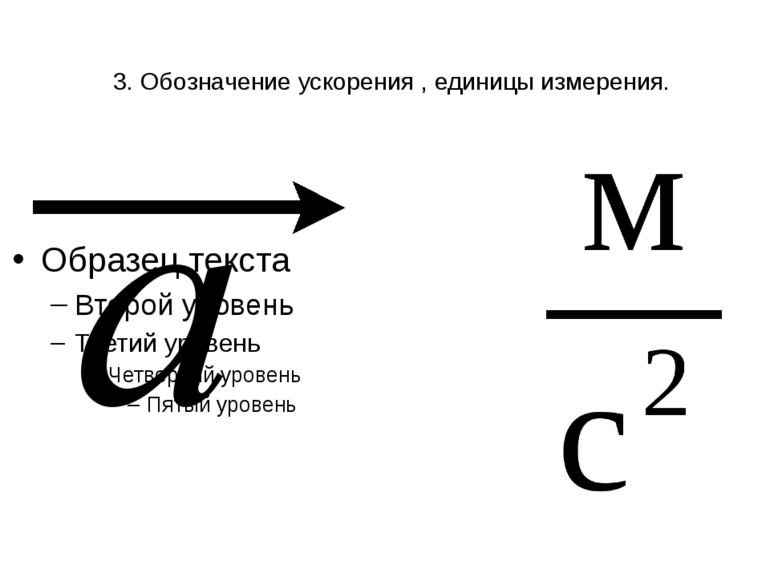
Угловое ускорение – что это?

Угловое ускорение (varepsilon) – физическая величина, характеризующая изменение угловой скорости при движении тела.

Единица измерения: (lbrackvarepsilonrbrack=frac1{с^2}) или (с^{-2})

Угловая скорость

Круговым движением точки вокруг оси называют движение, где траектория точки – окружность с центром, который лежит на оси вращения, перпендикулярной плоскости окружности.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Угловая скорость (omega) – векторная физическая величина, характеризующая скорость изменения угла поворота при круговом движении точки или твердого тела.

При движении по окружности (круговом движении) скорость меняет свое направление, значит такое движение не может считаться равномерным, оно ускоренное или равноускоренное (в частных случаях).

Вектор угловой скорости направлен вдоль оси вращения.

Основные формулы для вычисления угловой скорости

Для равномерного вращения (когда за равные отрезки времени тело поворачивается на один и тот же угол):

1. (omega=frac nt), где (n) – количество оборотов за единицу времени (t).
2. (omega=fracvarphi t), где (varphi) – угол поворота, (t) – время, за которое он совершен.
3. (omega=frac{2pi}T), где (Т) – период обращения (время, за которое тело/точка совершает один оборот).
4. (omega=2pinu), где (nu) – числом оборотов в единицу времени.

Единица измерения угловой скорости в СИ: (lbrackomegarbrack=frac{рад}с)

Связь между угловой скоростью и нормальным (центростремительным) ускорением

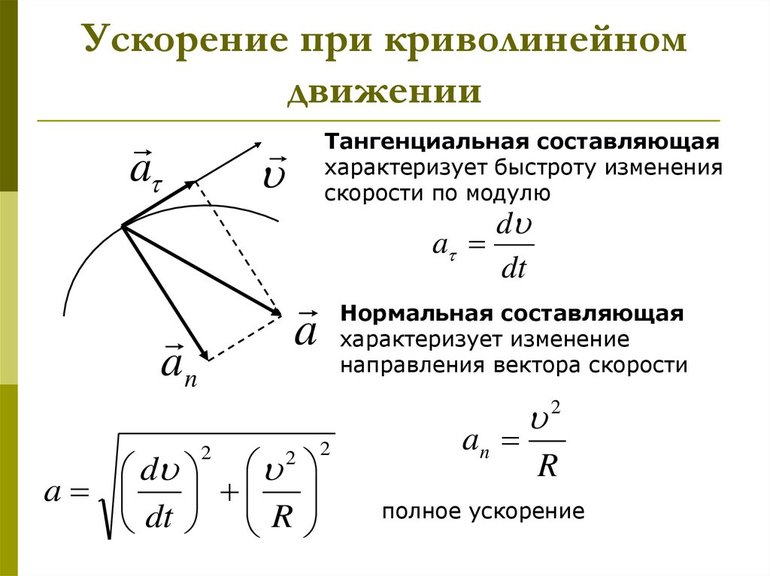
Центростремительное (нормальное) ускорение (a_n) – это составляющая полного ускорения, которая характеризует изменение направления вектора скорости при криволинейном движении. Другим компонентом полного ускорения является тангенциальное ускорение, оно характеризует изменение величины скорости.

Центростремительное ускорение определяется по формуле:

 (a_n=frac{V^2}R),

где (V) – скорость движения, (R) – радиус окружности.

Единица измерения в СИ: (lbrack a_nrbrack=frac м{с^2})

Итак, формула связывающая эти две величины:

(a_n=omega^2R)

Основные формулы для расчета углового ускорения

Угловое ускорение маховика

(varepsilon=fracomega t=frac{2pi n}t), где (n) – количество оборотов за единицу времени (t).

Среднее угловое ускорение

Средним угловым ускорением тела называют отношение изменения угловой скорости к отрезку времени, за который оно совершилось.

(leftlanglevarepsilonrightrangle=frac{triangleomega}{triangle t})

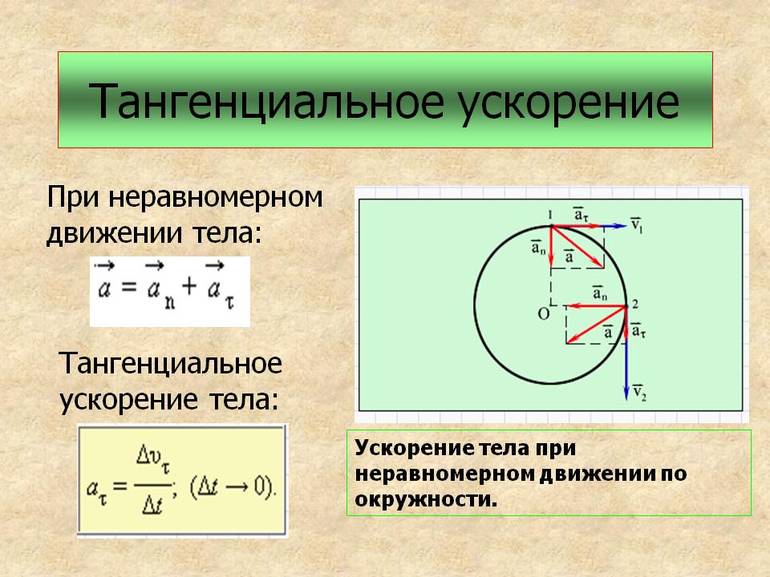
Тангенциальное ускорение

Тангенциальным (касательным) ускорением (a_tau) называют ту составляющую полного ускорения, которая направлена по касательной к траектории движения в данной точке. Тангенциальное ускорение описывает изменение скорости по модулю при криволинейном движении.

(a_tau=varepsilon r), где (varepsilon) – угловое ускорение, (r) –  радиус кривизны траектории в заданной точке.

Мгновенное угловое ускорение

Мгновенное угловое ускорение (alpha) есть первая производная угловой скорости по времени или вторая производная углового перемещения по времени.

(alpha=tg(varepsilon)=frac{;domega}{dt}=frac{d^2phi}{dt^2})

Движение по окружности

Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.

Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.

Если угол поворота мал, то ∆ l ≈ ∆ s .

Угловая скорость

При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.

Определение. Угловая скорость

Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .

ω = ∆ φ ∆ t , ∆ t → 0 .

Единица измерения угловой скорости — радиан в секунду ( р а д с ).

Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:

Нормальное ускорение

При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.

При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.

a n = ∆ v → ∆ t , ∆ t → 0

Модуль центростремительного ускорения можно вычислить по формуле:

a n = v 2 R = ω 2 R

Докажем эти соотношения.

Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .

В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.

По определению ускорения:

a → = ∆ v → ∆ t , ∆ t → 0

Взглянем на рисунок:

Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .

Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:

R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R

При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:

a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .

При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.

Запись центростремительного ускорения в векторной форме выглядит следующим образом:

Здесь R → — радиус вектор точки на окружности с началом в ее центре.

Тангенциальное ускорение

В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.

Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.

a τ = ∆ v τ ∆ t ; ∆ t → 0

Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t

Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.

Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .

Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω

Тангенциальное ускорение — определение, формула и измерение

Общие сведения

Первая лекция для студентов, изучающих кинематику, начинается с рассмотрения тангенциального ускорения, характеризуемого произвольным движением. По сути, рассматривается неравномерное прямолинейное движение общего вида. Кинематика входит в механику и изучает перемещение объектов без учёта сил, вызвавших их движение. Под перемещением понимают изменение положения в пространстве по отношению к другому физическому телу, которое и считается точкой отсчёта. Если изменение положения связать с координатами и временем, то образуется система отсчёта. С её помощью можно определить положение объекта в любой момент.

В кинематике любые процессы принято рассматривать, приняв тело за материальную точку. То есть его размерами и формой пренебрегают. При изменении за какой-то промежуток времени точка проходит путь, описывающийся линией — траекторией. Она является скалярной величиной, а само перемещение — векторной. Движение материальной точки может происходить с разной скоростью и ускорением. Быстроту движения разделяют на среднюю и мгновенную. Вторая определяется как предел, к которому стремится скорость на бесконечно малом временном интервале: v = Δs / Δt (Δt → 0).

Перемещение может происходить с ускорением. Это физическая величина, определяющая изменение быстроты перемещения. Иными словами, показывает изменение положения за единицу времени. Измеряется она в метрах на секунду в квадрате. В кинематике существует три вида ускорения:

• Тангенциальное — направленное вдоль касательного пути точки в определённый момент. Из-за происхождения слова его часто называют касательным.
• Нормальное — совпадающее с нормалью траектории изменения положения.
• Полное — определяющееся суммой тангенциального и нормального ускорений.

Но также используется понятие «вектор среднего ускорения тела». Определяется он как приращение вектора скорости за промежуток времени: aср = Δv / Δt. При этом он будет совпадать по направлению с вектором скорости, то есть направлен в сторону вогнутости траектории.

Угловое ускорение

Если имеется какая-то точка, находящаяся на вращающемся теле, то скорость её направлена по касательной. Когда движение равномерное, то линейная скорость связана с угловой равенством: v = w * r. А вот ускорение тела будет направлено по радиусу к центру окружности, причём модуль вычисляется как a = v / r либо если это точка на вращающемся теле: a = w2 * r.

В момент, когда тело поворачивается за небольшой промежуток времени на угол дельта фи, угловую скорость можно связать с условием поворота через формулу: w = Δ φ / Δ t. Если тело вращается равномерно, то промежуток времени может быть любым. В ином случае эта величина будет равна мгновенной угловой скорости.

Можно представить, что материальная точка движется неравномерно, то есть изменяется угловая скорость тела. Линейная скорость не будет представлять собой постоянную величину, в отличие от равномерного перемещения. Угол поворота равняется: w = v / r. Так как скорость не может быть константой, то отсюда следует, что и угловая скорость не будет постоянной величиной. Её изменение обозначают Δw. Она равняется разности конечной угловой скорости и начальной: Δw = wк — wн.

Изменение угловой скорости можно разделить на промежуток времени, за который оно поменяло значение: (wк — wн) / Δt. По сути, получается ускорение. Обозначается характеристика буквой эпсилон E и называется угловым ускорением. Измеряется характеристика в радианах на секунду в квадрате. Её смысл заключается в описании физической величины через отношение изменения угловой скорости тела за небольшой промежуток времени к длительности этого промежутка.

Пусть есть дуга окружности с центром. В начальный момент времени у тела есть скорость, направленная по касательной к траектории v0. Через некоторое время точка переместится по окружности на небольшое расстояние. Так как движение неравномерное, модуль скорости изменится v ≠ v0. Для того чтобы найти ускорение тела, нужно воспользоваться следующей формулой: a = Δv / Δt, при этом Δv = v — v0.

Чтобы найти эту разность, нужно воспользоваться правилом треугольника. Для этого следует перенести вектор V0 к V и соединить их линией. Радиус от центра к материальной точке можно обозначить R. Дельта V можно представить, как сумму взаимно перпендикулярных векторов. Один из них будет направленных тангенциально к радиусу, в физике обозначают его Δ Vτ, а другой радиально Δ Vr. В итоге: ΔV = Δ Vτ + Δ Vr.

Вывод формулы

Для доказательства формулы необходимо рассмотреть плоскую систему координат, в которой материальная точка изменяет своё положение по криволинейной траектории. В начальный момент её скорость будет равняться V0. Через некоторое время она изменится и станет V. На графике в плоском измерении это можно представить в виде синусоиды. В определённый момент времени скорость превышает начальную: V > V0. На схеме вектор нулевой скорости направлен из точки t0 вверх по касательной, а вектор V с нижней точки синусоиды параллельно оси ординаты.

Исходя из графика, можно сделать два вывода:

• Через промежуток времени Δt скорость изменяется как по направлению, так и по модулю: Δt = t — t0.
• Вектор изменения скорости, определяемый по правилу треугольника, будет равняться разности существующей скорости на данный момент и начальной: Δv = v — v0.

Для того чтобы построить вектор изменения Δv, нужно из конечной точки отрезка V0 провести линию к рассматриваемой точки, характеризующейся во времени скоростью V. Вершины полученного треугольника можно обозначить буквами ABD. Из верхнего угла B на сторону AD можно опустить медиану. Точка пересечения со стороной пусть будет C. Получается, что вектор Δv можно разложить на две составляющие — отрезки BC и СD. Причём медиана равняется Δvn, а изменение по оси ординаты Δvt.

Для разложения необходимо использовать вектор АС, длина которого совпадает с Vo по модулю: |AC| = |AB| = V0. Так как Δvn — результирующий вектор, то его можно вычислить через сумму: Δv = Δvn + Δvt. Причём первый член в равенстве характеризует изменение быстроты за промежуток времени по направлению, а второй — по модулю. Исходя из того, что t не равняется нулю, на него можно разделить левую и правую часть равенства: Δv / Δt = Δvn / Δt + Δvt / Δt. Если дельта-времени стремится к нулю, то формулу можно переписать в виде: lim Δv / Δt = lim Δvn / Δt + lim Δvt / Δt.

Учитывая связь между ускорениями и то, что полное значение состоит из суммы изменения быстроты движения по модулю и направлению, можно утверждать о верности формулы: a = at + an. Так как направление векторов ускорения и скорости всегда совпадают, то последний можно представить, как параметр, состоящий из двух взаимно перпендикулярных компонент:

• at — тангенциальной составляющей, совпадающей с отрезком V;
• an — перпендикулярным по отношению расположения V вектором.

Используя теорему Пифагора, можно сказать, что модуль полного ускорения равняется корню квадратному из суммы квадратов тангенциального и нормального ускорения: a = √at 2 + an 2 .

Решение простых примеров

В школьном курсе на уроках физики учащимся для закрепления материала предлагается решить определённый тип задач, используя определение тангенциального ускорения. Это типовые примеры, объясняющие суть характеристики и её применение в реальной практике. Вот некоторые из них.

1. Вычислить все ускорения точки, лежащей на окружности, через десять секунд после воздействия на диск вращателя. При этом учесть, что радиус окружности составит 20 см, а угол между валом и радиус вектором тела соответствует закону: j =3-t+0.2t 3 . Для решения примера необходимо использовать формулы для нахождения угловой скорости и ускорения. Подставив заданные значения, можно получить: w = d φ / dt = -1 + 0,2 * 3t 2 и e = dw / dt = 0,6 * 2t. Применив формулу связи, легко найти ускорение: at = R * E * (0,6 * 2t) = 1,2 * Rt = 24 м 2 /с. Подставив в формулу нормального ускорения значения, можно вычислить и его an = V 2 / R = R * (0,6 * 10 2 — 1) 2 / 0,2 = 696 м/с 2 . Отсюда полное ускорение будет равняться: a = √ 24 2 + 696 2 = 697 м/с 2 .
2. Материальное тело перемещается по окружности, имеющей радиус 20 см. При этом тангенциальное ускорение равняется 5 см на секунду в квадрате. Определить, сколько понадобится времени, чтобы ускорения сравнялись и нормальное стало больше тангенциального в два раза. Исходя из условия, можно утверждать, что движение является равноускоренным. Поэтому можно применить формулы: an = V2 / t; at = V / t. Отсюда: t = V / at, а V = √an * R. Подставив второе выражение в первое, получится: t = (√an * R) / at. При равенстве ускорений an = at, будет верной запись: t = √R / at = √20 / 5 = 2 с. Для второго случая an = 2at, поэтому: t = (√2 * 20) / 5 = 2,8 c.

Но не всегда решаемые задания можно решить, обойдясь одной формулой. При этом значения тех или иных величин могут быть довольно сложными для проведения вычислений. В таких случаях есть резон использовать так называемые онлайн-калькуляторы. Это специализированные сайты, выполняющие подсчёт в автоматическом режиме. Из таких сервисов можно выделить: сalc, widgety, webmath. Указанные интернет-решители работают на русском языке, так что вопросов, как с их помощью выполнять расчёты, возникнуть не должно.

Сложная задача

Пусть имеется физическое тело, которое движется, замедляясь по окружности радиусом R так, что в каждый момент времени её тангенциальное и нормальное убыстрение равны друг другу по модулю. Необходимо найти зависимость скорости и полного ускорения от времени и пройденного пути. В начальный момент скорость равняется V0.

Согласно условию, тангенциальное ускорение будет отрицательным, так как точка движется, замедляясь. Для понимания задачи можно изобразить схему движения. Для этого необходимо нарисовать окружность и указать на ней вектор начальной скорости, тангенциального и нормального ускорения. Изобразить вектор полного ускорения как сумму векторов.

Нормальное ускорение можно выразить через скорость и радиус: an = V 2 / R. Затем необходимо записать формулу для тангенциального ускорения: at = dV / dt. Так как они равны, то справедливым будет равенство: V 2 / R = dV / dt. Анализируя уравнение, можно сделать вывод, что так как скорость и радиус положительный, то слева будет стоять величина со знаком плюс. Но, с другой стороны, со временем скорость убывает, поэтому с правой стороны нужно поставить знак минус: V 2 / R = — dV / dt.

Полученное уравнение является дифференциальным и показывает зависимость скорости от времени. Равенство можно преобразовать, умножив на отношение dt / V 2 . В итоге должно получиться выражение: dV / V 2 = — dt / R. Это уравнение можно проинтегрировать. При этом пределами интеграла с левой стороны будет V0 и V, а с правой — 0 и t. Получился обыкновенный степенной интеграл, который будет равняться: 1 / V = dt / R.

Подставив пределы, можно получить равенство: (1 / V) — (1 / V0) = t / R. Из полученной формулы следует выразить скорость: V = (V0 * R) / (R + V0 * t). Поделив числитель и знаменатель на радиус, ответ примет вид: V (t) = V0 / (1 + (V0 * t / R)).

Теперь можно найти тангенциальное убыстрение, так как оно представляет производную от скорости. После взятия производной получится: at = dV / dt = — V02 / R (1 + V0 * t / R)2 = — V2 / R. Отсюда можно написать, что модуль полного ускорения будет равняться: a = √2 *|ar| = (√2 * V2) / R. Осталось найти путь. Он совпадает с длиной дуг и равняется интегралу модуля скорости от времени. После решения должно получиться равенство: S (t) = R * ln (1 + V0 * t / R). Задача решена.

Движение материальной точки по окружности. Центростремительное ускорение.

Линейная и угловая скорости

Движение по окружности нас окружает постоянно – это может быть мотоциклист на мототреке, вращение грузика на веревке, движение по выгнутому круглому мосту, любой поворот на дороге тоже можно рассматривать, как движение по части окружности и т.д.

Давайте представим, что мы смотрим сверху на мототрек (см. рис.1.). Пусть точка (А) это мотоциклист, который движется с постоянной линейной скоростью (vec), и за какое-то время (t) он переместится по дуге окружности (^<’>) в точку (^<’>). Его пройденный путь будет равен длине дуги окружности (^<’>).

Определение Линейная скорость – это путь, который проходит мотоциклист за единицу времени (например, за секунду):

Понятно, что чем больший путь (большую длину дуги) успевает пройти тело за одно и тоже время, тем быстрее оно движется, тем больше его линейная скорость. Линейная скорость — это обычная скорость, к которой мы все привыкли. Обратите внимание, что вектор линейной скорости всегда направлен по касательной к траектории, в нашем случае – по касательной к окружности. Чуть позже нам это пригодится.

И так, при движении по окружности можно двумя способами измерять скорость – при помощи линейной скорости (какое расстояние проходит тело за единицу времени) и при помощи угловой скорости (на какой угол поворачивается тело за единицу времени). Эти скорости, очевидно, должны быть связаны между собой.

Но прежде чем, вывести это соотношение, представьте, что отрезок (AO) вращается по окружности (см.Рис.1.) и за время (t) переходит в отрезок (^<’>O) — точка (A) переходит в точку (^<’>), а точка (B) – в точку (^<’>).

При этом точка (A) проходит за время (t) расстояние равное длине дуги окружности (^<’>), а точка (B) за тоже самое время (ведь обе точки лежат все время на одной прямой) расстояние (^<’>).

А на какой угол успевают повернуться точки (A) и (B) за одно и тоже время (t)?

Из рисунка 1 видно, что они обе поворачиваются на один и тот же угол (Deltavarphi). А так как угловая скорость по определению, это отношение угла ко времени, то угловые скорости точек (A) и (B) одинаковые.

И так, что мы имеем – оказывается, что при удалении линейная скорость растет, а угловая скорость при этом не меняется. Тогда логичной выглядит следующая формула, связывающая угловую и линейную скорости:

где (V) – линейная скорость,

(omega) – угловая скорость,

(R) – радиус вращения.

Период и частота вращения

Важными характеристиками любого вращательного движения являются частота и период:

Определение Период – время, за которое тело совершает полный оборот.

В нашем примере с мотоциклистом, период – это время, за которое мотоциклист проезжает один полный круг.

Из курса геометрии вспоминаем, что длину дуги окружности можно посчитать как (2*pi*R), где (R) – радиус окружности. Тогда в случае равномерного движения период можно посчитать по формуле, как расстояние деленое на скорость: $$T=frac<2*pi*R>;$$ Подставив сюда формулу ((1)) для линейной скорости через угловую: $$T=frac<2*pi><omega>;$$ Где (V) –линейная скорость вращения.

В системе СИ период измеряется в ([^<-1>]).

Определение Частота – количество оборотов за единицу времени.

В случае с мотоциклистом, частота – это сколько кругов он успевает проехать, например, за один час. Обычно частоту измеряют в оборотах в секунду.

Период и частота вращения связаны между собой выражением: $$T=frac<1><nu>;$$ Отсюда можно получить формулы для частоты, подставив период: $$nu=frac<2*pi*R>=frac<omega><2*pi>;$$

Скорость точки, находящейся на краю вращающегося диска равна (V_A=15(м/с)), а точки, расположенной на 0,2 (м) ближе к центру вращения равна (V_B=10(м/с)). Найти частоту вращения и радиус диска.

Решение: Точка (А) находится дальше от центра на (20 (см)), а значит ее скорость больше, чем у точки (В). По условию так и есть. Так как обе точки находятся на одном радиусе, то угловые скорости у них одинаковые. Распишем угловые скорости для точек (А) и (В) и приравняем: $$omega_A=frac;$$ $$omega_B=frac;$$ $$omega_A=omega_B;$$ $$frac=frac;$$ Из условия (A0=BO+0.2): $$frac=frac;$$ $$frac<15>=frac<10>;$$ $$15*BO=(BO+0,2)*10;$$ $$5*BO=2;$$ $$BO=0,4.$$ Мы нашли радиус окружности по которой вращается точка (В), тогда радиус точки (А) будет на (0,2(м)) больше — (0,6(м)).

Для того, чтобы найти частоту, воспользуемся формулой: $$nu=frac<2*pi*R_A>=frac<15><2*3,14*0,6>=3,98(об/сек);$$ Ответ: (R=0,6(м)) и (nu=3,98(об/сек).)

Центростремительное (нормальное) ускорение

Вернемся к нашему примеру с мотоциклистом, двигающимся по мототреку в форму окружности. (См. Рис.3.) Для начала, представим, что линейная скорость у мотоциклиста постоянна, то есть он двигается равномерно, а значит его ускорение должно быть равно нулю. Это действительно так, но при движении по окружности (или любой другой криволинейной траектории) даже с постоянной скоростью возникает новый вид ускорения – центростремительное, еще его называют «нормальное», ускорение. Оно появляется по причине изменения направления вектором скорости.

На самом деле, для решения задач понимать природу центростремительного ускорения совсем необязательно. Достаточно просто помнить, что при любом криволинейном движении появляется такое ускорение. Его можно вычислить по формуле: $$a_n=frac;$$ где (V) –линейная скорость;

(R) – радиус окружности.

Подставим сюда линейную скорость через угловую — (V=omega*R). И получим еще одну формулу для центростремительного ускорения: $$a_n=omega^2*R;$$ Важно! Центростремительное ускорение всегда перпендикулярно скорости и направлено к центру окружности.

Тангенциальное ускорение

Теперь представим, что мотоциклист едет по круглому мототреку не с постоянной скоростью, а равноускорено/равнозамедлено. В этом случае говорят, говорят, что мотоциклист движется с тангенциальным ускорением.

Тангенциальное ускорение – это обычное ускорение, к которому мы привыкли в курсе кинематики. Оно показывает на сколько успевает измениться скорость за единицу времени, например, за секунду.

Тангенциальное ускорение всегда направлено по касательной к траектории. Если тело ускоряется, то оно сонаправлено с линейной скоростью, а если замедляется, то направлено в противоположную сторону. (см.Рис.3, показано синей стрелкой (vec>))

При равноускоренномравнозамедленном движении тангенциальное ускорение можно посчитать по формуле: $$a_<tau>=frac;$$ где (V_к) – конечная скорость;

(V_н) – начальная скорость;

(t) – время, за которое скорость изменилась с (V_н) до (V_к).

При любом неравномерном движение по криволинейной траектории (окружности), у тела обязательно есть два вида ускорений – нормальное, направленное к центру, перпендикулярно скорости, и тангенциальное, направленное по касательной к траектории. Нормальное ускорение отвечает за изменение направления вектора линейной скорости, а тангенциальное за изменение величины линейной скорости.

Если тело движется с постоянной скоростью, то тангенциальное ускорение равно (0).

Если тело движется по прямой, то нормальное ускорение равно (0).

Векторно сложим эти два ускорения по правилу параллелограмма, и получим вектор общего ускорения, которым обладает тело при движении по окружности. (см. Рис.3., фиолетовая стрелка (vec)).

Колесо радиуса R вращается с постоянной скоростью. Во сколько раз отличаются центростремительные ускорения двух точек расположенный на расстояниях (R/2) и (R/3) от центра колеса

Решение: Так как любая точка колеса вращается с одинаковой угловой скоростью (omega), то воспользуемся формулой для центростремительного ускорения через угловую скорость: $$a_n=omega^2*r;$$ Пусть точка А вращается по окружности радиусом (R/2), а точка В — (R/3). $$a_=omega^2*frac<2>;$$ $$a_=omega^2*frac<3>;$$ $$frac>>=frac<omega^2*frac<2>><omega^2*frac<3>>=frac<2>*frac<3>=1,5$$ Ответ:(frac>>=1.5.)

источники:

http://nauka.club/fizika/tangentsialno%D0%B5-uskoreni%D0%B5.html

http://sigma-center.ru/circularmotion