Как найти эпюру нормальных напряжений

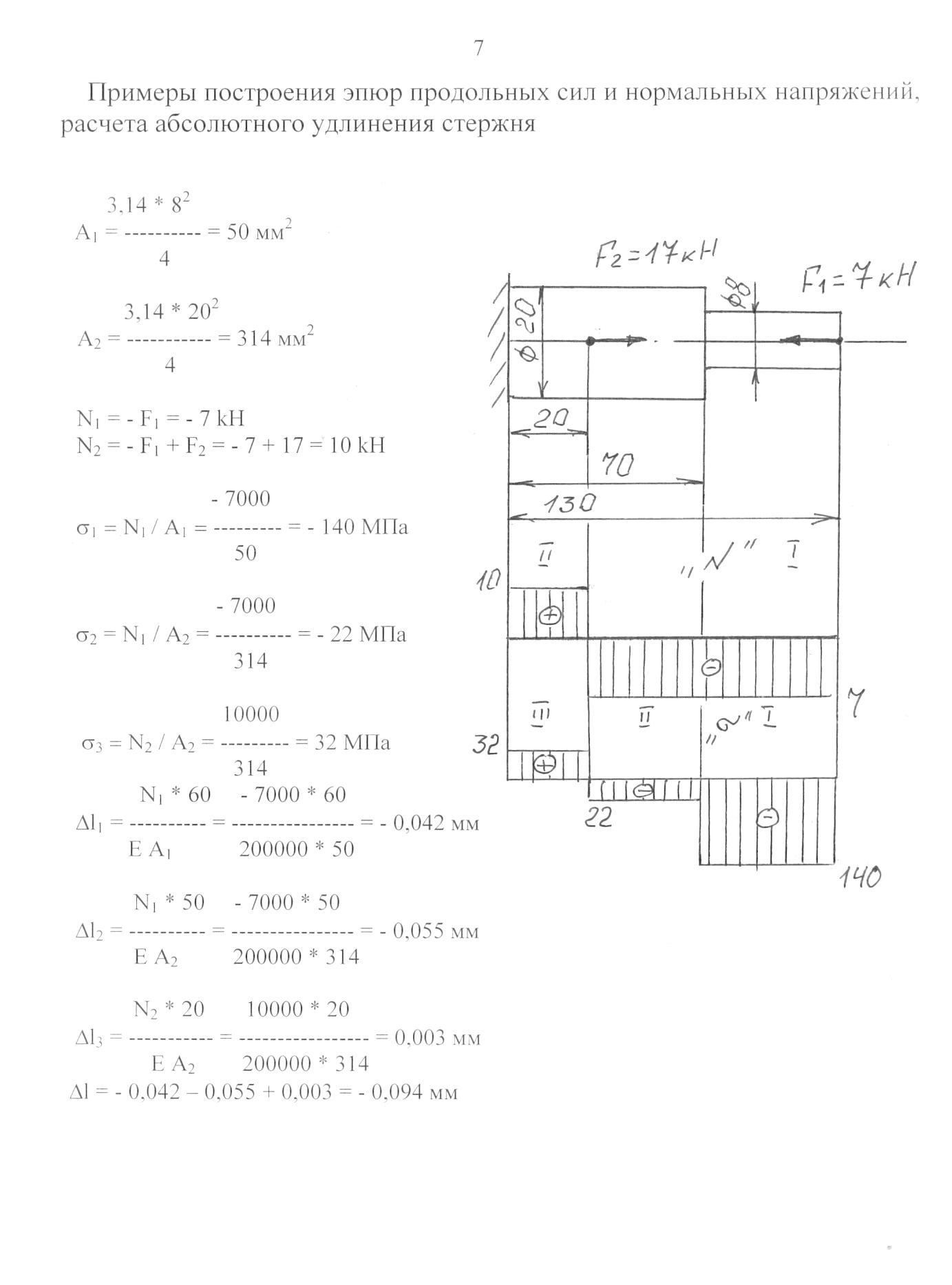
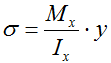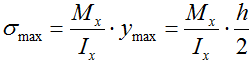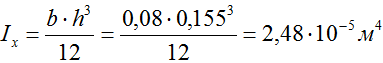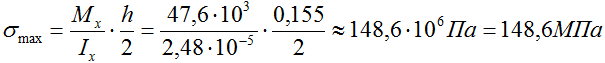Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.

Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!

Что же давай приступим к изучению!

Построение эпюры продольных сил

В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.

Что такое эпюра?

Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.

Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.

Что такое продольная сила?

Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.

Расчёт эпюры продольных сил

Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.

То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.

Правило знаков для продольных сил

Правило знаков для продольных сил следующее:

• если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
• если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках

На первом участке сила F₁ растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:

Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F₁, также действует сила F₂, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:

Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке

Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.

Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.

Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:

То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.

Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:

А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.

Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.

Построение эпюры нормальных напряжений

В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.

Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.

Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A₁=2 см², а на втором и третьем A₂ = A₃ = 4 см².

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.

Построение эпюры осевых перемещений поперечных сечений

Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.

Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:

Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.

Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:

А также удлинения (или укорочения) участка между расчетными сечениями:

В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).

Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.

Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.

Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину W_D (т. к. значение W_D — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.

Учёт распределённой нагрузки

А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил

На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:

Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:

Рассчитываем продольную силу на третьем участке:

Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений

Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений

Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче: 

Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):

Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.

Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.

То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.

Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:

Отмечаем найденное значение на эпюре перемещений:

Пример решения задачи на построение эпюры нормальных напряжений σ при изгибе стальной балки прямоугольного сечения.

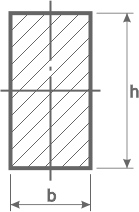
Задача

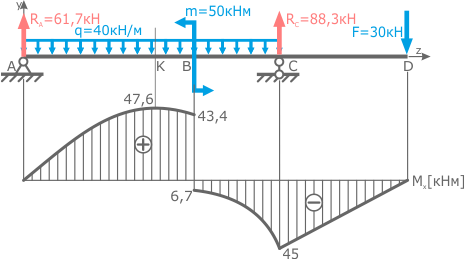
Построить эпюру распределения нормальных напряжений для подобранного ранее прямоугольного сечения двухопорной балки с размерами h=155мм и b=80мм.

Изгибающий момент в опасном сечении балки M_{x max}=47,6кНм.

Другие примеры решений >
Помощь с решением задач >

Пример решения

Предыдущие пункты решения задачи:

1. Определение опорных реакций,
2. Построение эпюр поперечных сил и изгибающих моментов,
3. Подбор размеров прямоугольного сечения балки.

Рассмотрим пример построения эпюры распределения нормальных напряжений в опасном сечении балки.

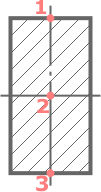
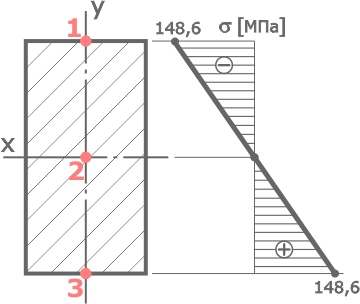
Прямоугольное сечение имеет три характерных точки:

1 – верхняя,

2 – центр тяжести (середина высоты),

3 – самая нижняя точка.

Для построения эпюры достаточно найти значения в любых двух точках, потому что при изгибе нормальная составляющая полных напряжений по высоте сечения меняется линейно.

где I_x – осевой момент инерции сечения,
y – расстояние от оси х проходящей через центр тяжести сечения до точки в которой рассчитывается напряжение.

Очевидно, что на самой оси x (точка №2) где координата y=0 напряжения отсутствуют.

Наибольшие значения нормальных напряжений будут на максимальном удалении от оси x, то есть при y_max=h/2 (в точках 1 и 3).

Рассчитаем момент инерции прямоугольного сечения

Тогда максимальные напряжения

При изгибе верхний и нижний слой балки испытывают продольную деформацию разных знаков.

Знаки напряжений в точках 1 и 3 определяются по построенной ранее эпюре изгибающих моментов M_x.

В данном случае по ней видно, что в опасном сечении балки эпюра моментов имеет положительное значение (+47,6 кНм), что согласно правила знаков при изгибе говорит о том, что в рассматриваемом месте балки сжимаются верхние слои (нижние соответственно растягиваются).

Другие видео

Поэтому в соответствии с правилом знаков для напряжений, нормальные напряжения в верхней точке 1 будут отрицательны (потому что сжатие), а в точке 3 – положительны (растяжение) или σ_т1=-148,6МПа, σ_т3=148,6МПа.

По полученным данным строим эпюру

Как видно по построенной эпюре, нормальные напряжения не превышают заданных допустимых значений, что говорит о том, что размеры прямоугольного сечения были подобраны верно, и прочность балки обеспечена.

Другие примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Растяжением –
сжатием
называется такой вид деформации, при
котором в поперечном сечении бруса
возникает только продольная сила N.

Прямые брусья,
работающие на растяжение – сжатие,
называются стержнями.

Продольной
силой
называется равнодействующая всех
внутренних нормальных сил, возникающих
в этом сечении.

Продольная сила
в любом напряженном сечении бруса
определяется методом сечений: она равна
алгебраической сумме проекций всех
внешних сил, приложенных по одну сторону
от рассматриваемого сечения, на продольную
ось.

Если продольная
сила по всей длине бруса не постоянна,
то строят эпюру «N».
Эпюра
– это график изменения внутреннего
силового фактора по длине бруса.

Правила
построения эпюр продольных сил:

1. Разбиваем брус
   на участки, границами которых являются
   сечения, где приложены внешние силы.

2. В пределах каждого
   участка применяют метод сечений и
   определяют продольную силу. При
   этом если внешняя сила растягивает
   оставленную часть стержня, т.е. направлена
   от сечения — продольная сила положительна;
   если внешняя сила сжимает оставленную
   часть стержня, т.е. направлена к сечению
   – продольная сила отрицательна.

3. Откладываем
   полученные значения и строим эпюру
   продольных сил. Если на участке не
   действует равномерно распределенная
   нагрузка, то эпюра ограничена прямой,
   параллельной нулевой линии.

4. Правильность
   построения эпюр продольных сил
   определяется следующим образом: в
   сечениях, где приложена внешняя сила,
   на эпюре есть «скачки», равные по
   величине приложенной силе.

Правила построения
эпюр нормальных напряжений:

1. Разбиваем брус
   на участки, границами которых являются
   точки приложения внешних сил и сечения,
   где меняется площадь.

2. На каждом участке
   вычисляем нормальные напряжения по
   формуле

N



А

1. Строим эпюру
   нормальных напряжений, по которой
   определяем опасное сечение. При
   растяжении – сжатии опасным является
   сечение, в котором величина нормальных
   напряжений наибольшая.

При растяжении
длина детали увеличивается, а сечение
уменьшается; при сжатии – наоборот.

∆l
= l
– l₀
— абсолютное
удлинение.

∆l

относительное
удлинение или продольная деформация.

l₀

Закон Гука при
растяжении – сжатии: 

Е – модуль
упругости первого рода, характеризует
жесткость материала.

Величина
абсолютного удлинения вычисляется по
формуле Гука:

Nl

∆l
= ——-

EA

Алгоритм решения
задач на построение эпюр продольных
сил и

нормальных
напряжений, расчет абсолютного удлинения
стержня

1. Разбить нулевую
   линию на участки для построения эпюры
   продольных сил. Границы участков
   провести в сечениях, где приложены
   внешние силы.

1. На каждом участке
   вычислить продольную силу методом
   сечений.

1. Отложить полученные
   значения и построить эпюру продольных
   сил. Правильность контролируется так:
   в сечениях, где к стержню приложены
   внешние силы, на эпюре продольных сил
   есть «скачки», численно равные этим
   силам.

1. Разбить нулевую
   линию на участки для построения эпюры
   нормальных напряжений. Границами
   участков являются сечения, в которых
   меняется площадь и приложены внешние
   силы.

1. На каждом участке
   вычислить нормальное напряжение по
   формуле

N

 = ——

A

1. Отложить полученные
   значения и построить эпюру нормальных
   напряжений. По эпюре определить опасное
   сечение детали. Опасными являются
   сечения участка, на котором нормальные
   напряжения наибольшие.

1. Для каждого участка
   на эпюре нормальных напряжений рассчитать
   абсолютное удлинение по формуле Гука.

1. Определить
   суммарную величину абсолютного удлинения
   для всей детали в целом: найти
   алгебраическую сумму абсолютных
   удлинений всех участков. При этом если
   суммарная величина положительна –
   стержень удлинился, если отрицательна
   – стержень укоротился.

Анализ наиболее
часто встречающихся ошибок.

Методические
рекомендации по их устранению

Следует
помнить, что на эпюре продольных сил
границы участков проходят в точках
приложения внешних сил, а на эпюре
нормальных напряжений – в точках
приложения внешних сил и в сечениях,
где меняется площадь стержня.

Чтобы правильно
подставить значения в формулу нормальных
напряжений, нужно с участка эпюры
напряжений, для которого ведется расчет,
подняться на эпюру нормальных сил и
посмотреть, каково значение продольной
силы именно на этом участке. Затем
подняться на чертеж детали и посмотреть,
какова площадь сечения стержня именно
на этом участке.

При расчете
абсолютного удлинения в формулу Гука
продольную силу следует подставлять с
эпюры продольных сил, а величину площади
сечения и длины данного участка – с
чертежа детали.

В формулу нормальных
напряжений и в формулу Гука следует
подставлять значение продольной силы
для данного участка.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

МИНИСТЕРСТВО
ОБРАЗОВАНИЯ НИЖЕГОРОДСКОЙ ОБЛАСТИ

Государственное
бюджетное образовательное учреждение

среднего
профессионального образования

«ПЕРЕВОЗСКИЙ
СТРОИТЕЛЬНЫЙ КОЛЛЕДЖ»

Методическая разработка
учебного занятия

тема «Построение эпюр
продольных сил, нормальных напряжений и перемещений»

Перевоз,

2014г.

Организация-разработчик: ГБОУ СПО «Перевозский
строительный колледж»

Разработчик: М.Н. Кокина

Методическая
разработка учебного занятия на тему «Построение эпюр продольных сил, нормальных
напряжений и перемещений» по дисциплине «Техническая механика»/ Перевозский
строит. колледж; Разр.: М.Н. Кокина. – Перевоз, 2014. –18 с.

В данной работе указаны цель учебного занятия, задачи. Подробно
рассмотрен ход занятия, в приложении представлен демонстрационный и раздаточный
материал. Методическая разработка написана с целью
систематизации учебного материала.

Методическая разработка предназначена для преподавателей и студентов,
обучающихся по специальности 270802, 08.02.01 «Строительство и эксплуатация
зданий и сооружений».

Работа может быть использована при проведении, занятий, открытого
занятия, олимпиады. Студентам может быть полезна при подготовке к зачету,
экзамену.

Оглавление

Введение

План-конспект открытого учебного занятия по
дисциплине «Техническая механика»

Подготовка
к занятию

План
учебного занятия

Ход
занятия

Приложения

 

Введение

Методическая разработка учебного занятия на тему «Построение эпюр
продольных сил, нормальных напряжений и перемещений» по дисциплине «Техническая
механика» предназначена для студентов 2 курса, специальности 270802, 08.02.01
«Строительство и эксплуатация зданий и сооружений».

Выбор указанной темы обусловлен тем, что данные понятия и методы
являются опорной базой для целого ряда технических дисциплин.

В ходе учебного занятия использовались:

Ø   
компьютерные и мультимедийные технологии;

Ø   
интерактивная доска;

Ø   
ноутбук;

Ø   
объяснительно-иллюстративный, репродуктивный,
частично-поисковый методы обучения;

Ø   
раздаточные материалы.

В ходе изучения темы «Построение эпюр продольных сил, нормальных напряжений
и перемещений» у обучающихся формируются следующие компетенции:

Ø    ПК 1.3.Выполнять несложные расчеты и
конструирование строительных конструкций.

Ø    ОК 1 Понимать сущность и социальную значимость своей будущей профессии,
проявлять к ней устойчивый интерес.

Ø    ОК 2 Организовывать собственную деятельность, определять методы и
способы выполнения профессиональных задач, оценивать их эффективность и
качество.

Ø    ОК 3 Принимать решения в стандартных и нестандартных ситуациях и нести
за них ответственность.

Ø    ОК 4 Осуществлять поиск, анализ и оценку информации, необходимой для
постановки и решения профессиональных задач, профессионального и личностного
развития.

Ø    ОК 5 Использовать информационно-коммуникационные технологии для
совершенствования профессиональной деятельности.

Ø    ОК 6 Работать в коллективе и команде, обеспечивать ее сплочение,
эффективно общаться с коллегами, руководством, потребителями.

Ø    ОК 7 Брать на себя ответственность за работу членов команды
(подчиненных), за результат выполнения заданий.

План-конспект открытого учебного занятия по дисциплине «Техническая механика»

Преподаватель: Кокина
Марина Николаевна

Группа: 2-131,
специальность 270802 «Строительство и эксплуатация зданий и сооружений».

Тема занятия: Построение
эпюр продольных сил, напряжений и перемещений

Вид занятия: практическое.

Тип занятия: комбинированный урок с использованием компьютерных и мультимедийных технологий с
элементами игры.

Форма проведения: работа в группах,
самостоятельная работа.

Межпредметная связь: «Математика», «Материаловедение», «Физика».

Основная цель учебного занятия: Научиться строить эпюры продольных сил, напряжений
и определять перемещение для бруса при растяжении или сжатии.

Задачи учебного занятия:

Учебная:

– рассмотреть алгоритм
нахождения продольной силы методом сечений и построения ее эпюры;

— научиться вычислять нормальное напряжение
для растяжения или сжатия в поперечном сечении для ступенчатого бруса и строить
эпюру для данного напряжения;

— научиться определять перемещение свободного
конца бруса.

Развивающая:

— развитие
интеллектуальных качеств обучающихся, познавательного интереса и способностей;

— развитие умения использовать полученные
знания.

Воспитательная:

– формирование сознательного отношения к
изучаемому материалу;

– воспитание культуры труда, формирование
навыков самостоятельной работы.

Методы обучения:

1. Объяснительно-иллюстративный.
2. Репродуктивный.
3. Частично-поисковый.

Средства обучения:

– интерактивная доска;

– ноутбук.

Раздаточный материал:

— карточки-задания;

Учебная литература:

1.                 
Олофинская, В.П. Техническая механика. – М.:
ФОРУМ-ИНФРА-М, 2011

2. Олофинская, В.П. Техническая механика. Сборник тестовых заданий. – М.:
ФОРУМ, 2011

Подготовка к
занятию

1.Разбить группу на две равносильные команды.

2.Выдать задания командам:

a) Выбрать капитана;

b) Придумать название команды и ее девиз;

c) Составить кроссворд по теме «Растяжение и сжатие» (10
слов);

План
учебного занятия

1.     
Организационный момент (3 минуты);

2.     
Актуализация ранее полученных знаний. (12 минут);

3.     
Актуализация материала на примере решения задач (15
минут);

4.     
Закрепление материала (55 минут);

5.     
Подведение итогов и результатов занятий (5 минут);

Ход занятия

1.                 
Организационный момент. (3 минуты)

1.      Проверка присутствующих. Объявление темы и целей занятия. (Слайд 1)

2.      Представление жюри. В состав жюри входят приглашенные преподаватели.
(По ходу занятия члены жюри вносят баллы в итоговую ведомость – приложение 1).

3.      Знакомство с командами. Визитная карточка. (5 баллов)

2.                 
Актуализация ранее полученных знаний. (12
минут)

Мы изучили тему «Растяжение и сжатие прямого бруса» в
разделе «Сопротивление материалов». Познакомились с основными понятиями и
определениями. Изучили методику нахождения величины внутренних усилий.
Рассмотрели принципы построения эпюр. Сегодня мы в течение занятия повторим эту
тему, обобщим и систематизируем полученные знания, отработаем навыки вычисления
внутренних усилий и напряжений и построения их эпюр. Работать будем в командах.
Но, прежде, чем приступить к решению, давайте повторим теоретический материал.

Разминка (фронтальный
опрос).

Сейчас мы с вами проведем небольшой
блиц-опрос по теме «Растяжение и сжатие прямого бруса». Каждой команде по
очереди предстоит ответить на вопросы. Право первого ответа мы разыграем с
помощью интерактивного игрального кубика. Если выпадает четное число, то первой
отвечает вторая команда, если нечетное – первая.

Правильный ответ – 10 баллов.

1.                 
Дайте определение понятия Сопротивление материалов
(Слайд 2)

2.                 
Установите соответствие между понятиями и
определениями (Слайд 3).

3.                 
Покажите на схеме положение внутренних усилий.
(Слайд 4)

4.                 
Какой внутренний силовой фактор возникает при растяжении
или сжатии? (Слайд 5)

5.                 
Какой метод используется для определения продольной
силы? (Слайд 6).

6.                 
Установите порядок выполнения действий метода
сечений? (Слайд 7).

7.                 
Как называется диаграмма, график, показывающий
изменение какой-либо величины по длине бруса. (Слайд 8).

8.                 
Кто вывел данную экспериментальную формулу? (Слайд
9).

9.                 
Что понимается под напряжением? (Слайд 10)

10.             
Составить формулу для определения нормального
напряжения при растяжении или сжатии. (Слайд 11)

3. Актуализация материала на примере решения задач (15 минут)

Ознакомиться с примером построения эпюр продольных сил, напряжений и
перемещений.  (Слайд 12)

Задача 1.  Двухступенчатый
стальной брус нагружен силами F₁=30 кН F₂=40 кН.

Построить эпюры продольных сил и нормальных напряжений по
длине бруса. Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа. Определить перемещение ∆l
свободного конца бруса, приняв Е=2∙10 ⁵ МПа. Площади поперечных
сечений А₁=1,5см²;А ₂ =2см².

Решение.

Разбить брус на участки, начиная от свободного конца.
Границами участков являются сечения, в которых приложены внешние силы, а для
напряжений также и место изменения размеров поперечного сечения.

Определить по методу сечений продольную силу для каждого
участка (ординаты эпюры N) и построить эпюры продольных
сил N. Проведя – параллельно оси бруса базовую (нулевую)
линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые
значения ординат. Через концы ординат провести линии, проставить знаки и
заштриховать эпюру линиями, параллельными ординатам.

Для построения эпюры нормальных напряжений определяем
напряжения в поперечных сечениях каждого из участков. В пределах каждого
участка напряжения постоянные, т.е. эпюра на данном участке изображается прямой,
параллельной оси бруса.

Перемещение свободного конца бруса определяем как сумму
удлинений (укорочений) участков бруса, вычисленных по формуле Гука.

Разбиваем брус на участки.

Определяем ординаты эпюры N на
участках бруса:

N₁= — F₁= -30кН

N₂= — F₂= -30кН

N₃= —F₁+F₂= -30+40=10 кН

Строим эпюру продольных сил

Вычисляем ординаты эпюры нормальных напряжений

σ₁ === –200МПа

σ₂ === –150МПа

σ ₃=== 50МПа

Строим эпюры нормальных напряжений.

4. Проверяем прочность бруса, если допускаемое напряжение [σ] = 160 МПа.

Выбираем максимальное по модулю расчетное напряжение. Iσ_max
I = 200 МПа

Подставляем в условие прочности Iσ_max
I ≤ [σ]

200 МПа ≤ 160 МПа. Делаем вывод, что
прочность не обеспечена.

5. Определяем перемещение свободного конца бруса Е = 2∙10
⁵ МПа.

∆l=∆l₁+∆l₂+∆l₃

∆l₁=== –
0,5мм

∆l₂=== –
0,225мм

∆l₃===
0,05мм

∆l= — 0,5 – 0,225 + 0,05 = –
0,675мм

Брус укоротился на 0,675мм

4.                 
Закрепление материала. (55 минут) (Слайд 13,
Слайд 14)

a)     
Задание – эстафета (25 минут)

Двухступенчатый стальной брус нагружен силами F₁, F₂.

Построить эпюры продольных сил и нормальных напряжений по
длине бруса.  Проверить прочность бруса, если допускаемое напряжение [σ] = 160 МПа. Определить перемещение ∆l
свободного конца бруса, приняв Е=2∙10 ⁵ МПа. Площади поперечных
сечений А₁=5 см²;А ₂ =10 см². Длина
l = 0,5 м. Первая команда F₁= 50 кН, F₂ = 30 кН. Вторая команда F₁= 30 кН, F₂ = 50
кН.

                                                          
F₁

              l           
l                  l

 

                l           
l                      l

Задание каждого этапа эстафеты – 5 баллов

1 этап эстафеты (по 1 человеку от команды)

Разбить брус на участки. Пронумеровать эти участки.

2 этап эстафеты (по 1 человеку от команды)

Найти величину продольной силы на первом участке.

3 этап эстафеты (по 1 человеку от команды)

Найти величину продольной силы на втором участке.

4 этап эстафеты (по 1 человеку от команды)

Найти величину продольной силы на третьем участке.

5 этап эстафеты (по 1 человеку от команды)

Построить эпюру для продольной силы.

6 этап эстафеты (по 1 человеку от команды)

Найти величину нормального напряжения на первом участке.

7 этап эстафеты (по 1 человеку от команды)

Найти величину нормального напряжения на втором участке.

8 этап эстафеты (по 1 человеку от команды)

Найти величину нормального напряжения на третьем участке.

9 этап эстафеты (по 1 человеку от команды)

Построить эпюру для нормального напряжения.

10  этап эстафеты (по 1 человеку от команды)

Проверить прочность бруса. Допускаемое напряжение [σ] = 160 МПа.

11 этап эстафеты (конкурс капитанов) – 10 баллов

Определить перемещение свободного конца бруса.

b)     Работа в группах (Карточки с заданиями) (10 минут) (Слайд 15)

Каждой команде необходимо выполнить задание. Задания мы разыграем с
помощью интерактивного игрального кубика. Если выпадает нечетное число, то
первое задание достается первой команде, если четное – то второй. Второе
задание автоматически переходит к другой команде. Время выполнения – 10 минут
задано на интерактивном таймере. (Карточки – задания приложение 2)

c)      Разгадывание кроссвордов. (10 минут) (Слайд 16)

Команды отгадывают кроссворд, составленный соперниками.  Время
разгадывания – 10 минут задано на интерактивном таймере.

Каждый правильный ответ 5 баллов.

d)     Творческое задание. (10 минут) (Слайд 17)

Сочинить стихотворение
со словами:

Растяжение

Сжатие

Эпюра

Сила

Гук

Прочность

Выполнение данного задания  — 10  баллов.

5.                 
Подведение итогов (5 минут) (Слайд 18)

Заполнить таблицу:

Я знал	Я узнал	Я хочу узнать

Пока обучающиеся заполняют
таблицу, жюри подсчитывает количество баллов, набранное каждой командой.

Объявление победителей. Выставление оценок.

Спасибо за работу на занятии! (Слайд 19)

Приложения

Приложение
1.

Итоговая ведомость

Вид задания	1 команда Название                           Капитан	2 команда Название                              Капитан
Визитная карточка команды Максимальное количество баллов — 5
Фронтальный опрос Максимальное количество баллов – 5 за каждый правильный ответ
Эстафета
1 этап эстафеты Максимальное количество баллов – 5
2 этап эстафеты Максимальное количество баллов – 5
3 этап эстафеты Максимальное количество баллов – 5
4 этап эстафеты Максимальное количество баллов – 5
5 этап эстафеты Максимальное количество баллов – 5
6 этап эстафеты Максимальное количество баллов – 5
7 этап эстафеты Максимальное количество баллов – 5
8 этап эстафеты Максимальное количество баллов – 5
9 этап эстафеты Максимальное количество баллов – 5
10 этап эстафеты Максимальное количество баллов – 5
11 этап эстафеты (конкурс капитанов) Максимальное количество баллов – 10
Работа в группах (карточки с заданиями) Максимальное количество баллов – 10
Разгадывание кроссвордов За каждый правильный ответ — 5 баллов
Творческое задание Максимальное количество баллов – 10
Итого

Приложение
2 

Карточки – задания

Задание 1

Для стального прямого бруса построить эпюры продольных сил и нормальных
напряжений. Проверить
прочность бруса, если допускаемое напряжение [σ] = 160 МПа.

Задание 2

Для стального прямого бруса построить эпюры продольных сил и нормальных
напряжений. Проверить прочность бруса, если
допускаемое напряжение [σ] = 160 МПа.

Приложение
3

Слайды

 

                           Слайд
1                                                           Слайд 2

 

                           Слайд
3                                                           Слайд 4

 

                           Слайд 5                                                           Слайд
6

 

                           Слайд
7                                                           Слайд 8

 

                           Слайд
9                                                           Слайд 10

 

                           Слайд
11                                                           Слайд 12

 

                           Слайд
13                                                           Слайд 14

 

                           Слайд
15                                                           Слайд 16

 

                           Слайд
17                                                           Слайд 18

 

Слайд 19