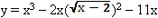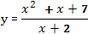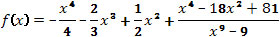Как найти эскиз графика производной

По графику производной y= f ‘ (x) можно не только исследовать поведение функции y=f(x) , но и попытаться построить ее график.

Поскольку для одной функции первообразных существует бесконечное множество, график функции по графику производной можно построить лишь схематично: точки экстремума и промежутки возрастания и убывания функции определить можно, а нули функции и экстремумы — нет.

Дан график производной: y= f ‘ (x):

Построить график функции y=f(x).

Решение:

Точки x=x2, x=x3, x=x4,  в которых производная y= f ‘ (x) обращается в нуль — это точки экстремума функции y=f(x).

В точках x=x2 и x=x4 производная меняет знак с «-«на «+», поэтому x2 и x=x4 — точки минимума функции y=f(x).

В точке x=x3 производная меняет знак с «+» на «-«, поэтому x=x3 — точка максимума функции.

На промежутках [x1;x2] и [x3;x4]  f ‘ (x)<0, поэтому y=f(x) на этих промежутках убывает.

На промежутках [x2;x3] и [x4;x5]  f ‘ (x)>0, поэтому для y=f(x)  они являются промежутками возрастания.

Сказать что-то более определенное о нулях и других значениях функции y=f(x) не получится. Данный эскиз графика y=f(x) — один из множества графиков первообразных для функции  y= f ‘ (x).  Другие могут быть получены из него параллельным переносом вдоль оси oy.

Если график производной y= f ‘ (x) представляет собой прямую,  параллельную оси ox (y=b, где b- число),, то функция y=f(x) — линейная. Она является возрастающей, если b>0, убывающей, если b<0, и постоянной, если b=0.

Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).

Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.

Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.

Ответ: (11.)

Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.

Практическая
работа по теме « Построение графика производной методом касательных»

 Ты уже знаешь, что такое производная?  Знаю, тема
очень большая и необычная, но надо понять , иначе нет смысла идти дальше.
Наверное , у тебя возникло много вопросов, например такие как:  за что отвечает
угловой коэффициент, почему и где берем  tgφ, как связать
функцию и ее производную и вообще :что показывает производная, зачем нужно ее
изучать? Если возникли трудности на первых уроках при определении производной,
то я настоятельно попрошу еще раз вернуться к теме « Производная» Сегодня я
предлагаю выполнить практическую работу по теме « Построение графика
производной методом касательных» и проанализировать полученные из нее выводы ,
которые тебе помогут глубже осознать всю связь функции  и ее производной

 Производная
функции в конкретной точке равна тангенсу  угла наклона касательной к графику
функции в этой точке или угловому коэффициенту этой касательной==k

 Ты видишь мы
провели касательную в точке ( показываю) , потом выберем две точки А и В таким
образом чтобы были целыми их координаты, затем достроим до прямоугольного
треугольника и найдем тангенс угла наклона касательной по отношению к
положительному направлению оси  Ox- это угол ВАС;  tg∠BAC=​AC​​/BC​​=​5/​​6​​=1,2

 Значит
и производная в точке  равна 1,2.

 При
построении графика производной учтем:

1.     
Если касательная параллельна оси Ox,
то тангенс угла наклона равен нулю , а значит и
значения производной в этих точках равны нулю и эти точки мы построим в первую
очередь

2.       Проведем касательные в некоторых точках на промежутках
возрастания и убывания функции и определим значения тангенса угла наклона в
этих точках касания , а значит их значения производных

3.       Повторим еще раз определение тангенса  и  обговорим 
следующее:

  Если 
в определении тангенса мы возьмем прилежащий к углу катет равный единице, тогда
значение тангенса , а значит и значение производной в точке будет равно длине
противолежащего отрезка.  Воспользуемся этим при построении  графика
производной по данной функции

При построении
графика производной наряду с функцией видны « необычные вещи»

Давайте вместе их
проанализируем:

·        
Производная функции- это тоже функция, не
похожая на исходную, но определяется ею и полностью зависит от нее,  между ними
есть взаимосвязь. Какая же?

Из
графиков видно, что  на участках возрастания функции угол между касательной и положительной
осью абсцисс  тем больше , где больше скорость изменения функции и наоборот:
там, где угол уменьшается, скорость изменения меньше. Значит производная
показывает  скорость изменения функции от точки к точке, т.е  производная – это
мгновенная скорость. При возрастании функции скорость возрастания производной
замедляется и становится равной нулю там , где функция достигает свой максимум.
Когда функция достигнет свой максимум  она изменит свое направление и достигнет
свой минимум ,а значит остановится ,следовательно скорость будет равна нулю.

·        
 Сравнивая и анализируя графики функции и
ее производной убеждаемся , что при возрастании функции ее производная
принимает только положительные значения, а при убывании функции- только
отрицательные значения

Данная
практическая работа позволяет мне  подготовить учащихся к ЕГЭ, где они
осознанно видеть взаимосвязь между функцией и ее производной

Применение
производных функций — важный элемент в практической части науки и производства.
Не зря нас в старшей школе и университете учили строить сложные графики,
исследовать и работать над функциями.  Без производных и дифференциальных
исчислений невозможно было бы рассчитать жизненно важные показатели и величины.
Человечество научилось моделировать различные процессы и исследовать их, решать
сложные математические задачи. Действительно, математика — царица всех наук,
потому что эта наука лежит в основе всех других естественных и технических
дисциплин.

Введение

Методика исследования функции, построение ее графика, включает в себя 2 этапа:

1. исследование без производной;

2. исследование с помощью производной.

Построение графика и исследование функции  без производной

При исследовании функции  без производной нахождение интервалов знакопостоянства и определение знаков функции на них выполнить очень затруднительно. Однако некоторые свойства данной функции можно узнать:

1. Область определения функции – это множество всех действительных чисел.

 

2. Если x стремится к , то и данная функция стремится к . Следовательно, множество значений функции – это вся числовая ось.

             

3. График этой функции симметричен относительно точки .

Пояснение

Рассмотрим функцию

Эта функция позволяет найти интервалы знакопостоянства и построить эскиз графика (см. Рис. 1).

Эта функция нечетная:

График нечетной функции симметричен относительно точки с координатами .

Рис. 1. График функции

При прибавлении 4 к функции  график сдвинется на 4 единицы вверх по оси  (см. Рис. 2): корни  и  пропадают, а корень  сдвигается влево. Следовательно, график функции  будет симметричен относительно точки .

Рис. 2. Схематичное изображение графиков функции  и

Нам удалось установить, что функция  имеет как минимум один корень, который меньше чем .

 

Построение графика и исследование функции  с помощью производной

 

Приравниваем производную к 0 и находим критические точки:

 

 – критические точки

Выделим интервалы знакопостоянства производной, которые определяют интервалы монотонности самой функции (см. Рис. 3).

До точки  функция возрастала (производная была положительна), после этой точки функция убывает (производная отрицательная), следовательно,  – это точка максимума.

До точки  функция убывала, после этой точки функция возрастает, следовательно,  – это точка минимума.

Рис. 3. График производной функции

Найдем значения функции в точках минимума и максимума:

 

 

Можно сделать вывод, что функция возрастает от  до 6 и от 2 до ; функция убывает от 6 до 2.

На рисунке 4 показан график функции . Этот график читается следующим образом:

Если аргумент возрастает от  до , то функция возрастает от  до 6; если аргумент от  до 1, то функция убывает от 6 до 2; если аргумент возрастает от 1 до , то функция возрастает от 2 до .

Рис. 4. График функции

Результаты исследования функции

1.  при  и при

2.  при

3.  – т. max

 

 – т. min

 

3. . Наибольшего и наименьшего значения функции не существует.

Задача

Найти число корней уравнения  в зависимости от параметра .

Решение

1. Перенесем  в правую часть уравнения:

 

2. Построим график функции  (см. Рис. 5) (как построить график этой функции см. выше).

Рис. 5. Иллюстрация к задаче

3. Рассечем этот график семейством прямых , при разных . Найдем точки пересечения этих прямых с графиком функции  (см. Рис. 6).

Рис. 6. Иллюстрация к задаче

Уравнение  имеет один корень при каждом  из множества , а также из множества .

Уравнение  имеет два корня при  и при .

Уравнение имеет три корня при всех  из множества .

Ответ: 1 корень:  

2 корня: ; ;

3 корня: .

Частные случаи для задачи

1. Найти все значения параметра , при каждом из которых данное уравнение имеет ровно два различных корня.

Ответ: уравнение  имеет два корня при  и при .

2. Найти наибольшее натуральное значение параметра a, при котором уравнение имеет три различных корня.

Решение

Уравнение имеет три корня при всех  из множества . В это множество входят такие натуральные числа: 3, 4, 5. Наибольшее из них – это 5.

Ответ: .

---

Общий план построения графика и исследования функции  

Общий план состоит из двух этапов:

1. Этап А: исследование без производной.

2. Этап Б: исследование с производной.

Этап А

1. Найти область определения функции .

2. Выделить интервалы знакопостоянства функции и определить знаки функции на них (для этого нужно приблизительно оценить расположение корней или точно найти их).

3. Найти точку пересечения графика с осью , для этого приравнять  и вычислить .

4. Выяснить специфику функции:

— четность, нечетность, периодичность;

— наличие центра или оси симметрии.

5. Построить эскиз графика в окрестностях каждого корня (в окрестностях корня функция может возрастать, убывать, иметь точку максимума или минимума (см. Рис. 7)).

Рис. 7. Эскиз графиков в окрестностях корня

6. Построить эскиз графика функции в окрестностях точек разрыва области определения . Точки разрыва – это, как правило, корни знаменателя. Они могут определять вертикальные асимптоты.

7. Построить график функции в окрестностях бесконечно удаленных точек: .

Этап Б

1. Найти производную функции .

2. Найти интервалы знакопостоянства производной и определить знаки производной на них. Эти интервалы определяют интервалы монотонности самой функции.

3. Найти критические точки, исследовать их на экстремум.

4. Построить и описать график функции .

Предложенная схема работает особенно хорошо для функций вида: , где  и  – многочлены.

Список литературы

1. Мордкович А.Г., Семенов П. В. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.

2. Мордкович А.Г. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений. – М.: Мнемозина, 2009.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики). – М.: Просвещение, 1996.

4. Колягин Ю.М., Сидоров Ю.В., Ткачева М.В., Федорова М.В., Шабунин М.И. Алгебра и начала математического анализа, 10 класс. Учебник для учащихся общеобразовательных учреждений (профильный уровень). – М.: Мнемозина, 2009.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт «ЯКласс» (Источник)

2. Интернет-сайт «Вся элементарная математика» (Источник)

3. Интернет-сайт YouTube (Источник)

Домашнее задание

1. Задание 45.13, 45.15(а), 45.3 (б) (стр. 265) – Мордкович А.Г. Алгебра и начала математического анализа, 10 класс. В 2 ч. Ч. 2. Задачник (Источник)

2. Исследуйте функцию и постройте ее график .

Цели урока:

• Обучающая
  (Систематизировать и обобщить знания учащихся по вопросу)
  • Систематизировать и обобщить знания учащихся по вопросу нахождения промежутков возрастания, убывания;
  • Систематизировать и обобщить знания учащихся по вопросу нахождения экстремумов функции;
  • Систематизировать и обобщить знания учащихся по вопросу исследования и построения графиков функции с помощью производной;
  • Отработать задания тестов ЕГЭ, закрепить навыки чтения и исследования функции с помощью производной.
• Развивающая
  • Способствовать развитию общения как метода научного познания, аналитико-синтетического мышления, смысловой памяти и произвольного внимания;
  • Способствовать развитию навыков исследовательской деятельности (планирование своей деятельности, выдвижение гипотез, анализ и обобщение полученных результатов).
• Воспитательная
  • Развивать у учащихся культуру общения, способствовать развитию творческой деятельности учащихся, потребности к самообразованию.

Ход урока

I. Закрепление и систематизация изученного материала

1) Математический диктант.

Учащиеся выполняют задание в рабочей тетради. Выполнения задания проверяют у друг друга. После провести устный опрос.

1. Что вы можете сказать о характере изменения функции, если:

а) f´(x) > 0 для всех x ∈ R

б) f´(x) < 0 для всех x ∈ R.

Ответ: а) возрастает, б) убывает.

2. Что можно сказать об угловом коэффициенте касательной к графику функции, если известно, что функция  : : а) возрастает, б) убывает?

Ответ: а) положительный, б) отрицательный.

3. Какие из данных функций возрастают, а какие убывают на всей числовой прямой:

а) у = х³ + х, б) у = — х⁵.

Ответ: а) возрастает, б) убывает.

4. Может ли значение функции в точке максимум быть меньше её значения в точке минимума.

Ответ: Да.

2) Решение задач.

Пример 1.

Работа с графиками производной, если известны свойства функции.

У каждого на столе карточки с заданиями. Разобрать решение совместно.

1. Найдите эскиз графика производной функции у = g´(x), если известно, что функция
у = g(x) убывает на всей числовой прямой (рис.1):

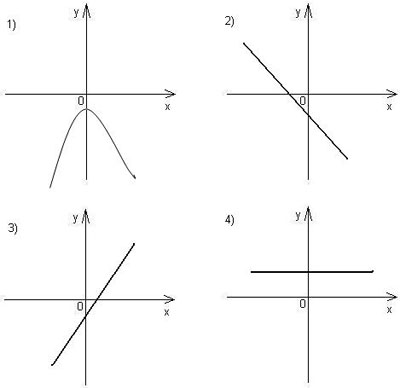
Рис. 1

2. Функция у = f(x)  задана своим графиком (рис.2). Определите, для каких значений х выполняется y = f´(x) > 0.

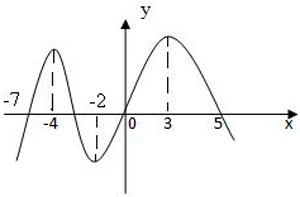
Рис. 2

1) (-∞; 4) U (-2; 3); 2) (-7; -3) U (0; 5); 3) (0; 4); 4) (-7; 4)

3. Функция у = f(x) задана своим графиком.  Укажите, в какой точке графика касательная к нему параллельна оси абсцисс.

1) (4;3); 2) (5;4); 3) (3;1)

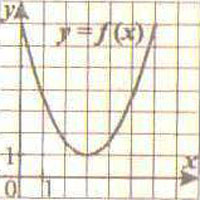
Рис. 3

4. Найдите эскиз графика производной функции у = g´(x), если известно, что функция
у = g(x) имеет единственный максимум:

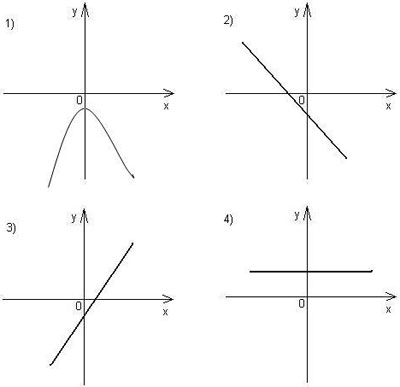
Рис. 4

5. Функция у = f(x) задана своим графиком. Определите, для каких значений х выполняется y = f´(x) < 0.

1) (-∞; 5) U (-2; 3); 2) (-7; -3) U(0; 5);  3) (0; 4);  4) (-7; 4)

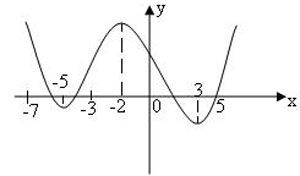
Рис. 5

6. К графику функции у = f(x)  в точке абсциссой х₀ = -3 проведена касательная. Определите коэффициент касательной, если на рис. изображен график производной данной функции.

1) 4; 2) 0; 3) 3; 4) 1.

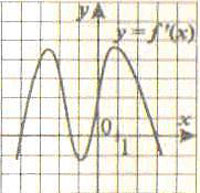
Рис. 6

7. На рис.7 изображен график производной некоторой функции. Укажите интервал, на котором функция убывает.

1) (-3; 0]; 2) (-2;2); 3) (-∞; 0]; 4) [0;+∞).

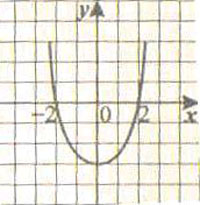
Рис. 7

8. Функция у = f(x) определена на промежутке [-7;7]. На рисунке изображен график ее производной. Найдите точку х₀, в которой функция у = f(x) принимает наименьшее значение.

1) 2; 2) 0; 3) – 4; 4) 7.

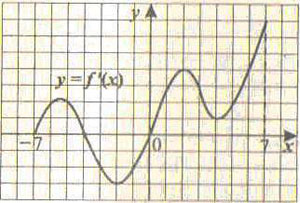
Рис. 8

9. Функция у = f(x) задана своим графиком. Укажите, в какой точке графика касательная к нему параллельна оси абсцисс.

1) (-3;-2); 2) (4;-2); 3) (3;1); 4)(-1;-3).

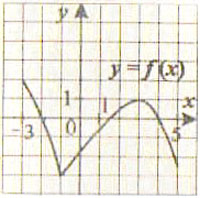
Рис. 9

Пример 2.

1. По графику функции у = f(x) , изображенному на рисунке, построить эскиз графика её производной.

№898.

2. По графику производной, изображенному на рисунке, построить график функции.

№899

4 человека выполняют задание на доске, остальные самостоятельно оформляют решение в тетрадях. Выполнение задания проверяют самостоятельно, сравнивая свои графики с графиками, выполненными на доске.

3) Теоретическая разминка.

Ученики задают друг другу вопросы по теории.

Примерные вопросы:

1. Определение возрастающей,  убывающей, монотонной функции.
2. Определение точек максимума, минимума.
3. Определение точек экстремума.
4. Сформулировать алгоритм исследования функции на монотонность и экстремумы
5. Сформулировать достаточные условия экстремума.

II. Самостоятельная работа.

Исследовать функцию и построить ее график.

Каждый ученик исследует функцию, заданную графиком

I. у = х⁵ – 5х               II. у = 5х³ – 3х⁵

Поместить  правильные ответы на крыльях доски или демонстрируя через кодоскоп.

Ученики консультанты, чьи работы были проверены учениками, проверяют самостоятельную работу.

III. Работа над ошибками.

«Найдем ошибки!»

Предлагаются для обсуждения вопросы, которые содержат часто встречающиеся.

1) Определяя точки минимума функции, учащийся нашел, при каких значениях аргумента значения функции равны 0. Затем из этих значений он выбрал те, проходя через которые функция меняет знак с « — » на « + ». Эти точки он назвал точками минимума. Прав ли он?

2) Определяя точки минимума функции, учащийся нашел те значения аргумента, при которых обращается в 0. Эти точки он назвал точками минимума. Прав ли он?

3) График производной. Определяя точки минимума, ученик указал точку х = 2. Прав ли он?

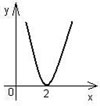
Рис. 10

4) График производной. Определяя точки минимума, ученик указал точки х = -4, х = 1, х = 3. Прав ли он?

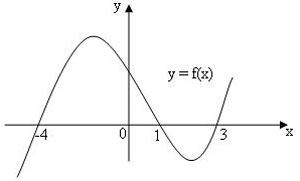
Рис. 11

5) График производной. Определяя точки минимума, ученик указал точку х = -2. Прав ли он?

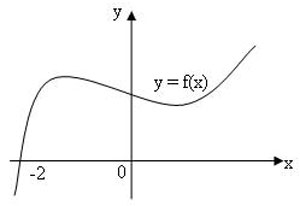
Рис. 12

IV. Проверка домашнего задания.

Предложить учащимся проиллюстрировать характерные свойства функций с помощью пословиц. Пословицы – это отражение устойчивых закономерностей, выверенных многовековым опытом народа.

«Графики функций – пословицы».

Примеры.

1) Повторение – мать учения.

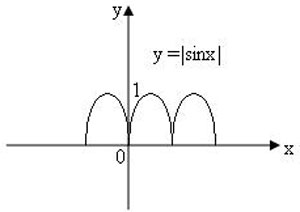
Рис. 13

2) Любишь с горки кататься, люби и саночки возить.

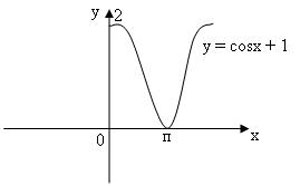
Рис. 14

3) Как аукнется, так и откликнется.

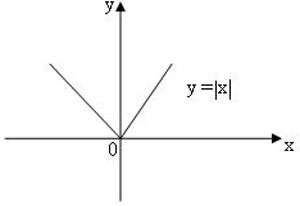
Рис. 15

V. Домашнее задание.

(С1): 1) Найти точки минимума функции

(С1): 2) Найти стационарные точки функции

(С1): 3) Найти точки максимума функции

4) Составить кроссворд по теме: «Геометрический и физический смысл производной» или рекламный ролик по теме «Вычисление производных».

VI. Подведение итогов урока.

Учебно-методическое обеспечение:

1. А. Г. Мордкович. Алгебра и начала анализа. Часть 1. Учебник.
2. А.Г.Мордкович и Пр. Алгебра и начала анализа. Часть 2. Задачник.
3. Л. А. Александрова. Алгебра и начала анализа. Самостоятельные работы / Под ред. А. Г. Мордковича.
4. Л. О. Денищева, Т. А. Корешкова. Алгебра и начала анализа. Тематические тесты и зачеты / Под ред. А. Г. Мордковича.
5. А. Г. Мордкович. Алгебра и начала анализа. Методическое пособие для учителя.
6. Тематические тесты. Математика. ЕГЭ-2009. Часть I(A1 – A10, B1 – B3) / Под редакцией Ф.Ф. Лысенко. – Ростов- на – Дону: Легион,2009. 256 с. (Серия «Готовимся к ЕГЭ»).
7. Тематические тесты. Математика. ЕГЭ-2009. Часть II (B4 – B8, C1 – C2 / Под редакцией Ф.Ф. Лысенко. – Ростов-на-Дону: Легион, 2009. 256 с. (Серия «Готовимся к ЕГЭ»).
8. Математика. 5-11 классы: игровые технологии на уроках / авт.- сост. Н.В. Барышникова. – Волгоград: Учитель, 2007. – 154 с.