Решение типовых примеров
1.20
Найти естественную область определения
функции
,
ее интервалы монотонности и точки
экстремума
.
Решение.
Областью определения данной функции
является множество
.
Производная этой
функции имеет вид
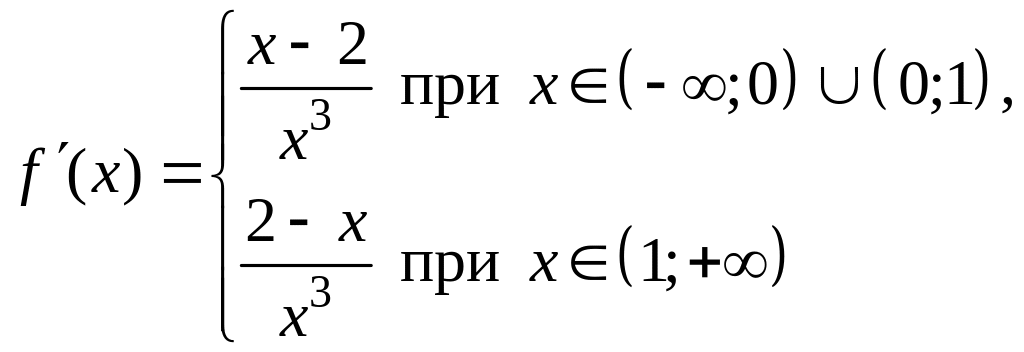
и обращается в
нуль в точке
.
При этом производная не существует в
точках
и
.
Поэтому точками возможного экстремума
являются
,
,
.
Они разбивают область определения на
четыре интервала монотонности:
,
,
,
.
Видно, что
при
,
при
.
Следовательно, функция
монотонно возрастает при
и
1;
монотонно убывает при
и
.
Согласно первому достаточному условию
локального экстремума, в точке
функция имеет локальный максимум,
,
а в точке
– локальный минимум,
.
2.20 Найти глобальный экстремум функции , определенной на :
.
Решение.
Областью определения данной функции
является множество
.
Определяем точки
возможного экстремума (стационарные
точки) функции
:
,
.
Значит,
и
.
Так как при
имеем
,
при
имеем
,
то
является точкой максимума. Так как при
имеем
и при
имеем
,
то
является точкой минимума.
Вычисляем значения
на концах отрезка
и в стационарных точках, принадлежащих
отрезку:
,
,
,
.
Тогда
,
Наименьшее значение
данная функция принимает на левом конце
отрезка в точке
,
наибольшее – в точке
и на правом конце отрезка в точке
.
График данной функции изображен на
рисунке 18.
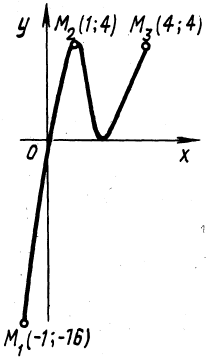
Рисунок 18
– График функции
на отрезке
3.20 Найти
глобальный экстремум функции
,
определенной на
.
Решение.
Естественной областью определения
данной функции является множество
.
Для определения наибольшего и наименьшего
значений функции на интервале
.
найдем локальные экстремумы. Вычислим
производную:
,
.
В точке
производная не существует. Критическими
точками являются точки
,
.
Для всех
справедливо неравенство
и
.
Поэтому наименьшее значение данной
функции на
равно нулю.
Рассмотрим точку
.
Заметим, что
и
.
Поэтому наибольшее значение данной
функции на
не существует (см. рис.19).
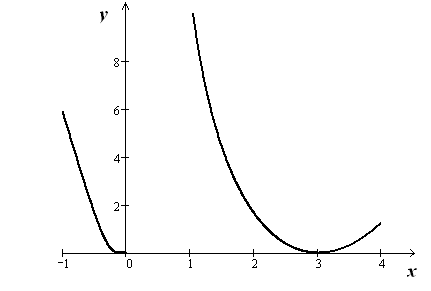
Рисунок 19
– График функции
,
4.20
Решить геометрическую задачу:
Боковая
сторона равнобедренной трапеции равна
ее меньшему основанию. Каков должен
быть угол при большем основании, чтобы
площадь трапеции была наибольшей?
Решение.
На рисунке 20
изображена трапеция
.
Пусть
.
Тогда по условию
.
Пусть BE
и
CF
– высоты трапеции; BE=CF.
Полагая BAD=,
выразим площадь трапеции как функцию
от
:
,
.
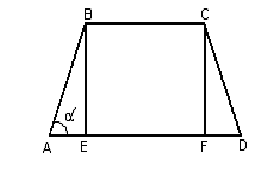
Рисунок
20
– Геометрическая интерпретация задачи
3.20
Площадь
трапеции
равна
.
Из
геометрических соображений имеем:
,
.
Тогда
площадь трапеции равна
.
Исследуем
функцию
,
определенную при
,
на экстремум.
.
Решая
уравнение
,
получим:
и
.
Отсюда
,
,
,
.
Единственным решением этого уравнения,
лежащим на
является
.
Убедимся, что при
функция
достигает максимума.
.
Так
как
,
,
,
то
.
Значит, при
функция
достигает наибольшего значения на
интервале
.
Угол при большем основании трапеции
равен
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нахождение области определения сложной функции — Студопедия
Поделись
Рассмотрим для начала сложную функцию f, которой соответствует формула . Какова же область определения сложной функции f ? Это множество всех x из области определения функции f2, для которых f2(x) входит в область определения функции f1.
Таким образом, область определения сложной функции — это пересечение двух множеств: множества всех таких x, что , и множества всех таких x, для которых . То есть, областью определения сложной функции f является множество всех x, удовлетворяющих условию .
Записанная система представляет собой систему неравенств, решением которой является искомая область определения сложной функции .
Таким образом, нахождение областей определения сложных функций сводится к решению систем неравенств различного вида.
Давайте рассмотрим решения нескольких примеров, в которых находятся области определения сложных функций.
Мы не будем подробно описывать решения систем неравенств, так как это выходит за рамки этой статьи.
Пример.
Найдите область определения сложной функции .
Решение.
Исходную сложную функцию можно записать в виде , то есть, f1 – логарифмическая функция с основанием e, а f2 – степенная функция с показателем 2.
Обратившись к известным областям определения основных элементарных функций, имеем и .
Тогда
Следовательно, областью определения заданной сложной функции является множество всех действительных чисел, кроме нуля.
Ответ:
.
Пример.
Какова область определения функции ?
Решение.
Перепишем данную функцию в виде . Теперь стало видно, что нам требуется найти область определения сложной функции f=f1(f2), где f1 – степенная функция с показателем , а f
2 – функция арксинус.
Нам известны области определения основных элементарных функций, откуда мы и заключаем, что и .
Осталось решить систему неравенств: .
Для решения неравенства вспомним свойства функции арксинус. Арксинус возрастает на всей области определения и обращается в ноль при x=0, следовательно, .
Вернемся к системе неравенств: .
Таким образом, областью определения исходной сложной функции является интервал .
Ответ:
.
Теперь давайте рассмотрим сложную функцию вида . Область определения функции f находится как решение системы вида
Пример.
Найдите область определения сложной функции .
Решение.
Заданную сложную функцию можно представить в виде , где f1 – функция синус, f2 – функция корень четвертой степени, f
3 – логарифмическая функция с основанием 10.
Нам известно, что .
Тогда область определения сложной функции f найдем, решив систему неравенств:
Условие равносильно условию , следовательно,
Ответ:
.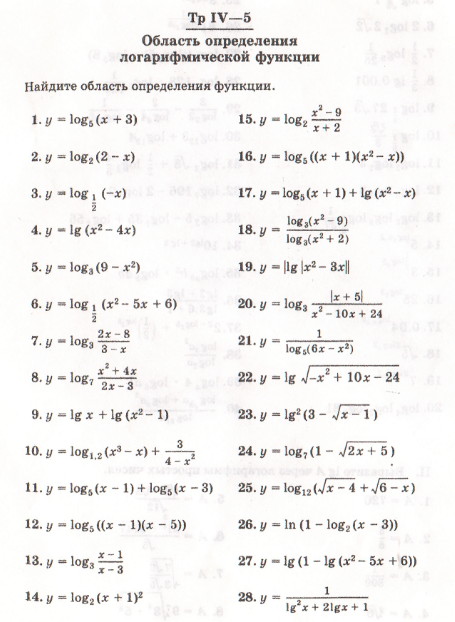
Замечание. В разобранных выше примерах мы специально брали сложные функции, составленные только из основных элементарных функций, чтобы лучше донести принцип нахождения области определения сложных функций. В следующих пунктах этой статьи мы разберем примеры нахождения областей определения сложных функций, составленных не только из основных элементарных функций, но и из элементарных функций.
К началу страницы
Домен и диапазон функции
Содержание:
- Что такое домен и диапазон функции?
- Как найти домен и диапазон функции
- Диапазон (статистика)
- Закрытый домен
- Кодовый домен
- Частотный диапазон
- Домен интеграции
- Интервальный домен
- Домен — это набор значений x, которые можно поместить в функцию. Другими словами, это набор всех возможных значений независимой переменной.
- Диапазон — это набор значений y, которые выводятся для домена.
- Кодовый домен подобен диапазону, но с одним большим отличием: кодовый домен может содержать все возможных выходных данных
, а не только те, которые действительно появляются.
Посмотрите видео для краткого обзора:
Домен и область действия
Посмотрите это видео на YouTube.
- Проверить известные домены/диапазоны,
- Угадай и проверь,
- Графики,
- Таблица значений.
Сначала посмотрите, сможете ли вы выяснить, какой тип функции у вас есть (это не всегда ясно).
Многие функции имеют бесконечный набор для домена. «Бесконечное множество» — это просто множество всех возможных чисел. Например, вы можете ввести любое число в функцию y = x 2 , и она все равно выдаст вам результат. Но как насчет диапазона? Отрицательное число никогда не будет отображаться для этой функции; отрицательный раз отрицательный всегда будет положительным.
y = -10 2 = -10 * -10 = 100.
Имеет смысл, что диапазон для x 2 равен 0 > ∞.
Некоторые функции имеют определенные домены и диапазоны. Краткое описание приведено ниже или просмотрите наш плейлист на YouTube, в котором есть серия очень коротких видеороликов о поиске доменов и диапазонов для различных функций.
- Линейные функции обычно имеют область определения и диапазон всех действительных чисел. См.: Линейные функции (видео).
- Полиномиальные функции имеют область определения всех действительных чисел. Диапазон зависит от степени и старшего коэффициента. См.: Полиномиальные функции.
- Квадратичные (квадратичные) функции имеют область определения всех действительных чисел. Диапазон зависит от знака старшего коэффициента: y ≥ min (+) или y ≥ max, (-). См.: Квадратичные функции.
- Функции абсолютного значения имеют область определения всех действительных чисел.
Диапазон зависит от вершины и знака выражения абсолютного значения. См.: Функция абсолютного значения.
- Функция квадратного корня имеет область определения x ≥ 0 и диапазон y ≥ 0. Другие функции квадратного корня, такие как √(x – 5), см.: Квадратный корень и радикальные функции.
- Рациональные функции f(x) = 1/x имеют область определения x ≠ 0 и диапазон значений x ≠ 0. Если у вас более сложная форма, например f(x) = 1 / (x – 5), вы можете найти домен и диапазон с помощью обратной функции или графика. См. Рациональные функции.
- Синусоидальные функции и функции косинуса имеют область определения всех действительных чисел и диапазон -1 ≤ y ≤ 1.
Совет: Ознакомьтесь с формами основных функций, таких как синус/косинус и многочлены. Таким образом, вы сможете разумно найти область определения и диапазон функции, просто взглянув на уравнение.
Если у вас нет сильных навыков алгебры, вы можете пропустить этот метод и вместо этого попробовать графические или табличные методы.
По сути, используйте свои навыки алгебры, чтобы найти домен и диапазон для функции, угадывая и проверяя! Несколько общих советов:
- Деление на ноль запрещено ). В качестве примера предположим, что у вас есть функция:
f(x) = 1/(x 2 – 9).
Вы можете исключить любые значения x (домен), которые делают знаменатель равным нулю. - Для домена число под знаком квадратного корня не может быть отрицательным . Например, вы не можете найти домен для √-10, потому что решение — мнимое число.
- Попробуйте ввести в функцию разные x-значения
для y, чтобы посмотреть, что произойдет. Ищите такие тенденции, как: всегда положительные, всегда отрицательные или наборы чисел, которые не работают. Попробуйте ввести очень большое (например, миллион) или очень маленькое (например, отрицательное значение миллиона) и посмотрите, сработает ли это.
Пример : Найти область определения и диапазон функции с помощью алгебры
Найти область определения и диапазон для:
Область определения:
- Числитель имеет квадратный корень; числа под этим не могут быть отрицательными (см.
№ 2 выше). Таким образом, у вас могут быть только числа для x, большие или равные -2.
- Знаменатель : Вы не можете разделить на ноль, вы не можете получить -3 + 3, так как это даст ноль. Например, 3 2 – 9 = 0,
.
Домен для этой конкретной функции: x >
-2, x ≠ 3.
Диапазон
Диапазон для этой функции — это набор всех значений f(x), исключая F(x) = 0. Здесь навыки алгебры получить тренировку!
- Числитель : Глядя на функцию, вы должны сразу увидеть, что числитель становится равным 0, когда x = -2:
√(2 + 2) = √0 = 0, - Знаменатель:
- Работая с -2, знаменатель становится: (-2) 2 – 9 = 5. Таким образом, f(-2) = 0/-5 = 0,
- Если вы вставите несколько значений x между 2 и 3 в (x 2 – 9), вы увидите, что функция приближается к отрицательной бесконечности.
- Вставьте еще несколько значений x, превышающих x = 3, обратите внимание, что функция стремится к положительной бесконечности.
- Чем больше становятся значения x, тем меньше становятся значения функции (но на самом деле они никогда не достигают нуля).
Постройте график функции и посмотрите, где находятся ваши значения x и y. Большинство графических калькуляторов помогут вам увидеть домен функции (или указать, какие значения могут быть недопустимы). Например, если вы нарисуете x 2 , будет ясно, что домен не может включать отрицательные числа. Если у вас нет графического калькулятора, попробуйте этот бесплатный онлайн-калькулятор. Всегда увеличивайте и уменьшайте масштаб графика, чтобы проверить непрерывность или отсутствующие области.
График для x 2 и 4x 2 +25 (используя онлайн-калькулятор HRW.
Из приведенного выше графика видно, что диапазон для x 2 (зеленый) и 4x 2 +25 (красный график) является положительным; На этом этапе вы можете предположить, что это набор из всех положительных действительных чисел, основываясь на графике
Составьте таблицу значений на вашем графическом калькуляторе ( См.
Включите ввод x от -10 до 10, затем несколько больших чисел (например, один миллион). Используйте калькулятор, чтобы найти значения y для значений x. Если калькулятор говорит вам, что значения или не определены, или что значения могут достигать предела (число, к которому функция приближается, но никогда не достигает), это должно помочь вам определить диапазон.
В статистике диапазон является мерой разброса: это разница между самым высоким и самым низким значением в наборе данных. Чтобы найти его, вычтите наименьшее число из наибольшего.
Несколько конкретных примеров поиска статистических диапазонов см. в разделе Как найти диапазон в статистике.
Другие значения «диапазона»
В исчислении диапазон равен всем выходным значениям функции . В некоторых областях математики диапазон может — что может сбивать с толку — также означать просто весь диапазон чисел — например, диапазон цен на мобильные телефоны может составлять от 40 до 550 долларов.
Закрытый домен — это домен, содержащий все его граничные точки. Если домен содержит набор всех внутренних точек (исключая границу), домен является открытым доменом . Незакрытый домен (это не то же самое, что открытый домен) содержит некоторые граничные точки, но не все.
Если домен содержит все точки в пределах ограниченного расстояния от начала координат, он называется ограниченным доменом . Неограниченная область имеет точки, не находящиеся внутри границы; Другими словами, они находятся на произвольном расстоянии от начала координат.
Непрерывная функция в ограниченной закрытой области D будет иметь максимальное значение и минимальное значение в D.
Закрытая область в других контекстах
конкретная система ответа на вопрос (QA). Например, система под названием САМОЛЕТ может хорошо отвечать на вопросы о воздушной скорости, ускорении и грузоподъемности конкретного самолета, но не очень хороша за пределами этой конкретной области.
В разработка программного обеспечения закрытый домен — это просто домен, все границы которого закрыты. Открытый домен — это домен, в котором открыты все границы.
Целостно замкнутые области находятся в коммутативной алгебре. Целостно замкнутая область A — это область целостности (ненулевое коммутативное кольцо, в котором произведение любых двух ненулевых элементов также не равно нулю), интегральное замыкание которой в своем поле частных есть само A.
Кодовый домен A (или целевой набор) содержит все значения (выходные данные) функции.
Когда мы говорим, что функция f: X → Y (что означает «набор значений X выводит набор значений Y»), кодовый домен — это Y . Другими словами, выходные данные функции ограничены доменом кода.
Диапазон аналогичен, но разница в том, что диапазон представляет собой набор фактических значений функции (фактических выходов).
Графическое представление кода домена
На приведенном ниже изображении показана взаимосвязь между доменом, совместным доменом и диапазоном.
- Красный овал — домен . Каждый вход для функции f является членом этой области и может быть представлен x.
- Синий овал (рассматриваемый в целом, включая желтый подраздел) — это кодовый домен . Это представляет все возможные числа, которые могут быть получены на выходе. Каждый экземпляр домена отображается функцией f в этот кодовый домен.
- Желтый овал, — подмножество этого целевого домена, — диапазон , содержащий все фактические экземпляры f(x).
Примеры кода домена
Возьмем функцию f(x) = x 2 , ограниченную вещественными числами, поэтому f: ℝ → ℝ.
Здесь целевым набором f являются все действительные числа (ℝ), но поскольку все значения x 2 положительны*, фактическое изображение или диапазон f равен ℝ + 0 .
*Любой отрицательный ввод приведет к положительному результату (например, -2 * -2 = +4).
Целевые наборы и композиция
Целевые наборы приобретают решающее значение, когда мы начинаем обсуждать композиции функций. Композиция «f∘g» читается как «f из g» или «f после g» и представляет собой составную функцию, которая включает в себя взятие члена домена g, отправку его через функцию g и передачу этого вывода через f. .
Композиция действительна тогда и только тогда, когда область определения второй функции совпадает с областью определения первой функции. В нашем примере композиция действительна только в том случае, если кодовый домен g совпадает с доменом f.
Анализ частотной области — это когда сигнал изучается относительно частоты , а не относительно времени . Исследуемые данные нанесены с частотой по оси x и амплитудой по оси y; это показывает, как энергия сигнала распределяется в зависимости от частоты.
Функция может быть представлена либо временной областью либо частотной областью; каждый полезен для разных целей. Представление сигнала во временной области может быть преобразовано в частотное представление с использованием преобразования Фурье или аналогичных манипуляций.
Преобразование Фурье преобразует представление во временной области (красный) в частотную область (синий). Пики в области представляют частоты компонентов.
Важность и использование анализа в частотной области
Термин впервые появился в 1953 году в технике связи. Однако сегодня этот анализ используется во многих различных областях, в том числе:
- Геология,
- Химия,
- Дистанционное зондирование,
- Обработка изображений,
- Электротехника,
- Связь.
Анализ в частотной области называют краеугольным камнем системной инженерии и важной частью набора инструментов почти любого ученого, инженера или статистика.
Это представление часто позволяет охарактеризовать сигнал или серию сигналов с помощью простой алгебры, в отличие от сложных дифференциальных уравнений, которые используются для представления сигнала во временной области. Простые вычисления, связанные с обработкой этих сигналов, делают его особенно полезным для инженеров. Возможно, что более важно, частотный анализ позволяет вам увидеть циклическое поведение, которое могло бы быть не сразу очевидным в представлении во временной области.
При интегрировании некоторой функции по замкнутому интервалу [a, b] этот интервал называется областью интегрирования . Например:
Областью интегрирования для этой функции является закрытый интервал [1, 3].
Область интегрирования может быть бесконечной (т. е. от -∞ до ∞), как показывает следующий несобственный интеграл:
Пример несобственного интеграла с бесконечной областью интегрирования.
Несобственные интегралы нельзя вычислить напрямую; Они вычисляются как пределы обычных интегралов.
В трех измерениях все становится немного сложнее, но в большинстве случаев область у основания объекта является областью интеграции.
Область интегрирования на 3D-форме обычно является базой (показана красными линиями на этом изображении).
Как нарисовать область интегрирования
Начертить область для любого интеграла легко, если у вас есть только один интеграл (см. пример в шаге 1 ниже). Для нескольких интегралов, если вы разбиваете их на шаги, это становится намного менее сложным.
Пример задачи: Нарисуйте область интегрирования для следующего повторного интеграла:
Решение:
Шаг 1: Нарисуйте границы интегрирования для первого интеграла. Границы даны как x = от 0 до 1, поэтому:
Шаг 2: Нарисуйте границы второго интеграла на том же графике из шага 1. Примечание: Если границы интегрирования не являются целыми числами (второй интеграл здесь есть e, число Эйлера), вы можете использовать графический калькулятор (я использовал калькулятор на Desmos.
Шаг 3: Найдите заштрихованную область, соответствующую определению обоих интегралов. В этом примере вы затеняете только область от 0 до 1, которая также находится в пределах [e, e x ].
Вот и все!
Вообще говоря, интервальный домен — это домен, ограниченный интервалом [1]. Например, входные данные (например, значения x) для конкретной функции могут быть ограничены интервалом [0, 1]. Интервалы могут быть закрытыми, открытыми или полузакрытыми/полуоткрытыми.
Функция, определенная на полуоткрытом интервале «область интервала» из [5.5, 10).
Интервальная область в теории областей
В теории областей термин «интервальная область», впервые предложенный Д. С. Скоттом в 1972 г. [2], представляет собой способ аппроксимации действительных чисел. Он получил свое название, потому что реалы разделены на интервалы для вычислений.
Аппроксимации иногда необходимы для вычислений над несчетными пространствами, такими как вещественные числа (ℝ) или некоторые функциональные пространства. Области интервалов не так просто определить, как «интервалы», с которыми вы сталкиваетесь в исчислении; Алгебраические структуры, состоящие из набора плюс одна или несколько бинарных операций, удовлетворяющих определенным аксиомам, необходимы для демонстрации различий между многими эквивалентными (и неэквивалентными) версиями интервальной области [3].
Теоретическая основа Скотта для дифференциального исчисления изначально была разработана для функций с одной переменной. Недавно он был распространен на функции нескольких переменных [3]. Это расширение переводит интервальную область в аппроксимации кривых и поверхностей [4].
Теория доменов и алгебраические структуры выходят за рамки этой статьи, но если вам интересно, прочитайте статью Джесс Бланк в Computer Journal Интервальные домены и вычислимые последовательности: пример редукции доменов [5].
Область интервалов: ссылки
[1] Klippert, J. (1989). Расширенное расширенное исчисление: подсчет разрывов функции с действительным знаком с интервальной областью. Журнал «Математика»
Том. 62, № 1 (февраль 1989 г.), стр. 43-48 (6 страниц)
[2] Скотт, Д. С. (1972) Теория решеток, типы данных и семантика. В
Растин, Р. (редактор), Формальная семантика языков программирования,
стр. 65
[3] Эдалат, А. (1995a) Теория предметной области и интеграция. Теоретическая информатика 151 163–193.
[4] Edalat, A. & Lieutier, A. (2004). Теория доменов и дифференциальное исчисление (функции одной переменной). Мат. Структура в Комп. Наука, том. 14, стр. 771–802. c2004 Cambridge University PressDOI: 10.1017/S0960129504004359 Напечатано в Соединенном Королевстве
[5] Blanck, J. (2012). Интервальные домены и вычислимые последовательности: пример сокращения доменов. Компьютерный журнал (5 сентября).
Домен и диапазон: другие ссылки
Кэссиди, Стив.
Кулкарни. Частота Дом. и преобразования Фурье. Получено с https://www.princeton.edu/~cuff/ele201/kulkarni_text/frequency.pdf 16 июня 2018 г.
Лю, Г. Исчисление нескольких переменных. Получено 31 августа 2020 г. с: https://www.math.ucla.edu/~azhou/teaching/18W/hw-solutions.pdf
MIT Department of Machine Engineering. 2.14 Раздаточный материал; Введение в частоту. Обработка домена. Получено с http://web.mit.edu/2.14/www/Handouts/FreqDom.pdf 16 июня 2018 г.
Ци, П. (2019). Ответы на сложные открытые вопросы в масштабе. Получено 7 января 2020 г. с: http://ai.stanford.edu/blog/answering-complex-questions/
Rogawski, J. (2007). Многомерное исчисление. WH Freeman.
Тиан, Дж. Инженерия качества программного обеспечения: тестирование, обеспечение качества и количественное улучшение.
Чжоу, А. Проблема.
ЦИФРОВАТЬ ЭТО КАК:
Stephanie Glen . «Домен и диапазон функции» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/types-of-functions/domain-and-range-of-a-function/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Как найти область определения функции
Обновлено 7 декабря 2020 г.
Автор Lisa Maloney
Когда вы впервые начинаете изучать функции, вам, возможно, придется рассматривать их как машину: вы вводите значение, x в функцию, и как только оно будет обработано машиной, другое значение — назовем его y — выскакивает из дальнего конца.
Стратегия поиска домена
Если вы только изучаете функции и домены, обычно предполагается, что доменом функции являются «все действительные числа». Поэтому, когда вы приступаете к определению домена, часто проще всего использовать свои знания математики, особенно алгебры, чтобы определить, какие числа не являются действительными членами домена. Поэтому, когда вы видите инструкции «найти домен», часто проще всего прочесть их в голове как «найти и исключить любые числа, которые не могут быть в домене».
В большинстве случаев это сводится к проверке (и устранению) потенциальных входных данных, которые могут привести к тому, что дроби станут неопределенными или будут иметь 0 в знаменателе, и поиску потенциальных входных данных, которые дадут вам отрицательные числа под знаком квадратного корня.
Пример нахождения домена
Рассмотрим функцию
f(x) = frac{3}{x — 2}
, которая на самом деле означает, что любое введенное вами число будет плюхаться вместо x в правой части уравнения. Например, если вы вычислили f (4), вы получили бы
f(4) = frac{3}{4 — 2}
, что дает 3/2.
А что, если вы вычислили f (2) или, другими словами, вместо 9 ввели 20039 х ? Тогда у вас будет
f(2) = frac{3}{2 — 2}
, что упрощается до 3/0, что является неопределенной дробью.
Здесь показан один из двух распространенных случаев, когда число может быть исключено из домена функции. Если задействована дробь, и входные данные приведут к тому, что знаменатель этой дроби будет равен нулю, то входные данные должны быть исключены из области определения функции.
Небольшое исследование покажет вам, что абсолютно любое число , кроме 2 вернет действительный (хотя иногда и беспорядочный) результат для рассматриваемой функции, поэтому областью применения этой функции являются все числа, кроме 2.
Другой пример поиска области
исключить возможные члены области определения функции: иметь отрицательную величину под знаком квадратного корня или любой радикал с четным индексом. Рассмотрим пример функции
f(x) = sqrt{5 — x}
Если x ≤ 5, то количество под радикальным знаком будет либо 0, либо положительным, и возвратит действительный результат. Например, если x = 4,5, у вас будет
f(4,5) = sqrt{5 — 4,5} = sqrt{0,5}
, что, несмотря на беспорядок, все же возвращает правильный результат. И если x = −10, у вас будет
f(-10) = sqrt{5 — (-10)} = sqrt{5 + 10} = sqrt{15}
, что, снова возвращает допустимый, если запутанный результат.
Но представьте, что х = 5,1. В тот момент, когда вы на цыпочках перейдете разделительную линию между 5 и любыми числами, превышающими ее, вы получите отрицательное число под корнем:
f(5.
Область определения функции
Сегодня потренируемся в отыскании области определения выражения и функции.
Когда отыскивают область определения функции, то часто она совпадает с областью определения выражения, задающего функцию: такая область определения называется естественной. Но бывает и так, что условия задачи накладывают особые ограничения: например, естественная область определения функции от (-8) до 8, но аргумент этой функции — время (или вес). Понятно тогда, что время (как и вес) не может быть отрицательной величиной и тогда естественная область определения такой функции сужается до промежутка (0; 8).
При отыскании области определения функции надо помнить о следующих ограничениях:
1. При извлечении корня четной степени подкоренное выражение обязано быть неотрицательным (что не запрещает ему быть равным нулю). 2. Знаменатель дроби не может быть равным нулю. 3. Выражение, стоящее под знаком логарифма, не может быть отрицательным или равняться нулю. 4. Выражение, стоящее под знаком арксинуса или арккосинуса, не может превышать 1 по модулю
Также надо помнить, что область определения всегда нужно искать для исходной функции, до каких-либо преобразований.
Например, функции 





1. Найдите область определения выражения:
Перепишем выражение:
Так как выражение стоит под корнем четной степени, значение его не должно быть отрицательным:

Дробь положительна, если числитель и знаменатель ее одновременно положительны или отрицательны. У нас в числителе положительное число, поэтому знаменатель неотрицателен. Кроме того, знаменатель не может быть равен нулю, поэтому неравенство становится таким:

Получили квадратное неравенство. Находим корни квадратного уравнения, чтобы выяснить точки перемены знака:
Наносим полученные точки на координатную прямую и расставляем знаки. Так как 
Ответ: 
2. Найдите область определения выражения:
Так как выражение стоит под корнем четной степени, значение его не должно быть отрицательным:

Получили квадратное неравенство. Находим корни квадратного уравнения, чтобы выяснить точки перемены знака:
Наносим полученные точки на координатную прямую и расставляем знаки. Так как 
Ответ: ![{x}in=[{{5-sqrt{41}}/4};{{5+sqrt{41}}/4}] {x}in=[{{5-sqrt{41}}/4};{{5+sqrt{41}}/4}]](https://easy-physic.ru/img_formuls/math_986_d5283fd254f051616bcd6dad000a9347.png)
3. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения 


Изображаем полученные точки на числовой оси, ставим знаки:
Точки закрашены, концы интервалов входят в решение. Тогда область определения функции: 



4. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения 



Изображаем полученные точки на числовой оси:
Решение системы неравенств:
Область определения функции: 

5. Найдите область определения функции:
Очевидно, что область определения функции будет совпадать с областью определения выражения
– ищем естественную область определения функции. Данное выражение имеет смысл только при 

Рассмотрим два случая:
Решение:
Или
Решение:
Область определения функции: 

6. Найти область определения функции:
Решение:
Ответ:
7. Найти область определения функции:
Решение:
Ответ:
8. Найти область определения функции:
Решение:
Ответ:

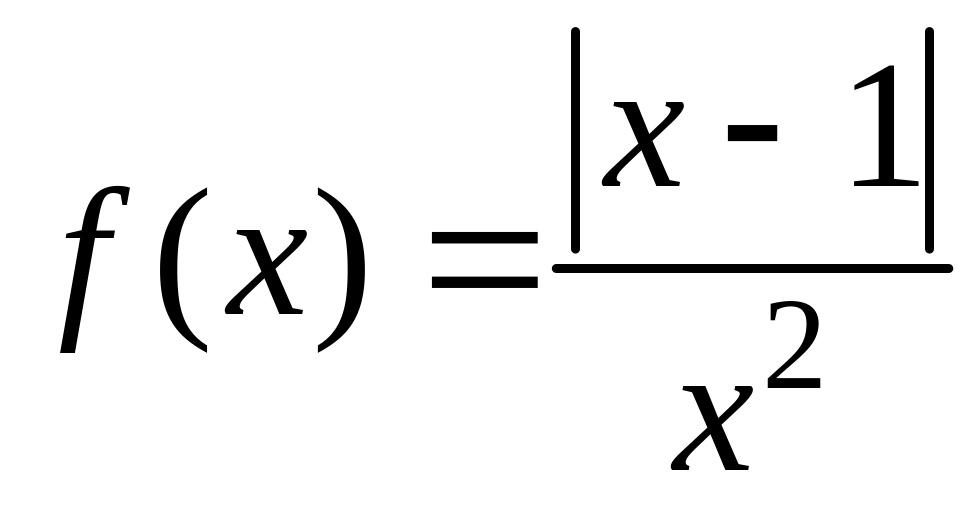
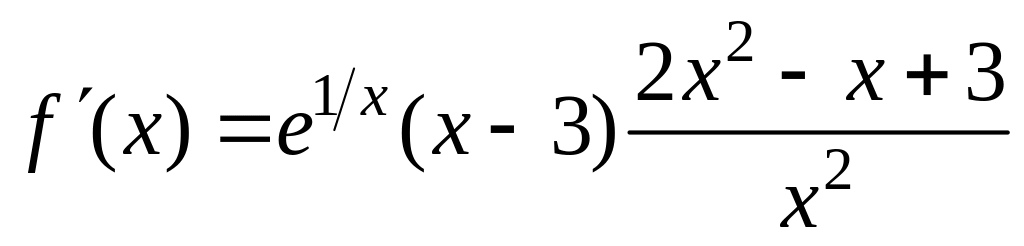
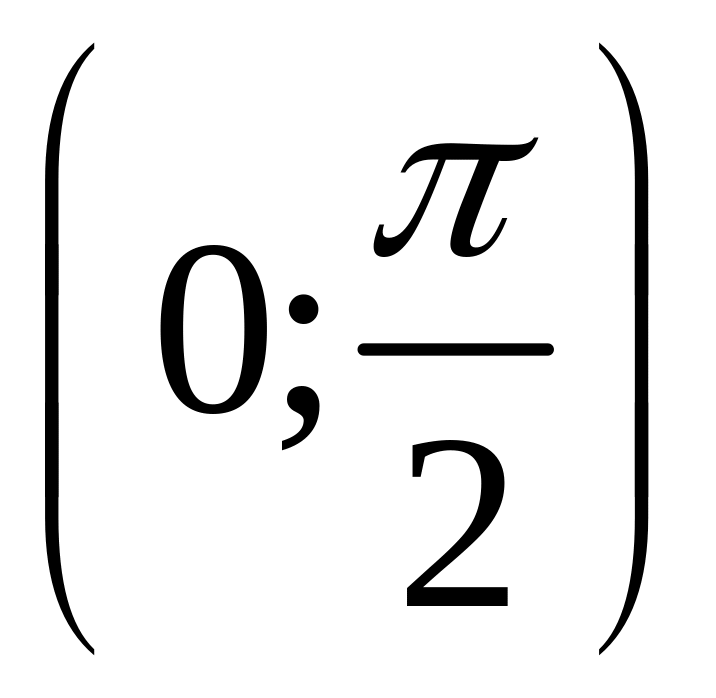
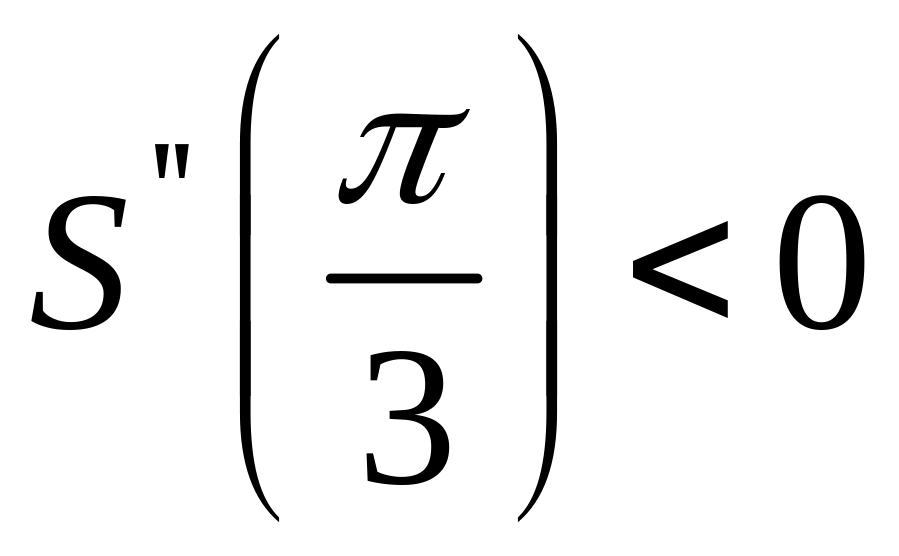

 Диапазон зависит от вершины и знака выражения абсолютного значения. См.: Функция абсолютного значения.
Диапазон зависит от вершины и знака выражения абсолютного значения. См.: Функция абсолютного значения.  № 2 выше). Таким образом, у вас могут быть только числа для x, большие или равные -2.
№ 2 выше). Таким образом, у вас могут быть только числа для x, большие или равные -2. 


















































