Как найти евклидово расстояние между двумя точками - Исправление недочетов и поиск решений вместе с Examum.ru

Не важно, начинаете вы осваивать Data Science или работаете в этой сфере не первый год, вам наверняка пригодятся эти метрики. Разбираемся, что они из себя представляют и чем отличаются друг от друга.

Евклидово расстояние (расстояние по прямой)

Евклидово расстояние самое интуитивное для понимания: именно Евклидову метрику мы представляем, когда кто-то просит нас измерить расстояние между точками.

Евклидово расстояние — это прямая линия между двумя точками с координатами X и Y. Например, одной из таких точек может быть город на карте с его координатами долготы и широты.

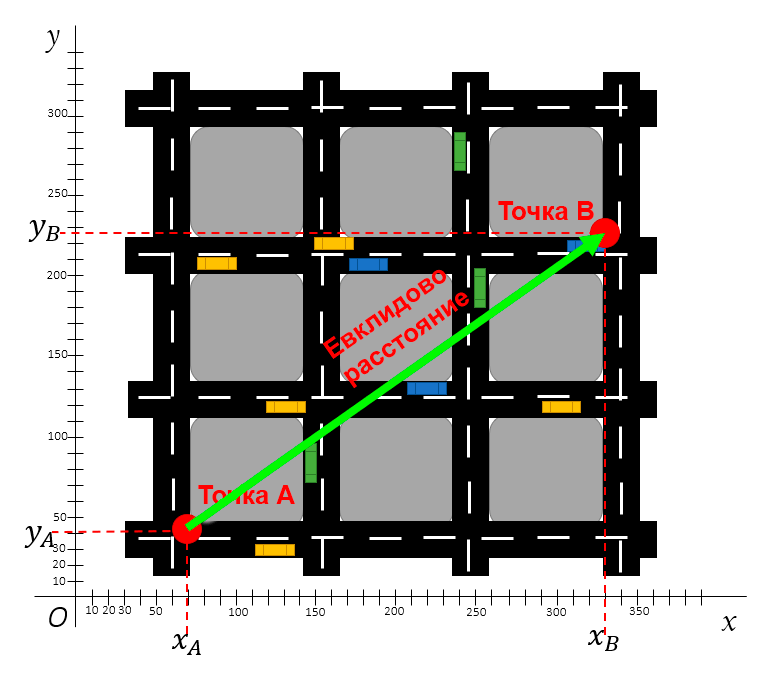
Евклидово расстояние характеризуется прямой линией. Допустим, вам нужно измерить расстояние по прямой между точками A и B на карте города, приведённой ниже.

Евклидово расстояние между двумя точками считается по теореме Пифагора

Для расчёта Евклидового расстояния вам понадобятся лишь координаты этих двух точек. Дистанцию между ними можно будет рассчитать по формуле Пифагора.

Теорема Пифагора гласит, что можно рассчитать длину «диагональной стороны» (гипотенузы) прямого треугольника, зная длины его горизонтальной и вертикальной стороны (катетов). Формула выглядит так: a² + b² = c².

Пример расчёта Евклидового расстояния

Прим. ред. В четвёртой строке вычислений допущена ошибка: (-260)^2 = 67 600, а не 76 600. Тогда результат будет равен ~321.

Расстояние L1 также известно как расстояние городских кварталов, манхэттенское расстояние, расстояние такси, метрика прямоугольного города — оно измеряет дистанцию не по кратчайшей прямой, а по блокам. Расстояние L1 измеряет дистанцию между городскими блоками: это расстояние всех прямых линий пути.

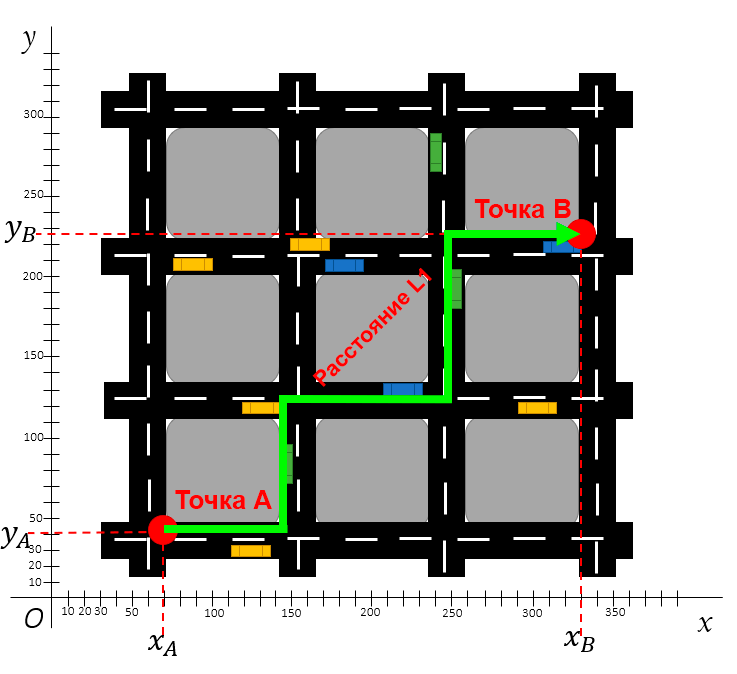
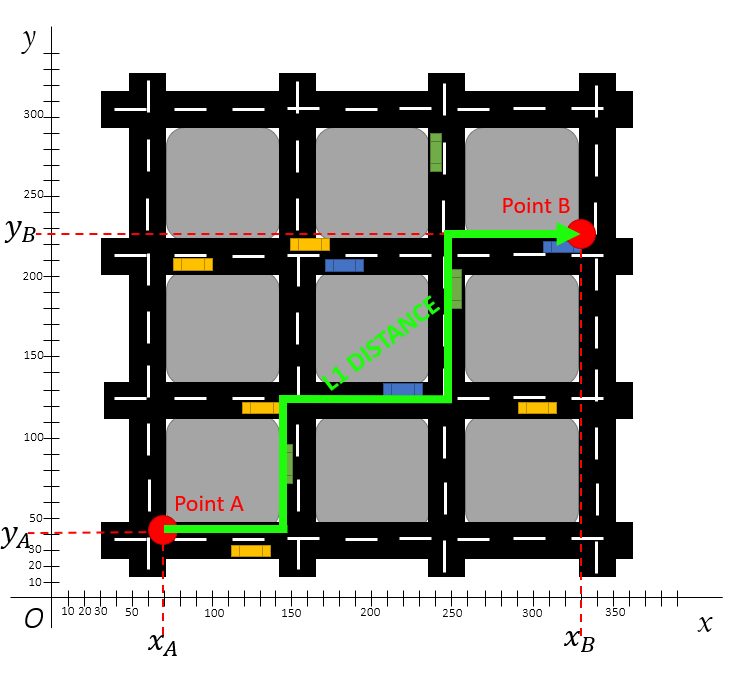
На следующем изображении показано расстояние L1 между двумя точками.

Расстояние L1 между двумя точками по блокам

Кроме показанного пути существует несколько альтернативных способов. Например, от точки A можно подняться на два блока вверх, а потом на три блока вправо, либо же на три блока вправо и два блока вверх.

Но расстояние L1 — это всё же просто дистанция, а поэтому траектория здесь не имеет значения. Единственное, что нужно понимать, это примерный путь: нужно пройти какое-то количество X блоков на восток и Y блоков на север. Сумма расстояний этих блоков и будет расстоянием L1 от точки A до точки B.

Пример расчёта расстояния L1 между двумя точками

Расстояние Чебышёва (метрика шахматной доски)

Расстояние Чебышёва известно ещё как расстояние шахматной доски. Чтобы понять принцип такой метрики, нужно представить короля на шахматной доске — он может ходить во всех направлениях: вперёд, назад, влево, вправо и по диагонали.

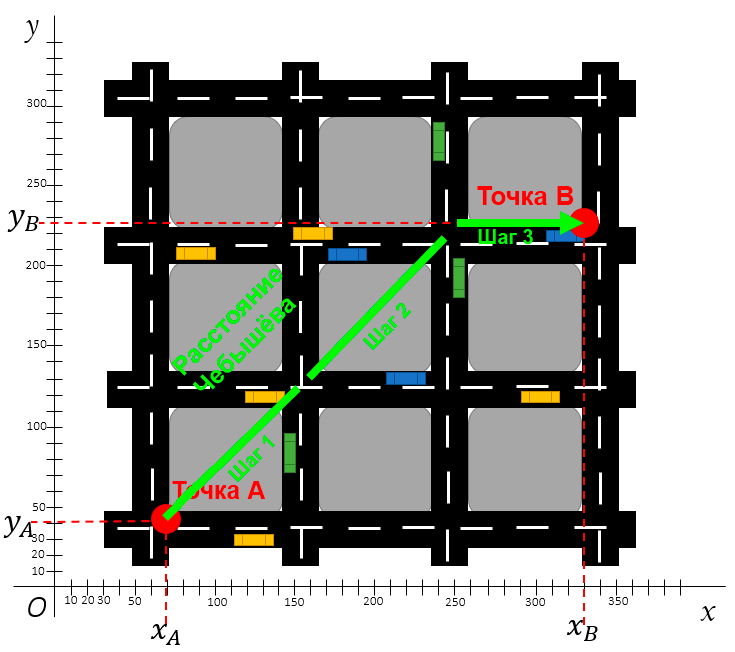
Расстояние Чебышёва между двумя точками

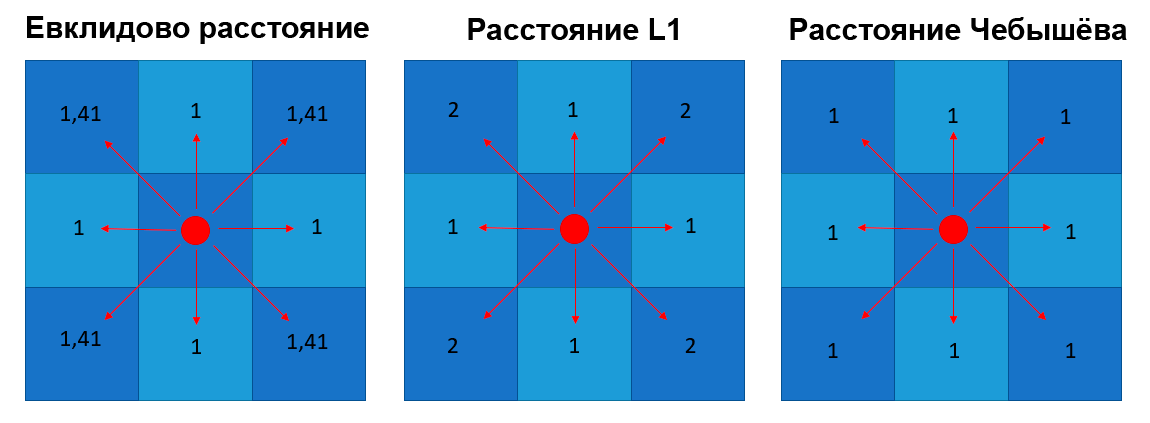
Разница расстояния L1 и расстояния Чебышёва в том, что при переходе на одну клетку по диагонали в первом случае засчитывается два хода (например вверх и влево), а во втором случае засчитывается всего один ход.

Ещё эти оба расстояния отличаются от Евклидового расстояния тем, что у Евклидового движение по диагонали рассчитывается по теореме Пифагора.

Сравнение путей 3 метрик

Расстояние Чебышёва можно представить как проход по шахматной доске.

Вот ещё один пример представления расстояния Чебышёва. Допустим, у вас есть дрон с двумя независимыми моторами: первый мотор тянет дрон вперёд, второй — в сторону. Оба мотора могут работать одновременно и равномерно на максимуме своей мощности.

Поэтому дрон может передвинуться на одну клетку по диагонали так же быстро, как по горизонтали или вертикали.

Посмотрите ещё раз на карту города по расстоянию Чебышёва. Первый шаг — оба мотора работают одновременно, второй шаг идентичен первому, а на третьем шаге мотор, тянущий дрон вперёд, отключается, и дрон смещается в сторону.

Таким образом, расстояние Чебышёва определяется как самая большая дистанция на одной оси.

Пример расчёта расстояния Чебышёва между двумя точками

Прим. ред. Полученный результат является условным и некорректно сравнивать его с другими результатами.

Перевод статьи «3 distances that every data scientist should know»

Источник

Время на прочтение
5 мин

Количество просмотров 28K

В этом руководстве мы рассмотрим, как рассчитать евклидово расстояние между двумя точками в Python с помощью Numpy.

Что такое евклидово расстояние?

Евклидово расстояние — это фундаментальная метрика расстояния, относящаяся к системам в евклидовом пространстве.

Евклидово пространство — это классическое геометрическое пространство, с которым вы знакомитесь на уроке математики, обычно связанное с 3 измерениями. Хотя его также можно приписать к любой неотрицательной целочисленной размерности.
Евклидово расстояние — кратчайшая прямая между двумя точками в евклидовом пространстве.

Название происходит от Евклида, который широко известен как «отец геометрии», так как это было единственное пространство, которое люди в то время обычно задумывали. Со временем в физике и математике наблюдались различные типы пространства, такие как пространство Аффин.

В 3-мерном евклидовом пространстве кратчайшая прямая между двумя точками всегда будет прямой линией между ними.

Учитывая этот факт, евклидово расстояние не всегда является наиболее полезной метрикой для отслеживания при работе со многими размерностями, мы сосредоточимся на 2D и 3D евклидовом пространстве для расчета евклидова расстояния.

Вообще говоря, евклидова расстояние широко используется в разработке 3D-миров, а также алгоритмов машинного обучения, которые включают в себя метрики расстояния, такие как K-ближайшие соседи. Как правило, евклидово расстояние будет представлять, насколько похожи две точки данных, предполагая, что некоторая кластеризация на основе других данных уже была выполнена.

Математическая формула

Математическая формула расчета евклидова расстояния между 2 точками в 2D пространстве:

$d(p,q) = sqrt[2]{(q_1-p_1)^2 + (q_2-p_2)^2 }$

Формула легко адаптируется к 3D-пространство, а также к любому размеру:

$d(p,q) = sqrt[2]{(q_1-p_1)^2 + (q_2-p_2)^2 + (q_3-p_3)^2 }$

Общая формула может быть упрощена до:

$d(p,q) = sqrt[2]{(q_1-p_1)^2 + ... + (q_n-p_n)^2 }$

Острый глаз может заметить сходство между евклидовым расстоянием и теоремой Пифагора:

На самом деле существует связь между ними — евклидовое расстояние рассчитывается с помощью теоремы Пифагора, учитывая декартовы координаты двух точек.

Из-за этого евклидова расстояние иногда называют расстоянием Пифагора, хотя прежнее название гораздо более известно.

Примечание: Две точки являются векторами, но выход должен быть скалярным.

Мы будем использовать NumPy для расчета этого расстояния для двух точек, и один и тот же подход используется для 2D и 3D пространств:

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')

ax.scatter(0, 0, 0)
ax.scatter(3, 3, 3)
plt.show()

Расчет евклидова расстояния в Python с помощью NumPy

Во-первых, нам нужно будет установить библиотеку NumPy:

$ pip install numpy

Теперь давайте импортируем его и настроим две наши точки с декартовыми координатами (0, 0, 0) и (3, 3, 3):

import numpy as np
# Initializing the points
point_1 = np.array((0, 0, 0))
point_2 = np.array((3, 3, 3))

Вместо того, чтобы выполнять расчет вручную, мы будем использовать вспомогательные методы NumPy, чтобы сделать его еще проще!

np.sqrt() и np.sum()

Операции и математические функции, необходимые для расчета евклидова расстояния, довольно просты: сложение, вычитание, а также функция квадратного корня. Несколько слагаемых также можно заменить суммой:

$d(p,q) = sqrt[2]{(q_1-p_1)^2 + (q_2-p_2)^2 + (q_3-p_3)^2 }$

NumPy предоставляет нам функцию np.sqrt(), представляющую функцию квадратного корня, а также функцию np.sum(), которая представляет собой сумму. При этом расчет евклидова расстояния в Python прост и интуитивно понятен:

# Get the square of the difference of the 2 vectors
square = np.square(point_1 - point_2)
# Get the sum of the square
sum_square = np.sum(square)

Данная формула дает нам довольно простой результат:

(0-3)^2 + (0-3)^2 + (0-3)^2

Что равно 27. Осталось все, что получить квадратный корень из этого числа:

# The last step is to get the square root and print the Euclidean distance
distance = np.sqrt(sum_square)
print(distance)

Это приводит к:

5.196152422706632

В истинном питоновом духе это можно сократить до одной строки:

И вы даже можете вместо этого использовать встроенные методы pow() и sum() математического модуля Python, хотя они требуют, чтобы вы немного поработали с вводом, который удобно абстрагируется с помощью NumPy, так как функция pow() работает только со скалярами (каждый элемент в массиве индивидуально) и принимает аргумент — в какой степени вы увеличиваете число.

Этот подход, однако, интуитивно больше похож на формулу, которую мы использовали раньше:

from math import *
distance = np.sqrt(sum(pow(a-b, 2) for a, b in zip(point_1, point_2)))
print(distance)

Это также приводит к:

5.196152422706632

np.linalg.norm()

Функция np.linalg.norm() представляет математическую норму. По сути, нормой вектора является его длина. Эта длина не обязательно должна быть евклидовым расстоянием, а может быть и другими расстояниями. Евклидово расстояние-это норма L2 вектора (иногда известная как евклидова норма), и по умолчанию функция norm() использует L2 — параметр ord имеет значение 2.

Если бы вы установили для параметра ord какое-то другое значение p, вы бы рассчитали другие p-нормы. Например, норма L1 вектора-это расстояние Манхэттена!

Имея это в виду, мы можем использовать функцию np.linalg.norm() для легкого и гораздо более чистого вычисления евклидова расстояния, чем использование других функций:

distance = np.linalg.norm(point_1-point_2)
print(distance)

Это приводит к печати расстояния L2/евклида:

5.196152422706632

Нормализация L2 и нормализация L1 широко используются в машинном обучении для нормализации входных данных.

np.dot()

Мы также можем использовать точечное произведение для расчета евклидова расстояния. В математике точечное произведение является результатом умножения двух векторов равной длины, а результатом является единственное число — скалярное значение. Из-за возвращаемого типа его иногда также называют «скалярным продуктом». Эту операцию часто называют внутренним произведением для двух векторов.

Для расчета точечного произведения между 2 векторами вы можете использовать следующую формулу:

$vec{p} cdot vec{q} = {(q_1-p_1) + (q_2-p_2) + (q_3-p_3) }$

С помощью NumPy мы можем использовать функцию np.dot(), передавая два вектора.

Если мы вычислим точечное произведение разницы между обеими точками с той же разницей — мы получим число, которое находится в зависимости от евклидова расстояния между этими двумя векторами. Извлечение квадратного корня из этого числа дает нам расстояние, которое мы ищем:

# Take the difference between the 2 points
diff = point_1 - point_2
# Perform the dot product on the point with itself to get the sum of the squares
sum_square = np.dot(diff, diff)
# Get the square root of the result
distance = np.sqrt(sum_square)
print(distance)

Конечно, вы также можете сократить это до однострочного:

distance = np.sqrt(np.dot(point_1-point_2, point_1-point_2))
print(distance)

5.196152422706632

Использование встроенной системы math.dist()

В Python есть встроенный метод в математическом модуле, который вычисляет расстояние между 2 точками в трехмерном пространстве. Однако это работает только с Python 3.8 или более поздней версии.

math.dist()принимает два параметра, которые являются двумя точками, и возвращает евклидово расстояние между этими точками.

Примечание: Обратите внимание, что две точки должны иметь одинаковые размеры (т.е. оба в 2d или 3d пространстве).

Теперь, чтобы вычислить Евклидово расстояние между этими двумя точками, мы просто заправляем их в метод thedistdist():

import math
distance = math.dist(point_1, point_2)
print(distance)

5.196152422706632

Заключение

Данная метрика используется во многих контекстах в интеллектуальном анализе данных, машинном обучении и ряде других областей и является одной из фундаментальных метрик расстояния.

Источник

From Wikipedia, the free encyclopedia

Using the Pythagorean theorem to compute two-dimensional Euclidean distance

In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points.
It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore occasionally being called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras, although Euclid did not represent distances as numbers, and the connection from the Pythagorean theorem to distance calculation was not made until the 18th century.

The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances between different types of objects, such as the distance from a point to a line. In advanced mathematics, the concept of distance has been generalized to abstract metric spaces, and other distances than Euclidean have been studied. In some applications in statistics and optimization, the square of the Euclidean distance is used instead of the distance itself.

Distance formulas[edit]

One dimension[edit]

The distance between any two points on the real line is the absolute value of the numerical difference of their coordinates, their absolute difference. Thus if and are two points on the real line, then the distance between them is given by:^[1]

A more complicated formula, giving the same value, but generalizing more readily to higher dimensions, is:^[1]

${displaystyle d(p,q)={sqrt {(p-q)^{2}}}.}$

In this formula, squaring and then taking the square root leaves any positive number unchanged, but replaces any negative number by its absolute value.^[1]

Two dimensions[edit]

In the Euclidean plane, let point have Cartesian coordinates $(p_{1},p_{2})$ and let point have coordinates $(q_{1},q_{2})$ . Then the distance between and is given by:^[2]

${displaystyle d(p,q)={sqrt {(q_{1}-p_{1})^{2}+(q_{2}-p_{2})^{2}}}.}$

This can be seen by applying the Pythagorean theorem to a right triangle with horizontal and vertical sides, having the line segment from to as its hypotenuse. The two squared formulas inside the square root give the areas of squares on the horizontal and vertical sides, and the outer square root converts the area of the square on the hypotenuse into the length of the hypotenuse.^[3]

It is also possible to compute the distance for points given by polar coordinates. If the polar coordinates of are and the polar coordinates of are , then their distance is^[2] given by the law of cosines:

${displaystyle d(p,q)={sqrt {r^{2}+s^{2}-2rscos(theta -psi )}}.}$

When and are expressed as complex numbers in the complex plane, the same formula for one-dimensional points expressed as real numbers can be used, although here the absolute value sign indicates the complex norm:^[4]

Higher dimensions[edit]

Deriving the -dimensional Euclidean distance formula by repeatedly applying the Pythagorean theorem

In three dimensions, for points given by their Cartesian coordinates, the distance is

${displaystyle d(p,q)={sqrt {(p_{1}-q_{1})^{2}+(p_{2}-q_{2})^{2}+(p_{3}-q_{3})^{2}}}.}$

In general, for points given by Cartesian coordinates in -dimensional Euclidean space, the distance is^[5]

${displaystyle d(p,q)={sqrt {(p_{1}-q_{1})^{2}+(p_{2}-q_{2})^{2}+cdots +(p_{n}-q_{n})^{2}}}.}$

The Euclidean distance may also be expressed more compactly in terms of the Euclidean norm of the Euclidean vector difference:

Objects other than points[edit]

For pairs of objects that are not both points, the distance can most simply be defined as the smallest distance between any two points from the two objects, although more complicated generalizations from points to sets such as Hausdorff distance are also commonly used.^[6] Formulas for computing distances between different types of objects include:

The distance from a point to a line, in the Euclidean plane^[7]
The distance from a point to a plane in three-dimensional Euclidean space^[7]
The distance between two lines in three-dimensional Euclidean space^[8]

Properties[edit]

The Euclidean distance is the prototypical example of the distance in a metric space,^[9] and obeys all the defining properties of a metric space:^[10]

Another property, Ptolemy’s inequality, concerns the Euclidean distances among four points , , , and . It states that

For points in the plane, this can be rephrased as stating that for every quadrilateral, the products of opposite sides of the quadrilateral sum to at least as large a number as the product of its diagonals. However, Ptolemy’s inequality applies more generally to points in Euclidean spaces of any dimension, no matter how they are arranged.^[11] For points in metric spaces that are not Euclidean spaces, this inequality may not be true. Euclidean distance geometry studies properties of Euclidean distance such as Ptolemy’s inequality, and their application in testing whether given sets of distances come from points in a Euclidean space.^[12]

According to the Beckman–Quarles theorem, any transformation of the Euclidean plane or of a higher-dimensional Euclidean space that preserves unit distances must be an isometry, preserving all distances.^[13]

Squared Euclidean distance[edit]

A cone, the graph of Euclidean distance from the origin in the plane

A paraboloid, the graph of squared Euclidean distance from the origin

In many applications, and in particular when comparing distances, it may be more convenient to omit the final square root in the calculation of Euclidean distances. The value resulting from this omission is the square of the Euclidean distance, and is called the squared Euclidean distance.^[14] For instance, the Euclidean minimum spanning tree can be determined using only the ordering between distances, and not their numeric values. Comparing squared distances produces the same result but avoids an unnecessary square-root calculation and sidesteps issues of numerical precision.^[15] As an equation, the squared distance can be expressed as a sum of squares:

${displaystyle d^{2}(p,q)=(p_{1}-q_{1})^{2}+(p_{2}-q_{2})^{2}+cdots +(p_{n}-q_{n})^{2}.}$

Beyond its application to distance comparison, squared Euclidean distance is of central importance in statistics, where it is used in the method of least squares, a standard method of fitting statistical estimates to data by minimizing the average of the squared distances between observed and estimated values,^[16] and as the simplest form of divergence to compare probability distributions.^[17] The addition of squared distances to each other, as is done in least squares fitting, corresponds to an operation on (unsquared) distances called Pythagorean addition.^[18] In cluster analysis, squared distances can be used to strengthen the effect of longer distances.^[14]

Squared Euclidean distance does not form a metric space, as it does not satisfy the triangle inequality.^[19] However it is a smooth, strictly convex function of the two points, unlike the distance, which is non-smooth (near pairs of equal points) and convex but not strictly convex. The squared distance is thus preferred in optimization theory, since it allows convex analysis to be used. Since squaring is a monotonic function of non-negative values, minimizing squared distance is equivalent to minimizing the Euclidean distance, so the optimization problem is equivalent in terms of either, but easier to solve using squared distance.^[20]

The collection of all squared distances between pairs of points from a finite set may be stored in a Euclidean distance matrix, and is used in this form in distance geometry.^[21]

Generalizations[edit]

In more advanced areas of mathematics, when viewing Euclidean space as a vector space, its distance is associated with a norm called the Euclidean norm, defined as the distance of each vector from the origin. One of the important properties of this norm, relative to other norms, is that it remains unchanged under arbitrary rotations of space around the origin.^[22] By Dvoretzky’s theorem, every finite-dimensional normed vector space has a high-dimensional subspace on which the norm is approximately Euclidean; the Euclidean norm is the
only norm with this property.^[23] It can be extended to infinite-dimensional vector spaces as the L² norm or L² distance.^[24] The Euclidean distance gives Euclidean space the structure of a topological space, the Euclidean topology, with the open balls (subsets of points at less than a given distance from a given point) as its neighborhoods.^[25]

Other common distances on Euclidean spaces and low-dimensional vector spaces include:^[26]

Chebyshev distance, which measures distance assuming only the most significant dimension is relevant.
Manhattan distance, which measures distance following only axis-aligned directions.
Minkowski distance, a generalization that unifies Euclidean distance, Manhattan distance, and Chebyshev distance.

For points on surfaces in three dimensions, the Euclidean distance should be distinguished from the geodesic distance, the length of a shortest curve that belongs to the surface. In particular, for measuring great-circle distances on the earth or other spherical or near-spherical surfaces, distances that have been used include the haversine distance giving great-circle distances between two points on a sphere from their longitudes and latitudes, and Vincenty’s formulae also known as «Vincent distance» for distance on a spheroid.^[27]

History[edit]

Euclidean distance is the distance in Euclidean space; both concepts are named after ancient Greek mathematician Euclid, whose Elements became a standard textbook in geometry for many centuries.^[28] Concepts of length and distance are widespread across cultures, can be dated to the earliest surviving «protoliterate» bureaucratic documents from Sumer in the fourth millennium BC (far before Euclid),^[29] and have been hypothesized to develop in children earlier than the related concepts of speed and time.^[30] But the notion of a distance, as a number defined from two points, does not actually appear in Euclid’s Elements. Instead, Euclid approaches this concept implicitly, through the congruence of line segments, through the comparison of lengths of line segments, and through the concept of proportionality.^[31]

The Pythagorean theorem is also ancient, but it could only take its central role in the measurement of distances after the invention of Cartesian coordinates by René Descartes in 1637. The distance formula itself was first published in 1731 by Alexis Clairaut.^[32] Because of this formula, Euclidean distance is also sometimes called Pythagorean distance.^[33] Although accurate measurements of long distances on the earth’s surface, which are not Euclidean, had again been studied in many cultures since ancient times (see history of geodesy), the idea that Euclidean distance might not be the only way of measuring distances between points in mathematical spaces came even later, with the 19th-century formulation of non-Euclidean geometry.^[34] The definition of the Euclidean norm and Euclidean distance for geometries of more than three dimensions also first appeared in the 19th century, in the work of Augustin-Louis Cauchy.^[35]

References[edit]

^ ^a ^b ^c Smith, Karl (2013), Precalculus: A Functional Approach to Graphing and Problem Solving, Jones & Bartlett Publishers, p. 8, ISBN 978-0-7637-5177-7
^ ^a ^b Cohen, David (2004), Precalculus: A Problems-Oriented Approach (6th ed.), Cengage Learning, p. 698, ISBN 978-0-534-40212-9
^ Aufmann, Richard N.; Barker, Vernon C.; Nation, Richard D. (2007), College Trigonometry (6th ed.), Cengage Learning, p. 17, ISBN 978-1-111-80864-8
^ Andreescu, Titu; Andrica, Dorin (2014), «3.1.1 The Distance Between Two Points», Complex Numbers from A to … Z (2nd ed.), Birkhäuser, pp. 57–58, ISBN 978-0-8176-8415-0
^ Tabak, John (2014), Geometry: The Language of Space and Form, Facts on File math library, Infobase Publishing, p. 150, ISBN 978-0-8160-6876-0
^ Ó Searcóid, Mícheál (2006), «2.7 Distances from Sets to Sets», Metric Spaces, Springer Undergraduate Mathematics Series, Springer, pp. 29–30, ISBN 978-1-84628-627-8
^ ^a ^b Ballantine, J. P.; Jerbert, A. R. (April 1952), «Distance from a line, or plane, to a point», Classroom notes, American Mathematical Monthly, 59 (4): 242–243, doi:10.2307/2306514, JSTOR 2306514
^ Bell, Robert J. T. (1914), «49. The shortest distance between two lines», An Elementary Treatise on Coordinate Geometry of Three Dimensions (2nd ed.), Macmillan, pp. 57–61
^ Ivanov, Oleg A. (2013), Easy as π?: An Introduction to Higher Mathematics, Springer, p. 140, ISBN 978-1-4612-0553-1
^ ^a ^b ^c ^d Strichartz, Robert S. (2000), The Way of Analysis, Jones & Bartlett Learning, p. 357, ISBN 978-0-7637-1497-0
^ Adam, John A. (2017), «Chapter 2. Introduction to the «Physics» of Rays», Rays, Waves, and Scattering: Topics in Classical Mathematical Physics, Princeton Series in Applied Mathematics, Princeton University Press, pp. 26–27, doi:10.1515/9781400885404-004, ISBN 978-1-4008-8540-4
^ Liberti, Leo; Lavor, Carlile (2017), Euclidean Distance Geometry: An Introduction, Springer Undergraduate Texts in Mathematics and Technology, Springer, p. xi, ISBN 978-3-319-60792-4
^ Beckman, F. S.; Quarles, D. A., Jr. (1953), «On isometries of Euclidean spaces», Proceedings of the American Mathematical Society, 4 (5): 810–815, doi:10.2307/2032415, JSTOR 2032415, MR 0058193
^ ^a ^b Spencer, Neil H. (2013), «5.4.5 Squared Euclidean Distances», Essentials of Multivariate Data Analysis, CRC Press, p. 95, ISBN 978-1-4665-8479-2
^ Yao, Andrew Chi Chih (1982), «On constructing minimum spanning trees in k-dimensional spaces and related problems», SIAM Journal on Computing, 11 (4): 721–736, doi:10.1137/0211059, MR 0677663
^ Randolph, Karen A.; Myers, Laura L. (2013), Basic Statistics in Multivariate Analysis, Pocket Guide to Social Work Research Methods, Oxford University Press, p. 116, ISBN 978-0-19-976404-4
^ Csiszár, I. (1975), «I-divergence geometry of probability distributions and minimization problems», Annals of Probability, 3 (1): 146–158, doi:10.1214/aop/1176996454, JSTOR 2959270, MR 0365798
^ Moler, Cleve and Donald Morrison (1983), «Replacing Square Roots by Pythagorean Sums» (PDF), IBM Journal of Research and Development, 27 (6): 577–581, CiteSeerX 10.1.1.90.5651, doi:10.1147/rd.276.0577
^ Mielke, Paul W.; Berry, Kenneth J. (2000), «Euclidean distance based permutation methods in atmospheric science», in Brown, Timothy J.; Mielke, Paul W. Jr. (eds.), Statistical Mining and Data Visualization in Atmospheric Sciences, Springer, pp. 7–27, doi:10.1007/978-1-4757-6581-6_2
^ Kaplan, Wilfred (2011), Maxima and Minima with Applications: Practical Optimization and Duality, Wiley Series in Discrete Mathematics and Optimization, vol. 51, John Wiley & Sons, p. 61, ISBN 978-1-118-03104-9
^ Alfakih, Abdo Y. (2018), Euclidean Distance Matrices and Their Applications in Rigidity Theory, Springer, p. 51, ISBN 978-3-319-97846-8
^ Kopeikin, Sergei; Efroimsky, Michael; Kaplan, George (2011), Relativistic Celestial Mechanics of the Solar System, John Wiley & Sons, p. 106, ISBN 978-3-527-63457-6
^ Matoušek, Jiří (2002), Lectures on Discrete Geometry, Graduate Texts in Mathematics, Springer, p. 349, ISBN 978-0-387-95373-1
^ Ciarlet, Philippe G. (2013), Linear and Nonlinear Functional Analysis with Applications, Society for Industrial and Applied Mathematics, p. 173, ISBN 978-1-61197-258-0
^ Richmond, Tom (2020), General Topology: An Introduction, De Gruyter, p. 32, ISBN 978-3-11-068657-9
^ Klamroth, Kathrin (2002), «Section 1.1: Norms and Metrics», Single-Facility Location Problems with Barriers, Springer Series in Operations Research, Springer, pp. 4–6, doi:10.1007/0-387-22707-5_1
^ Panigrahi, Narayan (2014), «12.2.4 Haversine Formula and 12.2.5 Vincenty’s Formula», Computing in Geographic Information Systems, CRC Press, pp. 212–214, ISBN 978-1-4822-2314-9
^ Zhang, Jin (2007), Visualization for Information Retrieval, Springer, ISBN 978-3-540-75148-9
^ Høyrup, Jens (2018), «Mesopotamian mathematics» (PDF), in Jones, Alexander; Taub, Liba (eds.), The Cambridge History of Science, Volume 1: Ancient Science, Cambridge University Press, pp. 58–72
^ Acredolo, Curt; Schmid, Jeannine (1981), «The understanding of relative speeds, distances, and durations of movement», Developmental Psychology, 17 (4): 490–493, doi:10.1037/0012-1649.17.4.490
^ Henderson, David W. (2002), «Review of Geometry: Euclid and Beyond by Robin Hartshorne», Bulletin of the American Mathematical Society, 39: 563–571, doi:10.1090/S0273-0979-02-00949-7
^ Maor, Eli (2019), The Pythagorean Theorem: A 4,000-Year History, Princeton University Press, pp. 133–134, ISBN 978-0-691-19688-6
^ Rankin, William C.; Markley, Robert P.; Evans, Selby H. (March 1970), «Pythagorean distance and the judged similarity of schematic stimuli», Perception & Psychophysics, 7 (2): 103–107, doi:10.3758/bf03210143, S2CID 144797925
^ Milnor, John (1982), «Hyperbolic geometry: the first 150 years», Bulletin of the American Mathematical Society, 6 (1): 9–24, doi:10.1090/S0273-0979-1982-14958-8, MR 0634431
^ Ratcliffe, John G. (2019), Foundations of Hyperbolic Manifolds, Graduate Texts in Mathematics, vol. 149 (3rd ed.), Springer, p. 32, ISBN 978-3-030-31597-9

Источник

Метрики расстояния играют важную роль в машинном обучении. Они обеспечивают прочную основу для нескольких алгоритмов машинного обучения, таких как k-ближайшие соседи для обучения с учителем и кластеризация k-средних для обучения без учителя. В зависимости от типа данных выбираются разные метрики расстояния. Итак, важно знать различные метрики расстояния и интуицию, лежащую в основе этого.

Эффективный показатель расстояния повышает производительность нашей модели машинного обучения, будь то задачи классификации или кластеризации.

Допустим, мы хотим создать кластеры с использованием алгоритма k-ближайшего соседа для решения задачи классификации или регрессии. Как мы можем сказать, что две точки похожи друг на друга?

Это произойдет, если их функции похожи. Когда мы наносим эти точки на график, они будут ближе друг к другу на расстоянии.

Следовательно, мы можем вычислить расстояние между точками, а затем определить сходство между ними. Теперь возникает вопрос: как рассчитать это расстояние и каковы разные показатели расстояния в машинном обучении?

Об этом мы и поговорим в этой статье. Мы рассмотрим 6 типов показателей расстояния в машинном обучении.

Типы показателей расстояния в машинном обучении

Евклидово расстояние

2. Манхэттенское расстояние

3. Расстояние Минковского

4. Расстояние Хэмминга.

5. Косинусное расстояние

1. Евклидово расстояние

Евклидово расстояние представляет собой кратчайшее расстояние между двумя точками.

Формула евклидова расстояния может использоваться для расчета расстояния между двумя точками данных на плоскости.

Евклидово расстояние обычно используется при вычислении расстояния между двумя строками данных, которые имеют числовые значения, такие как значения с плавающей запятой или целые числа.

Если столбцы имеют значения с разными масштабами, их следует нормализовать или стандартизировать перед вычислением евклидова расстояния. В противном случае столбцы с большими значениями будут преобладать при измерении расстояния.

Евклидово расстояние вычисляется как квадратный корень из суммы квадратов разностей между двумя векторами.

Где,

n = количество измерений

pi, qi = точки данных

Этот расчет связан с векторной нормой L2 (обсуждается позже).

А теперь остановимся и посмотрим внимательно! Вам знакома эта формула? Да, эта формула взята из «теоремы Пифагора».

Напишем код Евклидова расстояния на Python. Сначала мы импортируем библиотеку SciPy, которая содержит заранее написанные коды для большинства функций расстояния, используемых в Python:

Вот как мы можем вычислить евклидово расстояние между двумя точками в Python.

2. Манхэттенское расстояние

Манхэттенское расстояние — это сумма абсолютных разностей между точками по всем измерениям.

Мы используем расстояние Манхэттена, также известное как расстояние между кварталом или геометрия такси, если нам нужно рассчитать расстояние между двумя точками данных на сетке, как на шахматной доске. или городские кварталы.

Название такси связано с интуитивным пониманием того, что рассчитывает мера: кратчайший путь, по которому такси может проехать между городскими кварталами (координаты на сетке).

Допустим, мы хотим вычислить расстояние, d между двумя точками данных — A и B.

Расстояние d будет рассчитано с использованием абсолютной суммы разницы между его декартовыми координатами, как показано ниже:

А обобщенная формула для n-мерного пространства имеет вид:

Где,

n = количество измерений

pi, qi = точки данных

Манхэттенское расстояние связано с векторной нормой L1 (обсуждается позже).

Если вы попытаетесь визуализировать расчет расстояния, он будет выглядеть примерно так:

На картинке выше представьте, что каждая ячейка представляет собой здание, а линии сетки — дороги. Теперь, если мы хотим перейти от точки P к точке Q, отмеченной на изображении, и следовать по небесно-голубым и темно-синим путям, мы увидим, что путь не прямой и есть повороты. В этом случае мы используем метрику расстояния Манхэттена для расчета пройденного расстояния. Розовая линия, соединяющая две точки P и Q, — это расстояние Манхэттена. Теперь расстояние d будет вычислено, как показано желтой линией.

Когда в ML предпочтительнее использовать метрику манхэттенского расстояния?

Манхэттенское расстояние предпочтительнее метрики евклидова расстояния, поскольку размерность данных увеличивается. Это происходит из-за того, что известно как проклятие размерности. Для получения дополнительной информации посетите эту ссылку.

Теперь мы рассчитаем Манхэттенское расстояние между двумя точками. В SciPy есть функция под названием cityblock, которая возвращает расстояние Манхэттена между двумя точками.

3. Расстояние Минковского

Расстояние Минковского — это обобщенная форма евклидова и манхэттенского расстояния.

Расстояние Минковского рассчитывает расстояние между двумя точками.

Это обобщение евклидовых и манхэттенских мер расстояния и добавляет параметр, называемый «порядок» или «p», который позволяет вычислять различные меры расстояния.

Расстояние Минковского рассчитывается следующим образом:

Где «p» — параметр порядка.

Когда p установлено в 1, расчет аналогичен манхэттенскому расстоянию. Когда p установлено на 2, это то же самое, что и евклидово расстояние.

p = 1: расстояние Манхэттена.
p = 2: евклидово расстояние.

Промежуточные значения обеспечивают контролируемый баланс между двумя показателями.

Расстояние Минковского связано с векторной нормой Lp (обсуждается позже).

Расстояние Минковского обычно используется при реализации алгоритма машинного обучения, который использует меры расстояния, поскольку он дает контроль над типом меры расстояния, используемой для векторов с действительными значениями, с помощью гиперпараметра «p», который можно настраивать. .

Давайте вычислим расстояние Минковского порядка 3:

Когда порядок (p) равен 1, он будет представлять манхэттенское расстояние, а когда порядок в приведенной выше формуле равен 2, он будет представлять евклидово расстояние. Давайте проверим, что в Python:

Здесь мы видим, что когда порядок равен 1, расстояние Минковского и Манхэттенское расстояние одинаковы.

Давайте также проверим евклидово расстояние:

Когда порядок равен 2, мы видим, что расстояния Минковского и Евклидовы одинаковы.

Читая эту статью, вы наверняка встречали слова L1 нормы, L2 нормы. Итак, давайте обсудим их подробнее.

Вектор Норма

Вычисление размера или длины вектора часто требуется либо напрямую, либо как часть векторно-метрической операции.

Длина вектора называется векторной нормой или величиной вектора.

Длина вектора — это неотрицательное число, которое описывает протяженность вектора в пространстве и иногда называется величиной вектора или нормой.

Длина вектора всегда является положительным числом, за исключением вектора всех нулевых значений. Он рассчитывается с использованием некоторых показателей расстояния, которые суммируют расстояние вектора от начала векторного пространства. Например, начало векторного пространства для вектора с 3 элементами — (0, 0, 0).

Мы рассмотрим несколько распространенных вычислений векторных норм, используемых в машинном обучении.

Вектор L1 Норма

Длину вектора можно вычислить, используя норму L1. Норма L1, представленная как || v || 1, вычисляется как сумма абсолютных значений вектора, где абсолютное значение скаляра использует обозначение | a1 |. Ясно, что норма — это вычисление манхэттенского расстояния от начала координат векторного пространства.

||v||1 = |a1| + |a2| + |a3|

Норма L1 вектора может быть вычислена в NumPy с помощью функции norm () с параметром для указания порядка нормы, в данном случае 1.

Вектор L2 Норма

Норма L2, представленная как || v || 2, вычисляется как квадратный корень из суммы квадратов векторных значений. Очевидно, что норма — это вычисление евклидова расстояния от происхождение векторного пространства.

|| v || 2 = sqrt (a1² + a2² + a3²)

Норма L2 вектора может быть вычислена в NumPy с помощью функции norm () с параметрами по умолчанию.

Vector Lp Norm

Норма Lp, представленная как || v || p, вычисляется следующим образом из начала координат векторного пространства:

||v||p=(a1^p + a2^p + a3^p)^(1/p)

Очевидно, что норма — это вычисление расстояния Минковского от начала координат векторного пространства.

До сих пор мы рассмотрели метрики расстояния, которые используются, когда мы имеем дело с непрерывными или числовыми переменными. Но что, если у нас есть категориальные переменные? Как мы можем определить сходство между категориальными переменными? Здесь мы можем использовать другую метрику расстояния, называемую расстоянием Хэмминга.

4. Расстояние Хэмминга.

Расстояние Хэмминга измеряет сходство двух строк одинаковой длины. Расстояние Хэмминга между двумя строками одинаковой длины — это количество позиций, на которых соответствующие символы различаются.

Давайте разберемся в концепции на примере. Допустим, у нас есть две строки:

«евклидово» и «манхэттенское»

Поскольку длины этих строк равны, мы можем вычислить расстояние Хэмминга. Мы будем идти по символам и сопоставлять строки. Первый символ обеих строк (e и m соответственно) разный. Точно так же второй символ обеих строк (u и a) отличается. и так далее.

Посмотрите внимательно — семь символов разные, тогда как два символа (последние два символа) похожи:

Следовательно, расстояние Хэмминга здесь будет 7. Обратите внимание, что чем больше расстояние Хэмминга между двумя струнами, тем более непохожими будут эти струны (и наоборот).

Давайте посмотрим, как мы можем вычислить расстояние Хэмминга двух строк в Python.

Как мы видели в приведенном выше примере, расстояние Хэмминга между «евклидовым» и «манхэттенским» равно 7. Мы также видели, что расстояние Хэмминга работает только тогда, когда у нас есть строки одинаковой длины.

Давайте посмотрим, что происходит, когда у нас есть строки разной длины:

Это вызывает ошибку, в которой говорится, что длины массивов должны быть одинаковыми. Следовательно, расстояние Хэмминга работает только тогда, когда у нас есть строки или массивы одинаковой длины.

Это некоторые из мер сходства или матриц расстояний, которые обычно используются в машинном обучении.

5. косинусное расстояние и косинусное сходство:

Косинусное сходство — это показатель, используемый для измерения того, насколько похожи документы независимо от их размера. Математически он измеряет косинус угла между двумя векторами, проецируемыми в многомерное пространство. Косинусное сходство является преимуществом, потому что даже если два похожих документа находятся далеко друг от друга на евклидово расстояние (из-за размера документа), есть вероятность, что они все еще могут быть ориентированы ближе друг к другу. Чем меньше угол, тем выше косинусное подобие.

Формула косинусного подобия может быть получена из уравнения скалярных произведений:

Таким образом, косинусное подобие определяется как Cos θ, а косинусное расстояние равно 1- Cos θ. Пример:-

На приведенном выше изображении две точки данных показаны синим цветом, угол между этими точками составляет 90 градусов, а Cos 90 = 0. Следовательно, показанные две точки не похожи, и их косинусное расстояние равно 1 — Cos 90 = 1. .

Теперь, если угол между двумя точками равен 0 градусов на приведенном выше рисунке, то косинусное сходство, Cos 0 = 1 и косинусное расстояние равно 1- Cos 0 = 0. Тогда мы можем интерпретировать, что две точки на 100% похожи друг на друга. Другие.

На приведенном выше рисунке представьте, что значение θ составляет 60 градусов, затем по формуле подобия косинуса Cos 60 = 0,5, а расстояние косинуса равно 1-0,5 = 0,5. Таким образом, точки на 50% похожи друг на друга.

Давайте код для лучшего понимания. Для этого нам нужно импортировать библиотеку cosine_similarity.

Обратите внимание, что первое значение массива — 1.0, потому что это косинусное сходство между первым документом с самим собой. Также обратите внимание, что из-за наличия похожих слов в третьем документе («Солнце в небе яркое») он получил более высокий балл.

Заключение

В этой статье мы узнали о нескольких популярных метриках расстояния / сходства и о том, как их можно использовать для решения сложных задач машинного обучения. Мы изучили метрики расстояния Минковского, Евклида, Манхэттена, Хэмминга и косинуса и их использование.

Манхэттенское расстояние обычно предпочтительнее, чем более распространенное евклидово расстояние, когда данные имеют высокую размерность. Расстояние Хэмминга используется для измерения расстояния между категориальными переменными, а показатель косинусного расстояния в основном используется для определения степени сходства.

Спасибо за внимание! 😊 Если вам понравилось, нажмите 👏 значок . Это отличное упражнение для ваших пальцев, которое поможет другим людям увидеть историю.

Источник

Алгоритмы, Математика, Data Mining

Рекомендация: подборка платных и бесплатных курсов таргетированной рекламе — https://katalog-kursov.ru/

Будь вы новичок в работе с данными или, напротив, матёрый профессионал, вам никуда не деться от работы с различными видами расстояний (так же называемых «метриками»).

Ниже разобраны три базовых метрики, с которыми вам рано или поздно придётся столкнуться.

1. Евклидово расстояние (расстояние по прямой линии)

Из всех расстояний Евклидово самое простое для восприятия: именно его мы интуитивно представляем в первую очередь, когда кто-то просит нас оценить дистанцию.

Евклидова метрика — это прямая линия между двумя точками с заданными координатами X и Y. Двух координат (широты и долготы) нам, в свою очередь, достаточно, чтобы однозначно указать объект на карте.

Рассмотрим часть условного города:

Для расчёта Евклидова расстояния между точками A и B нам понадобятся лишь их координаты (Xn, Yn) и формула из теоремы Пифагора.

Теорема говорит нам о том, как рассчитать длину гипотенузы ( c ) прямоугольного треугольника, зная длины его катетов (a и b): a? + b? =c?. Таким образом:

2. Расстояние L1 (расстояние городских кварталов)

Расстояние L1 так же известное как расстояние городских кварталов, манхеттенское расстояние, метрика прямоугольного города, метрика городского квартала или метрика такси измеряет дистанцию не по прямой, а блоками.

Картинка ниже показывает, как это работает:

В отличие от Евклидова, в расстоянии L1 не один, а несколько кратчайших путей из точки A в точку B. Например, можно сначала пойти на два блока вверх и на три вправо после.

Но L1 — расстояние, поэтому конкретная траектория для расчётов не важна. Важно лишь знать, сколько блоков нужно пройти на север и сколько на восток. Сумма их расстояний и будет нашей метрикой.

3. Расстояние Чебышёва (метрика шахматной доски)

Расстояние Чебышёва иногда называют L-бесконечность метрикой («L Infinity Distance»). Легче всего понять как она работает, если представить движение короля по шахматной доске: он может передвигаться во всех направлениях: вперёд, назад, влево, вправо и по диагонали.

Главное отличие от расстояния L1 в том, как считается движение по диагонали: это два шага в L1 (один вправо + один вверх), но всего один шаг в расстоянии Чебышёва.

Обе метрики в свою очередь отличаются от Евклидовой, где движение по диагонали займёт корень из двух шагов (т.е. примерно 1,41):

Слева направо: дистанции в Евклидовой метрике, L1 метрике, метрике Чебышёва.

Другим примером расстояния Чебышёва будет движение квадрокоптера с двумя независимыми моторами: один, чтобы лететь вперёд-назад, второй, чтобы вправо-влево. Оба мотора могут работать одновременно на максимальной мощности.

Тогда движение по диагонали (если оба мотора включены) займёт столько же времени, сколько движение по горизонтали или вертикали (если включен только один соответствующий мотор).

Можно догадаться, что расстояние Чебышёва определяется как наибольшая дистанция по одной из осей.

Надеюсь, эта статья открыла для вас что-то новое или, напротив, помогла освежить знания. Удачи в применении метрик на практике!

Источник