Время на прочтение
5 мин
Количество просмотров 28K
В этом руководстве мы рассмотрим, как рассчитать евклидово расстояние между двумя точками в Python с помощью Numpy.
Что такое евклидово расстояние?
Евклидово расстояние — это фундаментальная метрика расстояния, относящаяся к системам в евклидовом пространстве.
-
Евклидово пространство — это классическое геометрическое пространство, с которым вы знакомитесь на уроке математики, обычно связанное с 3 измерениями. Хотя его также можно приписать к любой неотрицательной целочисленной размерности.
-
Евклидово расстояние — кратчайшая прямая между двумя точками в евклидовом пространстве.
Название происходит от Евклида, который широко известен как «отец геометрии», так как это было единственное пространство, которое люди в то время обычно задумывали. Со временем в физике и математике наблюдались различные типы пространства, такие как пространство Аффин.
-
В 3-мерном евклидовом пространстве кратчайшая прямая между двумя точками всегда будет прямой линией между ними.
Учитывая этот факт, евклидово расстояние не всегда является наиболее полезной метрикой для отслеживания при работе со многими размерностями, мы сосредоточимся на 2D и 3D евклидовом пространстве для расчета евклидова расстояния.
Вообще говоря, евклидова расстояние широко используется в разработке 3D-миров, а также алгоритмов машинного обучения, которые включают в себя метрики расстояния, такие как K-ближайшие соседи. Как правило, евклидово расстояние будет представлять, насколько похожи две точки данных, предполагая, что некоторая кластеризация на основе других данных уже была выполнена.
Математическая формула
Математическая формула расчета евклидова расстояния между 2 точками в 2D пространстве:
Формула легко адаптируется к 3D-пространство, а также к любому размеру:
Общая формула может быть упрощена до:
Острый глаз может заметить сходство между евклидовым расстоянием и теоремой Пифагора:
На самом деле существует связь между ними — евклидовое расстояние рассчитывается с помощью теоремы Пифагора, учитывая декартовы координаты двух точек.
Из-за этого евклидова расстояние иногда называют расстоянием Пифагора, хотя прежнее название гораздо более известно.
Примечание: Две точки являются векторами, но выход должен быть скалярным.
Мы будем использовать NumPy для расчета этого расстояния для двух точек, и один и тот же подход используется для 2D и 3D пространств:
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection = '3d')
ax.scatter(0, 0, 0)
ax.scatter(3, 3, 3)
plt.show()Расчет евклидова расстояния в Python с помощью NumPy
Во-первых, нам нужно будет установить библиотеку NumPy:
$ pip install numpyТеперь давайте импортируем его и настроим две наши точки с декартовыми координатами (0, 0, 0) и (3, 3, 3):
import numpy as np
# Initializing the points
point_1 = np.array((0, 0, 0))
point_2 = np.array((3, 3, 3))Вместо того, чтобы выполнять расчет вручную, мы будем использовать вспомогательные методы NumPy, чтобы сделать его еще проще!
np.sqrt() и np.sum()
Операции и математические функции, необходимые для расчета евклидова расстояния, довольно просты: сложение, вычитание, а также функция квадратного корня. Несколько слагаемых также можно заменить суммой:
NumPy предоставляет нам функцию np.sqrt(), представляющую функцию квадратного корня, а также функцию np.sum(), которая представляет собой сумму. При этом расчет евклидова расстояния в Python прост и интуитивно понятен:
# Get the square of the difference of the 2 vectors
square = np.square(point_1 - point_2)
# Get the sum of the square
sum_square = np.sum(square)Данная формула дает нам довольно простой результат:
(0-3)^2 + (0-3)^2 + (0-3)^2Что равно 27. Осталось все, что получить квадратный корень из этого числа:
# The last step is to get the square root and print the Euclidean distance
distance = np.sqrt(sum_square)
print(distance)Это приводит к:
5.196152422706632В истинном питоновом духе это можно сократить до одной строки:
И вы даже можете вместо этого использовать встроенные методы pow() и sum() математического модуля Python, хотя они требуют, чтобы вы немного поработали с вводом, который удобно абстрагируется с помощью NumPy, так как функция pow() работает только со скалярами (каждый элемент в массиве индивидуально) и принимает аргумент — в какой степени вы увеличиваете число.
Этот подход, однако, интуитивно больше похож на формулу, которую мы использовали раньше:
from math import *
distance = np.sqrt(sum(pow(a-b, 2) for a, b in zip(point_1, point_2)))
print(distance)Это также приводит к:
5.196152422706632np.linalg.norm()
Функция np.linalg.norm() представляет математическую норму. По сути, нормой вектора является его длина. Эта длина не обязательно должна быть евклидовым расстоянием, а может быть и другими расстояниями. Евклидово расстояние-это норма L2 вектора (иногда известная как евклидова норма), и по умолчанию функция norm() использует L2 — параметр ord имеет значение 2.
Если бы вы установили для параметра ord какое-то другое значение p, вы бы рассчитали другие p-нормы. Например, норма L1 вектора-это расстояние Манхэттена!
Имея это в виду, мы можем использовать функцию np.linalg.norm() для легкого и гораздо более чистого вычисления евклидова расстояния, чем использование других функций:
distance = np.linalg.norm(point_1-point_2)
print(distance)Это приводит к печати расстояния L2/евклида:
5.196152422706632Нормализация L2 и нормализация L1 широко используются в машинном обучении для нормализации входных данных.
np.dot()
Мы также можем использовать точечное произведение для расчета евклидова расстояния. В математике точечное произведение является результатом умножения двух векторов равной длины, а результатом является единственное число — скалярное значение. Из-за возвращаемого типа его иногда также называют «скалярным продуктом». Эту операцию часто называют внутренним произведением для двух векторов.
Для расчета точечного произведения между 2 векторами вы можете использовать следующую формулу:
С помощью NumPy мы можем использовать функцию np.dot(), передавая два вектора.
Если мы вычислим точечное произведение разницы между обеими точками с той же разницей — мы получим число, которое находится в зависимости от евклидова расстояния между этими двумя векторами. Извлечение квадратного корня из этого числа дает нам расстояние, которое мы ищем:
# Take the difference between the 2 points
diff = point_1 - point_2
# Perform the dot product on the point with itself to get the sum of the squares
sum_square = np.dot(diff, diff)
# Get the square root of the result
distance = np.sqrt(sum_square)
print(distance)Конечно, вы также можете сократить это до однострочного:
distance = np.sqrt(np.dot(point_1-point_2, point_1-point_2))
print(distance)5.196152422706632Использование встроенной системы math.dist()
В Python есть встроенный метод в математическом модуле, который вычисляет расстояние между 2 точками в трехмерном пространстве. Однако это работает только с Python 3.8 или более поздней версии.
math.dist()принимает два параметра, которые являются двумя точками, и возвращает евклидово расстояние между этими точками.
Примечание: Обратите внимание, что две точки должны иметь одинаковые размеры (т.е. оба в 2d или 3d пространстве).
Теперь, чтобы вычислить Евклидово расстояние между этими двумя точками, мы просто заправляем их в метод thedistdist():
import math
distance = math.dist(point_1, point_2)
print(distance)5.196152422706632Заключение
Данная метрика используется во многих контекстах в интеллектуальном анализе данных, машинном обучении и ряде других областей и является одной из фундаментальных метрик расстояния.
17 авг. 2022 г.
читать 1 мин
Евклидово расстояние между двумя векторами, A и B, рассчитывается как:
Евклидово расстояние = √ Σ(A i -B i ) 2
куда:
- Σ — греческий символ, означающий «сумма».
- A i — i -е значение в векторе A
- B i — i -е значение в векторе B
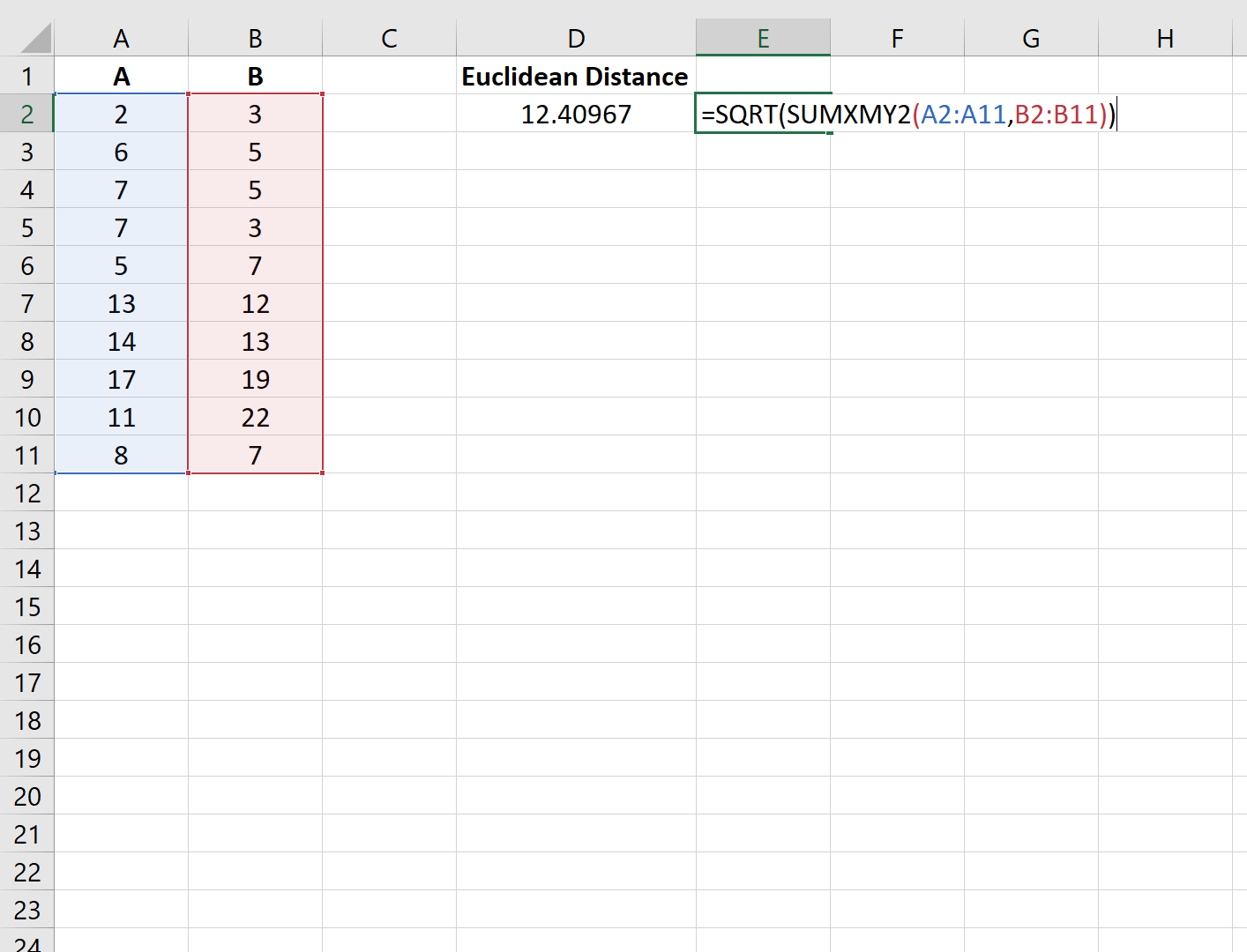
Чтобы вычислить евклидово расстояние между двумя векторами в Excel, мы можем использовать следующую функцию:
= SQRT ( SUMXMY2 (RANGE1, RANGE2))
Вот что делает формула в двух словах:
- SUMXMY2 находит сумму квадратов разностей соответствующих элементов диапазона 1 и диапазона 2.
- SQRT извлекает квадратный корень из этой суммы квадратов разностей.
Конечный результат, если евклидово расстояние между двумя диапазонами.
Например, предположим, что у нас есть следующие два вектора, A и B, в Excel:
Мы можем использовать следующую функцию для вычисления евклидова расстояния между двумя векторами:
Евклидово расстояние между двумя векторами оказывается равным 12,40967 .
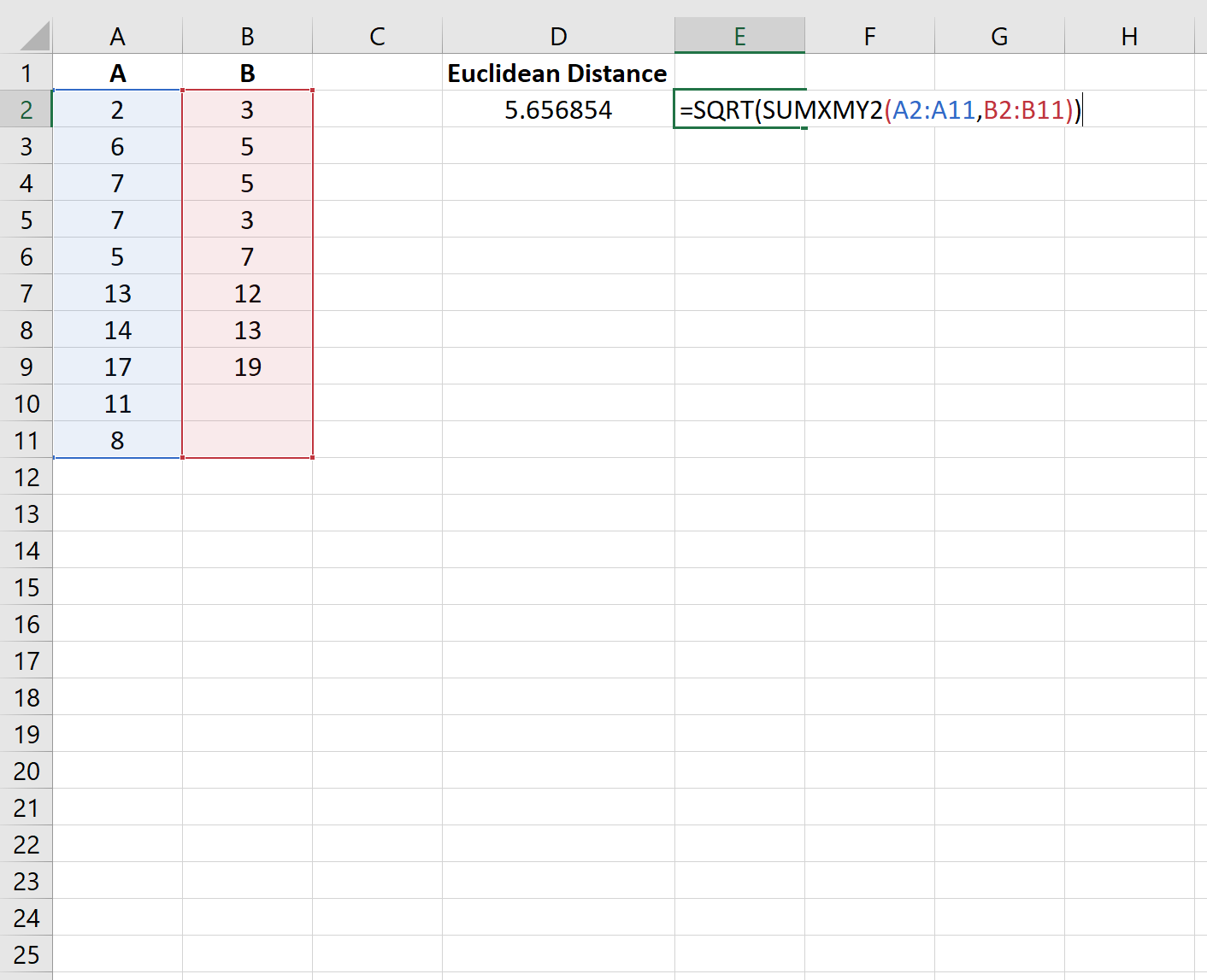
Обратите внимание, что эта функция будет включать только полные парные наблюдения при вычислении евклидова расстояния.
Например, последние две строки в столбце A не будут включены в расчет евклидова расстояния между следующими двумя векторами:
Евклидово расстояние между двумя векторами оказывается равным 5,656854 .
Дополнительные ресурсы
Как рассчитать евклидово расстояние в R
Как рассчитать евклидово расстояние в Python
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Не важно, начинаете вы осваивать Data Science или работаете в этой сфере не первый год, вам наверняка пригодятся эти метрики. Разбираемся, что они из себя представляют и чем отличаются друг от друга.
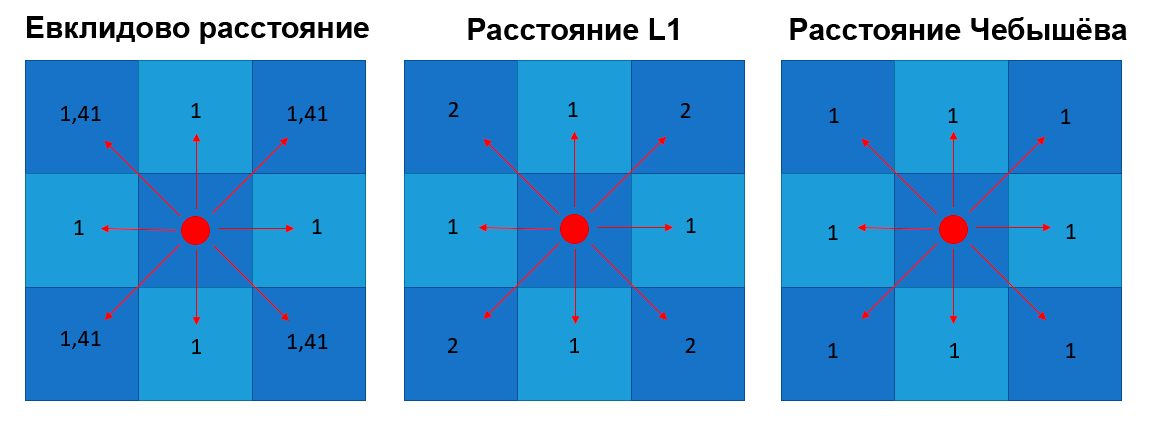
Евклидово расстояние (расстояние по прямой)
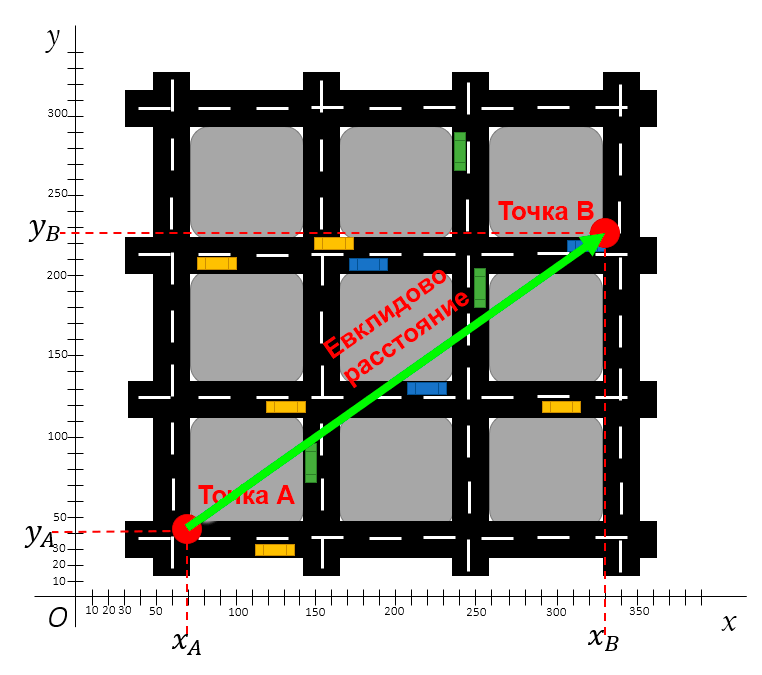
Евклидово расстояние самое интуитивное для понимания: именно Евклидову метрику мы представляем, когда кто-то просит нас измерить расстояние между точками.
Евклидово расстояние — это прямая линия между двумя точками с координатами X и Y. Например, одной из таких точек может быть город на карте с его координатами долготы и широты.
Евклидово расстояние характеризуется прямой линией. Допустим, вам нужно измерить расстояние по прямой между точками A и B на карте города, приведённой ниже.
Евклидово расстояние между двумя точками считается по теореме Пифагора
Для расчёта Евклидового расстояния вам понадобятся лишь координаты этих двух точек. Дистанцию между ними можно будет рассчитать по формуле Пифагора.
Теорема Пифагора гласит, что можно рассчитать длину «диагональной стороны» (гипотенузы) прямого треугольника, зная длины его горизонтальной и вертикальной стороны (катетов). Формула выглядит так: a² + b² = c².
Пример расчёта Евклидового расстояния
Прим. ред. В четвёртой строке вычислений допущена ошибка: (-260)^2 = 67 600, а не 76 600. Тогда результат будет равен ~321.
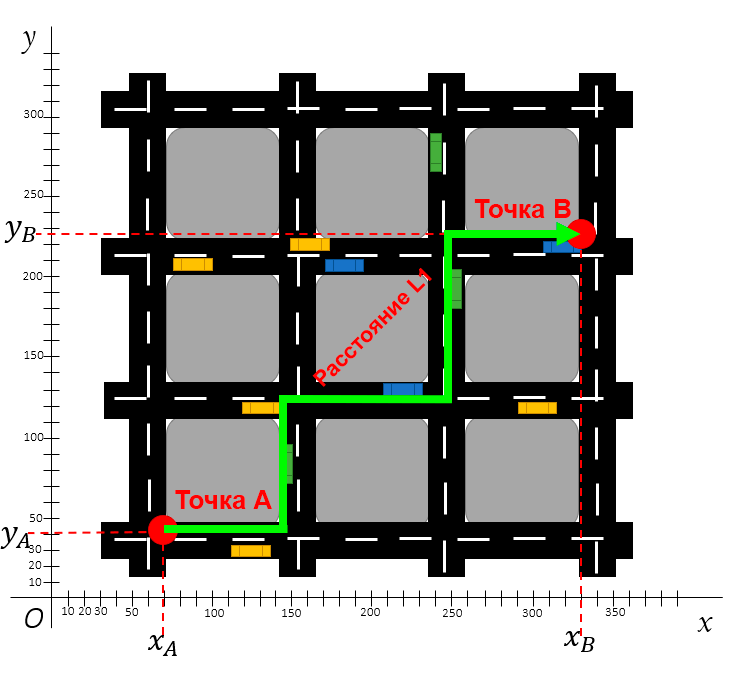
Расстояние L1 также известно как расстояние городских кварталов, манхэттенское расстояние, расстояние такси, метрика прямоугольного города — оно измеряет дистанцию не по кратчайшей прямой, а по блокам. Расстояние L1 измеряет дистанцию между городскими блоками: это расстояние всех прямых линий пути.
На следующем изображении показано расстояние L1 между двумя точками.
Расстояние L1 между двумя точками по блокам
Кроме показанного пути существует несколько альтернативных способов. Например, от точки A можно подняться на два блока вверх, а потом на три блока вправо, либо же на три блока вправо и два блока вверх.
Но расстояние L1 — это всё же просто дистанция, а поэтому траектория здесь не имеет значения. Единственное, что нужно понимать, это примерный путь: нужно пройти какое-то количество X блоков на восток и Y блоков на север. Сумма расстояний этих блоков и будет расстоянием L1 от точки A до точки B.
Пример расчёта расстояния L1 между двумя точками
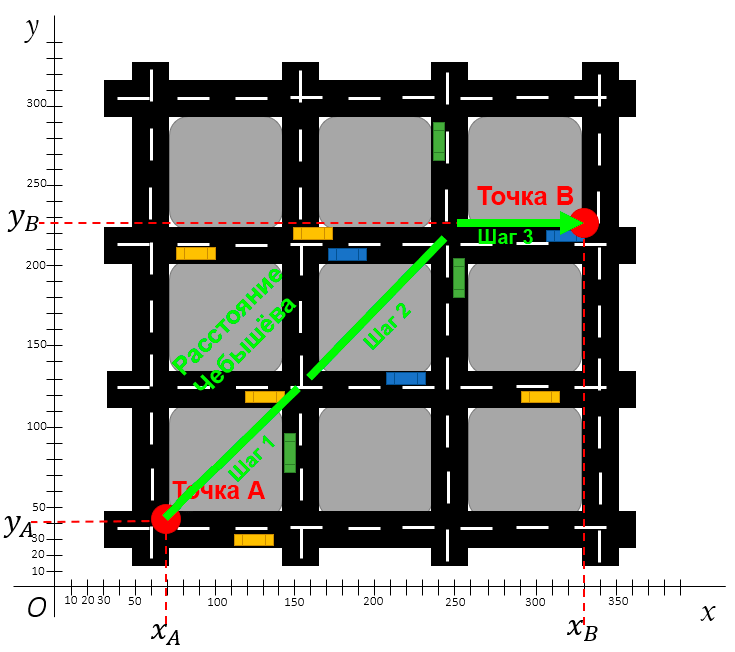
Расстояние Чебышёва (метрика шахматной доски)
Расстояние Чебышёва известно ещё как расстояние шахматной доски. Чтобы понять принцип такой метрики, нужно представить короля на шахматной доске — он может ходить во всех направлениях: вперёд, назад, влево, вправо и по диагонали.
Расстояние Чебышёва между двумя точками
Разница расстояния L1 и расстояния Чебышёва в том, что при переходе на одну клетку по диагонали в первом случае засчитывается два хода (например вверх и влево), а во втором случае засчитывается всего один ход.
Ещё эти оба расстояния отличаются от Евклидового расстояния тем, что у Евклидового движение по диагонали рассчитывается по теореме Пифагора.
Сравнение путей 3 метрик
Расстояние Чебышёва можно представить как проход по шахматной доске.
Вот ещё один пример представления расстояния Чебышёва. Допустим, у вас есть дрон с двумя независимыми моторами: первый мотор тянет дрон вперёд, второй — в сторону. Оба мотора могут работать одновременно и равномерно на максимуме своей мощности.
Поэтому дрон может передвинуться на одну клетку по диагонали так же быстро, как по горизонтали или вертикали.
Посмотрите ещё раз на карту города по расстоянию Чебышёва. Первый шаг — оба мотора работают одновременно, второй шаг идентичен первому, а на третьем шаге мотор, тянущий дрон вперёд, отключается, и дрон смещается в сторону.
Таким образом, расстояние Чебышёва определяется как самая большая дистанция на одной оси.
Пример расчёта расстояния Чебышёва между двумя точками
Прим. ред. Полученный результат является условным и некорректно сравнивать его с другими результатами.
Перевод статьи «3 distances that every data scientist should know»
Расстояние d между точками в пространстве A11;y1;z1>, A22;y2;z2> представляется формулой
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.3 / 5. Количество оценок: 8
Оценок пока нет. Поставьте оценку первым.
3 комментария
найти расстояние между точками с(-2;1;-2) д (-1;2;1) м (-1;0;2) н (1;-1;2) найти 3 вектора сд — 2 вектора мн
Расчет евклидова расстояния с помощью NumPy
В этом руководстве мы рассмотрим, как рассчитать евклидово расстояние между двумя точками в Python с помощью Numpy.
Что такое евклидово расстояние?
Евклидово расстояние — это фундаментальная метрика расстояния, относящаяся к системам в евклидовом пространстве.
Евклидово пространство — это классическое геометрическое пространство, с которым вы знакомитесь на уроке математики, обычно связанное с 3 измерениями. Хотя его также можно приписать к любой неотрицательной целочисленной размерности.
Евклидово расстояние — кратчайшая прямая между двумя точками в евклидовом пространстве.
Название происходит от Евклида, который широко известен как «отец геометрии», так как это было единственное пространство, которое люди в то время обычно задумывали. Со временем в физике и математике наблюдались различные типы пространства, такие как пространство Аффин.
В 3-мерном евклидовом пространстве кратчайшая прямая между двумя точками всегда будет прямой линией между ними.
Учитывая этот факт, евклидово расстояние не всегда является наиболее полезной метрикой для отслеживания при работе со многими размерностями, мы сосредоточимся на 2D и 3D евклидовом пространстве для расчета евклидова расстояния.
Вообще говоря, евклидова расстояние широко используется в разработке 3D-миров, а также алгоритмов машинного обучения, которые включают в себя метрики расстояния, такие как K-ближайшие соседи. Как правило, евклидово расстояние будет представлять, насколько похожи две точки данных, предполагая, что некоторая кластеризация на основе других данных уже была выполнена.
Математическая формула
Математическая формула расчета евклидова расстояния между 2 точками в 2D пространстве:
Формула легко адаптируется к 3D-пространство, а также к любому размеру:
Общая формула может быть упрощена до:
Острый глаз может заметить сходство между евклидовым расстоянием и теоремой Пифагора:
На самом деле существует связь между ними — евклидовое расстояние рассчитывается с помощью теоремы Пифагора, учитывая декартовы координаты двух точек.
Из-за этого евклидова расстояние иногда называют расстоянием Пифагора, хотя прежнее название гораздо более известно.
Примечание: Две точки являются векторами, но выход должен быть скалярным.
Мы будем использовать NumPy для расчета этого расстояния для двух точек, и один и тот же подход используется для 2D и 3D пространств:
Расчет евклидова расстояния в Python с помощью NumPy
Во-первых, нам нужно будет установить библиотеку NumPy:
Теперь давайте импортируем его и настроим две наши точки с декартовыми координатами (0, 0, 0) и (3, 3, 3):
Вместо того, чтобы выполнять расчет вручную, мы будем использовать вспомогательные методы NumPy, чтобы сделать его еще проще!
Операции и математические функции, необходимые для расчета евклидова расстояния, довольно просты: сложение, вычитание, а также функция квадратного корня. Несколько слагаемых также можно заменить суммой:
NumPy предоставляет нам функцию np.sqrt(), представляющую функцию квадратного корня, а также функцию np.sum(), которая представляет собой сумму. При этом расчет евклидова расстояния в Python прост и интуитивно понятен:
Данная формула дает нам довольно простой результат:
Что равно 27. Осталось все, что получить квадратный корень из этого числа:
В истинном питоновом духе это можно сократить до одной строки:
И вы даже можете вместо этого использовать встроенные методы pow() и sum() математического модуля Python, хотя они требуют, чтобы вы немного поработали с вводом, который удобно абстрагируется с помощью NumPy, так как функция pow() работает только со скалярами (каждый элемент в массиве индивидуально) и принимает аргумент — в какой степени вы увеличиваете число.
Этот подход, однако, интуитивно больше похож на формулу, которую мы использовали раньше:
Это также приводит к:
np.linalg.norm()
Функция np.linalg.norm() представляет математическую норму. По сути, нормой вектора является его длина. Эта длина не обязательно должна быть евклидовым расстоянием, а может быть и другими расстояниями. Евклидово расстояние-это норма L2 вектора (иногда известная как евклидова норма), и по умолчанию функция norm() использует L2 — параметр ord имеет значение 2.
Если бы вы установили для параметра ord какое-то другое значение p, вы бы рассчитали другие p-нормы. Например, норма L1 вектора-это расстояние Манхэттена!
Имея это в виду, мы можем использовать функцию np.linalg.norm() для легкого и гораздо более чистого вычисления евклидова расстояния, чем использование других функций:
Это приводит к печати расстояния L2/евклида:
Нормализация L2 и нормализация L1 широко используются в машинном обучении для нормализации входных данных.
Мы также можем использовать точечное произведение для расчета евклидова расстояния. В математике точечное произведение является результатом умножения двух векторов равной длины, а результатом является единственное число — скалярное значение. Из-за возвращаемого типа его иногда также называют «скалярным продуктом». Эту операцию часто называют внутренним произведением для двух векторов.
Для расчета точечного произведения между 2 векторами вы можете использовать следующую формулу:
С помощью NumPy мы можем использовать функцию np.dot(), передавая два вектора.
Если мы вычислим точечное произведение разницы между обеими точками с той же разницей — мы получим число, которое находится в зависимости от евклидова расстояния между этими двумя векторами. Извлечение квадратного корня из этого числа дает нам расстояние, которое мы ищем:
Конечно, вы также можете сократить это до однострочного:
Использование встроенной системы math.dist()
В Python есть встроенный метод в математическом модуле, который вычисляет расстояние между 2 точками в трехмерном пространстве. Однако это работает только с Python 3.8 или более поздней версии.
math.dist()принимает два параметра, которые являются двумя точками, и возвращает евклидово расстояние между этими точками.
Примечание: Обратите внимание, что две точки должны иметь одинаковые размеры (т.е. оба в 2d или 3d пространстве).
Теперь, чтобы вычислить Евклидово расстояние между этими двумя точками, мы просто заправляем их в метод thedistdist():
Заключение
Данная метрика используется во многих контекстах в интеллектуальном анализе данных, машинном обучении и ряде других областей и является одной из фундаментальных метрик расстояния.
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Евклидово пространство
Одной из важнейших задач геометрии является задача измерения расстояния между двумя объектами. В произвольном линейном пространстве мы пока не можем определить насколько «близки» между собой объекты. В настоящем разделе понятие расстояния между двумя векторами — элементами линейного пространства — будет вводиться посредством скалярного произведения векторов. Насколько обоснован такой порядок введения понятий:
$ mbox<> qquad $ скалярное произведение $ to $ длина ?
Ведь в аналитической геометрии последовательность кажется более «естественной»: скалярное произведение двух векторов $ X_<> $ и $ Y_<> $ определялось как произведение длин этих векторов на косинус угла между ними: $ langle X,Y rangle = |X| cdot |Y| cdot cos (widehat) $. Тем не менее, формально непротиворечива и обратная схема: если допустить, что скалярное произведение любых двух векторов может быть как-то вычислено (например, в $ mathbb R^ <3>$ по формуле $ langle X,Y rangle = x_1y_1+x_2y_2+x_3y_3 $ при заданных прямоугольных координатах $ (x_1,x_2,x_3) $ и $ (y_1,y_2,y_3) $ векторов $ X_<> $ и $ Y_<> $), то и длину векторов и угол между ними можно выразить через подходящие скалярные произведения: $$ |X|=sqrt< langle X,X rangle>,qquad widehat=arccos frac< langle X,Y rangle><sqrt<langle X,X rangle langle Y,Y rangle>> .$$
Определения
Вещественное линейное пространство $ mathbb E_<> $ называется евклидовым 1) , если в этом пространстве определена функция, ставящая в соответствие паре векторов $ \subset mathbb E $ вещественное число, называемое скалярным произведением векторов 2) $ X_<> $ и $ Y_<> $, и обозначаемое $ langle X,Y rangle_<> $ или $ (X,Y)_<> $; при этом фцнкция подчиняется аксиомам:
1. $ langle X,Y rangle= langle Y,X rangle $ для $ < X,, Y>subset mathbb E $;
2. $ langle X_1+X_2,Y rangle = langle X_1,Y rangle + langle X_2,Y rangle $ для $ < X_1,, X_2,, Y >subset mathbb E $;
3. $ langle lambda, X,Yrangle=lambda, langle X,Yrangle $ для $ < X,Y>subset mathbb E, lambda in mathbb R $;
4. $ langle X,X rangle>0 $ для $ forall Xne mathbb O $, $ langle mathbb O,mathbb O rangle =0 $.
Из аксиом 1 и 2 вытекает свойство линейности скалярного произведения и по второму вектору:
2′. $ langle X,Y_1+Y_2 rangle = langle X,Y_1 rangle + langle X,Y_2 rangle $ для $ subset mathbb E $.
Пример 1. Пространство $ mathbb R_<>^ $, рассматриваемое как пространство вещественных векторов-столбцов. Для векторов
$$ X=left[begin x_1 \ vdots \ x_n end right] quad mbox < и >quad Y=left[begin y_1 \ vdots \ y_n end right] $$ их скалярное произведение определим обобщением привычной из геометрии формулы $$ langle X,Y rangle = sum_^n x_jy_j = X^<top>Y ; $$ в последней формуле $ <>^ <top>$ означает транспонирование. Будем называть это скалярное произведение стандартным. Легко проверить выполнимость аксиом 1 — 4 .
Однако стандартное определение скалярного произведения вовсе не является единственно допустимым; формально скалярное произведение можно ввести и другим способом. Рассмотрим (пока произвольную) вещественную квадратную матрицу $ A_<> $ порядка $ n_<> $ и положим $$ begin langle X,Y rangle = X^ <top>A Y & = & a_<11>x_1y_1+a_<12>x_1y_2+ dots + a_<1n>x_1y_n &+ \ &+&a_<21>x_2y_1+a_<22>x_2y_2+ dots + a_<2n>x_2y_n &+ \ &+& dots &+ \ &+&a_x_ny_1+a_x_ny_2+ dots + a_x_ny_n & . end $$ (Здесь векторы $ X_<> $ и $ Y_<> $ из $ mathbb R_<>^ $ снова рассматриваются как столбцы.) Если матрица $ A_<> $ является положительно определенной, то все аксиомы скалярного произведения будут удовлетворены.
Зачем нужна такая возможность в неоднозначности определения скалярного произведения в одном и том же пространстве? — Ответ на этот вопрос откладывается до следующего пункта. А пока приведу одно замечание 3) .
Пример 2. Пространство $ mathbb P_ $ полиномов одной переменной степеней $ le n_<> $ с вещественными коэффициентами. Скалярное произведение полиномов
$$ p(x)=a_<0>x^n+a_1x^+dots + a_n quad mbox < и >quad q(x)=b_<0>x^n+b_1x^+dots + b_n $$ введем формулой $$ langle p(x), q(x) rangle = sum_^n a_j b_j. $$ Легко проверить справедливость всех аксиом.
В том же пространстве $ mathbb P_ $ можно ли определить скалярное произведение формулой
$$ langle p(x),q(x) rangle = sum_^m p(x_k) q(x_k) quad npu _^m subset mathbb R ? $$
Пример 3. Линейное пространство $ mathbb R^ $ вещественных квадратных матриц порядка $ n_<> $. Скалярное произведение введем формулой
Вторая интерпретация формулы связана с операцией $ operatorname $ нахождения следа матрицы, т.е. суммы элементов ее главной диагонали: $$ langle A,B rangle = operatorname left(Acdot B^ <top>right) , . $$ Эквивалентность последнего представления определению устанавливается непосредственной проверкой.
На основании аксиом скалярного произведения, его вычисление для произвольных векторов $ X_<> $ и $ Y_<> $ может быть сведено к вычислению скалярных произведений векторов произвольного базиса. В самом деле, если система $ \> $ составляет базис пространства $ mathbb E $, то, разложив оба вектора по этому базису $$X=x_1X_1+ dots +x_nX_n quad u quad Y=y_1X_1+ dots +y_nX_n , $$ получаем: $$langle X,Y rangle=langle x_1X_1+ dots +x_nX_n , y_1X_1+ dots +y_nX_n rangle=$$ $$ = left< begin &&x_1y_1 langle X_1,X_1 rangle + x_1y_2 langle X_1,X_2 rangle + dots + x_1y_n langle X_1,X_n rangle + \ &+&x_2y_1 langle X_2,X_1 rangle + x_2y_2 langle X_2,X_2 rangle + dots + x_2y_n langle X_2,X_n rangle+ \ &+ & dots qquad + \ &+&x_ny_1 langle X_n,X_1 rangle + x_ny_2 langle X_n,X_2 rangle + dots + x_ny_n langle X_n,X_n rangle end right> = $$ $$ =(x_1,x_2,dots,x_n)left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_n rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_n rangle \ dots & & & dots \ langle X_n,X_1 rangle & langle X_n,X_2 rangle & dots & langle X_n,X_n rangle end right) left(begin y_1 \ y_2 \ vdots \ y_n endright) . $$ Итак, при изменении векторов $ X_<> $ и $ Y_<> $ в последней формуле изменятся лишь строка и столбец координат, а промежуточная матрица останется неизменной. Задание этой матрицы, следовательно, полностью определит скалярное произведение в $ mathbb E_<> $. Фактически задание скалярного произведения в разобранном выше примере пространства $ mathbb R^ $ по формуле $ langle X,Y rangle=X^<top>AY $ можно рассматривать именно как частный случай этого при подходящем подборе базисных векторов. Согласно рассуждениям из примера $ 1_<> $, матрица $$ left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_n rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_n rangle \ dots & & & dots \ langle X_n,X_1 rangle & langle X_n,X_2 rangle & dots & langle X_n,X_n rangle end right) $$ должна обладать некоторыми принципиальными свойствами. Так оно и окажется, см. ☟ НИЖЕ.
Матрицей Грама системы векторов 4) $ > $ называется квадратная матрица $$ G(X_1,dots,X_m)=left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right) = left[ (X_j,X_k) right]_^m . $$ Ее определитель называется определителем Грама 5) (или грамианом) системы векторов $ > $: $$ <mathfrak G>(X_1,dots,X_m)=left| begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right| = det left[ langle X_j,X_k rangle right]_^m . $$
С помощью матрицы Грама формула скалярного произведения записывается в виде $$ langle X,Y rangle =[x_1,dots,x_n] G(X_1,dots,X_n) left[ begin y_1 \ vdots \ y_n end right] . $$
Пример 4. В пространстве $ mathbb R^ $ столбцов из $ n_<> $ элементов при стандартном способе задания скалярного произведения
$$ langle X,Y rangle = sum_^n x_jy_j quad npu quad X=[x_1,dots,x_n]<^<top>>, Y=[y_1,dots,y_n]<^<top>> $$ матрицу Грама системы векторов $ ,x_,dots,x_]^ <top>>_^m $ можно представить в виде произведения матриц $$ G(X_1,dots,X_)=left( begin x_ <11>& x_ <12>& dots & x_ <1n>\ x_ <21>& x_ <22>& dots & x_ <2n>\ dots & & & dots \ x_ & x_ & dots & x_ end right) left( begin x_ <11>& x_ <21>& dots & x_ \ x_ <12>& x_ <22>& dots & x_ \ vdots & & & vdots \ x_ <1n>& x_ <2n>& dots & x_ end right) . $$ Произведение имеет вид $ Mcdot M^ <top>$ и, согласно теореме Бине-Коши, определитель этого произведения равен $ 0_<> $ при $ m>n_<> $ и неотрицателен при $ m le n $. НИЖЕ будет установлено, что обнаруженные свойства определителя Грама являются универсальными: они выполняются в произвольном евклидовом пространстве. См. также, «обращение» этого результата — задача 4 ☞ ЗДЕСЬ.
Свойства
Теорема. Имеет место неравенство Коши–Буняковского:
$$ langle X,Y rangle ^2 le langle X,X rangle langle Y,Y rangle quad npu forall \subset mathbb E . $$
Доказательство для случая $ mathbb R^_<> $ приведено ☞ ЗДЕСЬ. Для доказательства общего случая используем одну вспомогательную конструкцию. Из аксиомы 4 следует, что для $ forall lambda in mathbb R $ будет выполнено $ langle lambda, X — Y,, lambda, X — Y rangle ge 0 $. Имеем: $$ 0 le langle lambda, X — Y,, lambda, X — Y rangle le lambda^2 langle X,X rangle — 2,lambda langle X,Y rangle +(Y,Y) . $$ Квадратное относительно $ lambda_<> $ неравенство будет выполнено при всех вещественных значениях этого параметра тогда и только тогда, когда дискриминант квадратного трехчлена будет отрицателен: $$ mathcal D=langle X,Y rangle^2 — langle X,X rangle langle Y,Y rangle le 0 . $$ ♦
С помощью скалярного произведения, введенного в предыдущем пункте, можно доказать справедливость интегральной формы неравенства:
$$ left( int_a^b p(t)q(t) d,t right)^2 le int_a^b p^2(t) d,t cdot int_a^b q^2(t) d,t $$ для произвольных полиномов 6) $ subset mathbb R [x] $.
Длиною вектора $ X_<> $ в евклидовом пространстве $ mathbb E_<> $ называется число $$ |X| = sqrt <langle X,X rangle> ; $$ здесь квадратный корень понимается как корень арифметический: $ |X| ge 0 $. Расстоянием между векторами $ X_<> $ и $ Y_<> $ называется число $ |X-Y| $.
В $ mathbb R^_<> $ при скалярном произведении, заданном стандартным способом формулой
$$ langle X,Y rangle = sum_^n x_jy_j quad npu quad X=[x_1,dots,x_n]<^<top>>, Y=[y_1,dots,y_n]<^<top>> , $$ длина вектора $ X_<> $ определяется естественным (с точки зрения геометрии) способом: $ |X|=sqrt $.
С помощью введенного определения неравенство Коши-Буняковского можно переписать в виде $$ |langle X,Y rangle| le |X| cdot |Y| quad npu forall \subset mathbb E , $$ где $ | cdot | $ в левой части означает модуль, а в правой части — длину.
Теорема. Имеет место неравенство треугольника
$$ |X+Y| le |X|+|Y| quad npu forall \subset mathbb E . $$
Доказательство. На основании неравенства Коши-Буняковского, имеем: $$ 0 le langle X+Y,, X+Y rangle=langle X,X rangle+2langle X,Y rangle+langle Y,Y rangle le |X|^2+2, |X| cdot |Y| +|Y|^2=left(|X|+|Y| right)^2 . $$ ♦
Углом между векторами $ X_<> $ и $ Y_<> $ называется угол $$varphi = widehat = arccos frac<langle X,Y rangle> <|X|cdot |Y|> .$$ Ввиду неравенства Коши-Буняковского это определение непротиворечиво: дробь под знаком арккосинуса не превосходит 1 по абсолютной величине. Векторы $ X_<> $ и $ Y_<> $ называются ортогональными: $ X bot Y $ если угол между ними равен $ pi/2 $, или, что то же, $ langle X,Y rangle=0 $.
Введенное таким определением понятие является естественным обобщением понятия угла на плоскости и в трехмерном пространстве. Хотя в пространствах размерностей больших $ 3_<> $ человеческие мозги думать не приучены, тем не менее, абстракция находит практическое применение в задаче информационного поиска.
Пусть задача заключается в сравнении двух текстовых документов «на похожесть». Имеются некоторые наборы ключевых слов, описывающих каждый из этих документов. Составим объединение этих наборов, упорядочим получившийся набор (пронумеруем слова), посчитаем частоты вхождений каждого из слов в каждый из документов. Получим два вектора: $$ X_1=(f_<11>,f_<12>,dots), X_2=(f_<21>,f_<22>,dots) , $$ описывающие каждый из документов. Здесь $ f_ in <0,1,2,dots, >$ — количество вхождений $ k_<> $-го слова в $ j_<> $-й документ. Для оценки близости векторов, на первый взгляд, кажется естественным вычислить расстояние между ними стандартным способом: $$ |X_1-X_2| = sqrt < sum_(f_<1k>-f_<2k>)^2> . $$ Однако, по здравому размышлению, понимаем, что при таком способе, документы различные по объему (общему количеству слов) будут слишком сильно отличаться друг от друга, при том, что могут оказаться близкими по сути (как будет отличаться большая статья от собственного реферата). Поэтому имеет смысл усреднить частоты в обоих текстах, т.е. рассматривать расстояние между векторами $ X_1/|X_1| $ и $ X_2/|X_2| $ единичной длины: $$ left|frac<|X_1|>-frac<|X_2|>right| = sqrt<2left( 1- frac<langle X_1,X_2 rangle> <|X_1|cdot |X_2|>right)> ; $$ скалярное произведение под знаком корня вычисляется стандартным способом: $ langle X_1,X_2 rangle=sum_ f_<1k>f_ <2k>$. Отсюда и возникает понятие косинусного расстояния: величина $$ frac<langle X_1,X_2 rangle> <|X_1|cdot |X_2|>$$ неотрицательна (поскольку компоненты векторов $ X_1,X_2 $ неотрицательны), и чем ближе она к $ 1_<> $ тем меньше расстояние между между нормированными векторами. Эта величина называется также похожестью или cходством 
Теорема [Пифагор]. Если $ X bot Y $, то $ |X+Y|^2=|X|^2+|Y|^2 $.
Если векторы $ X_1,dots,X_k $ попарно взаимно ортогональны, то
Пример. Найти расстояние между полиномами
$$p(x)=x^<100>-1/2,x^<85>-1/2,x^<64>+5,x^<34>-5,x^<32>+5,x^2+1 quad u quad q(x)=5,x^2+1 $$ если скалярное произведение задается формулой а) $ displaystyle langle p(x), q(x) rangle = sum_^ <100>a_j b_j $ ; б) $ displaystyle langle p(x), q(x) rangle = int_<-1>^1 p(t)q(t) d, t $.
Решение. Для случая а) нам достаточно просто вычислить сумму квадратов коэффициентов разности $ p(x)-q(x) $: расстояние равно $ sqrt <103/2>$.
Для случая б) нам придется иметь дело с интегралом $$ int_<-1>^1 left(p(t)-q(t) right)^2 d, t = int_<-1>^1 left(t^<100>-1/2,t^<85>-1/2,t^<64>+5,t^<34>-5,t^ <32>right)^2 d, t , $$ который, несмотря на свой громоздкий вид, может быть вычислен элементарными приемами математического анализа. В этом случае расстояние будет равно $ sqrt <95965413818,big/ 16503052280715>$.
Ответ. а) $ approx 7.176 $ ; б) $ approx 0.076 $.
Теперь прокомментируем последний пример. В разделе, посвященном полиному одной переменной, имеется теорема о непрерывной зависимости корней полинома от его коэффициентов. Смысл этого результата в следующем: если коэффициенты полиномов
$$f(x)=x^n+a_1x^+dots+a_n quad u quad <tilde f>(x)=x^n+<tilde a>_1x^+dots+<tilde a>_n$$ из $ mathbb C[x] $ близки, то и корни этих полиномов (при соответствующей нумерации) будут близки на комплексной плоскости. В этой теореме мера близости полиномов оценивается по формуле $$ sqrt[n]<sum_^n|a_k-<tilde a>_k| gamma^ > quad npu quad gamma = max_> left( sqrt[j] <|a_j|> , sqrt[j]<|<tilde a>_j|> right) , $$ которая, хоть и не совпадает с формулой $$ sqrt<sum_^n left(a_k-<tilde a>_k right)^2> , $$ определяющей расстояние в пространстве полиномов, но идейно ей близка. Вычисленное в предыдущем примере расстояние между полиномами $ p_<>(x) $ и $ q_<>(x) $ по формуле а) оказывается достаточно большим в том смысле, что если для полинома $ p_<>(x) $ искать полином, имеющий почти такое же расположение корней на $ mathbb C_<> $, то полином $ q_<>(x) $ окажется неподходящим кандидатом. 9)
Другое дело, если ставится задача приближения полинома $ p_<>(x) $ только на интервале $ [-1,1] $ — тогда полином $ q_<>(x) $ может оказаться вполне полезным. Выясним сначала природу интеграла, возникшего при решении. Пусть сначала $ p_<>(x) $ и $ q_<>(x) $ — произвольные, но (для простоты рассуждений) неотрицательные на интервале $ [a_<>,b] $ полиномы. Геометрический смысл интеграла $ int_a^b p(t) d, t $ — площадь криволинейной трапеции на плоскости $ (x_<>,y) $, ограниченной прямыми $ x=a_<>,,x=b,,y=0 $ и графиком $ y=p(x) $. Следовательно, геометрический смысл интеграла $$ int_a^b left| p(t)-q(t) right| d, t $$ — площадь фигуры, ограниченной прямыми $ x=a,,x=b_<> $ и графиками $ y=p(x), y=q(x) $ (заштрихована коричневым на рисунке). Чем меньше эта площадь, тем «теснее» друг к другу на отрезке $ [a_<>,b] $ расположены графики $ y=p(x) $ и $ y=q(x) $. Величина $$ sqrt <int_a^b left( p(t)-q(t) right)^2 d, t> , $$ вообще говоря, не совпадает с предыдущей, но смысл ее тот же: она позволяет оценивать близость графиков на всем отрезке $ [a_<>,b] $. Ответ в примере для варианта б) позволяет заключить, что на отрезке $ [-1,1] $ полином $ p_<>(x) $ неплохо приближается своими младшими одночленами, т.е. на указанном отрезке график $ y=p(x) $ не должен слишком сильно отличаться от параболы $ y=5,x^2+1 $.
Подводя итог приведенным рассуждениям, можно только повторить: метод, выбираемый для оценки близости между объектами, может зависеть от поставленной задачи. Микроскоп не пригоден для наблюдения за большими объектами, а телескоп — за малыми.
Следующий результат также имеет название, взятое из планиметрии, где он формулируется так: сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин его сторон.
Теорема. В евклидовом пространстве имеет место равенство параллелограмма
$$ |X+Y|^2+|X-Y|^2 =2(|X|^2+|Y|^2) quad npu forall \subset mathbb E . $$
Ортогонализация
Пусть $ dim mathbb E=n $ и векторы $ $ составляют базис $ mathbb E_<> $. Этот базис называется ортогональным если векторы попарно ортогональны: $ X_jbot X_k $; базис называется нормированным если каждый его вектор имеет единичную длину: $ |X_j|=1 $; базис называется ортонормированным если он ортогонален и нормирован, т.е. $$langle X_j,X_k rangle=delta_ ,quad npu quad subset <1,dots,n > .$$ Здесь $ delta_^<> $ — символ Кронекера.
Ортогональный базис будем обозначать $ <mathfrak E>_1,dots, <mathfrak E>_n $.
Чему равно расстояние между двумя векторами ортонормированного базиса?
В пространстве $ mathbb R_<>^ $ стандартным ортогональным базисом является базис, состоящий из векторов $$ <mathfrak e>_j = big[underbrace<0,dots,0,1>_,0,dots,0big]^ <top>quad npu quad j in <1,dots,n> . $$ Существование же ортогонального базиса в произвольном евклидовом пространстве еще требует доказательства. Предварительно установим следующий результат.
Теорема. Если ненулевые векторы $ X_1,dots, X_ $ попарно ортогональны, то они линейно независимы.
Доказательство. В самом деле, если $$ lambda_1 X_1 + dots + lambda_n X_n = mathbb O , $$ то, домножив это равенство скалярно на $ X_ <1>$, получим $$ lambda_1 langle X_1,X_1 rangle + dots + lambda_n langle X_1,X_n rangle = 0 . $$ Поскольку $ langle X_1,X_j rangle=0 $ для $ jin <2,dots,n>$, то $ lambda_1 langle X_1,X_1 rangle=0 $, откуда $ lambda_1=0 $. Аналогично показывается, что и все остальные $ lambda_j $ равны 0. ♦
Задача. Пусть имеется произвольная система $ $ линейно независимых векторов. Требуется построить систему ортогональных векторов $ left<<mathfrak E>_1,dots, <mathfrak E>_k right> $ такую, чтобы линейные оболочки любых подсистем совпадали: $$ <mathcal L>left(X_1,dots,X_m right) =<mathcal L>left(<mathfrak E>_1,dots, <mathfrak E>_m right) quad npu quad min <1,dots,k> . $$ Иными словами, вектор $ <mathfrak E>_1 $ должен линейно зависеть от $ X_ <1>$, вектор $ <mathfrak E>_2 $ должен линейно выражаться через $ X_1,X_2 $, $ <mathfrak E>_3 $ — через $ X_1,X_2,X_3 $ и т.д.
Алгоритм ортогонализации Грама — Шмидта 10)
В случае $ m_<>=1 $ возьмем $ <mathfrak E>_1=X_1 $: поскольку вектор $ X_ <1>$ входит в линейно независимую систему , то $ <mathfrak E>_1 ne mathbb O $. Далее, будем искать $ <mathfrak E>_2 $ в виде $$<mathfrak E>_2=X_2 + alpha_ <21><mathfrak E>_1 $$ при пока неопределенном коэффициенте $ alpha_ <21>$. Очевидно, что при таком выборе $ <mathfrak E>_2 $ условие $ <mathcal L>(X_1,X_2)=<mathcal L>(<mathfrak E>_1,<mathfrak E>_2) $ будет выполнено. Подберем $ alpha_ <21>$ так, чтобы выполнялось $ <mathfrak E>_2 bot <mathfrak E>_1 $. $$0=langle <mathfrak E>_1,<mathfrak E>_2 rangle=langle <mathfrak E>_1,X_2 rangle+alpha_ <21>langle <mathfrak E>_1,<mathfrak E>_1 rangle Rightarrow alpha_<21>=-langle <mathfrak E>_1,X_2 rangle big/ langle <mathfrak E>_1,<mathfrak E>_1 rangle . $$ Таким образом, коэффициент $ alpha_ <21>$, а вместе с ним и вектор $ <mathfrak E>_2 $ определяются единственным образом. При этом $ <mathfrak E>_2ne mathbb O $, ибо, в противном случае, векторы $ X_2 $ и $ <mathfrak E>_1=X_1 $ были бы л.з., что противоречит предположению о линейной независимости системы $ $. Продолжаем процесс далее: вектор $ <mathfrak E>_3 $ ищем в виде $$<mathfrak E>_3=X_3 + alpha_ <31><mathfrak E>_1 + alpha_ <32><mathfrak E>_2 $$ при пока неопределенных коэффициентах $ alpha_ <31>$ и $ alpha_ <32>$. Условие $ <mathcal L>(X_1,X_2,X_3)=<mathcal L>(<mathfrak E>_1,<mathfrak E>_2,<mathfrak E>_3) $ выполняется поскольку $$alpha_ <31><mathfrak E>_1 + alpha_ <32><mathfrak E>_2 in <mathcal L>(X_1,X_2) subset <mathcal L>(X_1,X_2,X_3) .$$ Подберем скаляры $ alpha_ <31>$ и $ alpha_ <32>$ так, чтобы выполнялось $ <mathfrak E>_3 bot <mathfrak E>_1 $ и $ <mathfrak E>_3 bot <mathfrak E>_2 $. Два этих условия задают систему линейных уравнений $$left< begin langle X_3,<mathfrak E>_1 rangle + alpha_ <31>langle <mathfrak E>_1, <mathfrak E>_1 rangle + alpha_ <32>langle <mathfrak E>_2 , <mathfrak E>_1 rangle &=0 ,\ langle X_3,<mathfrak E>_2 rangle + alpha_ <31>langle <mathfrak E>_1, <mathfrak E>_2 rangle + alpha_ <32>langle <mathfrak E>_2 , <mathfrak E>_2 rangle &=0 , end right. iff begin alpha_<31>=-langle X_3,<mathfrak E>_1 rangle big/ |<mathfrak E>_1|^2 \ alpha_<32>=-langle X_3,<mathfrak E>_2 rangle big/ |<mathfrak E>_2|^2 end $$
Процесс продолжается далее аналогично. Допустим, что векторы $ <mathfrak E>_1,dots,<mathfrak E>_ $ уже построены, они ненулевые, попарно ортогональные и $$ <mathcal L>left(X_1,dots,X_ right)= <mathcal L>left(<mathfrak E>_1,dots, <mathfrak E>_ right) .$$ Вектор $ <mathfrak E>_ $ ищем в виде: $$ <mathfrak E>_ =X_k+alpha_ <mathfrak E>_1 + alpha_ <mathfrak E>_2 +dots + alpha_ <mathfrak E>_ $$ при пока неопределенных коэффициентах $ alpha_,dots ,alpha_ $. Условие $ <mathcal L>left(X_1,dots,X_,X_k right)= <mathcal L>left(<mathfrak E>_1,dots, <mathfrak E>_,<mathfrak E>_ right) $ выполнено и, кроме того, $ <mathfrak E>_ne mathbb O $ (в противном случае $ X_k in <mathcal L>left(<mathfrak E>_1,dots, <mathfrak E>_ right) =<mathcal L>left(X_1,dots,X_ right) $, т.е. система $ ,X_k > $ линейно зависима. Коэффициенты $ alpha_, dots ,alpha_ $ подбираются из условий $ <mathfrak E>_ bot <mathfrak E>_1,dots, <mathfrak E>_ bot <mathfrak E>_ $. Получающаяся система линейных уравнений имеет единственное решение $$alpha_=- langle X_k,<mathfrak E>_1 rangle big/ |<mathfrak E>_1|^2 ,dots, alpha_=-langle X_k,<mathfrak E>_ rangle big/ |<mathfrak E>_|^2 , $$ и это решение определяет единственный вектор $ <mathfrak E>_ $. ♦
Пример. Ортогонализовать систему векторов
$$ X_1=left[1,0,0,0,1 right], X_2=left[1,1,0,1,1 right], X_3=left[1,1,1,1,1 right] $$ при стандартном способе задания скалярного произведения в $ mathbb R^5 $.
Пример. Пусть в пространстве полиномов скалярное произведение задается формулой
$$ langle p(x),q(x) rangle=int_<-1>^ <1>p(t)q(t) d, t .$$ Построить ортогональный базис этого пространства.
Решение. Искомый базис строится ортогонализацией канонического базиса $ 1,x,x^2,dots, x^n $. В результате получаем систему полиномов: $$1, x, x^2-frac<1><3>, x^3-frac<3><5>, x, x^4-frac<6><7>, x^2+frac<3><35>,dots $$ Полиномы, получающиеся из этих нормированием: $$P_0(x)=1, P_1(x)= x, P_2(x)=frac<1><2>(3,x^2-1), P_3(x)= frac<1><2>( 5,x^3-3, x), $$ $$ P_4(x)= frac<1><8>(35,x^4-30, x^2+3),dots $$ $$ P_n(x)=frac<1> <2^n>sum_^ <lfloor n/2 rfloor>frac<(-1)^k(2n-2k)!> x^ $$ известны как полиномы Лежандра. Здесь $ lfloor mbox < >rfloor $ означает целую часть числа. Рекуррентное соотношение $$kP_(x)-(2k-1),xP_(x)+(k-1),P_(x) equiv 0, quad kge 2 ;$$ позволяет найти полином $ P_(x) $ если уже вычислены $ P_(x) $ и $ P_(x) $. ♦
В ортонормированном базисе пространства $ mathbb E_<> $ матрица Грама из формулы скалярного произведения $$ langle X,Y rangle=(x_1,dots,x_n) G(X_1,dots,X_n) left( begin y_1 \ vdots \ y_n end right) $$ становится единичной и в таком базисе скалярное произведение становится стандартным : $$ langle X,Y rangle=sum_^n x_jy_j .$$
Следующая теорема устанавливает связь между двумя ортонормированными базисами в одном и том же пространстве.
Теорема. Матрица перехода от одного ортонормированного базиса к другому является ортогональной.
В пространстве $ mathbb R^_<> $ матрица, составленная из столбцов произвольного ортонормированного базиса, является ортогональной.
Матричный формализм алгоритма Грама-Шмидта: QR-разложение
Рассмотрим пример из предыдущего пункта об ортогонализации системы векторов в $ mathbb R^5 $; только векторы будем рассматривать столбцами: $$ X_1=left[begin 1 \ 0 \ 0 \ 0 \ 1 end right], X_2=left[ begin 1 \ 1 \ 0 \ 1 \ 1 end right], X_3=left[ begin 1 \ 1 \ 1 \ 1 \ 1 end right] , . $$ Составим из них матрицу $$ A_ <5times 3>= left[ X_1,X_2,X_3 right] , . $$ Алгоритм Грама-Шмидта означает некоторые действия со столбцами этой матрицы, и эти действия могут быть записаны на языке матричного формализма, а именно — с помощью операции умножения этой матрицы на последовательность матриц определенного вида. В самом деле, на первом шаге алгоритма, «все остается на месте»: столбец $ <mathfrak E>_1 $ совпадает с $ X_ <1>$, а оставшиеся столбцы мы пока не трогаем. Формально это «бездействие» можно записать с помощью умножения матрицы $ A_<> $ на единичную матрицу порядка $ 3_<> $. $$ Acdot E_ <3>= left[<mathfrak E>_1,X_2,X_3 right] , . $$ Следующий шаг алгоритма уже менее тривиален: в получившейся матрице производятся действия над первыми двумя столбцами. При этом первый столбец остается неизменным, последний — тоже, а изменяется лишь второй: $$ <mathfrak E>_2 = X_2 + alpha_ <21><mathfrak E>_1 , . $$ Для получившейся на первом шаге матрицы, это действие эквивалентно домножению ее справа на матрицу $$ R_2 = left( begin 1 & alpha_ <21>& 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end right) , . $$ Если значение $ alpha_ <21>$ вычисляется как указано в алгоритме: $$alpha_<21>=- langle <mathfrak E>_1,X_2 rangle big/ langle <mathfrak E>_1,<mathfrak E>_1 rangle =- langle X_1,X_2 rangle big/ langle X_1,X_1 rangle , , $$ то получившаяся матрица $$ Acdot E_ <3>R_2 = left[<mathfrak E>_1,<mathfrak E>_2,X_3 right] $$ имеет первые два столбца ортогональными. Следующее преобразование получившейся системы столбцов равносильно домножению получившейся матрицы справа на матрицу вида $$ R_3 = left( begin 1 & 0 & alpha_ <31>\ 0 & 1 & alpha_ <32>\ 0 & 0 & 1 end right) , . $$ Если значения $ alpha_ <31>$ и $ alpha_ <32>$ вычисляются как указано в алгоритме, то получившаяся матрица $$ Acdot E_ <3>R_2 R_3 = left[<mathfrak E>_1,<mathfrak E>_2,<mathfrak E>_3 right] $$ имеет систему своих столбцов ортогональной. Можно произвести еще одно дополнительное домножение $$ Acdot E_ <3>R_2 R_3 cdot left( begin 1/langle <mathfrak E>_1,<mathfrak E>_1 rangle & 0 & 0 \ 0 & 1/langle <mathfrak E>_2,<mathfrak E>_2 rangle & 0 \ & 0 & 1/ langle <mathfrak E>_3,<mathfrak E>_3 rangle end right) , , $$ превратив полученную матрицу в матрицу с ортонормированной системой столбцов.
Теперь обдумаем полученный результат. Матрицы, на которые производились домножения матрицы $ A_<> $ имеют довольно специфическую форму: они — либо диагональные, либо же отличаются от единичной матрицы в одном их своих столбцов. Эти матрицы могут быть отнесены к типу матриц элементарных преобразований системы столбцов произвольной матрицы $ A_<> $. Все они являются верхнетреугольными, и их произведение $ R_<> $ относится к тому же типу. Обратная к верхнетреугольной также является верхнетреугольной. В результате, можно получить разложение матрицы $ A_<> $ в произведение $$ A=Q_<5times 3>R^ <-1>, , $$ где вторая матрица в произведении является верхнетреугольной, а первая имеет свои столбцы ортонормированными.
Теорема [о QR-разложении]. Для любой вещественной матрицы $ A_^<> $ ранга $ n 11) $ tilde R_ $, такие, что $$ A=Q tilde R , . $$
Пример. Для матрицы из предыдущего примера имеем:
$$ left( begin 1 & 1 & 1 \ 0 & 1 & 1 \ 0 & 0 & 1 \ 0 & 1 & 1 \ 1 & 1 & 1 end right) = $$ $$ =left( begin 1/sqrt <2>& 0 & 0 \ 0 & 1/sqrt <2>& 0 \ 0 & 0 & 1 \ 0 & 1/sqrt <2>& 0 \ 1/sqrt <2>& 0 & 0 end right) left< left( begin 1 & -1 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end right) left( begin 1 & 0 & -1 \ 0 & 1 & -1 \ 0 & 0 & 1 end right) left( begin 1/sqrt <2>& 0 & 0 \ 0 & 1/sqrt <2>& 0 \ 0 & 0 & 1 end right) right>^ <-1>$$ $$ = left( begin 1/sqrt <2>& 0 & 0 \ 0 & 1/sqrt <2>& 0 \ 0 & 0 & 1 \ 0 & 1/sqrt <2>& 0 \ 1/sqrt <2>& 0 & 0 end right)left( begin sqrt <2>& sqrt <2>& sqrt <2>\ 0 & sqrt <2>& sqrt <2>\ 0 & 0 & 1 end right) , . $$ ♦
Для квадратной неособенной вещественной матрицы $ A_<> $ матрица $ Q_<> $ в QR-разложении будет ортогональной.
Последний результат имеет уже самостоятельное значение, не относящееся к материалам настоящего раздела. Например, его можно использовать для обращения матрицы $ A_<> $. Дело в том, что ортогональная матрица обращается достаточно просто: $ Q^ <-1>= Q^ <top>$.
Расстояние от точки до многообразия
Задача. Найти расстояние от заданного вектора $ X_<> $ до заданного множества $ mathbb Ssubset mathbb E $.
Такая постановка требует немедленного уточнения: что такое расстояние от вектора до множества? Обратясь за помощью к геометрии, мы можем ввести это понятие, основываясь на понятии расстояния между точками: например, расстояние от точки $ Xin mathbb R^2 $ до множества $ mathbb S subset mathbb R^2 $ определить как минимальное из возможных расстояний между точками $ X_<> $ и $ Y_<> $, где $ Yin mathbb S $. Следующий пример показывает, что наше определение оказывается ущербным.
Пример. Множество
Доказать следующие свойства операции $ perp $:
а) $ left(mathbb E_1^<^<bot>> right)^<^<bot>>=mathbb E_1 $; б) $ left(mathbb E_1 +mathbb E_2 right)^<^<bot>>=mathbb E_1^<^<bot>> cap mathbb E_2^<^<bot>> $; в) $ left(mathbb E_1 cap mathbb E_2 right)^<^<bot>>=mathbb E_1^<^<bot>>+mathbb E_2^<^<bot>> $.
Доказать, что в пространстве квадратных матриц со скалярным произведением, заданным формулой
$$ langle A,B rangle = operatorname left(Acdot B^ <top>right) = sum_^n a_b_ , $$ подпространство кососимметричных матриц является ортогональным дополнением подпространства симметричных матриц.
Вычисление расстояния
Теорема $ 2 $ из предыдущего пункта позволяет сформулировать результат, на котором и будет основано решение задачи вычисления расстояния.
Теорема 1. Для любого вектора $ Xin mathbb E $ существует единственное представление его в виде $$ X=X^<^<parallel>>+X^<^<bot>> quad npu X^<^<parallel>>in mathbb E_1, X^<^<bot>> in mathbb E_1^<^<bot>> . $$
В этом разложении вектор $ X^<^<parallel>> $ называется ортогональной проекцией вектора $ X_<> $ на $ mathbb E_1 $, а вектор $ X^<^<bot>> $ — ортогональной составляющей вектора $ X_<> $ относительно $ mathbb E_1 $ или же перпендикуляром, опущенным из точки $ X_<> $ на подпространство $ mathbb E_1 $.
Теорема 2. Длина перпендикуляра, опущенного из точки $ X_<> $ на подпространство $ mathbb E_1 $ , равна расстоянию от этой точки до подпространства: $$left|X^<^<bot>>right|=min_ |X-Y| . $$
Доказательство. $$ X^<^<bot>>=left( X-X^<^<parallel>> right) perp mathbb E_1 Rightarrow X^<^<bot>> perp left( -Y+X^<^<parallel>> right) quad npu forall Y in mathbb E_1 . $$ По теореме Пифагора: $$ left|X^<^<bot>> right|^2+ left|X^<^<parallel>> -Y right|^2 =left|X^<^<bot>>+ X^<^<parallel>> -Y right|^2 = |X-Y|^2 Rightarrow $$ $$ Rightarrow left|X^<^<bot>> right|^2le |X-Y|^2 Rightarrow left|X^<^<bot>> right|le min_ |X-Y| . $$ С другой стороны, указанный минимум достигается при $ Y=X^<^<parallel>> $ поскольку $ left|X^<^<bot>> right|=left|X-X^<^<parallel>>right| $. ♦
Итак, задача, поставленная в начале ☞ ПУНКТА, решается вычислением $ left|X^<^<bot>> right| $. Для нахождения последнего числа сначала найдем базис $ $ подпространства $ mathbb E_1 $. Далее, ищем $ X^<^<parallel>> $, принадлежащий $ mathbb E_1 $, в виде линейной комбинации базисных векторов: $$ X^<^<parallel>>=alpha_1 X_1 + dots + alpha_k X_k . $$ Для нахождения скаляров $ alpha_1,dots , alpha_k $ используем тот факт, что вектор $ X^<^<bot>>=X-X^<^<parallel>> $ должен быть ортогонален $ mathbb E_1 $, а значит, ортогонален каждому $ X_j $: $$langle X-X^<^<parallel>>, X_j rangle =0 iff langle X^<^<parallel>>, X_j rangle=langle X,X_j rangle . $$ Получаем систему линейных уравнений: $$ left< begin alpha_1 langle X_1,X_1 rangle &+ alpha_2 langle X_1,X_2 rangle &+ dots &+ alpha_k langle X_1,X_k rangle &= langle X,X_1 rangle, \ alpha_1 langle X_2,X_1 rangle & + alpha_2 langle X_2,X_2 rangle &+ dots &+ alpha_k langle X_2,X_k rangle &= langle X,X_2 rangle, \ dots & & & & dots \ alpha_1 langle X_k,X_1 rangle & + alpha_2 langle X_k,X_2 rangle &+ dots &+ alpha_k langle X_k,X_k rangle &= langle X,X_k rangle. end right. $$ с матрицей, которая нам уже известна как матрица Грама системы векторов: $ G(X_1,dots,X_k) $. Для однозначной разрешимости относительно $ alpha_1,dots , alpha_k $ необходимо и достаточно (см. ☞ теорема Кронекера-Капелли ), чтобы определитель этой матрицы — т.е. определитель Грама $ mathfrak G(X_1,dots,X_k) $ — был отличен от нуля.
Матрица Грама обращается в единичную если векторы $ X_1,dots,X_k $ входят в состав ортонормированного базиса пространства $ mathbb E_<> $. Следовательно, по крайней мере в этом частном случае, система уравнений будет иметь единственное решение. В одном из последующих ☟ ПУНКТОВ будет установлен и более общий факт: $$ mathfrak(Y_1,dots,Y_k)=0 iff quad mbox < система векторов >quad quad mbox < линейно зависима. >$$ Этот факт позволяет нам заключить, что, поскольку векторы $ $ — базисные для подпространства $ mathbb E_1 $, то система уравнений имеет единственное решение относительно $ alpha_1,dots , alpha_k $: $$alpha_1=alpha_1^<*>,dots , alpha_k=alpha_k^ <*> .$$ Теперь может быть найдена проекция вектора $ X_<> $ на $ mathbb E_1 $: $$ X^<^<parallel>>=alpha_1^ <*>X_1 + dots + alpha_k^ <*>X_k , $$ а затем и составляющая: $ X^<^<bot>>=X-X^<^<parallel>> $.
Пример. Найти расстояние от точки $ X=[1,1,2,2,2] $ до подпространства
$$ mathbb E_1= left< Xin mathbb R^5 left| begin x_1&-x_2&-x_3&+x_4 & &= 0, \ 2,x_1&-x_2&-x_3&+2,x_4 &-x_5 &=0 end right. right> , $$ если скалярное произведение определяется стандартно: $ langle X,Y rangle=sum_^5 x_jy_j $.
Решение. Базис $ mathbb E_1 $ составляет фундаментальная система решений системы линейных уравнений, например: $$X_1=[0,-1,1,0,0], X_2=[-1,0,0,1,0], X_3=[1,1,0,0,1] .$$ Составляем матрицу Грама этой системы векторов и выписываем систему уравнений: $$ left( begin 2 & 0 & -1 \ 0 & 2 & -1 \ -1 & -1 & 3 end right) left( begin alpha_1 \ alpha_2 \ alpha_3 end right) = left( begin 1 \ 1 \ 4 end right) Rightarrow alpha_1=frac<7><4>,, alpha_2=frac<7><4>,, alpha_3=frac<5> <2> . $$ Ортогональная проекция вектора $ X_<> $ на $ mathbb E_1 $: $$ X^<^<parallel>>= frac<7> <4>X_1 + frac<7> <4>X_2 + frac<5> <2>X_3=left[frac<3><4>,, frac<3><4>,, frac<7><4>,, frac<7><4>,, frac<5> <2>right] , $$ а ортогональная составляющая вектора $ X_<> $ относительно $ mathbb E_1 $: $$ X^<^<bot>>=X-X^<^<parallel>>= left[frac<1><4>,, frac<1><4>,, frac<1><4>,, frac<1><4>,, — frac<1> <2>right] quad Rightarrow left|X^<^<bot>>right| =frac<1><sqrt<2>> . $$
Ответ. $ 1/sqrt <2>$.
Альтернативный способ вычисления расстояния от точки до линейного многообразия, заданного системой линейных уравнений ☞ ЗДЕСЬ.
Расстояние от точки $ X_<> $ до линейного подпространства, базисными векторами которого являются $ X_1,dots,X_k $, вычисляется по формуле: $$ d=sqrt<frac<<mathfrak G>(X_1,dots,X_k, X)><<mathfrak G>(X_1,dots,X_k)>> . $$
Доказательство ☞ ЗДЕСЬ.
Пример. В пространстве полиномов с вещественными коэффициентами степеней не выше $ 5_<> $ со скалярным произведением, заданным формулой
$$langle p(x),q(x) rangle = int_<-1>^1 p(t)q(t) d,t $$ найти расстояние от полинома $ p(x)= -x^5+x^3-3,x+1 $ до линейного подпространства четных полиномов.
Решение. Базис подпространства четных полиномов состоит, например, из $ 1,x^2,x^4 $. Имеем: $$ <mathfrak G>(1,x^2,x^4)=left| begin int_<-1>^1 1 cdot 1 d,t & int_<-1>^1 1 cdot t^2 d,t & int_<-1>^1 1 cdot t^4 d,t \ int_<-1>^1 1 cdot t^2 d,t & int_<-1>^1 t^2 cdot t^2 d,t & int_<-1>^1 t^2cdot t^4 d,t \ int_<-1>^1 1 cdot t^4 d,t & int_<-1>^1 t^2 cdot t^4 d,t & int_<-1>^1 t^4 cdot t^4 d,t end right|=left| begin 2 & 2/3 & 2/5 \ 2/3 & 2/5 & 2/7 \ 2/5 & 2/7 & 2/9 end right|=frac<2048> <496125> ; $$ $$ <mathfrak G>(1,x^2,x^4,p(x))=left| begin 2 & 2/3 & 2/5 & 2 \ 2/3 & 2/5 & 2/7 & 2/3 \ 2/5 & 2/7 & 2/9 & 2/5 \ 2 & 2/3 & 2/5 & 3632/495 end right|=frac<5410816> <245581875> . $$ Отношение полученных определителей даст квадрат расстояния: $$ d^2=2642/495 . $$ К этому же ответу можно было прийти и быстрее если заметить, что при заданном скалярном произведении любой четный полином ортогонален любому нечетному полиному. Следовательно для выделения у $ p(x) $ ортогональной составляющей относительно подпространства четных полиномов достаточно оставить в его каноническом виде только нечетные одночлены. Расстояние равно норме полинома $ p(x)-1 $. ♦
Подводя итог: определители Грама полностью решают задачу о вычислении расстояния от точки до линейного подпространства в любом евклидовом пространстве; этот результат легко обобщается на произвольное линейное многообразие.
Теорема 3. Расстояние от точки $ X_<> $ до линейного многообразия $ mathbb M=X_0+mathbb E_1 $ равно длине ортогональной составляющей вектора $ X-X_0 $ относительно подпространства $ mathbb E_1 $.
Доказательство. Геометрический смысл понятен из рисунков, иллюстрирующих решение проблемы в $ mathbb R^ <3>$: надо свести задачу к случаю из предыдущей теоремы с помощью сдвига всей конструкции на вектор $ (-X_0) $.
Формальности: $$ min_ |X-Y| =min_ |X-(X_0+Z)|= min_ |(X-X_0)-Z)| . $$ Последняя величина — это расстояние от точки $ X-X_0 $ до $ mathbb E_1 $ ; согласно теореме $ 2 $ оно равно длине ортогональной составляющей вектора $ X-X_0 $ относительно $ mathbb E_1 $. ♦
Расстояние от точки $ X_<> $ до линейного многообразия, заданного параметрически
Вычисление расстояния между линейными многообразиями (и некоторыми другими объектами, заданными алгебраическими уравнениями) ☞ ЗДЕСЬ.
Угол между вектором и линейным многообразием
Углом между вектором $ Xin mathbb E $ и линейным подпространством $ mathbb E_1 subset mathbb E $ назовем число — точную нижнюю грань множества углов между $ X_<> $ и всевозможными векторами $ Y in mathbb E_1 $. Углом между вектором $ Xin mathbb E $ и линейным многообразием $ mathbb M=X_0+mathbb E_1 $ называется угол между $ X_<> $ и $ mathbb E_1 $.
Теорема. Угол между вектором $ Xin mathbb E $ и линейным подпространством $ mathbb E_1 subset mathbb E $ равен углу между этим вектором и его ортогональной проекцией $ X^<^<parallel>> $ на $ mathbb E_1 $.
Эта теорема сводит задачу к решенной в предыдущих пунктах задаче вычисления расстояния от вектора до подпространства, только теперь интерес смещается от ортогональной составляющей вектора к его ортогональной проекции.
Пример. Определить угол между вектором $ X_0=[1,0,3,0] $ и линейной оболочкой
Решение. Воспользуемся результатом, приведенным ☞ ЗДЕСЬ (для правильной стыковки рассматриваем все векторы как столбцы): $$ X_<ast>=L(L^ <top>L_<>)^ <-1>L^ <top>X_0 , . $$ Здесь $$ L=left(begin 5 & 1 & 2 \ 3 & 1 & -1 \ 4 & 4 & 1 \ -3 & 5 & 2 end right), qquad L^ <top>L = left(begin 59 & 9 & 5 \ 9 & 43 & 15 \ 5 & 15 & 10 end right), $$ $$ (L^ <top>L )^ <-1>= left(begin 41/2312 & -3/2312 & -2/289\ -3/2312 & 113/2312 & -21/289\ -2/289 & -21/289 & 307/1445 end right) $$ $$ L(L^ <top>L_<>)^ <-1>L^<top>= left(begin 9/10 & -1/5 & 1/5 & -1/10 \ -1/5 & 3/5 & 2/5 & -1/5 \ 1/5 & 2/5 & 3/5 & 1/5\ -1/10 & -1/5 & 1/5 & 9/10 end right), quad X_<ast>= left(begin 3/2 \ 1 \ 2 \ 1/2 end right) , . $$ $$ widehat>=arccos frac <langle X_0,X_<ast>rangle ><sqrt< langle X_0,X_0rangle langle X_<ast>,X_ <ast>rangle>>= arccos frac<sqrt<3>><2>= frac<pi> <6>, . $$ ♦
Свойства матрицы Грама
Теорема. $ <mathfrak G>(X_<1>,dots,X_m)=0 $ тогда и только тогда, когда система векторов $ ,dots,X_m > $ линейно зависима.
Доказательство. Если система векторов $ ,dots,X_m> $ линейно зависима, то имеет место равенство $$alpha_1 X_1+alpha_2 X_2+dots+alpha_ X_=mathbb O$$ при некотором нетривиальном наборе скаляров $ alpha_1=alpha_1^<*>,dots,alpha_m=alpha_m^ <*>$. Домножим это соотношение (скалярно) на векторы $ X_1,X_2,dots,X_m $, получим систему уравнений, которую перепишем в матричном виде: $$ left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right) left( begin alpha_1 \ alpha_2 \ vdots \ alpha_m end right)= left( begin 0 \ 0 \ vdots \ 0 end right) . $$ Если рассмотреть эту систему относительно переменных $ alpha_<1>,dots,alpha_m $, то она оказывается однородной и, по предположенному, будет иметь нетривиальное решение $ alpha_1=alpha_1^<*>,dots,alpha_m=alpha_m^ <*>$ . Следовательно (см. ☞ ТЕОРЕМА КРОНЕКЕРА-КАПЕЛЛИ ) ее определитель равен нулю: $ <mathfrak G>(X_<1>,dots,X_m)=0 $.
Обратно, если определитель Грама равен нулю, то предыдущая система имеет нетривиальное решение относительно $ alpha_<1>,dots,alpha_m $. Пусть $ alpha_1=alpha_1^<star>,dots,alpha_m=alpha_m^ <star>$ — какое-то из этих решений. Составим вектор $$X^<star>= alpha_1^ <star>X_1+alpha_2^ <star>X_2+dots+alpha_^ <star>X_ $$ и вычислим скалярное произведение его на самого себя: $$ langle X^<star>,X^ <star>rangle = $$ $$ = (alpha_1^ <star>,alpha_2^ <star>,dots,alpha_m^ <star>) underbrace<left( begin langle X_1,X_1 rangle & langle X_1,X_2 rangle & dots & langle X_1,X_m rangle \ langle X_2,X_1 rangle & langle X_2,X_2 rangle & dots & langle X_2,X_m rangle \ dots & & & dots \ langle X_m,X_1 rangle & langle X_m,X_2 rangle & dots & langle X_m,X_m rangle end right) left(begin alpha_1^ <star>\ alpha_2^ <star>\ vdots \ alpha_m^ <star>endright)>_<=mathbb O_>=0 . $$ Таким образом длина вектора $ X^ <star>$ равна нулю, и, следовательно, по аксиоме 4 , сам вектор $ X^ <star>$ — нулевой. Но тогда система векторов $ ,dots,X_m> $ линейно зависима. ♦
Ранг матрицы Грама совпадает с рангом системы порождающих ее векторов:
Если какой-то главный минор матрицы Грама обращается в нуль, то и все главные миноры бóльших порядков обращаются в нуль.
Теорема. $ <mathfrak G>(X_<1>,dots,X_m) ge 0 $ для любого набора векторов $ ,dots,X_m > $.
Доказательство ☞ ЗДЕСЬ
Матрица Грама линейно независимой системы векторов является положительно определенной. Матрица Грама произвольной системы векторов является положительно полуопределенной.
Дальнейшие свойства матрицы и определителя Грама ☞ ЗДЕСЬ
Задачи
Источник
Материалы этого раздела составлены на основе книги
Шилов Г.Е. Математический анализ. Конечномерные линейные пространства. М.Наука.1969
http://habr.com/ru/post/579914/
http://vmath.ru/vf5/euclid_space
From Wikipedia, the free encyclopedia
Using the Pythagorean theorem to compute two-dimensional Euclidean distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of a line segment between the two points.
It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, therefore occasionally being called the Pythagorean distance. These names come from the ancient Greek mathematicians Euclid and Pythagoras, although Euclid did not represent distances as numbers, and the connection from the Pythagorean theorem to distance calculation was not made until the 18th century.
The distance between two objects that are not points is usually defined to be the smallest distance among pairs of points from the two objects. Formulas are known for computing distances between different types of objects, such as the distance from a point to a line. In advanced mathematics, the concept of distance has been generalized to abstract metric spaces, and other distances than Euclidean have been studied. In some applications in statistics and optimization, the square of the Euclidean distance is used instead of the distance itself.
Distance formulas[edit]
One dimension[edit]
The distance between any two points on the real line is the absolute value of the numerical difference of their coordinates, their absolute difference. Thus if 

A more complicated formula, giving the same value, but generalizing more readily to higher dimensions, is:[1]
In this formula, squaring and then taking the square root leaves any positive number unchanged, but replaces any negative number by its absolute value.[1]
Two dimensions[edit]
In the Euclidean plane, let point 





This can be seen by applying the Pythagorean theorem to a right triangle with horizontal and vertical sides, having the line segment from 

It is also possible to compute the distance for points given by polar coordinates. If the polar coordinates of 



When 

Higher dimensions[edit]
Deriving the 
In three dimensions, for points given by their Cartesian coordinates, the distance is
In general, for points given by Cartesian coordinates in 
The Euclidean distance may also be expressed more compactly in terms of the Euclidean norm of the Euclidean vector difference:
Objects other than points[edit]
For pairs of objects that are not both points, the distance can most simply be defined as the smallest distance between any two points from the two objects, although more complicated generalizations from points to sets such as Hausdorff distance are also commonly used.[6] Formulas for computing distances between different types of objects include:
- The distance from a point to a line, in the Euclidean plane[7]
- The distance from a point to a plane in three-dimensional Euclidean space[7]
- The distance between two lines in three-dimensional Euclidean space[8]
Properties[edit]
The Euclidean distance is the prototypical example of the distance in a metric space,[9] and obeys all the defining properties of a metric space:[10]
Another property, Ptolemy’s inequality, concerns the Euclidean distances among four points 



For points in the plane, this can be rephrased as stating that for every quadrilateral, the products of opposite sides of the quadrilateral sum to at least as large a number as the product of its diagonals. However, Ptolemy’s inequality applies more generally to points in Euclidean spaces of any dimension, no matter how they are arranged.[11] For points in metric spaces that are not Euclidean spaces, this inequality may not be true. Euclidean distance geometry studies properties of Euclidean distance such as Ptolemy’s inequality, and their application in testing whether given sets of distances come from points in a Euclidean space.[12]
According to the Beckman–Quarles theorem, any transformation of the Euclidean plane or of a higher-dimensional Euclidean space that preserves unit distances must be an isometry, preserving all distances.[13]
Squared Euclidean distance[edit]
A cone, the graph of Euclidean distance from the origin in the plane
A paraboloid, the graph of squared Euclidean distance from the origin
In many applications, and in particular when comparing distances, it may be more convenient to omit the final square root in the calculation of Euclidean distances. The value resulting from this omission is the square of the Euclidean distance, and is called the squared Euclidean distance.[14] For instance, the Euclidean minimum spanning tree can be determined using only the ordering between distances, and not their numeric values. Comparing squared distances produces the same result but avoids an unnecessary square-root calculation and sidesteps issues of numerical precision.[15] As an equation, the squared distance can be expressed as a sum of squares:
Beyond its application to distance comparison, squared Euclidean distance is of central importance in statistics, where it is used in the method of least squares, a standard method of fitting statistical estimates to data by minimizing the average of the squared distances between observed and estimated values,[16] and as the simplest form of divergence to compare probability distributions.[17] The addition of squared distances to each other, as is done in least squares fitting, corresponds to an operation on (unsquared) distances called Pythagorean addition.[18] In cluster analysis, squared distances can be used to strengthen the effect of longer distances.[14]
Squared Euclidean distance does not form a metric space, as it does not satisfy the triangle inequality.[19] However it is a smooth, strictly convex function of the two points, unlike the distance, which is non-smooth (near pairs of equal points) and convex but not strictly convex. The squared distance is thus preferred in optimization theory, since it allows convex analysis to be used. Since squaring is a monotonic function of non-negative values, minimizing squared distance is equivalent to minimizing the Euclidean distance, so the optimization problem is equivalent in terms of either, but easier to solve using squared distance.[20]
The collection of all squared distances between pairs of points from a finite set may be stored in a Euclidean distance matrix, and is used in this form in distance geometry.[21]
Generalizations[edit]
In more advanced areas of mathematics, when viewing Euclidean space as a vector space, its distance is associated with a norm called the Euclidean norm, defined as the distance of each vector from the origin. One of the important properties of this norm, relative to other norms, is that it remains unchanged under arbitrary rotations of space around the origin.[22] By Dvoretzky’s theorem, every finite-dimensional normed vector space has a high-dimensional subspace on which the norm is approximately Euclidean; the Euclidean norm is the
only norm with this property.[23] It can be extended to infinite-dimensional vector spaces as the L2 norm or L2 distance.[24] The Euclidean distance gives Euclidean space the structure of a topological space, the Euclidean topology, with the open balls (subsets of points at less than a given distance from a given point) as its neighborhoods.[25]
Other common distances on Euclidean spaces and low-dimensional vector spaces include:[26]
- Chebyshev distance, which measures distance assuming only the most significant dimension is relevant.
- Manhattan distance, which measures distance following only axis-aligned directions.
- Minkowski distance, a generalization that unifies Euclidean distance, Manhattan distance, and Chebyshev distance.
For points on surfaces in three dimensions, the Euclidean distance should be distinguished from the geodesic distance, the length of a shortest curve that belongs to the surface. In particular, for measuring great-circle distances on the earth or other spherical or near-spherical surfaces, distances that have been used include the haversine distance giving great-circle distances between two points on a sphere from their longitudes and latitudes, and Vincenty’s formulae also known as «Vincent distance» for distance on a spheroid.[27]
History[edit]
Euclidean distance is the distance in Euclidean space; both concepts are named after ancient Greek mathematician Euclid, whose Elements became a standard textbook in geometry for many centuries.[28] Concepts of length and distance are widespread across cultures, can be dated to the earliest surviving «protoliterate» bureaucratic documents from Sumer in the fourth millennium BC (far before Euclid),[29] and have been hypothesized to develop in children earlier than the related concepts of speed and time.[30] But the notion of a distance, as a number defined from two points, does not actually appear in Euclid’s Elements. Instead, Euclid approaches this concept implicitly, through the congruence of line segments, through the comparison of lengths of line segments, and through the concept of proportionality.[31]
The Pythagorean theorem is also ancient, but it could only take its central role in the measurement of distances after the invention of Cartesian coordinates by René Descartes in 1637. The distance formula itself was first published in 1731 by Alexis Clairaut.[32] Because of this formula, Euclidean distance is also sometimes called Pythagorean distance.[33] Although accurate measurements of long distances on the earth’s surface, which are not Euclidean, had again been studied in many cultures since ancient times (see history of geodesy), the idea that Euclidean distance might not be the only way of measuring distances between points in mathematical spaces came even later, with the 19th-century formulation of non-Euclidean geometry.[34] The definition of the Euclidean norm and Euclidean distance for geometries of more than three dimensions also first appeared in the 19th century, in the work of Augustin-Louis Cauchy.[35]
References[edit]
- ^ a b c Smith, Karl (2013), Precalculus: A Functional Approach to Graphing and Problem Solving, Jones & Bartlett Publishers, p. 8, ISBN 978-0-7637-5177-7
- ^ a b Cohen, David (2004), Precalculus: A Problems-Oriented Approach (6th ed.), Cengage Learning, p. 698, ISBN 978-0-534-40212-9
- ^ Aufmann, Richard N.; Barker, Vernon C.; Nation, Richard D. (2007), College Trigonometry (6th ed.), Cengage Learning, p. 17, ISBN 978-1-111-80864-8
- ^ Andreescu, Titu; Andrica, Dorin (2014), «3.1.1 The Distance Between Two Points», Complex Numbers from A to … Z (2nd ed.), Birkhäuser, pp. 57–58, ISBN 978-0-8176-8415-0
- ^ Tabak, John (2014), Geometry: The Language of Space and Form, Facts on File math library, Infobase Publishing, p. 150, ISBN 978-0-8160-6876-0
- ^ Ó Searcóid, Mícheál (2006), «2.7 Distances from Sets to Sets», Metric Spaces, Springer Undergraduate Mathematics Series, Springer, pp. 29–30, ISBN 978-1-84628-627-8
- ^ a b Ballantine, J. P.; Jerbert, A. R. (April 1952), «Distance from a line, or plane, to a point», Classroom notes, American Mathematical Monthly, 59 (4): 242–243, doi:10.2307/2306514, JSTOR 2306514
- ^ Bell, Robert J. T. (1914), «49. The shortest distance between two lines», An Elementary Treatise on Coordinate Geometry of Three Dimensions (2nd ed.), Macmillan, pp. 57–61
- ^ Ivanov, Oleg A. (2013), Easy as π?: An Introduction to Higher Mathematics, Springer, p. 140, ISBN 978-1-4612-0553-1
- ^ a b c d Strichartz, Robert S. (2000), The Way of Analysis, Jones & Bartlett Learning, p. 357, ISBN 978-0-7637-1497-0
- ^ Adam, John A. (2017), «Chapter 2. Introduction to the «Physics» of Rays», Rays, Waves, and Scattering: Topics in Classical Mathematical Physics, Princeton Series in Applied Mathematics, Princeton University Press, pp. 26–27, doi:10.1515/9781400885404-004, ISBN 978-1-4008-8540-4
- ^ Liberti, Leo; Lavor, Carlile (2017), Euclidean Distance Geometry: An Introduction, Springer Undergraduate Texts in Mathematics and Technology, Springer, p. xi, ISBN 978-3-319-60792-4
- ^ Beckman, F. S.; Quarles, D. A., Jr. (1953), «On isometries of Euclidean spaces», Proceedings of the American Mathematical Society, 4 (5): 810–815, doi:10.2307/2032415, JSTOR 2032415, MR 0058193
- ^ a b Spencer, Neil H. (2013), «5.4.5 Squared Euclidean Distances», Essentials of Multivariate Data Analysis, CRC Press, p. 95, ISBN 978-1-4665-8479-2
- ^ Yao, Andrew Chi Chih (1982), «On constructing minimum spanning trees in k-dimensional spaces and related problems», SIAM Journal on Computing, 11 (4): 721–736, doi:10.1137/0211059, MR 0677663
- ^ Randolph, Karen A.; Myers, Laura L. (2013), Basic Statistics in Multivariate Analysis, Pocket Guide to Social Work Research Methods, Oxford University Press, p. 116, ISBN 978-0-19-976404-4
- ^ Csiszár, I. (1975), «I-divergence geometry of probability distributions and minimization problems», Annals of Probability, 3 (1): 146–158, doi:10.1214/aop/1176996454, JSTOR 2959270, MR 0365798
- ^ Moler, Cleve and Donald Morrison (1983), «Replacing Square Roots by Pythagorean Sums» (PDF), IBM Journal of Research and Development, 27 (6): 577–581, CiteSeerX 10.1.1.90.5651, doi:10.1147/rd.276.0577
- ^ Mielke, Paul W.; Berry, Kenneth J. (2000), «Euclidean distance based permutation methods in atmospheric science», in Brown, Timothy J.; Mielke, Paul W. Jr. (eds.), Statistical Mining and Data Visualization in Atmospheric Sciences, Springer, pp. 7–27, doi:10.1007/978-1-4757-6581-6_2
- ^ Kaplan, Wilfred (2011), Maxima and Minima with Applications: Practical Optimization and Duality, Wiley Series in Discrete Mathematics and Optimization, vol. 51, John Wiley & Sons, p. 61, ISBN 978-1-118-03104-9
- ^ Alfakih, Abdo Y. (2018), Euclidean Distance Matrices and Their Applications in Rigidity Theory, Springer, p. 51, ISBN 978-3-319-97846-8
- ^ Kopeikin, Sergei; Efroimsky, Michael; Kaplan, George (2011), Relativistic Celestial Mechanics of the Solar System, John Wiley & Sons, p. 106, ISBN 978-3-527-63457-6
- ^ Matoušek, Jiří (2002), Lectures on Discrete Geometry, Graduate Texts in Mathematics, Springer, p. 349, ISBN 978-0-387-95373-1
- ^ Ciarlet, Philippe G. (2013), Linear and Nonlinear Functional Analysis with Applications, Society for Industrial and Applied Mathematics, p. 173, ISBN 978-1-61197-258-0
- ^ Richmond, Tom (2020), General Topology: An Introduction, De Gruyter, p. 32, ISBN 978-3-11-068657-9
- ^ Klamroth, Kathrin (2002), «Section 1.1: Norms and Metrics», Single-Facility Location Problems with Barriers, Springer Series in Operations Research, Springer, pp. 4–6, doi:10.1007/0-387-22707-5_1
- ^ Panigrahi, Narayan (2014), «12.2.4 Haversine Formula and 12.2.5 Vincenty’s Formula», Computing in Geographic Information Systems, CRC Press, pp. 212–214, ISBN 978-1-4822-2314-9
- ^ Zhang, Jin (2007), Visualization for Information Retrieval, Springer, ISBN 978-3-540-75148-9
- ^ Høyrup, Jens (2018), «Mesopotamian mathematics» (PDF), in Jones, Alexander; Taub, Liba (eds.), The Cambridge History of Science, Volume 1: Ancient Science, Cambridge University Press, pp. 58–72
- ^ Acredolo, Curt; Schmid, Jeannine (1981), «The understanding of relative speeds, distances, and durations of movement», Developmental Psychology, 17 (4): 490–493, doi:10.1037/0012-1649.17.4.490
- ^ Henderson, David W. (2002), «Review of Geometry: Euclid and Beyond by Robin Hartshorne», Bulletin of the American Mathematical Society, 39: 563–571, doi:10.1090/S0273-0979-02-00949-7
- ^ Maor, Eli (2019), The Pythagorean Theorem: A 4,000-Year History, Princeton University Press, pp. 133–134, ISBN 978-0-691-19688-6
- ^ Rankin, William C.; Markley, Robert P.; Evans, Selby H. (March 1970), «Pythagorean distance and the judged similarity of schematic stimuli», Perception & Psychophysics, 7 (2): 103–107, doi:10.3758/bf03210143, S2CID 144797925
- ^ Milnor, John (1982), «Hyperbolic geometry: the first 150 years», Bulletin of the American Mathematical Society, 6 (1): 9–24, doi:10.1090/S0273-0979-1982-14958-8, MR 0634431
- ^ Ratcliffe, John G. (2019), Foundations of Hyperbolic Manifolds, Graduate Texts in Mathematics, vol. 149 (3rd ed.), Springer, p. 32, ISBN 978-3-030-31597-9