Евклидово
пространство. Длина (норма) вектора
Определение
1.Скалярным
произведением двух
векторов x =
(x1, x2,
… xn)
и y =
(y1, y2,
… yn) n-мерного
пространства называется число
(x, y)
= x1×y1 + x2×y2 +
… + xn×yn .
Определение
2.Евклидовым
пространством называется
линейное (векторное) пространство, в
котором задано скалярное произведение
векторов, удовлетворяющее определенным
условиям (аксиомам).
Определение
3.Длиной (нормой)
вектора в евклидовом пространстве
называется корень квадратный из его
скалярного квадрата
.
23.
Неравенства Коши – Буняковского,
треугольника
Неравенство
Коши-Буняковского
Доказывается
как следствие из следующей теоремы:
Теорема.
Пусть
–
произвольная, не обязательно линейно
зависимая система векторов. Тогда
детерминант матрицы, составленной из
их попарных скалярных произведений,
положителен,
если векторы линейно независимы, и равен
нулю, если они линейно зависимы.
Первое
утверждение следует из предложения 2
(Детерминант матрицы Грама любого базиса
положителен), так как линейно независимые
векторы составляют базис в своей линейной
оболочке.
Докажем
второе утверждение. Если векторы линейно
зависимы, то выполнено равенство
,
в котором среди коэффициентов есть
отличные от нуля. Умножая это равенство
скалярно на каждый из векторов. Мы придем
к системе линейных уравнений
Которой
удовлетворяют коэффициенты
.
Так как система имеет нетривиальное
решение, детерминант её матрицы равен
нулю.
Следствие.
Для
любых двух векторов в евклидовом
пространстве имеет место неравенство
Коши-Буняковского
причем
оно выполнено как равенство тогда и
только тогда, когда векторы линейно
зависимы.
Неравенство
треугольника.
Из
неравенства Коши-Буняковского следует
еще одно важное неравенство, называемое
неравенством
треугольника,
Знак
равенства имеет место, если
,
т.е. если угол междуx
и
y
равен
нулю, и только в этом случае. Неравенство
треугольника для векторов – направленных
отрезков – означает, что длина стороны
треугольника меньше суммы длин остальных
сторон.
24.
Угол между двумя векторами евклидова
пространства.
2 Длина вектора. Угол между векторами.
Определим
с помощью введенного понятия скалярного
произведения длину вектора и угол между
векторами.
Определение
2.2
Длиной вектора
в
евклидовом пространстве называется
число
|
|
(4) |
Длину
вектора
будем
обозначать через.
Естественно
пожелать, чтобы угол между векторами,
длина вектора и скалярное произведение
были связаны обычным соотношением:
скалярное произведение векторов равно
произведению их длин на косинус угла
между ними. Так как в этой фразе смысл
всех слов, кроме слов «угол между
векторами», нам уже известен, то этим
предписывается следующее
Определение
2.3
Углом
между векторами
и
мы
назовем число
т.е.
положим
|
|
(5) |
Векторы
и
называютсяортогональными,
если угол между ними равен
,
т.е. если
С помощью
введенных понятий можно перенести на
евклидовы пространства ряд теорем
элементарной геометрии 2.4.
Рассмотрим
один пример. Если
и
—
ортогональные векторы, тоестественно
считать диагональю прямоугольника со
сторонамии
.
Докажем, что
т.е.
квадрат
длины диагонали прямоугольника равен
сумме квадратов длин двух его непараллельных
сторон
(теорема Пифагора).
Доказательство.
По
определению квадрата длины вектора
В силу
дистрибутивности скалярного произведения
(аксиома 3)
В силу
ортогональности векторов
и
Следовательно,
что
и требовалось доказать.
Эту
теорему можно обобщить: если
векторы
попарно
ортогональны, то
25.
Ортонормированный базис.
В евклидовом
пространстве существуют специальные,
особо удобные базисы, называемые
ортонормированными базисами. Эти
базисы играют ту же роль, что и декартов
прямоугольный базис в аналитической
геометрии. Перейдем к определению
ортонормированного базиса.Определение.Будем говорить, что n элементов e1,…,enn-мерного евклидова пространства Е
образуютортонормированный базисэтого пространства, если эти элементы
попарно ортогональны и норма каждого
из этих элементов равна единице, т. е.
если
Для того
чтобы установить корректность
сформулированного определения, следует
доказать, что входящие в это определение
элементы e1,…,enобразуют
один из базисов рассматриваемого
n-мерного пространства Е, а для этого, в
силу теоремы 2.5, достаточно доказать,
что эти элементы e1,…,enлинейно независимы, т.е. что равенство
α1e1+ α2e2+ … + αn en =
0
(4.11)
возможно,
лишь когда α1= α2= … = αn= 0.
Докажем это. Пусть k — любой из
номеров 1,2, …,n. Умножая равенство (4.11)
скалярно на элемент еkи пользуясь
аксиомами скалярного произведения и
соотношениями (4.10), мы получим, что αk=
0.
Докажем теперь следующую основную
теорему.Теорема 4.3.Во всяком
n-мерном евклидовом пространстве Е
существует ортонормированный базис.
Доказательство. Согласно
определению размерности в пространстве
Е найдется n линейно независимых элементов
f1, f2,…, fn.
Докажем,
что можно построить n элементов e1,e2
,…,en, линейно выражающихся
через f1, f2,…, fnи
образующих ортонормированный базис
(т.е. удовлетворяющих соотношениям
(4.10)).
Проведем доказательство
возможности построения таких элементов
e1,e2 ,…,enметодом
математической индукции.
Если имеется
только один элемент f1, то для
построения элемента e1с нормой,
равной единице, достаточно нормировать
элемент f1, т.е. умножить этот
элемент на число,
обратное его норме (напомним, что
среди линейно независимых элементов
f1, f2,…, fnне может быть
нулевого элемента, так что норма f1больше нуля). Мы получим при этом
элемент
e1=f1
с нормой, равной единице.
Считая,
что m — целое число, меньшее n, предположим,
что нам удалось построить m элементов
e1,e2 ,…,em, линейно
выражающихся через f1, f2,…,
fm, попарно ортогональных и имеющих
нормы, равные единице. Докажем, что к
этим элементам
e1,e2 ,…,emможно
присоединить еще один элемент em+1,
линейно выражающийся через f1,
f2,…, fm+1, ортогональный к
каждому из элементов e1,e2 ,…,emи имеющий норму, равную единице.
Убедимся
в том, что этот элемент em+1имеет
вид
em+1 =
αm+1[fm+1 — (fm+1,em),em— (fm+1,em-1),em-1— … —
(fm+1,e1)e1],
(4.12)
где αm+1— некоторое вещественное число.
В
самом деле, элемент em+1линейно
выражается через f1, f2,…,
fm+1 (в силу того, что он линейно
выражается через e1,e2 ,…,em,
fm+1, акаждый из элементов e1,e2
,…,emлинейно выражается через
f1, f2,…, fm).
Отсюда
сразу же следует, что при αm+1≠ 0
элемент em+1заведомо не является
нулевым (ибо, в противном случае, являлась
бы нулевым элементом некоторая линейная
комбинация линейно независимых элементов
f1, f2,…, fm+1 , в которой,
в силу (4.12), отличен от нуля коэффициент
при fm+1).
Далее из того, что
элементы e1,e2 ,…,emпопарно ортогональны и имеют нормы,
равные единице, и из соотношения (4.12)
сразу же вытекает, что скалярное
произведение (em+1, ek) равно
нулю для любого номера k, равного 1, 2,…,
m.
Для завершения индукции остается
доказать, что число αm+1можно
выбрать так, что норма элемента (4.12)
будет равна единице. Выше уже установлено,
что при αm+1≠ 0 элемент em+1,
а, стало быть, и элемент, заключенный в
(4.12) в квадратные скобки, не является
нулевым.
Стало быть, для того чтобы
нормировать элемент, заключенный в
квадратные скобки, следует взять число
αm+1обратным положительной норме
этого, заключенного в квадратные скобки,
элемента. При этом норма em+1будет
равна единице.
Теорема доказана.
Доказанная теорема
приводит к следующему осуществляемому
шаг за шагом алгоритму построения по
данной системе n линейно независимых
элементов f1, f2,…, fnсистемы n попарно ортогональных элементов
e1,e2 ,…,en, норма каждого
из которых равна единице:
Указанный
алгоритм обычно называют процессом
ортогонализациилинейно независимых
элементов f1, f2,…, fn.Замечание. Конечно, в каждом
n-мерном евклидовом пространстве Е
существует много ортонормированных
базисов.
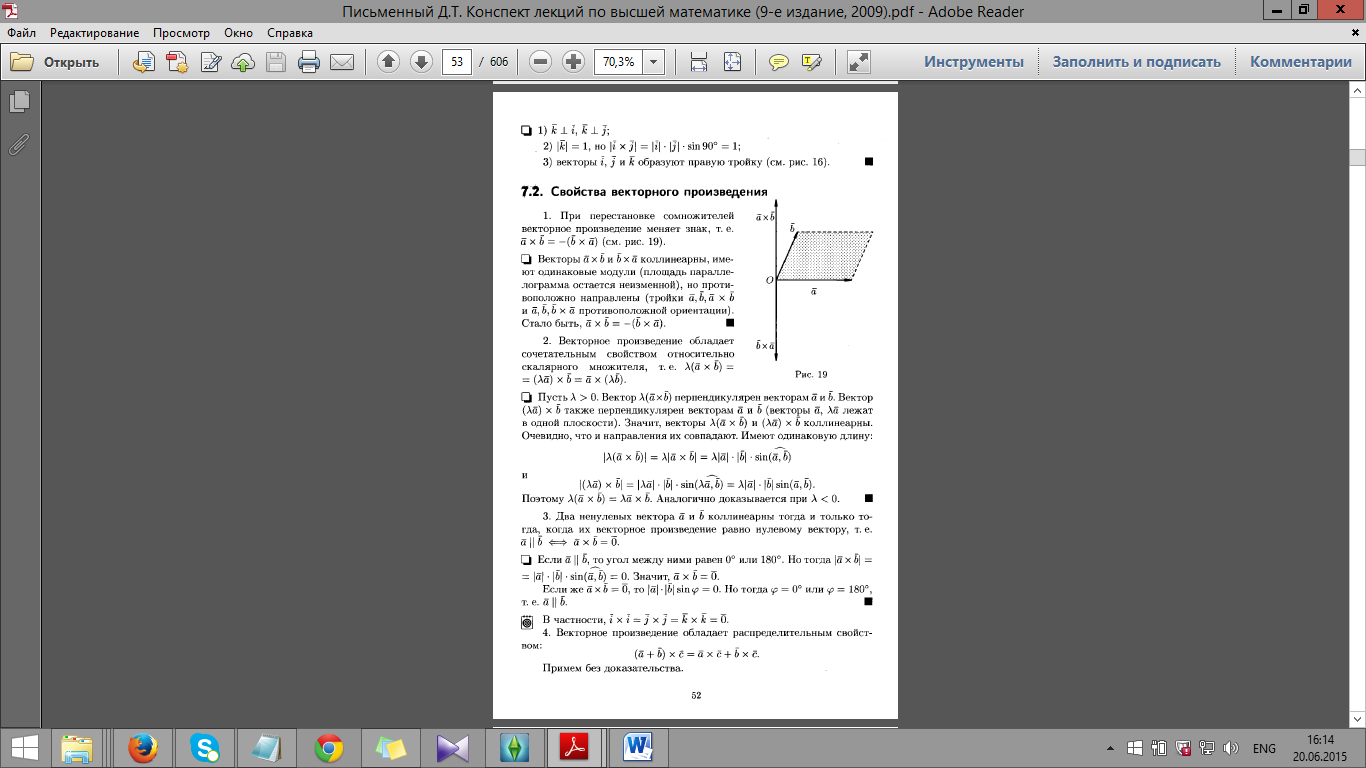
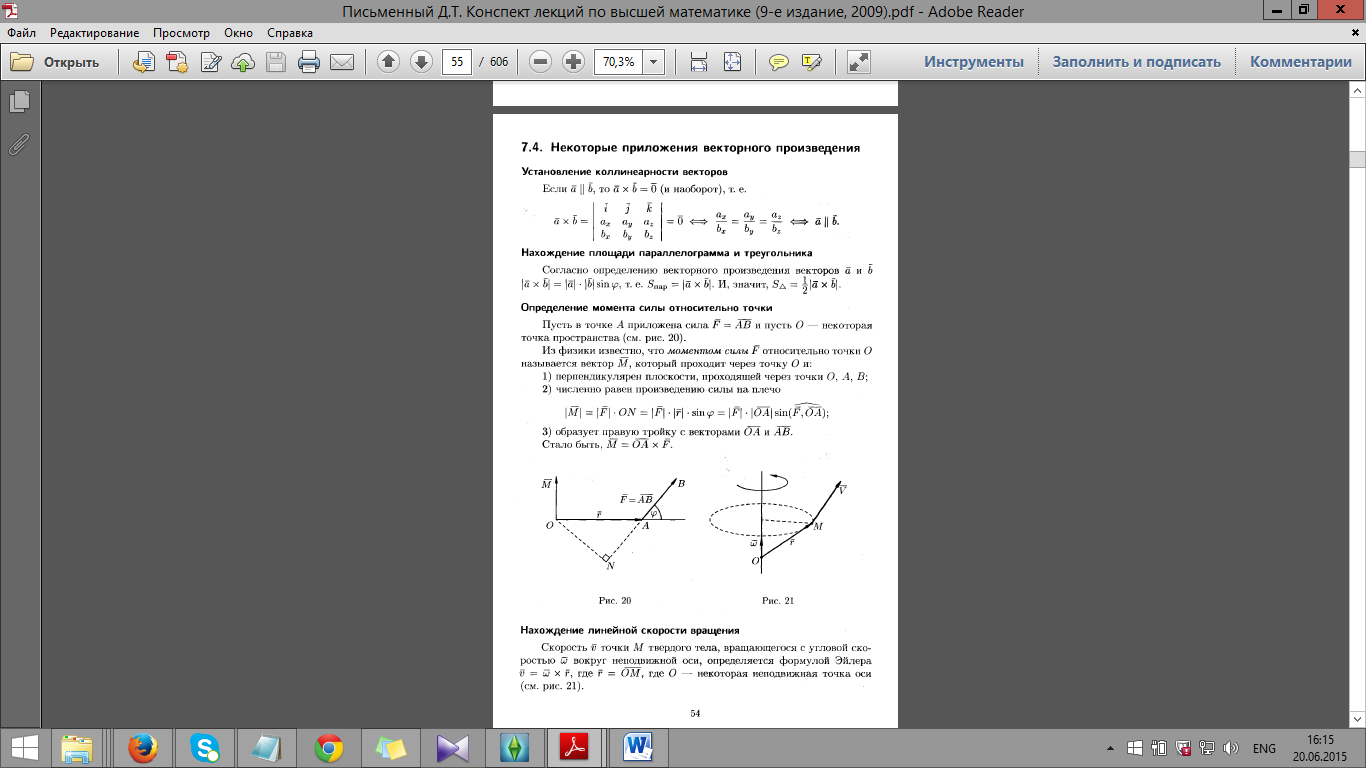
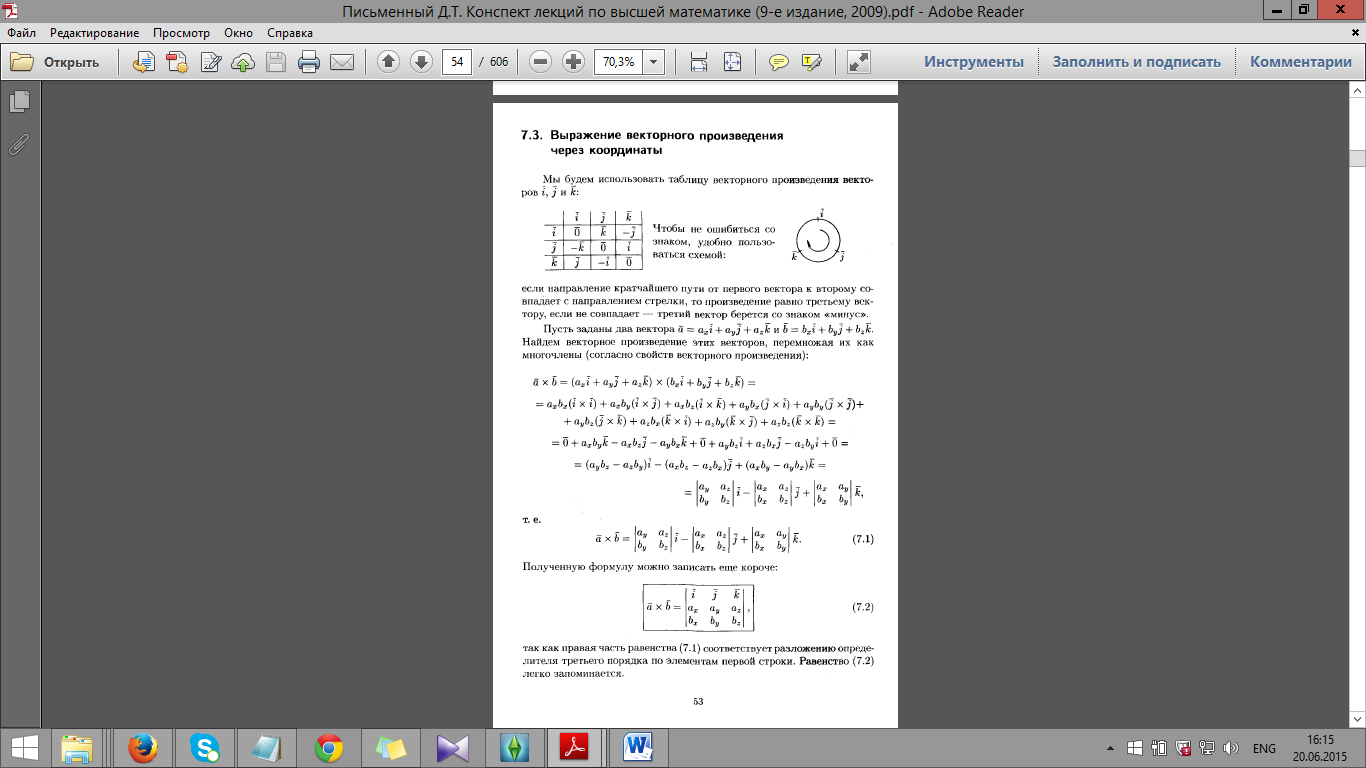
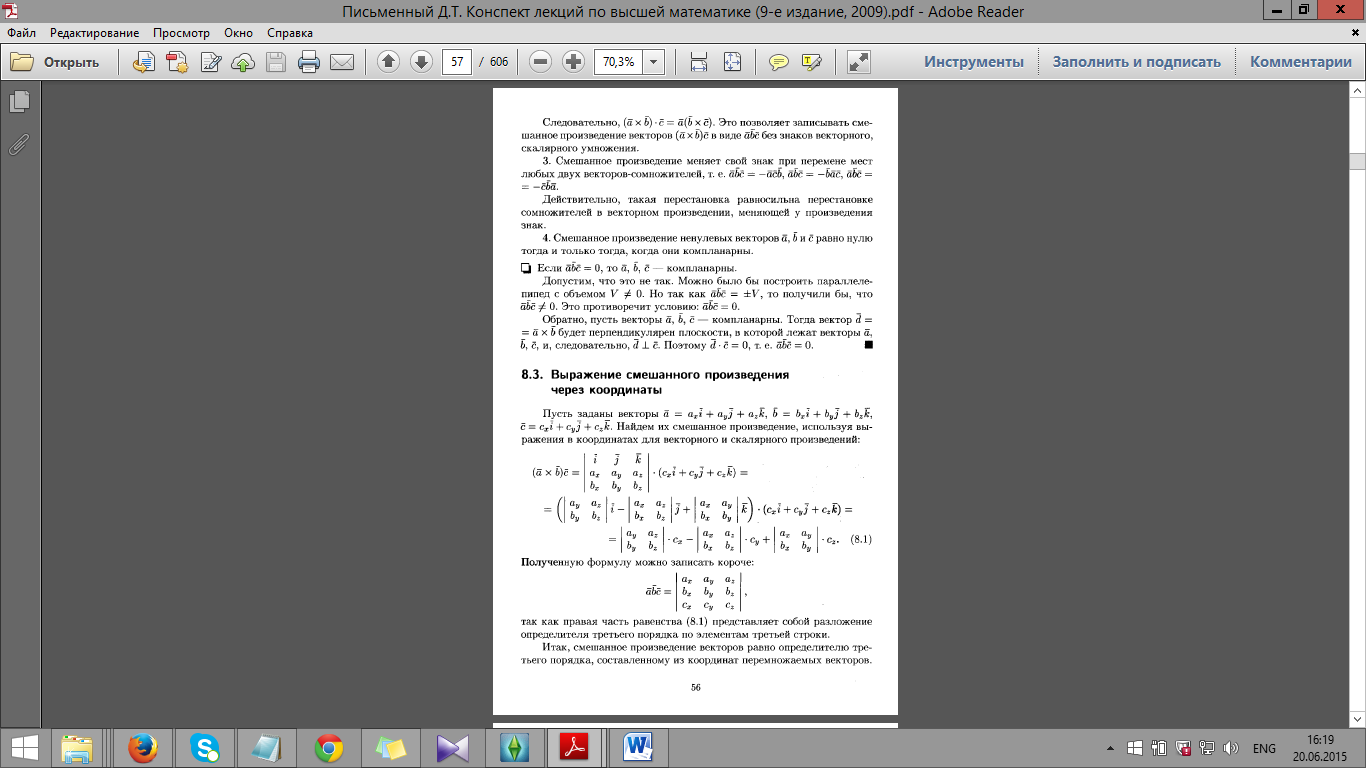
26. Векторное
произведение векторов, его свойства.
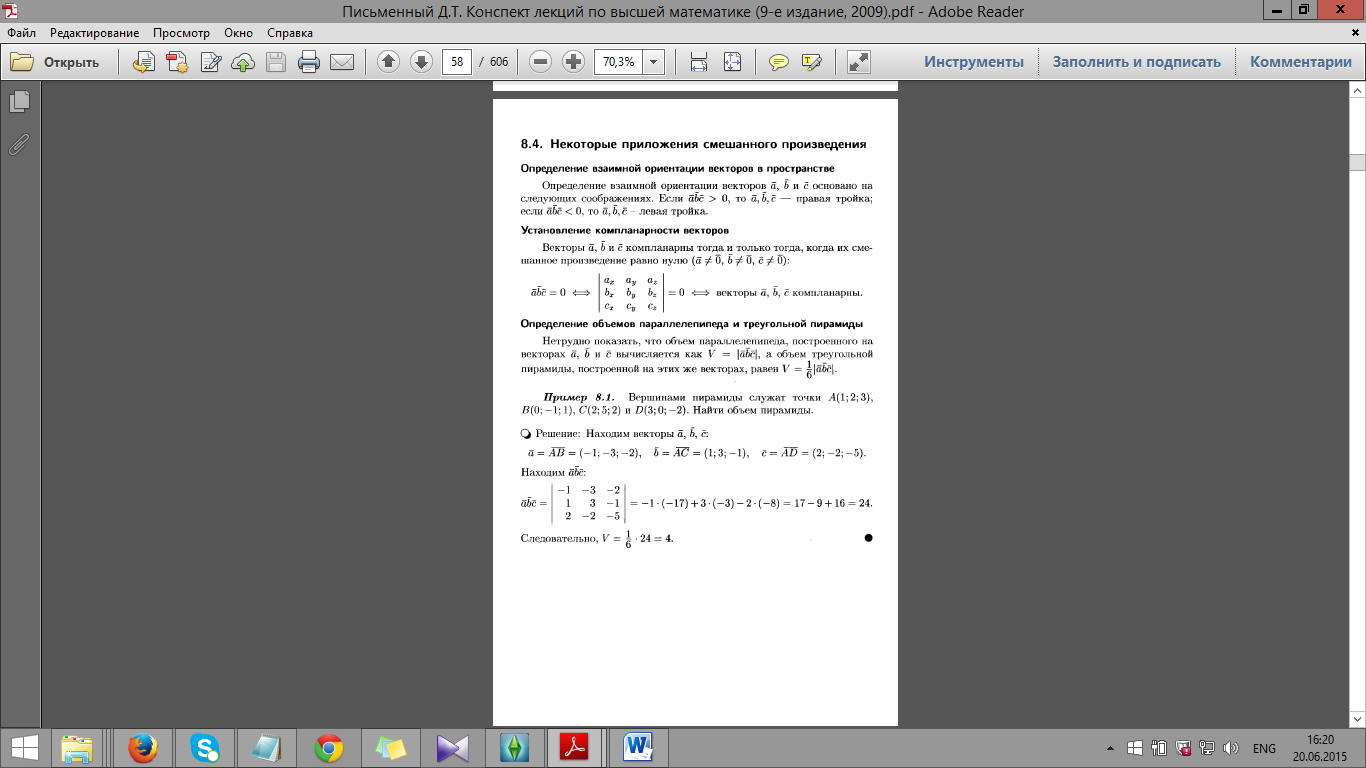
27.
Смешанное произведение векторов, его
свойства, геометрический смысл.
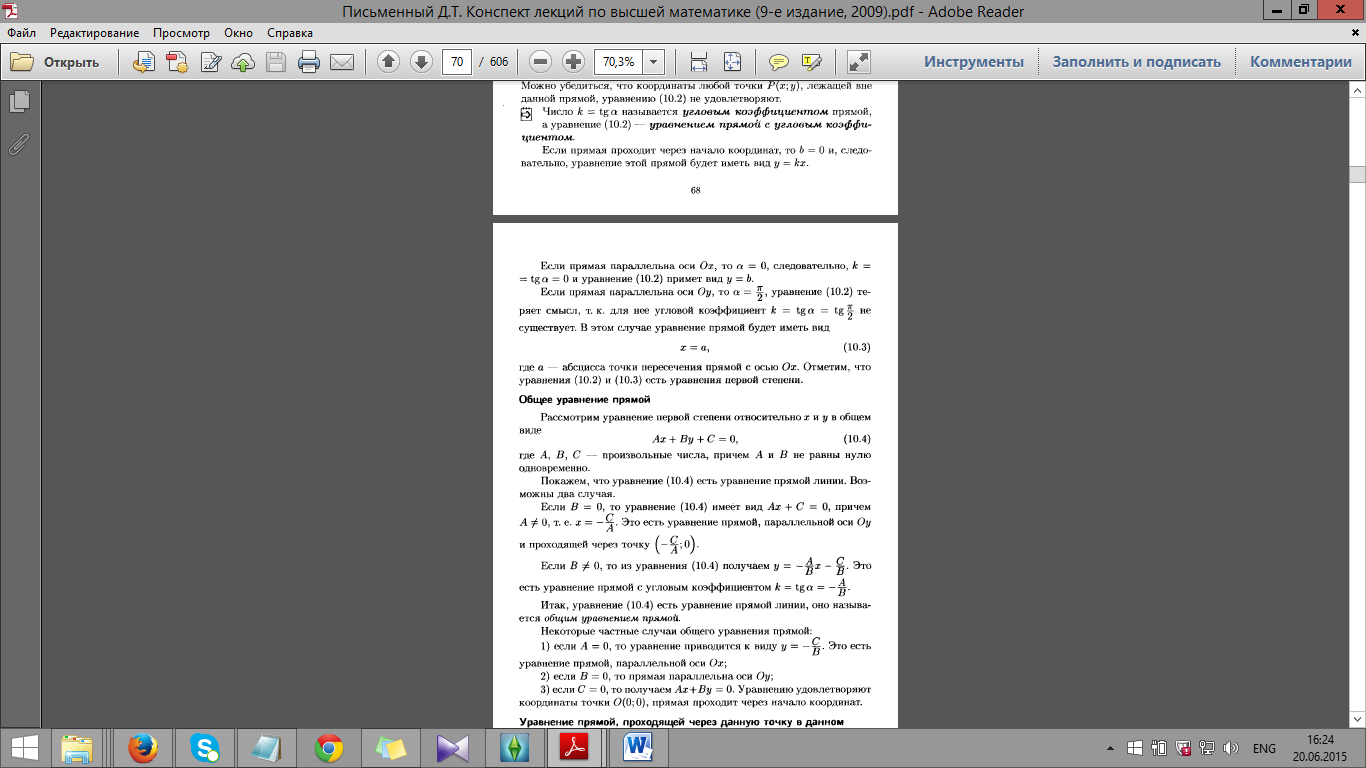
28.
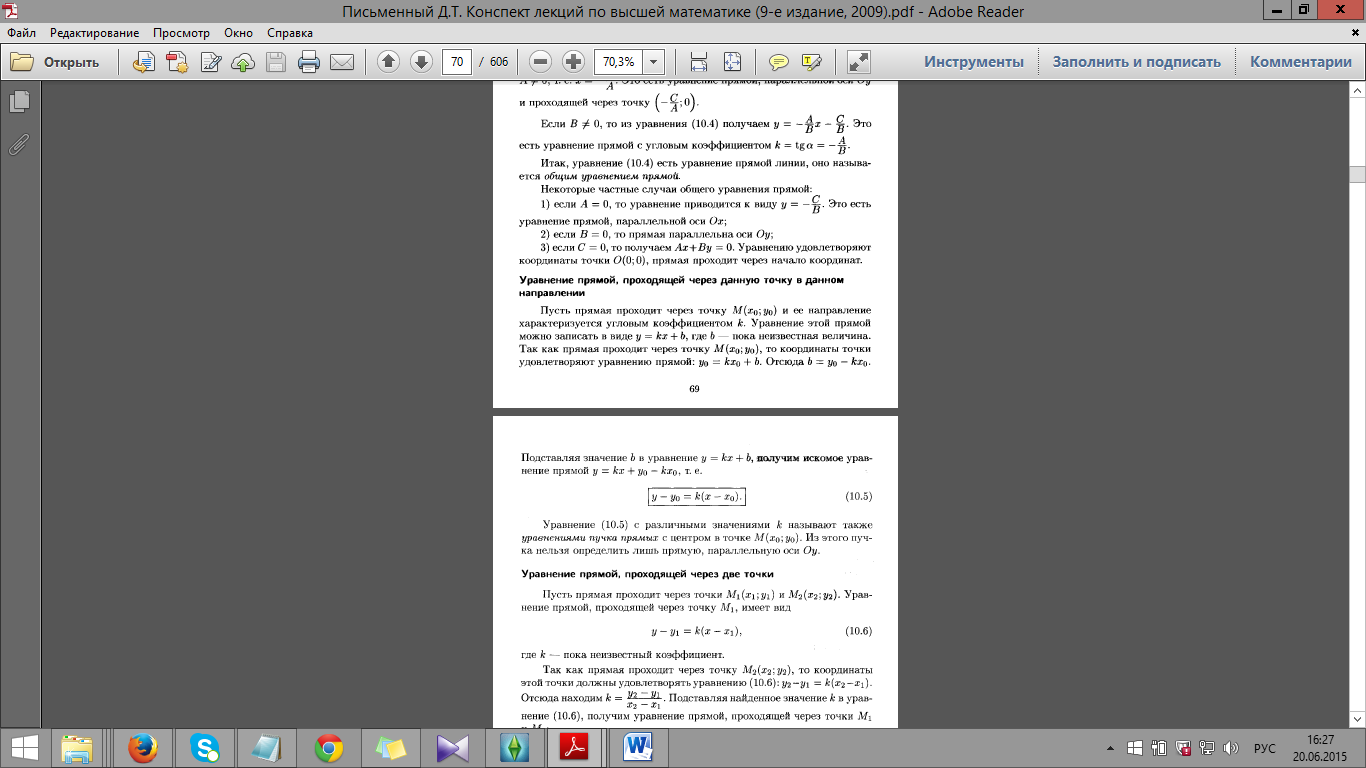
Уравнение прямой с угловым коэффициентом.
29.
Общее уравнение прямой на плоскости.
30.
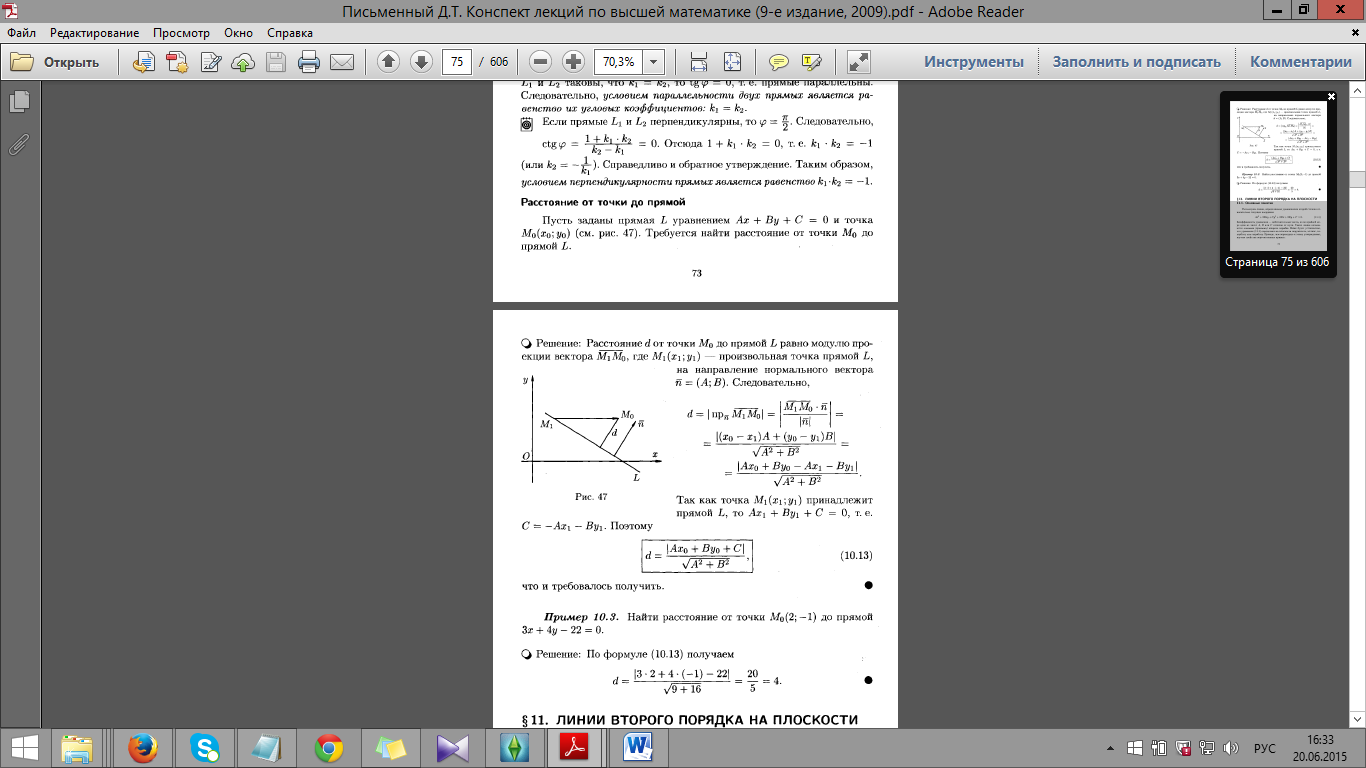
Уравнение прямой, проходящей через
точку
31.
Уравнение прямой, проходящей через две
и
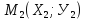
Уравнение прямой в отрезках.
32.
Уравнение прямой, проходящей через
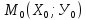
перпендикулярно
33.
Угол между двумя прямыми на плоскости.
Условия ∥,
двух
прямых.
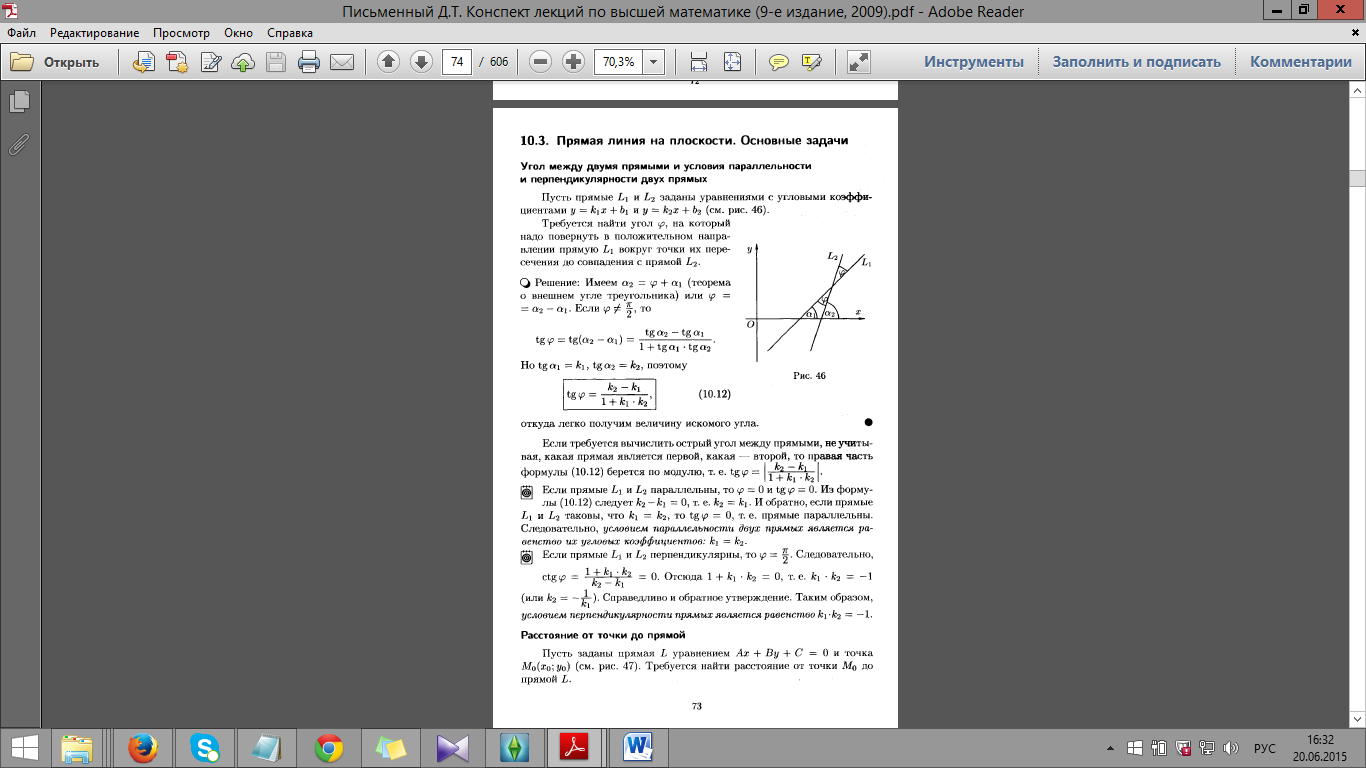
34.
Расстояние от точки
до
прямой, заданной уравнением
35.
Уравнение плоскости, проходящей через
точку,
перпендикулярно
вектору
36.
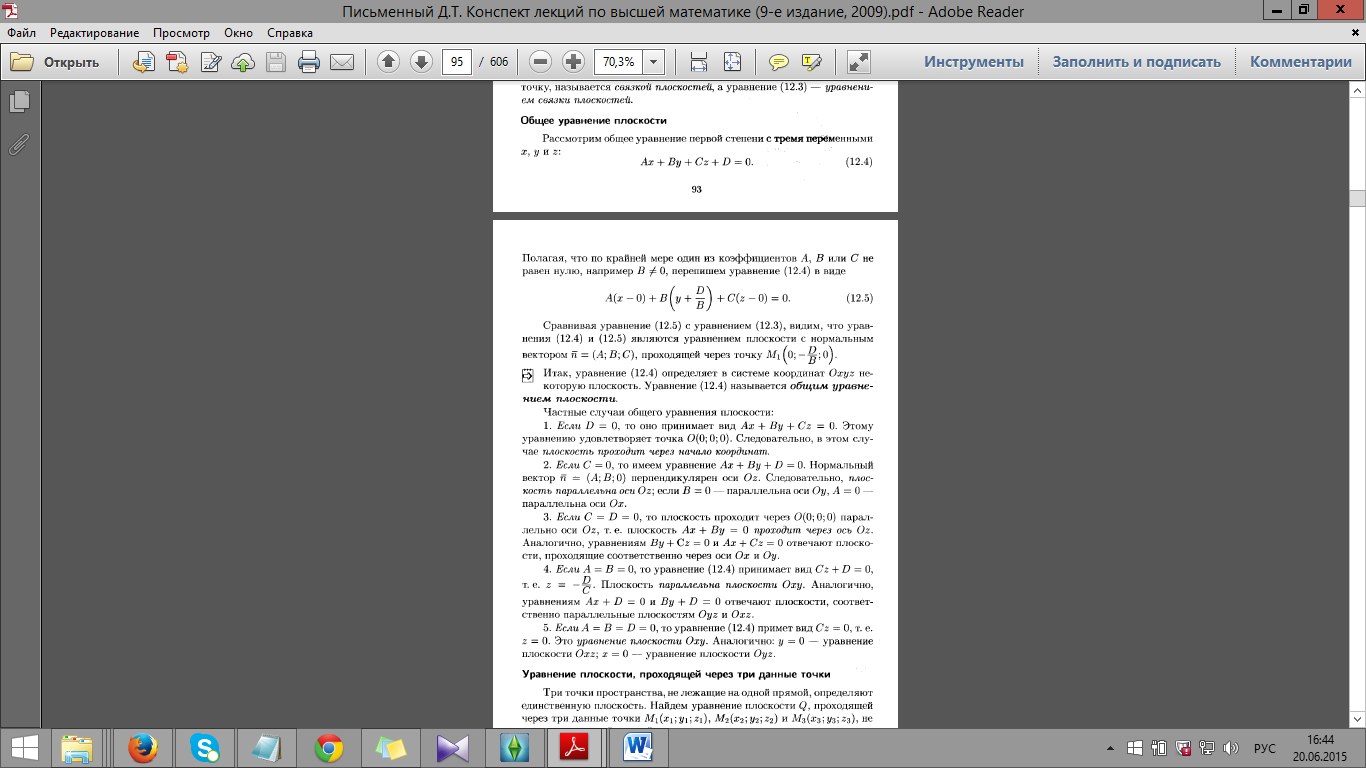
Общее уравнение плоскости.
37.
Уравнение плоскости, проходящей через
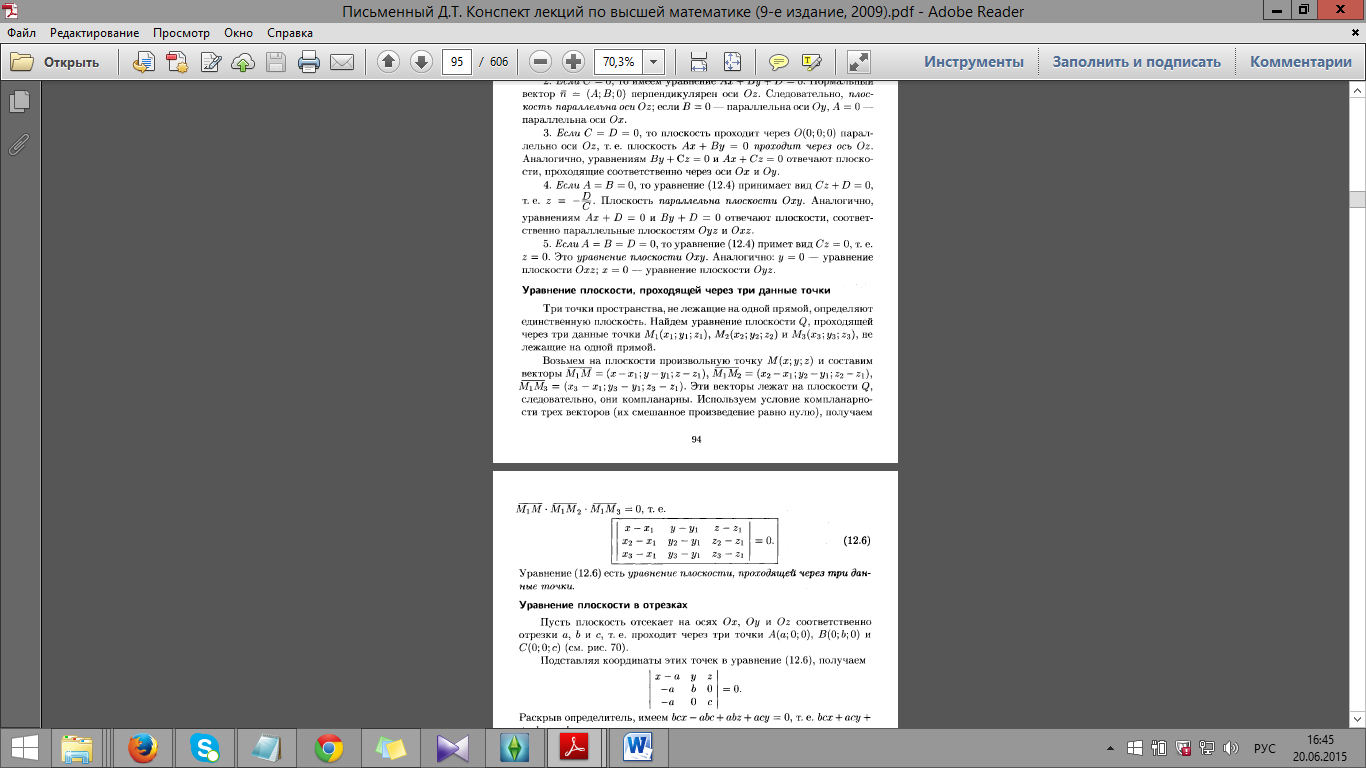
3 точки, не лежащие на одной прямой.
38.
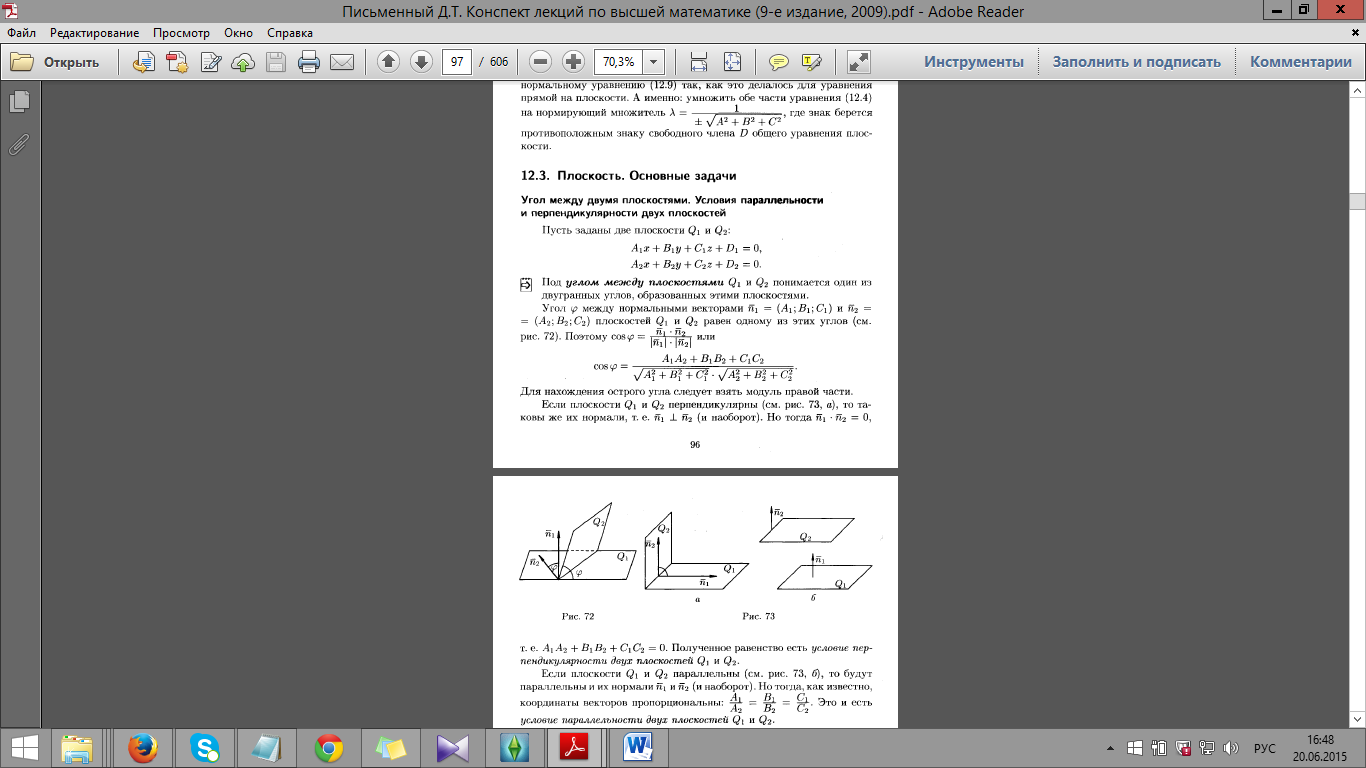
Угол между двумя плоскостями.
39.
Условия ∥,
двух
плоскостей.
40.
Расстояние от точки
до
плоскости, заданной уравнением
41.
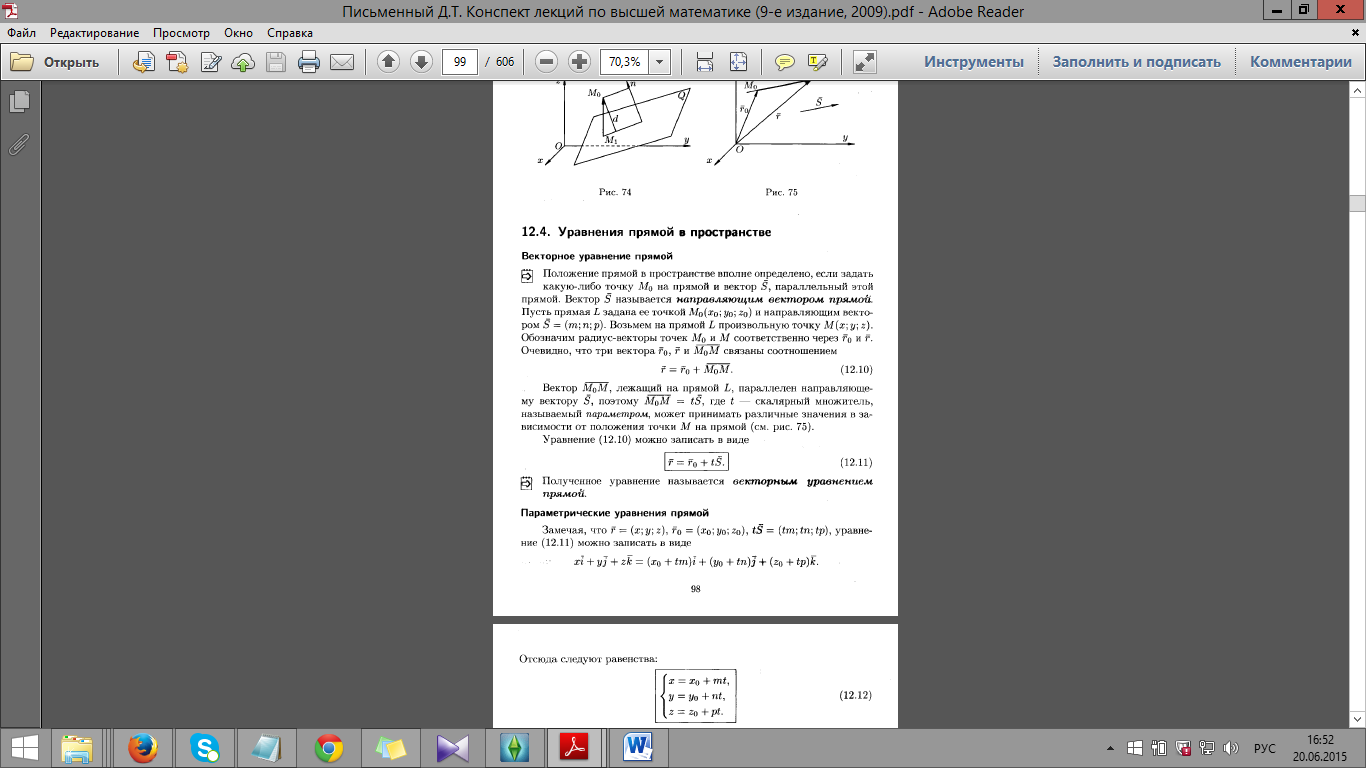
Векторное уравнение прямой в пространстве.
42.
Параметрические уравнения прямой в
пространстве.
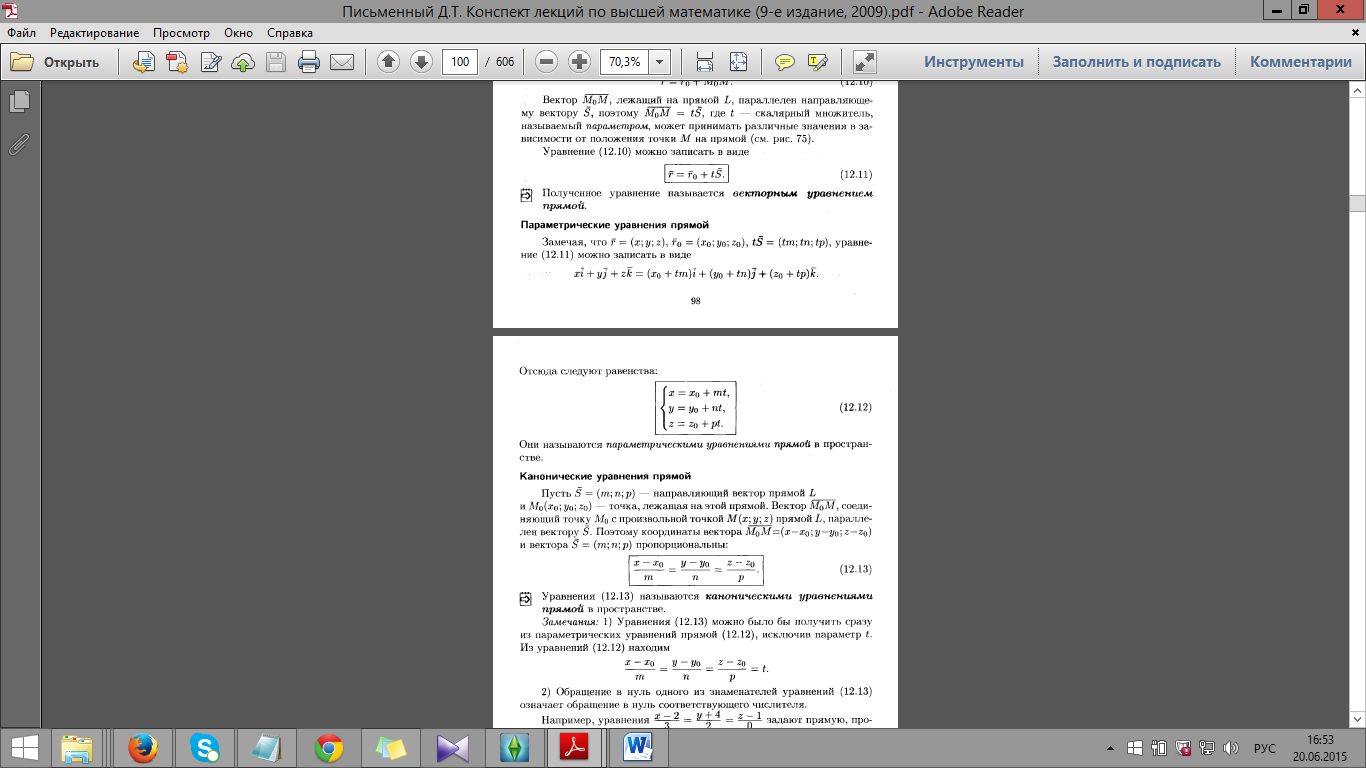
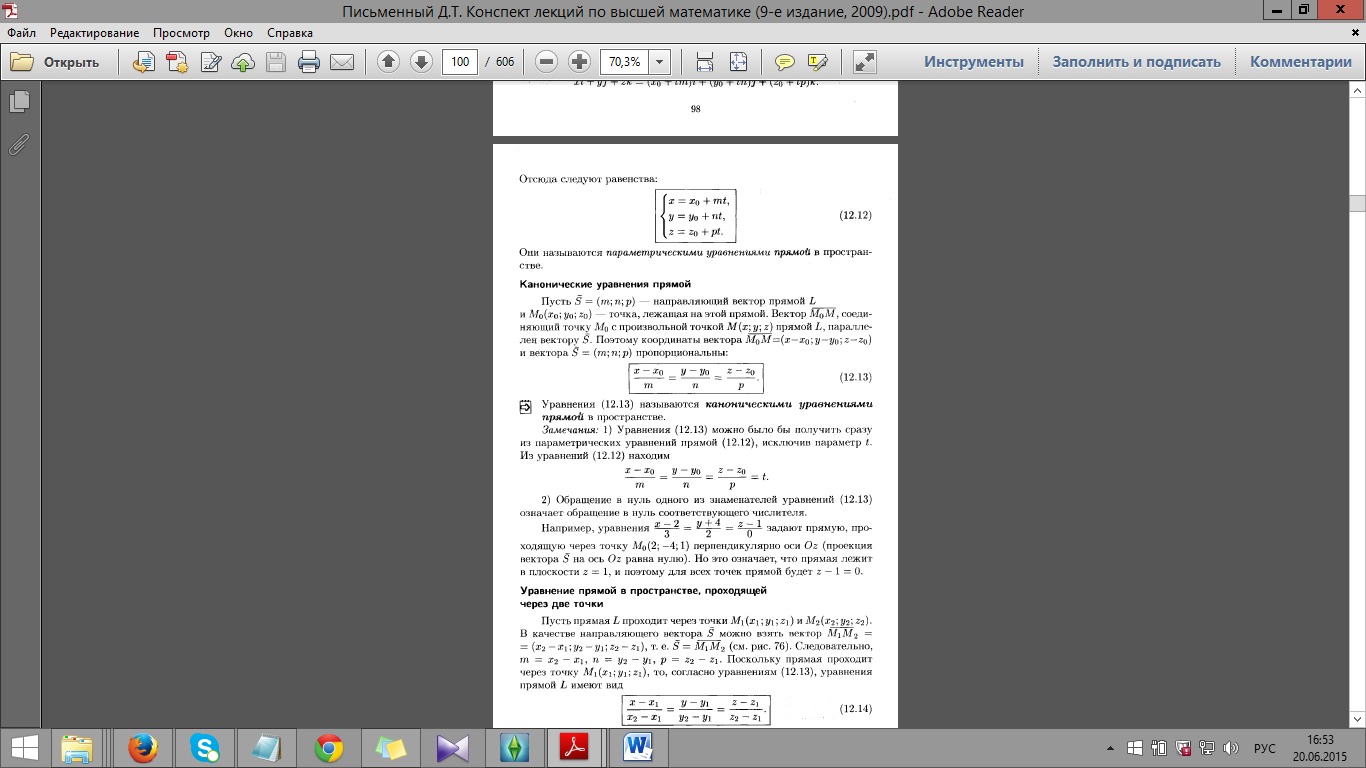
43.
Канонические уравнения прямой в
пространстве.
44.
Уравнение прямой, проходящей через две
точки
45)
46)
47)
48)
49,50)
51)
52)
55)
56)
57)
58)
59)
60)
61)
62)
63)
64)
65,66)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Норма (модуль, длина) вектора
В пространстве V каждому вектору x∈V ставим в соответствие некоторое неотрицательное число 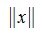
тогда и только тогда, когда x=0.
.
(неравенство треугольника).
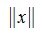
Примеры норм в линейных пространствах
1. max-норма, или m – норма:
2. l-норма:
3. Евклидова норма:
Пример вычисления нормы (длины, модуля) вектора
Вычислим нормы вектора
1. m-норма:
2. l-норма:
3. Евклидова норма:
|
|
Линейная алгебра для исследователей данных
Время на прочтение
5 мин
Количество просмотров 14K

«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».
Ирвинг Капланский
Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.
В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.
Произведения векторов
Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy
называется следующее вещественное число:
Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество
.
Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть
След
Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:
След обладает следующими свойствами:
-
Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.
-
Для любых матриц A,B ∈ ℝⁿˣⁿ: tr(A + B) = trA + trB.
-
Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.
-
Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.
-
Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).
Нормы
Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:
Заметим, что ‖x‖₂²=xᵀx.
Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:
-
Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).
-
f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).
-
Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).
-
Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)
Другими примерами норм являются норма l₁
и норма l∞
Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как
Нормы также могут быть определены для матриц, например норма Фробениуса:
Линейная независимость и ранг
Множество векторов {x₁, x₂, …, xₙ} ⊂ ℝₘ называют линейно независимым, если никакой из этих векторов не может быть представлен в виде линейной комбинации других векторов этого множества. Если же такое представление какого-либо из векторов множества возможно, эти векторы называют линейно зависимыми. То есть, если выполняется равенство
для некоторых скалярных значений α₁,…, αₙ-₁ ∈ ℝ, то мы говорим, что векторы x₁, …, xₙ линейно зависимы; в противном случае они линейно независимы. Например, векторы
линейно зависимы, так как x₃ = −2xₙ + x₂.
Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.
Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:
-
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.
-
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).
-
Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).
-
Для любых матриц A,B ∈ ℝᵐˣⁿ: rank(A + B) ≤ rank(A) + rank(B).
Ортогональные матрицы
Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м
атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.
Непосредственно из определений ортогональности и нормированности следует, что
Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n < m), но ее столбцы являются ортонормированными, то UᵀU = I, но UUᵀ ≠ I. Поэтому, говоря об ортогональных матрицах, мы будем по умолчанию подразумевать квадратные матрицы.
Еще одно удобное свойство ортогональных матриц состоит в том, что умножение вектора на ортогональную матрицу не меняет его евклидову норму, то есть
для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.
Область значений и нуль-пространство матрицы
Линейной оболочкой множества векторов {x₁, x₂, …, xₙ} является множество всех векторов, которые могут быть представлены в виде линейной комбинации векторов {x₁, …, xₙ}, то есть
Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,
Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть
Квадратичные формы и положительно полуопределенные матрицы
Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:
Заметим, что
-
Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как
(или просто A > 0), а множество всех положительно определенных матриц часто обозначают
.
-
Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как
(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают
.
-
Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной
-
, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx < 0.
-
Далее, симметричная матрица A ∈ 𝕊ⁿ называется отрицательно полуопределенной (
), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.
-
Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что
и
.
Собственные значения и собственные векторы
Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство
На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).
Перевод статьи был подготовлен в преддверии старта курса «Математика для Data Science». Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.
-
ЗАПИСАТЬСЯ НА ДЕМОУРОК
Евклидова норма в двух реальных измерениях
Евклидова норма , стандартная норма или стандарт 2 находится в математике , обычно используемой векторную норму . В двух- и трехмерном евклидовом пространстве евклидова норма соответствует описательной длине или величине вектора и может быть вычислена с помощью теоремы Пифагора . В более общем смысле, евклидова норма также определена для вещественных и комплексных векторных пространств любой конечной размерности, а затем является нормой, полученной из стандартного скалярного произведения .
Как норма, индуцированная скалярным произведением , она имеет ряд других свойств в дополнение к трем аксиомам нормы , например, справедливость неравенства Коши-Шварца и уравнения параллелограмма , а также инвариантность относительно унитарных преобразований . Для ортогональных векторов сама евклидова норма удовлетворяет более общей форме теоремы Пифагора.
Такие термины, как евклидово расстояние и евклидова топология, получены из евклидовой нормы . Это может быть обобщена на бесконечномерных векторных пространствах, например , в пространствах последовательностей через ℓ 2 нормы и функциональных пространств через L 2 нормы .
Определения
Реальные векторы в двух и трех пространственных измерениях
Вектор в евклидовой плоскости может быть о его компонентах и в декартовой системе координат с помощью представляющих. Длиной или величина вектора осуществляется количество штрихов характеризуются вектором и могут с помощью теоремы Пифагора пути

рассчитываться. В трехмерном евклидовом пространстве длина вектора становится аналогичной двумерному случаю, когда
определяется. В физике количества вектора иногда отличающийся тем , что , опуская количество штрихов и вектор стрелка: . Векторы выделены жирным шрифтом в тексте, иногда просто Смелый опущено: . Естественная длина вектора также называется евклидовой нормой или 2-нормой вектора и, чтобы отличать ее от других векторных норм , обозначается символом или .
Действительные векторы конечной размерности
Если векторное пространство вещественные мерные векторы , то евклидова норма вектора определяется как корень из суммы квадратов компонент вектора:
-
.
Для одномерного вектора абсолютное значение действительного числа является частным случаем, а для двух- или трехмерного вектора его длина на плоскости или в пространстве получается, как в предыдущем разделе. Евклидова норма — это стандартное скалярное произведение двух вещественных векторов
полученный, потому что он применяется
-
.
Комплексные векторы конечной размерности
Если теперь векторное пространство комплексных -мерных векторов , то евклидова норма вектора определяется как корень из суммы квадратов абсолютных значений компонент вектора:
-
.
Столбцы суммы в определении не должны быть пропущены. Частный случай для одномерного вектора — это модуль комплексного числа, соответствующий длине его вектора в гауссовой плоскости . Евклидова норма — это стандартное скалярное произведение двух комплексных векторов
индуцированная, где сопряженное комплексного числа . Он снова применяется
-
.
Примеры
Евклидова норма действительного вектора равна
-
.
Евклидова норма комплексного вектора равна
-
.
характеристики
Далее предполагается общий случай вещественных или комплексных векторов конечной размерности с или . Следующие свойства являются лишь частными случаями соответствующих свойств общих норм, индуцированных скалярным произведением .
Аксиомы нормы
Евклидова норма удовлетворяет трем аксиомам нормы . определённость
означает, что если длина вектора равна нулю , это должен быть нулевой вектор . Абсолютная однородность
утверждает, что, когда компоненты вектора умножаются на число , длина вектора изменяется с величиной этого числа. Неравенство треугольника ( субаддитивность )
наконец, заявляет, что длина суммы двух векторов не больше суммы двух длин. Равенство применяется именно тогда, когда два вектора указывают в одном направлении. Доказательство неравенства треугольника основано на неравенстве Коши-Шварца
-
.
Сфера единства и сфера единства
Единичная сфера (синий) и открытая единичная сфера (красный) в двух измерениях
Евклидова норма является специальной р -норма для выбора и, следовательно , также называется 2-нормой. Единичная сфера евклидовой нормы, то есть множество
Векторы со стандартным топливом имеют два реальных измерения в форме круга , в трех реальных измерениях форму сферической поверхности и в общих размерах форму шара . Аналогично этому называют сумму
-
или же.
замкнутая или открытая единичная сфера евклидовой нормы. Он имеет форму круглого диска в двух реальных измерениях и форму сферы в трех и более измерениях . Евклидова норма также может быть определена как функционал Минковского, используя его единичную сферу .
Уравнение параллелограмма
Евклидова норма достаточна для всех векторов в параллелограмм уравнения
и является единственной p -нормой с этим свойством, см. также теорему Жордана-фон Неймана .
Унитарная инвариантность
Евклидова норма — также как единственная p- норма — инвариантна относительно унитарных преобразований . Поэтому, если унитарная матрица (в комплексном случае) или ортогональная матрица (в реальном случае) , то применяется
-
,
как насчет свойства смещения стандартного скалярного произведения
следует. Евклидова норма не меняется при унитарных преобразованиях. Для вещественных векторов такими преобразованиями являются, например, вращения вектора вокруг нулевой точки . Это свойство проявляется, например, при численном решении линейных задач наименьших квадратов с использованием метода наименьших квадратов для QR-разложений .
Производные термины
угол
Используя стандартное скалярное произведение и евклидову норму, угол между двумя действительными векторами можно определить как
Быть определенным. При таком определении угла получается следующее обобщение закона косинуса :
-
.
Существует ряд различных определений углов между комплексными векторами. В общем, два вектора называются ортогональными, если они являются скалярным произведением . Затем к ортогональным векторам применяется более общая форма теоремы Пифагора.

-
.
Евклидово расстояние
Отношения между скалярным произведением, нормой, метрикой и топологией
Кроме того, с помощью евклидовой нормы, метрика может быть получена путем вычисления разности между двумя векторами
-
,
евклидовой метрики . Метрика позволяет измерить расстояние между двумя векторами. Поскольку евклидова метрика происходит от нормы, она инвариантна относительно сдвигов .
Евклидова топология
Кроме того, топология , евклидовая топология, может быть определена с помощью евклидовой нормы или метрик на векторном пространстве . Это стандартная топология, которая порождается системой множеств открытых сфер
-
,
которые содержат все векторы на расстоянии меньше, чем от данного вектора . Об этом ε-шарах можно тогда сказать, как условия непрерывности и предела, определить: например, стремится к последовательности векторов тогда и только тогда, когда к пределу , если для действительного. Фактически, все нормы в векторном пространстве эквивалентны евклидовой норме и, следовательно, порождают ту же топологию.
Обобщения
Если вы рассматриваете матрицу с действительными или комплексными элементами как соответственно длинный вектор, евклидова норма также может быть определена для матриц и тогда называется нормой Фробениуса . Евклидова норма также может быть обобщена на бесконечномерные векторные пространства над действительными или комплексными числами, а затем частично имеет свои собственные имена. Наиболее важные обобщения заключаются в следующем.
ℓ 2 стандартных
ℓ 2 -норме является обобщением евклидовой нормы в пространстве последовательностей квадратично суммируемых последовательностей . Вот только конечная сумма заменяется на Бесконечного и ℓ 2 норма затем дается как

-
.
Пространство является гильбертово пространство со скалярным произведением двух последовательностей
-
.
L 2 стандарт
Кроме того, евклидова норма может быть обобщена на функциональное пространство функций, интегрируемых на множестве квадратично , что происходит в два этапа. Во-первых, -норма является квадратичной интегрируемой по Лебегу функцией при

-
,
определяется, в результате чего по сравнению с ℓ 2 нормы только сумма была заменена интегралом. Изначально это только полунорма , поскольку не только нулевая функция, но и все функции, которые отличаются от нулевой функции только в терминах набора с нулевой мерой Лебега, интегрируются в ноль. Поэтому, принимая во внимание количество классов эквивалентности функций , которые почти везде одинаковы, и получает на этом L 2 -пространстве L 2 нормы по
-
.
Пространство представляет собой гильбертово пространство со скалярным произведением двух функций
-
.
Его также можно обобщить с меры Лебега на общие меры .
Общие векторные пространства
В более общем смысле евклидова норма может быть определена в любых бесконечномерных векторных пространствах через связанный базис Гамеля . Если такая Хамель основа имеет , где множество индексов , то каждый вектор может быть представлен в виде линейной комбинации с коэффициентами (здесь лишь конечное число коэффициентов могут отличаться от 0). Евклидова норма вектора тогда определяется как
и тем самым из скалярного произведения
индуцированный для векторов .
Иногда норма, индуцированная произвольным скалярным произведением на вещественном пространстве скалярных произведений, также называется евклидовой нормой.
литература
- Герберт Amann, Joachim Эшер : анализ I . Биркхойзер, Базель 2006 г., ISBN 3-7643-7755-0 .
- Альбрехт Бойтельшпахер : линейная алгебра . 6-е издание. Vieweg, 2003 г., ISBN 3-528-56508-X .
- Бронштейн и др.: Математика в мягкой обложке . 7-е издание. Харри Дойч, 2008, ISBN 978-3-8171-2007-9 .
- Герд Фишер: линейная алгебра . 9-е издание. vieweg, ISBN 3-528-57217-5 .
веб ссылки
- Эрик В. Вайсштейн : L ^ 2 норма . В: MathWorld (английский).
Индивидуальные доказательства
- ↑ б Amann, Эшер: анализ I . 2006, стр. 169 .
- ^ Клаус Шарнхорст: Углы в сложных векторных пространствах . В: Acta Applicandae Math. Volume. 69 , 2001, с. 95-103 .
- ↑ Scheja, Storch: Учебник алгебры: включая линейную алгебру . 2-й том. Vieweg, 1988, стр. 465 .
- ^ Бронштейн и др.: Taschenbuch der Mathematik . 2008, стр. 368 .
- ↑ Beutelspacher: Linear Algebra . 2003, стр. 259 .
Евклидовы пространства
Определение евклидова пространства
Вещественное линейное пространство называется евклидовым, если каждой паре элементов
этого пространства поставлено в соответствие действительное число
, называемое скалярным произведением, причем это соответствие удовлетворяет следующим условиям:
В скалярном произведении вектор
— первый, а вектор
— второй сомножители. Скалярное произведение
вектора
на себя называется скалярным квадратом. Условия 1–4 называются аксиомами скалярного произведения. Аксиома 1 определяет симметричность скалярного произведения, аксиомы 2 и 3 — аддитивность и однородность по первому сомножителю, аксиома 4 — неотрицательность скалярного квадрата
.
Линейные операции над векторами евклидова пространства удовлетворяют аксиомам 1–8 линейного пространства, а операция скалярного умножения векторов удовлетворяет аксиомам 1–4 скалярного произведения. Можно сказать, что евклидово пространство — это вещественное линейное пространство со скалярным произведением. Поскольку евклидово пространство является линейным пространством, на него переносятся все понятия, определенные для линейного пространства, в частности, понятия размерности и базиса.
Простейшие следствия из аксиом скалярного произведения
1. Аксиомы 2 и 3 скалярного произведения можно заменить одним условием линейности скалярного произведения по первому сомножителю:
2. Условие линейности скалярного произведения по первому сомножителю в силу симметричности (аксиома 1) справедливо и для второго сомножителя, т.е. скалярное произведение линейно по любому сомножителю.
3. Линейность скалярного произведения по любому сомножителю распространяется на линейные комбинации векторов:
для любых векторов и действительных чисел
.
4. Если хотя бы один сомножитель — нулевой вектор, то скалярное про изведение равно нулю:
Действительно, представим нулевой вектор в виде , где
— произвольный вектор из
. Тогда из аксиомы 3 получаем:
Неравенство Коши-Буняковского
Для любых векторов и
евклидова пространства
выполняется неравенство Коши-Буняковского:
(8.25)
В самом деле, для любого действительного числа и любых векторов
и
справедливо неравенство:
Следовательно, дискриминант квадратного трехчлена (переменной ) не больше нуля, т.е.
. Отсюда следует (8.25). Заметим, что равенство нулю дискриминанта возможно только в случае существования такого корня
, для которого
. Это условие равносильно коллинеарности векторов
и
. Напомним, что ненулевые векторы
и
называются коллинеарными, если существует такое число
, что
. Нулевой вектор считается коллинеарным любому вектору. Неравенство Коши-Буняковского выполняется как равенство только для коллинеарных векторов и как строгое неравенство для неколлинеарных.
Примеры евклидовых пространств
Определяя для элементов линейного пространства операцию скалярного произведения, получаем евклидово пространство. Если скалярное произведение можно ввести разными способами в одном и том же линейном пространстве, то и получаемые евклидовы пространства будут разными. Приведем примеры евклидовых пространств, соответствующих рассмотренным ранее примерам линейных пространств.
1. В нулевом линейном пространстве скалярное произведение можно определить единственным способом, положив
. Аксиомы скалярного произведения при этом выполняются.
2. В пространствах векторы (свободные или радиус- векторы) рассматриваются как направленные отрезки. В курсе элементарной геометрии вводятся понятия длины вектора и величины угла между векторами, а затем определяется скалярное произведение:
. Аксиомы 1—4 для этого скалярного произведения выполняются. Поэтому пространства
являются евклидовыми. Неравенство Коши-Буняковского в этом пространстве означает, что
. Геометрический смысл: длина проекции не превосходит длины наклонной (катет короче гипотенузы).
3. В пространстве скалярное произведение столбцов
и
можно задать формулой:
(8.26)
где — квадратная симметрическая положительно определенная матрица n-го порядка. Проверим выполнение аксиом 1-4. Аксиома 1 (симметричность) выполняется в силу симметричности матрицы
, поскольку число при транспонировании не изменяется, т.е.
. Свойство линейности по первому сомножителю (см. п.1 простейших следствий из аксиом) для (8.26) выполняется:
Значит, выполняются аксиомы 2 и 3. Аксиома 4 также выполняется, так как квадратичная форма положительно определенная. Таким образом, пространство
со скалярным произведением (8.26) является евклидовым пространством. В частности, если в качестве матрицы
взять единичную матрицу, формула (8.26) примет вид:
(8.27)
Это скалярное произведение считается стандартным в пространстве . Неравенство (8.25) Коши-Буняковского в «-мерном арифметическом пространстве
со скалярным произведением (8.27) трансформируется в неравенство Коши:
Приведем примеры формул, которые не задают скалярного произведения в
1) — аксиомы 1, 4 выполняются, а аксиомы 2, 3 — нет;
2) — аксиомы 1, 2, 3 выполняются, а аксиома 4 — нет.
4. Пространство решений однородной системы
линейных уравнений со скалярным произведением (8.27) является евклидовым пространством.
5. В пространстве действительных функций, определенных и непрерывных на данном промежутке
, скалярное произведение можно задать формулой:
(8.28)
В самом деле, аксиомы 1, 2, 3 для (8.28) выполняются в силу свойств определенного интеграла. Проверим выполнение аксиомы 4. Для ненулевой функции
, так как, если в какой-нибудь точке
функция
, то в силу непрерывности она отлична от нуля в некоторой окрестности точки
, целиком лежащей в интервале
. Поэтому интеграл от
в этой окрестности больше нуля.
Таким образом, пространство со скалярным произведением (8.28) является евклидовым. Скалярное произведение (8.28) считается стандартным в пространстве
. Для разрывных функций формула (8.28) не определяет скалярного произведения, так как нарушается аксиома 4. Неравенство (8.25) Коши-Буняковского в пространстве
со скалярным произведением (8.28) трансформируется в неравенство Шварца:
6. В пространстве многочленов с действительными коэффициентами скалярное произведение можно задать формулой (8.28), так как многочлены являются непрерывными функциями.
В пространстве многочленов степени не выше, чем
, зададим скалярное произведение многочленов
и
формулой:
(8.29)
Выражение в правой части (8.29) симметрично для коэффициентов двух многочленов, поэтому аксиома 1 выполняется. Аксиомы 2, 3 следуют из линейности выражения по коэффициентам каждого многочлена. Проверим аксиому 4. Запишем скалярный квадрат . Заметим, что
только при
, т.е. в случае нулевого много члена
. Следовательно, формула (8.29) задает скалярное произведение в пространстве
.
В пространстве определим произведение формулой:
(8.30)
В силу симметричности и линейности правой части (8.30) по значениям многочленов, заключаем, что аксиомы 1-3 выполняются. Проверим выполнение аксиомы 4. Приравняв скалярный квадрат нулю, получаем
Это возможно только при . Из этих трех равенств не следует, однако, что многочлен
нулевой. Например, ненулевой многочлен
удовлетворяет трем равенствам. Следовательно, в пространстве
формула (8.30) не задает скалярного произведения. Напротив, в пространстве
формула (8.30) определяет скалярное произведение. Так как из равенств
следует, что многочлен степени не выше второй тождественно равен нулю.
Длина вектора и угол между векторами в евклидовом пространстве
Длиной (нормой) вектора в евклидовом пространстве
называется число
.
Имея в виду обозначение, длину называют также модулем вектора. Рассматривается арифметическое значение квадратного корня, которое определено для любого вектора из-за неотрицательности подкоренного выражения (аксиома 4). Поэтому каждый вектор имеет положительную длину, за исключением нулевого, длина которого равна нулю:
.
Углом между ненулевыми векторами и
евклидова пространства
называется число
то есть
и
Представив неравенство Коши-Буняковского (8.25) в виде можно сделать вывод, что абсолютное значение выражения
не превосходит единицы, т.е. величина угла определена для любой пары ненулевых векторов. Заметим, что угол между коллинеарными векторами равен нулю или
.
Длина вектора и угол между векторами называются основными метрическими понятиями .
Из неравенства Коши-Буняковского (8.25) следует неравенство треугольника:
Докажем последнее неравенство. Применяя оценку , получаем
то есть .
Пример 8.17. Даны векторы евклидовых пространств:
а) — элементы пространства
со скалярным произведением (8.27):
;
б) — элементы пространства
со скалярным произведением (8.26):
в) — элементы пространства
со скалярным произведением (8.28):
.
г) — элементы пространства
со скалярным произведением (8.29):
;
д) — элементы пространства
со скалярным произведением (8.30):
В каждом пространстве найти длины двух данных векторов и угол между ними.
Решение. а) Находим скалярные произведения:
Следовательно, .
б) Находим скалярные произведения:
Следовательно, .
в) Находим скалярные произведения:
Следовательно, .
г) Находим скалярные произведения:
Следовательно, .
д) Находим скалярные произведения:
Следовательно, .
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

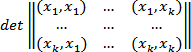
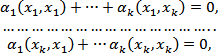
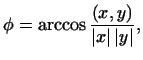
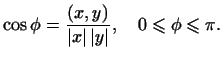
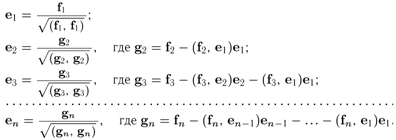



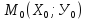



































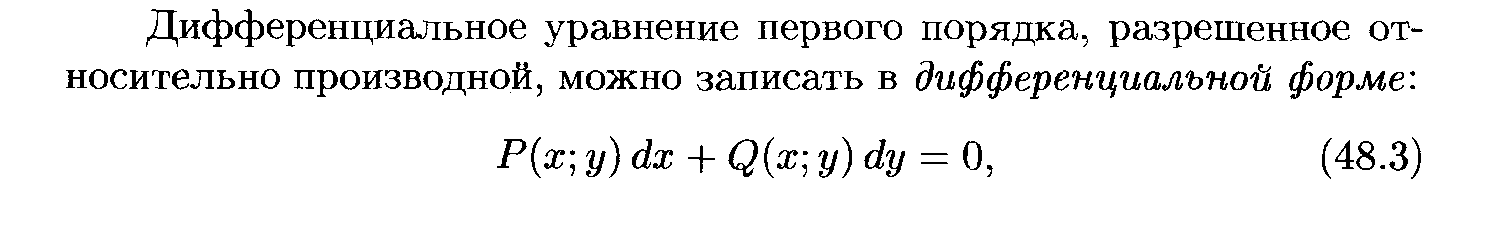






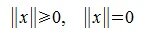 тогда и только тогда, когда x=0.
тогда и только тогда, когда x=0.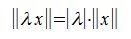 .
.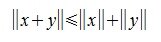 (неравенство треугольника).
(неравенство треугольника).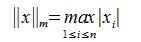

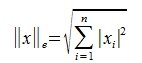
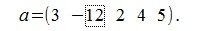

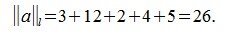








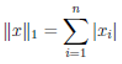







































































![[е] в L ^ {2} ( Omega)](https://wikimedia.org/api/rest_v1/media/math/render/svg/a90011eada9282d431f24c351554aac562f9dc41)
![| , [е] , | _ {L ^ {2} ( Omega)} = | f | _ {{ mathcal {L}} ^ {2} ( Omega)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3acd4af1682b70d5d9cf00c1f4b66e1464a413d)









