Как найти f x при нечетной функции

Четные и нечетные функции

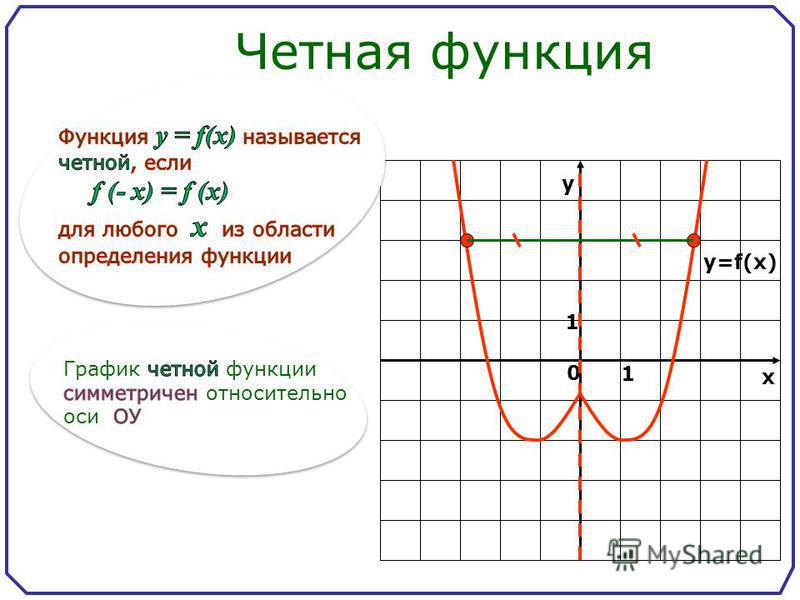
Функция y=f(x) называется четной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство

f(-x)=f(x).

График четной функции симметричен относительно оси ординат.

Например, y = x^2, y = cos x, y = left |x right | — четные функции.

Функция y=f(x) называется нечетной, если ее область определения симметрична относительно нуля и для любого x из ее области определения выполняется равенство

f(-x)=-f(x).

График нечетной функции симметричен относительно начала координат.

Например, y = x^3, y = sin x, y = tg x, y=frac{1}{x} — нечетные функции.

Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида.

Если вы учитесь в матклассе или на первом курсе вуза — вам могут встретиться вот такие задания:

1. Проверьте, является ли функция f(x)=frac{x}{3}-frac{3}{x} четной (нечетной). 

Область определения функции f(x):

xne 0.

Проверим, является ли f(x) чётной или нечётной. Если f(-x)=f(x), функция четна. Если f(-x)=-f(x), функция нечетна.

f(-x)=-frac{x}{3}+frac{3}{x}=-(frac{x}{3}-frac{3}{x})=-f(x) — значит, функция f(x)=frac{x}{3}-frac{3}{x} нечётная, её график симметричен относительно нуля.

2. Проверьте, является ли функция f(x)=x^2+cosx четной (нечетной).

Область определения: все действительные числа.

f(x) — чётная, как сумма двух чётных функций.

f(-x)={(-x)}^2+cos(-x)=x^2+cosx=f(x).

Её график симметричен относительно оси y.

3. Проверьте, является ли функция f(x)=frac{sqrt{1-x^2}}{left|xright|} четной (нечетной).

D(f):xin [-1;0)cup (0;1] .

Область определения функции симметрична относительно нуля.

f(-x)=frac{sqrt{1-{(-x)}^2}}{left|-xright|}=frac{sqrt{1-x^2}}{left|xright|};

f(x) — чётная, её график симметричен относительно оси y.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Четные и нечетные функции» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Чётные и нечётные функции

11 декабря 2021

Сегодня мы разберём:

  1. Определение чётных и нечётных функций
  2. Как проверить, является функция чётной или нечётной
  3. Как выглядят графики чётных и нечётных функций
  4. Дополнение. Задачи с параметром

1. Определение

Определение 1. Функция $fleft( x right)$, определённая на множестве $M$, называется чётной, если:

  1. $M$ — симметричное относительно нуля множество.
  2. $fleft( -x right)=fleft( x right)$.

Определение 2. Функция $fleft( x right)$, определённая на множестве $M$, называется нечётной, если:

  1. $M$ — симметричное относительно нуля множество.
  2. $fleft( -x right)=-fleft( x right)$.

Определение 3. Во всех остальные случаях, когда функция $fleft( x right)$ не является ни чётной,
ни нечётной, её называют функцией общего вида.

Примеры чётных функций:

  • Квадратичная: $fleft( x right)={{x}^{2}}$; любая степенная функция с чётным показателем: ${{x}^{4}}$, ${{x}^{8}},$ да хоть ${{x}^{128}}$.
  • Модуль: $fleft( x right)=left| x right|$. С модулем будет отдельный разговор — он обращает любую функцию в чётную.

Примеры нечётных функций:

  • Любая степенная функция с нечётным показателем: $fleft( x right)={{x}^{3}}$, ${{x}^{5}}$, ${{x}^{2n+1}}$.
  • Корень третьей степени: $fleft( x right)=sqrt[3]{x}$.
  • Обратная пропорциональность: $fleft( x right)={1}/{x};$.

2. Исследование функции на чётность

Чтобы узнать, является функция чётной или нечётной (или вообще общего вида), нужны две проверки:

  1. Область определения. Если она не симметрична относительно нуля, то функция общего вида. Если симметрична — переходим ко второй проверке.
  2. Зная $fleft( x right)$, считаем $fleft( -x right)$ и $-fleft( x right)$. Если $fleft( -x right)=-fleft( x right)$, то функция нечётная. А если $fleft( -x right)=fleft( x right)$, то функция чётная.

Главное, чтобы функция была задана формулой, а не таблицей, графиком или ещё как. Тогда исследование на чётность занимает несколько секунд. Мы сейчас убедимся в этом, но сначала важное замечание.

Что значит «симметричное относительно нуля множество»? Это значит, что если $xin M$, то и $-xin M$. Малейшее нарушение этого правила — хотя бы в одной точке — и множество уже не симметрично.

Примеры симметричных множеств:

[begin{align} & left( -infty ;+infty right) \ & left( -5;0 right)bigcup left( 0;5 right) \ & left[ -sqrt{2}-1;sqrt{2}+1 right] \ end{align}]

Примеры несимметричных множеств:

[begin{align} & left( -infty ;9 right)bigcup left( 9;+infty right) \ & left[ -3;3 right) \ & left[ 0;+infty right) \ end{align}]

Первые два множества несимметричны всего в одной точке (кстати, какой?). Но этого достаточно, чтобы прекратить исследование и отнести функцию к общему виду.

Разберём несколько примеров. Для начала — стандартный:

Исследуйте на чётность / нечётность функцию

[fleft( x right)={{x}^{3}}-4x]

Эта функция определена для всех действительных чисел: $xin mathbb{R}$. Это симметричное относительно нуля множество. Пока всё хорошо.

Считаем $fleft( -x right)$ и $-fleft( x right)$:

[begin{align} fleft( -x right) & ={{left( -x right)}^{3}}-4cdot left( -x right)= \ & =-{{x}^{3}}+4x; \ -fleft( x right) & =-left( {{x}^{3}}-4x right)= \ & =-{{x}^{3}}+4x end{align}]

Получили, что $fleft( -x right)=-fleft( x right)$. Значит, функция нечётная.

А вот более хитрый случай:

Исследуйте на чётность / нечётность функцию

[fleft( x right)=frac{x}{4-x}]

Область определения. Перед нами рациональная дробь. Её знаменатель должен быть отличен от нуля:

[begin{align} 4-x & ne 0 \ x & ne 4 \ end{align}]

Следовательно, область определения

[M=left( -infty ;4 right)bigcup left( 4;+infty right)]

Это множество несимметрично, поскольку $x=-4$ принадлежит этому множеству, а $x=4$ не принадлежит. Всё: функция $fleft( x right)$ — общего вида.

Дальше попробуйте сами:

Исследуйте на чётность / нечётность функцию

[begin{align} fleft( x right) & =frac{x-3}{x-3} \ gleft( x right) & =frac{3}{2+left| x right|} \ kleft( x right) & ={{left( 5-x right)}^{3}}-{{left( 5+x right)}^{3}} \ end{align}]

Ответ: $fleft( x right)$ — общего вида; $gleft( x right)$ — чётная; $kleft( x right)$ — нечётная.

Умение быстро определять чётность — чрезвычайно полезный навык. Особенно когда вы начнёте решать задачи с параметрами и всевозможные варианты ДВИ.

3. График чётной и нечётной функции

Всего два факта, которые нужно знать:

Теорема 1. График чётной функции $y=fleft( x right)$ симметричен относительно оси $OY$.

Теорема 2. График нечётной функции $y=fleft( x right)$ симметричен относительно начала координат.

Чтобы построить график чётной функции, достаточно построить его правую часть (для $xge 0$), а затем симметрично отразить относительно оси $OY$.

С нечётной функцией, на первый взгляд, всё то же самое. Сначала вновь строим правую часть графика (для $xge 0$), а затем отражаем её относительно начала координат. Однако практика показывает, что центральная симметрия даётся начинающим ученикам чуть сложнее, чем осевая.

Ниже приведены графики нескольких чётных функций. Попробуйте построить их самостоятельно.

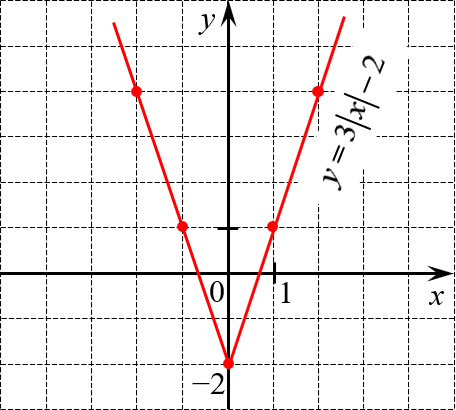
Постройте график функции

[y=3left| x right|-2]

Функция чётная. Пусть $xge 0$. Тогда функция примет вид

[y=3x-2]

Это линейная функция. Её график — прямая. С учётом отражения относительно оси $OY$ получим:

Постройте график функции

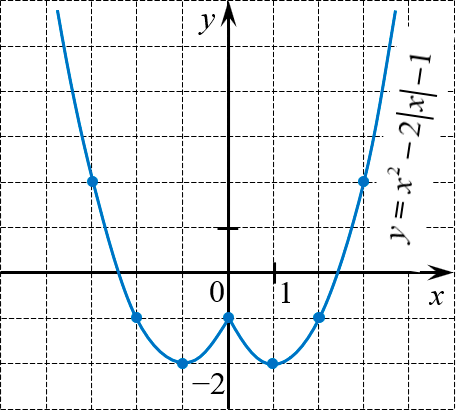
[y={{x}^{2}}-2left| x right|-1]

Функция чётная. При $xge 0$ видим привычную квадратичную функцию

[y={{x}^{2}}-2x-1]

Её график — парабола с вершиной ${{x}_{0}}={-b}/{2a};={2}/{2};=1$. После отражения получим

Постройте график функции

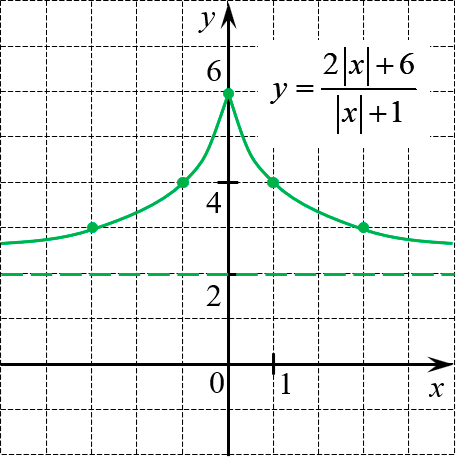
[y=frac{2left| x right|+6}{left| x right|+1}]

Функция чётная. При $xge 0$ получим привычную рациональную дробь. Выделим целую часть:

[y=frac{4}{x+1}+2]

Это обычная гипербола, сдвинутая на 1 влево и на 2 вверх. Итого получим:

Обратите внимание на последний график. При всяком сдвиге и симметрии желательно показывать не только новое положение самого графика, но и положение всех ориентиров: вспомогательная система координат, вертикальные и горизонтальные асимптоты (особенно актуально для гипербол) и т.д.

Зачем всё это нужно? Исследование функции на чётность и нечётность незаменимо для решения сложных уравнений и задач с параметром:

  1. Графический метод решения задач с параметром;
  2. Метод мажорант;
  3. Вместе с периодичностью используется в тригонометрии.

4. Дополнение. Задачи с параметром

Чётность функций редко встречается сама по себе. Прежде всего это инструмент для решения сложных задач.

Известно, что $fleft( x right)={{x}^{8}}+a{{x}^{4}}+1$ и $fleft( 2 right)=353$. Найдите $fleft( -2 right)$ и значение параметра $a$.

Решение. Очевидно, что функция $fleft( x right)$ чётная:

[begin{align} fleft( -x right) & ={{left( -x right)}^{8}}+a{{left( -x right)}^{4}}+1= \ & ={{x}^{8}}+a{{x}^{4}}+1=fleft( x right) end{align}]

Следовательно можем найти $fleft( -2 right)$:

[fleft( -2 right)=fleft( 2 right)=353]

Кроме того, подставим $x=2$ и $fleft( 2 right)=353$ в формулу, задающую функцию:

[begin{align} 353 & ={{2}^{8}}+acdot {{2}^{4}}+1 \ 16a& =96 \ a& =6 end{align}]

Задача решена. Ответы:

[begin{align} fleft( -2 right) & =353; \ a & =6. end{align}]

И ещё одна задача. Попробуйте решить её самостоятельно:

Известно, что $fleft( x right)=frac{6075}{{{x}^{5}}+k{{x}^{3}}}$ и $fleft( 3 right)=15$. Найдите $fleft( -3 right)$ и значение параметра $k$.

Решение. Функция чётная при любом $kin mathbb{R}$ (докажите это!), поэтому

[fleft( -3 right)=-fleft( 3 right)=-15]

Поскольку $fleft( 3 right)=15$, имеем:

[begin{align} fleft( 3 right) & =frac{6075}{{{3}^{5}}+kcdot {{3}^{3}}}=frac{15}{1} \ & … \ k& =6 end{align}]

Ответ: $fleft( -3 right)=-15$; $k=6$.

А чтобы действительно разобраться с чётностью, обязательно изучите ещё две темы:

  • Сдвиги графиков вдоль осей;
  • Графики функций с модулем.

После этого половина задач с параметром перестанет казаться вам сложными.:)

Смотрите также:

  1. Задача B15 — исследование функции с помощью производной
  2. Тест к уроку «Что такое числовая дробь» (средний)
  3. Следствия из теоремы Виета
  4. C2: расстояние между двумя прямыми
  5. Процент: налоги и зарплата. Считаем с помощью коэффициентов
Источник

Четность и нечетность функции ☑️ как определить, примеры решения задач

Общие сведения

Исследование функции на четность и нечетность — базовый элемент, показывающий ее поведение, которое зависит от значения аргумента. Последний является независимой переменной, соответствующей определенным допустимым значениям. Множество чисел, которое может принимать неизвестная независимого типа, называется областью определения. Областью значений функции вида y = f (x) являются все значения зависимой переменной «y».

Теперь следует сформулировать список базовых знаний, которые необходимы для анализа выражений на четность. Если нужно выполнить другие процедуры исследования, то его следует расширить. Например, для нахождения максимума следует ознакомиться с производной. Необходимый минимум знаний о функциях следующий:

  1. Область определения — D (f).
  2. Виды.
  3. Правила.
  4. Свойства для четных и нечетных.
  5. Классификация.

Первый элемент необходим для выявления аргумента, при котором можно узнать его недопустимые значения, а также определить симметричность. От свойств и вида также зависит четность. Первое рекомендуется применять в частных случаях, например, произведение двух нечетных тождеств. Результат следует проверять при помощи соответствующего программного обеспечения. Например, онлайн-калькулятор четности и нечетности функций позволяет следить за правильностью решения.

Область определения

Первый элемент, который нужен для анализа, следует рассмотреть подробнее. Область определения функции z = g (y) специалисты рекомендуют обозначать литерой «D». Полная запись выглядит таким образом: D (z). Кроме того, следует выяснить симметричность множества. Под последним понимается некоторый интервал, который нужно найти.

D (z) записывается в виде множества. Например, D (z) = [1;8]. Запись значит ограниченность аргумента, принимающего значения от 1 включительно до 8 включительно, то есть следующие цифры: 1, 2, 3, 4, 5, 6, 7 и 8.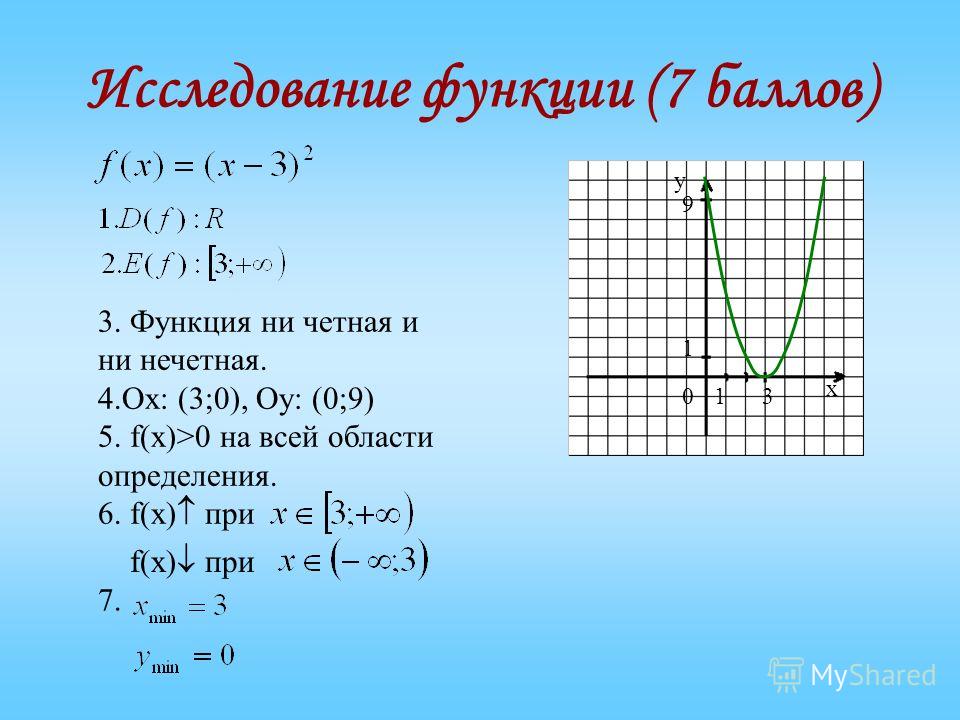 Если указана запись в виде (1;4), то ее нужно трактовать таким образом: от 1 не включительно до 4 не включительно, то есть в интервал входят только числа 2 и 3.

Для определения величины D (z) необходимо решить неравенство, корнем которого являются все значения аргумента. Для этих целей можно использовать и специализированное программное обеспечение. Математики рекомендуют свести пользование решебниками и программами к минимуму, поскольку не всегда предоставится возможность воспользоваться ими на экзаменах или контрольных.

Основные виды

Исследование функции зависит от ее вида, который нужно правильно определять. Для начала следует обозначить сложность, поскольку от этого параметра зависят дальнейшие действия и свойства, которыми придется руководствоваться. Математики производят разделение таким образом:

  • Простые: алгебраические, трансцендентные и тригонометрические.
  • Составные или сложные.

Алгебраические делятся на рациональные (без корня) и иррациональные (наличие радикала). Первые состоят из целых и дробных. D (z) для этих типов — все множество действительных чисел. Если функция представлена в виде обыкновенной дроби, то значение аргумента, приводящее к пустому множеству (знаменатель равен нулю), нужно исключить. Когда аргумент находится под знаком радикала (корня), тогда она считается иррациональной. Однако следует проверить, чтобы под корнем четной степени не было отрицательного значения, которое приводит к неопределенности.

Все функции, содержащие sin, cos, tg и ctg, являются тригонометрическими. Кроме того, arcsin, arccos, arctg и arcctg — обратные тригонометрические. Трансцендентные можно разделить на такие три группы: показательные, степенные и логарифмические.

Второе отличается от первого формулой. Другой тип классификации основан на периодичности. В зависимость от этого параметра все функции делятся на периодические и непериодические.

Параметр периодичности означает повторение ее поведения через определенный период Т.

Существует еще один критерий. Он называется монотонностью. В зависимости от него, функции бывают монотонными и немонотонными. Первая группа характеризуется постоянностью, то есть она либо убывает, либо возрастает. Все остальные могут убывать и возрастать на определенных промежутках. Примером является y = cos (x), поскольку она является убывающей и возрастающей через определенный период.

Правила для выявления

Для того чтобы исследовать на четность, существует два правила или теоремы, которые записываются в виде двух формул. Четная — функция вида w (x), для которой справедливо такое равенство: w (-x) = w (x). Для нечетной соотношение немного другое: w (-x) = w (x). Однако бывают выражения, к которым не применимы эти тождества. Они принадлежат общему виду.

Для оптимизации решения специалисты рекомендуют использовать некоторую последовательность действий или специальный алгоритм. Он позволяет определить четность за минимальный промежуток времени и без ошибок. Необходимо обратить внимание на пункты или шаги, по которым выполняется подробная оценка:

  • Разложить при необходимости на простые элементы.
  • Определить D (z). Если ее график симметричный, то нужно переходить к следующему шагу. В противном случае результатом является функция общего вида.
  • Проверить, подставив в выражение отрицательное значение аргумента w (-x).
  • Выполнить сравнение: w (-x) = w (x).
  • Сделать соответствующий вывод.

Если w (-x) = w (x), то это свидетельствует о четности. При выполнении тождества w (-x) = -w (x) функция является нечетной. Важно обратить внимание на D, поскольку в некоторых точках равенства и условия могут не выполняться. Это свидетельствует о том, что искомая функция принадлежит к общему виду, то есть не является четной и нечетной.

Одним интересным способом является графический метод (принцип). Для его реализации нужно выполнить построение графика. Если он будет симметричным относительно оси ординат ОУ, то равенство w (-x) = w (x) будет выполняться. В случае симметричности относительно начала системы координат (точка пересечения осей абсцисс и ординат), будет справедливым равенство w (-x) = -w (x).

Следствия из утверждений

Свойства или следствия из утверждений расчетов позволяют оптимизировать процесс решения, поскольку нет необходимости выполнять какие-либо действия. Очень часто приходится тратить много времени на задание, которое можно решить за несколько минут.


Математики выделяют следующие свойства для таких функций:

  • Симметричность графика: четная — относительно ОУ, а нечетная — относительно начала координат.
  • Функция эквивалентна сумме четной и нечетной.
  • Результат комбинации четных эквивалентен четной, а нечетных — нечетной.
  • Результирующее произведение: 2 четных — четное, 2 нечетных — четная, а 2 разной четности — нечетной.
  • Композиция: 2 нечетных — нечетна, четная и нечетная — четна, любая с четной — четна (не наоборот).
  • При взятии производной от четной результирующая является нечетной, а от нечетной — четной.
  • Определенный интеграл вида ∫(g (x))dx с границами от -А до А равен двойным интегралам ∫(g (x))dx с границей от -А до 0 и от 0 до А: ∫(g (x))dx |(-A;A) = 2∫(g (x))dx |(-A;0) = 2∫(g (x))dx |(0;A).
  • Определенный интеграл нечетной функции с границами -А и А равен 0.
  • Ряд Маклорена: четные степени соответствуют четной и наоборот.
  • Ряд Фурье: четная содержит только выражения с cos, а нечетная — sin.

Второе свойство можно записать математически таким образом: z (x) = y (x) + w (x). Выражение y (x) можно выразить следующим образом: y (x) = [z (x) — z (-x)] /2. Тождество w (x) выражается через z (x) формулой: w (x) = [z (x) + z (-x)] /2.

Классификация по четности

Специалисты давно уже исследовали некоторые функции. Примеры четных и нечетных можно классифицировать по признаку четности. Эти данные значительно ускоряют процесс анализа любого выражения. К нечетным функциям относятся следующие (следует учитывать, что аргумент «x» принадлежит множеству действительных чисел Z):

  • Возведение в степень, показатель которой является целым и нечетным.
  • Сигнум (sgn) — кусочно-постоянный тип, который задан несколькими формулами, объединенными в систему.
  • Радикал положительной нечетной степени.
  • Тригонометрические: sin (x), tg (x), ctg (x) и cosec (x).
  • Обратные тригонометрические: arcsin (x), arcctg (x), arcsec (x) и arccosec (x).
  • Гиперболические и их обратные выражения: гиперболические синус и косинус, а также ареасинус, ареатангенс и ареакотангенс.
  • Гудермана и обратная ей: gd (x) = arctg (sh (x)) и arcgd (x) = arch (sec (x)). 2) / 2c 2 ].
  • Кардинальный синус: sinc (x).

Остальные составляют класс общего вида, который не принадлежит к четным и нечетным. При решении задач необходимо иметь таблицу всех функций, которая должна быть составлена перед обучением. Следует учитывать, что на экзаменах и контрольных функции, используемые для описания каких-либо процессов, практически не исследуются. Зная алгоритм, не составит особого труда проверить выражение на четность. Следующим этапом, который поможет закрепить теоретические знания, считается практика.

Пример решения

Задачи исследования функции на четность встречаются редко, поскольку этот элемент входит в полный анализ ее поведения. Пусть дано тождество z (y) = (y 2 — y — 2) / (y 2 — 1). В этом случае следует действовать по алгоритму:

  • Состоит из двух элементов: g (y) = y 2 — y — 2 и h (y) = y 2 — 1.
  • Область значений: D (y 2 — y — 2) = (-бесконечность; +бесконечность) и D (y 2 — 1) = (-бесконечность; -1) U (-1;1) U (1; +бесконечность).
    2 — 1 = y 2 — 1.
  • В двух случаях функции являются нечетными: в первом — изменение знака, а во втором — от четной отнимается 1. Следовательно, искомое выражение является нечетной функцией.

Задачу можно решить вторым способом — проанализировать составляющие элементы. Например, знаменатель всегда будет нечетным, поскольку от четного y 2 отнимается нечетное число (6 — 1 = 5). Этот способ используется в некоторых языках программирования, для написания подпрограмм и процедур, позволяющих проверить или отобрать все нечетные значения. Числитель также является нечетным, поскольку он содержит нечетный элемент «y». Если построить график, используя любой из веб-ресурсов, то он окажется симметричным относительно начала координат.

Первое свойство свидетельствует о том, что функция является нечетной. Некоторые новички делают распространенную ошибку, считая, что отношение нечетных есть величина четная. Однако такое утверждение не применимо в этом случае. Если бы было произведение двух нечетных выражений, то результат являлся бы четным. Об этой особенности свидетельствует свойство под номером 4.

Таким образом, для исследования функции на предмет ее четности или нечетности нужно воспользоваться специальным алгоритмом, который рекомендуют математики. Он позволит выполнить операцию без ошибок и за короткий промежуток времени.

Нечётные и чётные функции | это… Что такое Нечётные и чётные функции?

Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Такое название возникло как обобщение чётности степенных функций: функция f(x) = xn чётна тогда и только тогда, когда n чётно, и нечётна тогда и только тогда, когда n нечётно.

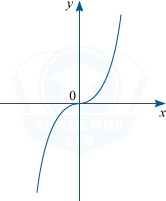
 — пример нечётной функции.

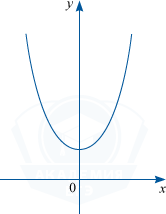
 — пример чётной функции.

нечётная

ни чётная, ни нечётная.

Другие определения:

  • Нечётная функция — функция, меняющая знак при изменении знака независимого переменного (симметричная относительно центра координат).
  • Чётная функция — функция, не изменяющая своего значения при изменении знака независимого переменного (симметричная относительно оси ординат).
  • Индифферентная функция[источник не указан 240 дней] — функция, не обладающая симметрией. В эту категорию относят функции не подпадающие под предыдущие 2 категории.

Содержание

  • 1 Определения
  • 2 Свойства
  • 3 Примеры
    • 3.1 Нечётные функции
    • 3.2 Чётные функции
  • 4 Вариации и обобщения

Определения

Определения вводятся для любой симметричной относительно нуля области определения , например, отрезка или интервала.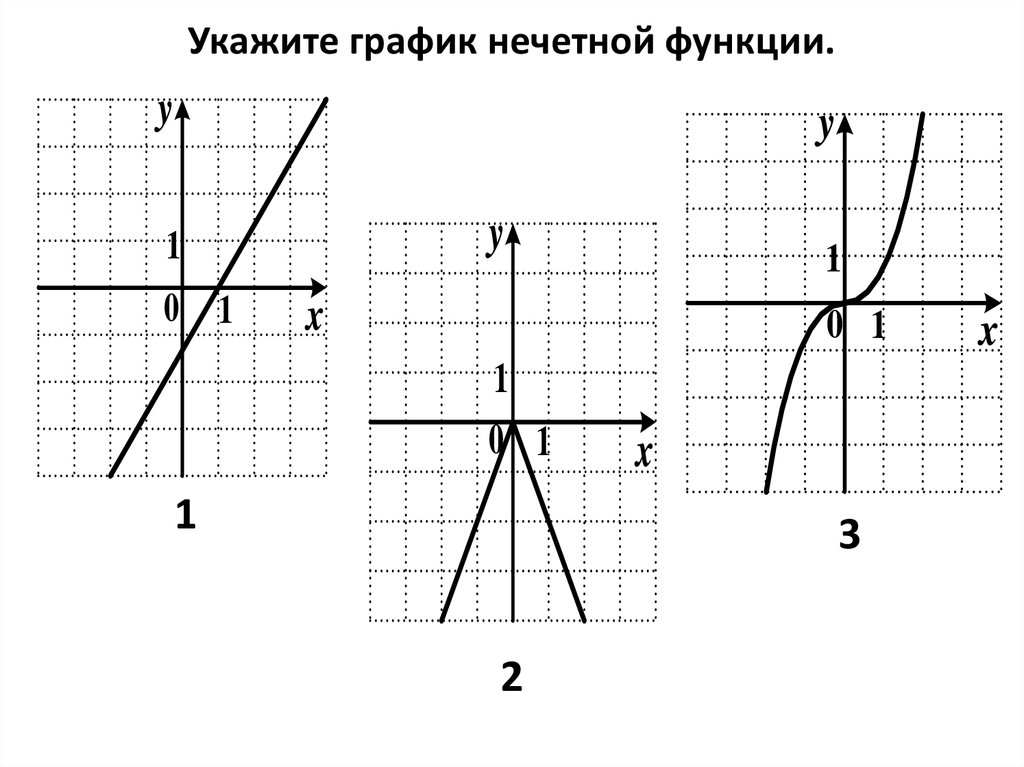

  • Функция называется чётной, если справедливо равенство
  • Функция называется нечётной, если справедливо равенство
  • Если не выполняется ни одно из этих равенств, то функция называется индифферентной[источник не указан 240 дней]

(или функцией общего вида).

Свойства

  • График нечётной функции симметричен относительно начала координат .
  • График чётной функции симметричен относительно оси ординат .
  • Произвольная функция может быть единственным образом представлена в виде суммы нечётной и чётной функций:

где

  • Функция  — единственная функция, одновременно являющаяся нечётной и чётной.
  • Сумма, разность и вообще любая линейная комбинация чётных функций чётна, а нечётных — нечётна.
  • Функция, обратная чётной, чётна, а нечётной — нечётна.
  • Произведение двух функций одной чётности чётно.
  • Произведение двух функций разной чётности нечётно.
  • Композиция двух нечётных функций нечётна.
  • Композиция чётной функции с чётной/нечётной чётна.
  • Композиция любой функции с чётной чётна (но не наоборот!).
  • Производная чётной функции нечётна, а нечётной — чётна.
    • То же верно про производную третьего, пятого и вообще любого нечётного порядка.
  • Производная чётного порядка имеет ту же чётность, что и первоначальная функция.

Примеры

Нечётные функции

  • Нечётная степень где  — произвольное целое число.
  • Синус .
  • Тангенс .

Чётные функции

  • Чётная степень где  — произвольное целое число.
  • Косинус .
  • Абсолютная величина (модуль) .

Вариации и обобщения

  • Понятие чётности и нечётности функций естественно обобщаются на случай отображений между векторными пространствами.

Четные и нечетные функции

Пусть f(x) — функция.

Чтобы узнать, является ли f(x) четным или нечетным, мы должны заменить ‘x’ на ‘-x’ в f(x). Мы должны заключить f(x) как четную или нечетную функцию из результата f(-x), как показано ниже.

1. Если f(-x)  =  f(x), то f(x) является четной функцией

2. Если f(-x)  =  — f(x), то f(x) является нечетной функцией

Если f(-x) не равно ни f(x), ни -f(x), мы должны заключить, что f(x) не является ни четным, ни нечетным.

Сумма или разность двух четных функций всегда четна.

Сумма или разность двух нечетных функций всегда нечетна.

Применение

Несмотря на то, что у нас есть много применений четных и нечетных функций, давайте рассмотрим важное применение четных и нечетных функций в интегральном исчислении.

Если f(x) является четной функцией, 

Если f(x) является нечетной функцией, 

Примеры

Пример 1: 

Пусть f(x)  =  x 3 , является ли f(x) нечетной или четной функцией ?

Решение: 

Чтобы узнать, является ли f(x) нечетной или четной функцией, подставим x = -x в f(x).

Тогда имеем

f(-x)  =  (-x) 3

f(-x)  =  -x 3

f(-x)  =  4

2 , f(x) — нечетная функция.

Пример 2 : 

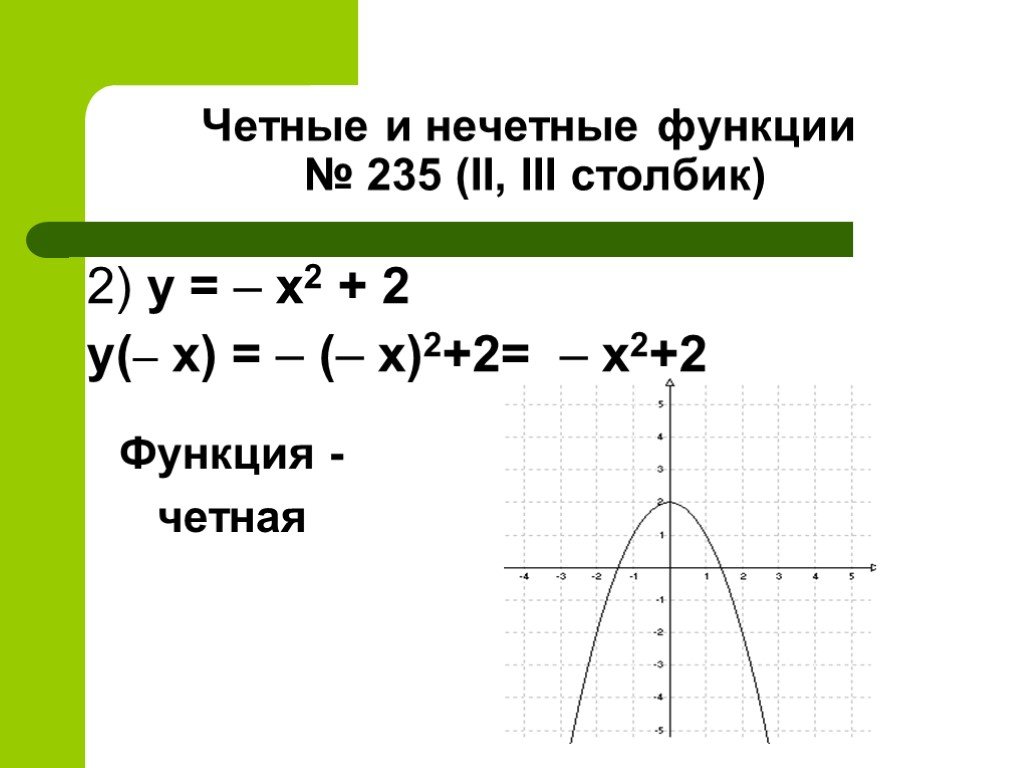
Пусть f(x)  =  x 2   + 2, является ли f(x) нечетной или четной функцией?

Решение: 

Чтобы узнать, является ли f(x) нечетной или четной функцией, подставьте -x вместо x в f(x).

Тогда имеем

f(-x)  =  (-x) 2  + 2

f(-x)  =  x 2  + 2

f(-x)  = 9 0f0(x4)

Итак, f(x) — четная функция.

Пример 3 : 

Пусть f(x)  =  x 3  — 2x, является ли f(x) нечетной или четной функцией?

Решение: 

Чтобы узнать, является ли f(x) нечетной или четной функцией, подставьте -x вместо x в f(x).

Тогда имеем

f(-x)  =  (-x) 3  — 2(-x)

f(-x)  =  -x 3  +  2x

f(-x) 9000 =  -(x 3  — 2x)

f(-x)  =  -f(x)  

Итак, f(x) — нечетная функция.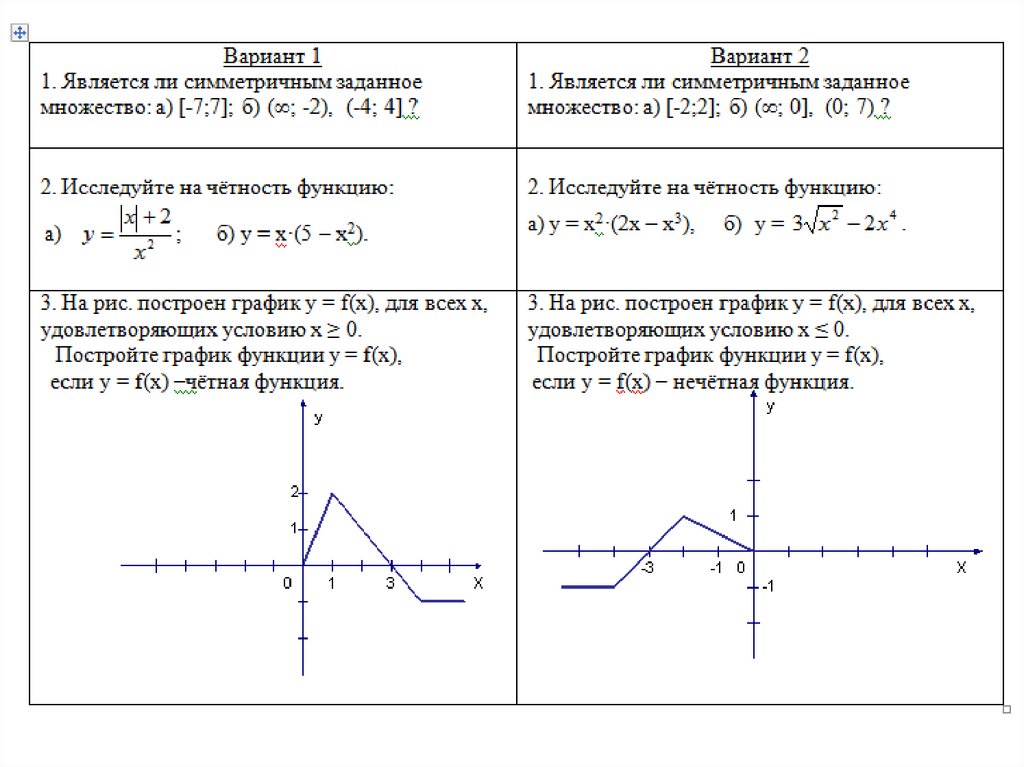

Пример 4 : 

Пусть f(x)  =  5x 3  + x 2 — 1, является ли f(x) нечетной или четной функцией?

Решение: 

Чтобы узнать, является ли f(x) нечетной или четной функцией, подставьте -x вместо x в f(x).

Тогда имеем

f(-x)  =  5(-x) 3  + (-x) 2  — 1

f(-x)  =  5(-x 3 )-900 x 2 -1

F (-x) = -5x 3 -x 2 -1

F (-x) = -(5x 3 + x 2 + 1)

f(-x) не может быть выражено как f(x) или -f(x).

Итак, f(x) не является ни четной, ни нечетной функцией.

Пример 5 : 

Пусть f(x)  =  x 4 + 2x 2   + 5, является ли f(x) нечетной или четной функцией?

Решение: 

Чтобы узнать, является ли f(x) нечетной или четной функцией, подставьте -x вместо x в f(x).

Тогда имеем

f(-x)  =  (-x) 4  + 2(-x) 2  + 2

f(-x)  =  x 4+ 04 + 2x 20 0 2

f(-x)  =  f(x)

Итак, f(x) — четная функция.

Важное примечание: 

В тригонометрических отношениях, если у нас есть отрицательный угол, мы должны понимать, что угол будет падать в IV -й квадрант .

В IV -м -м квадранте тригонометрические отношения ‘cos’ и ‘sec’ положительны, а все остальные тригонометрические отношения отрицательны.

Решение: 

Пусть f(x)  = sinx

Чтобы узнать, является ли f(x) нечетной или четной функцией, подставьте -x вместо x в f(x).

Тогда имеем

f(-x)  =  sin(-x)

Поскольку угол отрицательный, он попадает в IV -й квадрант . В IV -м -м квадранте «грех» отрицательный.

Итак, у нас есть

f(-x)  =  — sinx

f(-x)  =  — f(x)

 f(x) — нечетная функция  

Итак, sinx — нечетная функция.

Пример 7 :  

Является ли функция cosx четной или нечетной ?

Решение: 

Чтобы узнать, является ли функция f(x) четной или нечетной, подставьте -x вместо x в f(x).

Тогда у нас есть

f(-x)  =  cos(-x)

Поскольку угол отрицательный, он попадает в IV -й -й квадрант. В IV -й -й квадрант «cos» положительный.

Итак, у нас есть

f(-x)  =  cosx

f(-x)  =  f(x)

f(x) — четная функция

Итак, cosx — четная функция.

Пример 8 :  

Является ли tanx нечетным или четным ?

Решение: 

Пусть f(x)  = tanx

Чтобы узнать, является ли f(x) нечетной или четной функцией, подставьте -x вместо x в f(x).

Тогда у нас есть

f(-x)  = tan(-x)

Поскольку угол отрицательный, он попадает в IV -й -й квадрант. В IV -м квадранте «тангенс» отрицательный.

Итак, у нас есть

f(-x)  =  — tanx

f(-x)  =  — f(x)

 f(x) — нечетная функция  

Итак, tanx — нечетная функция.

Пример 9 :  

Пусть f(x)  =  sinx + tanx, является ли f(x) нечетной или четной функцией?

Решение: 

Чтобы узнать, является ли f(x) нечетной или четной функцией, подставьте -x вместо x в f(x).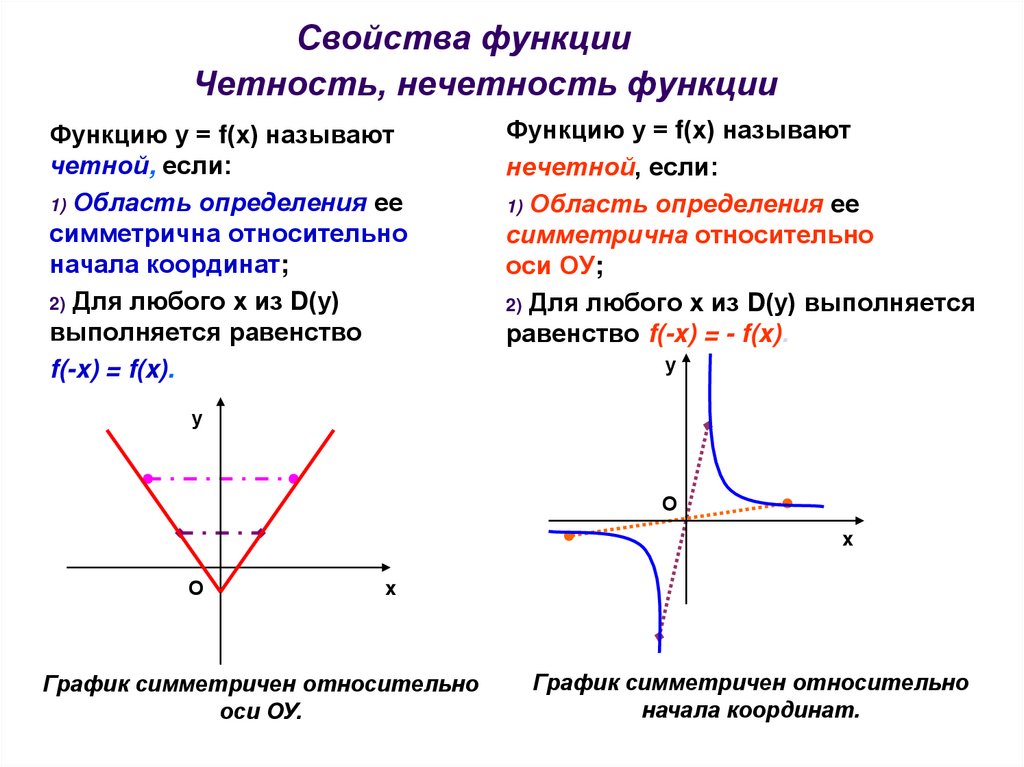

Тогда у нас есть

f(-x)  =  sin (-x) + tan(-x)

Поскольку угол отрицательный, он попадает в IV -й -й квадрант. В IV -м -м квадранте и «sin», и «tan» отрицательные.

Итак, имеем

f(-x)  =  — sinx — tanx

f(-x)  =  — (sinx + tanx)

f(-x)  =  — f(x)

Итак, f (x) — нечетная функция.

Примечание: Сумма или разность двух нечетных функций всегда нечетна.

Пример 10 :  

Пусть f(x)  =  secx + cosx, является ли f(x) нечетной или четной функцией?

Решение: 

Чтобы узнать, является ли функция f(x) четной или нечетной, подставьте -x вместо x в f(x).

Тогда у нас есть

f(-x)  =  sec(-x) + cos(-x)

Поскольку угол отрицательный, он попадает в IV -й -й квадрант. В IV -й квадрант и «sec», и «cos» положительны.

Итак, у нас есть

f(-x)  =  secx + cosx

f(-x)  =  f(x)

Итак, f(x) — четная функция.

Примечание: Сумма или разность двух четных функций всегда четна.

Помимо материалов, перечисленных выше, если вам нужны какие-либо другие материалы по математике, пожалуйста, используйте наш пользовательский поиск Google здесь.

Пожалуйста, отправьте ваш отзыв на [email protected]

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

Интегрирование четных и нечетных функций

Результаты обучения

  • Применение интегралов четных и нечетных функций

В Модуле 1: Функции и графики мы видели, что четная функция — это функция, в которой [latex]f(text{−}x)=f(x)[/latex] для всех [latex]x[/latex ] в области, то есть график кривой не изменится, если [latex]x[/latex] заменить на −[latex]x[/latex]. Графики четных функций симметричны относительно оси [latex]y[/latex]. Нечетная функция — это функция, в которой [latex]f(text{−}x)=text{−}f(x)[/latex] для всех [latex]x[/latex] в домене, а граф функция симметрична относительно начала координат.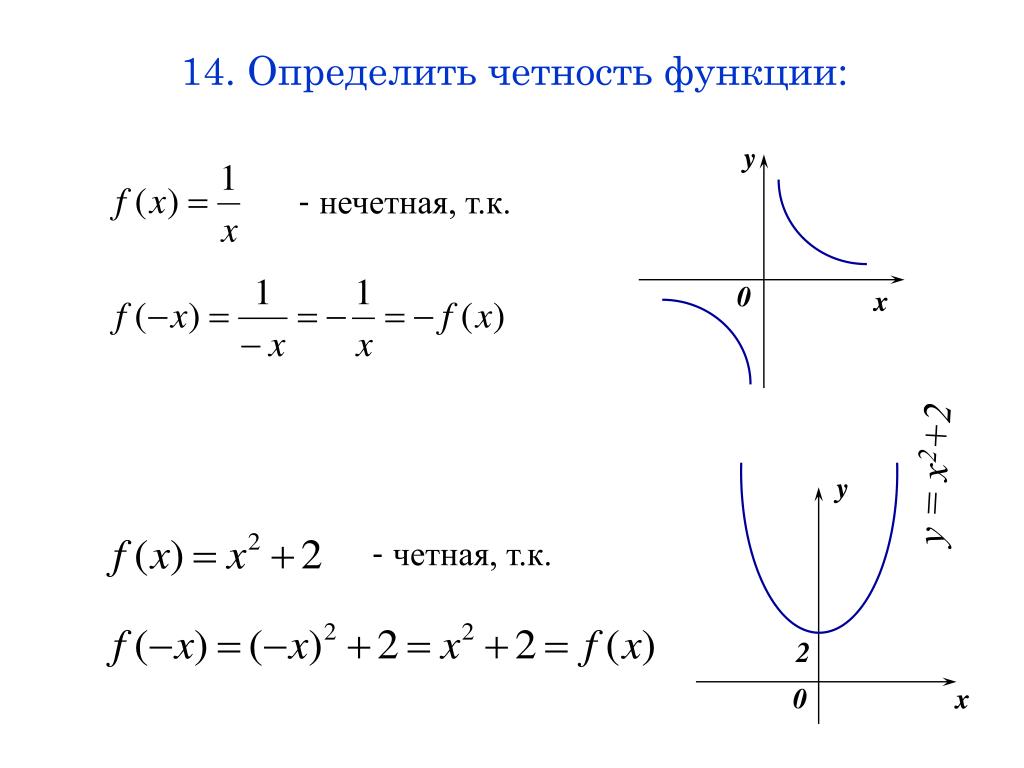

Интегралы четных функций, когда пределы интегрирования от −[latex]a[/latex] до [latex]a[/latex], включают две равные площади, поскольку они симметричны относительно [latex]y[/ латекс]-ось. Интегралы нечетных функций, когда пределы интегрирования равны [латекс]влево[текст{−}а,авправо],[/латекс] равны нулю, поскольку площади выше и ниже [латекс]х[/ латекс]-оси равны.

Интегралы четных и нечетных функций

Для непрерывных четных функций, таких что [latex]f(text{−}x)=f(x),[/latex] 9{8}-2)dx[/latex] и убедитесь, что формула интегрирования для четных функций верна.

Показать решение

Посмотрите следующее видео, чтобы увидеть работающее решение примера: Интеграция четной функции.

Скрытые субтитры и расшифровка информации для видео

Пример: интегрирование нечетной функции

Вычислить определенный интеграл от нечетной функции [латекс]-5 sin x[/латекс] по интервалу [латекс]влево[текст{−}pi ,pi справа].

Источник

Способы задания функции

Пусть функция задается формулой: y=2x^{2}-3. Назначая любые значения независимой переменной x, можно вычислить, пользуясь данной формулой соответствующие значения зависимой переменной y. Например, если x=-0,5, то, пользуясь формулой, получаем, что соответствующее значение y равно y=2 cdot (-0,5)^{2}-3=-2,5.

Взяв любое значение, принимаемое аргументом x в формуле y=2x^{2}-3, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:

x −2 −1 0 1 2 3
y −4 −3 −2 −1 0 1

Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.

Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x. Наиболее часто, это будет приближенное значение функции.

Четная и нечетная функция

Функция является четной функцией, когда f(-x)=f(x) для любого x из области определения. Такая функция будет симметрична относительно оси Oy.

Функция является нечетной функцией, когда f(-x)=-f(x) для любого x из области определения. Такая функция будет симметрична относительно начала координат O (0;0).

Функция является ни четной, ни нечетной и называется функцией общего вида, когда она не обладает симметрией относительно оси или начала координат.

Исследуем на четность нижеприведенную функцию:

f(x)=3x^{3}-7x^{7}

D(f)=(-infty ; +infty ) с симметричной областью определения относительно начала координат. f(-x)= 3 cdot (-x)^{3}-7 cdot (-x)^{7}= -3x^{3}+7x^{7}= -(3x^{3}-7x^{7})= -f(x).

Значит, функция f(x)=3x^{3}-7x^{7} является нечетной.

Периодическая функция

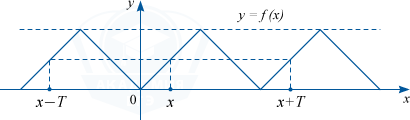
Функция y=f(x), в области определения которой для любого x выполняется равенство f(x+T)=f(x-T)=f(x), называется периодической функцией с периодом T neq 0.

Повторение графика функции на любом отрезке оси абсцисс, который имеет длину T.

График периодической функции с периодом T

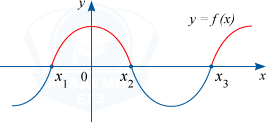
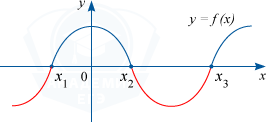
Промежутки, где функция положительная, то есть f(x) > 0 — отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих выше оси абсцисс.

f(x) > 0 на (x_{1}; x_{2}) cup (x_{3}; +infty )

График функции f(x) с промежутками на которых функция положительна

Промежутки, где функция отрицательная, то есть f(x) < 0 — отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

f(x) < 0 на (-infty; x_{1} ) cup (x_{2}; x_{3} )

График функции f(x) с промежутками на которых функция отрицательна

Ограниченность функции

Ограниченной снизу принято называть функцию y=f(x), x in X тогда, когда существует такое число A, для которого выполняется неравенство f(x) geq A для любого x in X.

Пример ограниченной снизу функции: y=sqrt{1+x^{2}} так как y=sqrt{1+x^{2}} geq 1 для любого x.

Ограниченной сверху называется функция y=f(x), x in X тогда, когда существует такое число B, для которого выполняется неравенство f(x) neq B для любого x in X.

Пример ограниченной снизу функции: y=sqrt{1-x^{2}}, x in [-1;1] так как y=sqrt{1+x^{2}} neq 1 для любого x in [-1;1].

Ограниченной принято называть функцию y=f(x), x in X тогда, когда существует такое число K > 0, для которого выполняется неравенство left | f(x) right | neq K для любого x in X.

Пример ограниченной функции: y=sin x ограничена на всей числовой оси, так как left | sin x right | neq 1.

Возрастающая и убывающая функция

О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) > y(x_{2}).

Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) < y(x_{2}).

Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0).

а) Если при x > 0 четная функция возрастает, то убывает она при x < 0

График четной функции

б) Когда при x > 0 четная функция убывает, то возрастает она при x < 0

График четной функции

в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x < 0

График нечетной функции

г) Когда нечетная функция будет убывать при x > 0, то она будет убывать и при x < 0

График нечетной функции

Экстремумы функции

Точкой минимума функции y=f(x) принято называть такую точку x=x_{0}, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}), и для них тогда будет выполняться неравенство f(x) > f(x_{0}). y_{min} — обозначение функции в точке min.

Точкой максимума функции y=f(x) принято называть такую точку x=x_{0}, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}), и для них тогда будет выполняется неравенство f(x) < f(x^{0}). y_{max} — обозначение функции в точке max.

Необходимое условие

Согласно теореме Ферма: f'(x)=0 тогда, когда у функции f(x), что дифференцируема в точке x_{0}, появится экстремум в этой точке.

Достаточное условие

  1. Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
  2. x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0}.

Наибольшее и наименьшее значение функции на промежутке

Шаги вычислений:

  1. Ищется производная f'(x);
  2. Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку [a; b];
  3. Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции, а большее — наибольшим.
Источник

Четность и нечетность функции

Определения и свойства четных и нечетных функций

ОПРЕДЕЛЕНИЕ

Функция

(
f(x)
) называется четной функцией, если для любого x из области определения выполняется равенство (
f(-x)=f(x)
)

Функция (
f(x)
) называется нечетной функцией, если для любого x из области определения выполняется равенство (
f(-x)=-f(x)
)

Если ни одно из условий (
f(-x)=f(x)
) или (
f(-x)=-f(x)
) не выполняется, то говорят, что функция (
f(x)
) не является ни четной, ни нечетной (или функцией общего вида)

График четной функции симметричен относительно оси ординат, график нечетной функции симметричен относительно начала координат.

При исследовании функции на четность и нечетность можно использовать следующие свойства:

1.Сумма двух четных функций четна, а сумма двух нечетных функций нечетна.

2.Произведение двух четных функций является четной функцией, равно как и произведение двух нечетных функций. Произведение четной и нечетной функции — нечетная функция.

3.Если функция (
f(x)
) четная (нечетная), то и функция (
frac{1}{f(x)}
) четная (нечетная).

Примеры решения задач

ПРИМЕР 1

  • Задание

    Используя определение исследовать на четность и нечетность следующие функции

    (
    f_{1}(x)=2 x^{4}-3 x^{2}+6 ; 2 ) f_{2}(x)=8 x^{3}-7 x ; 3 ) f_{3}(x)=x^{4}-4 x+5
    )

  • Решение

    1) Рассмотрим значение функции (
    f_{1}(x)=2 x^{4}-3 x^{2}+6
    ) в точке (
    (-x)
    ) :

    (
    f_{1}(x)=2 x^{4}-3 x^{2}+6
    )

    Для заданной функции выполняется условие (
    f_{1}(-x)=f_{1}(x)
    ) ,следовательно, она четная.

    2) Найдем значение функции (
    f_{2}(x)=8 x^{3}-7 x
    ) в точке (
    (-x)
    ) :

    (
    f_{2}(-x)=8 cdot(-x)^{3}-7 cdot(-x)=-8 x^{3}+7 x=-left(8 x^{3}-7 xright)=-f_{2}(x)
    )

    Для этой функции выполняется условие (
    f_{2}(-x)=-f_{2}(x)
    ),следовательно, она является нечетной.

    3) Найдем значение функции (
    f_{3}(x)=x^{4}-4 x+5
    ) в точке (
    (-x)
    ) :

    (
    f_{3}(-x)=(-x)^{4}-4 cdot(-x)+5=x^{4}+4 x+5
    )

    Таким образом, (
    f_{3}(-x) neq f_{3}(x) ; f_{3}(-x) neq-f_{3}(x)
    ) , значит, функция (
    f_{3}(x)=x^{4}-4 x+5
    ) не является ни четной, ни нечетной.

  • Ответ

    1) (
    f_{1}(x)=2 x^{4}-3 x^{2}+6
    ) — четная;

    2) (
    f_{2}(x)=8 x^{3}-7 x
    ) — нечетная;

    3) (
    f_{3}(x)=x^{4}-4 x+5
    ) — ни четная, ни нечетная.

    ПРИМЕР 2

  • Задание

    Исследовать функцию (
    f(x)=frac{x^{2}+4}{3 x^{6}+x^{4}+7}
    ) на четность, используя свойства четных и нечетных функций.

  • Решение

    Исследуем отдельно четность функции, которые находятся в числителе и знаменателе:

    (
    g(-x)=(-x)^{2}+4=x^{2}+4=g(x)
    )

    то есть функция (
    g(x)
    ) четная; аналогично

    (
    h(-x)=3(-x)^{6}+(-x)^{4}+7=3 x^{6}+x^{4}+7=h(x)
    )

    а тогда и функция (
    h(x)
    ) четная.

    По свойству 3, так как (
    h(x)
    ) — четная, то четной будет и функция (
    frac{1}{h(x)}=frac{1}{3 x^{6}+x^{4}+7}
    ) .Тогда исходную функцию (
    f(x)
    ) можно представить в виде произведения четных функций (
    f(x)=g(x) cdot frac{1}{h(x)}
    ) , следовательно, по свойству 2, (
    f(x)
    ) — четная.

  • Ответ

    Исследованная функция четная.

    • Источник

    Понравилась статья? Поделить с друзьями:
  • Как найти площадь параллелограмма abcd ответ
  • Как найти инфо по делу
  • Как исправить переключатель на смесителе
  • Как найти наградной лист вов по фамилии
  • Как найти числа если дано среднее арифметическое