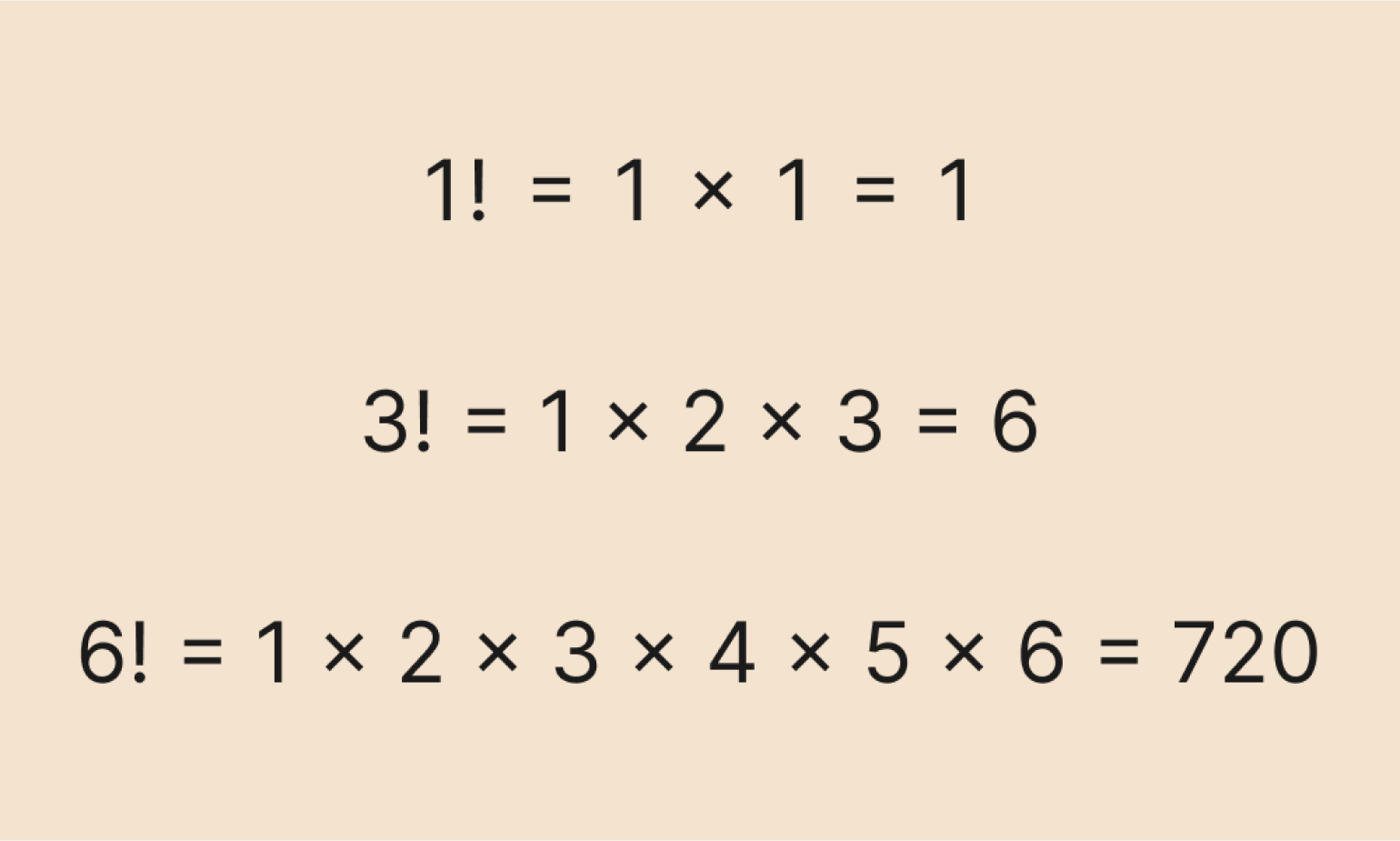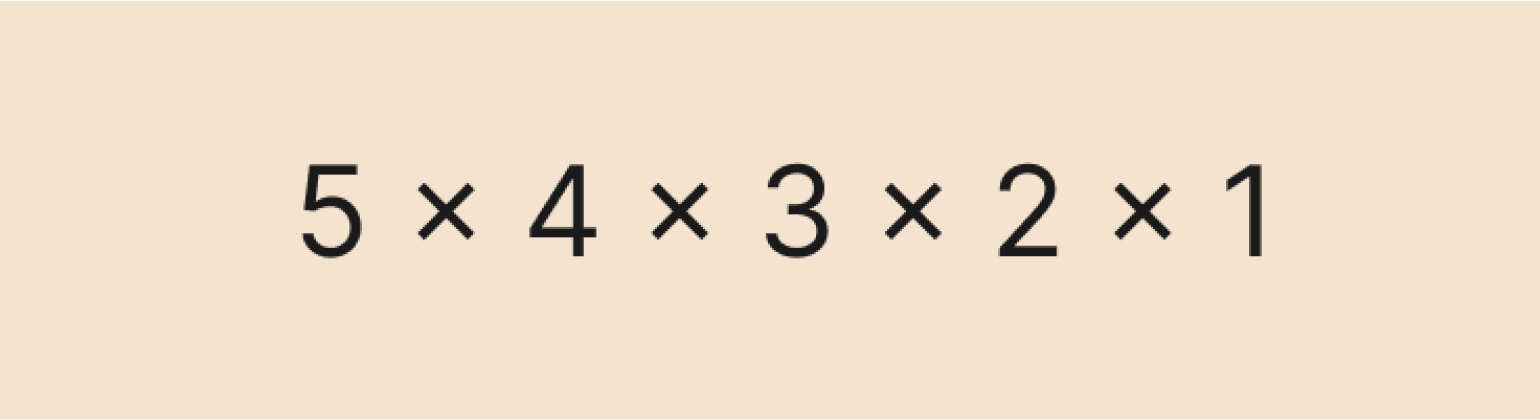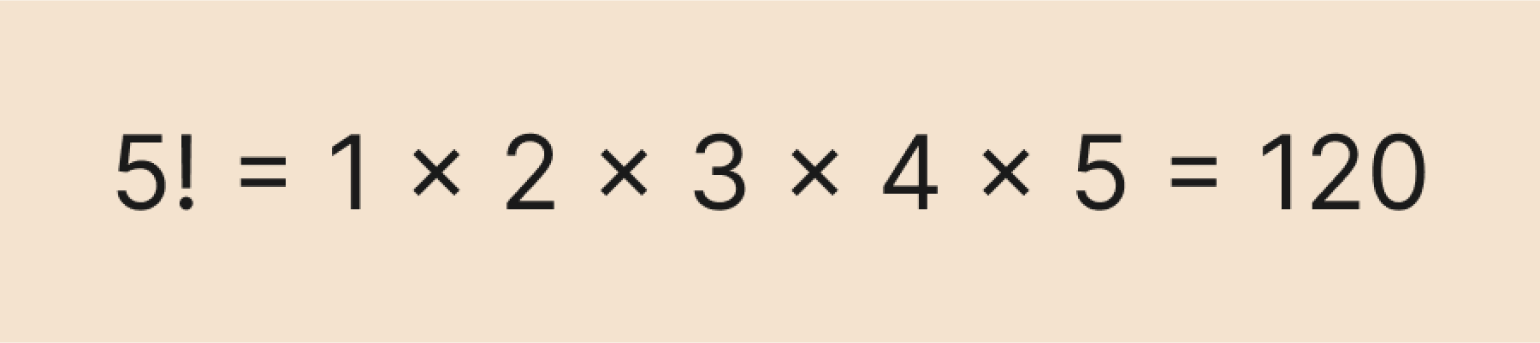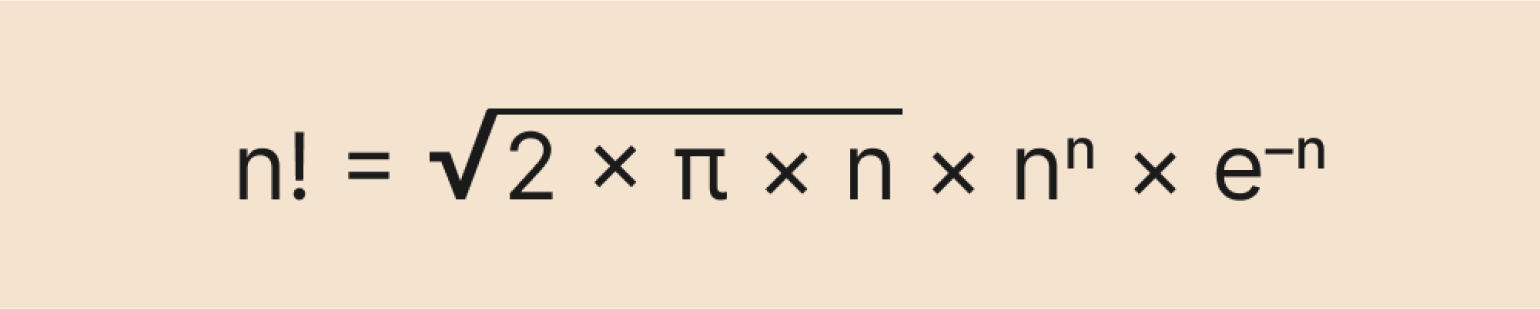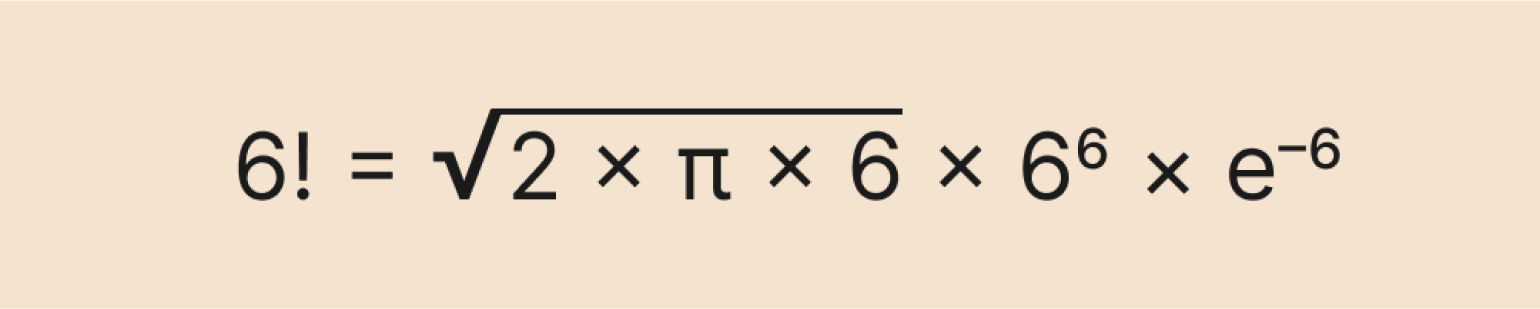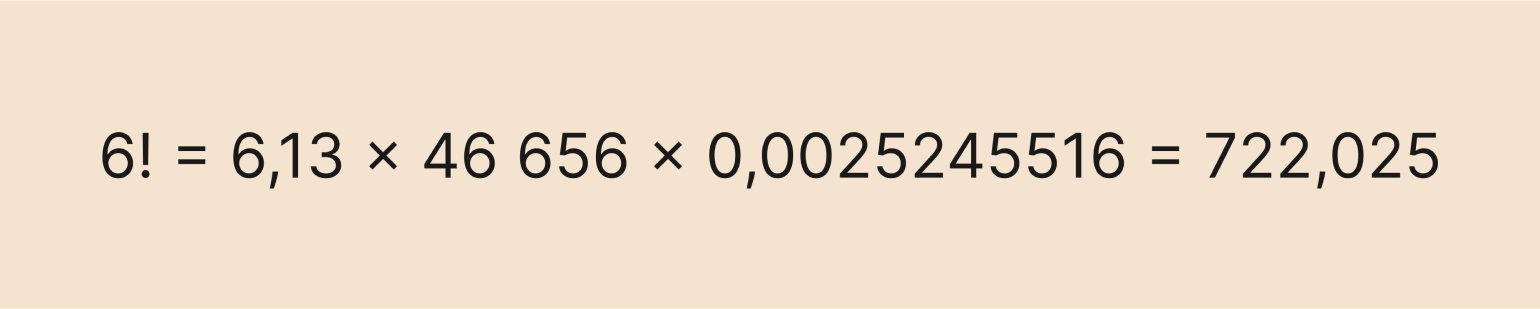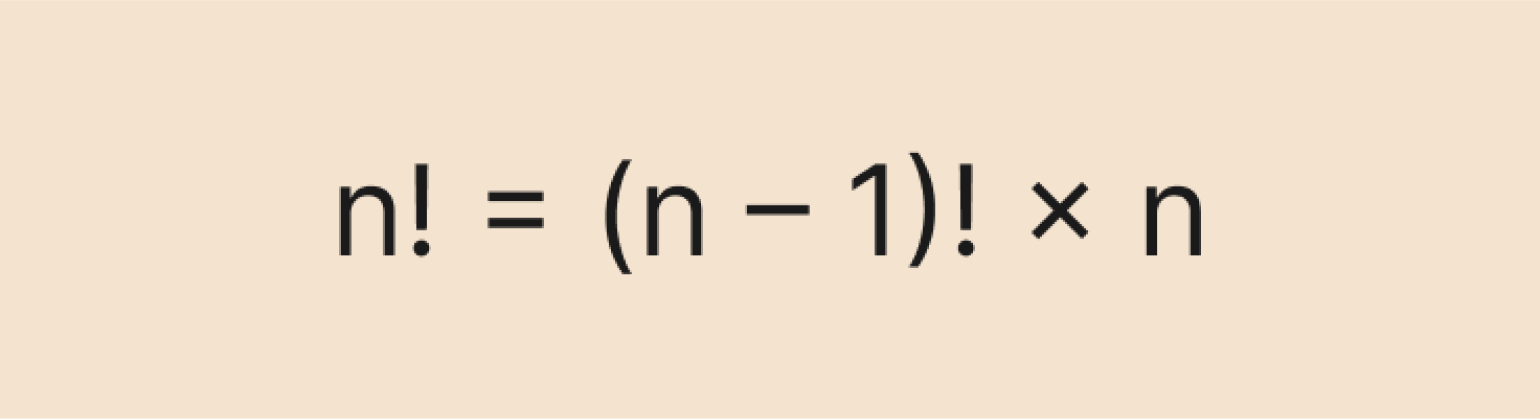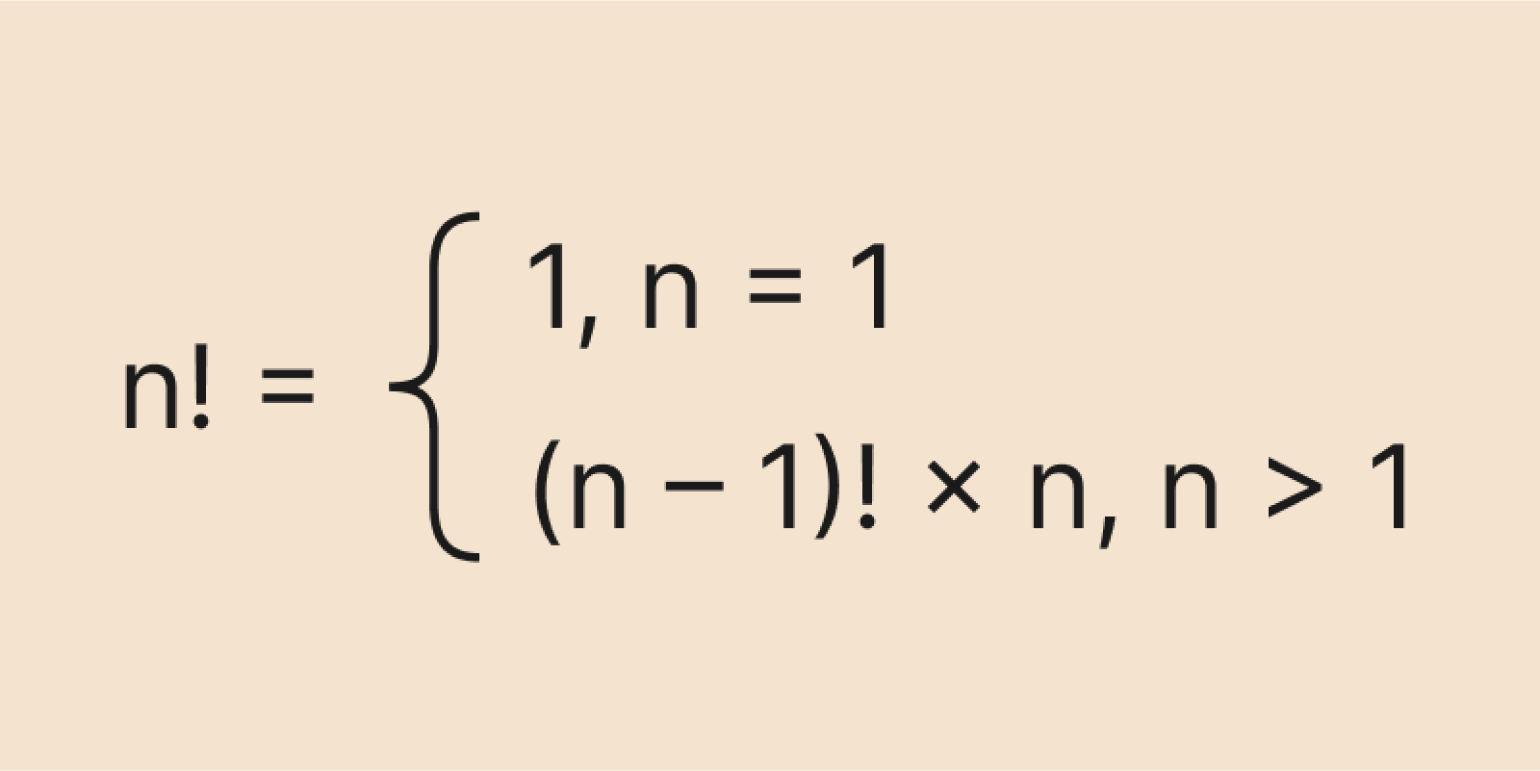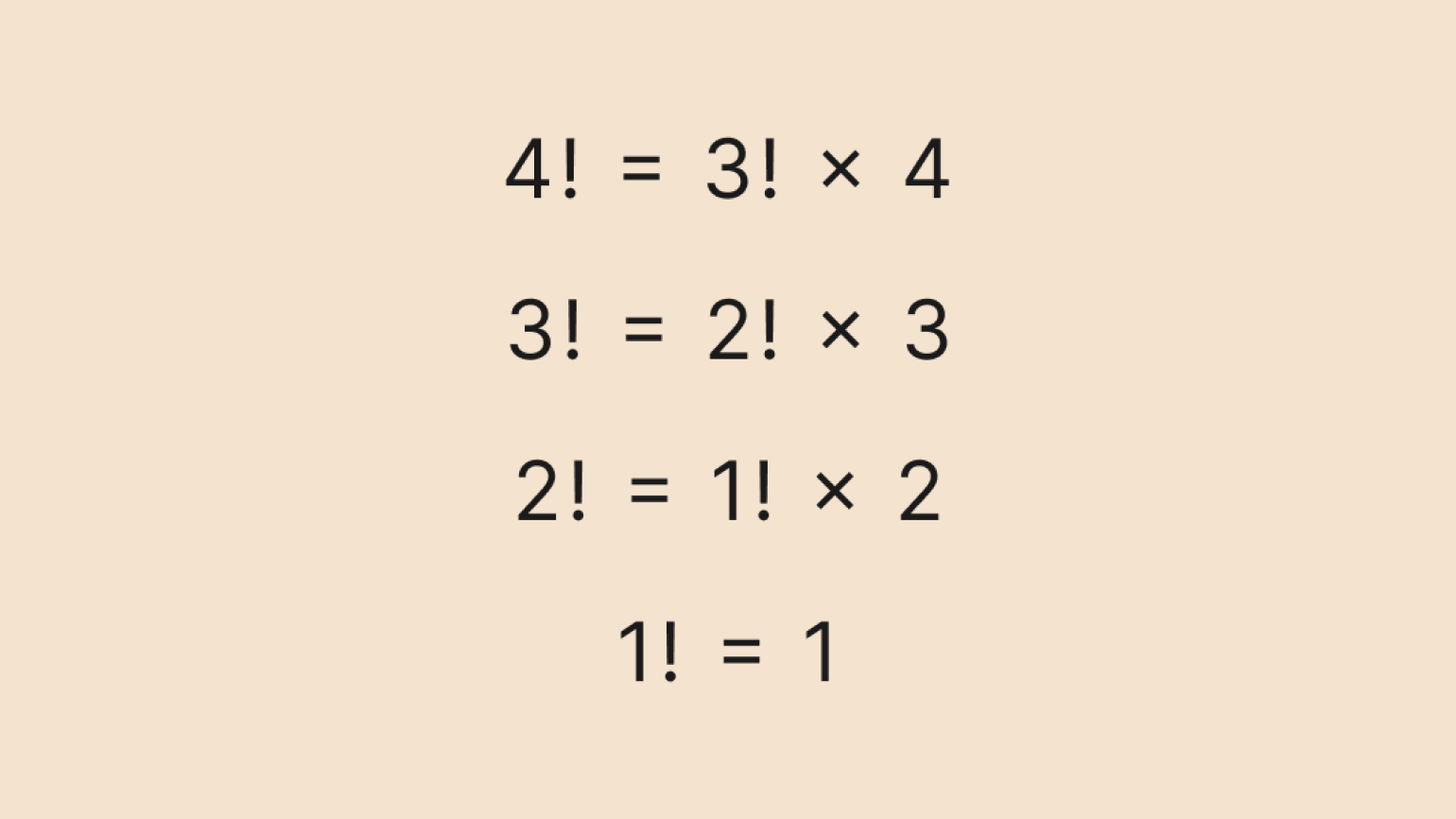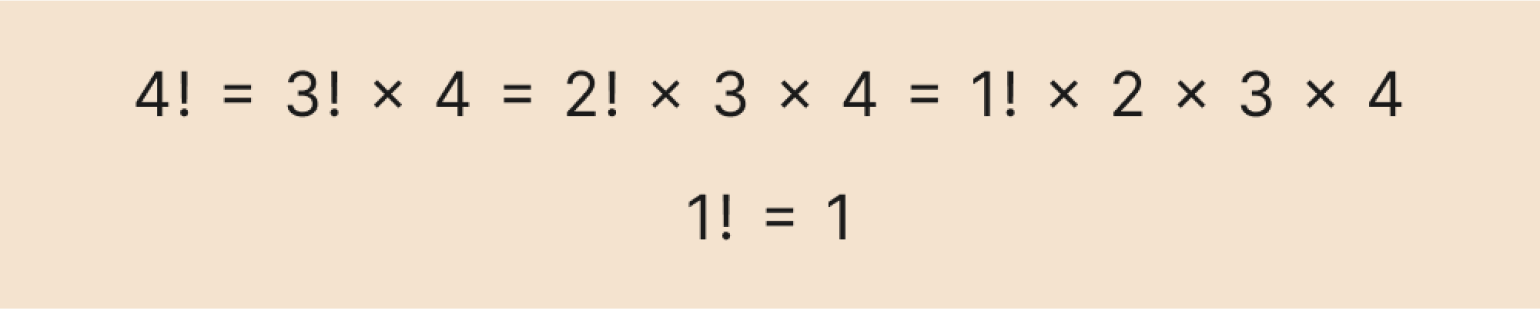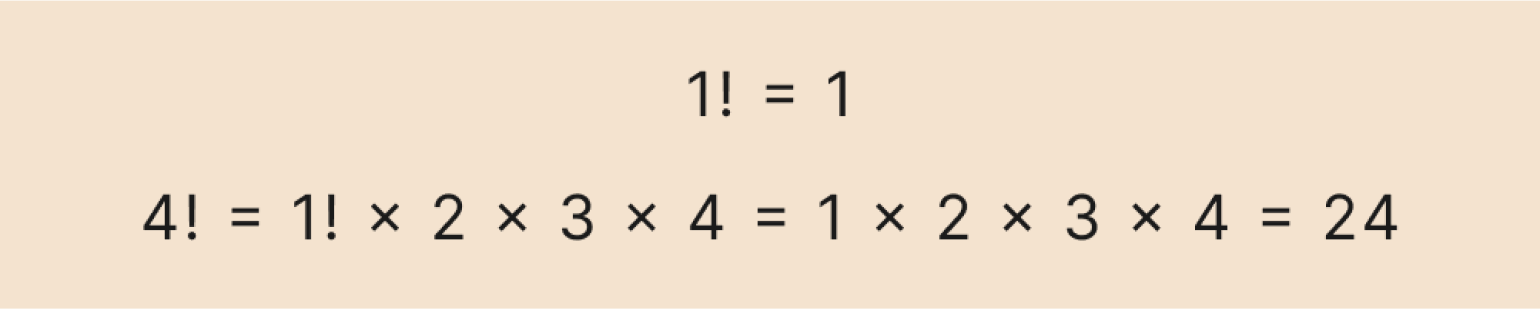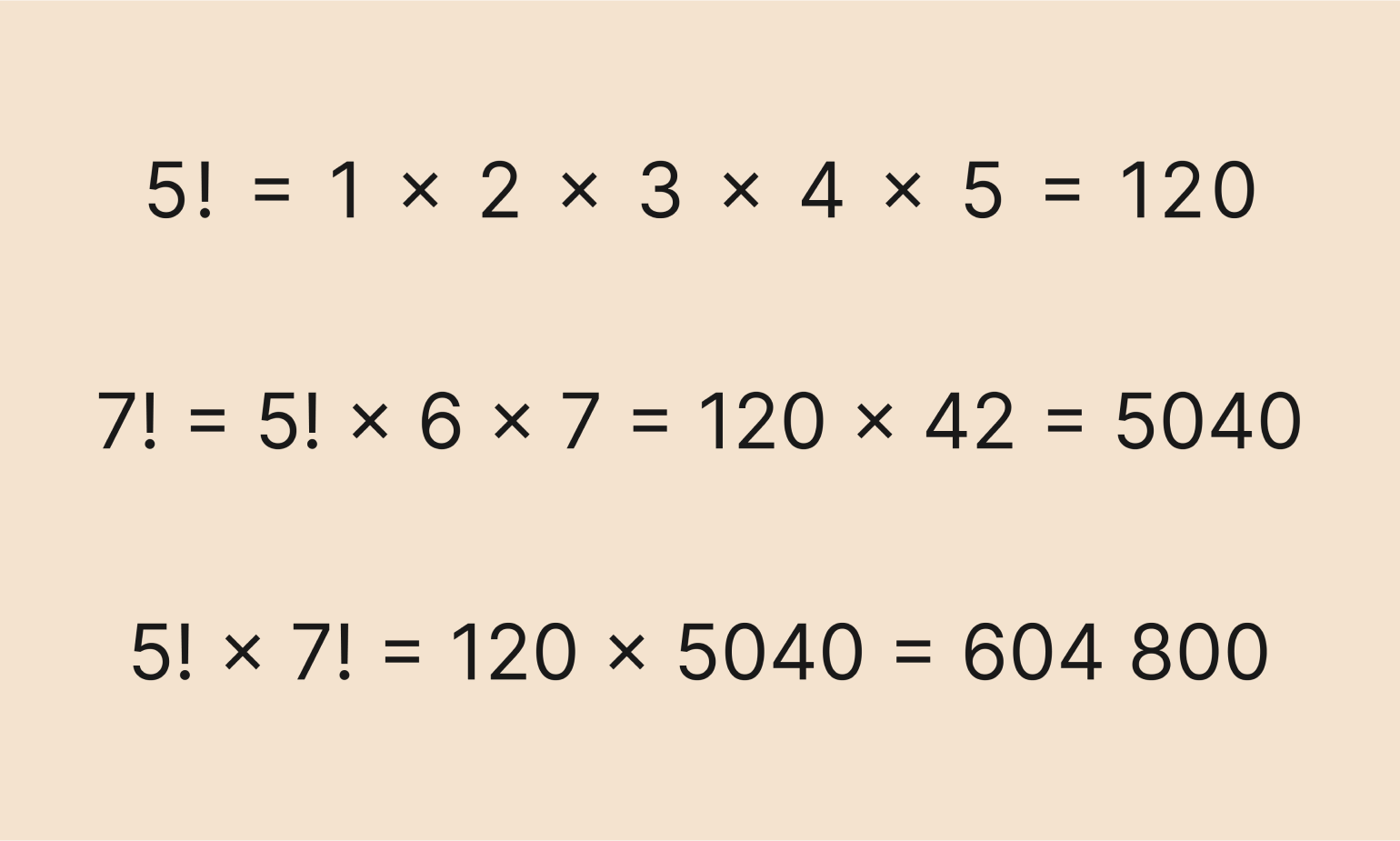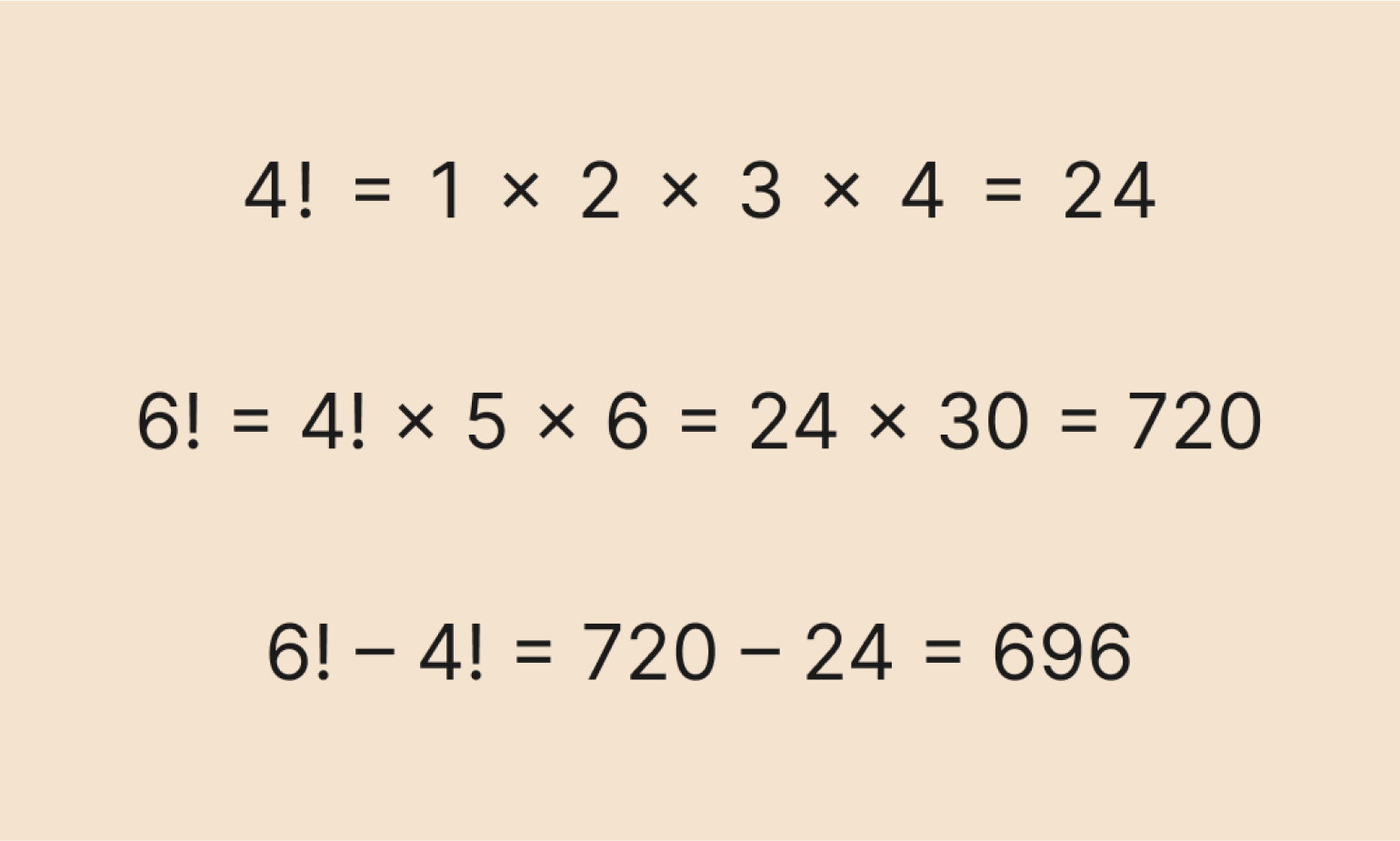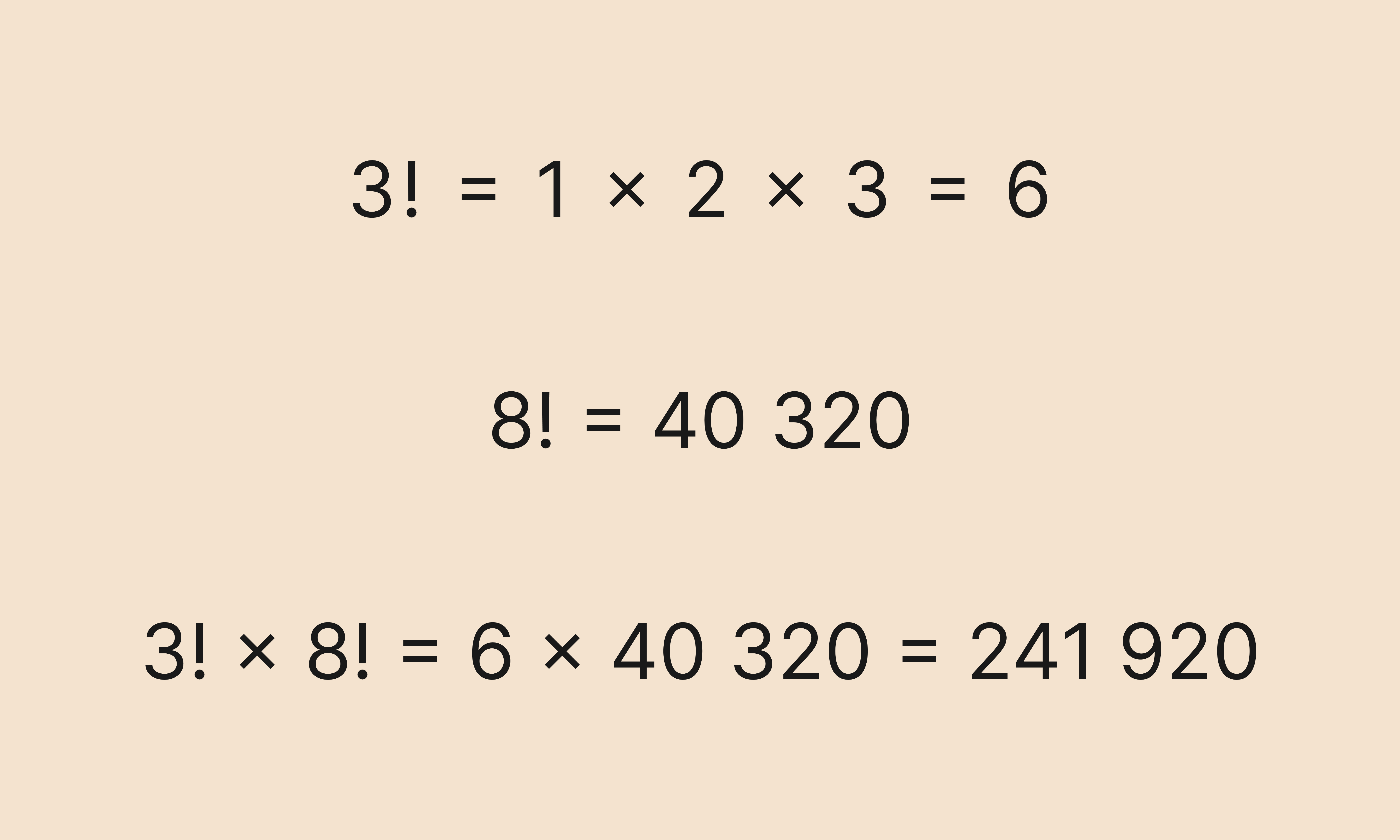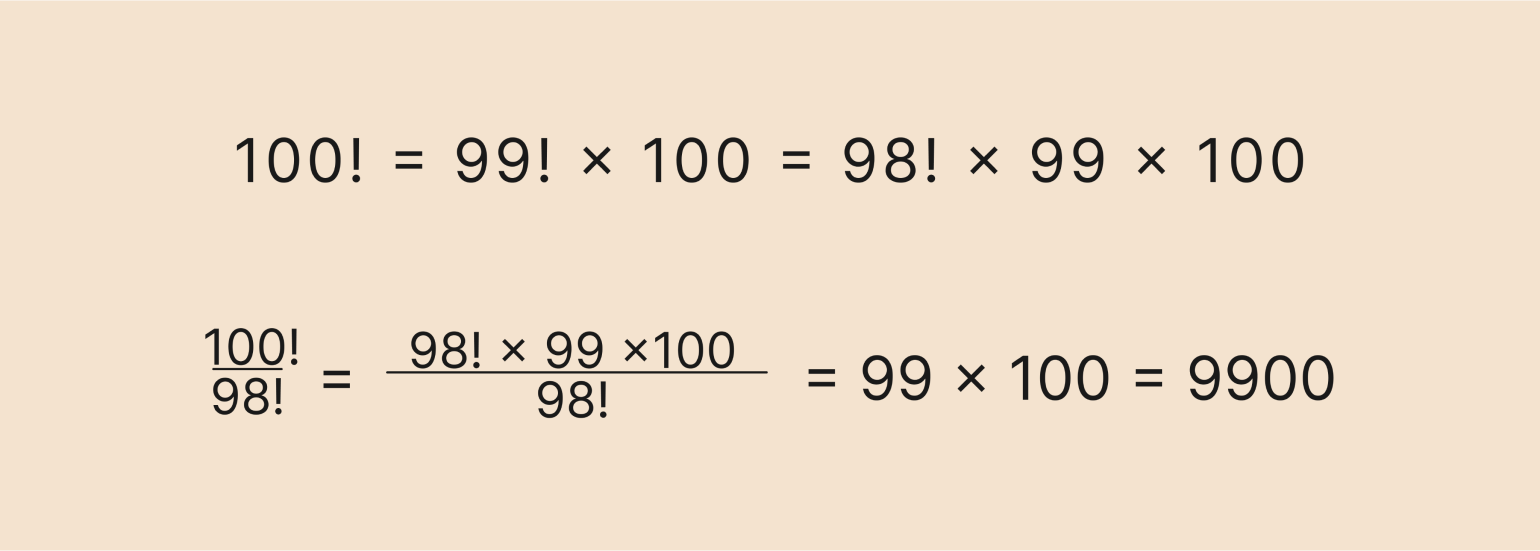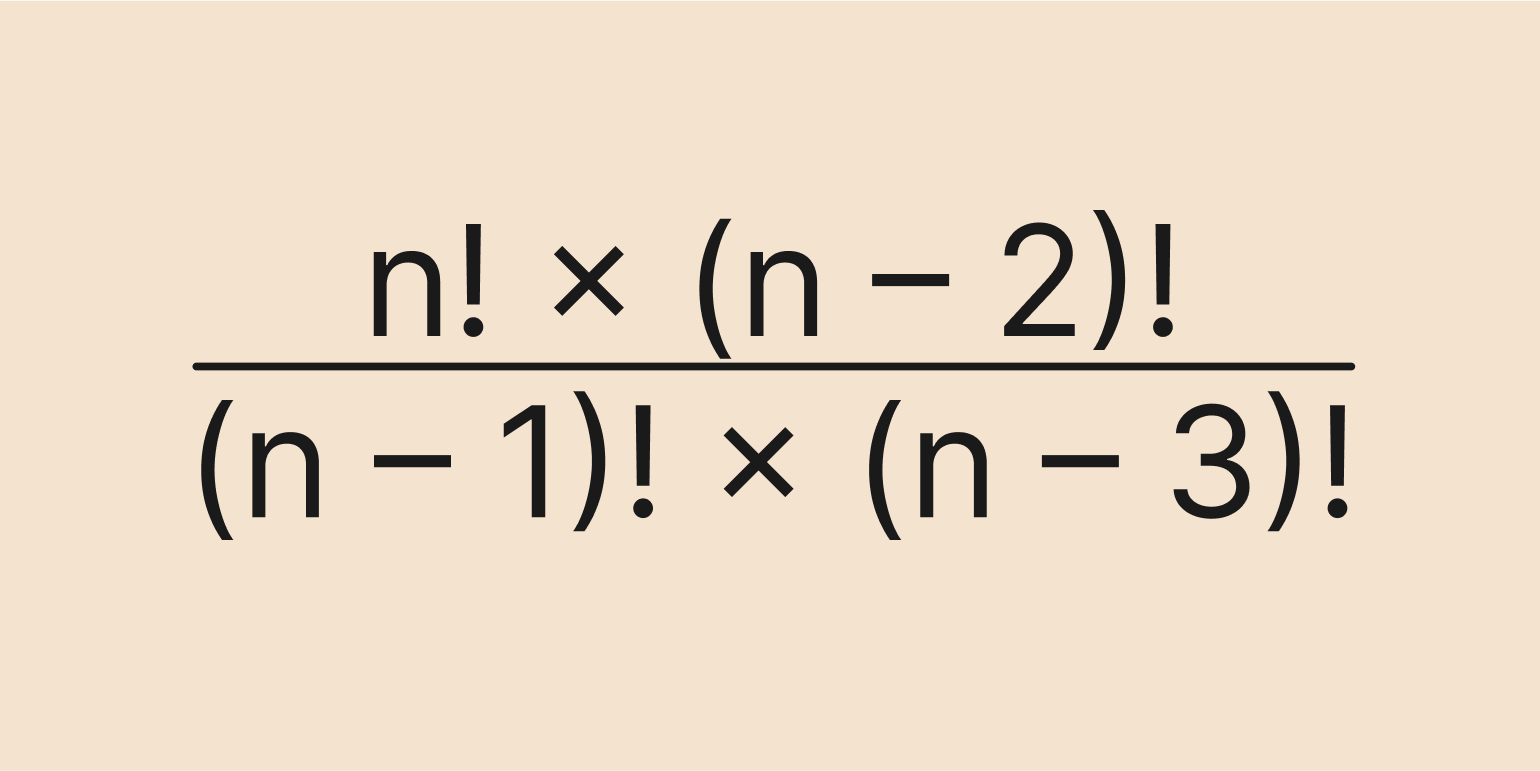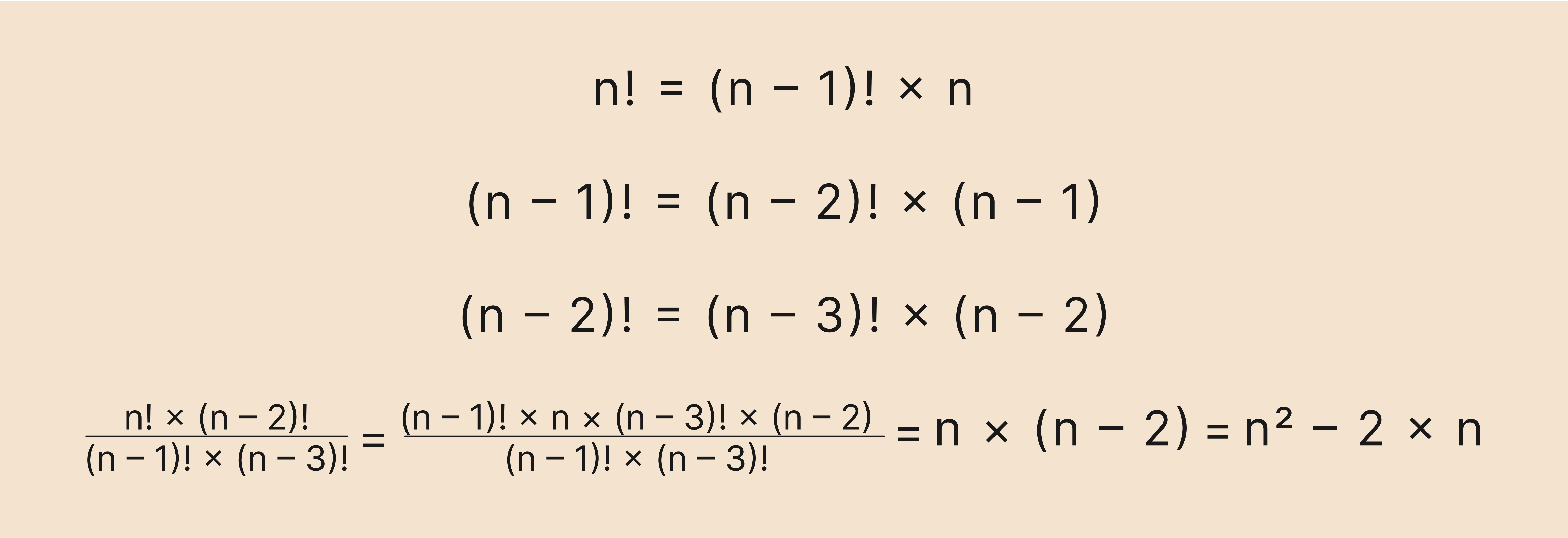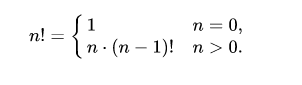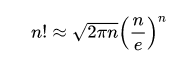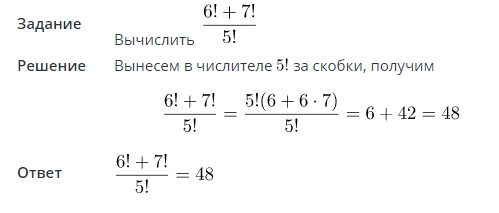#статьи
- 19 май 2023
-
0
Что такое факториал и как его вычислить
Статья, после которой вы начнёте щёлкать факториалы как орешки.
Иллюстрация: Катя Павловская для Skillbox Media
Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.
Даже если вы уже давно окончили школу, факториалы всё равно могут доставить немало приятных флешбэков — например, если вы обучаетесь программированию и знакомитесь с задачками на рекурсию или комбинаторику. Поэтому мы решили максимально просто объяснить, что такое факториал, как его вычислять и зачем он вообще нужен.
Эта статья будет полезна как опытным программистам, которые хотят освежить знания, так и тем, кто ещё учится: школьникам, студентам и совсем зелёным джунам.
Содержание:
- Что такое факториал
- Для чего он нужен
- Основные свойства и формулы
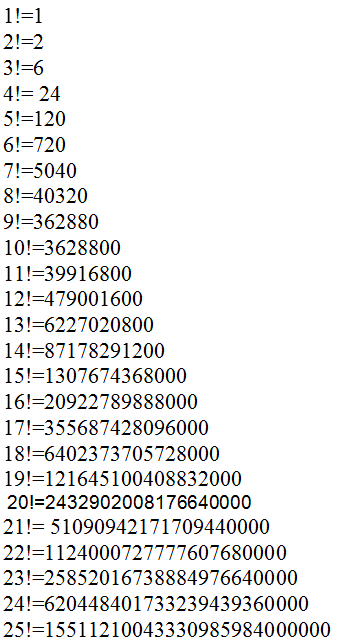
- Шпаргалка: таблица факториалов
- Решаем задачи на факториалы
- Что запомнить
Факториал числа n — это произведение всех натуральных чисел от единицы до n. Обозначается факториал символом восклицательного знака: !.
Это определение из учебника, и оно пока звучит сложновато — неясно, зачем эти факториалы вообще нужны и как они могут пригодиться в науке и технике. Но об этом чуть позже — для начала давайте посмотрим на примеры факториалов:
Чтобы вычислить их, нам нужно перемножить все числа от единицы до числа, стоящего под знаком факториала — так гласит определение. Получаем выражения:
Ещё в математическом определении сказано, что факториал не может быть отрицательным или дробным — то есть вот такие факториалы вычислить нельзя:
Факториалы незаменимы там, где нужно быстро посчитать количество комбинаций и сочетаний разных предметов. В математике этому посвящён даже целый раздел — комбинаторика. Её методы используют много где: от лингвистики до криптографии и анализа ДНК. И во всех этих сферах факториал помогает упрощать сложные вычисления.
Разберём на примере, как это работает.
Допустим, у вас есть пять шоколадок и вы решили раздать их пяти друзьям — каждому по одной. Задача — выяснить, сколько существует способов раздать эти шоколадки. Начинаем размышлять:
- первую шоколадку можно отдать одному из пяти друзей;
- вторую — одному из четырёх друзей, потому что один уже получил свою шоколадку;
- третью — одному из трёх, потому что двое уже наслаждаются своими шоколадками;
- четвёртую — одному из двух;
- пятую — последнему другу.
Получается, что способов раздать первую шоколадку — 5, вторую — 4, третью — 3, четвёртую — 2, а пятую — всего 1. По правилам математики, чтобы выяснить общее количество всех вариантов, нужно перемножить их между собой. Ну а кто мы такие, чтобы с этими правилами спорить?
Смотрим на выражение выше и понимаем: ведь оно идеально вписывается в определение факториала — произведение натуральных чисел от одного до n (в нашем случае n равно 5). Следовательно, это выражение можно коротко и изящно записать в виде факториала:
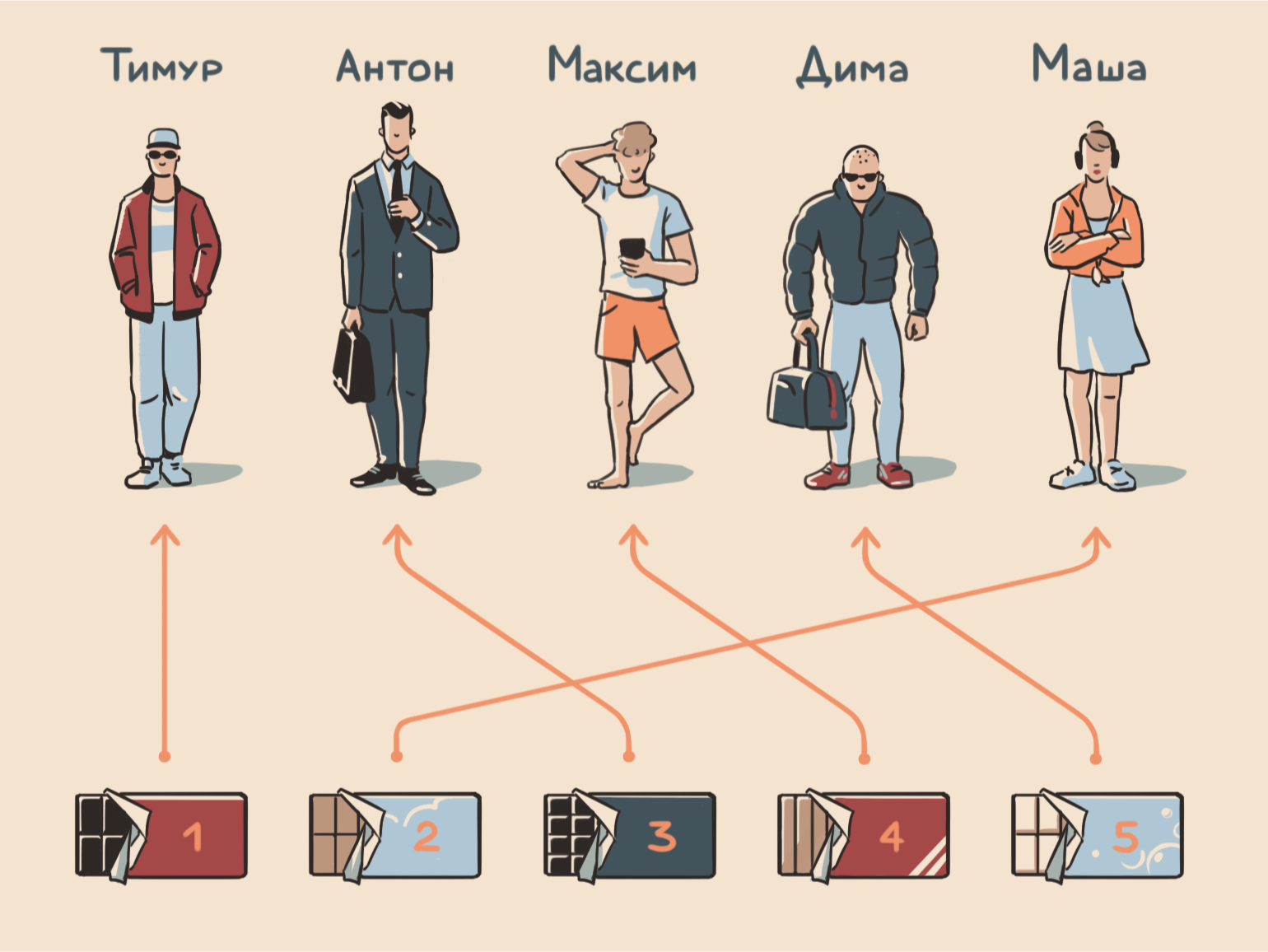
Выходит, что всего способов раздать пять шоколадок пяти друзьям существует 120. Вот как может выглядеть один из них:
Конечно, в жизни вам вряд ли придётся считать количество способов раздать друзьям шоколадки. Но, например, в статистике, теории вероятностей, матанализе и программировании факториалы используют сплошь и рядом. Так что, если видите себя в будущем на матмехе или, на худой конец, в IT, то лучше познакомиться с ними хотя бы бегло.
Так как факториалы используются в разных областях математики, свойств у них довольно много — каждая область привносит какие-то свои методы вычислений. Одно из свойств вы уже знаете: факториал — это всегда целое положительное число. Вот ещё несколько, которые стоит запомнить:
- Факториал нуля равен единице — 0! = 1.
- Факториал единицы тоже равен единице: 1! = 1.
- Рекурсия: n! = (n – 1)! × n. Это основное свойство факториалов, о нём мы чуть подробнее поговорим дальше.
Мы видим, что каждое свойство описывается какой-то формулой — и некоторые из этих формул могут быть весьма полезны. Они позволяют нам находить факториалы проще и быстрее, чем простым перемножением натуральных чисел. Разберём эти формулы тоже.
Чтобы вычислить факториал, не используя так много операций умножения, придумали формулу Стирлинга. Вот как она выглядит:
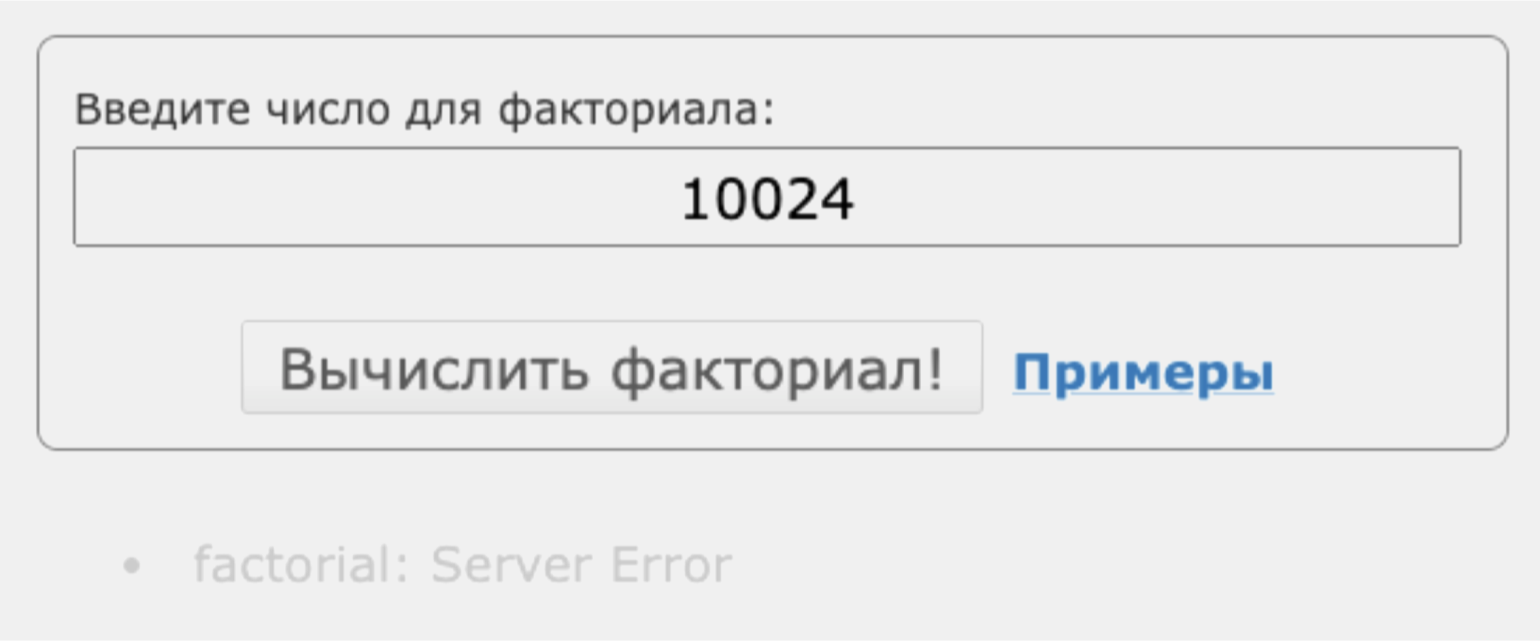
Выглядит страшно, но на самом деле она очень полезная. Её используют, когда хотят приблизительно узнать факториал большого числа. Обычным способом это будет сделать сложно даже мощному компьютеру — например, попробуйте посчитать в онлайн-калькуляторе факториал числа 10 024 (спойлер: это может занять несколько часов и даже дней).
Скришнот: «Контрольная работа РУ — калькуляторы онлайн» / Skillbox Media
Давайте попробуем вычислить факториал числа 6 по этой формуле:
Число e примерно равно 2,71, а π — 3,14. Подставляем их в выражение и получаем ответ:
Получили приближённое значение настоящего факториала, который равен 720. Но можно сделать ответ и более точным. Для этого нужно добавить больше знаков после запятой всем переменным — например, если взять 20 знаков, то ответ будет таким:
Это уже больше похоже на правду. Хотя погрешность всё равно есть.
Рекуррентная формула позволяет вычислить факториал числа n, основываясь на факториале предыдущего числа — (n – 1). Выглядит она так:
В целом рекуррентная формула не приносит нам большой пользы, так как всё равно приходится вычислять факториал предыдущего числа. Если он равен какому-то большому числу (например, 100), то использование формулы теряет смысл — слишком уж много вычислений это потребует.
Рекуррентная формула основана на главном свойстве факториалов — рекурсии: n! = (n – 1)! × n. Это свойство особенно полезно при решении задач по комбинаторике: так мы можем быстро сокращать факториалы и упрощать выражения.
Однако рекуррентная формула хорошо подходит для алгоритмов — в частности, для программирования. Мы можем задать начальное значение: например, что 0! = 1 или 1! = 1, а затем считать следующие факториалы по формуле:
Получим алгоритм для вычисления факториалов. Не очень эффективный, но простой.
Давайте вычислим по этой формуле факториал числа 4. Сначала распишем рекуррентную формулу до базового значения — факториала числа 1:
Можно записать это и в сокращённом виде:
Теперь последовательно подставляем значение факториала, которое мы уже знаем, и вычисляем результат:
Получили ответ — 24. Ничего сложного, просто перемножаем числа.
Кстати, всю эту формулу можно обернуть в реально работающую функцию на языке Python:
def factorial(n): # Определяем функцию if n == 0 or n == 1: # Базовый случай return 1 else: # Рекуррентный случай return factorial(n-1) * n # Вызываем эту же функцию, но с меньшим аргументом print(factorial(4)) # Печатаем факториал 4 # Вывод: # 24
Можете попробовать запустить её в онлайн-интерпретаторе и посмотреть, как работает. Тут есть один нюанс: Python не даст вам посчитать факториал числа больше 998, так как у него есть ограничение на количество вызовов функции — в программировании это называется глубиной рекурсии.
Чтобы быстро находить, чему равен факториал, можно запомнить или сохранить в заметки вот такую табличку. Она рассчитана всего на 12 чисел, но для большинства учебных задач этого хватит.
| 1! | 1 |
| 2! | 2 |
| 3! | 6 |
| 4! | 24 |
| 5! | 120 |
| 6! | 720 |
| 7! | 5040 |
| 8! | 40 320 |
| 9! | 362 880 |
| 10! | 3 628 800 |
| 11! | 39 916 800 |
| 12! | 479 001 600 |
С теорией вроде разобрались — теперь попробуем решить несколько задач с факториалами, чтобы закрепить знания на практике.
Задача: перемножить два факториала.
Решение:
Сперва нужно вычислить значения факториалов, а затем перемножить полученные значения:
Обратите внимание: во второй строке мы применили рекуррентную формулу, чтобы быстрее вычислить факториал числа 7.
Задача: вычесть из одного факториала другой.
Решение:
Используем тот же подход, что и в предыдущей задаче: сначала вычисляем факториалы, а затем получаем ответ на всё выражение.
Вроде бы ничего сложного, главное — не запутаться в умножении.
Задача: умножить один факториал на другой:
Решение:
Вычисляем факториалы, потом перемножаем их значения:
Во второй строке мы воспользовались таблицей выше и быстро нашли значение факториала от числа 8.
Задача: сократить дробь и вычислить её значение.
Решение:
Здесь мы воспользуемся рекуррентной формулой для вычисления факториала и разложим верхний факториал на множители:
В первой строке мы применили рекуррентную формулу два раза, а во второй — просто сократили одинаковые факториалы в числителе и в знаменателе.
Задача: сократить дробь.
Решение:
Хотя здесь нет конкретных чисел, но принцип решения остаётся таким же: используем рекуррентную формулу и сокращаем одинаковые значения в числителе и знаменателе.
Главное — не запутаться и правильно применить рекуррентную формулу.
- Факториал — это произведение всех натуральных чисел от 1 до данного числа. Например, факториал числа 5 будет равен 1 × 2 × 3 × 4 × 5 = 120.
- Его используют во многих областях науки — например, комбинаторике, теории вероятностей и математическом анализе.
- Помимо стандартной формулы для вычисления факториала можно использовать формулы Стирлинга и рекуррентную формулу.
- Формула Стирлинга нужна для того, чтобы посчитать факториал без большого числа операций умножения.
- Рекуррентная формула позволяет вычислить факториал на основе предыдущего факториала.

Научитесь: Профессия Data Scientist
Узнать больше
Часто нужно с использованием закона умножения вычислить произведения натуральных чисел по порядку, начиная с (1).
Например,
1⋅2⋅3⋅4⋅5⋅6⋅7
и т. д. Не всегда важно вычислить числовое произведение. Чтобы можно было короче записать выражения такого вида, в математике используется знак «(!)».
Произведение всех натуральных чисел от 1 до (n) включительно называется факториалом числа n и записывается
n!
(читается как «эн факториал»).
Принято, что (0! = 1).
Пример:
1 задание.
Вычисли значение выражения.
a)
5!+4!=5⋅4⋅3⋅2⋅1+4⋅3⋅2⋅1=120+24=144
.
b)
7!−5!4!=7⋅6⋅5⋅4!−5⋅4!4!=5⋅4!(42−1)4!=5⋅41=205
((4!) выносится за скобки. В дроби равные факториалы можно сокращать).
c)
80!79!+59!58!=80⋅79!79!+59⋅58!58!=80+59=139
.
Каждый больший факториал можно выразить меньшим факториалом, т. е.
(n! = n(n-1)! = n(n-1)(n-2)! = n(n-1)(n-2)(n-3)!) и т. д.
Пример:
2 задание.
Сократи дробь:
.
3 задание.
Упрости выражение:
.
При увеличении значения (n) значение (n!) стремительно возрастает. Знак факториала удобно использовать, если нужно записывать большие числа.
Пример:
сколькими различными способами можно составить список учеников, если в нём должно быть (25) различных учеников?
1⋅2⋅3⋅…⋅24⋅25=25!
Ответ: список можно составить (25!) различными способами.
Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала.
Это очень просто, вот пример:
7! = 1 * … * 7 = 5040.
Факторизация — разложение функции на множители.
Таблица факториалов
Свойства факториалов
Рекуррентная формула
Комбинаторная интерпретация
Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.
Формула Стирлинга
Позволяет не перемножать большие числа. Обычно необходим только главный член:
Можно ли вычислить 0,5 или -3,217? Нет, нельзя. Но можно использовать нечто под названием «Гамма-функция», что намного сложнее.
Расчет по предыдущему значению
Функцию легко вычислить из предыдущего значения:
-
3! = 3 × 2! = 6;
-
41160 = 5! +8! + 6!
А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0.
Однако было решено, что в случае 0 результат будет равен 1.
Некоторые очень большие значения
Онлайн калькулятор поможет сделать вычисление – всего лишь надо найти знак, похожий на «x!» или «n!». Нужно обратить внимание, что браузеры могут испытывать затруднения при попытке отобразить более крупные числа и может произойти сбой.
Некоторые браузеры могут не позволять копировать, поэтому необходимо будет загрузить большие результаты в виде текстового файла.
Примеры вычисления факториалов больших чисел:
-
70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);
-
100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;
-
200! это примерно 7 88657867867364479050355236321393 x 103743.
Как найти функцию в Паскаль? Вычисление легко реализуется на разных языках программирования. Можно выбрать два метода: итеративный, то есть он создает цикл, в котором временная переменная умножается на каждое натуральное число от 1 до n, или рекурсивный, в котором функция вызывает себя до достижения базового варианта 0! = 1.
Программа на языке Паскаль:
На языке Си вычисления делаются с помощью рекурсивной функции. Следует заметить, что если начать вычислять факториал отрицательного числа в неаккуратно написанной функции, то это приведет к зацикливанию.
Факториал дроби (½) — это половина квадратного корня pi = (½)√π.
Примеры задач с решениями
Задание 1
Задание 2
Использование факториалов
Математика и многие ее области используют функцию. В комбинаторике функция была введена именно для расчета перестановки. Также понятие тесно связано с биномом ньютона (формула бинома Ньютона необходима для разложения степени (x + y) n в многочлен).
A factorial is a mathematical operation that you write like this: n!. It represents the multiplication of all numbers between 1 and n.
So if you were to have 3!, for example, you’d compute 3 x 2 x 1 (which = 6). Let’s see how it works with some more examples.
Definition of a Factorial
The factorial of a number is the multiplication of all the numbers between 1 and the number itself. It is written like this: n!. So the factorial of 2 is 2! (= 1 × 2).
To calculate a factorial you need to know two things:
0! = 1n! = (n - 1)! × n
The factorial of 0 has value of 1, and the factorial of a number n is equal to the multiplication between the number n and the factorial of n-1.
For example, 5! is equal to 4! × 5.
Here the first few factorial values to give you an idea of how this works:
| Factorial | Multiplication | Result |
|---|---|---|
| 0! | 1 | 1 |
| 1! | 1 | 1 |
| 2! | 1 × 2 | 2 |
| 3! | 1 × 2 × 3 | 6 |
| 4! | 1 × 2 × 3 × 4 | 24 |
| 5! | 1 × 2 × 3 × 4 × 5 | 120 |
| 6! | 1 × 2 × 3 × 4 × 5 × 6 | 720 |
| 7! | 1 × 2 × 3 × 4 × 5 × 6 × 7 | 5040 |
| 8! | 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 | 40,320 |
| 9! | 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 | 362,880 |
What is a Factorial Used For?
Practically speaking, a factorial is the number of different permutations you can have with n items: 3 items can be arranged in exactly 6 different ways (expressed as 3!).
For example, let’s see all the arrangements you can have with the three items, A, B and C:
ABC
ACB
BAC
BCA
CAB
CBAAnd in fact, 3! = 6.
How to Calculate the Factorial of 0
Looking at the factorial from this point of view, what’s the factorial of 0?
Well, how many different ways can you arrange 0 elements?
There is exactly 1 way to arrange zero elements. And that’s making a sequence of zero elements.
Factorial Use Cases
You typically use a factorial when you have a problem related to the number of possible arrangements. Let’s look at some example problems.
Factorial example problem 1: the letters in the word «camper»
How many different ways can you arrange the letters of the word camper?
The word camper has 6 letters, so the number of possible arrangements is given by the factorial of 6: 6! = 6 × 5 × 4 × 3 × 2 × 1 = 720. That would have been a pretty big number of arrangements to find by hand, wouldn’t it?
Factorial example problem 2: drawing colored balls from a bag
Let’s say there are three balls in a bag – one green, one blue, and one yellow.
If you draw the three balls in sequence, what chance is there that you’ll get the yellow first, the green one second, and the blue one last?
Maybe now you are wondering what chances have to do with factorials – well, in a moment you will see.
There are 6 possible sequences in which the balls can be drawn: 3! = 6.
There is a chance of 1 over the total number of possibilities to get the yellow-green-blue sequence, so that is 1/(3!) or 1/6 or 16.7% chance to get the desired outcome.
How to Calculate a Factorial Programmatically with JavaScript
There are two ways to calculate factorials programmatically in JavaScript:
How to calculate a factorial in JS with recursion
Let’s get back to the two things to know when calculating a factorial – that is 0! = 1 and n! = (n - 1)! × n. We can use the first one to create the base case of the recursive function, because in that case we know the result already.
function factorial(n) {
if (n === 0) {
return 1;
}
}The second thing to know about how to calculate a factorial, n! = (n - 1)! × n, can be the recursive case.
function factorial(n) {
if (n === 0) {
return 1;
} else {
return factorial(n-1) * n;
}
}
How to calculate a factorial with a JavaScript while loop
We said before that 0! = 1. So, to calculate the factorial of a number with a loop, we can initialize a variable to 1, and multiply the numbers from n to 1 by the variable inside the loop.
In this way, if the input is higher than 1, the output will easily be 1.
function factorial(n) {
let result = 1;
for (n > 1) {
result *= n;
n--;
}
return result;
}Conclusion
The factorial is a pretty important operator to know if you are interested in statistics and probabilities.
In this article you have learned a how to calculate a factorial, a simple application, and you have seen how to calculate it using JavaScript.
Have fun with it!
Learn to code for free. freeCodeCamp’s open source curriculum has helped more than 40,000 people get jobs as developers. Get started
- Факториал
- Таблица факториалов
- Примеры решения факториалов
- Калькулятор факториалов
Факториал
ЧТО ТАКОЕ ФАКТОРИАЛ
Для нахождения факториала нужно умножить все целые числа от выбранного нами числа до 1.
Факториал обозначается символом «!»
Пример факториалов:
4! = 4 · 3 · 2 · 1 = 24
5! = 5 · 4 · 3 · 2 · 1 = 120
Обычно говорят 4! как «факториал четырех».
ВЫЧИСЛЕНИЕ ФАКТОРИАЛА
Можно легко рассчитать факториал, зная значение факториала предыдущего числа:
Можно это записать в виде таблицы:
| n | n! | ||
| 1 | 1 | 1 | 1 |
| 2 | 2 x 1 | = 2 x 1! | = 2 |
| 3 | 3 x 2 x 1 | = 3 x 2! | = 6 |
| 4 | 4 x 3 x 2 x 1 | = 4 x 3! | = 24 |
| 5 | 5 x 4 x 3 x 2 x 1 | = 5 x 4! | = 120 |
| 6 | и так далее | и так далее |
Для точного определения факториала любого числа следует воспользоваться таблицей факториалов
- Чтобы вычислить 6!, нужно 5!=120 умножить на 6, получается 720
- Чтобы вычислить 8!, нужно 7!=5040 умножить на 8, получается 40.320
Пример:
9! равно 362.880. Попробуйте посчитать 10!
10! = 9!х10
10! = 362.880 х 10 = 3.628.800
ФОРМУЛА ФАКТОРИАЛА
Существует правило как найти n факториал:
n! = n × (n — 1)!
Которое означает:
«факториал любого числа — это число, умноженное на факториал предыдущего целого числа»
Итак, 12! = 12 × 11!, … и 100! = 100 × 99!, и т. д.
ФАКТОРИАЛ 0
Это очень интересная тема. Принято, что 0! = 1. А почему?
Никакое умножение чисел не приводит к 1, но давайте проследим факториалы в обратном порядке, скажем, от 4!:
И во многих задачах 0! = 1 просто имеет смысл.
ФАКТОРИАЛ ОТРИЦАТЕЛЬНОГО ЧИСЛА
Можем ли мы найти факториалы для чисел меньших нуля?
Нет. Факториалы для таких чисел не определены.
Почему? Легко объяснить на примере.
Пример
Начнем с 3! = 3 × 2 × 1 = 6 и спускаемся вниз:
2! = 3! / 3 = 6 / 3 = 2
1! = 2! / 2 = 2 / 2 = 1
0! = 1! / 1 = 1 / 1 = 1
(поэтому 0! = 1)
(−1)! = 0! / 0 = 1 / 0 = ой, деление на ноль не определено
И с этого момента все целочисленные факториалы не определены.
ФАКТОРИАЛ ДРОБНОГО ЧИСЛА
Можем ли мы найти факториалы для таких чисел, как 0,4 или −8,116?
Да мы можем! Но нам нужно углубиться в тему под названием Гамма-функция, которая выходит за рамки этой страницы.
И они могут быть отрицательными (кроме целых чисел).
Вот несколько значений дробных факториалов:
| (-1/2)! | √π |
| (1/2)! | (1/2)√π |
| (3/2)! | (3/4)√π |
| (5/2)! | (15/8)√π |
ПРИМЕНЕНИЕ ФАКТОРИАЛА
Факториалы незаменимы для вычисления количества перестановок, сочетаний и размещений.
Пример:
Сколько существует разных способов, с помощью которых 7 человек могут прийти первым, вторым и третьим ?
Список довольно длинный, если 7 человек обозначим как a, b, c, d, e, f и g, то список включает:
abc, abd, abe, abf, abg, acb, acd, ace, acf, … и т. д.
Формула для расчета: 7!/(7−3)! = 7!/4!
Выпишем умножение полностью:
(7 × 6 × 5 × 4 × 3 × 2 × 1)/(4 × 3 × 2 × 1) = 7 × 6 × 5
Пояснение: 4 × 3 × 2 × 1 сокращено, т.к. они встречаются в числителе и знаменателе, и осталось только 7 × 6 × 5 . получаем:
7 × 6 × 5 = 210
Итак, есть 210 различных способов, которыми 7 человек могут прийти первым, вторым и третьим.
Решено!
Пример:
Что такое 100! / 98!
Используя наши знания из предыдущего примера, мы можем сразу перейти к следующему:
100!/98! = 100 × 99 = 9900
Другие примеры задач с факториалом и их решение на странице решение факториалов.
ИНТЕРЕСНЫЕ ФАКТЫ
70! приблизительно 1,197857 … x 10100 , что чуть больше, чем в Googol (цифра 1, за которой следует сотня нулей).
100 факториал: 100! приблизительно 9,3326215443944152681699238856 x 10157
200 факториал: 200! приблизительно 7,8865786736479050355236321393 x 10374
Полезные материалы по теме
- Таблица факториалов
- Примеры решения факториалов
- Калькулятор факториалов