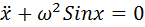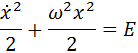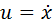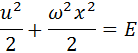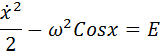Фазовые портреты «на пальцах» или что можно узнать о решениях диффура, не решая его
Время на прочтение
4 мин
Количество просмотров 83K
Очень часто в ряде наук встречается ситуация, когда модель рассматриваемого процесса сводится к дифференциальному уравнению. Причём, в большинстве реальных задач это уравнение довольно сложно решить, или совсем невозможно. И вот тут в полный голос звучит извечный вопрос: как быть?
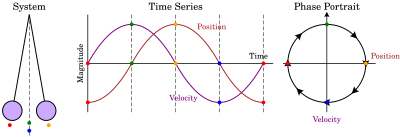
Встречайте: фазовые портреты (они же фазовые диаграммы). Простым языком, фазовый портрет — это то, как величины, описывающие состояние системы (a.k.a. динамические переменные), зависят друг от друга. В случае механического движения это координата и скорость, в электричестве это заряд и ток, в известной популяционной задаче это количество хищников и жертв и т.д.
Чем хороши фазовые портреты? А тем, что их можно построить не решая динамические уравнения системы. В некоторых случаях построение фазового портрета становится совсем простой задачей. Однако, одновременно с этим, фазовые портреты дают вдумчивому наблюдателю очень много информации о поведении системы.
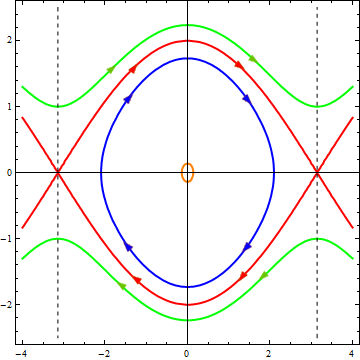
Начнём с простого примера — малых колебаний (так же называемых гармоническими). Малые колебания встречаются почти в каждой сфере естественных наук. Для определённости, будем рассматривать колебания металлического стержня, подвешенного за один из концов (частный случай так называемого физического маятника). Можно показать, что его колебания описываются следующим дифференциальным уравнением:
Где x — угол отклонения стержня от вертикали, точка над x означает производную по времени, а коэффициент перед синусом зависит от размера и массы стержня.
Если амплитуда (размах) колебаний достаточно мала, синус можно приближенно заменить его аргументом (вы ведь помните первый замечательный предел, нет?). В таком случае, уравнение принимает следующий вид:
Это уравнение легко решается регулярными методами, но, давайте, попробуем применить к нему метод фазовых портретов. Для этого, домножим уравнение на производную и проинтегрируем его один раз по времени:
Получилось выражение, первый член которого выглядит как кинетическая энергия. Это не случайно — на самом деле мы получили именно закон сохранения энергии. Постоянная Е в правой части (полная энергия системы на единицу массы) может принимать различные значения, которые соответствуют разным начальным состояниям системы.
Введём обозначение:
Полученный нами закон сохранения превратился в уравнение кривой на плоскости (x,u):
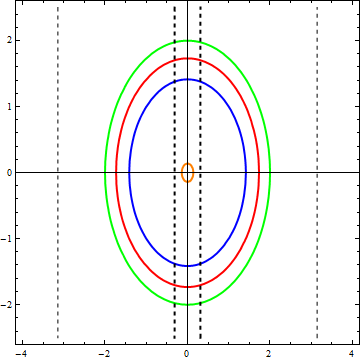
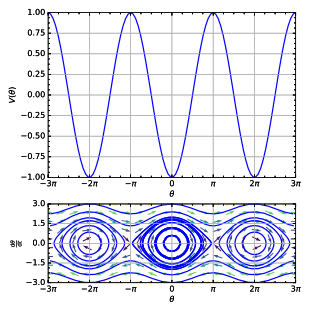
Для разных значений Е мы получим разные кривые. Нарисуем несколько таких линий для разных значений энергии:
По горизонтальной оси отложена величина x, по вертикальной — u
Каждая из полученных линий называется фазовой траекторией. Когда меняется состояние системы, изображающая её точка движется по одной из этих траекторий, стрелки указывают направление движения изображающей точки.
По графику видно, что значения скорости и координаты меняются циклическим образом, то есть периодически повторяются. Отсюда можно сделать вывод, что описываемая рассмотренным уравнением система будет совершать колебания. Бинго! Именно так ведёт себя маятник, и если решить уравнение, решение будет иметь вид периодических функций (а именно — комбинации синуса и косинуса).
Следует однако помнить, что замена синуса его аргументом оправдана лишь для малых углов отклонения (от 10 градусов и меньше), поэтому мы не можем доверять тем траекториям, которые выходят за границы области, ограниченной жирными пунктирными линиями, то есть из четырех приведенных траекторий лишь оранжевая достоверно отображает реальность. Кроме того, поскольку x это угол, то его значения, соответствующие 180 и -180 градусам описывают одно и то же положение стержня, то есть правая и левая пунктирные линии (тонкие) на графике это на самом деле одна и та же линия.
Теперь, поскольку нам понятна суть, можно перейти к чему-то посложнее. Выше мы очень сильно упростили уравнение и при этом ограничили себя только малыми колебаниями. Математик бы сказал, что мы линеаризовали уравнение и пренебрегли нелинейными эффектами. Так давайте включим в рассмотрение нелинейность. Вернёмся к самому первому уравнению — с синусом. Если мы повторим с ним то, что проделали с линейным уравнением, мы получим следующий закон сохранения:
В зависимости от значения энергии, мы опять получаем разные кривые, которые приведены на следующем рисунке, причем выбраны те же значения энергии, что и на первой диаграмме, и те же цвета для линий.
По горизонтальной оси отложена величина x, по вертикальной — u
Как видите, процессы происходящее в системе стали более разнообразными:
При малых энергиях (оранжевая и синяя траектории) существует колебательный режим, но колебания уже не являются гармоническими — фазовые траектории уже не имеют форму эллипсов.
При больших энергиях (зеленая траектория) колебаний уже нет, вместо этого мы получаем вращательное движение с переменной скоростью. И действительно, если достаточно сильно «толкнуть» стержень, он будет вращаться, замедляясь при подъёме и ускоряясь при спуске.
При определенном промежуточном значении энергии получается особый набор траекторий, которые отделяют друг от друга области соответствующие разным типам движения и поэтому называются сепаратрисами. И да, значение энергии для красной кривой было выбрано мной именно так, чтобы в нелинейном случае получилась сепаратриса. Каждая ветвь сепаратрисы это траектория, соответствующая особому типу движения. Посмотрим на диаграмму: движение начинается с очень маленькой скоростью от одного крайнего положения стержня, при приближении к положению равновесия скорость растёт, а после изображающая точка все более замедляясь уходит к крайнему положению, где и останавливается. Это соответствует тому, что мы поднимаем стержень вертикально вверх и отпускаем его, проносясь через положение равновесия он поднимается к верхней точке с другой стороны и останавливается.
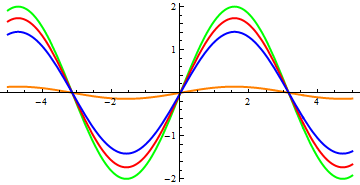
А теперь давайте посмотрим насколько близки к истине наши выводы, сделанные на основе фазовых портретов. Перед вами график решения линейного уравнения:
По горизонтальной оси отложено время, по вертикальной — x
… и нелинейного:
По горизонтальной оси отложено время, по вертикальной — x
Цветовая маркировка на этих графиках такая же, как и на фазовых портретах. Судить о том, насколько верные выводы были сделаны на основе фазовых портретов я предоставлю вам, дорогие читатели. Обращу ваше внимание только на один момент — колебания в линейном случае происходят синхронно — с одной и той же частотой. В нелинейном же случае, частота колебания с большей амплитудой (синяя линия) оказывается меньше, чем у колебания с малой амплитудой (оранжевая линия). Это служит еще одним подтверждением того, что нелинейные колебания не являются гармоническими.
Ну и напоследок: это всего лишь поверхностный экскурс в метод фазовых портретов, и словосочетание «на пальцах» попало в заголовок неспроста. Те же, кто решит углубиться в перипетии данного предмета, увидят, что за фазовыми портретами скрывается намного большее.
From Wikipedia, the free encyclopedia
Phase portrait of damped oscillator, with increasing damping strength. The equation of motion is
In mathematics, a phase portrait is a geometric representation of the trajectories of a dynamical system in the phase plane. Each set of initial conditions is represented by a different point or curve.
Phase portraits are an invaluable tool in studying dynamical systems. They consist of a plot of typical trajectories in the phase space. This reveals information such as whether an attractor, a repellor or limit cycle is present for the chosen parameter value. The concept of topological equivalence is important in classifying the behaviour of systems by specifying when two different phase portraits represent the same qualitative dynamic behavior. An attractor is a stable point which is also called a «sink». The repeller is considered as an unstable point, which is also known as a «source».
A phase portrait graph of a dynamical system depicts the system’s trajectories (with arrows) and stable steady states (with dots) and unstable steady states (with circles) in a phase space. The axes are of state variables.
Examples[edit]
Illustration of how a phase portrait would be constructed for the motion of a simple pendulum.
- Simple pendulum, see picture (right).
- Simple harmonic oscillator where the phase portrait is made up of ellipses centred at the origin, which is a fixed point.
- Damped harmonic motion, see animation (right).
- Van der Pol oscillator see picture (bottom right).
- Parameter plane (c-plane) and Mandelbrot set
Visualizing the behavior of ordinary differential equations[edit]
A phase portrait represents the directional behavior of a system of ordinary differential equations (ODEs). The phase portrait can indicate the stability of the system. [1]
| Unstable | Most of the system’s solutions tend towards ∞ over time |
| Asymptotically stable | All of the system’s solutions tend to 0 over time |
| Neutrally stable | None of the system’s solutions tend towards ∞ over time, but most solutions do not tend towards 0 either |
The phase portrait behavior of a system of ODEs can be determined by the eigenvalues or the trace and determinant (trace = λ1 + λ2, determinant = λ1 x λ2) of the system.[1]
| Eigenvalue, Trace, Determinant | Phase Portrait Shape |
|---|---|
| λ1 & λ2 are real and of opposite sign;
Determinant < 0 |
Saddle (unstable) |
| λ1 & λ2 are real and of the same sign, and λ1 ≠ λ2;
0 < determinant < (trace2 / 4) |
Node (stable if trace < 0, unstable if trace > 0) |
| λ1 & λ2 have both a real and imaginary component;
(trace2 / 4) < determinant |
Spiral (stable if trace < 0, unstable if trace > 0) |
See also[edit]
- Phase space
- Phase plane
References[edit]
- ^ a b c d Haynes Miller, and Arthur Mattuck. 18.03 Differential Equations. Spring 2010. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA. (Supplementary Notes 26 by Haynes Miller: https://ocw.mit.edu/courses/mathematics/18-03-differential-equations-spring-2010/readings/supp_notes/MIT18_03S10_chapter_26.pdf)
- Jordan, D. W.; Smith, P. (2007). Nonlinear Ordinary Differential Equations (fourth ed.). Oxford University Press. ISBN 978-0-19-920824-1. Chapter 1.
- Steven Strogatz (2001). Non-linear Dynamics and Chaos: With applications to Physics, Biology, Chemistry and Engineering. ISBN 9780738204536.
External links[edit]
- Linear Phase Portraits, an MIT Mathlet.
Фазовые портреты простых канонических систем
(a) Различные
действительные собственные значения
Система уравнений
имеет вид
Решением системы
является y1 =;
y2 =,откуда получаем
.
Возможны два варианта:
(а.1) Корни 1
и 2
противоположного знака.
П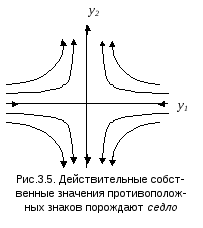
семействогипербол, имеющих
асимптотами осиу1
иу2,
которые так же являются траекториями.
Направления, по которым траектории
проходят через стационарную точку,
можно определить непосредственно из
решений приt,изменяющемся от0до.
Суммарный фазовый портрет такой системы
называетсяседлом.
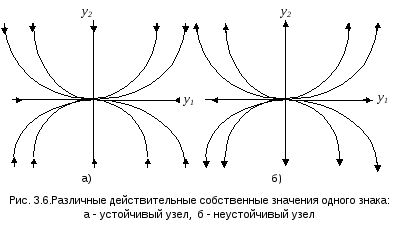
(а.2) Корни 1
и 2
одного знака.
Траектории в этом
случае образуют семейство степенных
функций, причем каждая траектория входит
в точку покоя или выходит из нее (в
зависимости от знака корней) с различных
направлений. Совокупная картина фазовых
траекторий называется в этом случае
узлом устойчивым илинеустойчивым
(рис.3.6).
(
Действительные кратные собственные
значения.
В этом случае
имеем систему уравнений
и
решение.
Откуда получаемy2=cy1,
т.е. интегральными линиями служат все
прямые, проходящие через начало координат.
Этозвездообразный(звездный)
узел.
(c)Действительные
кратные значения.
В этом случае система
уравнений принимает вид:
Получаем узел с
одним направлением входа устойчивый
при 0 < 0 и
неустойчивый при0
> 0. Такой фазовый портрет называетсявырожденным узлом. Узлы такого вида
представляют собой точки с координатами
(2n,0), где n=0,1,…
механической системы с трением, фазовый
портрет которой приведен на рис.3.4,b.
(d) Комплексные
собственные значения.
Система уравнений
имеет вид
Выполним замену
переменных:
Переходя в
плоскости y1 , y2
к полярным координатам, получим
систему уравнений
имеющую следующее
решение:
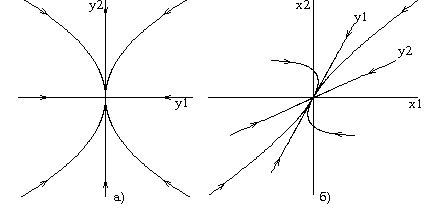
Последнее уравнение
задает логарифмические спирали,
выходящие (или входящие) из начала
координат (точки покоя). Направление
движения по траекториям приt,изменяющемся от 0 до,
определяется из решения системы
уравнений. При
< 0имеем устойчивый
фокус, а при
> 0-неустойчивый.
При =0получим
= с, т.е. в плоскостих,уполучается семейство подобных окружностей
с общими осями симметрии. Фазовый портрет
в этом случае называетсяцентром.
Рис.3.8.
Комплексные собственные значения
порождают:
а
— неустойчивый фокус, >0
б
— устойчивый фокус, <0
в
— центр, =0
Фазовый портрет простой линейной системы
Фазовый портрет простой
линейной системы
можно получить из фазового портрета
канонической системы
с
помощью преобразованияx=My,
где
являются координатами точкиx
относительно базиса{m1,
m2},
составленного из столбцов матрицыМ.
Отсюда оси
— это прямые, проходящие через начало
координат на плоскости
и имеющие направление векторовm1,
m2.
Влияние линейных преобразований вида
x=My
на фазовый портрет
канонической системы
Рис.3.10.
Влияние линейных преобразований на
фазовый портрет
показано на рис.3.9, где (а) — фазовый
портрет исходной канонической системы,
а (б) — фазовый портрет преобразованной
системы при матрице преобразований.
Рис.3.9.Влияние
линейных преобразований на фазовый
портрет:
а
– каноническая система,
б
– преобразованная система
мы можем найти решение для любой линейной
системы общего вида, если определим
соответствующую ей каноническую систему
и применим линейное преобразование
координат.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #