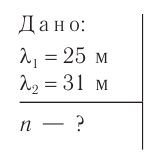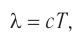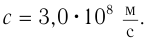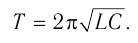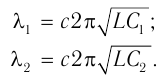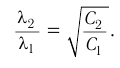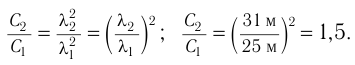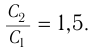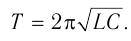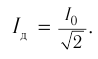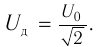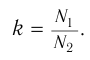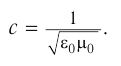Электромагнитные колебания
-
Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.
-
Колебательный контур
-
Энергетические превращения в колебательном контуре
-
Электромеханические аналогии
-
Гармонический закон колебаний в контуре
-
Вынужденные электромагнитные колебания
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: свободные электромагнитные колебания, колебательный контур, вынужденные электромагнитные колебания, резонанс, гармонические электромагнитные колебания.
Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.
Колебательный контур
Колебательный контур — это замкнутый контур, образованный последовательно соединёнными конденсатором и катушкой.
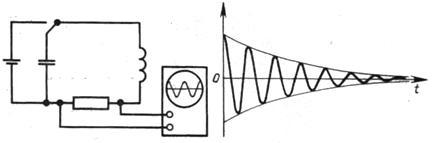
Зарядим конденсатор, подключим к нему катушку и замкнём цепь. Начнут происходить свободные электромагнитные колебания — периодические изменения заряда на конденсаторе и тока в катушке. Свободными, напомним, эти колебания называются потому, что они совершаются без какого-либо внешнего воздействия — только за счёт энергии, запасённой в контуре.
Период колебаний в контуре обозначим, как всегда, через . Сопротивление катушки будем считать равным нулю.
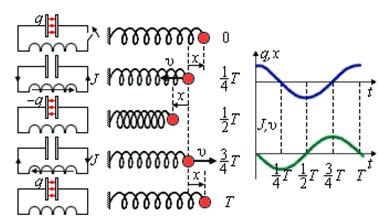
Рассмотрим подробно все важные стадии процесса колебаний. Для большей наглядности будем проводить аналогию с колебаниями горизонтального пружинного маятника.
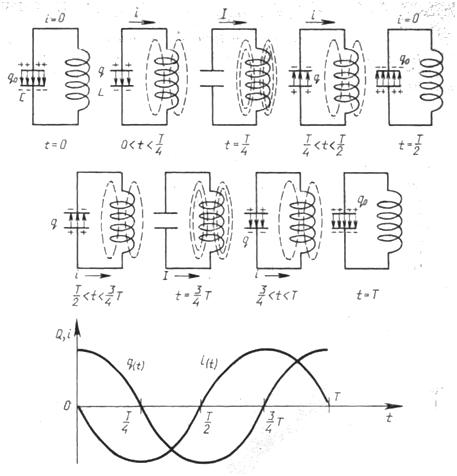
Начальный момент: . Заряд конденсатора равен
, ток через катушку отсутствует (рис. 1). Конденсатор сейчас начнёт разряжаться.
Рис. 1.
Несмотря на то, что сопротивление катушки равно нулю, ток не возрастёт мгновенно. Как только ток начнёт увеличиваться, в катушке возникнет ЭДС самоиндукции, препятствующая возрастанию тока.
Аналогия. Маятник оттянут вправо на величину и в начальный момент отпущен. Начальная скорость маятника равна нулю.
Первая четверть периода : . Конденсатор разряжается, его заряд в данный момент равен
. Ток
через катушку нарастает (рис. 2).
Рис. 2.
Увеличение тока происходит постепенно: вихревое электрическое поле катушки препятствует нарастанию тока и направлено против тока.
Аналогия . Маятник движется влево к положению равновесия; скорость маятника постепенно увеличивается. Деформация пружины
(она же — координата маятника) уменьшается.
Конец первой четверти : . Конденсатор полностью разрядился. Сила тока достигла максимального значения
(рис. 3). Сейчас начнётся перезарядка конденсатора.
Рис. 3.
Напряжение на катушке равно нулю, но ток не исчезнет мгновенно. Как только ток начнёт уменьшаться, в катушке возникнет ЭДС самоиндукции, препятствующая убыванию тока.
Аналогия. Маятник проходит положение равновесия. Его скорость достигает максимального значения . Деформация пружины равна нулю.
Вторая четверть: . Конденсатор перезаряжается — на его обкладках появляется заряд противоположного знака по сравнению с тем, что был вначале (рис. 4).
Рис. 4.
Сила тока убывает постепенно: вихревое электрическое поле катушки, поддерживая убывающий ток, сонаправлено с током.
Аналогия. Маятник продолжает двигаться влево — от положения равновесия к правой крайней точке. Скорость его постепенно убывает, деформация пружины увеличивается.
Конец второй четверти . Конденсатор полностью перезарядился, его заряд опять равен
(но полярность другая). Сила тока равна нулю (рис. 5). Сейчас начнётся обратная перезарядка конденсатора.
Рис. 5.
Аналогия. Маятник достиг крайней правой точки. Скорость маятника равна нулю. Деформация пружины максимальна и равна .
Третья четверть: . Началась вторая половина периода колебаний; процессы пошли в обратном направлении. Конденсатор разряжается (рис. 6).
Рис. 6.
Аналогия. Маятник двигается обратно: от правой крайней точки к положению равновесия.
Конец третьей четверти: . Конденсатор полностью разрядился. Ток максимален и снова равен
, но на сей раз имеет другое направление (рис. 7).
Рис. 7.
Аналогия. Маятник снова проходит положение равновесия с максимальной скоростью , но на сей раз в обратном направлении.
Четвёртая четверть: . Ток убывает, конденсатор заряжается (рис. 8).
Рис. 8.
Аналогия. Маятник продолжает двигаться вправо — от положения равновесия к крайней левой точке.
Конец четвёртой четверти и всего периода: . Обратная перезарядка конденсатора завершена, ток равен нулю (рис. 9).
Рис. 9.
Данный момент идентичен моменту , а данный рисунок — рисунку 1. Совершилось одно полное колебание. Сейчас начнётся следующее колебание, в течение которого процессы будут происходить точно так же, как описано выше.
Аналогия. Маятник вернулся в исходное положение.
Рассмотренные электромагнитные колебания являются незатухающими — они будут продолжаться бесконечно долго. Ведь мы предположили, что сопротивление катушки равно нулю!
Точно так же будут незатухающими колебания пружинного маятника при отсутствии трения.
В реальности катушка обладает некоторым сопротивлением. Поэтому колебания в реальном колебательном контуре будут затухающими. Так, спустя одно полное колебание заряд на конденсаторе окажется меньше исходного значения. Со временем колебания и вовсе исчезнут: вся энергия, запасённая изначально в контуре, выделится в виде тепла на сопротивлении катушки и соединительных проводов.
Точно так же будут затухающими колебания реального пружинного маятника: вся энергия маятника постепенно превратится в тепло из-за неизбежного наличия трения.
к оглавлению ▴
Энергетические превращения в колебательном контуре
Продолжаем рассматривать незатухающие колебания в контуре, считая сопротивление катушки нулевым. Конденсатор имеет ёмкость , индуктивность катушки равна
.
Поскольку тепловых потерь нет, энергия из контура не уходит: она постоянно перераспределяется между конденсатором и катушкой.
Возьмём момент времени, когда заряд конденсатора максимален и равен , а ток отсутствует. Энергия магнитного поля катушки в этот момент равна нулю. Вся энергия
контура сосредоточена в конденсаторе:
Теперь, наоборот, рассмотрим момент, когда ток максимален и равен , а конденсатор разряжен. Энергия конденсатора равна нулю. Вся энергия контура запасена в катушке:
В произвольный момент времени, когда заряд конденсатора равен и через катушку течёт ток
, энергия контура равна:
Таким образом,
(1)
Соотношение (1) применяется при решении многих задач.
к оглавлению ▴
Электромеханические аналогии
В предыдущем листке про самоиндукцию мы отметили аналогию между индуктивностью и массой. Теперь мы можем установить ещё несколько соответствий между электродинамическими и механическими величинами.
Для пружинного маятника мы имеем соотношение, аналогичное (1):
(2)
Здесь, как вы уже поняли, — жёсткость пружины,
— масса маятника,
и
— текущие значения координаты и скорости маятника,
и
— их наибольшие значения.
Сопоставляя друг с другом равенства (1) и (2), мы видим следующие соответствия:
(3)
(4)
(5)
(6)
Опираясь на эти электромеханические аналогии, мы можем предвидеть формулу для периода электромагнитных колебаний в колебательном контуре.
В самом деле, период колебаний пружинного маятника, как мы знаем, равен:
B соответствии с аналогиями (5) и (6) заменяем здесь массу на индуктивность
, а жёсткость
на обратную ёмкость
. Получим:
(7)
Электромеханические аналогии не подводят: формула (7) даёт верное выражение для периода колебаний в колебательном контуре. Она называется формулой Томсона. Мы вскоре приведём её более строгий вывод.
к оглавлению ▴
Гармонический закон колебаний в контуре
Напомним, что колебания называются гармоническими, если колеблющаяся величина меняется со временем по закону синуса или косинуса. Если вы успели забыть эти вещи, обязательно повторите листок «Механические колебания».
Колебания заряда на конденсаторе и силы тока в контуре оказываются гармоническими. Мы сейчас это докажем. Но прежде нам надо установить правила выбора знака для заряда конденсатора и для силы тока — ведь при колебаниях эти величины будут принимать как положительные, так и отрицательные значения.
Сначала мы выбираем положительное направление обхода контура. Выбор роли не играет; пусть это будет направление против часовой стрелки (рис. 10).
Рис. 10. Положительное направление обхода
Сила тока считается положительной , если ток течёт в положительном направлении. В противном случае сила тока будет отрицательной
.
Заряд конденсатора — это заряд той его пластины, на которую течёт положительный ток (т. е. той пластины, на которую указывает стрелка направления обхода). В данном случае
— заряд левой пластины конденсатора.
При таком выборе знаков тока и заряда справедливо соотношение: (при ином выборе знаков могло случиться
). Действительно, знаки обеих частей совпадают: если
, то заряд
левой пластины возрастает, и потому
.
Величины и
меняются со временем, но энергия контура остаётся неизменной:
(8)
Стало быть, производная энергии по времени обращается в нуль: . Берём производную по времени от обеих частей соотношения (8); не забываем, что слева дифференцируются сложные функции (Если
— функция от
, то по правилу дифференцирования сложной функции производная от квадрата нашей функции будет равна:
):
Подставляя сюда и
, получим:
Но сила тока не является функцией, тождественно равной нулю; поэтому
Перепишем это в виде:
(9)
Мы получили дифференциальное уравнение гармонических колебаний вида , где
. Это доказывает, что заряд конденсатора колеблется по гармоническому закону (т.е. по закону синуса или косинуса). Циклическая частота этих колебаний равна:
(10)
Эта величина называется ещё собственной частотой контура; именно с этой частотой в контуре совершаются свободные (или, как ещё говорят, собственные колебания). Период колебаний равен:
Мы снова пришли к формуле Томсона.
Гармоническая зависимость заряда от времени в общем случае имеет вид:
(11)
Циклическая частота находится по формуле (10); амплитуда
и начальная фаза
определяются из начальных условий.
Мы рассмотрим ситуацию, подробно изученную в начале этого листка. Пусть при заряд конденсатора максимален и равен
(как на рис. 1); ток в контуре отсутствует. Тогда начальная фаза
, так что заряд меняется по закону косинуса с амплитудой
:
(12)
Найдём закон изменения силы тока. Для этого дифференцируем по времени соотношение (12), опять-таки не забывая о правиле нахождения производной сложной функции:
Мы видим, что и сила тока меняется по гармоническому закону, на сей раз — по закону синуса:
(13)
Амплитуда силы тока равна:
Наличие «минуса» в законе изменения тока (13) понять не сложно. Возьмём, к примеру, интервал времени (рис. 2).
Ток течёт в отрицательном направлении: . Поскольку
, фаза колебаний находится в первой четверти:
. Синус в первой четверти положителен; стало быть, синус в (13) будет положительным на рассматриваемом интервале времени. Поэтому для обеспечения отрицательности тока действительно необходим знак «минус» в формуле (13).
А теперь посмотрите на рис. 8. Ток течёт в положительном направлении. Как же работает наш «минус» в этом случае? Разберитесь-ка, в чём тут дело!
Изобразим графики колебаний заряда и тока, т.е. графики функций (12) и (13). Для наглядности представим эти графики в одних координатных осях (рис. 11).
Рис. 11. Графики колебаний заряда и тока
Обратите внимание: нули заряда приходятся на максимумы или минимумы тока; и наоборот, нули тока соответствуют максимумам или минимумам заряда.
Используя формулу приведения
запишем закон изменения тока (13) в виде:
Сопоставляя это выражение с законом изменения заряда , мы видим, что фаза тока, равная
, больше фазы заряда
на величину
. В таком случае говорят, что ток опережает по фазе заряд на
; или сдвиг фаз между током и зарядом равен
; или разность фаз между током и зарядом равна
.
Опережение током заряда по фазе на графически проявляется в том, что график тока сдвинут влево на
относительно графика заряда. Сила тока достигает, например, своего максимума на четверть периода раньше, чем достигает максимума заряд (а четверть периода как раз и соответствует разности фаз
).
к оглавлению ▴
Вынужденные электромагнитные колебания
Как вы помните, вынужденные колебания возникают в системе под действием периодической вынуждающей силы. Частота вынужденных колебаний совпадает с частотой вынуждающей силы.
Вынужденные электромагнитные колебания будут совершаться в контуре, поключённом к источнику синусоидального напряжения (рис. 12).
Рис. 12. Вынужденные колебания
Если напряжение источника меняется по закону:
то в контуре происходят колебания заряда и тока с циклической частотой (и с периодом, соответственно,
). Источник переменного напряжения как бы «навязывает» контуру свою частоту колебаний, заставляя забыть о собственной частоте
.
Амплитуда вынужденных колебаний заряда и тока зависит от частоты : амплитуда тем больше,чем ближе
к собственной частоте контура
.При
наступает резонанс — резкое возрастание амплитуды колебаний. Мы поговорим о резонансе более подробно в следующем листке, посвящённом переменному току.
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Электромагнитные колебания» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Электромагнитные колебания и волны
Содержание
- Свободные электромагнитные колебания. Колебательный контур
- Вынужденные электромагнитные колебания. Резонанс
- Гармонические электромагнитные колебания
- Переменный ток. Производство, передача и потребление электрической энергии
- Емкостное сопротивление
- Электромагнитное поле
- Свойства электромагнитных волн
- Различные виды электромагнитных излучений и их применение
- Основные формулы раздела «Электромагнитные колебания и волны»
Свободные электромагнитные колебания. Колебательный контур
Электромагнитные колебания — это периодические изменения заряда, силы тока и напряжения, происходящие в электрической цепи. Простейшей системой для наблюдения электромагнитных колебаний служит колебательный контур.
Колебательный контур — это замкнутый контур, образованный последовательно соединенными конденсатором и катушкой.
Сопротивление катушки ( R ) равно нулю.
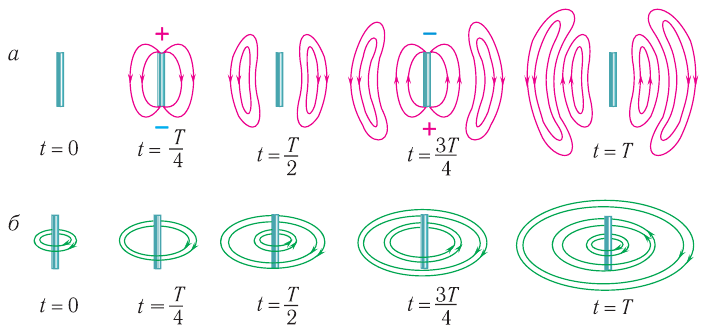
Если зарядить конденсатор до напряжения ( U_m ), то в начальный момент времени ( t_1=0 ), напряжение на конденсаторе будет равно ( U_m ). Заряд конденсатора в этот момент времени будет равен ( q_m=CU_m ). Сила тока равна нулю.
Полная энергия системы будет равна энергии электрического поля:
Конденсатор начинает разряжаться, по катушке начинает течь ток. Вследствие самоиндукции в катушке конденсатор разряжается постепенно.
Ток достигает своего максимального значения ( I_m ) в момент времени ( t_2=T/4 ). Заряд конденсатора в этот момент равен нулю, напряжение на конденсаторе равно нулю.
Полная энергия системы в этот момент времени равна энергии магнитного поля:
В следующий момент времени ток течет в том же направлении, постепенно (вследствие явления самоиндукции) уменьшаясь до нуля. Конденсатор перезаряжается. Заряды обкладок имеют заряды, по знаку противоположные первоначальным.
В момент времени ( t_3=T/2 ) заряд конденсатора равен ( q_m ), напряжение равно ( U_m ), сила тока равна нулю.
Полная энергия системы равна энергии электрического поля конденсатора.
Затем конденсатор снова разряжается, но ток через катушку течет в обратном направлении.
В момент времени ( t_4=3T/4 ) сила тока в катушке достигает максимального значения, напряжение на конденсаторе и его заряд равны нулю. С этого момента ток в катушке начинает убывать, но не сразу (явление самоиндукции). Энергия магнитного поля переходит в энергию электрического поля. Конденсатор начинает заряжаться, и через некоторое время его заряд равен первоначальному, а сила тока станет равной нулю.
Через время, равное периоду ( T ), система возвращается в начальное состояние. Совершилось одно полное колебание, дальше процесс повторяется.
Важно!
Колебания, происходящие в колебательном контуре, – свободные. Они совершаются без какого-либо внешнего воздействия — только за счет энергии, запасенной в контуре.
В контуре происходят превращения энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно. В любой произвольный момент времени полная энергия в контуре равна:
где ( i, u, q ) – мгновенные значения силы тока, напряжения, заряда в любой момент времени.
Эти колебания являются затухающими. Амплитуда колебаний постепенно уменьшается из-за электрического сопротивления проводников.
Вынужденные электромагнитные колебания. Резонанс
Вынужденными электромагнитными колебаниями называют периодические изменения заряда, силы тока и напряжения в колебательном контуре, происходящие под действием периодически изменяющейся синусоидальной (переменной) ЭДС от внешнего источника:
где ( varepsilon ) – мгновенное значение ЭДС, ( varepsilon_m ) – амплитудное значение ЭДС.
При этом к контуру подводится энергия, необходимая для компенсации потерь энергии в контуре из-за наличия сопротивления.
Резонанс в электрической цепи – явление резкого возрастания амплитуды вынужденных колебаний силы тока в колебательном контуре с малым активным сопротивлением при совпадении частоты вынужденных колебаний внешней ЭДС с частотой собственных колебаний в контуре.
Емкостное и индуктивное сопротивления по-разному изменяются в зависимости от частоты. С увеличением частоты растет индуктивное сопротивление, а емкостное уменьшается. С уменьшением частоты растет емкостное сопротивление и уменьшается индуктивное сопротивление. Кроме того, колебания напряжения на конденсаторе и катушке имеют разный сдвиг фаз по отношению к колебаниям силы тока: для катушки колебания напряжения и силы тока имеют сдвиг фаз ( varphi_L=-pi/2 ), а на конденсаторе ( varphi_C=pi/2 ). Это означает, что когда растет энергия магнитного поля катушки, то энергия электрического поля конденсатора убывает, и наоборот. При резонансной частоте индуктивное и емкостное сопротивления компенсируют друг друга и цепь обладает только активным сопротивлением. При резонансе выполняется условие:
Резонансная частота вычисляется по формуле:
Важно!
Резонансная частота не зависит от активного сопротивления ( R ). Но чем меньше активное сопротивление цепи, тем ярче выражен резонанс.
Чем меньше потери энергии в цепи, тем сильнее выражен резонанс. Если активное сопротивление очень мало ( (Rto0) ), то резонансное значение силы тока неограниченно возрастает. С увеличением сопротивления максимальное значение силы тока уменьшается, и при больших значениях сопротивления резонанс не наблюдается.
График зависимости амплитуды силы тока от частоты называется резонансной кривой. Резонансная кривая имеет больший максимум в цепи с меньшим активным сопротивлением.
Одновременно с ростом силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке. Эти напряжения становятся одинаковыми и во много раз больше внешнего напряжения. Колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. При резонансе амплитуды этих напряжений одинаковы и они компенсируют друг друга. Падение напряжения происходит только на активном сопротивлении.
При резонансе возникают наилучшие условия для поступления энергии от источника напряжения в цепь: при резонансе колебания напряжения в цепи совпадают по фазе с колебаниями силы тока. Установление колебаний происходит постепенно. Чем меньше сопротивление, тем больше времени требуется для достижения максимального значения силы тока за счет энергии, поступающей от источника.
Явление резонанса используется в радиосвязи. Каждая передающая станция работает на определенной частоте. С приемной антенной индуктивно связан колебательный контур. При приеме сигнала в катушке возникают переменные ЭДС. С помощью конденсатора переменной емкости добиваются совпадения частоты контура с частотой принимаемых колебаний. Из колебаний всевозможных частот, возбужденных в антенне, контур выделяет колебания, равные его собственной частоте.
Резонанс может привести к перегреву проводов и аварии, если цепь не рассчитана на работу в условиях резонанса.
Гармонические электромагнитные колебания
Гармоническими электромагнитными колебаниями называются периодические изменения заряда, силы тока и напряжения, происходящие по гармоническому – синусоидальному или косинусоидальному – закону.
В электрических цепях это могут быть колебания:
- силы тока – ( i=I_mcos(omega t+varphi+frac{pi}{2}); )
- напряжения – ( u=U_mcos(omega t+varphi); )
- заряда – ( q=q_mcos(omega t+varphi); )
- ЭДС – ( varepsilon=varepsilon_msinomega t. )
В этих уравнениях ( omega ) –циклическая частота, ( varphi ) – начальная фаза колебаний, амплитудные значения: силы тока – ( I_m ), напряжения – ( U_m ) и заряда – ( q_m ).
Важно!
Если в начальный момент времени заряд имеет максимальное значение, а сила тока равна нулю, то колебания заряда совершаются по закону косинуса с начальной фазой, равной нулю. Если в начальный момент времени заряд равен нулю, а сила тока максимальна, то колебания заряда совершаются по закону синуса.
Сила тока равна первой производной заряда от времени:
Амплитуда колебаний силы тока равна:
Колебания заряда и напряжения в колебательном контуре происходят в одинаковых фазах. Амплитуда напряжения равна:
Колебания силы тока смещены по фазе относительно колебаний заряда на ( pi/2 ).
Период свободных электромагнитных колебаний
Период свободных электромагнитных колебаний находится по формуле Томсона:
где ( L ) – индуктивность катушки, ( C ) – электроемкость конденсатора.
Циклическая частота: ( omega=frac{2pi}{T}=frac{1}{sqrt{LC}} )
Важно!
Период и циклическая частота не зависят от начальных условий, а определяются только индуктивностью катушки и электроемкостью конденсатора. Амплитуда колебаний заряда и силы тока определяются начальным запасом энергии в контуре.
При свободных гармонических колебаниях происходит периодическое преобразование энергии. Период колебаний энергии в два раза меньше, чем период колебаний заряда, силы тока и напряжения. Частота колебаний энергии в два раза больше частоты колебаний заряда, силы тока и напряжения.
Переменный ток. Производство, передача и потребление электрической энергии
Переменным называется ток, изменяющийся по величине и направлению по гармоническому закону.
Переменный ток представляет пример вынужденных электромагнитных колебаний. Для описания переменного электрического тока используют следующие величины:
• мгновенное значение силы тока – i;
• мгновенное значение напряжения – u;
• амплитудное значение силы тока – Im;
• амплитудное значение напряжения –Um.
Цепь переменного тока представляет собой колебательный контур, к которому приложена внешняя синусоидальная ЭДС. В цепь переменного тока могут включаться различные нагрузки: резистор, катушка, конденсатор.
Активное сопротивление
Проводник, преобразующий всю энергию электрического тока во внутреннюю, называется активным сопротивлением ( R ). (Эту величину мы раньше называли сопротивлением.) Активное сопротивление зависит от материала проводника, его длины и площади поперечного сечения и не зависит от частоты переменного тока.
В проводнике с активным сопротивлением колебания силы тока и напряжения совпадают по фазе:
Мгновенное значение мощности: ( p=i^2R, )
среднее значение мощности за период: ( overline{p}=frac{I_m^2R}{2}. )
Действующим значением силы переменного тока ( I_Д ) называют значение силы постоянного тока, который в том же проводнике выделяет то же количество теплоты , что и переменный ток за то же время:
Действующим значением напряжения переменного тока ( U_Д ) называют значение напряжения постоянного тока, который в том же проводнике выделяет то же количество теплоты, что и переменный ток за то же время:
Для цепи с активным сопротивлением выполняется закон Ома для мгновенных, амплитудных и действующих значений.
Индуктивное сопротивление
Катушка в цепи переменного тока имеет большее сопротивление, чем в цепи постоянного тока. В такой цепи колебания напряжения опережают колебания силы тока по фазе на ( pi/2 ). Колебания силы тока и напряжения происходят по закону:
Амплитуда силы тока в катушке:
где ( L ) – индуктивность катушки.
Индуктивным сопротивлением ( X_L ) называют физическую величину, равную произведению циклической частоты на индуктивность катушки:
Индуктивное сопротивление прямо пропорционально частоте. Физический смысл индуктивного сопротивления: ЭДС самоиндукции препятствует изменению в ней силы тока. Это приводит к существованию индуктивного сопротивления, уменьшающего силу тока.
Для цепи с индуктивным сопротивлением выполняется закон Ома.
Емкостное сопротивление
В цепи постоянного тока через конденсатор ток не идет. Для переменного тока конденсатор обладает конечным сопротивлением, обратно пропорциональным его емкости. В цепи переменного тока сопротивление конденсатора меньше, чем в цепи постоянного тока.
В такой цепи колебания напряжения отстают от колебаний силы тока по фазе на ( pi/2 ). Колебания силы тока и напряжения происходят по закону:
Амплитуда силы тока в катушке: ( I_m=Comega U_m. ).
Если ввести обозначение ( X_C=frac{1}{omega C} ), то получим соотношение между амплитудными значениями силы тока и напряжения, аналогичное закону Ома: ( I_m=frac{U_m}{X_C}. )
Емкостным сопротивлением ( X_C ) называют величину, обратную произведению циклической частоты на электроемкость конденсатора. Емкостное сопротивление обратно пропорционально частоте.
Физический смысл емкостного сопротивления: изменению переменного тока в любой момент времени противодействует электрическое поле между обкладками конденсатора.
В цепи переменного тока колебания силы тока и ЭДС происходят по синусоидальному закону с одинаковой циклической частотой ( omega ) и разностью фаз ( varphi ):
Соотношения амплитудных значений силы тока ( I_m ) и ЭДС ( varepsilon_m ) в цепи переменного тока связаны между собой законом Ома для цепи переменного тока:
Он гласит: амплитуда силы переменного тока прямо пропорциональна амплитуде ЭДС и обратно пропорциональна полному сопротивлению цепи:
Величина ( Z ) называется полным сопротивлением цепи переменного тока.
Электрическая энергия имеет перед другими видами энергии следующие преимущества:
- можно передавать на большие расстояния с малыми потерями;
- удобно распределять между потребителями;
- легко превращать в другие виды энергии.
В настоящее время производится и используется энергия переменного тока. Это связано с возможностью преобразовывать его напряжение и силу тока с малыми потерями энергии, что особенно важно при передаче электроэнергии на большие расстояния.
Различают следующие типы электростанций:
- тепловые;
- гидроэлектростанции;
- атомные.
Получение переменного тока
Переменный ток получают с помощью генератора переменного тока.
Генератор переменного тока (электромеханический генератор переменного тока) – это устройство, преобразующее механическую энергию в электрическую. В основе работы генератора переменного тока лежит явление электромагнитной индукции.
Процесс получения переменного тока можно рассмотреть на примере вращения витка провода в однородном магнитном поле. Магнитный поток через площадь витка равен:
Если период вращения витка ( T ), то угол ( alpha=frac{2pi t}{T}=omega t ).
Тогда ( Phi=BScosomega t. )
ЭДС индукции изменяется по закону ( e=-Phi’=BSomegasinomega t=varepsilon_msinomega t. )
Амплитуда ЭДС ( varepsilon_m=BSomega. )
Если рамка содержит ( N ) витков, то ( varepsilon_m=NBSomega. )
Основные части генератора переменного тока:
- обмотка статора с большим числом витков, в ней индуцируется ЭДС. Статор состоит из отдельных пластин из электротехнической стали для уменьшения нагрева от вихревых токов;
- ротор (вращающаяся часть генератора) создает магнитное поле. Для получения нужной частоты переменного тока может иметь несколько пар полюсов. На гидроэлектростанциях в генераторе число пар полюсов равно 40–50, на тепловых электростанциях – 10-16;
- клеммы для снятия напряжения.
Промышленные генераторы вырабатывают напряжение порядка 104 В. Промышленная частота переменного тока в нашей стране 50 Гц.
Передача электроэнергии
Электроэнергия производится в основном вдалеке от основных потребителей энергии, там, где есть топливные ресурсы.
С электростанции переменный ток по проводам линии электропередач (ЛЭП) поступает к различным потребителям электрической энергии. Для уменьшения потерь при передаче переменного тока необходимо использовать высокое напряжение. Чем длиннее линия, тем выше должно быть напряжение. В высоковольтных ЛЭП оно может достигать 500 кВ. Генераторы на электростанциях вырабатывают напряжение 16–20 кВ. Потребителям не нужно высокое напряжение. Возникает необходимость преобразования напряжения. С электростанции электрический ток поступает на повышающую подстанцию, затем передается по линии электропередач на понижающую подстанцию, где напряжение понижается до 6–10 кВ, а затем до 220–380 В. Для преобразования напряжения используют трансформатор.
Трансформатор – устройство, преобразующее переменное напряжение без изменения его частоты.
На схемах трансформатор обозначается:
Основные части трансформатора:
- замкнутый сердечник из электротехнической стали;
- две катушки-обмотки.
Катушка, подключаемая к источнику переменного напряжения, называется первичной обмоткой; катушка, к которой подключается нагрузка, – вторичной обмоткой.
Сердечник набирается из отдельных пластин для уменьшения потерь на нагревание вихревыми токами.
Принцип действия основан на явлении электромагнитной индукции. При подключении первичной обмотки к полюсам источника напряжения в ней возникает переменный ток. Напряжение изменяется с течением времени по гармоническому закону. С такой же частотой будут изменяться сила тока в катушке и магнитный поток, создаваемый этим током.
При изменении магнитного потока в каждом витке провода первичной обмотки возникает переменная ЭДС самоиндукции. Этот магнитный поток будет пронизывать и вторую катушку. В каждом ее витке возникает ЭДС индукции, изменяющаяся по гармоническому закону с той же частотой. Число витков в обмотках различно. Отношение ЭДС самоиндукции ( varepsilon_1 ) в первичной обмотке к ЭДС индукции во вторичной обмотке ( varepsilon_2 ) равно отношению числа витков в первичной обмотке ( N_1 ) к числу витков во вторичной обмотке ( N_2 ):
Режим работы
- Режим холостого хода – разомкнута цепь вторичной обмотки. Напряжение ( U_2 ) на ее концах в любой момент времени равно ЭДС индукции ( varepsilon_2 ), взятой с противоположным знаком. Поэтому можно записать:
где ( k ) – коэффициент трансформации.
Если ( k>1 ), то трансформатор понижающий, если ( k<1 ), то повышающий.
- Режим нагрузки. При подключении нагрузки к концам вторичной обмотки в ней возникает переменный ток. Напряжение ( U_2 ) на ее концах в любой момент времени отличается от ЭДС индукции ( varepsilon_2 ) на величину падения напряжения на внутреннем сопротивлении вторичной обмотки ( r ): ( U_2=varepsilon_2-I_2r ) или ( U_2=I_2R ).
Мощность тока в обмотках одинакова. Поэтому увеличение напряжения на входе повышающего трансформатора в ( k ) раз сопровождается уменьшением силы тока во вторичной катушке во столько же раз.
В трансформаторе нет потерь на трение, так как нет вращающихся частей. Потери в сердечнике состоят из потерь на нагревание и на перемагничивание.
Отношение мощности ( P_2 ), потребляемой нагрузкой, к мощности ( P_1 ), потребляемой первичной обмоткой трансформатора, называется коэффициентом полезного действия трансформатора:
КПД трансформатора – 98%.
Потребление электрической энергии: промышленность – около 70%; сельское хозяйство; транспорт; строительство; средства связи; в быту.
Электромагнитное поле
Электромагнитное поле – это особый вид материи, с помощью которого осуществляется электромагнитное взаимодействие заряженных тел или частиц.
Это понятие было введено Д. Максвеллом, развившим идеи Фарадея о том, что переменное магнитное поле порождает вихревое электрическое поле.
Всякое изменение магнитного поля порождает в окружающем пространстве вихревое электрическое поле, силовые линии которого замкнуты. Вихревое электрическое поле порождает появление вихревого магнитного поля и так далее. Эти переменные электрическое и магнитное поля, существующие одновременно, и образуют единое электромагнитное поле.
Характеристиками этого поля являются вектор напряженности и вектор магнитной индукции.
Если электрический заряд покоится, то вокруг него существует только электрическое поле.
Если напряженность электрического поля равна нулю, а магнитная индукция отлична от нуля, то обнаруживается только магнитное поле.
Если электрический заряд двигается с постоянной скоростью, то вокруг него существует электромагнитное поле.
Максвелл предположил, что при ускоренном движении зарядов в пространстве будет возникать возмущение, которое будет распространяться в вакууме с конечной скоростью. Когда это возмущение достигнет второго заряда, то изменится сила, с которой электромагнитное поле действует на этот заряд.
При ускоренном движении заряда происходит излучение электромагнитной волны. Электромагнитное поле материально. Оно распространяется в пространстве в виде электромагнитной волны.
Свойства электромагнитных волн
Электромагнитная волна – это изменяющееся во времени и распространяющееся в пространстве электромагнитное поле.
Существование электромагнитных волн было теоретически предсказано английским физиком Дж. Максвеллом в 1864 году. Электромагнитные волны были открыты Г. Герцем.
Источник электромагнитной волны – ускоренно движущаяся заряженная частица – колеблющийся заряд.
Важно!
Наличие ускорения – главное условие излучения электромагнитной волны. Интенсивность излученной волны тем больше, чем больше ускорение, с которым движется заряд.
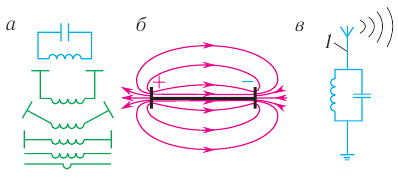
Источниками электромагнитных волн служат антенны различных конструкций, в которых возбуждаются высокочастотные колебания.
Электромагнитная волна называется монохроматической, если векторы ( vec{E} ) и ( vec{B} ) совершают гармонические колебания с одинаковой частотой (частотой волны).
Длина электромагнитной волны: ( lambda=cT=frac{c}{nu}, )
где ( c ) – скорость электромагнитной волны, ( T ) – период, ( nu ) – частота электромагнитной волны.
Свойства электромагнитных волн
- В вакууме электромагнитная волна распространяется с конечной скоростью, равной скорости света 3·108 м/с.
- Электромагнитная волна поперечная. Колебания векторов напряженности переменного электрического поля и магнитной индукции переменного магнитного поля взаимно перпендикулярны и лежат в плоскости, перпендикулярной к вектору скорости волны.
- Электромагнитная волна переносит энергию в направлении распространения волны.
Важно!
Электромагнитная волна в отличие от механической волны может распространяться в вакууме.
Плотность потока или интенсивность – это электромагнитная энергия, переносимая через поверхность единичной площади за единицу времени.
Обозначение – ( I ), единица измерения в СИ – ватт на квадратный метр (Вт/м2).
Важно!
Плотность потока излучения электромагнитной волны от точечного источника убывает обратно пропорционально квадрату расстояния от источника и пропорциональна четвертой степени частоты.
Электромагнитная волна обладает общими для любых волн свойствами, это:
- отражение,
- преломление,
- интерференция,
- дифракция,
- поляризация.
Электромагнитная волна производит давление на вещество. Это означает, что у электромагнитной волны есть импульс.
Различные виды электромагнитных излучений и их применение
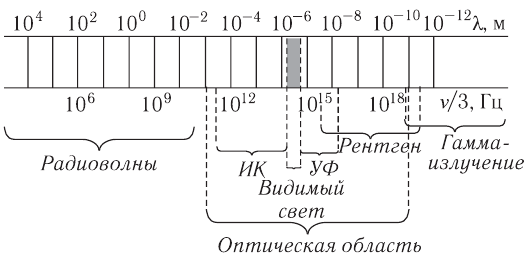
Электромагнитные излучения имеют длины волн от 10-12 до 104 м или частоты от 3·104 до 3·1020.
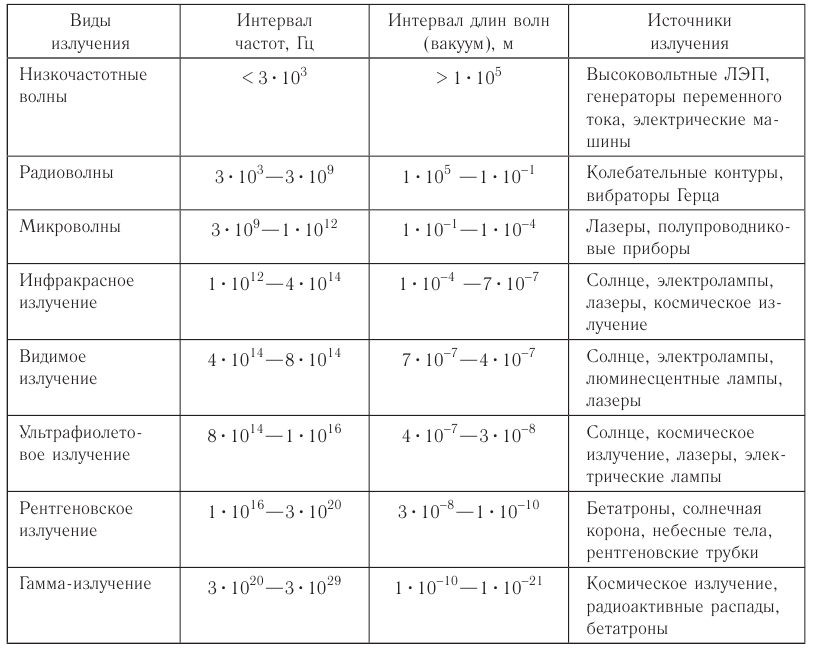
Различают следующие виды электромагнитных излучений:
- радиоволны;
- инфракрасное излучение;
- видимое излучение (свет);
- ультрафиолетовое излучение;
- рентгеновское излучение;
- гамма-излучение.
Границы между диапазонами условны, но излучения имеют качественные различия в свойствах. При переходе от излучений с малой частотой к излучениям с большей частотой волновые свойства проявляются слабее, а корпускулярные (квантовые) – сильнее.
Радиоволны
( lambda ) = 103–10-3 м, ( nu ) = 105–1011 Гц. Источники радиоволн – колебательный контур, вибратор.
Радиоволны делятся на:
- длинные (длина больше 1 км);
- средние (от 100 м до 1 км);
- короткие (от 10 до 100 м);
- ультракороткие (меньше 10 м).
Свойства: отражение, поглощение, интерференция, дифракция. Применение: радиосвязь, телевидение, радиолокация.
Радиосвязью называется передача информации с помощью радиоволн. Радиосвязь осуществляется с помощью модулированных радиоволн. Модуляцией радиоволны называется изменение ее параметров (амплитуды, частоты, начальной фазы) с частотой, меньшей частоты передаваемой волны.
Схема радиосвязи показана на рисунке:
Передача радиоволн. Генератор высокой частоты вырабатывает высокочастотные колебания несущей частоты. Звуковые колебания поступают в микрофон, где преобразуются в электромагнитные колебания. В модуляторе эти колебания преобразуются в модулированные колебания. После усиления модулированные колебания поступают в передающую антенну, которая излучает электромагнитные волны. На рисунке показан звуковой сигнал низкой частоты и модулированный высокочастотный сигнал.
Прием радиоволн. Электромагнитные колебания поступают в приемную антенну и вызывают электромагнитные колебания в приемном контуре. Эти колебания поступают в усилитель, а затем в детектор. В качестве детектора используют устройство с односторонней проводимостью. Это может быть полупроводниковый диод. В детекторе сигнал демодулируют (детектируют). Процесс детектирования заключается в выделении из высокочастотных модулированных колебаний колебаний низкой (звуковой) частоты. После сглаживания и усиления сигнал поступает в динамик. На рисунке показаны процессы детектирования (демодуляции) и сглаживания.
Радиолокацией называют обнаружение и определение местоположения объектов с помощью радиоволн. Излучение осуществляется короткими импульсами. В интервале времени между излучением двух последовательных импульсов осуществляется прием отраженного от объекта сигнала. Для радиолокации используют ультракороткие радиоволны.
Инфракрасное (тепловое) излучение
( lambda ) = 10-3 – 10-7 м, ( nu ) = 1011 – 1014 Гц. Источники – атомы и молекулы вещества.
Это излучение испускают все тела при температуре, отличной от 0 К. Свойства: нагревает вещество при поглощении; интерференция; дифракция; проходит через дождь, снег, дымку; невидимо; преломление, отражение. Применение: в приборах ночного видения, в физиотерапии, промышленности (для сушки). Регистрируют с помощью термопары, болометра, фотографическим методом.
Видимое излучение
( lambda ) = 8·10-7 – 4·10-7 м, ( nu ) = 4·1011 – 8·1014 Гц.
Это излучение воспринимается глазом. Свойства: отражение, преломление, поглощение, интерференция, дифракция.
Ультрафиолетовое излучение
( lambda ) = 10-8 – 4·10-7 м, ( nu ) = 8·1014 – 3·1015 Гц. Источники – кварцевые лампы.
Ультрафиолетовое излучение дают светящиеся пары ртути и твердые тела, у которых температура выше 1000°С. Свойства: химическое действие; большая проникающая способность; биологическое действие; невидимо. Применение: в медицине, промышленности. Регистрируют фотографическими методами.
Рентгеновское излучение
( lambda ) = 10-8 – 10-11 м, ( nu ) = 3·1016 – 3·1019 Гц. Источник – рентгеновские трубки.
Возникает при торможении быстрых электронов. Свойства: высокая химическая активность; биологическое действие; интерференция; дифракция на кристаллической решетке; высокая проникающая способность. Применение: в медицине, промышленности, науке.
Гамма-излучение
Длина волны меньше 10-11 м, частота от 1020 Гц и выше. Источник – ядерные реакции.
Свойства: высокая проникающая способность, сильное биологическое действие. Применение: в медицине, промышленности (дефектоскопия), науке.
Шкала электромагнитных излучений позволяет сделать вывод: все электромагнитные излучения обладают одновременно волновыми и квантовыми свойствами, которые дополняют друг друга.
Важно!
Волновые свойства сильнее выражены при малых частотах и больших длинах волн, а квантовые – при больших частотах и малых длинах волн.
Решение задач по теме «Электромагнитные колебания и волны»
По этой теме можно выделить четыре группы задач:
- на определение параметров колебательного контура;
- на уравнения гармонических электромагнитных колебаний;
- на применение закона Ома;
- на расчет мощности и КПД трансформатора.
Решение первой группы задач на определение параметров колебательного контура основано на использовании формулы Томсона (формулы периода свободных электромагнитных колебаний) и закона сохранения и превращения энергии в колебательном контуре. Поэтому необходимо записать уравнения для мгновенных значений заряда и напряжения на конденсаторе и силы тока в катушке; записать уравнение для полной энергии колебательного контура в произвольный момент времени. В качестве дополнительных формул могут понадобиться формулы электроемкости плоского конденсатора, индуктивности катушки и длины электромагнитной волны. Помните, что скорость распространения электромагнитной волны в вакууме равна скорости света – 3·108 м/с. В среде с показателем преломления ( n ) скорость света можно рассчитать по формуле: ( v=frac{c}{n}. )
Важно!
Амплитудное значение напряжения – ( U_m=frac{q_m}{C} ), амплитудное значение силы тока – ( I_m=q_momega ).
При решении второй группы задач на уравнения гармонических электромагнитных колебаний рекомендуется записать заданное в задаче уравнение и уравнение гармонических колебаний в общем виде. Сравнить эти уравнения и определить основные характеристики: амплитуду, частоту, фазу.
При решении задач на закон Ома нужно помнить, что электроизмерительные приборы показывают действующие значения напряжения и силы тока. Действующие значения величин пропорциональны амплитудным значениям. Важно помнить, что резонанс возникает при равенстве индуктивного и емкостного сопротивлений.
Решение четвертой группы задач на расчет мощности и КПД трансформатора опирается на знание формул КПД и мощности в цепи.
Основные формулы раздела «Электромагнитные колебания и волны»
Электромагнитные колебания и волны
3.2 (63.87%) 62 votes
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.
Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.
Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.
Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.
Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Содержание:
Электромагнитные колебания:
Мы проживаем в различных городах и селах нашей республики. Они находятся в сотнях и тысячах километров от столицы. Несмотря на большие расстояния между населенными пунктами, мы постоянно поддерживаем связь. Кроме этого, нам известна информация о событиях со всего мира. Эти новости мы узнаем по телевизору, радио, мобильным телефонам. Каким образом информация доходит до нас по телевидению, через радиоприемники, мобильные телефоны?
Передача на большие расстояния речи, музыки, изображений или другой информации в виде электромагнитных сигналов называется телекоммуникацией. Передача информации в виде электрических сигналов с помощью проводников была изобретена в 1837 году английскими учеными У. Куком и Ч. Уитсоном. Американский художник С. Морзе изобрел передачу информации с помощью специального алфавита, состоящего из точек и тире. Этот метод в дальнейшем стал широко применяться во всем мире. В 1876 году А.Г. Белл изобрел телефон. В настоящее время, если телефоны в наших домах и различных ведомствах связаны со станцией через металлические проводники, то междугородные и международные телефонные станции связаны кабелями оптических волокон. Информация по этим кабелям передается с помощью лазерных лучей. По одной паре кабель одновременно может поддерживать связь 6000 телефонных абонентов. Наши радиоприемники и телевизоры могут получать информацию вообще без проводов. Мобильные телефоны также поддерживают беспроводную связь. В этих случаях информация передается с помощью электромагнитных волн.
Как поступает информация по проводам и воздуху в виде речи, изображения и звука в мобильные телефоны, радиоприемники и телевизоры? Ответы на эти вопросы вы, уважаемые ученики, найдете в данной главе.
Свободные электромагнитные колебания
Простые электромагнитные колебания можно создать в электрической цепи, состоящей из конденсатора и катушки индуктивности. Построим электрическую цепь, состоящую из конденсатора, катушки индуктивности, источника постоянного тока и включателя (рис. 3.1). Для упрощения не будем учитывать сопротивление электрической цепи. При включении включателя с левой стороны батареи пластинки конденсатора С заряжаются. При этом между обкладками конденсатора создается электрическое поле с максимальной энергией
В результате зарядки верхней обкладки конденсатора положительным, а нижней обкладки отрицательным зарядом он становится источником тока (1 случай). В результате с положительной обкладки конденсатора наблюдается перемещение зарядов на отрицательную обкладку через катушку индуктивности, т.е. образуется ток. Вокруг этого тока создается магнитное поле. Этот ток из-за индуктивности катушки постепенно увеличивается и достигает максимального значения (смотрите график на рисунке). Магнитное поле, созданное вокруг тока, протекающего через катушку, будет тоже растущим (2 случай). В этом случае энергия электрического поля между обкладками конденсатора уменьшается до нуля. Энергия магнитного поля вокруг катушки постепенно растет и достигает своего максимального значения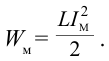
Из рассмотренных процессов сделаем следующие выводы:
- В цепи, состоящей из конденсатора и катушки индуктивности, заряд, переданный конденсатору из источника тока, в замкнутой цепи создаст переменный ток.
- Энергия, полученная от источника, сначала концентрируется в качестве энергии электрического поля между обкладками конденсатора, а затем превращается в энергию магнитного поля внутри катушки. Далее энергия магнитного поля превращается в энергию электрического поля и т.д., периодически происходят превращения.
Мы узнали, что любые процессы, которые периодически повторяются, называются колебаниями.
Значит, процесс в цепи, состоящей из конденсатора с и катушки, тоже имеет колебательный характер. Это явление называется электромагнитные колебания. Замкнутая цепь, состоящая из катушки (L) и конденсатора (С), в которой создаются электромагнитные колебания, называется колебательным контуром (рис. 3.3).
Формула определения периода (частоты) электромагнитного колебания в колебательном контуре найдена английским физиком У. Томсоном.
Здесь: Т-период колебания в секундах, 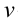
Когда происходят электромагнитные колебания в контуре, энергия электрического поля периодически превращается в энергию магнитного поля и наоборот. В идеальном колебательном контуре из-за отсутствия расхода энергии колебания не затухают. Полная энергия сохраняется и ее величина в любой момент времени равна:
Здесь: L- индуктивность катушки, С-емкость конденсатора, 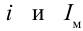
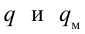
Явления, происходящие в колебательном контуре, — это превращение энергии электрического поля конденсатора в энергию магнитного поля катушки и наоборот — энергии магнитного поля катушки в энергию электрического поля конденсатора. Это явление можно сравнить с рассмотренным в 10-м классе примером, где потенциальная энергия растянутой пружины, пружинного маятника, превращается в кинетическую энергию груза и наоборот. Согласно этому в следующей таблице приведем аналогию величин, характеризующих механические и электрические колебания.
Механические величины:
Электрические величины:
Следует отметить, что электромагнитные и механические колебания имеют разную природу, но выражаются аналогичными уравнениями.
Пример №1
Емкость конденсатора колебательного контура равна 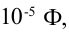
Дано: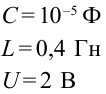
Формула:
Решение:
Графическое изображение колебания затухающие электромагнитные колебания
В рассмотренном колебательном контуре для создания возникающих электромагнитных колебаний сначала в момент времени t=0 на конденсатор подается заряд qM, не оказывая других внешних воздействий. Колебания, возникающие при отсутствии внешних воздействий, называются свободными колебаниями.
Учитывая схожесть электромагнитных колебаний с механическими колебаниями, изученными в 10-м классе, изменение заряда конденсатора можно записать следующей формулой:
Если учесть, что 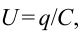
Сила тока в катушке определяется согласно следующей закономерности:
Периодическое изменение физических параметров с течением времени по закону синуса или косинуса называется гармоническими колебаниями.
Модуль наибольшего значения колеблющейся величины называется амплитудой колебания, или амплитудной величиной.
Амплитуда в механических колебаниях равна наибольшему отклонению тела от положения равновесия, а в электромагнитных колебаниях — наибольшему значению электрического заряда 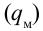
Для изображения зависимости величин гармонических колебаний от времени удобен графический метод.
Нарисуем графики зависимости заряда, напряжения и силы тока электромагнитных колебаний от времени. Для этого воспользуемся формулами (3-3), (3-4) и (3-5). Сравнивая эти уравнения, можно увидеть, что колебания отличаются друг от друга по фазовым смещениям, т.е. имеют сдвиг по фазе.
Нарисуем графики вышеназванных уравнений. Ось абсцисс указывает в долях период времени, над ним соответствующие фазы колебания. По оси ординат выставлены величины 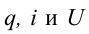
Если на этих графиках будет известен масштаб, то по оси абсцисс можно найти период (время), а по оси ординат — амплитуду или мгновенное значение колеблющихся величин. Таким же образом сравнивая графики, можно найти сдвиг по фазе. Например, при максимальном значении заряда и напряжения на обкладках конденсатора сила тока равна нулю.
Колебания силы тока в контуре по фазам опережают колебания заряда на 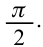
Как было сказано выше, колебания, возникающие в идеальных колебательных контурах, не затухают. В реальных контурах из-за того, что сопротивление R не равняется нулю, электрическая энергия превращается в тепло и амплитуда колебания со временем уменьшается (рис. 3.5).
Такие колебания называются затухающим и колебаниями.
Следует отметить, что согласно формуле 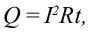
Затухающие колебания относятся к непериодичным колебаниям. Их уравнения выражаются через дифференциальные уравнения и являются сложными задачами, поэтому, не приводя их решения, ограничимся приведением их графиков.
Пример №2
На рисунке приведен график изменения тока в колебательном контуре. Объясните изменение энергии в промежутке времени: 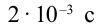
Решение: За приведенный промежуток времени 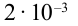
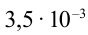
Значит, энергия электрического поля конденсатора уменьшается до нуля и растет энергия магнитного поля катушки, достигая максимального значения.
Генераторы электромагнитных колебаний на транзисторах
Мы узнали, что в колебательном контуре возникают высокочастотные электромагнитные колебания. Если наблюдать на экране осциллографа колебания, возникающие в колебательном контуре, то увидим, что с течением времени амплитуда колебания уменьшается (рис. 3.6).
Причиной этого является электрическое сопротивление проводников катушки контура, используемых для соединения. Известно, что, имея сопротивление, проводник нагревается. Электрическая энергия превращается в тепловую энергию. Поэтому возникающие в контуре свободные электромагнитные колебания являются затухающими колебаниями.
Для того чтобы колебания не затухали, израсходованную энергию нужно периодически передавать колебательному контуру с помощью батарейки. Это означает, что включатель в контуре не должен постоянно оставаться включенным, его надо периодически выключать. Вспомните из 10-го класса фазы колебания. Согласно этому, во время перезарядки обкладки конденсатора включатель должен соединиться в тот момент, когда знаки зарядов на обкладках соответствуют полюсам батарейки.
Как при этом должен работать включатель? Представим себе, что частота колебания контура равна 1 МГц. В этом случае потребуется включатель включать-выключать миллион раз в секунду! Эту задачу не смогут выполнить никакие механические или электромеханические устройства.
Такую задачу может выполнить только электронный прибор, т.е. транзистор. Вспомним приведенный в 10-м классе принцип работы транзистора 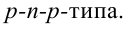
На рис. 3.7 приводится схема генератора, в котором создаются высокочастотные незатухающие колебания. Здесь контур, состоящий из L и С, подсоединен к источнику тока через транзистор. В момент включения протекающий через катушку L ток имеет растущий характер. Магнитное поле, возникающее вокруг нее, тоже будет расти. Это магнитное поле, проходящее сквозь катушку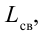
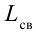
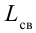
Таким образом, конденсатор С в контуре периодически заряжается от батарейки. Однако если источник напряжения подсоединяется в колебательный контур периодически, в те интервалы времени, когда обкладки конденсатора, подсоединенные к положительному полюсу, заряжаются положительно, конденсатор непрерывно заряжается. В этом случае колебания не затухнут. В противном случае колебания не возникнут. Значит, включение-выключение транзистора должно управляться колебаниями в контуре. Цепь база-эмиттер в транзисторе называется входной цепью, цепь коллектор-эмиттер — выходной цепью. Обычно напряжение (ток), приложенное во входной части на транзисторе, управляет выходным током. В транзисторных генераторах наоборот, напряжение при выходе (в контуре) управляет входным напряжением 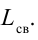
Чтобы обратная связь обеспечила колебания, напряжение входных и выходных цепей по фазе должно отличаться на 180°.
Частота электромагнитных колебаний, вырабатываемых генератором, выражается по формуле Томсона (3-1).
Таким образом, в генераторе образуются незатухающие автоколебания. Автоколебания являются вторым типом незатухающих колебаний. Основная их разница от вынужденных колебаний заключается в том, что им не нужны внешние периодичные действия. В этих системах имеется собственный источник энергии. Система сама обеспечивает и управляет пополнением израсходованной энергии. Любая система автоколебания состоит из следующих частей: источник энергии, колебательная система и электронный ключ.
Частоты автоколебания изменяются в очень широком диапазоне. Они используются для радиосвязи, телевидения, ЭВМ и в других устройствах.
Электромагнитные колебания могут быть как полезными, так и вредными для живых организмов. Каждый орган человеческого организма имеет свойственную ему резонансную частоту. Когда частота внешнего колебания равняется этой резонансной частоте, действия будут сильными. Доказано, что электромагнитные излучения влияют на психику человека.
В современной медицине все шире распространяются методы лечения с помощью высокочастотных электромагнитных колебаний. Кроме того, электромагнитные излучения оптического диапазона (УФ-излучения) используются для лечения и диагностики различных заболеваний.
Активное сопротивление в цепи переменного тока
В предыдущих темах мы познакомились с графическими изображениями изменения некоторых физических величин в зависимости от времени. Для их описания также широко применяется метод векторной диаграммы. Скажем, изменение тока в цепи задается уравнением
Возьмем вектор длиной 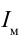
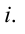
В повседневной жизни, быту и технике к цепи переменного тока подсоединяются различные бытовые приборы. Утюг, электрическая лампочка, вентилятор и т.д — в этих приборах электрическая энергия превращается в тепловую, световую, механическую и другие виды энергии. Когда эти приборы подсоединяются к источнику напряжения, то они оказывают различное сопротивление протеканию тока. Для изучения их природы попробуем подсоединить разные приборы к цепи переменного тока.
Сначала рассмотрим случай, когда к цепи переменного тока подсоединено заранее известное нам сопротивление (рис. 3.9). Пусть это сопротивление будет активным сопротивлением. Такое сопротивление называется активным, потому что когда через него протекает ток, электрическая энергия полностью превращается в другие виды (тепло, свет и др.) энергии. Проводник подсоединен к источнику переменного тока, имеющего сопротивление R и напряжение U. Это напряжение задается уравнением
Используя закон Ома для участка цепи, находим мгновенное значение силы тока, протекающего по сопротивлению R
Здесь 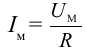
Если сопоставить уравнение изменения напряжения (3-6) с полученным уравнением для силы тока (3-7), можно прийти к выводу, что колебания напряжения и силы тока в активном сопротивлении будут происходить в одинаковой фазе. Графики колебания напряжения и силы тока приведены на рис. 3.10.
Зависимость между колебаниями напряжения и силы тока можно показать через векторную диаграмму (рис. 3.11).
На диаграмме амплитуда переменного тока и амплитуда переменного напряжения изображены в виде параллельных векторов, а угол между ними, т.е. разница фазы колебания равна нулю.
Частота потребляемого в быту электрического напряжения равна 50 Гц. Это означает, что в секунду электрическая лампочка накаливания 100 раз включается и выключается. Чувствительность человеческого глаза такова, что он способен уловить изменение процесса только до 16-20 раз в секунду, поэтому мы не чувствуем включение-выключение электрической лампочки с такой частотой. По этой причине важно знать мощность переменного тока.
Мощность цепи с активным сопротивлением
Мгновенная мощность переменного тока определяется как 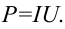
Здесь: 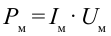
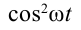
Как видно из рис. 3.12, величина мгновенной мощности переменного тока меняется периодически. По какой формуле в этом случае можно определить количество тепла, выделенного при протекании переменного тока в электрической плите? Для этого введем понятие эффективного значения переменного тока.
Эффективным значением переменного тока 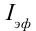
Опыты показывают, что эффективное значение силы тока связано с его максимальным значением и определяется следующей формулой:
Эффективное значение переменного напряжения можно записать формулой (3-9):
Пример №3
При подсоединении резистора в цепь переменного тока с максимальным напряжением 30 В по нему протекает максимальный ток 2 А. Найдите среднюю мощность, выделяемую в резисторе.
Дано: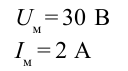
Формула:
Решение:
Конденсатор в цепи переменного тока
Опыты показывают, что, подсоединяя конденсатор к цепи постоянного тока, по ней ток не протекает, так как пространство между обкладками конденсатора разделено диэлектриком. Если конденсатор подсоединить к цепи переменного тока, то по ней ток течет.
Для изучения вопроса, от каких физических параметров зависит сила тока, протекающего через конденсатор, рассмотрим случай, когда к цепи переменного тока подсоединен только конденсатор (рис. 3.13).
Пусть емкость конденсатора равна С и приложенное напряжение изменяется согласно закономерности
сопротивление соединительных проводов R = 0. В этом случае напряжение конденсатора будет: 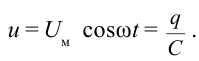
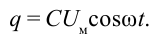
sinco=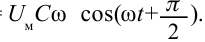
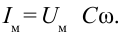
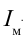
Если сопоставить это уравнение с напряжением, приложенным к конденсатору (3-11), мы увидим, что колебания силы тока в цепи опережают колебания напряжения на 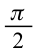
В этом случае значение амплитуды силы тока будет следующим:
Это выражение является законом Ома для участка цепи переменного тока с конденсатором. На месте активного сопротивления стоит величина 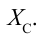
Отсюда вытекает, что сила тока, протекающего через конденсатор, зависит от емкости конденсатора и частоты переменного тока. Чем больше емкость и частота, тем меньше сопротивление цепи, и соответственно сила тока будет больше.
Пример №4
К цепи переменного тока с частотой 50 Гц подсоединен конденсатор емкостью 50 мкФ. Чему равно емкостное сопротивление цепи?
Дано: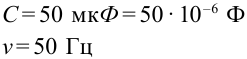
Формула:
Решение:
Катушка индуктивности в цепи переменного тока
Проведем такой опыт. К источнику постоянного тока последовательно подсоединим электрическую лампочку и катушку индуктивности. Обратим внимание на яркость лампочки. Затем последовательно подсоединим электрическую лампочку и катушку индуктивности к источнику с эффективным напряжением, равным постоянному напряжению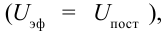
Сила тока, протекающего по катушке с индуктивностью L, изменяется согласно закономерности
Сопротивление соединительных проводов и катушки пусть будет
Ток, протекающий по катушке, из-за индуктивности катушки создаст электродвижущую силу (ЭДС) самоиндукции. Ее мгновенное значение определяется выражением
Здесь: 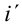
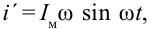
ЭДС цепи, напряжение на концах катушки и падение потенциала на активном сопротивлении связаны через следующее соотношение
Если учесть, что R = 0, формула (3-16) примет вид
тогда напряжение определяется следующей формулой:
Если сопоставить напряжение с мгновенным значением напряжения, то вытекает 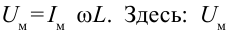
таком случае уравнение напряжения, приложенного к концам катушки, будет выглядеть так:
Если сопоставить это уравнение с выражением (3-14) силы тока, протекающего по катушке, можем увидеть, что колебания напряжения, приложенного к концам катушки, по фазе опережают колебания силы тока на 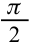
Если амплитудное значение напряжения катушки сопоставимо с законом Ома, написанным для участка цепи, известно, что произведение 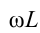
Тогда сопротивление катушки будет: 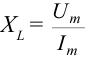
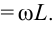
В таком случае амплитудное значение силы тока будет следующим:
Это выражение является законом Ома для участка цепи переменного тока с катушкой. На месте активного сопротивления стоит величина 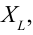
Отсюда вытекает, что сила тока, протекающего по катушке, зависит от индуктивности катушки и частоты переменного тока. Чем больше индуктивность и частота, тем больше будет сопротивление цепи, а сила протекающего тока соответственно будет меньше.
Пример №5
К цепи переменного тока с частотой 10 кГц подсоединена катушка с индуктивностью 5 Гн. Чему равно индуктивное сопротивление цепи?
Дано: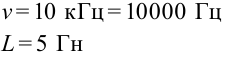
Формула:
Решение:
Закон ома для цепи переменного тока при последовательном соединении активного, индуктивного и емкостного сопротивления
Составим цепь, последовательно соединяя резистор с сопротивлением R, катушку индуктивности с индуктивностью L и конденсатор с емкостью С (рис. 3.19). На концы подаем переменное напряжение 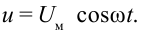
общее напряжение равно сумме векторов падения напряжения в потребителях:
Здесь: 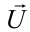
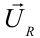
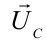
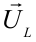
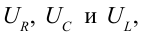
Амплитуду силы тока возьмем как вектор, направленный по горизонтальной оси (рис. 3.19). Фаза колебания напряжения в активном сопротивлении соответствует фазе колебания силы тока. Колебания напряжения в конденсаторе по фазе отстают на — от колебания силы тока. В катушке колебания напряжения опережают колебания силы тока на 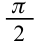
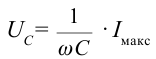
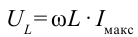
Чтобы найти общее напряжение (U), вектор 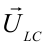
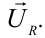
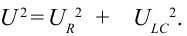
По закону Ома
Подставим в выражение (3-22)
Отсюда:
Это выражение называют законом Ома для полной цепи переменного тока.
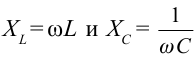
Здесь:
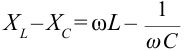
Выражение
называется полным сопротивлением цепи переменного тока.
Разницу фаз между колебаниями тока и колебаниями напряжения в цепи можно определить, используя векторную диаграмму:
Характерные свойства цепи переменного тока заключаются в том, что энергия, получаемая от генератора, выделяется в качестве тепловой энергии только в активном сопротивлении. В реактивном сопротивлении энергия не выделяется.
В реактивном сопротивлении энергия электрического поля периодически превращается в энергию магнитного поля и наоборот. В первой четверти периода, когда конденсатор заряжается, энергия передастся в цепь и накапливается в виде энергии электрического поля. В следующей четверти периода эта энергия снова передается в источник в виде энергии магнитного поля.
Пример №6
К источнику переменного тока с максимальным значением напряжения 120 В и частотой 100 Гц подсоединены активное сопротивление 200 Ом, конденсатор емкостью 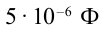
Дано: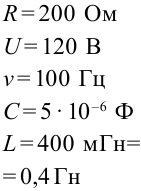
Формула:
Решение:
Явление резонанса в цепи переменного тока
Полное сопротивление электрической цепи в случае последовательного соединения цепи переменного тока, сопротивления R, катушки с индуктивностью L и конденсатора с емкостью С определяется выражением
Если 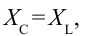
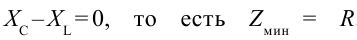
Значит, в этих условиях амплитуда силы тока резко возрастет. Это явление называется резонансом в электрической цепи. Для наблюдения резонанса должны выполняться следующие условия
Мы знаем, что частота свободного колебания в контуре колебания, где активное сопротивление равно нулю,определяется из выражения 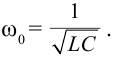
На рис. 3.21 приводится график зависимости амплитудного значения силы тока цепи от частоты внешних напряжений, приложенных к нему. График зависимости 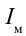
На рис. 3.21 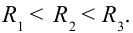
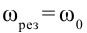
Рассмотренное явление резонанса называется резонансом напряжения.
Во время резонанса с увеличением тока напряжение в катушке и конденсаторе быстро растет. Их значение может быть больше, чем величины внешнего напряжения.
Во время резонанса амплитуда колебания напряжения индуктивной катушки и конденсатора будет:
В колебательных контурах выполняются условия 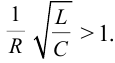
напряжение катушки и конденсатора будет больше, чем напряжение,
приложенное к цепи, а с уменьшением R оно будет увеличиваться. Другими словами, при больших значениях активного сопротивления резонанс на практике не наблюдается.
В период резонанса амплитудное значение переменного тока и амплитуда общего напряжения колеблется в одинаковой фазе.
Явление резонанса широко используют в технике. В радиоприемниках принцип выделения нужных сигналов среди множества радиосигналов основан на явлении резонанса. При этом значение емкости или индуктивности в колебательном контуре входной части приемника изменяется и его собственная частота настраивается на частоту сигнала той станции, которую необходимо принять. В контуре происходит резонанс именно для сигнала выбранной частоты, и созданное им напряжение будет самым большим. В электротехнических приборах тоже применяется явление резонанса, так как во время увеличения напряжения в катушке или конденсаторе может возникнуть электрический пробой.
Пример №7
К цепи переменного тока с частотой 50 Гц подсоединена катушка с индуктивностью 100 мГн и конденсатор емкостью С. При каком значении емкости конденсатора происходит явление резонанса?
Дано: 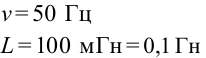
Формула
Решение:
Сила и мощность переменного тока
Как вам известно, работа, выполненная постоянным током, определяется как произведение напряжения, силы тока и времени прохождения тока:
Для определения работы, выполненной переменным током за короткий промежуток времени, его значение рассматриваем как постоянное. В таком случае мгновенное значение выполненной работы переменного тока тоже находится из похожей формулы:
Если напряжение, приложенное к концам цепи, изменяется согласно закономерности
то сила тока в нем тоже меняется по гармоническому закону со сдвигом по фазе: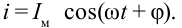
Работа, выполненная за единицу времени, называется мощностью. Поэтому мгновенное значение мощности переменного тока можно записать в виде
Здесь мощность с истечением времени меняется и по модулю, и по знаку. В первой половине периода, если мощность передается в цепь (р>0), то во второй половине часть мощности обратно передается в сеть питания (р< 0).
В некоторых случаях очень важно знать среднее значение мощности в течение длительного времени. Для этого достаточно определить мощность, приходящуюся на один период.
Для определения мощности, приходящейся на один период, формулу (3-31) преобразуем в вид, чтобы она не зависела от времени. Для этого используем формулу из курса математики — произведение двух косинусов:
В рассматриваемом нами случае 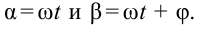
Среднее значение второго слагаемого в данном выражении в течение одного периода равно нулю. Значит, независимо от времени, средняя мощность, приходящаяся на один период, будет
Если учитывать выражение эффективных значений тока и напряжения, так как 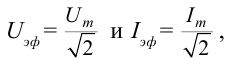
Эта величина называется мощностью переменного тока для участка цепи:
Согласно этому, работа, выполненная переменным током, определяется следующей формулой:
Таким образом, мощность и работа, выполненная переменным током участка цепи, определяется эффективными значениями силы тока и напряжения. Она также зависит от фазовых смещений между напряжением и силой тока. Множитель 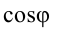
Если в цепи не будет реактивного сопротивления, тогда 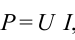
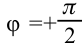
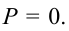
График зависимости мгновенного значения мощности можно найти путем произведения силы тока и напряжения, приходящегося на каждый момент. Из графика видно, что в одной четвертой части периода мощность имеет положительное значение и энергия передается на данный участок цепи. Но в следующей четверти периода мощность имеет отрицательное значение и энергия из этого участка цепи обратно возвращается в сеть питания. В одной четвертой части периода энергия, переданная в электрическую цепь, накапливается в виде магнитного поля тока, затем она возвращается в сеть.
При проектировании переменных электрических цепей обращают внимание на то, чтобы значение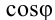
В отраслях промышленности и в сфере бытовых услуг широко применяются электрические двигатели. Они обладают большим индуктивным сопротивлением и маленьким активным сопротивлением.
Поэтому значение costp становится маленьким. Для его увеличения используют специальный компенсирующий конденсатор. Здесь нужно обращать внимание на то, чтобы электродвигатели не работали в холостую или с недостаточной нагрузкой. Обычно устройства со значением costp < 0,85 использовать не разрешается.
Пример №8
Катушка с индуктивностью 0,5 Гн и активным сопротивлением 100 Ом и конденсатор емкостью 10 мкФ соединены с источником переменного напряжения 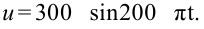
Дано: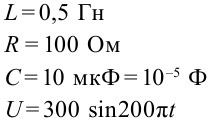
Формула:
Решение:
Самые важные понятия, правила и законы
- Свободные электромагнитные колебания: Колебания электрического и магнитного поля, возникающие в колебательном контуре, после одноразовой зарядки.
- Колебательный контур: Цепь, состоящая из катушки и конденсатора. Период колебания
- Затухающие колебания: Колебания, возникающие в колебательном контуре, при одноразовой передаче энергии конденсатору. Амплитуда колебания с течением времени уменьшается.
- Полная энергия в колебательном контуре:
- Гармонические колебания: Периодическое изменение физических величин, которые подчиняются закону sin или cos.
- Амплитуда колебания: Модуль наибольшего значения колеблющейся величины.
- Автоколебания: Возникновение незатухающих колебаний за счет источника внутри системы колебания.
- Генератор высокой частоты: Устройство, создающее незатухающие колебания в системе, состоящей из источника энергии, системы колебания и электронного ключа.
- Обратная связь: Передача из выходной цепи части электрического сигнала во входную цепь.
- Активное сопротивление-
:Сопротивление, превращающее энергию переменного тока безвозвратно в другие виды энергии.
- Реактивное сопротивление-
: Сопротивление, превращающее энергию переменного тока в энергию электрического или магнит- 1 ного поля, и наоборот.
- Мощность цепи с активным сопротивлением:
- Эффективные значения переменного тока и напряжения:
- Закон Ома для полного участка цепи переменного тока:
- Полное сопротивление цепи переменного тока:
- Разности фаз колебания тока и колебания напряжения в цепи :
- Явление резонанса: Увеличение амплитуды колебания при равных значениях частоты внешних вынуждающих сил и собственной частоты системы.
- Последовательный резонанс, или резонанс напряжения: Резкое увеличение напряжения на конденсаторе и катушке в цепи переменного тока при равных значениях частоты внешнего источника электричества и собственной частоты цепи.
- Мощность переменного тока:
- Работа, выполненная переменным током:
Электромагнитные колебания и волны
Карта электромагнитных колебаний:
Свободные электромагнитные колебания
Механическое колебательное движение — перемещение тела или системы тел в противоположных направлениях около положения устойчивого равновесия.
Периодическое колебательное движение — это движение тела или системы тел, повторяющееся через равные промежутки времени.
Свободные колебания — это колебания, происходящие в замкнутой системе под действием внутренних консервативных сил.
Гармоническое колебание — это свободное колебание системы, в процессе которого величины, характеризующие движение, изменяются по закону синуса или косинуса.
На рисунке изображен график изменения координаты тела по закону косинуса:
Амплитуда — максимальное отклонение колеблющегося тела от положения устойчивого равновесия.
• Частота колебаний — физическая величина, равная числу колебаний за 1 секунду:
Период колебаний — время, затраченное на одно полное колебание:
Частота и период колебаний — величины, обратные друг другу: 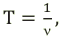
Циклическая частота — физическая величина, в 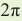
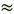
Обратимся к простой электрической цепи (с), содержащей конденсатор ёмкостью С и катушку индуктивностью L. Такую цепь называют LC-контуром. Если в LC-контуре зарядить конденсатор, то он сразу начинает разряжаться, а в катушке возникает ток. В результате происходящей самоиндукции сила тока в катушке постепенно растет и после полной разрядки конденсатора достигает максимального значения (d и е). Однако этот ток, сохранивший своё направление в результате самоиндукции, начинает снова заряжать конденсатор, и сила тока постепенно уменьшается. В момент, когда пластины конденсатора заряжаются зарядами, равными начальному значению, но противоположного знака, сила тока становится равной нулю (f). Перезарядка конденсатора через катушку периодически повторяется (g и h).
Таким образом, в LC-контуре происходят периодические изменения электрического и магнитного полей, т.е. характеризующих их величин — электрического заряда, силы тока и напряжения. В этом случае говорят, что в идеальном LC-контуре созданы свободные электромагнитные колебания. Поэтому обычно такой LC-контур называют идеальным колебательным контуром (контур, в котором не происходит потери энергии).
Свободные электромагнитные колебания — это периодические изменения электрического и магнитного полей и характеризующих их величин — электрического заряда, силы тока, напряжения и др., происходящие в колебательном контуре без поступления в него энергии от посторонних источников.
Несмотря на различие в происхождении механических и электромагнитных колебаний, они характеризуют единое свойство материи, заключающееся в периодичности происходящих процессов, вследствие этого подчиняются общим закономерностям — они описываются похожими уравнениями. Поэтому удобно (выгодно) исследовать электромагнитные колебания в аналогии с механическими, например, колебаниями пружинного и математического маятников (таблица З.1.).
Превращения энергии при электромагнитных колебаниях
Подготовьте электронную презентацию по теме «Превращения энергии при электромагнитных колебаниях». С этой целью вы можете воспользоваться аналогией превращений энергии при механических колебаниях пружинного маятника (таблица 3.2).
Полная энергия идеального колебательного контура в произвольный момент времени равна сумме энергий электрического и магнитного полей:
Однако в реальных колебательных контурах потребители обладают электрическим сопротивлением и поэтому потери энергии на его преодоление неизбежны. Это значит, что в реальном контуре энергия электрического ноля не может полностью превратиться в энергию магнитного ноля, некоторая его часть выделяется в виде тепла. Поэтому свободные электромагнитные колебания в реальном контуре являются затухающими.
Составьте план презентации, используя аналогию колебаний.
Вынужденные электромагнитные колебания: переменный ток
Электрический ток, в котором сила тока не меняет свое численное значение и направление, называется постоянным.
Источниками постоянного тока являются электрофорная машина, различные виды батарей (гальванический элемент), аккумулятор, солнечная батарея и используемый в физической лаборатории выпрямитель тока. Через поверхность S, ограниченную замкнутым контуром (рамкой), помещенным в однородное магнитное поле, проходит поток магнитной индукции.
Поток магнитной индукции (Ф) — скалярная физическая величина, численно равная произведению модуля индукции магнитного поля, площади контура, помещенного в это магнитное поле, и косинуса угла между вектором магнитной индукции и нормалью к площади контура:
Возникновение электрического тока в проводящем контуре в результате изменений магнитного потока, пронизывающего площадь, ограниченную этим контуром, называют явлением электромагнитной индукции.
ЭДС индукции, возникающая в замкнутом проводящем контуре, прямо пропорциональна скорости изменения магнитного потока, пронизывающего поверхность, ограниченную контуром:
Сила индукционного тока, возникающая в замкнутом проводящем контуре, согласно закону Ома для замкнутой цепи равна:
Возникновение ЭДС индукции в замкнутом проводящем контуре в результате изменений силы тока в нем, называют явлением самоиндукции.
При увеличении силы тока в замкнутом контуре от нуля до некоторого значения магнитный поток, пронизывающий этот контур, тоже увеличивается. В результате возникающая ЭДС самоиндукции создает в контуре электрический ток, направленный против протекающего по нему основного тока.
Вынужденные электромагнитные колебания
Вы выяснили, что в реальном колебательном контуре электромагнитные колебания всегда являются затухающими. Чтобы они были незатухающими, необходимо периодически сообщать энергию колебательному контуру. С этой целью к колебательному контуру последовательно подсоединяют источник (b), ЭДС которого меняется по гармоническому закону, например, по закону:
На схеме электрической цени источник переменного тока обозначают символом 
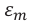
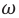
Вынужденные электромагнитные колебания — изменения электрического заряда, силы тока и напряжения, возникающие в контуре под действием переменной ЭДС внешнего источника тока с частотой, равной циклической частоте 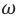
Вынужденные электромагнитные колебания можно рассматривать как переменный ток, проходящий через контур, содержащий резистор, конденсатор и катушку.
Переменный ток — это ток, направление и характеризующие параметры которого периодически меняются со временем.
Переменный ток приводит в движение электрические двигатели на заводах и фабриках, используется в быту в осветительных системах и приводит в действие почти все электрические приборы и др.
Получение переменного тока
Устройство, производящее переменный ток, называется генератором переменного тока, или индукционным генератором. Принцип работы генератора основан на явлении электромагнитной индукции. Самая простая модель такого генератора состоит из проводящего контура, вращающегося в однородном магнитном поле (с).
При вращении с циклической частотой 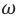
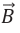
Согласно закону электромагнитной индукции, в контуре возникает ЭДС, меняющаяся по периодическому закону:
В результате на полюсах источника возникает напряжение, меняющееся по закону синуса:
Если к полюсам контура генератора подсоединить потребитель, например, лампу, то через нее будет проходить меняющийся по гармоническому закону индукционный ток — лампа периодически будет то ярко загораться, то гаснуть (d):
В выражениях (2), (3) и (4) символы 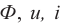
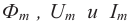
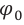
Генераторы переменного тока бывают различной конструкции. Обычно они состоят либо из катушки (ротора) с большим числом витков, способной вращаться в магнитном поле неподвижного постоянного магнита (статора), либо, наоборот, из двухполюсного магнита (ротора), способного вращаться внутри неподвижной катушки (статора). На тепловых электростанциях используются генераторы, состоящие из двухполюсных магнитных роторов (е).
Вращаясь с частотой 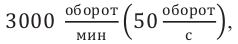
Другие величины, характеризующие переменный ток
При прохождении электрического тока по проводнику происходит процесс частичного превращения электрической энергии во внутреннюю, в результате проводник нагревается. В цепи переменного тока, несмотря на периодические изменения мгновенного значения мощности, среднее значение мощности остается постоянным в любом периоде:
Здесь 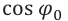
Отношения 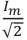
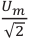
• Действующее значение силы тока равно силе такого постоянного тока, который выделяет в нем за равное время такое же количество тепла, что и переменный ток.
• Амперметр и вольтметр, используемые в цепи переменного тока, измеряют действующие значения силы тока и напряжения.
Цепи переменного тока, содержащие резистор, конденсатор и катушку
Резистор — проводник, изготовленный из особого сплава и имеющий зажимы. На электрических схемах резистор изображается прямоугольником и обозначается буквой R.
В микросхемах используют различные резисторы. Связь между силой тока на участке цепи, напряжением на его концах и сопротивлением участка определяется законом Ома:
Здесь R — сопротивление участка (проводника).
Сопротивление проводника зависит от его геометрических размеров и материала, из которого изготовлен:
Работа тока на участке цепи равна произведению силы тока в нем на напряжение на его концах и на время прохождения тока:
Мощность электрического тока равна отношению работы тока ко времени, за которое эта работа совершена:
Активное сопротивление в цепи переменного тока
Резистор в цепи переменного тока, сопротивление которого определяется выражением 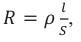
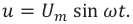
Конденсатор в цепи переменного тока
Как будут меняться величины, характеризующие переменный ток, в цепи переменного тока с конденсатором?
В каком случае в цепи с конденсатором существует ток
Оборудование: конденсатор (100 мкФ), лампа (4В), источники постоянного и переменного тока, ключ (2 шт.), соединительные провода.
Ход работы:
1. Соберите цепь, руководствуясь схемой (b).
2. Замкнув ключ 1, подсоедините конденсатор к источнику постоянного напряжения и наблюдайте за происходящим.
3. Разомкните ключ 1 и затем, замкнув ключ 2, подсоедините конденсатор к источнику переменного тока, одновременно продолжая наблюдать за происходящим.
4. Подсоедините лампу непосредственно к источнику переменного тока без конденсатора и сравните ее свечение (излучение) со свечением в цепи с конденсатором.
Обсуждение результата:
- При соединении конденсатора в какой цепи электрический ток существовал, и лампа светилась? Почему?
- В какой цепи переменного тока лампа светила ярче: с конденсатором или без? Почему?
При подсоединении конденсатора к источнику постоянного тока по цепи проходит кратковременный ток, лампа на миг загорается и сразу гаснет. Причиной кратковременности тока является наличие диэлектрика между пластинами конденсатора. Конденсатор, подсоединенный к источнику переменного тока, периодически перезаряжаясь, обеспечивает ток в цени и свечение лампы. Если лампа подсоединена к источнику переменного тока напрямую без конденсатора, то она светит ярче, чем в той же цепи с конденсатором. Уменьшение яркости свечения лампы свидетельствует о сопротивлении, которое создает конденсатор в этой цепи. Сопротивление, созданное конденсатором, называют ёмкостным сопротивлением и обозначают символом Хс. Соотношения между величинами, характеризующими цепь переменного тока с конденсатором, систематизированы в таблице 3.4.
Катушка в цепи переменного тока
Что произойдет, если цепь неременного тока будет состоять только из катушки?
Исследование цепи с катушкой.
Оборудование: катушка с железным сердечником (L = 5 Гн), лампа (4В), источник постоянного тока, источник переменного тока, ключ (2 шт.), соединительные провода.
Ход работы:
1. Соберите электрическую цепь на основе схемы (с).
2. Замкните ключ 1 и соедините катушку индуктивности L с источником постоянного тока. Обратите внимание на свечение лампы.
3. Затем разомкните ключ 1 и замкните ключ 2, соединив катушку с источником переменного тока и наблюдая за происходящим.
Обсуждение результата:
- При соединении участка цепи с лампой и катушкой к какому источнику тока лампа будет светить ярче?
- К какому выводу можно прийти из опыта?
Из исследования стало известно, что при подсоединении участка цепи с катушкой индуктивности и лампой к источнику переменного тока яркость свечения резко уменьшается. Это, в свою очередь, показывает, что катушка индуктивности обладает определенным сопротивлением. Сопротивление, которым обладает катушка, называют индуктивным сопротивлением и обозначают символом XL.
Соотношение между величинами, характеризующими цепь переменного тока с индуктивным сопротивлением, показано в таблице 3.5.
Кстати:
Лампы LED (светодиоды) вследствие своей высокой энергосберегаемости широко используются во всех осветительных системах. Несмотря на то, что лампы LED подключаются к сети переменного тока напряжением 220 В, их светодиоды работают на очень слабом постоянном токе. Постоянным током их обеспечивает помещенная в основание лампы микроэлектрическая цепь, снабженная полупроводниковым диодом и транзистором, катушкой, резистором и конденсатором.
Закон ома для цепи переменного тока с последовательным соединением активного, индуктивного и ёмкостного сопротивления
Закон Ома для полной цепи выражается следующим образом:
Сила тока в полной цепи прямо пропорциональна ЭДС источника и обратно пропорциональна полному сопротивлению цепи:
Амплитуда вынужденных колебаний колебательной системы зависит от частоты внешнего воздействия. С приближением значений частоты изменения внешнего воздействия к значению частоты собственных колебаний системы амплитуда вынужденных колебаний растет. В результате в системе возникает явление резонанса:
Резонанс — явление, выражающееся в резком возрастании амплитуды вынужденных колебаний в системе при совпадении частоты внешнего воздействия с частотой свободных колебаний системы:
Кривизна резонансной кривой зависит от значения силы трения. Кривая 1 соответствует малым значениям силы трения (максимально резкая), кривая 2 соответствует относительно большому значению силы трения, а кривая 3 соответствует наибольшему значению силы трения.
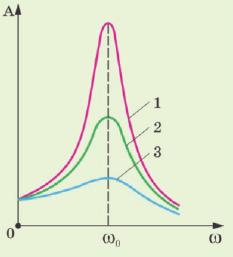
На предыдущем уроке были проанализированы особые, можно сказать, идеализированные состояния цепи переменного тока. Реальные цени переменного тока состоят из системы, включающей резистор, катушку и конденсаторы одновременно.
Представим, что цепь из последовательно соединенных резистора, конденсатора и катушки подсоединена к источнику переменного тока с ЭДС (с), меняющейся по гармоническому закону 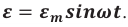
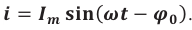
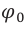
Согласно закону Ома, амплитудные значения силы тока и ЭДС (или общего напряжения на концах цени переменного тока) связаны друг с другом:
Здесь Um — амплитудное значение общего напряжения на концах цепи переменного тока, Z— полное сопротивление цепи переменного тока.
Полное сопротивление цепи переменного тока — физическая величина, равная отношению амплитудного значения общего напряжения на концах цепи переменного тока к амплитудному значению силы переменного тока:
Если разделить обе части последнего равенства на 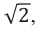
Полное сопротивление цепи из последовательно соединенных активного, ёмкостного и индуктивного сопротивлений зависит от этих сопротивлений:
Здесь 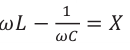
Если учесть выражение (2) в выражении (1), то закон Ома для цепи переменного тока можно записать таким образом:
Примечание. Вышеприведенные выражения можно получить на основе векторной диаграммы напряжений на разных участках цепи переменного тока, учитывая разность фаз колебаний силы тока и напряжения на этих сопротивлениях (d).
Как видно из диаграммы:
Если в выражении (2) учесть соответствующие падения напряжения, приведенные ниже:
используя векторную диаграмму, можно определить коэффициент мощности:
На рисунке (е) изображены графики зависимости амплитудных значений силы переменного тока от частоты колебаний ЭДС для трех резисторов с различными значениями сопротивлений. Анализ графиков показывает, что с уменьшением активного сопротивления 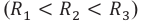
В это время частота колебаний силы переменного тока и ЭДС источника (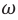
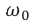
Передача электроэнергии. Трансформатор
Согласно закону сохранения энергии для полной цепи при прохождении электрического тока по металлическому проводнику ток совершает работу. Эта работа тратится на увеличение внутренней энергии проводника — на выделение тепла:
Количество теплоты, выделенное в проводнике с током, равно произведению квадрата силы тока на сопротивление проводника и на время прохождения тока по нему:
Соотношение между этими величинами впервые было экспериментально установлено английским ученым Д.Джоулем и русским ученым Э.Ленцем, поэтому его называют законом Джоуля-Ленца.
В параллельно соединенных проводниках напряжение (одинаково) неизменно, поэтому количество теплоты, выделяемое в них, обратно пропорционально сопротивлениям этих проводников:
Передача электроэнергии
При передаче на большие расстояния электроэнергии, произведенной генератором переменного тока, в проводах линии передачи происходят потери энергии в виде выделенного тепла, которое определяется на основе закона Джоуля-Ленца:
Как видим из формулы (1), одним из способов уменьшения потерь энергии является увеличение площади поперечного сечения проводов (S). Но этот способ не выгоден с практической точки зрения, так как в этом случае провода будут настолько массивными, что придется создать гигантские опорные столбы для их поддержки.
Самым выгодным способом снизить потери энергии является повышение напряжения и сохранение передаваемой мощности:
Поэтому для передачи вырабатываемого на электростанциях переменного тока напряжением 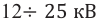
Значит, при передаче электроэнергии невозможно обойтись без необходимого элемента этого процесса — трансформатора — устройства для повышения-понижения напряжения (а).
Трансформатор
Трансформатор (лат. «transformare» — «превращать, преобразовывать») — электромагнитное устройство, предназначенное для увеличения-уменьшения напряжения переменного тока без изменения его мощности и частоты.
Схематическое изображение трансформатора и его условное обозначение на схеме показаны на рисунках (b) и (с). Он состоит из замкнутого сердечника (1), собранного из пластин, на который намотаны две катушки (обмотки). Первая катушка (2) называется первичной и подключается к источнику переменного напряжения, вторая катушка (3), называемая вторичной, присоединяется к нагрузке, т.е. к потребителям с общим сопротивлением
Переменный ток, проходящий через первичную обмотку, создает переменный магнитный поток, пронизывающий стальной сердечник и обе обмотки. Так как обе обмотки пересекает один и тот же магнитный поток, то в каждом витке этих обмоток возникает ЭДС индукции, равная
Если в первичной обмотке N1 витков, а во вторичной их N2, то ЭДС индукции в каждой из них будет равна соответственно:
Величина, равная отношению ЭДС, индуцированных в первичной и вторичной обмотках, называется коэффициентом трансформации (К) и равна отношению количества витков в соответствующих обмотках:
При разомкнутой вторичной обмотке (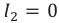
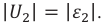
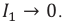
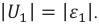
Из выражения (4) видно, что если 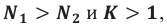
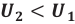
Если 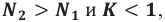
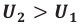
Активное сопротивление трансформатора близко к нулю, поэтому при работе в режиме нормальной нагрузки мощность в первичной цепи приблизительно равна мощности во вторичной цени: 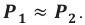
Значит, в обмотке трансформатора с малым напряжением сила тока принимает высокое значение, а в обмотке с большим напряжением сила тока принимает низкое значение. По этой причине провода в обмотке с малым числом витков и низким значением напряжения должны иметь большую площадь поперечного сечения, чем провода в обмотке с большим числом витков и высоким напряжением.
КПД трансформатора определяется следующим выражением:
Примечание. При подключении вторичной обмотки к потребителю коэффициент трансформации:
Здесь 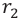
Электромагнитные волны
Волна — процесс распространения колебаний в пространстве с течением времени.
Волна — процесс переноса в среде энергии без переноса вещества.
Механическая волна — процесс распространения механических колебаний в среде. Механическая волна распространяется в упругой среде (в твердой, жидкой и газообразной) и не распространяется в вакууме. Существует два вида волн: продольные и поперечные.
В продольной волне колебания частиц среды происходят в направлении, параллельном направлению распространения волны. Продольная волна распространяется во всех средах (твердой, жидкой и газообразной). Она сопровождается чередованием сгущений и разряжений частиц среды.
В поперечной волне колебания частиц среды происходят в направлении, перпендикулярном направлению распространения волны. Поперечные волны распространяются только в твердых телах и на поверхности жидкостей. Они распространяются в виде чередующихся выпуклостей и впадин.
Одним из важнейших видов механических волн является звуковая волна, или просто звук. Она тоже представляет собой распространение колебаний в упругой среде.
Частота (период) волны — это частота (период) колебаний источника, создающего волну.
Длина волны — расстояние, на которое распространяется волна за время, равное периоду (t = Т) колебаний:
Скорость волны — это скорость распространения колебаний в среде:
Скорость волны не зависит от периода и частоты волны. Скорость волны зависит от свойств среды и его агрегатного состояния. Длина волны в однородной среде прямо пропорциональна периоду колебаний и обратно пропорциональна частоте колебаний частиц среды. При переходе волны из одной среды в другую частота и период волны не меняются, однако, так как скорость волны в различных средах различна, то и длина волны изменится.
Электромагнитная волна:
Явление электромагнитной индукции и явление самоиндукции показали, что изменяющееся со временем магнитное поле создает в пространстве вихревое переменное электрическое поле. Английский ученый Джеймс Клерк Максвелл (1831 — 1879) в опубликованной в 1873 году научной работе «Трактат об электричестве и магнетизме» обосновал предположение, что вихревое электрическое поле тоже создает в пространстве переменное магнитное поле. При этом силовые линии электрических и магнитных полей окружают друг друга.
Силовые линии нолей связаны следующими соотношениями:
Таким образом, быстро меняющееся электрическое поле порождает в этой же части пространства переменное магнитное поле, которое в свою очередь порождает вихревое электрическое поле и т.д. Переменные электрические и магнитные поля, одно порождая другое, охватывают все новые и новые части пространства — распространяются в пространстве с конечной скоростью в виде электромагнитных волн.
Электромагнитная волна — распространение в пространстве переменного электромагнитного поля. Являясь поперечной волной (g), электромагнитная волна характеризует изменение векторов напряженности электрического поля 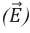
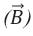
Некоторые свойства электромагнитных волн
Электромагнитные волны являются поперечными. Колебания векторов напряженности электрического поля 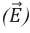
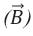
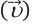
Электромагнитная волна распространяется и в среде, и в вакууме. Скорость её распространения в вакууме равна скорости распространения света в вакууме:
Здесь 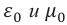
Скорость распространения электромагнитной волны в среде равна скорости распространения света в среде и зависит от свойств среды:
Здесь 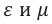
Длина электромагнитной волны в вакууме:
Длина электромагнитной волны в среде меньше, чем в вакууме, в n раз:
Электромагнитная волна обладает энергией. Часть энергии волны поглощается при попадании волны в проводник, в котором при этом возникает быстро меняющийся электрический ток.
Дошедшая до границы раздела двух сред электромагнитная волна претерпевает отражение и преломление.
Электромагнитная волна рассеивается в пространстве, поглощается в воде и т.д.
Излучение электромагнитных волн — открытый колебательный контур.
В обычном колебательном контуре происходит превращение энергий электрического и магнитного полей друг в друга, однако эти превращения выражаются поочередным накоплением энергии соответствующих полей то в конденсаторе, то в катушке. Поэтому за пределами колебательного контура, можно сказать, электромагнитная волна не фиксируется, то есть контур не излучает электромагнитные волны. Чтобы добиться излучения электромагнитной волны, необходимо повысить собственную частоту электромагнитных колебаний, создающих волну. Для этого следует уменьшить либо емкость, либо индуктивность в контуре, так как собственная частота электромагнитных колебаний в контуре равна
Учитывая эти закономерности, немецкий ученый Генрих Рудольф Герц (1857-1894) изменил форму колебательного контура и в 1886 году добился излучения контуром электромагнитных волн. Он удалил катушку, уменьшил площадь пластин конденсатора и отдалил их друг от друга. В результате закрытый контур превратился в открытый. Проводя опыты, периодически сообщая энергию такому контуру, называемому вибратором Герца, между кондукторами его конденсатора возникали высокочастотные электромагнитные колебания в форме искрового разряда. Одновременно на расстоянии 1-2 м параллельно вибратору был помещен приемный контур, не подсоединенный к какому-либо источнику энергии, резонатор, между кондукторами которого тоже возник такой же искровой разряд. Значит, высокочастотные электромагнитные колебания, возникшие в открытом колебательном контуре, распространили свою энергию в пространстве в виде электромагнитных волн, и эти волны были приняты резонатором (h).
Энергия электромагнитной волны
Презентацию рекомендуется провести на основе нижеприведенного плана. При этом рекомендуется воспользоваться электронными ресурсами и теоретическими сведениями.
План:
1. Энергия электромагнитных волн.
2. Шкала электромагнитных волн:
- а) радиоволны;
- 6) микроволны;
- в) инфракрасные волны;
- г) видимый свет;
- д) ультрафиолетовые волны;
- е) рентгеновское излучение;
- ж)
излучение.
При подготовке презентации по последнему пункту постарайтесь ответить на следующие вопросы: дата открытия этого излучения, характеристика, свойства, применение, действие на человеческий организм.
1. Энергия электромагнитной волны.
Электромагнитная волна несет в себе энергию. Эта энергия характеризуется следующими величинами:
• Плотность потока электромагнитного излучения (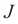
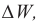
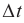
Если 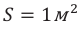
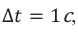
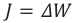
Плотность энергии электромагнитной волны равна энергии электромагнитного поля в единице объёма:
Единица измерения плотности энергии в СИ:
Электромагнитную энергию 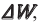
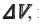
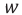
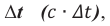
Подставив выражение (3) в формулу (1), выясняется, что плотность (интенсивность) потока излучения равна произведению плотности электромагнитной энергии на скорость его распространения:
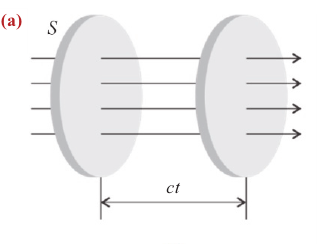
Самым простым источником, излучающим электромагнитные волны, является точечный источник — его размеры во много раз меньше расстояния, на котором оценивается его действие. Такой источник излучает одинаковые по интенсивности волны во всех направлениях (b). Если в формуле (1) учесть, что площадь сферы радиусом R. в центре которой помещен точечный источник, равна 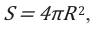
Если принять во внимание, что электромагнитные волны излучаются при ускоренном движении заряженных частиц, то напряженность электрического поля и индукция магнитного поля прямо пропорциональны ускорению этих частиц, а ускорение частиц прямо пропорционально квадрату частоты их колебаний:
Плотность электромагнитной энергии, как энергия электромагнитного поля, приходящаяся на единичный объём, равна сумме энергии электрического и магнитного полей:
Плотность (интенсивность) потока излучения пропорциональна плотности энергии, которая в свою очередь пропорциональна четвертой степени частоты излучения:
Мощность электромагнитного излучения точечного источника:
2. Шкала электромагнитных волн.
Некоторые сведения по этой теме можно получить по рисунку (см.: с).
Принципы радиосвязи
Самым простым видом механических волн являются звуковые волны.
Звуковые волны — это волны, распространяющиеся в упругой среде и вызывающие звуковые ощущения. Человеческое ухо воспринимает как звук только механические волны, колебания в которых происходят с частотой в пределах от 16 Гц до 20 ООО Гц. Важной особенностью звуковых волн является их отражение от препятствий на пути распространения. Метод определения местонахождения объектов с помощью звуковых волн называется звуколокацией (эхолокацией). Принцип работы прибора, называемого эхолотом, используемого для определения глубины морей и океанов, установления месторасположения крупных косяков рыб, основан на явлении отражения звука (эхо). Источник звука, расположенный под кораблем, испускает кратковременные звуковые сигналы.
Отраженный от объектов на глубине звуковой сигнал фиксируется специальным чувствительным прибором, находящимся на корабле. Учитывая скорость распространения звука в воде, промежуток времени между моментами отправления сигнала и его приема, легко можно вычислить расстояние до объекта:
По заказу Министерства обороны США Массачусетский технологический университет в 1961-1963 годах осуществил проект «Вест-форд» с помощью трех космических кораблей. На основе этого проекта в околоземное пространство было выпущено 480 миллионов медных иголок длиной 2 см каждая. Рассеявшись вокруг Земли, они образовали «игольную сферу» на расстоянии 
Принципы радиосвязи:
Опыты, проведенные Герцем, заинтересовали многих ученых мира и привели к исследованию путей осуществления радиотелеграфной и радиотелефонной связи.
Передача информации азбукой Морзе с помощью радиосвязи впервые была продемонстрирована русским физиком Александром Степановичем Поповым (1859-1905) 7-го мая 1895 года (эта дата и ныне отмечается в России как День радио). В 1896 году итальянский изобретатель Гульельмо Маркони (1874-1937) продемонстрировал передачу радиосигналами нескольких букв азбуки Морзе с помощью созданного им передающего устройства и прием этого радиосигнала помещенным на расстоянии 3 км аппаратом. В 1901 году, используя отражение радиоволн от земной ионосферы, он реализовал передачу информации с территории Англии на диаметрально противоположную сторону Атлантического океана — приемный аппарат в США (b).
Радиосвязь — это передача и прием информации (звук и изображение) с помощью электромагнитных волн.
В радиосвязи используются электромагнитные волны двух диапазонов:
- низкочастотные волны — плохо распространяются в пространстве, однако несут информацию;
- высокочастотные волны — распространяющиеся на очень большие расстояния в пространстве, но не несущие информации.
Основу радиосвязи составляют передающая сигналы радиостанция и принимающий эти сигналы радиоприемник.
В радиопередатчике происходят три основных процесса: 1) генерирование высокочастотных электромагнитных колебаний; 2) усиление этих высокочастотных колебаний до необходимой мощности; 3) изменение одного из параметров высокочастотных колебаний (амплитуды, частоты или фазы) в соответствии с передаваемой информацией.
Согласно упрощенной схеме передающей станции (с) она состоит из генератора на транзисторе (Т), колебательного контура, цепи микрофона (М) и передающей антенны (V). Генератор создает незатухающие высокочастотные электромагнитные волны (см. с, 1). Затем эти высокочастотные колебания модулируют (3) поступающими с микрофона низкочастотными колебаниями (2).
Модуляция — изменение амплитуды (частоты, фазы) высокочастотных электромагнитных колебаний в соответствии с амплитудой (частотой, фазой) низкочастотных звуковых колебаний.
Для осуществления амплитудной модуляции волн первичную обмотку трансформатора, подключенного к цепи передающей станции, подсоединяют к цени микрофона, а вторичную обмотку к источнику в цепи генератора на транзисторе. В результате высокочастотные колебания в колебательном контуре станции модулируются сигналами звуковой частоты. Полученные модулированные сигналы с помощью антенны излучаются в пространстве (см: с, 3).
Согласно упрощенной схеме приемной станции (радиоприемника) он состоит из следующих основных частей (d): принимающая антенна (Q), колебательный контур с конденсатором переменной мощности (С2), полупроводниковый диод — детектор (D), сглаживающий электрические сигналы конденсатор (Сз) и телефон (или громкоговоритель) (U). Принимаемые антенной радиоприемника электромагнитные волны создают в колебательном контуре переменный индукционный ток.
Меняя емкость конденсатора в контуре, уравниваем частоту его собственных колебаний с частотой колебаний определенной принимаемой электромагнитной волны. При этом резко возрастает амплитуда колебаний возникшего в контуре тока — возникает резонанс. В результате контур настраивается на прием сигнала определенной передающей станции. Далее осуществляется процесс отделения низкочастотных колебаний от принятых радиоприемником высокочастотных модулированных колебаний — детектирование (или демодуляция).
Демодуляция реализуется с помощью детектора (полупроводниковый диод). Ток, прошедший через детектор, превращается в односторонний пульсирующий ток (см: d, 4). Этот ток, пройдя через конденсатор Сз (фильтр), сглаживается. Сглаженный электрический сигнал превращается в колебания звуковой частоты (5), и они выводится на громкоговоритель телефона (радио).
Радиолокация
Электромагнитные волны отражаются от металлических (проводящих) пластин. Физическую основу радиолокации составляет именно это свойство электромагнитных волн.
Радиолокация — обнаружение различных объектов с помощью радиоволн.
Устройство для определения расстояния до объекта с помощью радиоволн называется радиолокатором (или радаром).
Радиолокатор — устройство, состоящее из радиопередатчика и радиоприемника ультракоротких волн (е).
Радиолокатор излучает радиоволны в виде коротких импульсов. В промежутке времени между двумя такими импульсами локатор автоматически превращается в антенну, принимающую отраженные от объекта сигналы. Таким образом, легко определяется расстояние (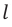
Здесь 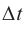
Определение электромагнитных колебаний
Электромагнитные колебания имеют много общего с механическими колебаниями: они подчиняются одинаковым количественным законам. Электромагнитные колебания – это периодические изменения заряда, силы тока и напряжения. Среди различных физических явлений электромагнитные колебания занимают особое место, они создают электромагнитные волны, которые получили широкое применение в электротехнике, радиотехнике и физической оптике.
Изучив подраздел, вы сможете:
- описывать условия возникновения свободных и вынужденных колебаний;
- проводить аналогии между механическими и электромагнитными колебаниями;
- исследовать графические зависимости заряда и силы тока от времени посредством компьютерного моделирования.
Свободные и вынужденные электромагнитные колебания
I. Свободные электромагнитные колебания. Уравнение свободных колебаний
Для создания колебательного процесса, в контуре можно использовать два способа: зарядить конденсатор (рис. 10) или создать внешним переменным магнитным полем ЭДС индукции в катушке.
Запишем закон Ома для колебательного контура:
где u − переменное напряжение на обкладках конденсатора, 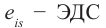
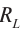
Если колебательный контур считать идеальным, т. е. 
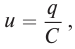
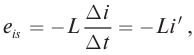
При малых значениях изменения аргумента, которым является промежуток времени, 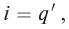
Подставив (3) в (2), получим уравнение, которое описывает процессы, происходящие в идеальном колебательном контуре, или закон Ома для колебательного контура:
Введем понятие «собственная циклическая частота колебаний»:
тогда формула (4) примет вид:
Получено уравнение (6), описывающее электромагнитные колебания в контуре.
Вспомните!
1. Конденсатор и катушка индуктивности, соединенные между собой в замкнутую цепь, представляют собой колебательный контур, в котором могут происходить электромагнитные колебания (рис. 11).
2. Сила тока – это заряд, прошедший в единицу времени через поперечное сечение проводника: 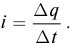
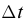
Возьмите на заметку:
Период и собственная частота электромагнитных колебаний, зависят только от емкости конденсатора С и индуктивности катушки L. Они не зависят от заряда, силы тока и напряжения.
Величины, характеризующие свободные колебания в колебательном контуре
Процессы, происходящие в колебательном контуре, характеризуются такими величинами, как: период, собственная частота, циклическая частота, заряд, сила тока, напряжение.
Мгновенное значение силы тока в колебательном контуре определим из уравнений (7) и (8), взяв первую производную от заряда:
Из полученных выражений следует, что максимальное значение силы тока в контуре зависит от максимального значения заряда:
Чем больше заряд на обкладках конденсатора, тем выше напряжение между ними: 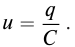
Автоколебательные системы. Вынужденные колебания
Автоколебательные системы позволяют получить незатухающие колебания различных частот. В этих системах есть свой источник, который компенсирует потери энергии в определенные моменты времени. Основные элементы автоколебательной системы изображены на рисунке 13:
Запомните!
Автоколебательные системы – это системы, в которых совершаются незатухающие колебания за счет поступления энергии от источника внутри системы.
Генератор на транзисторе
На рисунке 15 изображена схема автоколебательной электрической системы, получившей название «генератор на транзисторе». Роль клапана в нем выполняет транзистор. Обратную связь осуществляет катушка связи
Вспомните!
Вынужденные колебания – это колебания, происходящие под воздействием внешней периодически действующей силы.
Принцип действия генератора на транзисторе
Если на эмиттер 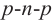
Транзистор – это полупроводниковый прибор с двумя 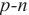
Вспомните! Индукционный ток всегда имеет такое направление, при котором его магнитное поле противодействует изменению магнитного потока, вызывающему этот ток.
Аналогии между механическими и электромагнитными колебаниями
I. Аналогия величин, характеризующих механические и электромагнитные колебания
Всем величинам, характеризующим механические колебания, можно найти аналоги среди величин, характеризующих электромагнитные колебания (таблица 1).
II. Энергии колебательных систем
Аналогия величин позволяет по формулам для механических колебаний записать формулы для электромагнитных колебаний. Например, кинетическая энергия пружинного маятника определяется массой и скоростью тела: 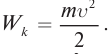
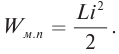
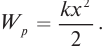
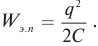
III. Закон сохранения энергии в применении к механическим и электромагнитным колебаниям
Выведем из положения равновесия пружинный маятник (рис. 21 а). Растянутая пружина в положении максимального отклонения обладает максимальной потенциальной энергией 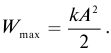
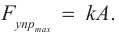
При отсутствии силы сопротивления выполняется закон сохранения полной механической энергии:
где 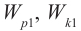
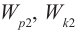
IV. Закон сохранения энергии в применении к электромагнитным колебаниям
Рассмотрим электромагнитные колебания в колебательном контуре (рис. 22 а). В начальный момент времени энергия электрического поля между обкладками конденсатора имеет максимальное значение и определяет полную энергию контура (таблица 3). При разрядке конденсатора заряд на его обкладках и энергия электрического поля уменьшаются. В катушке появляется ток, энергия магнитного поля катушки возрастает (рис. 22 б). Полная энергия контура равна сумме энергии электрического поля конденсатора и энергии магнитного поля катушки с током. Через четверть периода заряд на обкладках конденсатора становится равным нулю, сила тока в катушке достигает максимального значения 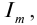
Полная энергия колебательного контура при отсутствии тепловых потерь остается величиной постоянной:
где 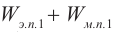
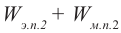
V. Графики электромагнитных колебаний
Определим сдвиг фаз величин, характеризующих электромагнитные колебания. Пусть заряд на конденсаторе меняется по закону:
Тогда изменение силы тока будет происходить по закону:
Напряжение на обкладках конденсатора меняется по закону:
Закон изменения ЭДС самоиндукции поля, созданного магнитным полем катушки, определим по формуле:
Все величины выражены через одну и ту же тригонометрическую функцию, определим разность фаз. Колебания силы тока опережают по фазе колебания заряда на конденсаторе на 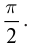
Возьмите на заметку:
Колебательный контур, активное сопротивление которого равно нулю, и в конденсаторе нет токов проводимости и других эффектов, приводящих к потерям энергии, называют идеальным колебательным контуром.
Интересно знать!
«Человек – колебательный контур» (рис. 24)
1. Живую клетку можно представить в виде колебательного контура с электрической емкостью и сопротивлением. Емкость клетки определяется свободно радикальными реакциями и системой антиоксидантной защиты, а сопротивление – ферментативным окислением.
2. В виде колебательного контура можно представить не только клетку, но и печень, а также систему кровообращения – каскад замкнутых проводников от петель капилляров до большого и малого кругов кровообращения.
3. Нервная система координирует работу всего организма.
4. Ритмы электрического потенциала органов человека:
- желудка и кишечника – 0,01…0,05 Гц;
- легких – 0,2…0,3 Гц;
- сердца – около 1,2 Гц;
- нервной системы – 10…1000 Гц;
- ритм электрической активности головного мозга – 8…10 Гц;
Итоги:
Глоссарий:
- Автоколебательные системы – системы, в которых совершаются незатухающие колебания за счет поступления энергии от источника внутри системы.
- Вынужденные колебания – колебания, происходящие под воздействием внешней периодически действующей силы.
- Идеальный колебательный контур – контур, активное сопротивление которого равно нулю, в конденсаторе нет токов проводимости и других эффектов, приводящих к потерям энергии.
- Свободные электромагнитные колебания – периодически повторяющиеся изменения силы тока в катушке и напряжения между обкладками конденсатора без потребления энергии от внешних источников.
- Электромагнитные колебания – периодические изменения заряда, силы тока и напряжения.
Электромагнитные колебания в контуре и формула Томсона
Перемещение проекции точки, движущейся по окружности
Зависимость координаты (смещения) материальной точки, совершающей гармонические колебания, от времени:
Зависимость проекции скорости 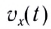
Зависимость проекции ускорения 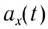
Уравнение гармонических колебаний:
х(t) — зависимость координаты материальной точки, совершающей гармонические колебания, от времени (решение уравнения гармонических колебаний).
Пружинный маятник
Период колебаний и циклическая частота пружинного маятника:
Уравнение движения пружинного маятника:
Математический маятник
Период колебаний и циклическая частота математического маятника:
Уравнение движения математического маятника:
Резонанс
Резонанс — явление резкого возрастания амплитуды вынужденных колебаний при совпадении циклической частоты 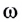
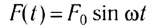
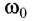
Рассмотрим электрическую цепь, содержащую конденсатор электроемкостью С и катушку (соленоид) индуктивностью L (рис. 188).
Такая цепь называется идеальным колебательным контуром или LC-контуром.
Пусть в начальный момент времени (t=0) конденсатор С заряжен так, что на его первой обкладке находится заряд 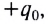
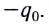
После замыкания цепи конденсатор начнет разряжаться, и в цепи появится электрический ток, сила I(t) которого будет меняться с течением времени. Поскольку при прохождении электрического тока через катушку индуктивности возникнет изменяющийся во времени магнитный поток, то в ней возникнет ЭДС самоиндукции, препятствующая изменению силы тока.
Вследствие этого, сила тока в колебательном контуре будет возрастать от нуля до некоторого максимального значения не мгновенно, а в течение некоторого промежутка времени, определяемого индуктивностью катушки.
В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального значения 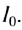
После разрядки конденсатора сила тока в катушке начинает убывать. Это также происходит не мгновенно, поскольку теперь ЭДС самоиндукции стремится скомпенсировать уменьшение тока и «поддерживает» его. Ток, создаваемый ЭДС самоиндукции катушки, заряжает обкладки конденсатора до начального напряжения обратной полярности — знак заряда на каждой обкладке оказывается противоположным начальному.
Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения 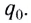
Таким образом, в идеальном LС-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
Свободные электромагнитные колебания в контуре — это периодические изменения заряда на обкладках конденсатора, силы тока в контуре и разности потенциалов на обоих элементах контура, происходящие без потребления энергии от внешних источников.
Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением ЭДС самоиндукции в катушке, которая «обеспечивает» эту перезарядку. Заметим, что заряд конденсатора q(t) и сила тока в катушке I(t) достигают своих максимальных значений 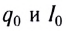
Наименьший промежуток времени, за который LС-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Период свободных электромагнитных колебаний в контуре определяется по формуле Томсона
Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство
Получим уравнение колебаний в LC-контуре, используя закон сохранения энергии. Продифференцировав выражение для его полной энергии по времени, с учетом того, что 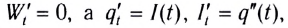
Переписав его в виде
замечаем, что это — уравнение гармонических колебаний с циклической частотой
Соответственно, период рассматриваемых колебаний
Сравним электромагнитные колебания с механическими колебаниями. Для этого воспользуемся таблицей 4, в которой сопоставляются аналогичные физические величины.
Из таблицы 4 следует, что аналогом энергии упругой деформации пружины можно считать электростатическую энергию конденсатора, аналогом кинетической энергии груза — энергию магнитного поля катушки.
Таблица 4
Сопоставление физических величин, характеризующих электромагнитные и механические колебания
Соответственно, зависимость заряда конденсатора от времени будет иметь такой же характер, как и зависимость координаты (смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону (но с другими начальными фазами) будут изменяться сила тока в цепи, напряжение на конденсаторе (катушке).
Для определения начальной фазы 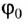
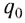
Полная энергия идеального колебательного контура сохраняется с течением времени, поскольку согласно закону Джоуля — Ленца в нем вследствие отсутствия резисторов не выделяется теплота. Реальный колебательный контур всегда имеет некоторое сопротивление R, обусловленное сопротивлением катушки, соединительных проводов и т. д. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они будут продолжаться сколь угодно долго.
С точки зрения механической аналогии идеальному колебательному контуру соответствует пружинный маятник без трения, а реальному — с трением.
Вычисление электромагнитных колебаний и волн
Явление возникновения ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.
Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.
Рис. 29. Колебательный контур (а); зарядка конденсатора от источника (б)
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью 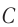
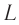
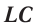
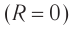
Подключив (при помощи ключа 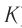
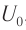
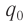
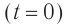
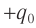
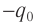
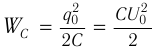
Рис. 30. Прохождение тока в колебательном контуре
Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа 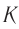
Таким образом, в контуре появится нарастающий по модулю электрический ток, сила 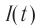
Вследствие этого модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения 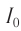
Рис. 31. Электромагнитные колебания в идеальном 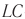
При разрядке конденсатора энергия его электростатического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):
где 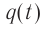
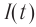
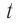
В момент полной разрядки конденсатора 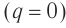
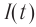
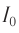
После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезаряжает конденсатор до начального напряжения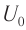
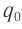
Таким образом, в идеальном 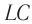
Свободные электромагнитные колебания в 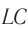
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд 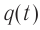
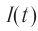
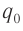
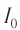
Наименьший промежуток времени, в течение которого 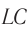
Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального 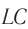
Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:
где 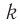
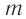
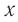
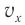
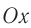
Период его колебаний:
Проанализируем соотношения (1) и (2). Видно, что энергия электростатического поля конденсатора 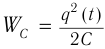
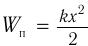
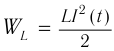
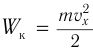
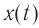
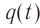
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника массу 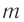
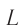
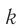
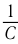
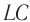
которая называется формулой Томсона.
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).
Таблица 4. Сопоставление физических величин, характеризующих механические и электромагнитные колебания
Для наблюдения и исследования электромагнитных колебаний применяют электронный осциллограф, на экране которого получают временную развертку колебаний (рис. 32).
Рис. 32. Гармонические электромагнитные колебания на экране осциллографа
Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты (проекции смещения) тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.
Для определения начальной фазы 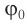
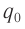
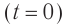
Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.
Полная энергия идеального колебательного контура 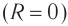
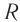
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.
Пример №9
Идеальный колебательный контур состоит из конденсатора емкостью 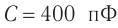
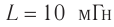
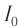
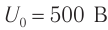
Решение
Максимальная энергия электростатического поля конденсатора:
а максимальная энергия магнитного поля катушки:
Так как контур идеальный 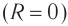
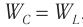
Отсюда
Ответ:
Вынужденные электромагнитные колебания
Магнитный поток 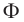
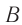
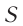
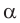
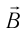
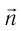
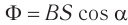
Закон электромагнитной индукции: ЭДС индукции в контуре равна скорости изменения пронизывающего его магнитного потока, взятой с противоположным знаком: 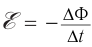
Незатухающие электромагнитные колебания находят широкое применение в науке и технике. Для получения незатухающих колебаний необходимо компенсировать потери энергии в контуре. Для механических колебаний это достигается действием периодической внешней силы, в результате чего в системе возникают вынужденные колебания. Аналогично этому вынужденные электромагнитные колебания в колебательном контуре происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения. При этом напряжение в цепи и сила тока изменяются как по знаку, так и по модулю.
Ток, сила и направление которого периодически меняются, называется переменным.
Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими синусоидальное напряжение. Такая же функциональная зависимость силы тока от времени позволяет, по сравнению с другими зависимостями, наиболее просто и экономично осуществлять передачу, распределение и использование электрической энергии.
Электротехническое устройство, предназначенное для преобразования механической энергии в энергию переменного электрического тока, называется генератором переменного тока.
Принцип действия индукционного генератора переменного тока основан на явлении электромагнитной индукции.
Пусть проводящая рамка площадью 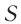
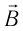
Рис. 33. Вращение проводящей рамки в магнитном поле
При равномерном вращении рамки угол 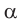
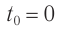
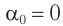
Подставляя полученное выражение для 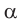
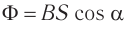
Поскольку магнитный поток, пронизывающий рамку, изменяется со временем (рис. 34), то в ней согласно закону Фарадея индуцируется ЭДС индукции 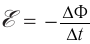
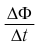
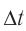
Поскольку 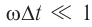
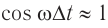
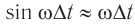
Окончательно
Отсюда
Следовательно,
Рис. 34. Возникновение ЭДС индукции при вращении проводящей рамки в магнитном поле
Как видно, ЭДС индукции изменяется по синусоидальному закону:
где 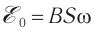
При подключении к выводам рамки устройства, потребляющего энергию, например нагрузки с достаточно большим сопротивлением 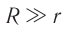
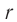
где 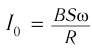
Анализируя выражения (1) и (2), можем сделать вывод, что в цепи, содержащей, кроме рамки, только активное сопротивление 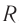
В общем случае (например, при наличии в цепи конденсатора и (или) катушки) колебания силы тока в цепи и напряжения на конденсаторе или катушке будут происходить с одинаковой частотой 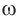
где 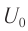
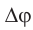
Рис. 35. Части индукционного генератора: 1 — индуктор; 2 — якорь; 3 — коллектор со щетками
Подчеркнем, что ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное, которое также остается неизменным в течение следующего полуоборота.
Основными частями индукционного генератора переменного тока являются (рис. 35):
- индуктор — постоянный магнит или электромагнит, который создает магнитное поле;
- якорь — обмотка, в которой индуцируется переменная ЭДС;
- коллектор — контактные кольца и скользящие по ним контактные пластинки (щетки) — устройство, посредством которого ток снимается или подводится к вращающимся частям.
Неподвижная часть генератора называется статором, а подвижная — ротором.
В зависимости от конструкции генератора его якорь может быть как ротором, так и статором. Для получения переменных токов большой мощности якорь делают неподвижным, чтобы конструктивно упростить схему передачи тока в промышленную сеть. Кроме того, это делает генератор более надежным в эксплуатации вследствие уменьшения искрения и обгорания щеток.
На современных гидроэлектростанциях падающая вода вращает вал электрогенератора с частотой 1—2 оборота в секунду. Таким образом, если бы якорь генератора имел только одну рамку (обмотку), то получался бы переменный ток частотой 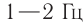
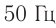
Для паровых турбин, ротор которых вращается очень быстро, используют якорь с одной обмоткой. В этом случае частота вращения ротора совпадает с частотой переменного тока, т. е. ротор должен делать 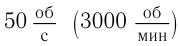
Для увеличения амплитудного значения ЭДС индукции нужно либо увеличивать индукцию магнитного поля, пронизывающего обмотки якоря, либо увеличивать число витков его обмоток. Для увеличения индукции магнитного поля 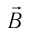
Мощные генераторы вырабатывают напряжение 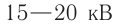
При подключении электрических цепей к источнику переменного тока возникают новые закономерности, которые и рассмотрим ниже.
Пусть источник тока создает переменное гармоническое напряжение:
Согласно закону Ома для участка цепи сила тока на участке цепи, содержащем только резистор сопротивлением 
где 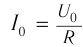
Рис. 36. Зависимости 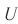
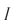
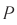
Сила тока во всей такой цепи также меняется с течением времени по синусоидальному закону.
Максимальные величины напряжения и силы тока 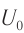
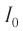
Значения напряжения 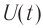
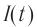
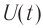
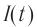
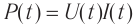
С учетом зависимости силы тока от времени перепишем выражение для мгновенной мощности на резисторе сопротивлением 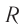
Поскольку мгновенная мощность изменяется со временем, то использовать эту величину на практике в качестве характеристики длительно протекающих процессов крайне неудобно.
Перепишем формулу для мгновенной мощности по-другому:
Первое слагаемое не зависит от времени. Второе слагаемое — переменная составляющая — функция косинуса двойного угла. Ее среднее значение за промежуток времени, равный (или кратный) периоду колебаний, равно нулю 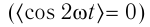
Поэтому среднее значение мощности переменного электрического тока за длительный по сравнению с периодом колебаний промежуток времени можно найти по формуле:
Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.
Действующее (эффективное) значение силы переменного тока равно силе такого постоянного тока, который, проходя в электрической цепи по резистору сопротивлением 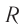
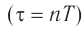
Поскольку для постоянного тока 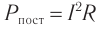
Аналогично можно ввести действующее значение и для напряжения:
Таким образом, выражения для расчета мощности, потребляемой резисторами в цепях постоянного тока, аналогичны и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
В цепях переменного тока большинство электроизмерительных приборов измеряют действующие значения тока и напряжения. Так, например, действующим значением напряжения в Беларуси в бытовых сетях переменного тока является 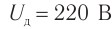
Необходимо отметить, что закон Ома для участка цепи переменного тока, содержащего только резистор сопротивлением 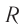
Таким образом, резисторы оказывают сопротивление как постоянному, так и переменному току, при этом в обоих случаях в них происходит превращение электрической энергии в энергию теплового движения частиц. Вследствие этого сопротивление резисторов 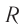
Преобразование переменного тока и трансформатор
Генераторы переменного тока создают в расчете на определенные значения напряжения. Для практического использования электрической энергии во всевозможных устройствах и приборах необходимы различные значения напряжений. Для этого используются трансформаторы (от лат. transformo — преобразую). Первую модель (прототип) трансформатора создал в 1831 г. Майкл Фарадей, намотав на железное кольцо две изолированные обмотки, которую использовал в своих экспериментах. Трансформатор был впервые использован для изменения напряжения в 1878 г. русским ученым Павлом Николаевичем Яблочковым для питания изобретенных им источников света — «электрических свечей».
Трансформатор (рис. 37, а) — это электромагнитное устройство, преобразующее переменный ток одного напряжения в переменный ток другого напряжения с сохранением его частоты.
Трансформатор, увеличивающий напряжение, называют повышающим, а уменьшающий напряжение — понижающим. Схематическое изображение и условное обозначение трансформатора показаны на рисунке 37 б, в.
Рис. 37. Трансформатор: а — общий вид; б — схематическое изображение; в — условное обозначение
Рис. 38. Различные расположения обмоток трансформаторов
Самый простой трансформатор состоит из двух обмоток (катушек), надетых на общий замкнутый сердечник (см. рис. 37, а). Обмотка трансформатора, на которую подается переменное напряжение, называется первичной, а обмотка, с которой снимается преобразованное переменное напряжение, — вторичной. Число витков в первичной обмотке трансформатора обозначим 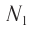
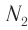
Обмотки трансформатора могут быть расположены на сердечнике различным образом (рис. 38).
Принцип действия трансформатора основан на явлении электромагнитной индукции. Магнитное поле, создаваемое переменным током в первичной обмотке (см. рис. 37, а), благодаря наличию замкнутого сердечника практически без потерь (без рассеяния) пронизывает витки вторичной обмотки. Для этого сердечник изготовляется из специального (ферромагнитного) материала, что позволяет создаваемое током в обмотках поле почти полностью локализовать внутри сердечника. В результате магнитный поток существует только внутри сердечника и одинаков во всех сечениях. Это дает возможность считать мгновенные значения магнитных потоков во всех сечениях сердечника одинаковыми.
Пусть первичная обмотка трансформатора подключена к источнику тока с переменной ЭДС и на нее подается напряжение 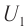
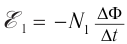
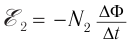
где 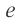
Вследствие малого активного сопротивления первичной обмотки
Режимом холостого хода трансформатора называется режим с разомкнутой вторичной обмоткой. В этом случае напряжение на вторичной обмотке равно индуцируемой в ней ЭДС:
Следовательно, в режиме холостого хода из соотношения (1) получаем:
т. е. действующее значение напряжения 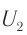
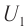
Как следует из выражения (2), в зависимости от отношения числа витков в обмотках напряжение 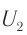
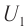
Тип трансформатора определяется коэффициентом трансформации, который равен отношению числа витков первичной катушки к числу витков вторичной:
Согласно выражению (2) отношение действующих значений напряжений на первичной и вторичной обмотках трансформатора в режиме холостого хода равно коэффициенту трансформации:
Как следует из соотношения (3), 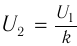
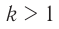
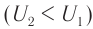
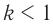
Рабочим ходом (режимом) трансформатора называется режим, при котором в цепь его вторичной обмотки включена некоторая нагрузка. Включение нагрузки во вторичную цепь трансформатора приводит к появлению в ней тока. Согласно правилу Ленца магнитный поток, создаваемый током во вторичной обмотке, стремится скомпенсировать изменение магнитного потока через витки вторичной обмотки, а значит, и через витки первичной обмотки (общий сердечник).
Это приводит к некоторому уменьшению магнитного потока в первичной обмотке, для компенсации которого действующее значение силы тока в первичной обмотке трансформатора увеличивается. Следовательно, после включения нагрузки трансформатора во вторичную обмотку сила тока в его первичной катушке увеличивается таким образом, чтобы суммарный магнитный поток через первичную обмотку достиг прежней величины.
Трансформатор не производит, а преобразовывает энергию. Согласно закону сохранения энергии мощность тока, выделяемая в цепи вторичной обмотки трансформатора в режиме нагрузки, поступает из цепи его первичной обмотки, т. е. от внешнего источника. Пренебрегая потерями энергии, связанными с нагреванием обмоток и работой по перемагничиванию сердечника, которые в современных трансформаторах не превышают 
Таким образом, повышая напряжение в несколько раз, трансформатор во столько же раз уменьшает силу тока.
Режимом короткого замыкания называется режим, при котором вторичная обмотка трансформатора замкнута без нагрузки. Данный режим опасен для трансформатора, поскольку в этом случае действующее значение тока во вторичной обмотке максимально и происходят электрическая и тепловая перегрузки системы.
При работе трансформатора всегда имеются энергетические потери, связанные с такими физическими процессами, как:
- нагревание обмоток трансформатора при прохождении электрического тока;
- работа по перемагничиванию сердечника;
- рассеяние магнитного потока.
Наиболее значительные энергетические потери при работе трансформатора обусловлены тепловым действием вихревых токов (токов Фуко), возникающих в сердечнике при изменении магнитного потока.
Для уменьшения тепловых потерь сердечники (магнитопроводы) трансформаторов изготовляют не из сплошного куска металла, а из тонких пластин специальной трансформаторной стали, разделенных тончайшими слоями диэлектрика (пластины покрывают лаком). Такая конструкция сердечника позволяет значительно увеличить его электрическое сопротивление, что приводит к уменьшению потерь на его нагревание.
Для предотвращения перегрева мощных трансформаторов используется масляное охлаждение.
Современные трансформаторы имеют очень высокие 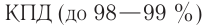
Пример №10
Определите силу тока 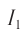
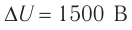
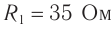
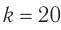
Решение
По закону Ома сила тока в первичной обмотке:
где 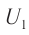
Коэффициент трансформации:
где 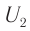
Тогда сила тока в первичной обмотке:
Ответ: 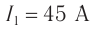
Производство, передача и потребление электрической энергии
Электрическая энергия вырабатывается на электростанциях. В зависимости от вида используемого носителя энергии все современные электростанции делятся на тепловые, гидроэлектростанции и атомные. Приведем характеристики основных типов электростанций.
Тепловые электростанции (ТЭС) используют теплоту, получаемую при сжигании угля, нефти, мазута, газа и других горючих ископаемых 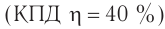
Гидроэлектростанции (ГЭС) используют энергию движущейся воды рек, водохранилищ и иных водных потоков 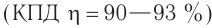
Атомные электростанции (АЭС) работают на энергии, выделяющейся при расщеплении ядер урана и плутония 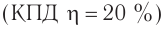
При передаче электроэнергии от электростанций к крупным промышленным центрам и городам наиболее часто используют проводные линии передач, которые являются надежным и сравнительно недорогим способом передачи энергии. Часть передаваемой энергии неизбежно теряется в соответствии с законом Джоуля — Ленца:
где 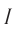
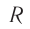
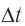
Как следует из закона Джоуля — Ленца, для уменьшения тепловых потерь в линиях передач необходимо уменьшать их сопротивление и действующее значение силы тока. Однако уменьшение сопротивления 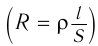
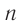
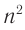
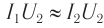
Рис. 39. Высоковольтная линия электропередачи
Поскольку генераторы переменного тока на электростанциях дают напряжения не более 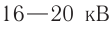
Для безопасного обслуживания потребителей энергии (станков, бытовых приборов и др.) напряжение их питания должно быть низким, что легко достигается при использовании понижающих трансформаторов. Понижение напряжения обычно происходит в несколько этапов.
Рассмотрим блок-схему передачи и распределения электроэнергии (рис. 40):
генератор переменного тока 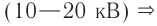
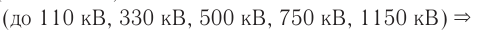
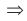
Рис. 40. Блок-схема передачи электроэнергии
В современном обществе потребление электроэнергии распределяется примерно следующим образом: промышленность — 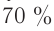
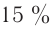
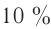
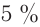
В настоящее время все большее распространение получают линии передач, работающие на постоянном токе. Хотя преобразование постоянного напряжения сложнее и дороже, но постоянный ток по сравнению с переменным обладает рядом преимуществ.
Во-первых, постоянный ток, в отличие от переменного, не создает переменные магнитные поля, которые индуцируют токи в близлежащих проводниках, что приводит к потерям мощности.
Во-вторых, постоянный ток можно передавать при более высоком напряжении, так как действующее напряжение в цепи равно амплитудному, и не следует опасаться электрического пробоя изолятора или воздуха при том же амплитудном напряжении.
Развитие цивилизации сопровождается непрерывным ростом энергопотребления на нашей планете. Однако запасы природного топлива (нефти, газа, угля, торфа) и иных полезных ископаемых на Земле ограничены, поскольку из-за изменения геологических условий их формирование в настоящее время практически прекратилось.
Явным лидером среди энергоносителей на сегодняшний день является нефть, поскольку ее сравнительно легко добывать, транспортировать, очищать и использовать. Помимо этого, нефть также является источником разнообразных синтетических материалов — красок, лекарств, синтетических волокон, пластмасс и др.
По различным оценкам, в настоящее время выработано около 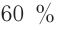
В нашей стране запасы нефти и угля не являются стратегическими. На территории Республики Беларусь к основным видам добываемых топливных ресурсов следует отнести дрова и торф.
Работа электростанций вследствие их значительной мощности существенным образом влияет на состояние окружающей среды и приводит к появлению следующих экологических проблем:
ГЭС — загрязнение атмосферы продуктами сгорания, изменение природного теплового баланса из-за рассеяния тепловой энергии;
ГЭС — изменение климата, нарушение экологического равновесия, уменьшение пахотных площадей;
АЭС — опасность радиоактивного загрязнения среды при авариях, проблемы захоронения радиоактивных отходов.
Одной из главных экологических проблем современности является рост выбросов в атмосферу продуктов сгорания топлива (в первую очередь углекислого газа). Углекислый газ «окутывает» Землю подобно пленке, препятствуя ее охлаждению. Это приводит к парниковому эффекту, при котором средняя температура на Земле медленно повышается. Соответственно, за последние десятилетия на планете происходит глобальное потепление, которое, согласно прогнозам ученых, может привести к необратимым изменениям в климате Земли.
Рост энергопотребления заставляет ученых и инженеров искать альтернативные источники энергии, которые имели бы возобновляемый характер, т. е., в отличие от нефти и газа, могли бы самостоятельно восстанавливаться с течением времени.
К возобновляемым источникам энергии относят ветер, недра Земли (геотермальную энергию), морские приливы, а также солнечное излучение, используемое напрямую.
Ветроэнергетика — использование кинетической энергии ветра для получения электроэнергии. Энергия ветра уже достаточно успешно преобразуется в электроэнергию в многочисленных небольших ветряных генераторах в зонах устойчивых ветров (рис. 41).
Рис. 41. Ветряные генераторы.
Проекты будущего предлагают использовать в качестве возобновляемых источников энергии колоссальную энергию океанических и воздушных течений, тропических ураганов и торнадо. Ключевая причина их формирования — неравномерное нагревание Солнцем различных участков поверхности Земли.
Геотермальная энергетика — использование естественного тепла Земли для выработки электрической энергии. Геотермальная энергия в местах естественных разломов земной коры используется для нужд человека. Например, столица Исландии — Рейкьявик полностью отапливается за счет геотермальных источников. Запасы геотермальной энергии достаточно велики, о чем можно судить по громадной разрушительной силе землетрясений и извержений вулканов и гейзеров.
Приливная энергетика использует энергию морских приливов. В настоящее время делаются первые шаги для использования энергии океанических приливов и отливов. Инженерная идея подобных проектов проста: использовать перепад уровней воды во время прилива и отлива для вращения водой гидротурбин, чтобы на соединенных с ними гидрогенераторах производить электричество.
Гелиоэнергетика — получение электрической энергии из энергии солнечного излучения. Развитие современных технологий позволяет эффективно использовать энергию, вырабатываемую солнечными батареями. Так, в южных широтах энергии подобных батарей, установленных на крыше, хватает для энергоснабжения небольшого дома. Современные технологии позволяют, используя солнечные батареи, получать электрическую энергию от солнечного излучения не только на Земле, но и в космосе (рис. 42). Есть смелые проекты, в которых предлагается разместить солнечные батареи в ближнем космосе на расстоянии 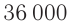
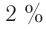
Рис. 42. Солнечные батареи в космосе
Водородная энергетика:
Самым распространенным перспективным источником энергии в масштабах Вселенной следует считать водород, поскольку его изотопы позволяют осуществить реакцию термоядерного синтеза . Энергия термоядерного синтеза предпочтительнее энергии ядерного расщепления , поскольку из одинаковой массы вещества при синтезе может быть извлечено в 10 раз больше энергии, чем при расщеплении. Кроме того, водород (топливо синтеза) гораздо легче добывать в Мировом океане, чего нельзя сказать об уране и тории, служащими топливом при реакциях ядерного расщепления. Немаловажным является и тот факт, что при реакции термоядерного синтеза не возникает радиоактивных отходов, поскольку ее основной продукт — гелий, являющийся инертным газом. А радиоактивные изотопы гелия 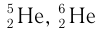
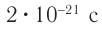
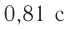
Возобновляемые источники энергии сравнительно безопасны, поскольку их использование не приводит к загрязнению окружающей среды.
Электромагнитные волны и их свойства. Шкала электромагнитных волн
Впервые гипотезу о существовании электромагнитных волн высказал в 1864 г. английский физик Джеймс Максвелл. В своих работах он показал, что источниками электрического поля могут быть как электрические заряды, так и магнитные поля, изменяющиеся во времени.
В свою очередь, магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическим током), либо переменными электрическими полями.
Рис. 43. Переменные электрические и магнитные поля, порождающие друг друга
Изменение индукции магнитного поля с течением времени вызывает появление в окружающем пространстве вихревого электрического поля. Силовые линии этого поля замкнуты и охватывают линии индукции магнитного поля, и напряженность электрического поля 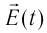
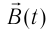
Таким образом, в вакууме возникает система изменяющихся и взаимно порождающих друг друга электрических и магнитных полей, охватывающих все большие и большие области пространства (рис. 44).
Совокупность связанных друг с другом периодически изменяющихся электрического и магнитного полей называют переменным электромагнитным полем. Согласно теории Максвелла электромагнитное поле распространяется в пространстве с конечной скоростью.
Рис. 44. Образование электромагнитной волны
Рассмотрим подробнее процесс образования электромагнитного поля в пространстве, окружающем проводник.
Пусть в проводнике возбуждены электромагнитные колебания, в результате чего сила электрического тока в нем непрерывно меняется. Поскольку сила тока связана со скоростью движения свободных зарядов в проводнике, то скорость движения последних также будет непрерывно изменяться с течением времени. Это говорит о том, что свободные заряды внутри проводника будут двигаться с ускорением.
Согласно теории Максвелла при ускоренном движении свободных зарядов в проводнике в пространстве вокруг него создается переменное магнитное поле, которое порождает переменное вихревое электрическое поле. Последнее, в свою очередь, вновь вызывает появление переменного магнитного поля уже на большем расстоянии от заряда и т. д. Таким образом, в пространстве вокруг проводника образуются взаимосвязанные электрические и магнитные поля, которые распространяются с течением времени в виде волны.
Электромагнитное поле, распространяющееся в вакууме или в какой-либо среде с конечной скоростью, называется электромагнитной волной (рис. 45).
Рис. 45. Электромагнитная волна
Электромагнитные волны являются поперечными. В них направления колебаний векторов напряженности 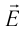
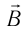
Подобно упругим механическим волнам, электромагнитные волны испытывают отражение от препятствий, но, в отличие от упругих волн, они могут распространяться и в вакууме.
Частота электромагнитных волн совпадает с частотой колебаний излучающих частиц. Максимальное значение ускорения при гармонических колебаниях пропорционально квадрату частоты колебаний: 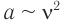
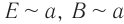
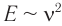
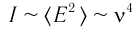
Одним из важнейших результатов теории Максвелла было теоретическое определение модуля скорости распространения электромагнитных волн (света). Согласно этой теории модуль скорости распространения с электромагнитной волны в вакууме связан с электрической постоянной 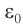
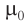
Скорость распространения электромагнитных волн в вакууме является максимально (предельно) достижимой величиной. В любом веществе скорость их распространения меньше 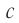
Совпадение скорости электромагнитных волн со скоростью света дало возможность Джеймсу Максвеллу предположить, что свет имеет электромагнитную природу. Благодаря этому произошло объединение в одно учение оптики и электромагнетизма.
Рис. 46. Схематическое изображение экспериментальной установки Герца: а — вибратор Герца; б — приемный контур
Электромагнитные волны были экспериментально открыты немецким физиком Генрихом Герцем в 1887 г. Для их генерации он использовал специальное устройство (рис. 46, а), впоследствии названное вибратором Герца.
Герц исследовал излучаемое вибратором электромагнитное поле. В воздушном зазоре между шарами при переменном напряжении, достигающем значения пробоя воздуха, происходил искровой разряд. При этом в вибраторе возникали электромагнитные колебания высокой частоты. Индикатором электромагнитных волн, возникающих в опытах Герца, служила искра, образующаяся в приемном контуре (рис. 46, б). Размеры приемного контура выбирались таким образом, чтобы собственная частота возникающих в нем колебаний была равна частоте излучаемых волн.
Изменяя положение приемного контура по отношению к вибратору и наблюдая появление в нем искры, Герц определял наличие поля в различных точках пространства. Таким образом, Герц экспериментально доказал существование электромагнитных волн.
Длина волны, возникшей в вибраторе Герца, была 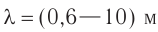
К 1889 г. Герц сумел не только убедительно доказать существование электромагнитных волн, но и установить их основные свойства:
- распространяются не только в различных средах, но и вакууме;
- в вакууме распространяются со скоростью, модуль которой
;
- отражаются и преломляются на границах раздела сред;
- являются поперечными.
Герц считал, что электромагнитные волны невозможно использовать для осуществления связи без проводов. Однако русский ученый Александр Степанович Попов 7 мая 1895 г. на заседании Русского физико-химического общества в Петербурге сообщил о возможности приема электромагнитных сигналов. 18 декабря 1897 г. он передал на расстояние 250 м первую в мире радиограмму из двух слов «Генрих Герц».
В 1901 г. итальянский инженер Г. Маркони впервые осуществил радиосвязь через Атлантический океан.
Исследования по передаче информации электромагнитными волнами, проведенные Поповым, показали, что для радиосвязи можно использовать колебательный контур.
Закрытый контур излучает слабо, так как электрическое поле сосредоточено в основном между обкладками конденсатора, а магнитное — в катушке, т. е. поля пространственно разделены. Такая система с сосредоточенными параметрами практически не излучает электромагнитные волны.
Проследим за изменениями в системе при увеличении расстояния 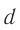
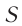
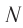
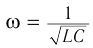
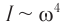
Рис. 47. Схема получения открытого колебательного контура (а); открытый колебательный контур (б); колебательный контур с антенной 1 (в)
Таким образом, для эффективного излучения контур необходимо «открыть», раздвинув обкладки конденсатора, т. е. создать условия «ухода» поля в пространство (рис. 47, а). Если заменить катушку прямым проводом, то частота со увеличится еще больше. В результате приходим к открытому колебательному контуру — это прямой провод (рис. 47, б). Однако в таком виде его невозможно использовать на практике, так как мощность излучения и в этом случае невелика. Интенсивное излучение начинается при достижении частот порядка сотен тысяч герц. Поэтому в действительности контур состоит из катушки и длинного провода — антенны (рис. 47, в). Один конец провода соединен с землей (заземлен), второй — поднят над поверхностью Земли. Длина антенны изготовляется кратной половине длины волны, так как в этом случае она настроена в резонанс с генератором колебаний, что обеспечивает оптимальные условия для излучения и приема электромагнитных волн. Вынужденные колебания высокой частоты в антенне создают в окружающем пространстве электромагнитное поле, и электромагнитные волны распространяются от антенны (рис. 48).
Рис. 48. Излучение электромагнитных волн простейшей антенной (диполем): а — расположение силовых линий электрического поля; б — расположение линий индукции магнитного поля
Спектр электромагнитного излучения удобно изображать в виде шкалы электромагнитных волн, приведенной на рисунке 49.
Рис. 49. Шкала электромагнитных волн
Свойства электромагнитных волн сильно зависят от их частоты. Излучение электронов, обусловленное их движением в проводниках, позволяет генерировать электромагнитные волны с частотой до 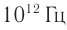
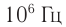
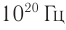
Классификация электромагнитных волн в зависимости от частот (длин волн) приведена в таблице 5.
Таблица 5. Классификация электромагнитных волн
В настоящее время электромагнитные волны находят широкое применение в науке и технике в таких процессах и явлениях, как:
- плавка и закалка металлов в электротехнической промышленности, изготовление постоянных магнитов (низкочастотные волны);
- телевидение, радиосвязь, радиолокация (радиоволны);
- мобильная связь, радиолокация (микроволны);
- сварка, резка, плавка металлов лазерами, приборы ночного видения (инфракрасное излучение);
- освещение, голография, лазеры (видимое излучение);
- люминесценция в газоразрядных лампах, лазеры (ультрафиолетовое излучение);
- рентгенотерапия, рентгеноструктурный анализ, лазеры (рентгеновское излучение);
- дефектоскопия, диагностика и терапия в медицине, исследование внутренней структуры атомов, военное дело (гамма-излучение).
Пример №11
Радиоприемник настроен на радиостанцию, работающую на длине волны 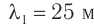
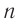
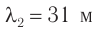
Решение
Длина волны определяется по формуле:
где
По формуле Томсона
Тогда для двух длин волн можем записать:
Разделив второе уравнение на первое, получим:
Отсюда
Ответ:
Формулы и определения
Идеальным колебательным контуром или 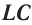
Период электромагнитных колебаний в идеальном колебательном контуре определяется формулой Томсона:
Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по резистору сопротивлением 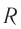
Действующее значение напряжения:
Сопротивление 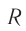
Трансформатор — электромагнитное устройство, преобразующее переменный ток одного напряжения в переменный ток той же частоты, но другого напряжения. Принцип действия трансформатора основан на явлении электромагнитной индукции.
Тип трансформатора определяется коэффициентом трансформации, который равен отношению числа витков первичной обмотки к числу витков вторичной обмотки трансформатора:
Если 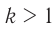
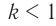
Совокупность связанных друг с другом изменяющихся электрического и магнитного полей называют электромагнитным полем.
Электромагнитными волнами называется распространяющееся в пространстве переменное электромагнитное поле.
Электромагнитные волны являются поперечными, так как колебания напряженности 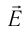
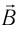
Модуль скорости распространения электромагнитных волн в вакууме равен модулю скорости распространения света:
- Свободные и вынужденные колебания в физике
- Вынужденные электромагнитные колебания
- Резонанс в физике
- Распространение механических волн в средах
- Уравнение Бернулли
- Механические колебания и волны в физике
- Гармонические колебания в физике
- Вынужденные колебания в физике
В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания.
Электромагнитными колебаниями называют периодические взаимосвязанные изменения заряда, силы тока и напряжения.
Свободными колебаниями называют такие, которые совершаются без внешнего воздействия за счет первоначально накопленной энергии.
Вынужденными называются колебания в цепи под действием внешней периодической электродвижущей силы
Свободные электромагнитные колебания – это периодически повторяющиеся изменения электромагнитных величин (q – электрический заряд, I – сила тока, U – разность потенциалов), происходящие без потребления энергии от внешних источников.
Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур или колебательный контур.
Колебательный контур – это система, состоящая из последовательно соединенных конденсатора емкости C, катушки индуктивности L и проводника с сопротивлением R
Рассмотрим закрытый колебательный контур, состоящий из индуктивности L и емкости С.
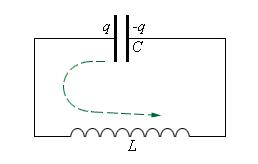
Чтобы возбудить колебания в этом контуре, необходимо сообщить конденсатору некоторый заряд от источника ε. Когда ключ K находится в положении 1, конденсатор заряжается до напряжения . После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер
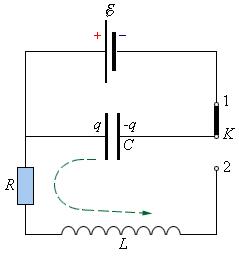
Свободные электромагнитные колебания можно наблюдать на экране осциллографа.
Как видно из графика колебаний, полученного на осцилографе, свободные электромагнитные колебания являются затухающими, т.е.их амплитуда уменьшается с течением времени. Это происходит потому, что часть электрической энергии на активном сопротивлении R превращается во внутреннюю энерги. проводника (проводник нагревается при прохождении по нему электрического тока).
Рассмотрим, как происходят колебания в колебательном контуре и какие изменения энергии при этом происходят. Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0).
Если зарядить конденсатор до напряжения U0 то в начальный момент времени t1=0 на обкладках конденсатора установятся амплитудные значения напряжения U0 и заряда q0 = CU0.
Полная энергия W системы равна энергии электрического поля Wэл:
Если цепь замыкают, то начинает течь ток. В контуре возникает э.д.с. самоиндукции
Вследствие самоиндукции в катушке конденсатор разряжается не мгновенно, а постепенно (так как, согламно правилу Ленца, возникающий индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван. Т.е. магнитное поле индукционного тока не дает мгновенно увеличиться магнитному потоку тока в контуре). При этом ток увеличивается постепенно, достигая своего максимального значения I0 в момент времени t2=T/4, а заряд на конденсаторе становится равным нулю.
По мере разрядки конденсатора энергия электрического поля уменьшается, но одновременно возрастает энергия магнитного поля. Полная энергия контура после разрядки конденсатора равна энергии магнитного поля Wм:
В следующий момент времени ток течет в том же направлении, уменьшаясь до нуля, что вызывает перезарядку конденсатора. Ток не прекращается мгновенно после разрядки конденсатора вследствии самоиндукции (теперь магнитное поле индукционного тока не дает магнитному потоку тока в контуре мгновенно уменьшиться). В момент времени t3=T/2 заряд конденсатора опять максимален и равен первоначальному заряду q = q0, напряжение тоже равно первоначальному U = U0, а ток в контуре равен нулю I = 0.
Затем конденсатор снова разряжается, ток через индуктивность течёт в обратном направлении. Через промежуток времени Т система приходит в исходное состояние. Завершается полное колебание, процесс повторяется.
График изменения заряда и силы тока при свободных электромагнитных колебаниях в контуре показывает, что колебания силы тока отстают от колебаний заряда на π/2.
В любой момент времени полная энергия:
При свободных колебаниях происходит периодическое превращение электрической энергии Wэ, запасенной в конденсаторе, в магнитную энергию Wм катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается постоянной.
Свободные электрические колебания аналогичны механическим колебаниям. На рисунке приведены графики изменения заряда q(t) конденсатора и смещения x(t) груза от положения равновесия, а также графики тока I(t) и скорости груза υ(t) за один период колебаний.
В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону
q(t) = q0cos(ωt + φ0)
Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний и период колебаний
— формула Томпсона
Амплитуда q0 и начальная фаза φ0 определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия.
Для колебаний заряда, напряжения и силы тока получаются формулы:
Для конденсатора:
q(t) = q0cosω0t
U(t) = U0cosω0t
Для катушки индуктивности:
i(t) = I0cos(ω0t + π/2)
U(t) = U0cos(ω0t + π)
Вспомомним основные характеристики колебательного движения:
q0, U0, I0 — амплитуда – модуль наибольшего значения колеблющейся величины
Т — период – минимальный промежуток времени через который процесс полностью повторяется
ν — Частота – число колебаний в единицу времени
ω — Циклическая частота – число колебаний за 2п секунд
φ — фаза колебаний — величина стоящая под знаком косинуса (синуса) и характеризующая состояние системы в любой момент времени.














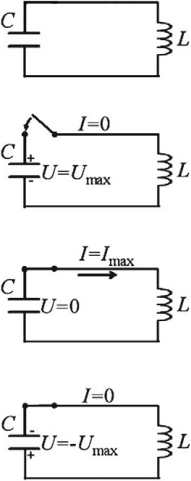
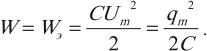
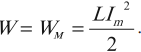
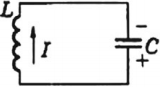
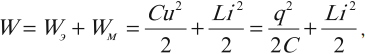
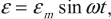
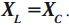
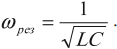
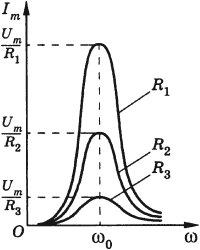
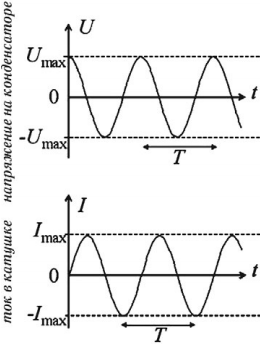
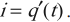
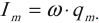
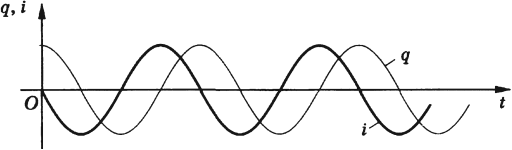
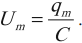
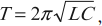
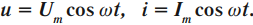
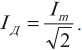
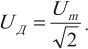
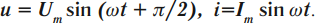
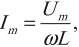
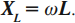
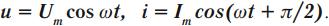
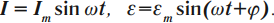
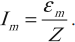
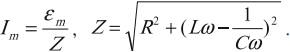
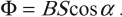
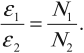
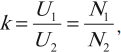
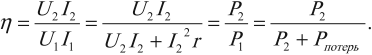
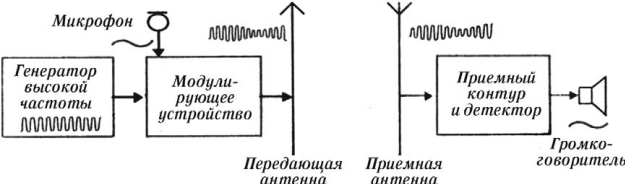
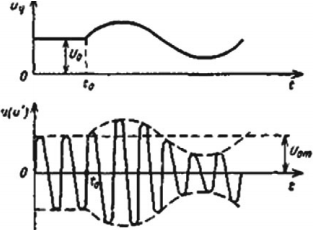
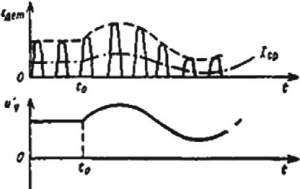















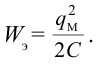
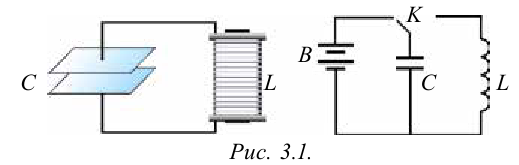
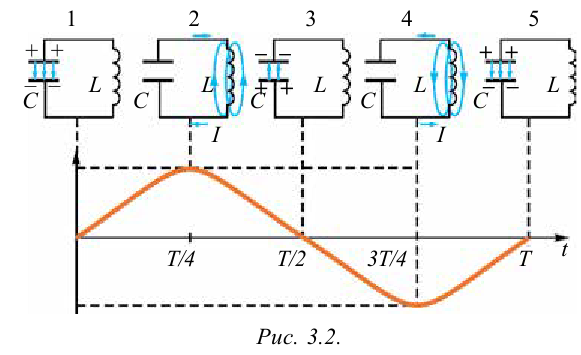
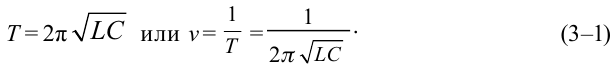
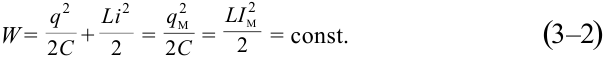
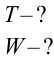
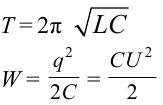
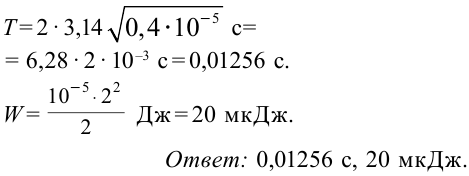


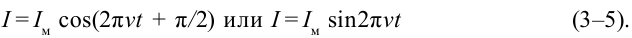
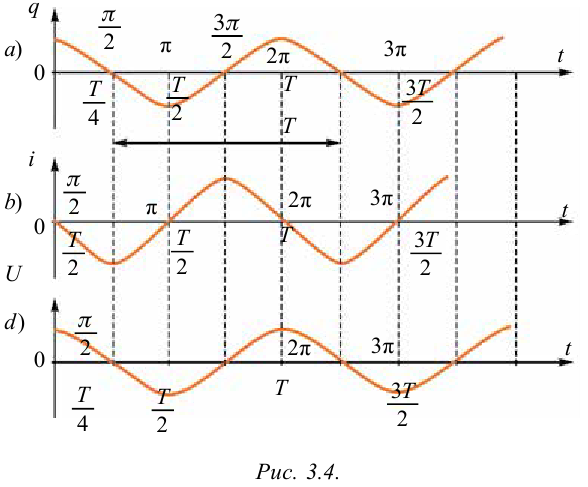
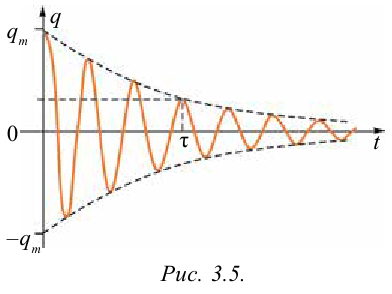
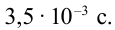
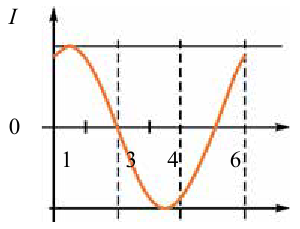
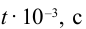
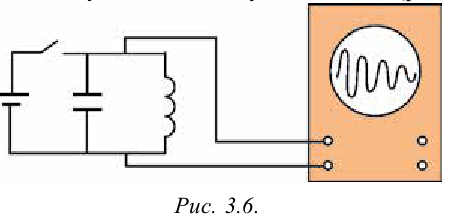
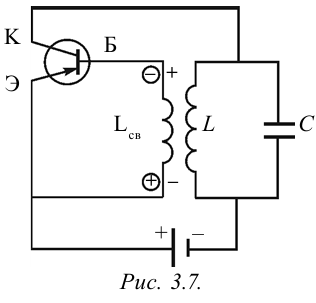
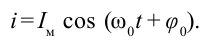
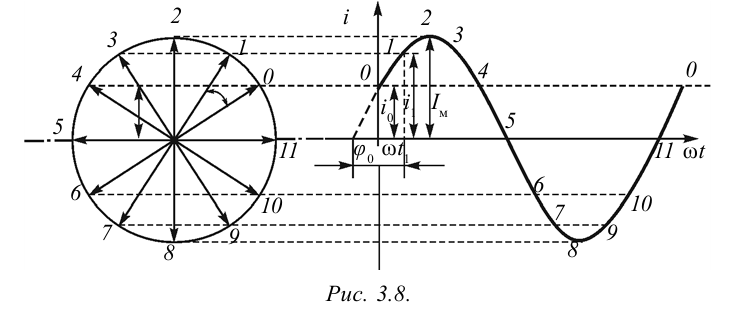
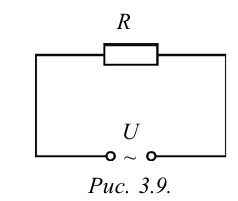

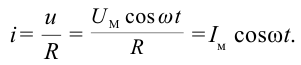

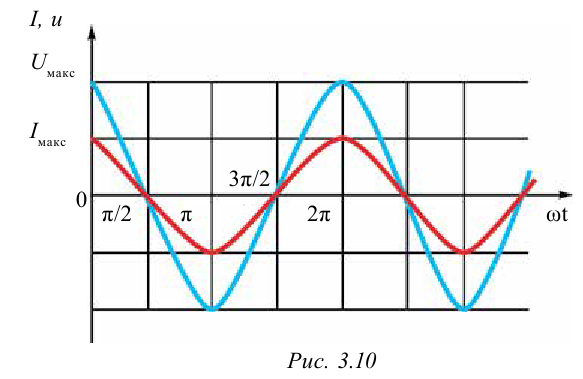
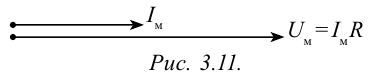
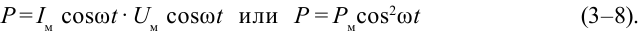

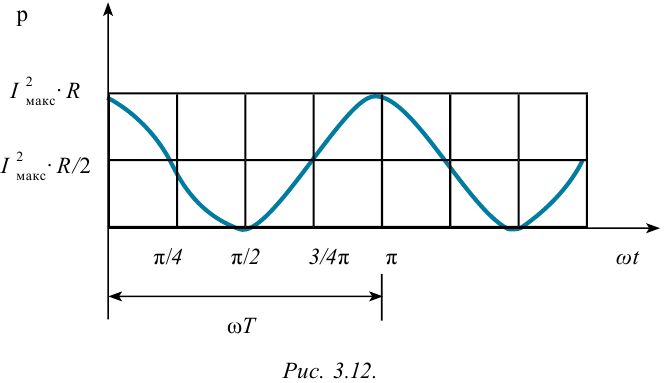

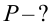
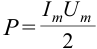

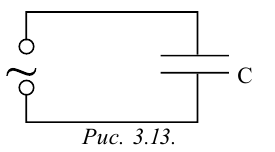

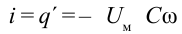


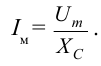
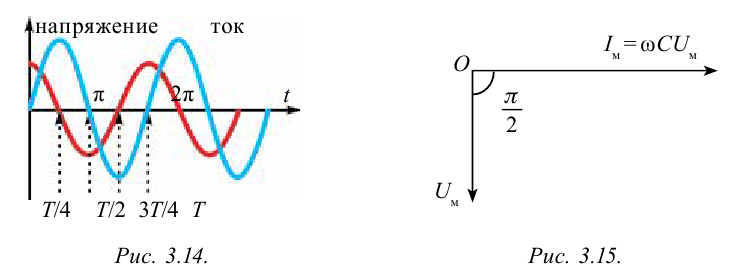
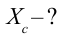
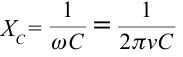
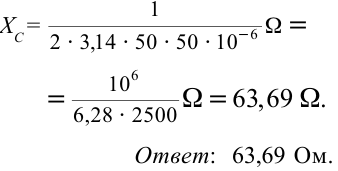
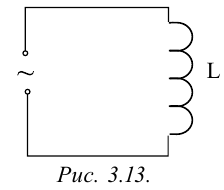

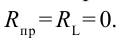

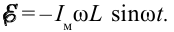

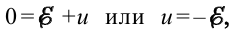
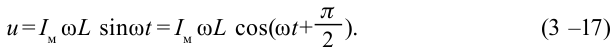

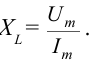
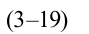
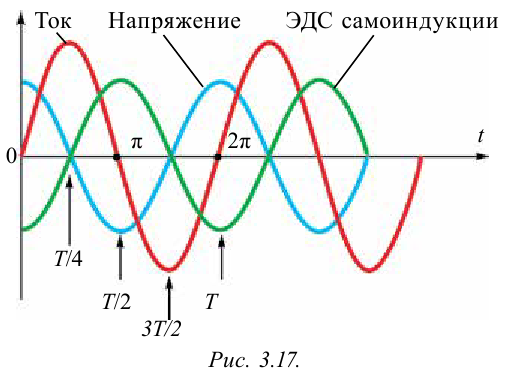
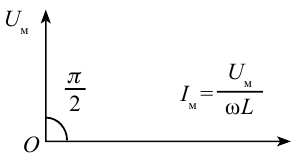
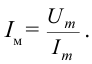
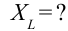
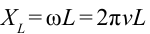
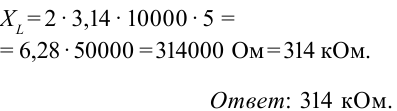


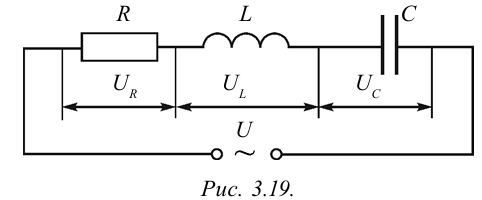
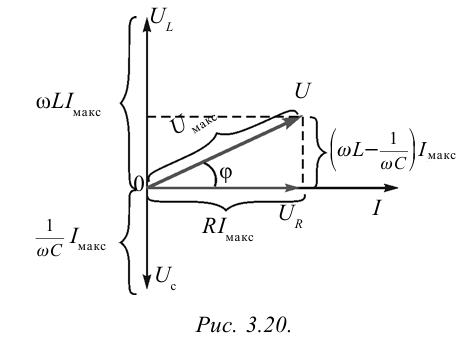
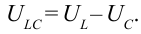
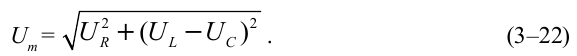
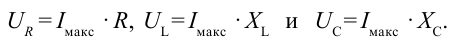
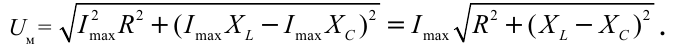
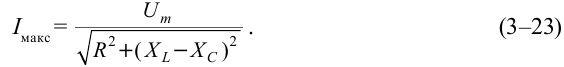
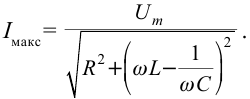

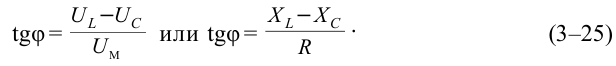
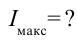
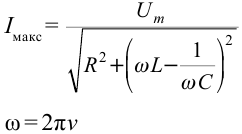

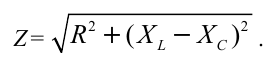

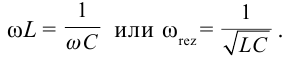
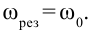
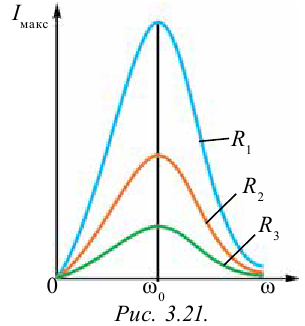
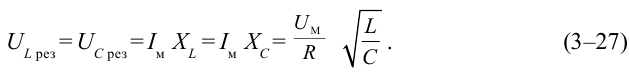
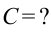
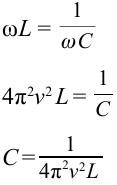
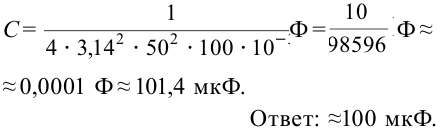


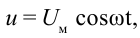
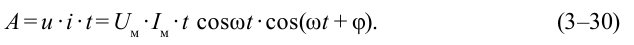
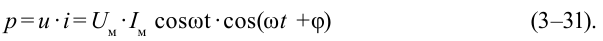
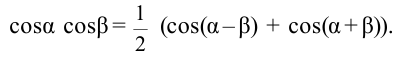
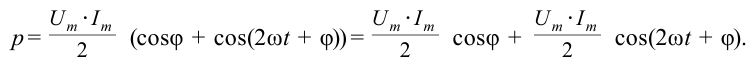
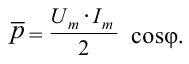
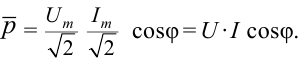


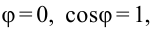
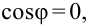
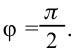
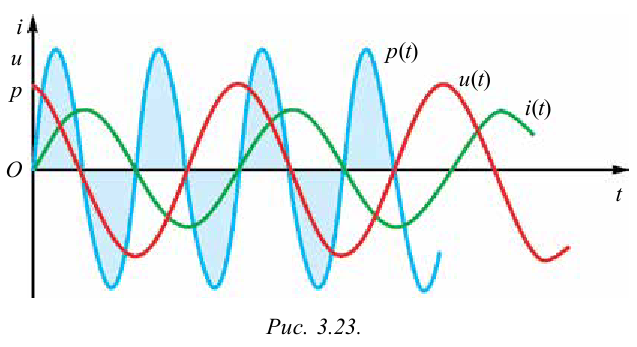
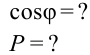
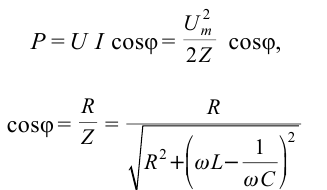

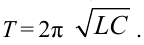
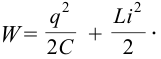
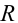 :Сопротивление, превращающее энергию переменного тока безвозвратно в другие виды энергии.
:Сопротивление, превращающее энергию переменного тока безвозвратно в другие виды энергии.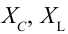 : Сопротивление, превращающее энергию переменного тока в энергию электрического или магнит- 1 ного поля, и наоборот.
: Сопротивление, превращающее энергию переменного тока в энергию электрического или магнит- 1 ного поля, и наоборот. 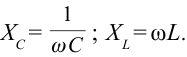
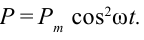
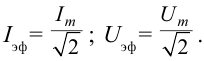
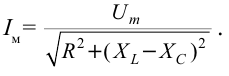
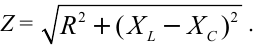
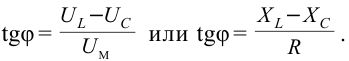
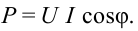
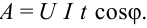
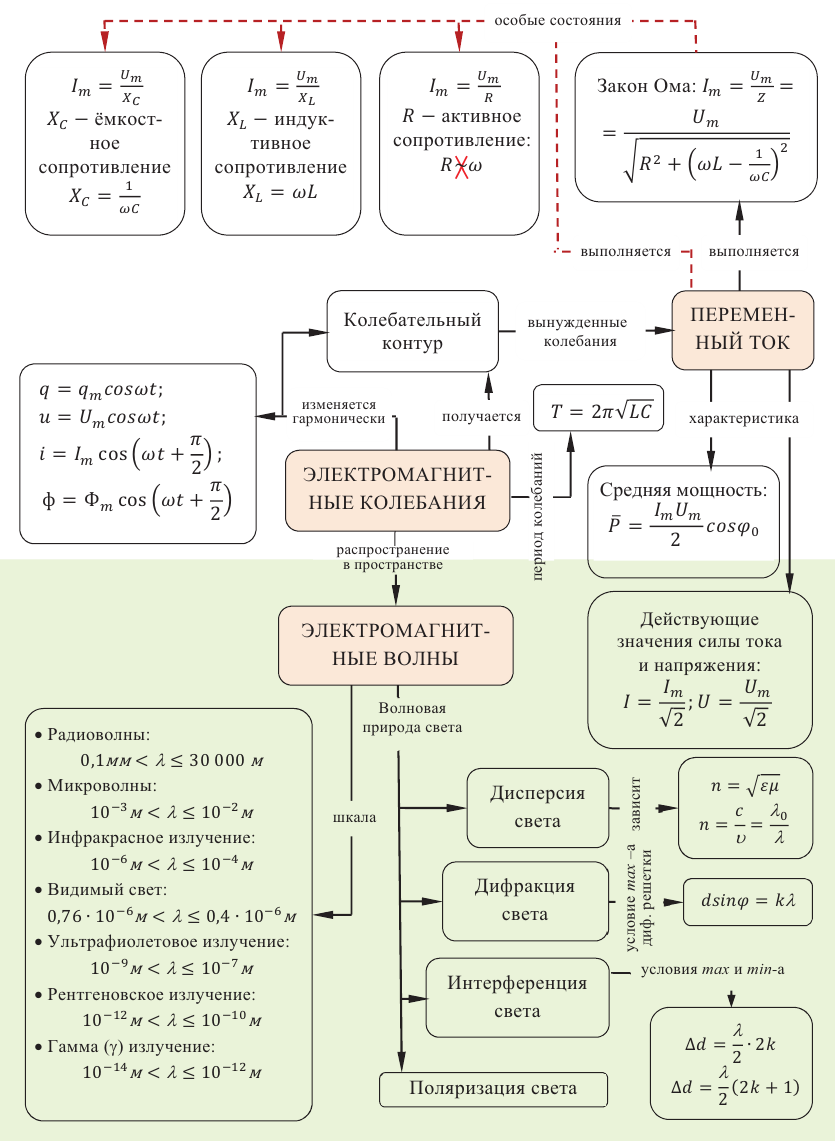
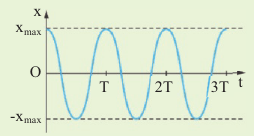
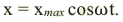
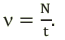
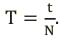
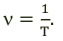
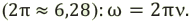
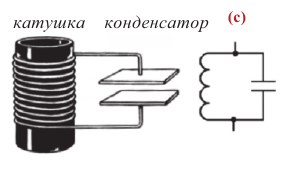

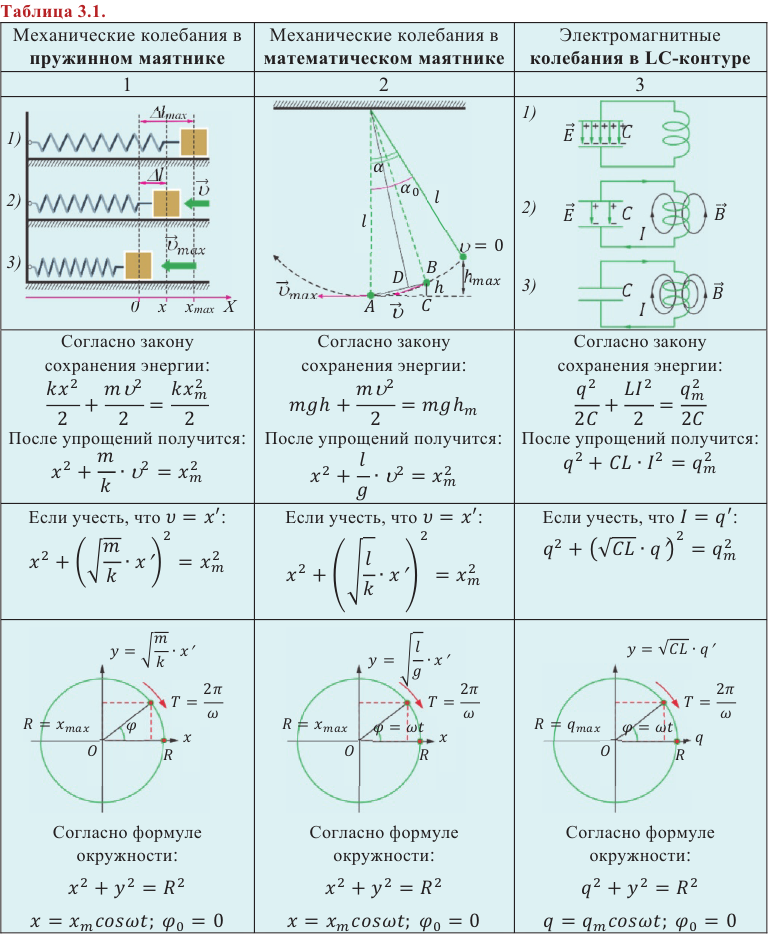
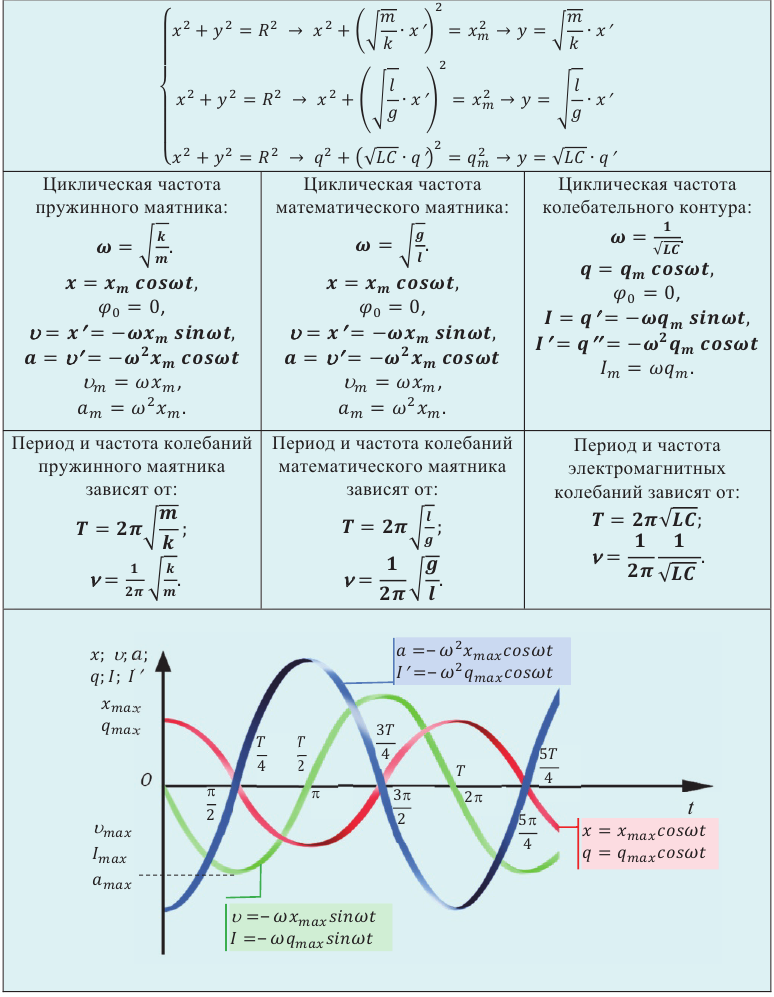
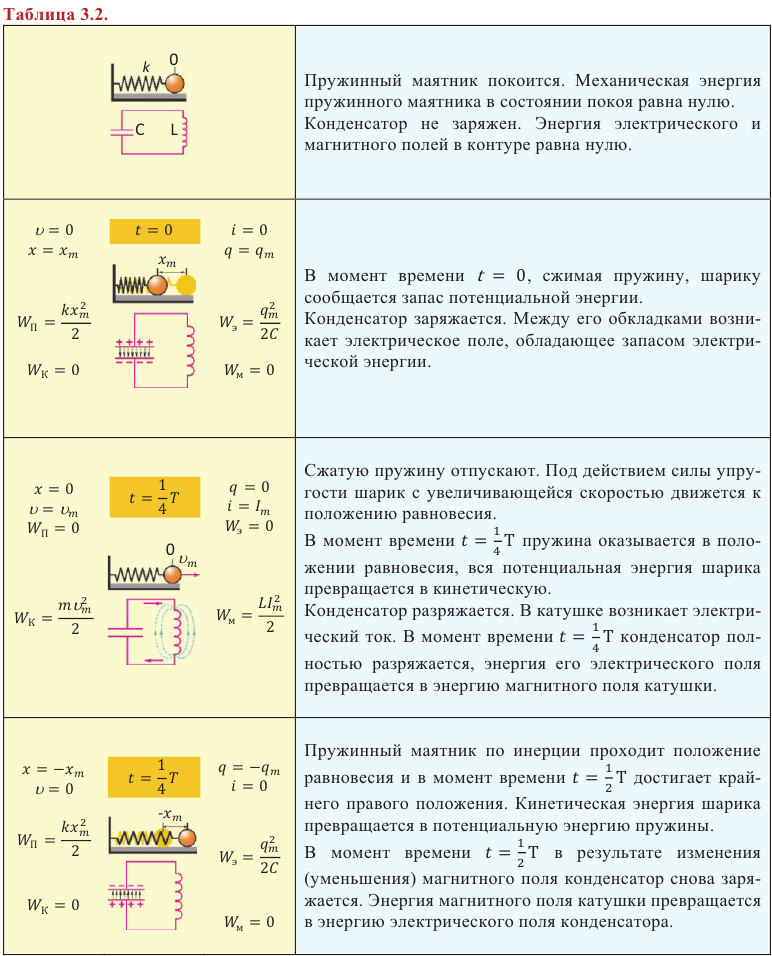
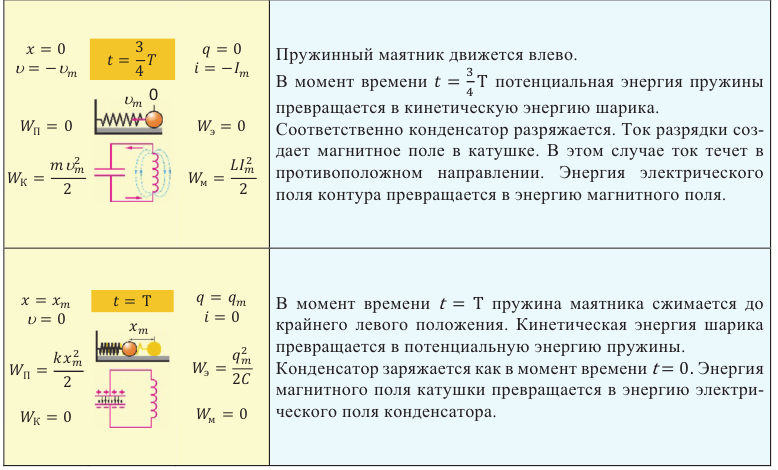
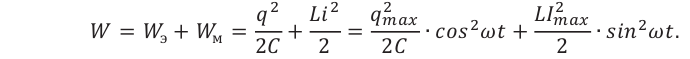
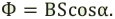
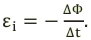
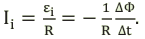
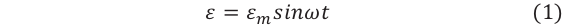
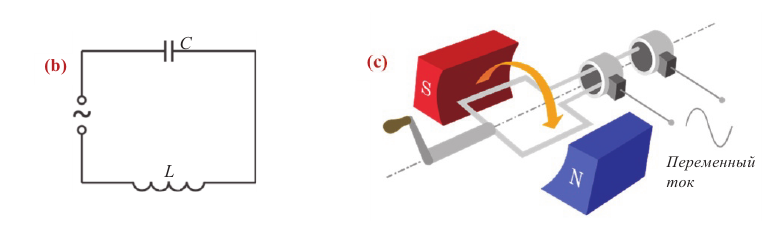
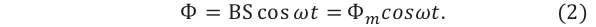
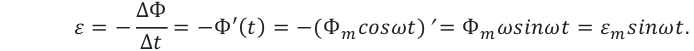
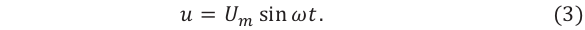
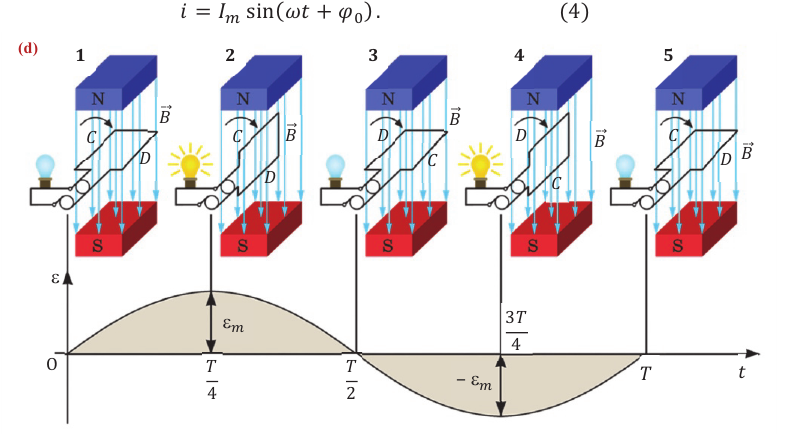

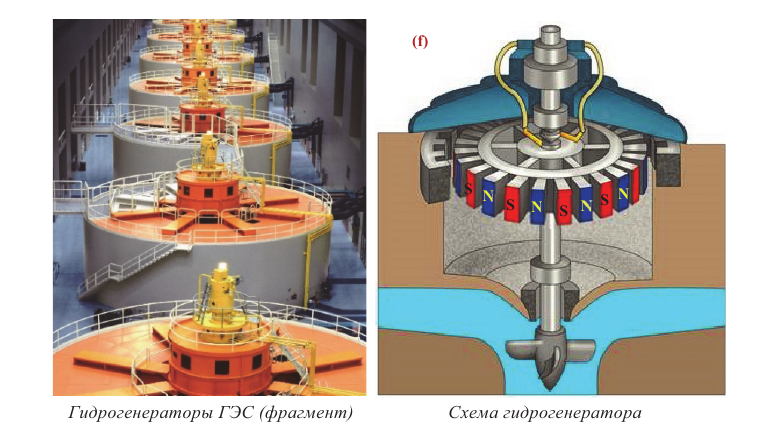
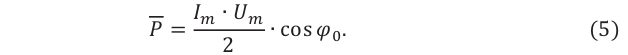
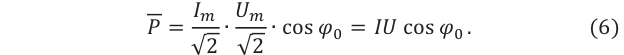
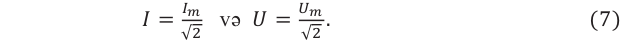

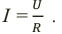

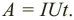

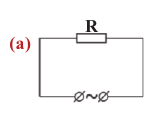
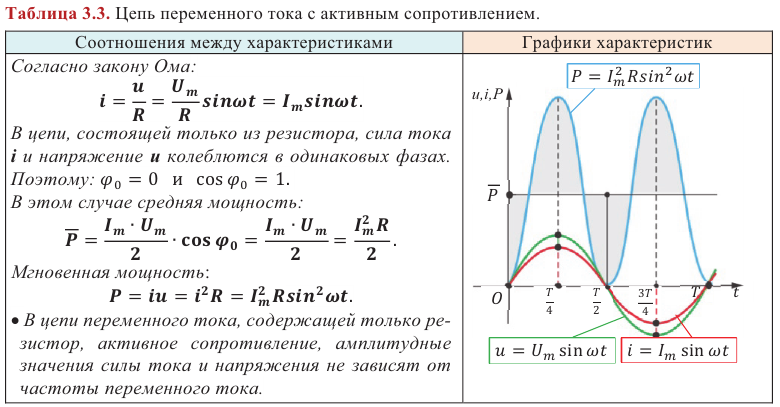
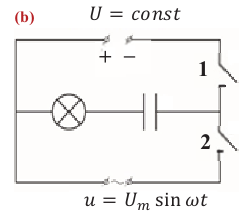
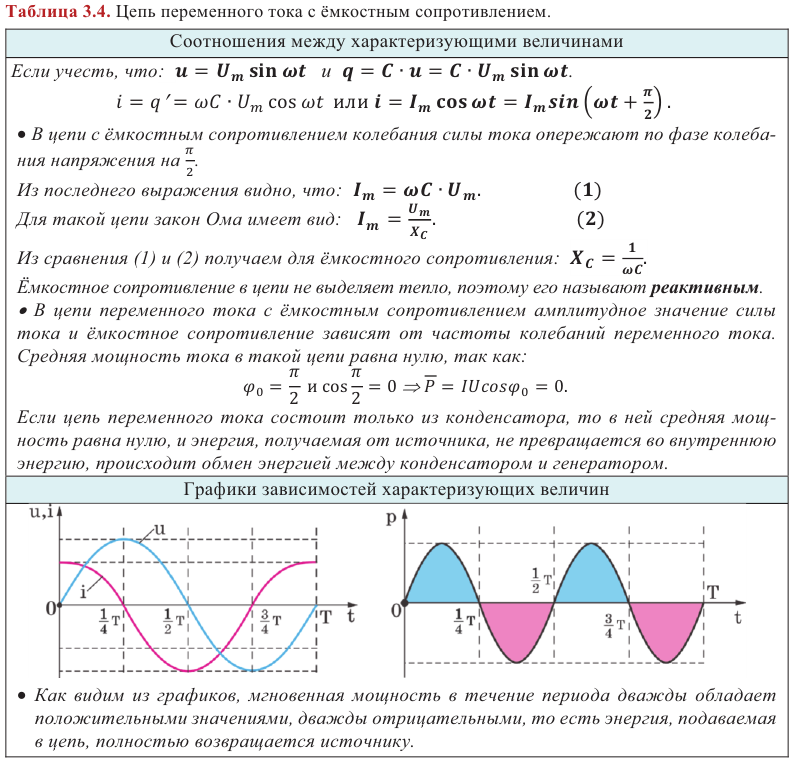
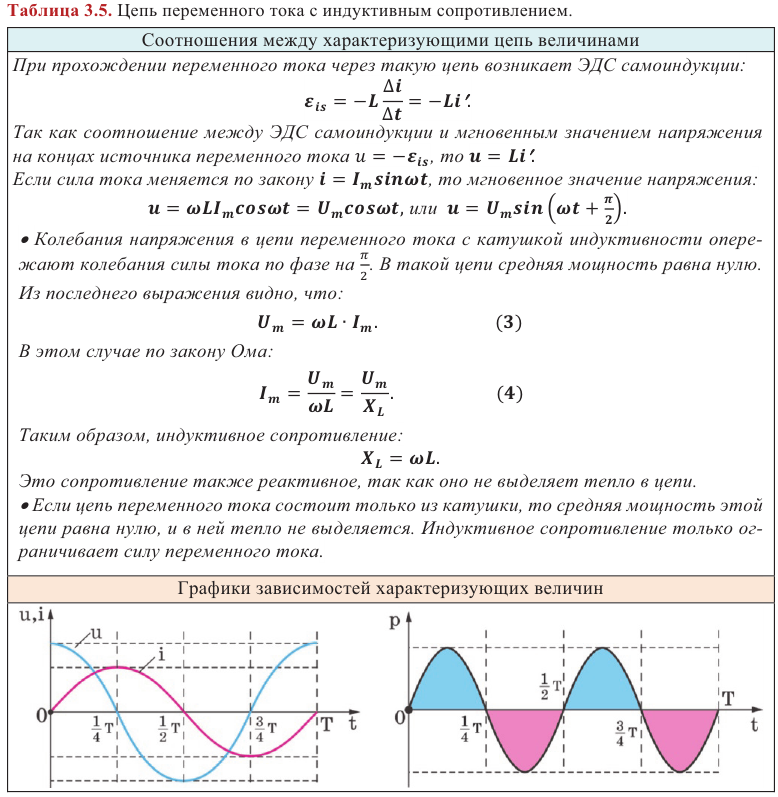

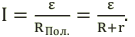
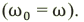
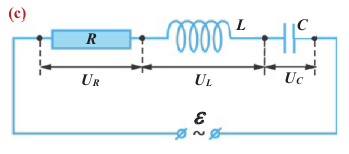
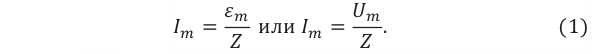


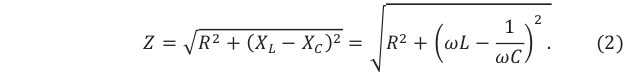
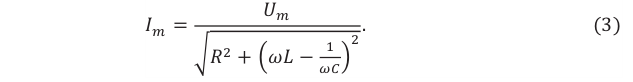
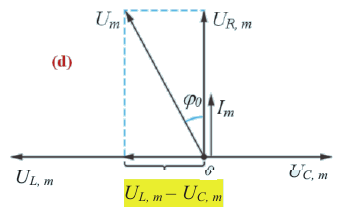
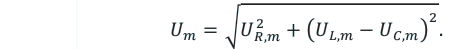
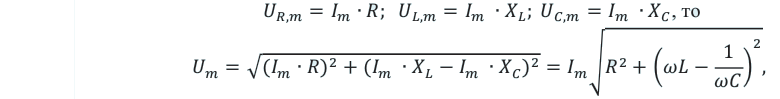

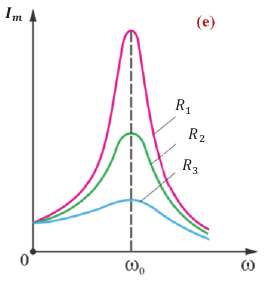
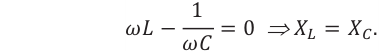
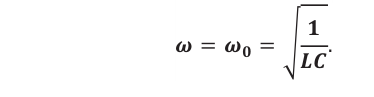



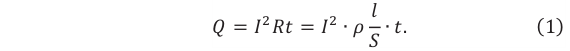
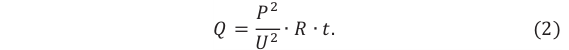
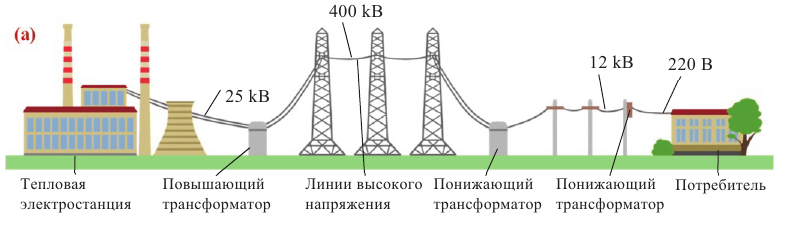
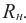
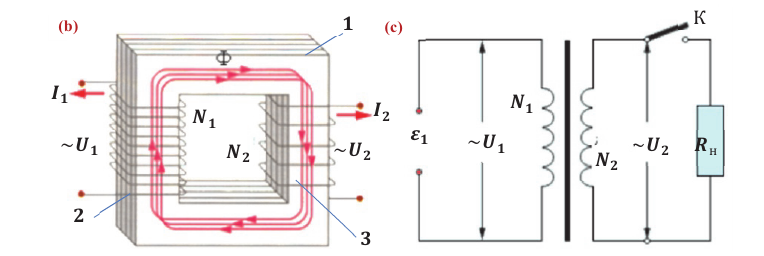
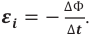
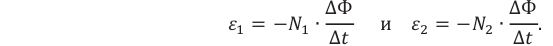
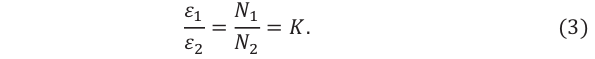
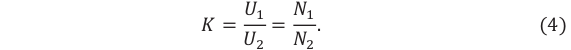
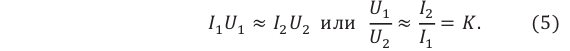
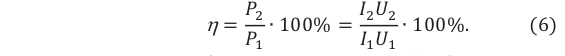
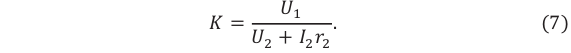
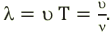
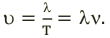
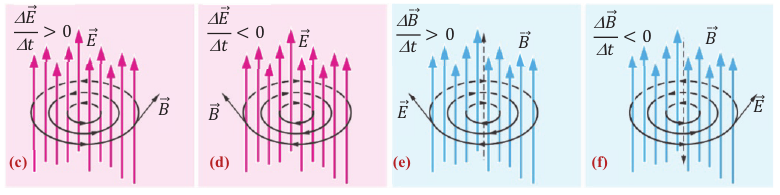
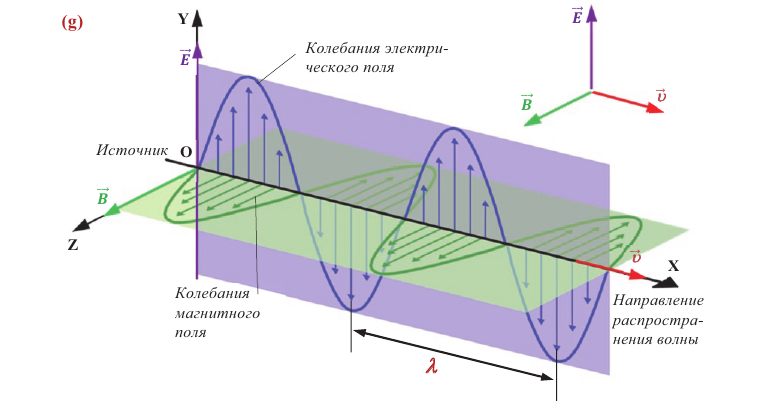
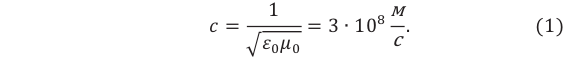
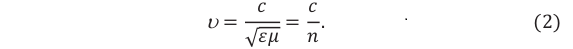
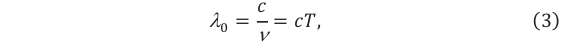
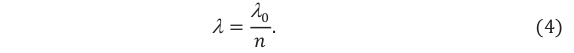
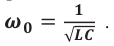
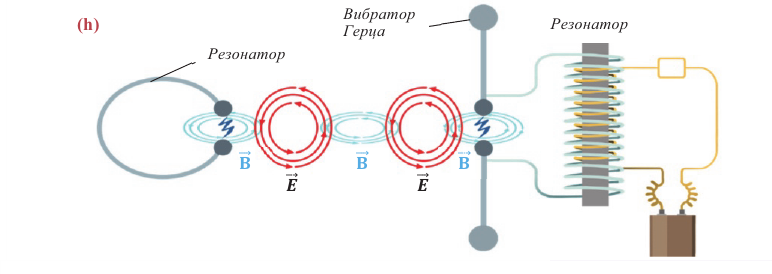
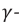 излучение.
излучение.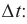
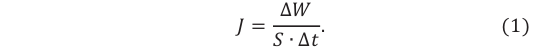
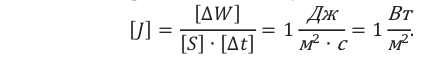

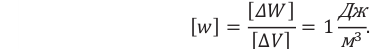
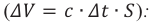
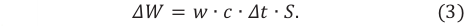
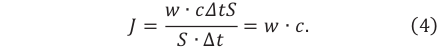
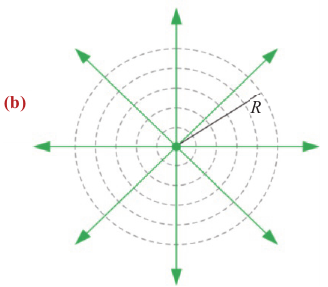
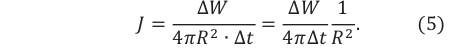
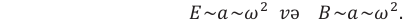
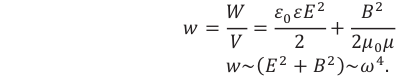

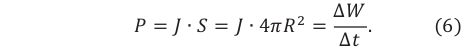
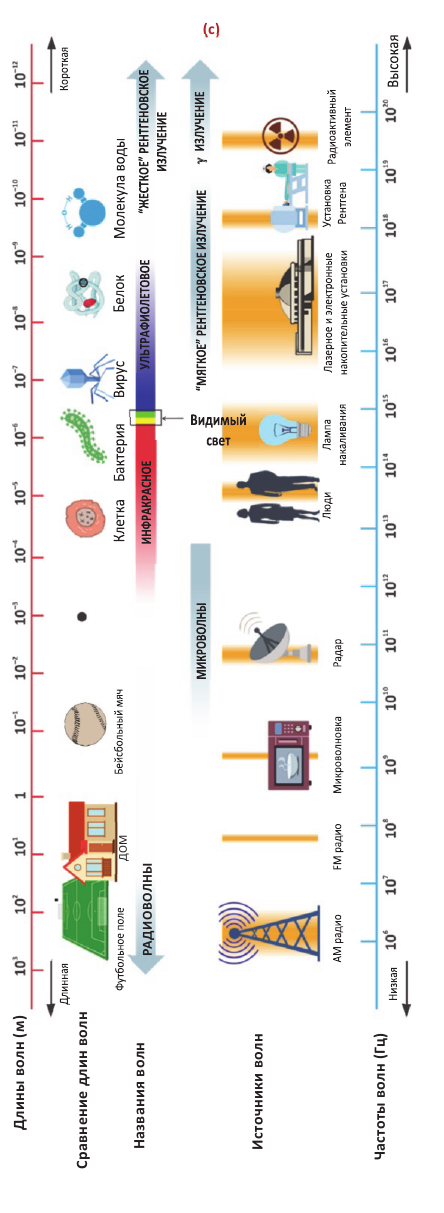


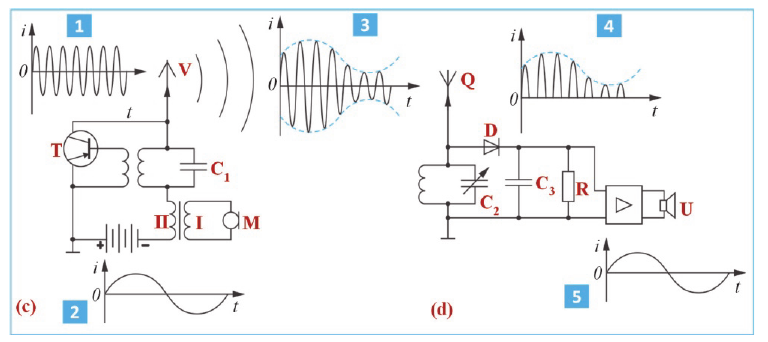
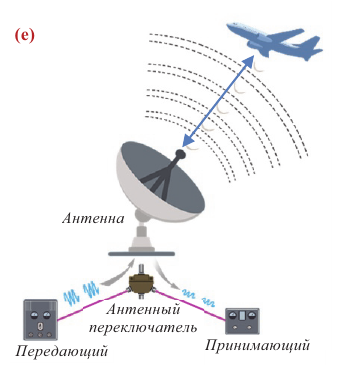

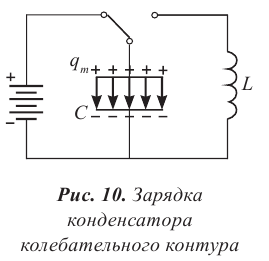






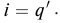
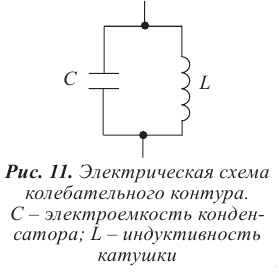
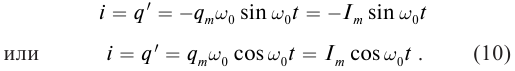

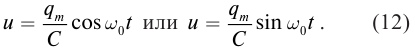
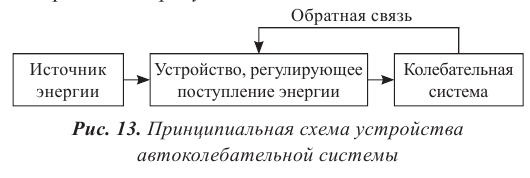
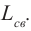
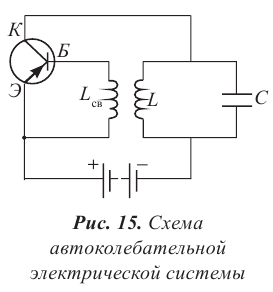
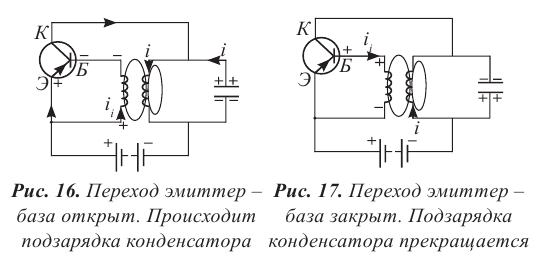
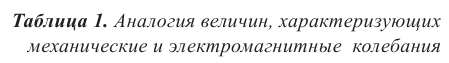
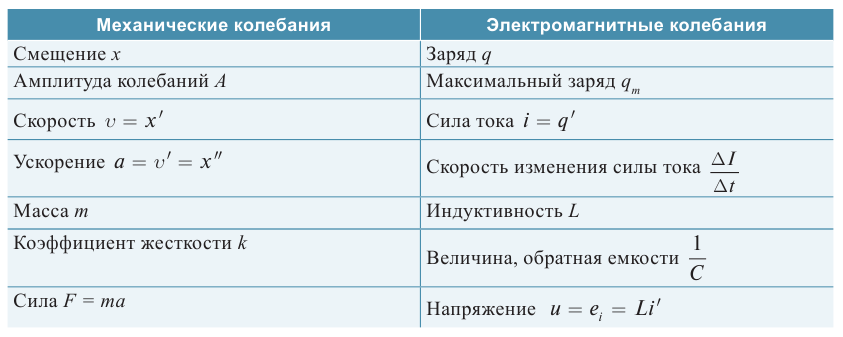
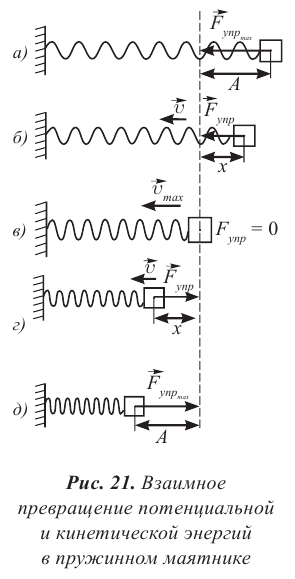
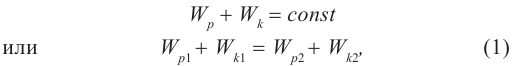
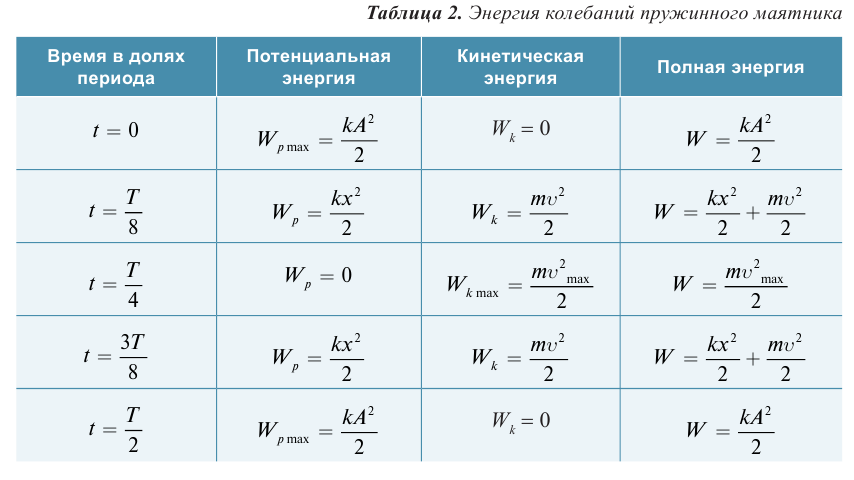
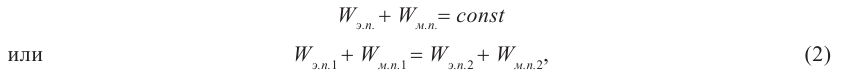
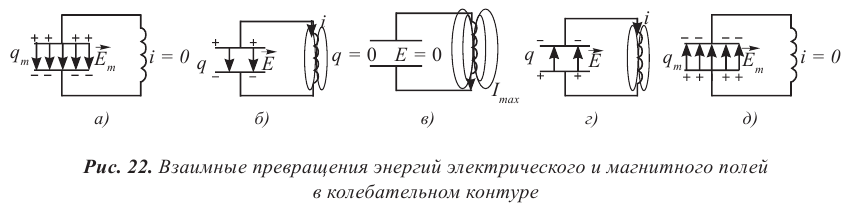


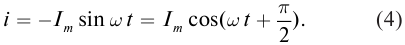
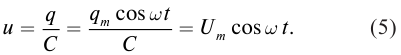
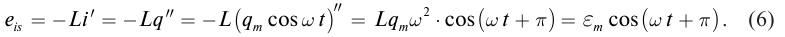
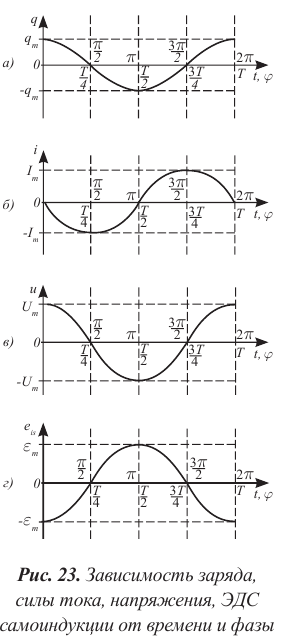


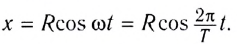
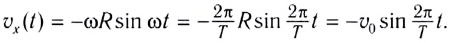
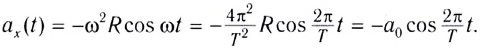
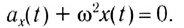
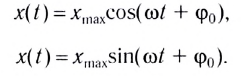
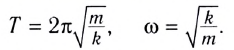
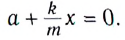
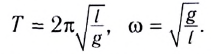
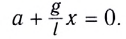
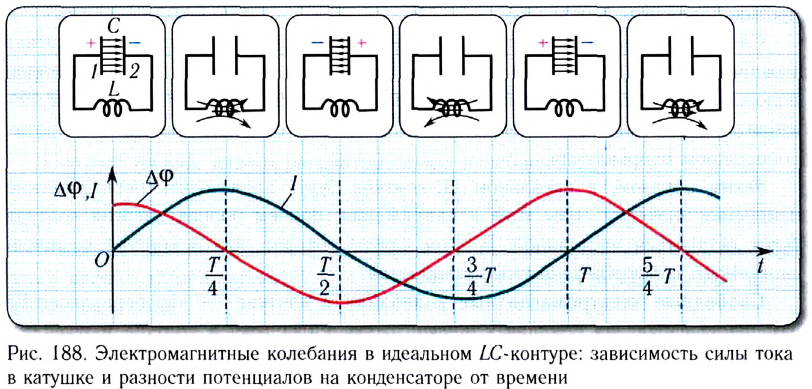
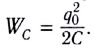
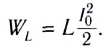
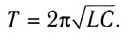
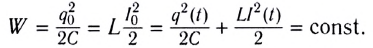
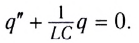
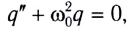
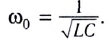
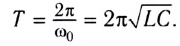

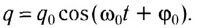
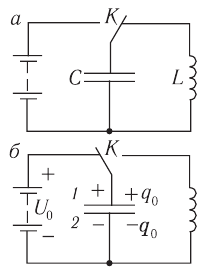
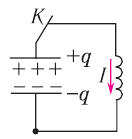
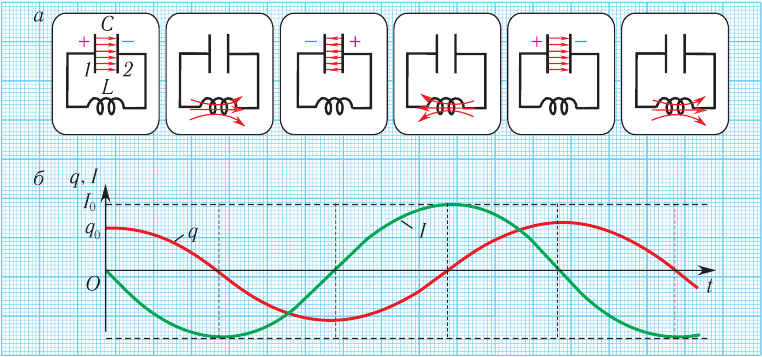
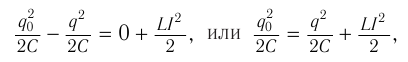
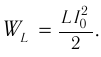
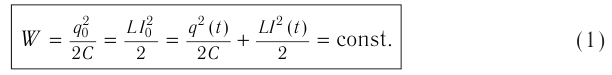




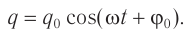
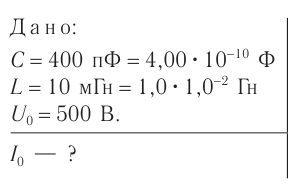
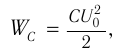
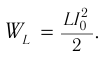
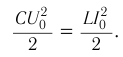
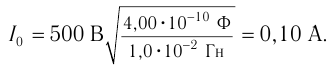
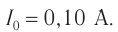
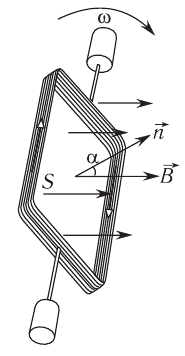
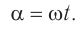
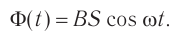
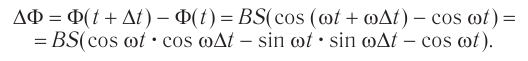
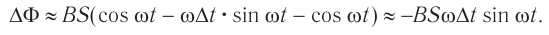
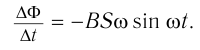
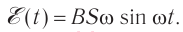
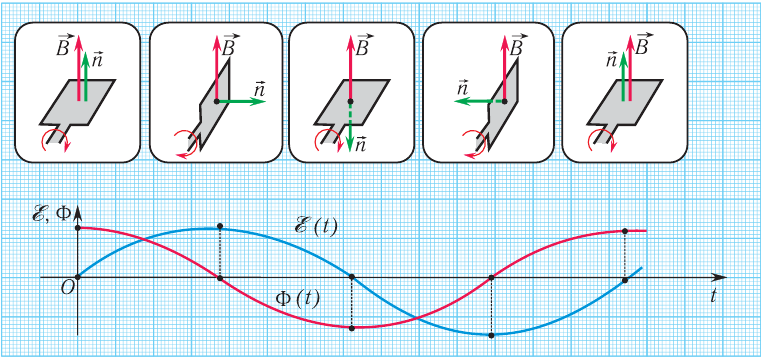

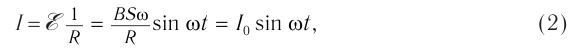
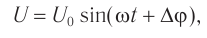
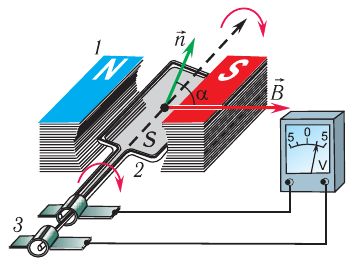
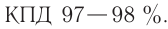
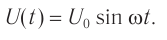
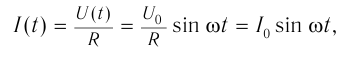
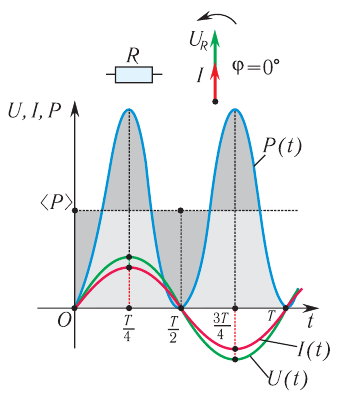
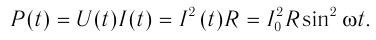
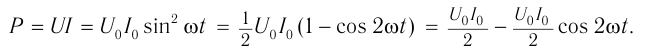
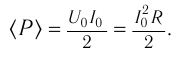
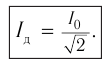
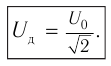
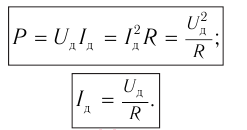
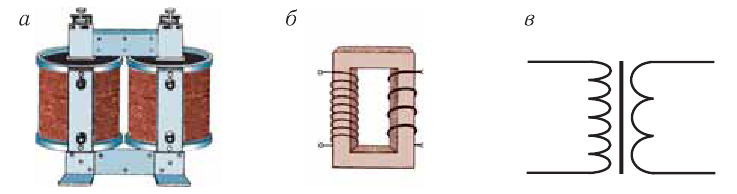


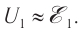
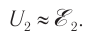

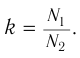

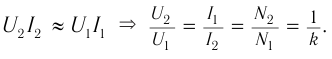
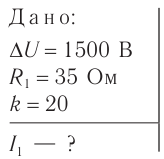
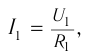
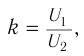
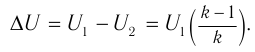
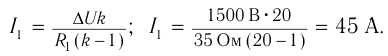


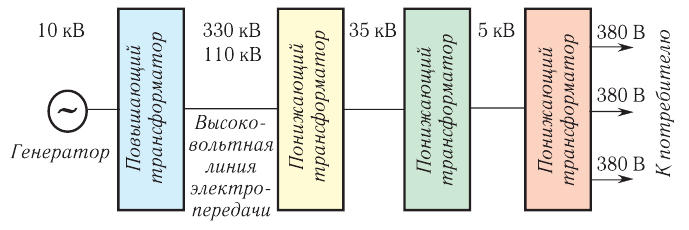


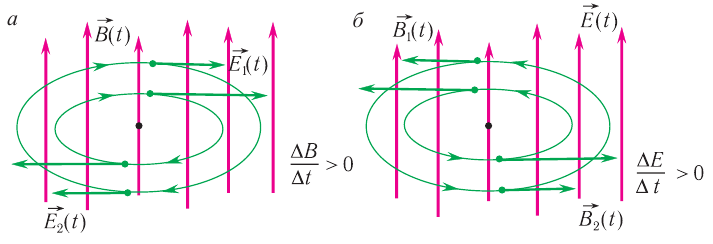
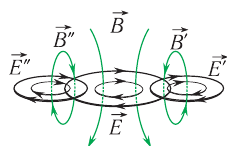
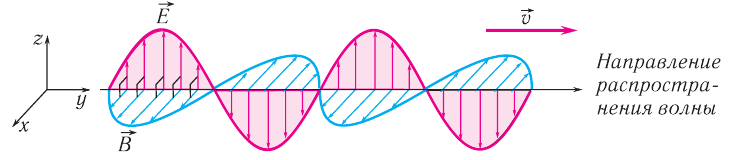
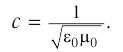
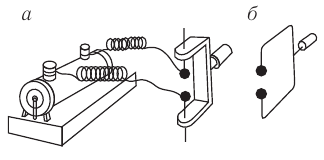
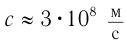 ;
;