Как найти фигуру с одинаковой площадью - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание:

§ 1 Сравнение фигур. Способы сравнения
§ 2 Площадь фигур. Сравнение площадей фигур
§ 3 Подведение итогов

§ 1 Сравнение фигур. Способы сравнения

На рисунке изображены геометрические фигуры: треугольники, круги, четырехугольники, квадраты. Все они разные по размеру. Вы легко сможете определить на глаз, какая из этих фигур имеет самый большой размер, а какая – самый маленький.

Гораздо сложнее сравнить фигуры, имеющие небольшую разницу в размерах, или фигуры, отличающиеся формой.

Чтобы сравнить их между собой, достаточно просто наложить одну на другую. Это приводит нас к выводу: квадрат больше круга. Второй способ: переведём на прозрачный лист бумаги фигуру и накладываем её на другую фигуру: овал оказывается больше прямоугольника.

§ 2 Площадь фигур. Сравнение площадей фигур

Говоря о размерах геометрических фигур, мы имеем в виду хорошо известные величины: длина, ширина. В данном случае мы сравнивали поверхности фигур, мысленно проводя по ним ладонью. Новая величина для определения размеров фигуры называется площадью.

Говорят, что площадь квадрата больше площади круга, а площадь круга меньше площади квадрата и, аналогично, площадь овала больше площади прямоугольника, а площадь прямоугольника меньше площади овала.

Таким образом, для того, чтобы сравнить площади фигур, надо одну из них наложить на другую.

В математике для нахождения площади геометрических фигур используют специальные формулы, в которых площадь обозначается заглавной латинской буквой S.

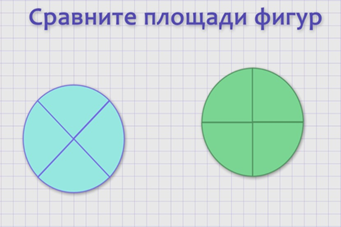
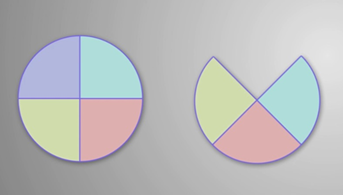
Попробуйте сравнить площади данных фигур.

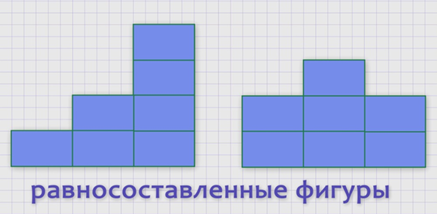
Обратите внимание, фигуры разделены на равные части. Сосчитаем, сколько частей образуют первую фигуру. Их 4. Вторая фигура также состоит из 4-х частей, но её части расположены по-другому. Таким образом, мы можем утверждать, что данные фигуры состоят из равного количества одинаковых частей. Такие фигуры называются равносоставленными.

Равносоставленные фигуры имеют одинаковую площадь. А вот форма равносоставленных фигур может быть разнообразной.

Итак, для того, чтобы получить равносоставленные фигуры, необходимо выполнить два условия:

во-первых, все части фигур должны иметь одинаковые размеры и форму;

во-вторых, количество частей также должно быть одинаковым.

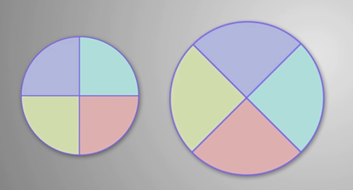
Что произойдёт, если не выполнить одно из условий? Например, некоторые части фигуры изменили свой размер. Площадь фигуры заметно увеличилась.

Сейчас мы уже не можем утверждать, что данные фигуры имеют одинаковую площадь.

А если изменить количество частей?

Фигура заметно уменьшилась в размере. Площади этих фигур также нельзя считать одинаковыми.

§ 3 Подведение итогов

Итак, подведем итог нашим рассуждениям: площади фигур (или предметов в окружающем мире) можно сравнивать разными способами. Наш глазомер легко справляется с простыми случаями сравнения площадей, например, площадь пола в вашем классе намного меньше площади пола в спортзале вашей школы!

Если нам нужно сравнить площади (размеры), например, двух похожих вещей, мы будем аккуратно накладывать их друг на друга. А если вам, как Тому Сойеру, придётся красить забор и сравнивать его с площадью забора, который покрасил ваш друг, то здесь не обойтись без сравнения количества одинаковых частей – досочек!

А вдруг ваши заборы окажутся равносоставленными фигурами?

Использованные изображения:

Источник

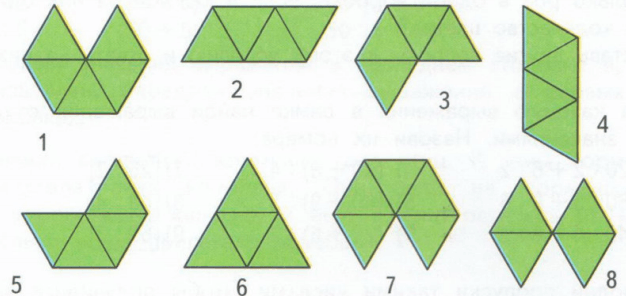
Найди на рисунке равные фигуры и назови их номера. найди фигуры с одинаковой площадью.

reshalka.com

ГДЗ учебник по математике 3 класс Дорофеев. Часть 2 страница 28. Номер №8

Решение

Равные фигуры, которые совпадут при наложении:
1) 1 и 7;
2) 2 и 4;
3) 3 и 5.
Площади фигур:
1) 5 (треугольников) − площадь первой фигуры;
2) 4 (треугольника) − площадь второй фигуры;
3) 4 (треугольника) − площадь третьей фигуры;
4) 4 (треугольника) − площадь четвертой фигуры;
5) 4 (треугольника) − площадь пятой фигуры;
6) 4 (треугольника) − площадь шестой фигуры;
7) 5 (треугольников) − площадь седьмой фигуры;
8) 4 (треугольника) − площадь восьмой фигуры.
Площади следующих фигур равны:
1) 1 и 7;
2) 2, 3, 4, 5, 6, 8.

Источник

mat:geom:area

Содержание

Площадь. Равновеликие фигуры

Равновеликие фигуры — плоские фигуры с одинаковыми площадями или геометрические тела с одинаковыми объемами.

Разрезанием на части и перекладыванием их можно любой многоугольник превратить в равновеликий ему квадрат.

Это следствие из теоремы Больяй — Гервина: равносоставленные фигуры являются равновеликими, а равновеликие многоугольники являются равносоставленными.

Понятие равносоставленности лежит в основе «метода разбиения», применяемого для вычисления площадей многоугольников: параллелограмм «разрезанием и перекладыванием» сводят к прямоугольнику, треугольник — к параллелограмму, трапецию — к треугольнику.

Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.

Достроим треугольник до прямоугольника. Площадь треугольника равна половине площади прямоугольника.

Проведем через середину боковой стороны трапеции прямую, параллельную второй боковой стороне. Площадь трапеции равна площади полученного параллелограмма.

Перекраивание трапеции в равносоставленный треугольник:

видео — Площадь трапеции. Сведение к площади треугольника

Подробнее

Равносоставленность

Равновеликие многогранники не всегда являются равносоставленными. Так, например, куб и равновеликий ему правильный тетраэдр не являются равносоставленными — так называемая теорема Дена.

Вопросы

Квадраты с равными сторонами равновелики?
Равносторонние треугольники с равными сторонами равновелики?
Равносторонние треугольники равновелики?

Задачи

Задача A

Доказать, что всякая прямая, проходящая через точку пересечения диагоналей параллелограмма, делит его на 2 равновеликие части.

Доказательство.

Задача B — Про торт и бесстыдную птичку

Решается на основании задачи A.

У бабушки было два внука, которые должны были приехать на выходные погостить. Она, как любая добропорядочная бабушка, приготовила для них торт. И поставила его на подоконник. Но пока он там стоял, над домом бабушки пролетала бесстыдная птичка. И так получилось, что она справила свою нужду аккурат на краешек торта. Бабушка увидав это не упала духом и решила, что этот кусочек она просто вырежет (см рисунок). Бабушка была очень справедливая, внуков любила одинаково, и к своей работе относилась трепетно. Помогите бабушке разделить весь оставшийся торт на две совершенно одинаковые по площади части.

Бабушка имеет идеальный глазомер, она легко способна находить на глаз середины и пересечения любых отрезков. И у бабушки есть замечательный нож, которым она умеет лихо отрезать куски торта по любой намеченной прямой.

Решение.

Задание

Начертите равновеликие треугольники.

Решение.

Задача

Доказать, что медиана делит треугольник на два равновеликих треугольника.

Решение.

Следствие. Диагонали параллелограмма разбивают его на четыре равновеликих треугольника.

Задача

Доказать, что медианы треугольника разбивают его на шесть равновеликих треугольников.

Решение.

Рассмотреть попарно эти шесть треугольников. У них одинаковые основания и одна и та же высота. Поэтому попарно треугольники имеют одинаковую площадь. В силу транзитивности все 6 треугольников равновелики.

Задача

Начертите треугольник ABC. Через вершину B проведите 2 прямые так, чтобы они разделили этот треугольник на 3 треугольника, имеющие равные площади.

Решение.

Задача

Постройте полукруг, равновеликий данному кругу.

Постройте круг, равновеликий данному полукругу.

Задача

Доказать, что круг на рисунке разбит на 9 равновеликих частей

Решение

Задача

Найти площадь четвертой части

Решение

mat/geom/area.txt

· Последние изменения: 2016/01/18 01:22 (внешнее изменение)

Источник

Определение.

Равновеликие фигуры — это фигуры, которые имеют одинаковые площади.

Равновеликие тела — это тела, которые имеют равные объёмы (равновеликие тела часто также называют равновеликими фигурами).Равные фигуры — это фигуры, которые совпадают при наложении (у них соответствующие стороны равны и соответствующие углы равны).

Равные фигуры имеют равные площади, поэтому равные фигуры являются также равновеликими. Обратное, вообще говоря, неверно.

Примеры равновеликих фигур.

рисунок 1

1) Прямоугольник и квадрат, изображенные на рисунке 1, — равновеликие фигуры.

Площадь прямоугольника

a=8, b=2, S=8∙2=16

Площадь квадрата

$[S = {c^2}]$

S=4²=16.

То есть, прямоугольник со сторонами a и b и квадрат со стороной c являются равновеликими, если

$[ab = {c^2}]$

рисунок 2

2) Треугольник и квадрат, изображенные на рисунке 2 — равновеликие фигуры, так как имеют равные площади.

Площадь квадрата S=3²=9.

Площадь треугольника

$[S = frac{1}{2}a{h_a},]$

$[ Rightarrow S = frac{1}{2} cdot 6 cdot 3 = 9.]$

Треугольник со стороной a и проведенной к ней высоте ha и квадрат со стороной c являются равновеликими, если

$[frac{1}{2}a{h_a} = {c^2}]$

рисунок 3

3) Треугольник и трапеция, изображенные на рисунке 3 — равновеликие, поскольку их площади равны.

Площадь треугольника

$[S = frac{1}{2}c{h_c},]$

$[ Rightarrow S = frac{1}{2} cdot 5 cdot 4 = 10.]$

Площадь трапеции

$[S = frac{{a + b}}{2} cdot h, Rightarrow S = frac{{7 + 3}}{2} cdot 2 = 10.]$

Треугольник со стороной c и проведенной к ней высотой hс и трапеция с основаниями a и b и высотой h являются равновеликими, если

$[frac{1}{2}c{h_c} = frac{{a + b}}{2} cdot h]$

Источник

ОТВЕТЫ К ЗАДАНИЯМ

8. Найди на рисунке равные фигуры и назови их номера. Найди фигуры с одинаковой площадью.

Равные фигуры, которые совпадут при наложении:
1) 1 и 7;
2) 2 и 4;
3) 3 и 5.
Площади фигур:
1) 5 треугольников
2) 4 треугольника
3) 4 треугольника
4) 4 треугольника
5) 4 треугольника
6) 4 треугольника
7) 5 треугольников
4 треугольника
Площади фигур 1 и 7 равны, площади фигур 2, 3, 4, 5, 6, 8 равны.

9. Мальчик посмотрел в зеркало и увидел в нем отражение часов. Можешь ли ты определить, сколько времени на этих часах?

Часы показывают 7 часов 5 минут.

1. Каждое из чисел 72, 15, 26, 39, 54, 81 замени суммой разрядных слагаемых.

72 = 70 + 2
15 = 10 + 5
26 = 20 + 6
39 = 30 + 9
54 = 50 + 4
81 = 80 + 1

2. Вычисли значение каждого выражения двумя способами. Выбери из них самый удобный.
(16 + 12) : 4
(9 + 21) : 3
(18 + 36) : 9

Решение

1) (16 + 12) : 4 = 28 : 4 = 7;
2) (16 + 12) : 4 = 16 : 4 + 12 : 4 = 4 + 3 = 7

1) (9 + 21) : 3 = 30 : 3 = 10
2) (9 + 21) : 3 = 9 : 3 + 21 : 3 = 3 + 7 = 10

1) (18 + 36) : 9 = 54 : 9 = 6;
2) (18 + 36) : 9 = 18 : 9 + 36 : 9 = 2 + 4 = 6

3. Вычисли.

(27 + 9) : 3 = 27 : 3 + 9 : 3 = 9 + 3 = 12
(32 + : 4 = 40 : 4 = 10
(15 + 15) : 6 = 30 : 6 = 5

4. У бригады стекольщиков было 60 стекол. Они вставили в 9 квартирах по 4 стекла. Сколько стекол у бригады осталось?

Было — 60 ст.
Вставили — 9 к. по 4 ст.
Осталось — ?

1) 9 * 4 = 36 (с.) − вставили
2) 60 − 36 = 24 (с.) − осталось у стекольщиков
Ответ: 24 стекла.

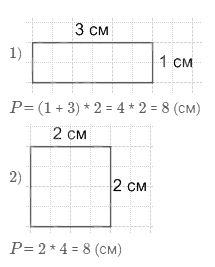
5. Начерти в тетради два разных прямоугольника, периметр каждого из которых равен 8 см.

Источник