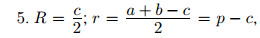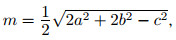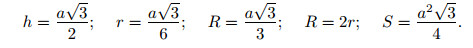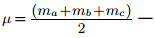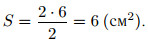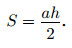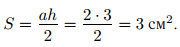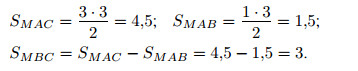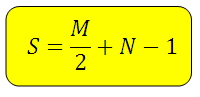Как найти фигуру в квадрате - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Определить площадь плоских фигур в квадратных сантиметрах (также обозначаемых как см²) достаточно просто. В самом легком случае, когда требуется рассчитать площадь квадрата или прямоугольника, она вычисляется произведением длины и ширины. Площадь других фигур (кругов, треугольников и так далее) можно определить с помощью целого ряда специальных математических формул. Также, если потребуется, можно без труда перевести площадь в квадратные сантиметры из других единиц измерения.

1

Определите длину измеряемой площади. У квадратов и прямоугольников по четыре стороны, расположенных под прямыми углами относительно друг друга. В случае с прямоугольниками, их противоположные стороны равны между собой, тогда как у квадратов равны все стороны. Измерьте одну из сторон квадрата или большую из сторон прямоугольника, чтобы определить ее длину в сантиметрах.^[1]
2
Определите ширину измеряемой площади. Далее измерьте в сантиметрах любую из сторон, смежных с той, которую вы измерили в первую очередь. Эта сторона будет находиться под углом в 90 градусов к первой. Вторая мерка будет обозначать ширину квадрата или прямоугольника.^[2]
- Так как у квадрата все стороны одинаковы, его длина будет равна ширине. Поэтому у квадрата можно изначально измерить только одну сторону.
3
Умножьте длину на ширину. Просто перемножьте длину и ширину фигуры, чтобы определить площадь квадрата или прямоугольника в квадратных сантиматрах.^[3]
- Например, допустим, что длина прямоугольника составляет 4 см, а ширина – 3 см. В таком случае площадь фигуры рассчитывается следующим образом: 4 × 3 = 12 квадратных сантиметров.
- В случае с квадратом (по причине равных сторон) можно просто умножить саму на себя длину одной из его сторон (другими словами, возвести ее «в квадрат» или «во вторую степень»), чтобы определить площадь фигуры в квадратных сантиметрах.
Реклама

1
Найдите площадь круга по формуле: S = π × r². Чтобы найти площадь круга в квадратных сантиметрах, необходимо знать расстояние в сантиметрах от центра круга до линии его окружности. Это расстояние называется радиусом окружности. Как только радиус будет известен, обозначьте его буквой r из вышеупомянутой формулы. Умножьте значение радиуса само на себя и на число π (3,1415926…), чтобы узнать площадь круга в квадратных сантиметрах.^[4]
- Например, площадь круга с радиусом 4 см составит 50,27 квадратных сантиметра в результате перемножения 3,14 и 16.
2
Вычислите площадь треугольника по формуле: S = 1/2 b × h. Площадь треугольника в квадратных сантиметрах вычисляется умножением половины длины его основания b (в сантиметрах) на его высоту h (в сантиметрах). Основанием треугольника выбирается одна из его сторон, тогда как высота треугольника – это перпендикуляр, опущенный к основанию треугольника из противоположной к нему вершины. Площадь треугольника можно вычислить через длину основания и высоту по любой из сторон треугольника и противоположной к ней вершине.^[5]
- Например, если длина основания треугольника составляет 4 см, а высота, проведенная к основанию – 3 см, площадь составит: 2 x 3 = 6 квадратных сантиметра.
3
Найдите площадь параллелограмма по формуле: S = b × h. Параллелограммы подобны прямоугольникам за одним исключением – их углы не обязательно равны 90 градусам. Соответственно, расчет площади параллелограмма производится аналогичным для прямоугольника способом: длина стороны основания в сантиметрах умножается на высоту параллелограмма в сантиметрах. За основание берут любую из сторон, а высота определяется длиной перпендикуляра к ней из противоположного тупого угла фигуры.^[6]
- Например, если длина основания параллелограмма составляет 5 см, а его высота – 4 см, его площадь составит: 5 x 4 = 20 квадратных сантиметров.
4
Вычислите площадь трапеции по формуле: S = 1/2 × h × (B+b). Трапеция – это четырехугольник две стороны которого параллельны между собой, а остальные две – нет. Чтобы определить площадь трапеции в квадратных сантиметрах, необходимо знать три мерки (в сантиметрах): длину более длинной параллельной стороны B, длину более короткой параллельной стороны b и высоту трапеции h (определяемую как кратчайшее расстояние между ее параллельными сторонами по перпендикулярному к ним отрезку). Сложите между собой длины двух параллельных сторон, поделите сумму пополам и умножьте на высоту, чтобы получить площадь трапеции в квадратных сантиметрах.^[7]
- Например, если более длинная из параллельных сторон трапеции равна 6 см, более короткая – 4 см, а высота – 5 см, площадь фигуры составит: ½ x (6+4) х 5 = 25 квадратных сантиметров.
5
Найдите площадь правильного шестиугольника: S = ½ × P × a. Приведенная формула верна только для правильного шестиугольника с шестью равными сторонами и шестью одинаковыми углами. Буквой P обозначается периметр фигуры (или произведение длины одной стороны на шесть, что справедливо для правильного шестиугольника). Буквой a обозначается длина апофемы – расстояние от центра шестиугольника до середины одной из его сторон (точки, расположенной посередине между двумя соседними вершинами фигуры). Перемножьте периметр и апофему в сантиметрах и поделите результат на два, чтобы найти площадь правильного шестиугольника.^[8]
- Например, если у правильного шестиугольника шесть равных сторон по 4 см (то есть его периметр P = 6 x 4 = 24 см), а длина апофемы равна 3,5 см, то его площадь составит: ½ x 24 x 3,5 = 42 квадратных сантиметра.
6
Вычислите площадь правильного восьмиугольника по формуле: S = 2a² × (1 + √2). Для расчета площади правильного восьмиугольника (с восемью равными сторонами и восемью одинаковыми углами) нужно знать только длину одной из сторон фигуры в сантиметрах (обозначенной в формуле буквой “a”). Подставьте соответствующее значение в формулу и вычислите результат.^[9]
- Например, если длина стороны правильного восьмиугольника равна 4 см, то площадь этой фигуры составляет: 2 х 16 x (1 + 1,4) = 32 x 2,4 = 76,8 квадратных сантиметров.
Реклама

1
Переведите все мерки в сантиметры, прежде чем производить расчет площади. Чтобы сразу рассчитать площадь в квадратных сантиметрах, необходимо подставлять все параметры в формулу расчета площади также в сантиметрах (это касается, длины, высоты, апофемы и так далее). Поэтому, если ваши исходные данные выражены в других единицах измерения (например, в метрах), сначала их следует перевести в сантиметры. Ниже приведены соотношения наиболее популярных единиц измерения.
- 1 метр = 100 сантиметров
- 1 сантиметр = 10 миллиметров
- 1 дюйм = 2,54 сантиметра
- 1 фут = 30,48 сантиметра
- 1 сантиметр = 0,3937 дюйма
2
Чтобы перевести площадь из квадратных метров в квадратные сантиметры, ее следует умножить на 10000 (то есть площадь одного квадратного метра в сантиметрах), или на произведение 100 см на 100 см. Если вы знаете площадь фигуры в квадратных метрах, ее можно перевести в квадратные сантиметры умножением на 10000.^[10]
- Например, 0,5 квадратного метра = 0,5 x 10000 = 5000 квадратных сантиметров.
3
Чтобы перевести в квадратные сантиметры площадь, выраженную в квадратных дюймах, умножьте ее на 6,4516. Как уже упоминалось, 1 дюйм равен 2,54 сантиметра, тогда как квадратный дюйм составляет 6,4516 квадратных сантиметров (или 2,54 x 2,54). Таким образом, если вам необходимо конвертировать в квадратные сантиметры площадь, равную 10 квадратным дюймам, следует умножить 10 на 6,4516, и у вас получится 64,5 квадратных сантиметров.^[11]
- Также следует упомянуть, что в одном гектаре содержится 10000 квадратных метров, тогда как каждый квадратный метр равен 10000 квадратных сантиметров. Поэтому, чтобы выразить один гектар в сантиметрах, следует умножить 10000 на 10000 и получится 100 миллионов квадратных сантиметров.
Реклама

Об этой статье

Эту страницу просматривали 154 010 раз.

Была ли эта статья полезной?

Источник

Две фигуры называют равными, если одну их них можно так наложить на другую,
что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Запомните!

Для вычисления площади квадрата нужно умножить его длину на саму себя.

S = a · a

Пример:

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см²

Формулу площади квадрата, зная
определение степени,
можно записать следующим образом:

S = a²

Площадь прямоугольника

Запомните!

Для вычисления площади прямоугольника нужно умножить его длину на ширину.

S = a · b

Пример:

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см²

Запомните!

Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Запомните!

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя
правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м²
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м²

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м²

Ответ: S = 65 м² — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Запомните!

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

Рассмотрим прямоугольник:

АС — диагональ прямоугольника
ABCD. Найдём площадь треугольников

ABC и
ACD

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см²

S_ABC = S_ABCD : 2

S_ABC = 20 : 2 = 10 см²

S_ABC =
S_ACD = 10 см²

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

3 декабря 2015 в 22:54

Ирина Петренко
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Ирина Петренко
Профиль
Благодарили: 0

Сообщений: 1

как написать правильно площадь треугольника?

0
Спасибо thanks
Ответить

9 декабря 2015 в 19:41
Ответ для Ирина Петренко

Тима Клюев
(^-^)
Профиль
Благодарили: 0

Сообщений: 8

(^-^)
Тима Клюев
Профиль
Благодарили: 0

Сообщений: 8

S(рисуешь мини треугольник) = ,,,,,

0
Спасибо thanks
Ответить

Источник

Признаки равенства треугольников

1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.

2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.

3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то треугольники равны.

Признаки равенства прямоугольных треугольников

1. По двум катетам.

2. По катету и гипотенузе.

3. По гипотенузе и острому углу

4. По катету и острому углу

Теорема о сумме углов треугольника и следствия из неё

1. Сумма внутренних углов треугольника равна 180°.

2. Внешний угол треугольника равен сумме двух внутренних не смежных с ним углов.

3. Сумма внутренних углов выпуклого n-угольника равна 180°(n − 2).

4. Сумма внешних углов n-угольника равна 360°

5. Углы со взаимно перпендикулярными сторонами равны, если они оба острые или оба тупые.

6. Угол между биссектрисами смежных углов равен 90°.

7. Биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны.

Основные свойства и признаки равнобедренного треугольника

1. Углы при основании равнобедренного треугольника равны.

2. Если два угла треугольника равны, то он равнобедренный.

3. В равнобедренном треугольнике медиана, биссектриса и высота, проведённые к основанию, совпадают.

4. Если в треугольнике совпадает любая пара отрезков из тройки: медиана, биссектриса, высота, — то он является равнобедренным.

Неравенство треугольника и следствия из него

1. Сумма двух сторон треугольника больше его третьей стороны

2. Сумма звеньев ломаной больше отрезка, соединяющего начало первого звена с концом последнего.

3. Против большего угла треугольника лежит бOльшая сторона.

4. Против большей стороны треугольника лежит больший угол.

5. Гипотенуза прямоугольного треугольника больше катета

6. Если из одной точки проведены к прямой перпендикуляр и наклонные, то

1) перпендикуляр короче наклонных;

2) большей наклонной соответствует большая ´ проекция и наоборот

Средняя линия треугольника.

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.

Теорема о средней линии треугольника.

Средняя линия треугольника параллельна стороне треугольника и равна её половине.

Теоремы о медианах треугольника

1. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1, считая от вершины.

2. Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный

3. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы

Свойство серединных перпендикуляров к сторонам треугольника.

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника

Теорема о высотах треугольника.

Прямые, содержащие высоты треугольника, пересекаются в одной точке.

Теорема о биссектрисах треугольника.

Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.

Свойство биссектрисы треугольника.

Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам

Признаки подобия треугольников

1. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.

2. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключенные между этими сторонами, равны, то треугольники подобны.

3. Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого, то треугольники подобны.

Площади подобных треугольников

1. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

2. Если два треугольника имеют равные углы, то их площади относятся как произведения сторон, заключающих эти углы.

В прямоугольном треугольнике

1. Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или на косинус прилежащего к этому катету острого угла.

2. Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к этому катету острого угла.

3. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.

4. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен 30°.

где a, b — катеты, а c — гипотенуза прямоугольного треугольника; r и R — радиусы вписанной и описанной окружностей соответственно

Теорема Пифагора и теорема, обратная теореме Пифагора

1. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.

2. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник — прямоугольный

Средние пропорциональные в прямоугольном треугольнике

Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу

Метрические соотношения в треугольнике

1. Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

2. Следствие из теоремы косинусов. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

3. Формула для медианы треугольника. Если m — медиана треугольника, проведённая к стороне c, то

где a и b — остальные стороны треугольника.

4. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.

5. Обобщённая теорема синусов. Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.

Формулы площади треугольника

1. Площадь треугольника равна половине произведения основания на высоту.

2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

3. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.

4. Площадь треугольника равна произведению трёх его сторон, делённому на учетверённый радиус описанной окружности.

5. Формула Герона:

где p — полупериметр; a, b, c — стороны треугольника.

Элементы равностороннего треугольника

Пусть h, S, r, R — высота, площадь, радиусы вписанной и описанной

окружностей равностороннего треугольника со стороной a. Тогда

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Чертежи

Обозначения

Формулы

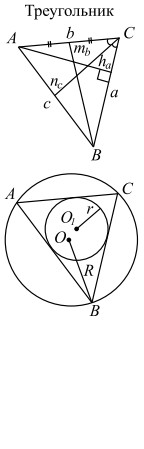a, b, c — стороны;
A, B, C — противолежащие
им углы;

h_a, h_b, h_c — высоты,
проведённые к
соответствующим
сторонам;

n_a, n_b, n_c — биссектрисы,
проведённые к
соответствующим сторонам;

b_a и b_c — отрезки, на
которые делится
биссектрисой сторона b;
m_a, m_b, m_c —
медианы, проведённые
к соответствующим
сторонам;

полусумма медиан;
R — радиус описанной
окружности;

r — радиус вписанной
окружности

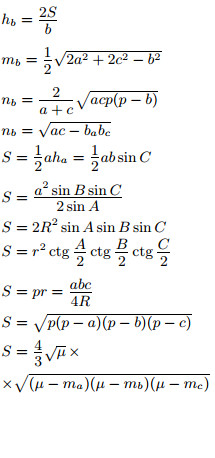Прямоугольный треугольник

Немного полезной информации

В этой главе мы рассмотрим простые виды задач по геометрии, а именно задачи, в которых нужно найти площади плоских фигур, нарисованных

на клетчатой бумаге или расположенных на координатной плоскости.

Для решения таких задач требуется знать не очень много формул, поэтому их решение доступно практически каждому.

Давайте вспомним эти формулы и разберём примеры их применения.

Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы (c) равен сумме квадратов катетов (a и b):

c² = a² + b²

Площадь прямоугольного треугольника равна половине произведения его катетов:

S =ab/2.

Напомним, что у прямоугольного

треугольника есть прямой угол, равный 90°. Сторона напротив прямого

угла (самая длинная) называется гипотенузой, две прилежащие к прямому углу стороны называют катетами.

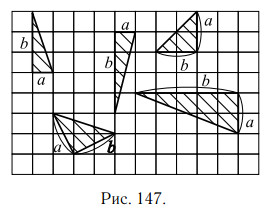
На рисунке 147 приведены чертежи некоторых прямоугольных треугольников, у которых показаны катеты a и b.

Задачи с решениями

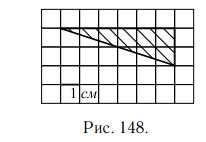
1. На клетчатой бумаге с клетками размером 1 см × 1 см изображён треугольник (см. рис. 148). Найдите его площадь в квадратных сантиметрах.

Решение.

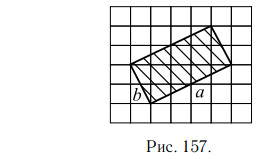
Площадь прямоугольного треугольника равна половине произведения

его катетов. В данном треугольнике катеты равны 2 см и 6 см (посчитаем

по клеточкам), поэтому площадь

Ответ: 6

Площадь треугольника

Немного полезной информации

Площадь произвольного треугольника равна половине произведения длины его стороны (a) на высоту (h), проведённую к этой стороне:

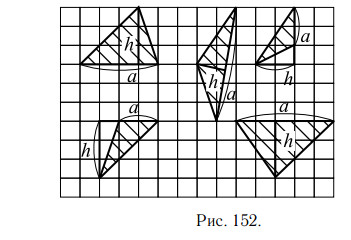
На рисунке 152 приведены чертежи некоторых треугольников, у которых обозначены одна из сторон a и высота, проведённая к этой стороне h.

Как правило, удобно брать ту сторону, которая проходит по линиям

клетчатой бумаги (или же проходит параллельно осям координат).

Задачи с решениями

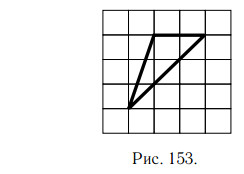
На клетчатой бумаге с клетками размером 1 см × 1 см изображён треугольник (см. рис. 153). Найдите его площадь в квадратных сантиметрах.

Решение.

1-й способ.

Площадь произвольного треугольника равна половине произведения

длины его стороны (a) на высоту (h), проведённую к этой стороне. Проведём высоту h. Треугольник тупоугольный, поэтому высота проводится вне

треугольника.

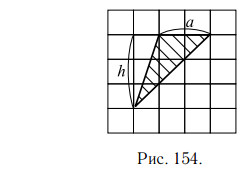
На рисунке 154 сторона a = 2 см, высота h = 3 см

Ответ: 3.

Заметим, что так как клетки имеют размер 1 см × 1 см, то площадь

в квадратных сантиметрах получится, если мы будем по рисунку считать

размер отрезков в клетках. Поэтому единицы длины в этих задачах можно

и не писать.

2-й способ.

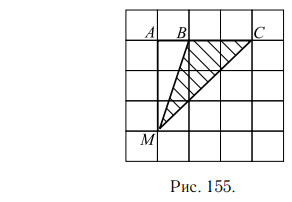
Достроим треугольник BCM до прямоугольного треугольника MCA

(см. рис. 155).

Тогда искомую площадь треугольника BCM можно найти как разность площадей двух прямоугольных треугольников MAC и MAB.

Катеты первого из них равны 3 см и 3 см, катеты второго — 3 см и 1 см.

Площадь прямоугольного треугольника равна половине произведения

его катетов, следовательно,

Ответ: 3.

Четырёхугольник

Параллелограмм.

Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.

Свойства и признаки параллелограмма

1. Диагональ разбивает параллелограмм на два равных треугольника.

2. Противоположные стороны параллелограмма попарно равны.

3. Противоположные углы параллелограмма попарно равны.

4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.

5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.

6. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.

7. Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.

Свойство середин сторон четырёхугольника.

Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.

Прямоугольник.

Прямоугольником называется параллелограмм с прямым углом.

Свойства и признаки прямоугольника

1. Диагонали прямоугольника равны.

2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник

Квадрат.

Квадратом называется прямоугольник, все стороны которого равны.

Формулы площади четырёхугольника

1. Площадь параллелограмма равна произведению основания на высоту

2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.

3. Площадь прямоугольника равна произведению двух его соседних сторон.

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Площадь четырёхугольника

Площадь прямоугольника равна произведению его смежных сторон:

S = ab.

На рисунке 156 приведены чертежи некоторых прямоугольников, у которых показаны смежные стороны a и b

Задачи с решениями

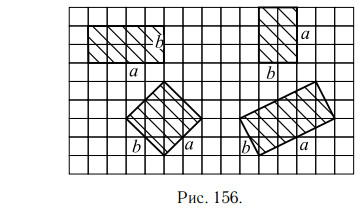
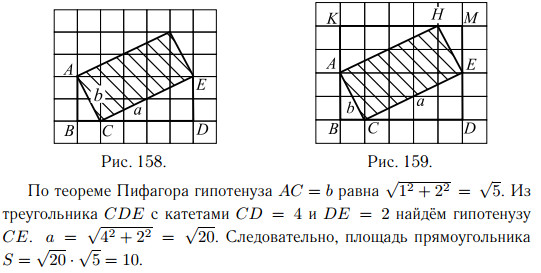
На клетчатой бумаге с клетками размером 1 см×1 см изображён прямоугольник (см. рис. 157). Найдите его площадь в квадратных сантиметрах.

Решение.

1-й способ.

Площадь прямоугольника равна произведению его смежных сторон a

и b. Для того чтобы найти стороны прямоугольника, рассмотрим прямоугольный треугольник ABC с катетами AB = 2 и BC = 1 и гипотенузой

AC = b (см. рис. 158).

Ответ: 10.

2-й способ.

Достроим прямоугольник ACEH до прямоугольника BKMD

(см. рис. 159). Чтобы найти площадь ACEH, нужно из площади прямоугольника BKMD вычесть площади прямоугольных треугольников

AKH, HME, EDC и ABC.

Так как площадь прямоугольного треугольника равна половине произведения катетов, то площадь каждого из двух больших треугольников

(AKH и EDC) равна 4, а площадь каждого из двух маленьких треугольников (HME и ABC) равна 1. Площадь прямоугольника BKMD равна 4 · 5 = 20. Следовательно, площадь искомого прямоугольника будет равна 20 − 1 − 1 − 4 − 4 = 10.

Ответ: 10.

Заметим, что подобным «достраиванием» можно найти площадь любого многоугольника на клетчатой бумаге.

Квадрат.

Квадратом называется прямоугольник, все стороны которого равны.

Свойства и признаки ромба

1. Диагонали ромба перпендикулярны.

2. Диагонали ромба делят его углы пополам

3. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.

4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

Площадь ромба равна половине произведения его диагоналей

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Четырёхугольник

Параллелограмм.

Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.

Свойства и признаки параллелограмма

1. Диагональ разбивает параллелограмм на два равных треугольника.

2. Противоположные стороны параллелограмма попарно равны.

3. Противоположные углы параллелограмма попарно равны.

4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.

5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.

Свойство середин сторон четырёхугольника.

Прямоугольник.

Прямоугольником называется параллелограмм с прямым углом.

Свойства и признаки прямоугольника

1. Диагонали прямоугольника равны.

2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник

Квадрат.

Квадратом называется прямоугольник, все стороны которого равны.

Формулы площади четырёхугольника

1. Площадь параллелограмма равна произведению основания на высоту

2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.

3. Площадь прямоугольника равна произведению двух его соседних сторон.

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Площадь четырёхугольника

Площадь прямоугольника равна произведению его смежных сторон:

S = ab.

На рисунке 156 приведены чертежи некоторых прямоугольников, у которых показаны смежные стороны a и b

Ромб

Квадрат.

Квадратом называется прямоугольник, все стороны которого равны.

Свойства и признаки ромба

1. Диагонали ромба перпендикулярны.

2. Диагонали ромба делят его углы пополам

3. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.

4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.

Площадь ромба равна половине произведения его диагоналей

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Трапеция

Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).

1. Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

Замечательное свойство трапеции.

Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.

Равнобедренная трапеция.

Трапеция называется равнобедренной, если её боковые стороны равны.

Свойства и признаки равнобедренной трапеции

1. Углы при основании равнобедренной трапеции равны.

2. Диагонали равнобедренной трапеции равны

3. Если углы при основании трапеции равны, то она равнобедренная.

4. Если диагонали трапеции равны, то она равнобедренная

5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований.

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Чертежи	Обозначения	Формулы
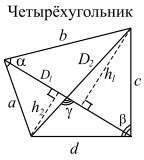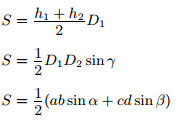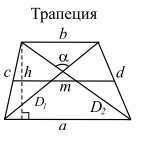	a, b, c, d — стороны; D₁, D₂ — диагонали; γ — угол между диагоналями; h₁, h₂ — длины перпендикуляров, опущенных на диагональ D₁; α, β — два противолежащих угла четырёхугольника.
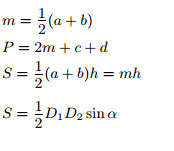	a, b — основания; c, d — боковые стороны; D1, D2 — диагонали; α — угол между диагоналями; m — средняя линия; h — высота

Площадь трапеции равна половине произведения суммы оснований (a + b) на высоту (h):

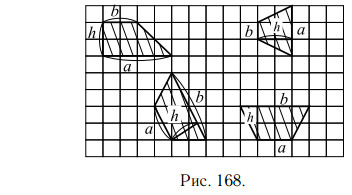
На рисунке 168 приведены чертежи некоторых трапеций, у каждой из

которых показаны основания a и b и высота h.

Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.

Основные формулы

Далее S — площадь фигуры, P — периметр, p — полупериметр.

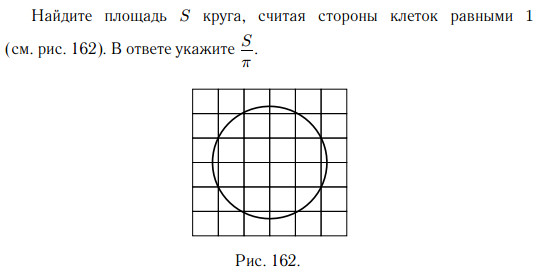
Площади круга и сектора

Площадь круга равна произведению числа π на квадрат радиуса:

S = πR².

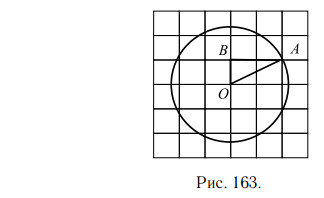
Решение.

Площадь круга равна произведению числа π на квадрат радиуса. Найдём радиус. Из центра O проведём радиус OA. В треугольнике OAB сторона OA — гипотенуза, катеты равны 1 и 2 (см. рис. 163)

Найдём гипотенузу по теореме Пифагора.

Ответ: 5

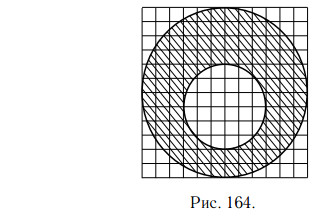
На клетчатой бумаге нарисовано два круга (см. рис. 164). Площадь

внутреннего круга равна 3. Найдите площадь заштрихованной фигуры.

Решение.

Радиус R внутреннего круга — 3 клетки, его площадь равна πR² = 3.

Радиус внешнего круга — 6 клеток, то есть 2R, поэтому его площадь равна

π · (2R)² = 3 · 4 = 12. Площадь заштрихованной фигуры равна разности 12 − 3 = 9.

Ответ: 9

Источник

Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.

Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.

В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.

ФОРМУЛА ПИКА

Площадь искомой фигуры можно найти по формуле:

М – количество узлов на границе треугольника (на сторонах и вершинах)

N – количество узлов внутри треугольника

*Под «узлами» имеется ввиду пересечение линий.

Найдём площадь треугольника:

Отметим узлы:

1 клетка = 1 см

M = 15 (обозначены красным)

N = 34 (обозначены синим)

Ещё пример. Найдём площадь параллелограмма:

Отметим узлы:

M = 18 (обозначены красным)

N = 20 (обозначены синим)

Найдём площадь трапеции:

Отметим узлы:

M = 24 (обозначены красным)

N = 25 (обозначены синим)

Найдём площадь многоугольника:

Отметим узлы:

M = 14 (обозначены красным)

N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.

А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.

Теперь взгляните на следующие фигуры:

Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:

Отметим узлы:

M = 11 (обозначены красным)

N = 5 (обозначены синим)

Ответ: 9,5

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение

Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.

Рассмотрим подход оговоренный в статье «Площадь четырёхугольника. Универсальный способ«.

Найдём площадь фигуры:

Опишем около неё прямоугольник:

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:

Ответ: 4,5

В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.

Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.

Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.

Больше полезных формул — в нашем ЕГЭ-Справочнике.

Смотри также материал: Как быстро выучить формулы

В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.

Вычисление длин отрезков, величин углов и площадей фигур по формулам

1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.

Средняя линия трапеции равна полусумме её оснований: $frac{AD+BC}{2}=frac{4+2}{2}=3.$

Ответ: 3.

2. Найдите величину угла ABC. Ответ дайте в градусах.

Величина вписанного угла alpha равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна ${90}^{circ}.$ Тогда $angle alpha =frac{{90}^{circ}}{2}={45}^{circ}.$

Ответ: 45.

3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на $frac{sqrt{5}}{2}.$

Решение:

Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:

${sin alpha }={sin angle AOB}=frac{4}{2sqrt{5}}=frac{2}{sqrt{5}}.$ Осталось умножить найденное значение синуса на $frac{sqrt{5}}{2}.$

$frac{2}{sqrt{5}}cdot frac{sqrt{5}}{2}=1$

Ответ: 1.

4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:

, где d_1 и d_2 — диагонали.

Получим:

Ответ: 12.

5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.

Площадь трапеции равна произведению полусуммы оснований на высоту:

Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции

Ответ: 18.

Нахождение площадей многоугольников сложной формы

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.

6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: 12,5 .

7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: 10,5 .

Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.

Согласно формуле Пика, площадь многоугольника равна В+Г/2-1

где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.

Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.

Посмотрим, как решается задача 7 с помощью формулы Пика:

Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.

Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.

Выбирайте — какой способ вам больше нравится.

8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки

Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.

Площадь каждого из больших треугольников равна $frac{1}{2}cdot 3cdot 2=3.$

Площадь каждого из маленьких треугольников равна $frac{1}{2}cdot 1cdot 2=1.$

Тогда площадь четырехугольника

9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки

Решение:

На рисунке изображен ромб с вырезанным из него квадратом.

Площадь ромба равна половине произведения его диагоналей.

Площадь вырезанного квадрата равна 4.

Площадь фигуры равна 36 — 4 = 32.

Ответ: 32.

Площадь круга, длина окружности, площадь части круга

Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.

Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.

10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как R=1 . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как R=1 ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть 360 градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Ответ: .

11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.

На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще $frac{1}{8}$ круга, то есть $frac{3}{8}$ круга.

Значит, нам надо умножить площадь круга на $frac{3}{8}$ . Получим:

$frac{3}{8}cdot 2,8 =1,05$

Ответ: 1,05.

12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.

Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна pi R^2 , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в ${frac{4}{3}}^2 = frac{16}{9}$ раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.

Ответ: 7.

Задачи на координатной плоскости

13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).

Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда

Ответ: 20

14. Найдите площадь четырехугольника, вершины которого имеют координаты

На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.

Ответ: 16.

Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник