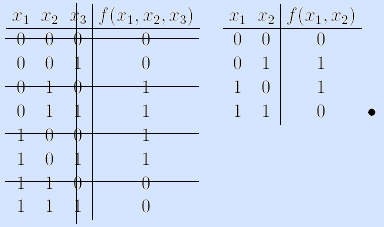Как найти фиктивную переменную по таблице - Исправление недочетов и поиск решений вместе с Examum.ru

Определение. Говорят, что булева функция f(x₁, …, x_i, …, x_n) существенно зависит от переменной x_i, если выполняется условие

В этом случае также говорят, что переменная x_i существенная, в противном случае ее называют фиктивной переменной.

Пример. Рассмотрим булеву функцию f(x₁, x₂, x₃) и исследуем ее переменные x₁ и x₃.

Из таблиц истинности видно, что переменная x₁ функции f(x₁, x₂, x₃) существенная, так как f(0,x₂, x₃) ≠ f(1,x₂, x₃). Переменная x₃ фиктивная, так как f(x₁, x₂, 0) = f(x₁, x₂, 1). •

Очевидно, что для выявления фиктивных переменных можно не строить в явном виде таблиц истинности левой и правой частей неравенства, а сравнивать соответствующие части вектора-столбца значений функции.

Алгоритм распознавания фиктивной переменной по таблице истинности.

– Для переменной x₁ сравниваются половины столбца значений функции: верхняя и нижняя, так как именно в верхней половине x₁=0, а в нижней x₁=1, если они совпадают, то переменная x₁ фиктивна;

– для переменной x₂ сравниваются четвертины столбца в каждой половине, так как именно в верхних четвертинах x₂ =0, а в нижних x₂ =1, если четвертины в каждой половине совпадают, то переменная x₂ фиктивна;

– и так далее (за четвертинами следуют 1/8, 1/16, … ).

Пример. Для булевой функции из предыдущего примера переменная x₁ существенна, так как верхняя половина столбца значений функции (0011) не равна нижней половине (1100). Переменная x₂ существенна, так как четвертины уже в первой половине различаются (00 и 11). Переменная x₃ фиктивна, так как осьмушки во всех четвертинах равны (0 и 0, 1 и 1, 1 и 1, 0 и 0). •

Выявление фиктивных переменных можно ускорить, используя следующее очевидное утверждение.

Достаточное условие отсутствия фиктивных переменных. Если вес вектора-столбца значений функции нечетен, то функция не может содержать фиктивных переменных.

Алгоритм удаления фиктивной переменной x_i состоит в вычеркивании из таблицы истинности всех строк, в которых x_i = 0 (или всех строк, в которых x_i = 1), и столбца x_i.

Пример (функция та же). Применив алгоритм для удаления фиктивной переменой x₃ (таблица слева), получаем результат (таблица справа).

Если переменная x_i функции f(x₁, …, x_n) фиктивна, то на наборах, соседних по i компоненте, функция принимает одинаковые значения. Отсюда следует способ выявления и удаления фиктивной переменной функции, заданной матрицей Грея.

Алгоритм распознавания фиктивной переменной по матрице Грея (основан на свойстве симметрии кода Грея).

Переменная фиктивна тогда и только тогда, когда точки на матрице расположены симметрично относительно осей этой переменной. Упрощенная матрица – это одна из ее симметричных половин.

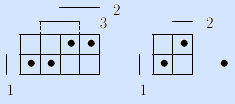
Пример (функция та же и представлена на левой матрице). Переменная x₃ функции фиктивна. Справа показан результат ее удаления.

Определение. Булевы функции назовем равными с точностью до фиктивных переменных, если равны (в смысле, определенном ранее) функции, полученные из исходных удалением фиктивных переменных (и именно это расширенное толкование равенства функций мы будем иметь в виду во всех дальнейших рассуждениях).

Пример. Рассмотрим функции f₁(x₁, x₂) и f₂(x₁, x₂). Удалив фиктивную переменную x₁ функции f₁(x₁, x₂) и фиктивную переменную x₂ функции f₂(x₁, x₂), получим равные функции f₁(x₂)=f₂(x₁)=f(x). Значит, исходные функции равны с точностью до фиктивных переменных.

В вышеприведённых таблицах выделена графа «фиктивные переменные», т.е. переменные, от которых функция на самом деле не зависит. Остановимся на этом понятии подробнее.

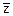
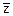
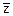
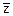
Пример: Рассмотрим булевы функции f(x,y) = xÚy и g(x,y,z) = (xÙy)Ú(хÙ )Ù(yÙz)Ú(yÙ ). Можно заметить, что в силу тождеств алгебры Буля g=(xÚy)Ù(zÚ ), а поскольку zÚ =1, то g = xÚy = f.

В этом примере функция, в которой присутствуют 3 переменных, в действительности зависит от 2-х. В дискретной математике, по сравнению с непрерывной, понятие фиктивных переменных играет большую роль.

Определение: Переменная х является существенной переменной для функции f(x, x₁,…, x_n-1), если существует хотя бы один набор (x₁,…, x_n-1) такой, что f(0, x₁,…, x_n-1) ≠ f(1, x₁,…, x_n-1)

В противном случае переменная называется фиктивной, или несущественной. Понятно, что в определении переменную можно ставить на любое место, и фиктивных переменных может быть несколько.

Ключевым понятием в теории булевых функций является понятие равенства функций. Для функций от одного и того же числа переменных нет необходимости рассматривать какое-то специальное определение равенства, ибо такие функции равны, если они совпадают как отображения одного о того же булева куба. Существование фиктивных переменных усложняет ситуацию, и проблема состоит в том, чтобы определить равенство булевых функций в целом, независимо от числа переменных.

Булевы функции f и g равны, если их существенные переменные совпадают и на каждом наборе значений этих переменных функции f и g принимают равные значения.

Кроме процедуры удаления фиктивных переменных используют и процедуру добавления к множеству переменных булевой функции одной или нескольких переменных.

В результате понятие фиктивной переменной позволяет любые две функции рассматривать как функции от одних и тех же переменных. Для этого надо рассмотреть объединение множеств переменных XUY и дополнить множества X и Y до объединения, вводя соответствующие переменные как фиктивные.

Нетрудно распространить описанную конструкцию на произвольное конечное множество функций и считать тем самым все функции этого множества функциями от одного и того же числа переменных.

Введём понятие проектирующей функции.

Функцию pr_i от n переменных, такую, что

называют (i-ой) проектирующей функцией. В общем случае нумерация множества переменных может быть не задана, и следует указывать не номер, а саму переменную.

Из определения следует, что проектирующая функция имеет единственную существенную переменную, а все остальные переменные проектирующей функции являются фиктивными. Далее мы всегда будем обозначать проектирующую функцию её символом – х, имея в виду возможность расширения на любое число переменных. Такое обозначение есть, конечно вольность, т.к. функция как бы отождествляется с аргументом. Отождествление функции и аргумента недопустимо, т.к. понятие переменной, хоть и связано с понятием функции, никак не есть частный случай понятия функции. Переменная – это имя, некий символ, но никак не функция. Тем не менее мы будем использовать это обозначение ради краткости.

Не нашли то, что искали? Воспользуйтесь поиском:

Вход в систему

Последние комментарии

ПСЗ
5 недель 4 дня назад
Наверное вот так вот ?
6 недель 5 дней назад
Спасибо
6 недель 5 дней назад
Эльдар
7 недель 4 дня назад
Умножение двух положительных чисел в Ассемблере МиК
7 недель 4 дня назад
Да
8 недель 16 часов назад
А вот почему, ВЛАД, .
8 недель 1 день назад
Почему? Я когда писал код,
8 недель 1 день назад
Продолжу.
8 недель 1 день назад
Снова Влад
8 недель 1 день назад

О существенных и фиктивных переменных булевых функций

Воспроизведём данное на лекции определение существенности переменной БФ.

Определение. Пусть задана некоторая БФ f(x₁, x₂, …,x_k, …,x_n_).

Переменная x_k этой функции называется существенной, если найдётся набор ДВОИЧНЫХ значений такой, что:

Рассмотрим пример. Пусть БФ f( x₁, x₂, x₃) задана таблицей:

f( x₁, x₂, x₃)

Исследуем переменные этой функции на существенность.

x₁– существенна, т.к., например, при f(x₁, 0, 1), имеем f(0, 0, 1)=0, f(1, 0, 1)=1. Т.е. f(0, 0, 1) <>f(1, 0, 1). Здесь нашлись двоичные значения = такие, что f(0,a₂,a₃) <>f(1,a₂,a₃).
x₂– не существенна, т.к. f(a₁, 0,a₃) = f(a₁, 1,a₃)на любых наборах двоичных значениий (проверьте это по таблице!).
x₃– существенна, т.к., например, при f(0, 0,x₃), имеем f(0, 0, 0)=1, f(0, 0, 1)=0. Т.е. f(0, 0, 0) <>f(0, 0, 1). Здесь нашлись двоичные значения = такие, что f(a₁,a₂, 0) <>f(a₁,a₂, 1).

Если в таблично заданной функции f( x₁, x₂, …,x_k, …,x_n), например, переменная x_k — не существенна, то для исключения её из таблицы и, соответственно, уменьшения арности указанной функции, необходимо:

вычеркнуть из таблицы столбец несущественной переменной x_k;
вычеркнуть из таблицы все строки, в пересечении которых с вычеркнутым столбцом стоят нули.

Так как x₂ в выше приведённом примере – не существенна (фиктивна), то действуя так, как описано выше, её из таблицы можно исключить.

В результате получим таблицу:

f(x₁, x₃)

При желании, в полученной таблице, переменные, для удобства, можно переименовать, например, в x₁, x₂, или в x, y. На функцию, как на отображение, такие переименования никакого влияния не окажут.

Ясно, что выполняя описанные операции в обратном порядке, фиктивные переменные можно в таблицу включать, формально увеличивая, тем самым, арность задаваемой этой таблицей БФ.

Определение . Две булевы функции f₁ и f₂ будем называть равными (эквивалентными), если таблицу f₂ можно получить из таблицы f₁ путём добавления и/или изъятия фиктивных переменных, а также, возможно, переименования (любых) переменных.

В дальнейшем, БФ рассматриваются с точностью до их равенства (т.е. равные функции нами различаться не будут).

Если функции f₁ и f₂ равны, то этот факт будем обозначать как f₁ = f₂.

Замечание. Возможность добавления фиктивных переменных позволяет считать что БФ, образующие любое рассматриваемое конечное множество всегда имеют одну и ту же арность.

Критерий фиктивности переменной БФ.

Пусть БФ f(x₁, x₂, …,x_k, …,x_n) определена таблично. Для выявления фиктивности её переменной x_k, удобно использовать следующий критерий:

Вычислим величину L=2 n- k+1 ;
Разобьём столбец значений функции (он последний в таблице) на равные отрезки длины L;
Если в каждом из полученных на шаге 2 отрезке верхняя половина отрезка совпадает с нижней его половиной, то проверяемая переменная x_k – фиктивна, иначе, она не фиктивна, т.е. существенна.

Задание. Убедитесь в том, что приведённый критерий работает, применив его к переменным x₁, x₂, x₃ рассмотренного выше примера табличного задания БФ f( x₁, x₂, x₃).

Источник

Равенство булевых функций. Фиктивные переменные

Ключевым понятием в теории булевых функций является понятие равных булевых функций. Для функций от одного и того же числа переменных нет необходимости рассматривать какое-то специальное определение равенства, ибо такие функции равны, если они совпадают как отображения булева куба $mathbb{B}^n$ в . Проблема состоит в том, чтобы определить равенство булевых функций независимо от числа переменных.

Пример 6.4. Рассмотрим булевы функции f(x,y)=xlor y и g(x,y,z)=xzlor xoverline{z}lor yzlor yoverline{z} .

Можно заметить, используя тождества булевой алгебры, что g(x,y,z)=(xlor y)(zlor overline{z}) , а поскольку zlor overline{z}=1 , то

g(x,y,z)=xlor y=f(x,y).

и функции и естественно рассматривать как равные, несмотря на то, что они зависят от разного числа переменных.

В примере 6.4 функция определена как функция от трех переменных, но значение переменного не влияет на значение функции. Обобщая ситуацию примера, можно ввести понятие фиктивного переменного булевой функции.

Определение 6.1. Переменное x_i называют фиктивным переменным булевой функции f(x_1,ldots,x_n) , если значение функции не зависит от значения этого переменного, т.е. если для любых значений переменных

$f(x_1,ldots,x_{i-1},0,x_{i+1},ldots,x_n)= f(x_1,ldots,x_{i-1},1,x_{i+1},ldots,x_n).$

Будем называть переменное , не являющееся фиктивным переменным функции , существенным переменным данной функции и говорить, что функция существенно зависит от переменного .

Пусть дана булева функция y=f(x_1,ldots,x_n) от переменных. Пусть существенными переменными этой функции являются переменные $x_{i_1},ldots, x_{i_r}$ , где rleqslant n и 1leqslant i_1<ldots<i_rleqslant n . Присваивая каждому фиктивному переменному функции произвольное значение, получим функцию widetilde{f} , такую, что она есть функция от переменных, т.е. есть отображение из $mathbb{B}^n$ в , и для любого набора $alpha_{i_1},ldots,alpha_{i_r}$ значений переменных $x_{i_1}, ldots,x_{i_r}$ имеет место равенство

$widetilde{f}(alpha_{i_1},ldots,alpha_{i_r})= f(x_1,ldots,alpha_{i_1},ldots, alpha_{i_r},ldots,x_n)$

независимо от значений фиктивных переменных функции (т.е. переменных, отличных $x_{i_1}, ldots,x_{i_r}$ ). Тем самым функция widetilde{f} оказывается уже функцией, определенной на некоторой r-мерной грани булева куба $mathbb{B}^n$ .

Договоримся только что описанный переход от функции к функции widetilde{f} , уже не имеющей фиктивных переменных, называть удалением фиктивных переменных (функции ).

Замечание 6.2. В качестве упомянутой выше r-мерной грани может быть взята любая грань с направлением, заданным номерами фиктивных переменных. Фиксация грани означает фиксацию конкретного набора значений фиктивных переменных. Тогда соответствующая этой грани функция widetilde{f} получается из исходной функции в результате подстановки вместо каждого фиктивного переменного того конкретного значения, которое задано указанным выше набором.

Вернемся к примеру 6.4. Удаляя фиктивное переменное , вместо функции получим либо функцию g(x,y,0) , которая определена на (двумерной) грани $mathbb{B}_{0}^{3;3}$ булева куба $mathbb{B}^3$ , либо функцию g(x,y,1) , определенную на грани $mathbb{B}_{1}^{3;3}$ . Направлением каждой из этих граней будет однокомпонентный кортеж (3), определенный номером фиктивного переменного .

С использованием понятий фиктивного и существенного переменного можно дать следующее определение равных булевых функций.

Определение 6.2. Булевы функции и называют равными, если их существенные переменные соответственно равны и на каждом наборе значений этих переменных функции и принимают равные значения.

Чтобы распознать по таблице булевой функции, является ли переменное x_i фиктивным, нужно рассмотреть все наборы с фиксированным значением i-й компоненты (один раз фиксировав это значение как 0, другой раз — как 1). Из определения 6.1 ясно, что переменное x_i фиктивно тогда и только тогда, когда для любых двух наборов, отличающихся только значением i-й компоненты, функция принимает равные значения.

Пример 6.5. а. Из табл. 6.4 следует, что мажоритарная функция не имеет фиктивных переменных, так как, например, f(0,0,1)=0 , а f(1,0,1)=1 , т.е. переменное x_1 существенное. Далее, f(1,0,0)=0 , но f(1,1,0)=1 , что означает существенность переменного x_2 ; для x_3 имеем , но , что означает существенность и этого переменного.

б. Ниже приведена таблица функции от четырех переменных (табл. 6.5). Рекомендуется проверить, что переменное x_2 является фиктивным и что остальные переменные существенны. Более того, анализ таблицы показывает, что эта функция есть не что иное, как мажоритарная функция, существенно зависящая от переменных x_1,,x_3 и x_4 .

$begin{aligned} mathit{Table~6.5}~&\ begin{array}{|c||c|c|c|c||c|} hline & x_1& x_2& x_3& x_4& g(x_1,x_2,x_3,x_4) \hline scriptstyle{mathsf{0}}& 0& 0& 0& 0& 0\ scriptstyle{mathsf{1}}& 0& 0& 0& 1& 0\ scriptstyle{mathsf{2}}& 0& 0& 1& 0& 0\ scriptstyle{mathsf{3}}& 0& 0& 1& 1& 1\ scriptstyle{mathsf{4}}& 0& 1& 0& 0& 0\ scriptstyle{mathsf{5}}& 0& 1& 0& 1& 0\ scriptstyle{mathsf{6}}& 0& 1& 1& 0& 0\ scriptstyle{mathsf{7}}& 0& 1& 1& 1& 1\ scriptstyle{mathsf{8}}& 1& 0& 0& 0& 0\ scriptstyle{mathsf{9}}& 1& 0& 0& 1& 1\ scriptstyle{mathsf{10}}& 1& 0& 1& 0& 1\ scriptstyle{mathsf{11}}& 1& 0& 1& 1& 1\ scriptstyle{mathsf{12}}& 1& 1& 0& 0& 0\ scriptstyle{mathsf{13}}& 1& 1& 0& 1& 1\ scriptstyle{mathsf{14}}& 1& 1& 1& 0& 1\ scriptstyle{mathsf{15}}& 1& 1& 1& 1& 1\hline end{array}& end{aligned}$

Кроме процедуры удаления фиктивных переменных используют и процедуру добавления к множеству переменных булевой функции одной или нескольких фиктивных переменных. Так, если дана функция $f(x_1,ldots,x_n)in mathcal{P}_{2,n}$ , то можно ввести новое фиктивное переменное у, определив новую, равную исходной, согласно определению 6.2, функцию от n+1 переменного таким образом:

$widehat{f}(x_1,ldots,x_n,y)= f(x_1,ldots,x_n)cdot (yloroverline{y})$ (см. пример 6.4).

Следует заметить, что фиктивное переменное можно (в новой функции widehat{f} ) «поставить на любое место». Или, говоря точнее, можно определить семейство функций $widehat{f}_i,~i=overline{1,n}$ , с фиктивным переменным так, что

$widehat{f}_i(x_1,ldots,y,x_i,ldots,x_n)= f(x_1,ldots,x_n)cdot (ylor overline{y}).$

Понятие фиктивного переменного позволяет также произвольные две булевы функции рассматривать как функции от одного и того же числа переменных.

Действительно, пусть функция f(x_1,ldots,x_n) есть функция от переменных, а функция g(y_1,ldots,y_m) — функция от переменных. Обозначим множества переменных функции и через и соответственно. Расширим множество переменных функции до Xcup Y , вводя переменные из Ysetminus Y (если они существуют) как фиктивные. Точно так же поступим с функцией , добавляя фиктивные переменные из множества Xsetminus Y (если, конечно, оно не пусто). Тогда получим функции и , равные, согласно определению 6.2, функциям и соответственно и определенные как функции от одного и того же числа переменных, составляющего мощность объединения множеств |Xcup Y| .

Нетрудно распространить описанную конструкцию на произвольное конечное множество булевых функций и считать тем самым все функции этого множества функциями от одного и того же числа переменных.

Проектирующая функция

В заключение рассмотрим понятие проектирующей функции.

Функцию $operatorname{pr}_i$ от переменных, такую, что $operatorname{pr}_i(x_1,ldots,x_i,ldots,x_n)=x_i,,$ называют (i-й) проектирующей функцией. В общем случае нумерация множества переменных может быть явно не задана, и тогда при определении проектирующей функции следует указывать не номер соответствующего переменного, а само переменное. В этом случае проектирующая функция $operatorname{pr}_x^X$ с множеством переменных этой функции и выделенным переменным xin X определяется так:

$operatorname{pr}_x^X(ldots,x,ldots)=x$

(за многоточиями «скрыты» переменные проектирующей функции, отличные от переменного ).

Из определения следует, что проектирующая функция $operatorname{pr}_x^X$ имеет единственное существенное переменное, а именно переменное . Все остальные переменные проектирующей функции являются фиктивными. Поэтому любые две проектирующие функции $operatorname{pr}_x^X$ и $operatorname{pr}_x^Y$ равны, согласно определению 6.2, при любых множествах переменных и , содержащих переменное .

Вместе с тем для двух различных переменных и проектирующие функции $operatorname{pr}_x^X$ и $operatorname{pr}_x^Y$ — разные функции. Так, $operatorname{pr}_1(x_1,x_2)$ — функция, отличная от функции $operatorname{pr}_2(x_1,x_2)$ поскольку, например, $operatorname{pr}_1(1,0)=1,~ operatorname{pr}_2(1,0)=0$ .

Впредь договоримся любую из множества равных между собой проектирующих функций $operatorname{pr}_x^X$ обозначать символом ее единственного существенного переменного.

Замечание 6.3. Такое обозначение проектирующих функций есть условность и определенная вольность, состоящая в том, что проектирующая функция $operatorname{pr}_x^X$ как бы отождествляется с самим переменным . Однако отождествление функции и переменного недопустимо, так как понятие переменного, хоть и связано с понятием функции, никак не есть частный случай понятия функции. Переменное — только имя, некое обозначение, которое используется при аналитическом задании функции, но никак не сама функция. Тем не менее ради краткости, мы сохраним обозначение как обозначение любой из проектирующих функций $operatorname{pr}_x^X$ и будем использовать иногда даже выражение «функция «, понимая под этим любую из указанного семейства проектирующих функций.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Скачать материал

Сейчас обучается 140 человек из 43 регионов

Сейчас обучается 75 человек из 34 регионов

Описание презентации по отдельным слайдам:

1 слайд

Существенные и фиктивные переменные
2 слайд

Определение
Говорят, что булева функция f(x1, …, xi, …, xn) существенно зависит от переменной xi, если выполняется условие:
f(x1, …, xi-1,0,xi+1, …, xn) ≠ f(x1, …, xi-1,1,xi+1, …, xn).
В этом случае также говорят, что переменная xi существенная, в противном случае ее называют фиктивной переменной.
Другими словами, переменная является несущественной, если ее изменение не изменяет значения функции
3 слайд

Пример 1. Рассмотрим булеву функцию f(x1, x2, x3) и исследуем ее переменные x1 и x3.
Из таблиц истинности видно, что переменная x1 функции f(x1, x2, x3) существенная, так как f(0,x2, x3) ≠ f(1,x2, x3). Переменная x3 фиктивная, так как f(x1, x2, 0) = f(x1, x2, 1).
4 слайд

Алгоритм распознавания фиктивной переменной по таблице истинности.
– Для переменной x1 сравниваются половины столбца значений функции: верхняя и нижняя, так как именно в верхней половине x1=0, а в нижней x1=1, если они совпадают, то переменная x1 фиктивна;
– для переменной x2 сравниваются четвертины столбца в каждой половине, так как именно в верхних четвертинах x2 =0, а в нижних x2 =1, если четвертины в каждой половине совпадают, то переменная x2 фиктивна;
– и так далее (за четвертинами следуют 1/8, 1/16, … ).
5 слайд

Пример 1. Булева функция f(x1, x2, x3)
Переменная x1 существенна, так как верхняя половина столбца значений функции (0011) не равна нижней половине (1100).
Переменная x2 существенна, так как четвертины уже в первой половине различаются (00 и 11).
Переменная x3 фиктивна, так как осьмушки во всех четвертинах равны (0 и 0, 1 и 1, 1 и 1, 0 и 0).
6 слайд

Достаточное условие отсутствия фиктивных переменных
Если вес вектора-столбца значений функции нечетен, то функция не может содержать фиктивных переменных.
7 слайд

Алгоритм удаления фиктивной переменной
Алгоритм удаления фиктивной переменной xi состоит в вычеркивании из таблицы истинности всех строк, в которых xi = 0 (или всех строк, в которых xi = 1), и столбца xi.
Пример (функция та же). Применив алгоритм для удаления фиктивной переменой x3, получаем результат
8 слайд

Пример
Определение.
Булевы функции назовем равными с точностью до фиктивных переменных, если равны функции, полученные из исходных удалением фиктивных переменных
Рассмотрим функции f1(x1, x2) и f2(x1, x2).
Удалив фиктивную переменную x1 функции f1(x1, x2) и фиктивную переменную x2 функции f2(x1, x2), получим равные функции f1(x2)=f2(x1)=f(x).
Значит, исходные функции равны с точностью до фиктивных переменных.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 264 580 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

Рейтинг:
5 из 5

11.12.2016
1008
10

11.12.2016
528
0

11.12.2016
494
2

11.12.2016
642
0

Рейтинг:
5 из 5

11.12.2016
811
1

11.12.2016
1304
17

11.12.2016
549
0

Вам будут интересны эти курсы:

Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Источник

Теоретические обоснования

Есть булевы функции, которые не меняют
своих значений при изменении значений
некоторых своих переменных. Например,
на значение функции

(см. табл. 2.4) не влияет значение переменной
,
поскольку
,
,
а на значение функции

не влияет значение переменной
,
поскольку
,
.
Переменные, значения которых не влияют
на значения функции, называют фиктивными.
Определим это понятие строго.

Определение. Переменная

называется фиктивной переменной
функции
,
если на всех наборах

значений переменных

выполняются равенства

В противном случае переменная

называется существенной, т.е. переменная

называется существенной переменной
функции
,
если найдется такой набор

значений переменных
,
что

Чтобы определения фиктивной и существенной
переменных легче было усвоить, адаптируем
их к каким-нибудь частным случаям.
Например,
определим

как фиктивную переменную функции
:
переменная

называется фиктивной переменной функции
,
если выполняются четыре равенства:
,
,
,
.

Теперь определим

как существенную переменную функции
:
переменная

называется существенной переменной
функции
,
если хотя бы одно из равенств
,
,
,

не выполняется.

Фиктивные переменные не влияют на
значения функции и с этой точки зрения
являются «лишними», поэтому естественно
поставить вопрос об их удалении.

Операция удаления (введения) фиктивных
переменных. Пусть для функции

переменная

является фиктивной. Возьмем таблицу
истинности функции
.
Вычеркнем из нее все строки, в которых
,
а также вычеркнем столбец переменной
.
Полученная таким образом таблица
будет задавать некоторую функцию
,
причем на любом наборе

значений переменных

для функций

и

выполнено равенство
.
О функции

говорят, что она получена из функции

путем удаления фиктивной переменной,
а о функции

говорят, что она получена из функции

путем введения фиктивной переменной.

Если одну функцию можно получить из
другой путем введения или удаления
фиктивных аргументов, то они считаются
равными.

Пример 7. Найти
фиктивные переменные функции и удалить
их:

а)
; б)
.

◄ а) Для наглядности рассуждений
построим таблицу истинности функции
(табл. 2.12).

Таблица 2.12

0	0	0
0	1	0
1	0	1
1	1	1

:
,
следовательно,

— существенная;

:
и
,
следовательно,

— фиктивная.

Чтобы
удалить фиктивную
переменную
,
нужно вычеркнуть из таблицы
истинности функции второй столбец, а
также третью и пятую строки (они закрашены
серым цветом). В результате получим
таблицу истинности функции
,
равной функции
.

б) Построим таблицу истинности функции
(табл. 2.13).

Таблица 2.13

0	0	0	1
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	1
1	1	0	0
1	1	1	1

:
,
,
,
,
следовательно,

— фиктивная;

:
,
следовательно,

— существенная;

:
,
,
значит,

— существенная.

Чтобы удалить
фиктивную переменную
,
нужно вычеркнуть из таблицы истинности
функции первый столбец и последние
четыре строки (они закрашены серым
цветом). В результате получим таблицу
истинности функции
,
равной функции
.
►

Пример 8. Из
функции

путем введения фиктивной переменной

получить функции
,
,
.

◄ Заготовим шаблон таблицы истинности
функции

(табл. 2.14), отведя первый столбец под
значения переменной
,
второй — под значения
,
третий — под значения
,
четвертый — под значения самой функции.

Значение функции

на каждой паре наборов вида

и

должны совпадать со значением функции

на наборе
.
Значит, в строках, соответствующих
наборам

и
,
надо проставить значение
,
в строках, соответствующих наборам

и
,
—
,
в строках, соответствующих наборам

и
,
—

и, наконец, в строках, соответствующих
наборам

и
,
—
.

Заготовим шаблон таблицы истинности
функции

(табл. 2.15), отведя первый столбец под
значения переменной
,
второй — под значения
,
третий — под значения
,
четвертый — под значения самой функции.
Столбец значений функции

заполним, исходя из того, что на каждой
паре наборов вида

и

значение функции

должны совпадать со значением функции

на наборе
.

Заготовим шаблон таблицы истинности
функции

(табл. 2.16), отведя первый столбец под
значения переменной
,
второй — под значения
,
третий — под значения
,
четвертый — под значения самой функции.
Столбец значений функции

заполним, исходя из того, что на каждой
паре наборов вида

и

значение функции

должны совпадать со значением функции

на наборе
.
►

Таблица 2.14		Таблица 2.15		Таблица 2.16

0	0	0	0		0	0	0	0	0	0	0	0
0	0	1	1		0	0	1	1	0	0	1	0
0	1	0	0		0	1	0	0	0	1	0	1
0	1	1	0		0	1	1	1	0	1	1	1
1	0	0	0		1	0	0	0	1	0	0	0
1	0	1	1		1	0	1	0	1	0	1	0
1	1	0	0		1	1	0	0	1	1	0	0
1	1	1	0		1	1	1	0	1	1	1	0

Удаление фиктивных переменных упрощает
дальнейшую работу с функцией. Однако
в некоторых случаях фиктивные переменные
полезно не удалять, а вводить. Дело в
том, что, выполнив такую операцию
неоднократно, можно перейти от данной
функции к функции, которая ей равна и
при этом зависит от любого наперед
заданного числа переменных (большего
исходного). Благодаря этому, рассматривая
одновременно несколько функций, можно
считать их зависящими от одного и того
же множества переменных (в качестве
такого множества можно взять объединение
множеств переменных всех этих функций).

Имея в виду вышесказанное, будем в
дальнейшем придерживаться следующих
договоренностей.

1.
Если число переменных специально
не оговаривается, функции рассматриваются
с точностью до фиктивных переменных,
т.е. предполагается, что с заданием
некоторой функции

заданы все равные ей функции, и для
обозначения равных функций используется
один и тот же функциональный символ.

2. При рассмотрении любой системы функций
будем предполагать (если не оговорено
противное), что все функции данной
системы зависят от одного числа
переменных. Такой подход позволит
избежать громоздких рассуждений.

Например, при
желании вместо системы функций
,
,

можно рассматривать систему равных им
функций
,
.

В первой части параграфа мы ввели на
описательном уровне понятия формулы
над множеством функций и функции,
заданной формулой. Теперь формализуем
эти понятия.

Пусть

— некоторое множество булевых функций,
—
некоторое счетное множество переменных.
Используя индукцию, определим множество
формул над

с переменными из
.
Одновременно будем определять числовую
характеристику

формулы
,
называемую ее глубиной, а также
множество ее подформул.

Определение. Базис
индукции. Каждая переменная

из

и каждая константа

из

является формулой глубины 0, т.е.
.
Множество подформул формулы
глубины 0 состоит из нее самой.

Индуктивный переход.
Пусть

— функция из
,

— формулы и
.
Тогда выражение

является формулой, ее глубина

равна
,
а множество подформул

включает саму формулу

и все подформулы
.

Используя индукцию по глубине формулы,
определим функцию, заданную формулой.

Определение. Базис
индукции. Пусть
.
Тогда

имеет вид
,
где

— переменная из
,
или
,
где

— константа из
.
В первом случае

задает тождественную функцию
,
во втором — функцию, тождественно равную
константе
.

Индуктивный переход.
По предположению индукции каждой
формуле глубины

сопоставлена некоторая функция. Пусть

— произвольная формула глубины
.
Следовательно, она имеет вид
,
где

— функция из
,

— формулы, для которых
,
и, значит, по предположению индукции
этим формулам уже сопоставлены некоторые
функции
,
,…,
.
Тогда формула

задает функцию

,
значение которой на каждом наборе

находится как значение функции

на наборе
.

Заметим, что, определяя индуктивно
функцию, заданную формулой, мы
воспользовались договоренностью
рассматривать функции с точностью до
фиктивных переменных и считали все
функции системы

зависящими от

переменных.

Зададимся вопросом: можно ли по виду
формулы, которой задана функция,
определить, какие из переменных этой
функции существенны, а какие фиктивны?
Очевидно, если функция задана формулой,
в которую некоторая переменная не
входит, то эта переменная фиктивная.
Обратное утверждение в общем случае
неверно, т.е. в формуле, задающей функцию,
могут присутствовать как существенные,
так и фиктивные переменные этой функции.
Убедимся в этом на примерах.

Пример 9. Указать
существенные и фиктивные переменные
функции

◄ Вначале упростим формулу, которой
задается функция, используя равносильность
:

Таким образом, значение функции
определяется исключительно значением
переменной
,
причем
,
Значит,

— существенная,

— фиктивные.►

Соседние файлы в папке discretka_1

Источник

Ключевым понятием в теории булевых функцuй является понятие равных булевых функций. Для функций от одного и того же числа переменных n нет необходимости рассматривать какое-
то специальное определение равенства, ибо такие функции
равны, если они совпадают как отображения булева куба Bⁿ в
В. Проблема состоит в том, чтобы определить равенство булевых
функций независимо от числа переменных.

Пример 6.4. Рассмотрим булевы функции f(x,y) =x ∨ y и
g(x,y,z) = xz ∨ xz ∨ yz ∨ yz.

Можно заметить, используя тождества булевой алгебры,
что

g(x,y,z) = (x ∨ y)(z ∨ z),

а поскольку z ∨ z = 1, то

g(x,y,z) = (х ∨ y) = f(x,y),

и функции f и g естественно рассматривать как равные, несмотря на то что они зависят от разного числа переменных. #

В примере 6.4 функция g определена как функция от трех
переменных, но значение переменного z не влияет на значение
функции. Обобщая ситуацию примера, можно ввести понятие
фиктивного переменного булевой функции.

Определение 6.1. Переменное x_i называют фиктивным
переменным булевой функции f(x₁, … ,x_n), если значение
функции не зависит от значения этого переменного, т .е.
если для любых значений переменных х₁, … , x_i-1, х_i+1, … , x_n

f(х₁, … , x_i-1, 0, х_i+1, … , x_n) = f(х₁, … , x_i-1, 1, х_i+1, … , x_n).

Будем называть переменное х, не являющееся фиктивным
переменным функции f, существенным переменным данной
функции и говорить, что функция f существенно зависит
от переменного х.

Пусть дана булева функция у = f(x₁, … ,x_n) от n переменных.
Пусть существенными переменными этой функции являются
переменные x_i₁, … ,x_{i_r}, где r ≤ n и 1 ≤ i₁<…r ≤ n.
Присваивая каждому фиктивному переменному функции f произвольное значение, получим функцию f, такую, что она есть функция от r переменных, т.е. есть отображение из B^r в В, и для любого набора α_i₁, … , α_{i_r} значенuй переменных x_i₁, …, x_{i_r}
имеет место равенство

f˜(α_i₁ , … ,α_{i_r}) = f(x₁, …, α_i₁, … ,α_{i_r},…,x_n)

независимо от значений фиктивных переменных функции f
(т.е. переменных, отличных от x_i₁ , …, x_{i_r}). Тем самым функция
f оказывается уже функцией, определенной на некоторой
r-мерной грани булева куба Bⁿ.

Договоримся только что описанный переход от функции f к
функции f, уже не имеющей фиктивных переменных, называть
удалением фиктивных переменных (функции f).

Замечание 6.2. В качестве упомянутой вьппе r-мерной
грани может быть взята любая грань с направлением, заданным
номерами фиктивных переменных. Фиксация грани означает
фиксацию конкретного набора значений фиктивных переменных.
Тогда соответствующая этой грани функция f получается
из исходной функции f в результате подстановки вместо каждого
фиктивного переменного того конкретного значения,
которое задано указанным вьппе набором.

Вернемся к примеру 6.4. Удаляя фиктивное переменное z,
вместо функции g получим либо функцию g(x,y,O), которая
определена на (двумерной) грани B^3,30 булева куба В³ , либо
функцию g(x,y,1), определенную на грани B^3,31 . Направлением
каждой из этих граней будет однокомпонентный кортеж (3),
определенный номером фиктивного переменного z. #

С использованием понятий фиктивного и существенного переменного
можно дать следующее определение равных булевых
функций.

Определение 6.2. Булевы функции f и g называют равными,
если их существенные переменные соответственно равны
и на каждом наборе значений этих переменных функции f
и g принимают равные значения.

Чтобы распознать по таблице булевой функции, является
ли переменное x_i фиктивным, нужно рассмотреть все наборы с
фиксированным значением i-й компоненты (один раз фиксировав это значение как 0, другой раз — как 1). Из определения 6.1 ясно, что переменное x_i фиктивно тогда и только тогда, когда
для любых двух наборов, отличающихся только значением i-й
компоненты, функция принимает равные значения.

Пример 6.5. а. Из табл. 6.4 следует, что мажоритарная
функция не имеет фиктивных переменных, так как, например,
f(0,0,1) = 0, а f(1,0,1) = 1, т.е. переменное х₁ существенное.
Далее, f(1,0,0) = 0, но f(1,1,0) = 1, что означает существенность
переменного х₂; для х₃ имеем f(1,0,0) = 0, но f(1,0,1) = 1,
что означает существенность и этого переменного.

б. Ниже приведена таблица функции g от четырех переменных
(табл. 6.5). Рекомендуется проверить, что переменное х₂
являетеся фиктивным и что остальные переменные существенны.
Более того, анализ таблицы показывает, что эта функция
есть не что иное, как мажоритарная функция, существенно зависящая от переменных х₁, х₃ и х₄. #

Кроме процедуры удаления фиктивных переменных используют
и процедуру добавления к множеству переменных булевой
функции одной или нескольких фиктивных переменных. Так,
если дана функция f(x₁, … ,x_n) ∈ P_2,n, то можно ввести новоефиктивное переменное у, определив новую, равную исходной,
согласно определению 6.2, функцию от n + 1 переменного таким
образом:

(см. пример 6.4).

Следует заметить, что фиктивное переменное можно (в
новой функции «поставить на любое место». Или, говоря
точнее, можно опред елить семейство функций с
фиктивным переменным у так, что

Понятие фиктивного переменного позволяет также произвольные
две булевы функции рассматривать как функции от
одного и того же числа переменных.

Действительно, пусть функция f(х₁, …, x_n) есть функция
от n переменных, а функция g(y₁, …, y_m) — функция от m переменных.
Обозначим множества переменных функции f и g
че рез Х и У соответственно. Расширим множество переменных
функции f до Х ∪ У, вводя переменные из УХ ( если они
существуют) как фиктивные. Точно так же поступим с функцией
g, добавляя фиктивные переменные из множества ХУ
(если, конечно, оно не пусто). Тогда получим функции и
, равные, согласно определению 6.2, функциям f и g соответственно
и определенные как функции от одного и того же числа
переменных, составляющего |X ∪ Y|.

В заключение рассмотрим понятие проектирующей функции.

Функцию pr_i от n переменных, такую, что

pr_i(x₁,…,x_i,…,x_n) = x_i,

называют (i-й) проектирующей функцией. В общем случае
нумерация множества переменных может быть явно не задана,
и тогда при определении проектирующей функции следует
указывать не номер соответствующего переменного, а само
переменное. В этом случае проектирующая функция pr^Xx c множеством переменных Х этой функции и выделенным переменным
х ∈ Х определяется так:

pr^Xx
(…,х,…) = х

(за многоточиями «скрыты» переменные проектирующей функции,
отличные от переменного х).

Из определения следует, что проектирующая функция pr^Xx имеет единственное существенное переменное, а именно переменное
х. Все остальные переменные проектирующей функции
являются фиктивными. Поэтому любые две проектирующие
функции pr^Xx и pr^Yx равны, согласно определению 6.2, при любых
множествах переменных Х и У, содержащих переменное х.

Вместе с тем для двух различных переменных х и у проектирующие функции pr^Xx и pr^Yx — разные функции. Так,
pr₁(x₁,x₂) — функция, отличная от функции pr₂(x₁,x₂), поскольку,
например, pr₁(1,0) = 1, pr₂(1,0) =0.

Впредь договоримся любую из множества равных между
собой проектирующих функций pr^Xx обозначать символом х ее единственного существенного переменного.

Замечание 6.3. Такое обозначение проектирующих функций
есть условность и определенная вольность, состоящая в
том, что проектирующая функция pr^Xx как бы отождествляется с самим переменным х. Однако отождествление функции и переменного
недопустимо, так как понятие переменного, хоть и
связано с понятием функции, никак не есть частный случай понятия функции. Переменное — только имя, некое обозначение, которое используется при аналитическом задании функции, но
никак не сама функция. Тем не менее ради краткости, мы
сохраним обозначение х как обозначение любой из проектирующих
функций pr^Xx и будем использовать иногда даже выражение «функция х», понимая под этим любую из указанного
семейства проектирующих функций.

Источник

Вход в систему

Навигация

Последние комментарии

О существенных и фиктивных переменных булевых функций

Равенство булевых функций. Фиктивные переменные

Проектирующая функция

Описание презентации по отдельным слайдам:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Другие материалы

Вам будут интересны эти курсы:

Теоретические обоснования