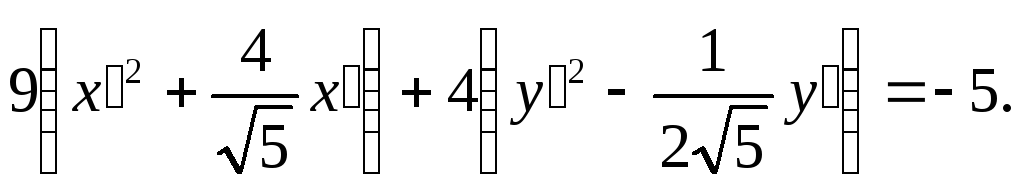Как найти фокальные радиусы точки - Исправление недочетов и поиск решений вместе с Examum.ru

Эллипс – это замкнутая плоская кривая, сумма расстояний от каждой точки до двух точек равняется постоянной величине.

Что такое эллипс и фокусное расстояние

Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна .

Обозначим фокусы эллипса $F_{1}$ и $F_{2}$ . Допустим, что расстояние $F_{1}{F_{2}}$ = – фокусное расстояние.

Рис. 1

$F_{1}, F_{2}$ – фокусы .

$F_{1} = (c, 0)$ ; $F_{2} = (- c ; 0)$ ,

– половина расстояния между фокусами;

– большая полуось;

– малая полуось.

Теорема:

Фокусное расстояние и полуоси связаны соотношением:

Если точка находится на пересечении эллипса с вертикальной осью, $r_{1} + r_{2} = 2 * sqrt{b^2 + c^2}$ (теорема Пифагора). Если же точка находится на пересечении его с горизонтальной осью, $r_1} + r_{2} = a - c + a + c$ . Так как по определению сумма $r_{1} + r_2}$ – постоянная величина, то приравнивая получается:

$a^2 = b^2 + c^2to{r_{1} + r_{2} = 2a$ .

Уравнение эллипса

Уравнение элиппса бывает двух видов:

Каноническое уравнение эллипса.
Параметрическое уравнение эллипса.

Сначала рассмотрим каноническое уравнение эллипса:

Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:

$1 = {x^2over{a^2}} + {y^2over{b^2}}$

Если центр эллипсa смещен в точку с координатами $(x_{0}, y_{0})$ тогда уравнение:

$1 = {(x - x_{0})^2over{a^2}} + {(y - y_{0})^2over{b^2}}$

Чтобы получить каноническое уравнение эллипса, разместим $F_{1}$ и $F_{2}$ на оси симметричной к началу координат. Тогда у фокусов будут такие координаты $F_{2}(-c, 0)$ и $F_{2}(c, 0)$ (см. рис. 2).

Пусть – произвольная точка эллипса. Обозначим через $r_{2}$ и $r_{1}$ – расстояние от точки к фокусам. Согласно с определением эллипса:

$r_{1} + r_{2} = 2a$

(1)

Рис. 2

Подставим в (1) $r_{1} = F_{1}M = sqrt{(x - c)^2 + (y - 0)^2}$ , $r_{2} = sqrt{(x + c)^2 + y^2}$ и освободимся от иррациональности, подняв обе части к квадрату, получим:

$r_{2} = 2a - r_{1}tosqrt{(x + c)^2 + y^2} = 2a - sqrt{(x - c)^2 + y^2}}to{x^2 + 2cx + c^2 + y^2} = 4a^2 - 4asqrt{(x - c)^2) + y^2} + x^2 - 2cx + c^2 + y^2to{4a}sqrt{(x - c^2 + y^2} = 4a^2 - 4cxarrowvert:4$

$asqrt{(x - c)^2 + y^2} =a^2 - cx$

(подносим к квадрату обе части): $to{a^2x^2 - 2ca^2x + a^2c^2 + a^2y^2} = {a^4 - 2ca^2x + c^2x^2to{(a^2 - c^2)x^2 + a^2y^2 = a^2(a^2 - c^2)arrowvert:a^2(a^2 - c^2)$ ,

${x^2over{a^2}} + {y^2over{a^2 - c^2}} = 1$

Обозначим: , получаем каноническое уравнение эллипса:

${x^2over{a^2}} + {y^2over{b^2}} = {1}$

(2)

Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из $Delta{F_{1}}MF_{2}$ у нас получается $F_{2}M + F_{1}M > F_{1}F_{2}to{r_{1} + r_{2}} > 2c$ . Так как $r_{1} + r_{2} = 2a$ , тогда , и поэтому .

Для построения эллипса обратим внимание, что если точка $M_{1}(x, y)$ принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки $M_{2}(-x, y), M_{3}(-x, -y), M_{4}(x, -y)$ тоже удовлетворяют это уравнение: из

${x^2over{a^2}} + {y^2over{b^2}} = 1to{(pm{x})^2over{a^2}} + {(pm{y})^2over{b^2}} = {1}$ .

Точки $M_{1}, M_{2}, M_{3}, M_{4}$ – расположены симметрично относительно осей координат. Значит, эллипс – фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.

Из уравнения (2) находим $y = pm{{b}over{a}}sqrt{a^2 - x^2$ , для первой четверти ${y} = {bover{a}}sqrt{a^2 - x^2}$ .

Если , тогда . Если же , тогда . Точки $A_{1}(a, 0)$ и $B_{1}(0, b)$ , а также симметричные с ними $A_{2}(-a, 0)$ , $B_{2}(0, -b)$ – вершины эллипса, точка – центр эллипса, $A_{1}A_{2}$ = большая ось, $B_{1}B_{2} = 2b$ – малая ось эллипса.

Если первой четверти, тогда из $y = {bover{a}}sqrt{a^2 - x^2$ получается, что при возрастании от к значение падает от к . (рис. 3)

Параметрическое уравнение выглядит так:

$left{ begin{aligned} x = a{cos}alpha\ y = b{sin}alpha end{aligned}quad {0leqalpha < 2pi right$

Основные свойства эллипса

Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.

1. Угол между касательной к эллипсу и фокальным радиусом $r_{1}$ равен углу между касательной и фокальным радиусом $r_{2}$ .

2. Уравнение касательной к эллипсу в точке с координатами $(x_{M}, y_{M})$ :

$1 = {x x_{M}over{a^{2}}} + {y y_{M}over{b^{2}}}$ .

3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).

4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.

5. Если вписать эллипс с фокусами $F_{1}$ и $F_{2}$ у треугольника , тогда выполняется соотношение:

= ${{overline{F_{1}A} * overline{F_{2}A}}over{overline{CA} * overline{AB}}} + {{overline{F_{1}B} * overline{F_{2}B}}over{overline{AB} * overline{BC}}} + {{overline{F_{1}C} * overline{F_{2}C}}over{overline{BC} * overline{CA}}}$

Эксцентриситет эллипса

Эксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначается

Значения эксентриситета характеризует степень “сплющенность” эллипса. Если , тогда $c = {sqrt{a^2 + b^2}} = 0to{varepsilon = 0}$ – получается круг. Если же , тогда – эллипс превращается в отрезок. В некоторых случаях . Для фокальных радиусов приведём без доказательства такие формулы:

$left{ begin{aligned} r_{1} = a - varepsilon{x},\ r_{2} = a + varepsilon, end{aligned} quad{xin[-a, a]. right$

Рис. 3

Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси и , тогда вычислим $c = {sqrt{a^2 + b^2}}$ – полуфокусное расстояние.

Строим фокусы $F_{1}$ и $F_{2}$ на расстоянии один от другого Концы не растянутой нити длиной закрепляем в точках $F_{1}$ и $F_{2}$ . Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.

Примеры решения задач

Задача

Задан эллипс уравнением ${x^2over{25}} + {y^2over{9}} = 1$ и точки $M_{0}(4; 1,8), M_{1}(3; 2,4)$ . Необходимо:

убедиться, что точки $M_{0}$ и $M_{1}$ лежат на эллипсе;
найти полуоси эллипса и координаты его фокусов;
найти расстояние от точки $M_{0}$ к фокусам;
убедиться, что сумма этих расстояний равна длине большой оси;
найти эксентриситет эллипса.

Решение

1. Подставим координаты точки $M_{0}$ в левую часть уравнения эллипса:

${x^2over{25}} + {y^2over{9}} = {4^2over25}} + {1,8 * 1,8over{9}} = {16over25}} + {36over{100}} = {16over{25}} + {9over25}} = 1$ – точка $M_{0}$ лежит на эллипсе. Аналогично для $M_{1}(3; 2,4)$ :

точка $M_{1}$ лежит на эллипсе.

2. С канонического ${x^2over{a^2}} + {y^2over{b^2}} = {1}$ и данного уравнения ${x^2over{25}} + {y^2over{9}} = 1$ эллипса выходит: $a^2 = {25},quad{b^2 = 9}to{a = 5, b = 3}.$ Из равенства получается:

$b^2 = a^2 - c^2to {c^2 = a^2 - b^2 = 25 - 9} = {16}to{c = 4}$ – полуфокусное расстояние. Координаты фокусов $F_{1}(4; 0)$ и $F_{2}(-4; 0)$ .

3. Найдём фокальные радиусы точки $M_{0}$ :

$r_{2} = F_{2}M_{0} = sqrt{(4 - (-4))^2 + 1,8^2} = sqrt{64 + 3,24} = sqrt{67,24} = 8,2$

$r_{1} = F_{1}M_{0} = sqrt{(4 - 4)^2 + 1,8^2} = 1,8.$

4. Найдём сумму $r_{1} + r_{2} = 1, 8 + 8.2 = 10 = 2 * 5 = 2a$ , что отвечает определению эллипса.

5. Эксцентриситет находится по формуле .

Задача

Найти оси, вершины и фокусы эллипса

Решение

Сведём обычное уравнение к каноническому:

$169x^2 + 25y^2 - 4225 = 0to{x^2over{25}} + {y^2over{169}} = 1$

, $b^2 = 169to{a = 5, b = 13}$ . Вершины эллипса в точках $A_{1}(5, 0)$ , $B_{1}(0, 13)$ , $A_{2}(-5, 0)$ , $B_{2}(0, -13)$ . Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае больше, чем , то эллипс, который вытянут вдоль оси , находим полуфокусное расстояние $c = sqrt{b^2 - a^2} = sqrt{169 - 25} = sqrt{144} = 12$ .

Фокусы в точках $F_{1}(0, 12)$ и $F_{2}(0, -12)$ . (см. рис. 3)

Рис. 4

Найти оси, вершины и фокусы эллипса $25x^2 + 144y^2 = 3600quad{:}arrowvertto{25x^2over{3600}} + {144y^2over{3600}} = {1}to{x^2over{144}} + {y^2over{25}} = {1}$ или ${X^2over{12^2}} + {y^2over{5^2}} = {1}$ . Построить эллипс.

Сравнивая последнее уравнение с уравнением (2), у нас получается:

, $b^2 = 5^2to{a = 12, b = 5}$ . Откуда находим оси эллипса: , и координаты вершин: $A_{1}(12, 0)$ , $A_{2} (-12, 0)$ , $B_{1}(0, 5)$ , $B_{2}(0, -5)$ . Дальше из формулы:

$b^2 = a^2 - c^2to{c^2 = a^2 - b^2 = 144 - 25 = 119}to{c = sqrt{119}}approx{10,91}$ . Значит, фокусами эллипса есть точки: $F_{1}(sqrt{119}, 0)$ и $F_{2}(-sqrt{119}, 0)$ . Для построения эллипса отложим на осях и вершины $A_{1}, B_{1}, A_{2}, B_{2}$ соответственно соединим их плавной линией, (см. задачу 1).

Замечание! Если в каноническом уравнении ${x^2over{a^2}} + {y^2over{b^2}} = {1}$ большей полуосью будет , тогда фокусы эллипса будут расположены на оси и тогда $c = sqrt{b^2 - a^2}$ .

Источник

Кривые второго порядка

Контрольные
вопросы:

Окружность.
Эллипс.
Гипербола.
Парабола.
Общее уравнение
кривой второго порядка.

1. Окружность
– это множество всех точек плоскости,
равноудаленных от данной точки (центра)
на данное расстояние.

Если R
– радиус окружности, точка С—
ее центр, то уравнение окружности имеет
вид

. (8)

Пример
4. найти
координаты центра и радиус окружности
.

Решение.

Разделим исходное
уравнение на 2, сгруппируем выражения
относительно х
и у:

Дополним выражения,
стоящие в скобках до полных квадратов:

или

Таким образом,
координаты центра окружности
,
радиус окружности равен.

2.
Эллипсом
называется множество всех точек
плоскости, сумма расстояний которых до
двух данных точек, называемых фокусами,
есть величина постоянная (ее обозначают
через 2а),
причем эта постоянная больше расстояния
между фокусами.

Если оси координат
расположены по отношению к эллипсу так,
как на рисунке 11, а фокусы эллипса
находятся на оси Ох
на равных расстояниях от начала координат
в точках
и,
то получится простейшее (каноническое)уравнение
эллипса:

. (9)

Здесь а
– большая, b
– малая полуось, причем а,
b
и с (с
– половина расстояния между фокусами)
связаны соотношением
.

Рис. 6

Форма эллипса
(мера его сжатия) характеризуется его
эксцентриситетом
.

Расстояния
некоторой точки эллипса М от его фокусов
называются фокальными
радиус-векторами
этой точки. Их обычно обозначают
и.
Для любой точки эллипса в силу определения.

Фокальные
радиус-векторы выражаются через абсциссу
точки эллипса по формулам:
(правый фокальный радиус-вектор),(левый фокальный радиус-вектор).

3.
Гиперболой
называется множество всех точек
плоскости, абсолютная величина разности
расстояний которых до двух данных точек,
называемых фокусами,
есть величина постоянная (ее обозначают
через 2а),
причем эта постоянная меньше расстояния
между фокусами.

Если поместить
фокусы гиперболы в точках
и,
то получимканоническое
уравнение гиперболы

, (10)

где
.
Гипербола состоит из двух ветвей и
расположена симметрично относительно
осей координат. Точкииназываются вершинами гиперболы. Отрезоктакой, что,
называетсядействительной
осью гиперболы,
а отрезок
такой, что,
—мнимой осью.
При этом
.

Прямая называется
асимптотой
гиперболы, если расстояние точки М(х;у)
гиперболы этой прямой стремится к нулю
при
или.
Гипербола имеет две асимптоты, уравнения
которых.

На рисунке 7 указано
взаимное расположение гиперболы и ее
асимптот. Отношение
называетсяэксцентриситетом
гиперболы.

Рис.7

Фокальные
радиус-векторы правой ветви гиперболы:
(правый фокальный радиус-вектор),(левый фокальный радиус-вектор).

Фокальные
радиус-векторы левой ветви гиперболы:
(правый фокальный радиус-вектор),(левый фокальный радиус-вектор).

4.
Параболой
называется множество всех точек
плоскости, равноудаленных от данной
точки, называемой фокусом,
и данной прямой, называемой директрисой.

Если директрисой
параболы является прямая
,
а фокусом – точка,
то уравнение параболы имеет вид

. (11)

Эта парабола
расположена симметрично относительно
оси абсцисс (рис. 8, где
).
Приветви параболы обращены в положительную
сторону.

Рис. 8

Длина фокального
радиус-вектора параболы
определяется по формуле().

5.
Общее уравнение кривой второго порядка
имеет вид

, (12)

где A,
B,
C,
D,
E,
F
– произвольные действительные числа.
Оно определяет на плоскости Оху
эллипс, гиперболу или параболу (с
возможными случаями распада и вырождения
этих кривых) с осями симметрии,
параллельными осям координат:

1) если
,
тогда определяемая этим уравнением
кривая есть эллипс (действительный,
мнимый или выродившийся в точку);

если
,
тогда соответствующая кривая является
гиперболой;
если
,
тогда уравнение определяет параболу.

Если кривая второго
порядка задана уравнением (12) то, применив
преобразование поворота осей координат
с использованием формул

,
,
(13)

следует при
соответствующем выборе α освободиться
в уравнении от члена с произведением
координат и свести исходное уравнение
к одному из трех вышеперечисленных
типов.

Пример 5.
Привести к каноническому виду уравнение

Решение.

1. Преобразуем
данное уравнение, использовав формулы
поворота осей координат:

или

Найдем α из условия
,
т.е. приравняем к нулю коэффициент при.
Получим уравнение.
Отсюда,.

Заметим, что эти
значения
соответствуют двум взаимно перпендикулярным
направлениям. Поэтому, взяввместо,
мы только меняем ролями осии(рис. 9).

Рис. 9

Пусть
,
тогда,;
возьмем положительные значенияsinα
и cosα.
Тогда уравнение принимает вид

или

2. Выражения, стоящие
в скобках, дополним до полных квадратов:

или

Приняв за новое
начало точку
,
применим формулы преобразования
координат,
получим

или
(уравнение эллипса).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

(схема 21)

Эллипсом называется
геометрическое место точек плоскости, сумма расстояний от каждой из которых до
двух данных точек этой плоскости, называемых
фокусами, есть величина постоянная, равная 2a.

Обозначим фокусы через F₁ и F₂,
расстояние между ними через 2c, а сумму расстояний от произвольной точки эллипса до
фокусов – через 2a. По определению 2a>2c, то есть a>c .

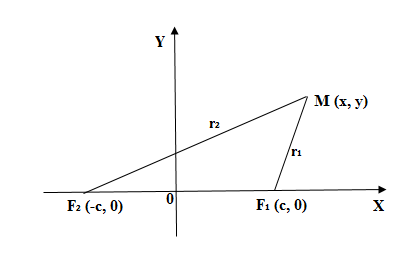
Выберем систему координат
так, чтобы
фокусы F₁ и F₂
лежали на оси 0x, а начало координат совпадало с серединой отрезка F₁F₂. Тогда фокусы имют координаты: F₁(–c;0) и F₂(c;0). Пусть M(x;y) –
произвольная точка эллипса (текущая точка). Тогда по определению эллипса можно записать

По сути, мы получили уравнение эллипса. Упростим его с помощью ряда несложных математических преобразований:

Так как, a>c, то a²–c²>0, то можно обозначить a²–c²=b². Тогда
последнее уравнение имеет вид:

(2.17)

Это
уравнение равносильно первоначальному. Оно называется каноническим уравнением
эллипса – кривой
второго порядка.

Установим форму эллипса, пользуясь его каноническим
уравнением.

1. Уравнение (2.17) содержит x и y
только в четных степенях, поэтому
если точка (x;y)
принадлежит эллипсу, то
ему также принадлежат
точки (–x;y), (x;–y), (–x;–y). Отсюда: эллипс симметричен относительно осей 0x и 0y, а также
относительно точки O(0;0), которую называют центром эллипса.

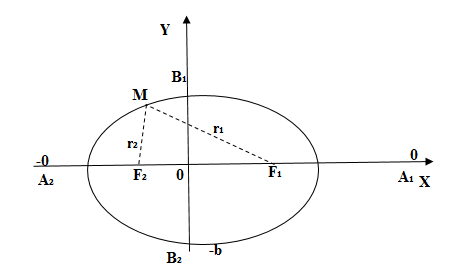
2. Найдем точки пересечения эллипса с осями координат.
Положив y=0, найдем точки A₁(a;0) и A₂(–a;0), в которых ось 0x пересекает эллипс. Положив в уравнении
(2.17) x=0, находим точки пересечения эллипса с осью 0y: B₁(0;b) и B₂(0;–b). Точки A₁, A₂, B₁, B₂ называются вершинами эллипса. Отрезки А₁А₂,
В₁В₂, а также
их длины 2a и 2b – соответственно большая и малая оси эллипса (рис. 2.4).

3. Из уравнения (2.17) следует, что каждое слагаемое в
левой части не превосходит единицы,
т.е.:

Следовательно, все точки эллипса лежат внутри
прямоугольника, ограниченного прямыми x= ± a
и y= ± b.

4. В уравнении (2.17) левая часть – сумма
неотрицательных слагаемых, т.е. при возрастании одного слагаемого другое будет
уменьшаться, если |x| возрастает, |y|
уменьшается и наоборот.

Из сказанного следует, что эллипс имеет форму
овальной замкнутой кривой. Форма эллипса зависит от отношения. При a=b эллипс превращается в окружность, уравнение эллипса
(2.17) принимает вид: x²+y²=a². Отношение половины расстояния между фокусами к большой полуоси эллипса – эксцентриситет эллипса . Причем
0<ε<1, так как 0<c<a.

Отсюда видно, что чем меньше эксцентриситет эллипса,
тем будет менее эллипс сплющенным; при ε=0 эллипс
превращается в окружность.

Пусть M(x;y) – произвольная точка эллипса с фокусами F₁ и F₂. Длины
отрезков |MF₁|=r₁ и |MF₂|=r₂ – фокальные
радиусы точки M, r₁+r₂=2a. Имеют место формулы: r₁=a+εx и r₂=a – εx.

Прямые – директрисы
эллипса.

Если r – расстояние от произвольной точки до какого–нибудь фокуса,
d –
расстояние от этой же точки до соответствующей этому фокусу директрисы (рис. 2.5), то отношениеесть величина
постоянная, равная эксцентриситету эллипса: .

Из равенства a²–c²=b²
следует, что a>b. Если же
наоборот, то уравнение (2.17) определяет эллипс, большая ось которого 2b лежит на
оси 0y, а малая ось 2a – на оси 0x. Фокусы такого
эллипса находятся в точках F₁(0;c) и F₂(0;–c), где . Данный эллипс будет растянут вдоль оси 0y.

Пример 2.5. Составить уравнение линии, для каждой точки
которой отношение расстояний от нее до
точки A(3;0) и до прямой x=12, равно числу ε=0,5. Полученное
уравнение привести к простейшему виду.

Решение. Пусть M(x;y) – текущая (произвольная) точка искомого
геометрического множества точек. Опустим перпендикуляр MB на прямую

. Тогда точка B(12;y). По условию задачи
.

По формуле расстояния между
двумя точками получаем:

Отсюда

Полученное уравнение представляет собой эллипс вида где, согласно формуле (2.17).

Определим фокусы эллипса F₁(–c;0) и F₂(c;0). Для эллипса справедливо равенство b²=a²–c²,
откуда c²=a²–b² =9 и c=3. То есть,
F₁(–3;0) и F₁(3;0)–
фокусы эллипса (точки F₂ и A совпадают).

Эксцентриситет эллипса

Примечание. Если эллипс (окружность) вращать вокруг одной из его
осей, то описываемая им поверхность будет эллипсоидом вращения (сферой)

Пример 2.6. В геодезии используется система географических координат,
основанная на понятии геоида. Геоид – поверхность Земли,
ограниченная уровенной поверхностью, продолженной под континенты. Поверхность
геоида отличается от физической поверхности Земли, на которой резко выражены
горы и океанические впадины.

Тело, поверхность которого более всего соответствует
поверхности геоида, имеет определенные размеры и ориентирована соответственно в
теле Земли, называется референц–эллипсоидом. В нашей стране с 1946 года для всех
геодезических работ принят референц–эллипсоид Красовского с
параметрами a=6 378 245 м, b=6 356 863 м, α=1: 298,3.

Линия, проходящая вертикально через центр эллипсоида
является полярной осью. Линия, проходящая через центр эллипсоида,
перпендикулярно к полярной оси, – экваториальной осью. При пересечении
поверхности эллипсоида плоскостью, проходящей через его центр, перпендикулярно
к полярной оси, образуется окружность, называемая экватором. Окружность,
полученная от пересечения поверхности эллипсоида плоскостью, параллельной
плоскости экватора, называется параллелью. Линия пересечения
поверхности эллипсоида с плоскостью, проходящей через заданную точку и полярную
ось, называется меридианом данной точки. Положение точки на земной поверхности
определяется пересечением параллели и меридиана, проходящих через нее. Угол φ между плоскостью экватора и отвесной
линией называется географической широтой. Для определения долгот
точек один из меридианов (Гринвичский) принимают за начальный или нулевой. Угол
λ, составленный плоскостью меридиана,
проходящего через данную точку, и плоскостью начального меридиана, называется
географической долготой

Гипербола – геометрическое место точек плоскости, модуль разности расстояний от
каждой из которых до двух данных точек этой плоскости – фокусов, есть величина
постоянная, равная 2a.

Обозначим фокусы через
F₁ и F₂, расстояние между ними через 2c, а модуль
разности расстояний от каждой точки
гиперболы до фокусов через 2a. По определению 2a<2c, то есть a<c.

Выберем систему координат x0y так, чтобы фокусы F₁ и F₂лежали на оси 0x, а начало координат совпало с серединой отрезка F₁F₂. Тогда фокусы будут иметь координаты F1(c;0) и F₂(–c;0). На этой основе выведем уравнение гиперболы. Пусть M(x;y) – ее произвольная точка. Тогда по определению |MF₁–MF₂|=2a, то есть. Проведя преобразования, аналогичные упрощениям уравнения эллипса, получим каноническое уравнение гиперболы:

, (2.18)

где
b²=a²–c².
Гипербола – линия 2–го порядка.

Установим форму гиперболы, исходя из ее канонического
уравнения.

1. Уравнение (2.18) содержит x и y только в
четных степенях. Следовательно, гипербола симметрична относительно осей координат
0x и 0y, и относительно точки O(0;0) – центра гиперболы.

2. Найдем точки пересечения гиперболы с осями координат. Положив в
уравнении (2.18) y=0, находим две точки пересечения гиперболы с осью 0x: A₁(a;0) и A₂(–a;0).

Положив в (2.18) x=0, получаем y²= – b²,
чего быть не может. Т.е. гипербола ось 0y не пересекает.

Точки A₁(a;0) и A₂(–a;0) – вершины гиперболы, а отрезок |A₁A₂|=2a – действительная ось. Отрезок |B₁B₂|=2b,
соединяющий точки B₁(0;b) и B₂(0;–b) – мнимая ось (рис. 2.6). Прямоугольник
со сторонами 2a и 2b – основной
прямоугольник гиперболы.

3. Из уравнения (2.18) следует, что уменьшаемое . Это означает, что точки гиперболы расположены справа
от прямой x=a (правая
ветвь гиперболы) и слева от прямой x=–a (левая
ветвь) (рис. 2.6).

4. Из уравнения (2.18) гиперболы видно, что
когда |x| возрастает, то |y| также
возрастает. Это
следует из того, что разность –
сохраняет значение, равноe единице. Следовательно, гипербола имеет форму,
состоящую из двух неограниченных ветвей.

Прямая L называется асимптотой некоторой неограниченной кривой, если расстояние d от точки M этой кривой до прямой L стремится к нулю при неограниченном
удалении точки M вдоль кривой
от начала координат.

Покажем, что гипербола имеет две асимптоты: . Так как
данные прямые и гипербола (2.18) симметричны относительно координатных
осей, то достаточно рассмотреть только точки, расположенные в первой четверти.

Возьмем на прямой точку N, имеющую
ту же абсциссу, что и точка M(x;y) на гиперболе . Найдем разность |MN|:

Очевидно: так как числитель есть величина постоянная, а знаменатель дроби увеличивается с возравстанием переменной х, то длина отрезка |MN| стремится
к нулю. Так как |MN| больше
расстояния d от точки M до прямой L, то d стремится к нулю тем более (и подавно). Следовательно, прямые

– есть
асимптоты гиперболы (рис. 2.7).

Построение гиперболы начинают с нанесения ее основного прямоугольника на координатную плоскость. Далее проводят диагонали этого прямоугольника, которые являются асимптотами гиперболы, затем отмечают ее вершины, фокусы и строят ветви гиперболы.

Эксцентриситет гиперболы –
отношение расстояния между фокусами к величине её действительной оси,
обозначается ε: . Так
как у гиперболы c>a, то
эксцентриситет ее больше единицы. Эксцентриситет характеризует форму гиперболы. Так как . Видно, что чем меньше
эксцентриситет гиперболы, тем меньше отношение ее полуосей, а
значит, тем более вытянут ее основной прямоугольник.

Эксцентриситет
равносторонней гиперболы равен . Действительно, . Фокальные радиусы

для точек
правой ветви гиперболы имеют вид: r₁=εx+a, r₂=εx–a; для точек
левой ветви: r₁=–(εx+a), r₂=–(εx–a).

Прямые называются директрисами
гиперболы. Тот факт, что для гиперболы ε>1, то означает: правая директриса расположена между центром и правой вершиной гиперболы,
левая – между центром и левой вершиной. Директрисы
гиперболы имеют тоже свойство , что и директрисы эллипса.

Уравнение определяет гиперболу с действительной осью 2b, расположенной на оси 0y, и мнимой осью 2a, расположенной на оси абсцисс (подобная гипербола изображена
на рисунке 2.7 пунктиром).

Значит, гиперболы
и
имеют общие
асимптоты. Такие гиперболы называются сопряженными.

Примечание. Если у кривой 2–го порядка смещен центр в некоторую
точку O’(x₀;y₀), то она
называется нецентральной кривой. Уравнение такой кривой имеет вид:

Примечание. При вращении гиперболы вокруг ее действительной оси
образуется двуполостный гиперболоид, вокруг ее мнимой оси – однополостный гиперболоид

Подробно данные уравнения рассмотрены в теме:
«Исследование общего уравнения 2–ой степени» (смотри схему 10), частными
случаями которого являются данные формулы.

Вопросы
для самопроверки

Источник

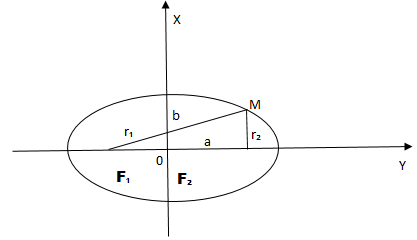
Эллипсом называют плоскую кривую, состоящую из точек, сумма расстояний которых от двух определённых точек плоскости является неизменной, строго заданной величиной, равной суммарной длине двух больших его полуосей (2a). Эти две точки называются фокусами эллипса.

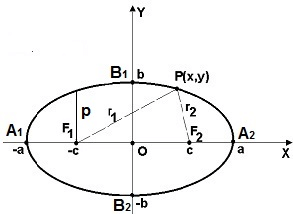
F₁ и F₂ – фокусы эллипса;

а – большая полуось;

b – малая полуось

с – фокусное расстояние

Теорема

Фокусное расстояние эллипса и его полуоси связаны между собой соотношением [boldsymbol{a^{2}=b^{2}+c^{2}}]

Доказательство:

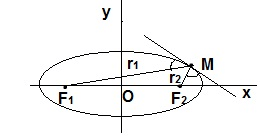
Когда точка M на линии эллипса находится на его пересечении с вертикальной осью, из теоремы Пифагора выходит, что

r₁ + r₂ = 2*√(b² + c²)

Когда точка M пересекает горизонтальную ось

r₁ + r₂ = а – c + а + c

По определению эллипса r₁ + r ₂= const

Это позволяет после приравнивания получить

a² = b² + c²

r₁ + r₂ = 2а

Что и требовалось доказать.

Уравнение эллипса

Каноническим уравнением эллипса называют уравнение [boldsymbol{1=left(x^{2} / a^{2}right)+left(y^{2} / b^{2}right)}]

Доказательство уравнения:

Введём прямоугольную декартову систему координат.

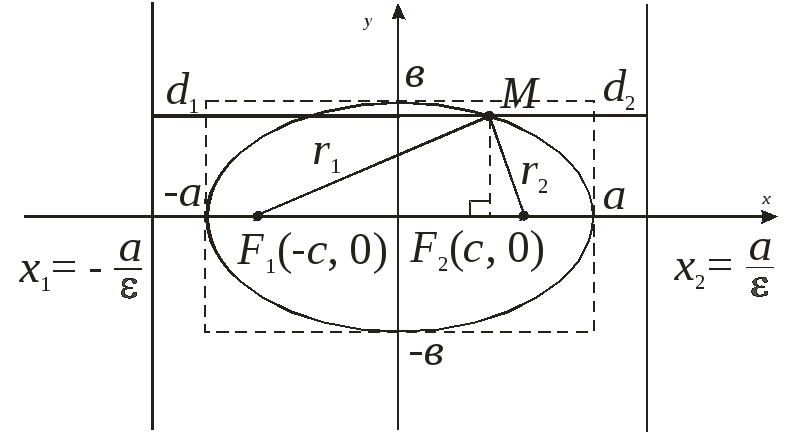
Сначала докажем, что координаты любой из точек на эллипсе удовлетворяют приведённому каноническому уравнению. Затем покажем, что любое из решений уравнения является координатами точки, лежащей на линии эллипса. Из этого будет следовать удовлетворение каноническому уравнению только тех точек, которые лежат на поверхности эллипса. Опираясь на этот факт и на определение эллипса можно будет однозначно сделать вывод, что написанное нами уравнением является каноническим уравнением или, как ещё говорят, основной формулой эллипса.

Пусть М(х, у) будет точкой эллипса, т.е. сумму её фокальных радиусов примем равной 2а, т. е. r₁ + r₂ = 2a.
С помощью формулы расстояния, разделяющего две точки на координатной плоскости, можно легко найти фокальные радиусы точки M.
r₁ = √[(x + c)² + y²]
r₂ = √[(x — c)² + y²]

Из этих уравнений получаем √[(x + c)² + y²] + √[(x — c)² + y²] = 2a

Если один из корней перенести в правую часть и возвести всё в квадрат, то придём к выражению
(x + c)² + y² = 4a² – 4a√[(x — c)² + y²] + (x – c)² + y²

После сокращения приходим к 2xc = 4a² – 4a√[(x-c)² + y²] – 2xc
После приведения подобных членов, сокращения на 4 и уединения радикала будем иметь
a√[(x-c)² + y²] = a² – xc

Возведём это выражение в квадрат
a²(x-c)² + a² y2 = a⁴ – 2a²xc + x²c²

Если раскрыть скобки и сократить на -2a² xc, то a²x² + a²c² + a²y² = a⁴ + x²c²
Отсюда легко получить (a² – c²)x² + a²y² = a²(a² – c²)
Из этого следует, что b²x² +a²y² = a²b²
Пусть некоторые числа (x, y) полностью удовлетворяют каноническому уравнению
1 = (x²/a²) + (y²/b²)
Пусть нам дана точка M(x,y) на координатной плоскости 0xy
Из канонического уравнения следует, что Y² = b²(1- x²/a²)
Если это равенство подставить в выражение для фокальных радиусов, которые имеет точка M, то можно получить
r₁ = √[(x + c)² +y²] = √[x²+2xc + c² +b²– b²x²/a²] = √[x²(1 – b²/a²) + 2xc +c² +b²] =
= √[x²(a² – b²)/a² + 2xc + (c² + b²)] = √[x²(c²/a²) + 2xc +a²] = √[x(c/a) +a]² = |a +xε|
т. е. r₁= |a +xε|
Отношение 2с/2a = c/a = ε называется эксцентриситетом эллипса. Оно у него всегда меньше 1.
То же самое просчитываем для r_2.
Т. к. x²/a² больше или равно 1 или x больше или равно большой полуоси (a), то можно сделать вывод о справедливости неравенства a≥|x|> |x|* ε = |xε|
Отсюда явно следует, что a+-|xε|>0 или a+-xε > 0 и r₁= a + xε, r₂ = a — xε
Из полученных равенств выходит, что r₁ + r₂ = 2a, это значит, что точка M однозначно является точкой эллипса. Это нам и нужно было доказать.

Свойства эллипса

У эллипса имеются две взаимно перпендикулярные оси симметрии.

Доказательство:
Переменные x и y в уравнение эллипса входят лишь во второй степени. Это означает, что если точка M с координатами (x,y) ему принадлежит, то и точки М₁(-x, y) и M₂ (x, -y) тоже принадлежат ему. Легко проверить, что указанные координаты удовлетворяют каноническому уравнению эллипса. M₁ симметрична по отношению к оси X, а M₂по отношению к оси Y. Получается, что у эллипса есть две взаимно перпендикулярные точки симметрии.
У эллипса есть центр симметрии.

Доказательство:
Если координаты точки М(x,y) будут удовлетворять уравнению эллипса, то и точка
N (–x; –y) ему тоже будет удовлетворять. M и N симметричны по отношению к началу координат. Это как раз и означает, что у эллипса имеется центр симметрии.
Эллипс пересекает каждую из осей в двух точках.

Доказательство:
Возьмём произвольную точку эллипса M(x,y). Расстояние этой точки до фокусов будет
r₁ = √[(x + c)² + y²]
r₂ = √[(x — c)² + y²]

Теперь давайте рассмотрим выражение

(x+-c)² + y² = x²+- 2xc + c²+ y² =
= x²+- 2xc + a² – b²+y² = x²+- 2xc+ a²— b² + b²(1-x²/a²) =
= (a² – b²)*x²/a² +-2xc +a² = c²*x²/a²+-2xa(c/a) + a² = (a +c*x/a)²

Эксцентриситет эллипса, как сказано ранее, меньше 1. Т. к. |x|≤ a, то a – εx > 0. Поэтому
F₁M = a + εx и F₂M = a – εx. Напомним, что ε – это эксцентриситет эллипса.

А теперь несколько свойств эллипса без доказательств.

Эллипс можно получить, сжав окружность.
Если через эллипс проходят две прямые, то отрезок, концами которого являются середины отрезков созданных при пересечении прямых, обязательно пересекает середину, центр эллипса.
Угол, созданный касательной к эллипсу и его радиусом, проходящем через фокусы указанной геометрической фигуры, в любых случаях пересекает середину эллипса.
Уравнение касательной к эллипсу в точке М, имеющей координаты x_M и y_M
1 = (x*x_M)/a² + (y*y_M)/b²
Эволюта эллипса представляет собой астероиду, растянутую вдоль его малой оси.
Угол между касательной к эллипсу и одним его фокальным радиусом (r₁) имеет ту же величину, что и угол, разделяющий касательную и другой фокальный радиус (r₂) фигуры.

Как построить эллипс

Расскажем, как построить эллипс по его большой и малой полуосям и с помощью циркуля.

Построение эллипса по его большой и малой осям

Считается самым простым, не требующим серьёзных навыков.

Проведите две перпендикулярные оси;

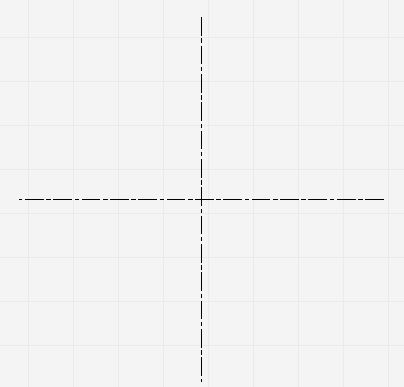
От места пересечения осей на вертикальной отложите верх и вниз отрезки. Они будут составлять малую ось эллипса. На горизонтальной отложите отрезки вправо и влево. Из них будет состоять большая ось;

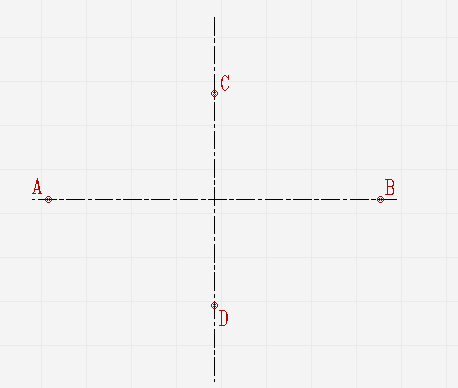
Проведите две концентрические окружности. Одну диаметром AB, диаметром CD;

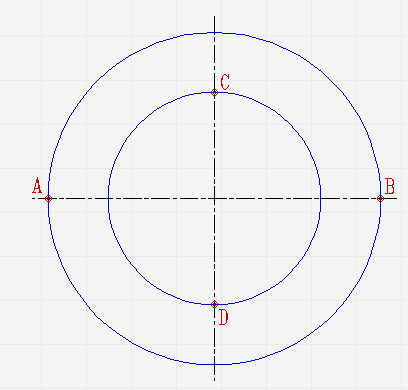
Проведите ещё диаметры в различных направлениях;

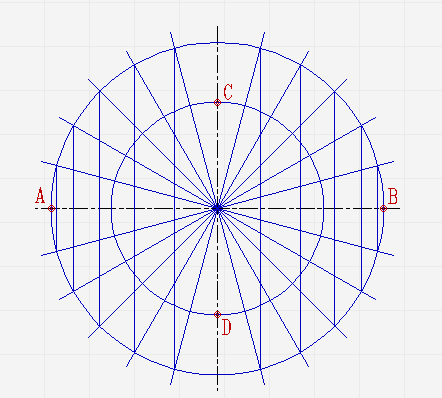
В местах, где лучи соприкасаются с окружностями, проведите линии параллельные малой и большой осям эллипса, пока они не пересекутся в точках, которые принадлежат эллипсу;

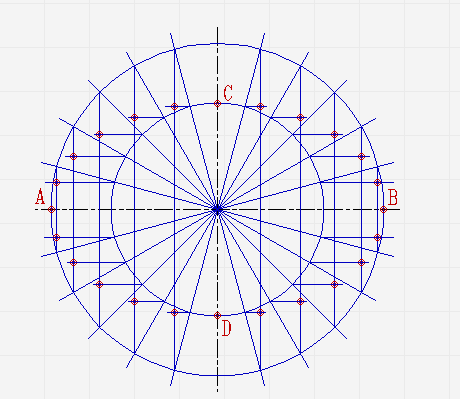
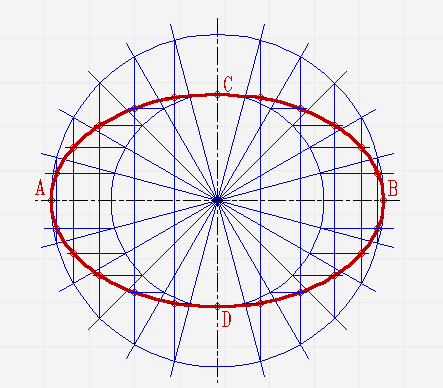
Соедините полученные точки плавной линией.

Нет времени решать самому?

Наши эксперты помогут!

Как построить эллипс с помощью циркуля

Во многом здесь всё аналогично предыдущему способу, поэтому перегружать текст иллюстрациями не будем.

Порядок действий следующий:

Проведите две перпендикулярные линии. Они будут осями эллипса, а точка их пересечения центром геометрической фигуры;
Определитесь с величиной большой и малой полуосей, если их значения не заданы в условии задачи;
Установите раствор циркуля на длину большой полуоси (a). Поместите циркуль в точку O и отметьте на одной из линий две точки, P₁и P₂. Установите раствор циркуля на длину малой полуоси. Опять поместите его в точку O и отметьте на другой из линий ещё две точки, обозначьте их как Q₁ и Q₂. Отрезки P₁P₂ и Q₁Q₂ будут большой и малой полуосями будущего эллипса;
Установите раствор циркуля на величину a. Поместите циркуль в точке Q₁или Q₂. После этого обозначьте циркулем на отрезке P₁P₂точки F_{1 и}F₂. Это будут фокусы фигуры.
Отметьте на P₁P₂любую точку и обозначьте её T. Поставьте в этой точке циркуль и измерьте этим инструментом расстояние до P₁. Затем начертите окружность данного радиуса из фокуса F₁. После этого нужно сделать ещё одну окружность с радиусом величиной с расстояние от T до P₂, но уже с центром из F₂;
Отметьте точки, в которых пересекаются обе окружности. Повторяйте процедуру, описанную в предыдущем пункте с новыми точками, отмечаемыми на отрезке P₁P₂;
Соедините точки пересечения окружностей сплошной линией, когда построите их достаточное количество. Так у вас получится построить фигуру эллипс с помощью циркуля.

Примеры решения задач

Задача 1

Эллипс задан уравнением 16x² + 25y² = 400. Требуется найти большую и малую полуоси эллипса, координаты его фокусов и эксцентриситет.

Решение:

Разделим полученное уравнение на 400. Этим мы приведём его к виду

(x²/25) + (y²/16) =1. Большая полуось равна 5, корню квадратному из 25, а малая 4, корню квадратному из 16.

Из соотношения a² = b² + c² находим фокусное расстояние. Оно равно

c=+-√(a² – b²) = +-√(25-16) = +-3, а значит координаты фокусов будут

F₁(-3,0)и F₂(3,0). Эксцентриситет ε = с/a = 3/5.

Ответ: a = 5, b = 4, ε = 3/5.

Задача 2

Выяснить, является ли эллипсом линия, заданная как

9x² + 25y² – 225 = 0

Преобразуем данное нам уравнение к каноническому виду. Для этого:

Перенесём 225 в правую сторону

9x² + 25y² = 225

Поделим обе части этого уравнения на 225

(9x²/225) + (25y²/225) = 1

Сократим дроби и получим

(x²/25) + (y²/9) = 1

Как видим, нам удалось получить каноническое уравнение эллипса в чистом виде, т. е. исходное уравнение представляет собой эллипс, что и требовалось выяснить.

Ответ: 9x² + 25y² – 225 = 0 является уравнением эллипса.

Задача 3

Составить каноническое уравнение эллипса если расстояние между фокусами равно 8, а большая ось 10.

Решение:

Если большая ось равняется 10, значит полуось будет 5.

Если фокусное расстояние равно 8, то число c из координат фокусов будет 4.

Далее нужно подставить и вычислить

4 = √(25-b²)

Возведём это уравнение в квадрат

16 = 25 – b²

Перенесём b² влево, а 16 вправо

b² = 25 – 16 =9

В результате этих не сложных преобразований и вычислений получим каноническое уравнение

(x²/25) + (y²/9) = 1

Ответ: (x²/25) + (y²/9) = 1.

Задача 4

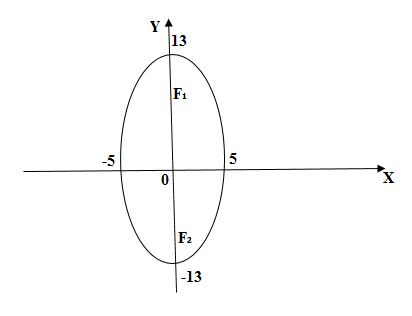
Получить каноническое уравнение эллипса, если его эксцентриситет равен 12/13, а большая полуось равна 26.

Решение:

Из уравнения эксцентриситета ε = с/a находим, что a = 13, а величина с = 12. Далее нужно вычислить квадрат длины меньшей полуоси

c = √(169 – b²)

Возведём обе части уравнения в квадрат

c² = 169 – b²

Отсюда

b² = 169 – 144 = 25

Далее остаётся лишь составить каноническое уравнение

(x²/169) + (y²/25) = 1

Ответ: (x²/169) + (y²/25) = 1

Задача 5

Найти фокусы у эллипса, который задан уравнением (x²/25) + (y²/16) = 1

Решение:

Нам нужно найти число с, которое определяет первые координаты фокусов

c = √(25-16) =3

Фокусы заданного эллипса будут равны

F₁(-3,0) и F₂(3,0).

Ответ: F₁(-3,0) и F₂(3,0).

Источник