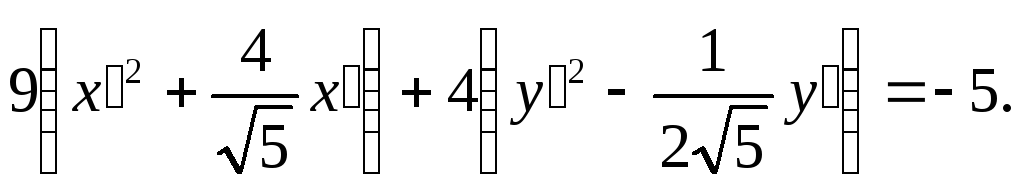Как найти фокальный радиус параболы

Кривые второго порядка

Контрольные
вопросы:

1. Окружность.

2. Эллипс.

3. Гипербола.

4. Парабола.

5. Общее уравнение
   кривой второго порядка.

1. Окружность
– это множество всех точек плоскости,
равноудаленных от данной точки (центра)
на данное расстояние.

Если R
– радиус окружности, точка С—
ее центр, то уравнение окружности имеет
вид

. (8)

Пример
4. найти
координаты центра и радиус окружности
.

Решение.

Разделим исходное
уравнение на 2, сгруппируем выражения
относительно х
и у:

.

Дополним выражения,
стоящие в скобках до полных квадратов:

или

.

Таким образом,
координаты центра окружности
,
радиус окружности равен.

2.
Эллипсом
называется множество всех точек
плоскости, сумма расстояний которых до
двух данных точек, называемых фокусами,
есть величина постоянная (ее обозначают
через 2а),
причем эта постоянная больше расстояния
между фокусами.

Если оси координат
расположены по отношению к эллипсу так,
как на рисунке 11, а фокусы эллипса
находятся на оси Ох
на равных расстояниях от начала координат
в точках
и,
то получится простейшее (каноническое)уравнение
эллипса:

. (9)

Здесь а
– большая, b
– малая полуось, причем а,
b
и с (с
– половина расстояния между фокусами)
связаны соотношением
.

Рис. 6

Форма эллипса
(мера его сжатия) характеризуется его
эксцентриситетом
.

Расстояния
некоторой точки эллипса М от его фокусов
называются фокальными
радиус-векторами
этой точки. Их обычно обозначают
и.
Для любой точки эллипса в силу определения.

Фокальные
радиус-векторы выражаются через абсциссу
точки эллипса по формулам:
(правый фокальный радиус-вектор),(левый фокальный радиус-вектор).

3.
Гиперболой
называется множество всех точек
плоскости, абсолютная величина разности
расстояний которых до двух данных точек,
называемых фокусами,
есть величина постоянная (ее обозначают
через 2а),
причем эта постоянная меньше расстояния
между фокусами.

Если поместить
фокусы гиперболы в точках
и,
то получимканоническое
уравнение гиперболы

, (10)

где
.
Гипербола состоит из двух ветвей и
расположена симметрично относительно
осей координат. Точкииназываются вершинами гиперболы. Отрезоктакой, что,
называетсядействительной
осью гиперболы,
а отрезок
такой, что,
—мнимой осью.
При этом
.

Прямая называется
асимптотой
гиперболы, если расстояние точки М(х;у)
гиперболы этой прямой стремится к нулю
при
или.
Гипербола имеет две асимптоты, уравнения
которых.

На рисунке 7 указано
взаимное расположение гиперболы и ее
асимптот. Отношение
называетсяэксцентриситетом
гиперболы.

Рис.7

Фокальные
радиус-векторы правой ветви гиперболы:
(правый фокальный радиус-вектор),(левый фокальный радиус-вектор).

Фокальные
радиус-векторы левой ветви гиперболы:
(правый фокальный радиус-вектор),(левый фокальный радиус-вектор).

4.
Параболой
называется множество всех точек
плоскости, равноудаленных от данной
точки, называемой фокусом,
и данной прямой, называемой директрисой.

Если директрисой
параболы является прямая
,
а фокусом – точка,
то уравнение параболы имеет вид

. (11)

Эта парабола
расположена симметрично относительно
оси абсцисс (рис. 8, где
).
Приветви параболы обращены в положительную
сторону.

Рис. 8

Длина фокального
радиус-вектора параболы
определяется по формуле().

5.
Общее уравнение кривой второго порядка
имеет вид

, (12)

где A,
B,
C,
D,
E,
F
– произвольные действительные числа.
Оно определяет на плоскости Оху
эллипс, гиперболу или параболу (с
возможными случаями распада и вырождения
этих кривых) с осями симметрии,
параллельными осям координат:

1) если
,
тогда определяемая этим уравнением
кривая есть эллипс (действительный,
мнимый или выродившийся в точку);

1. если
   ,
   тогда соответствующая кривая является
   гиперболой;

2. если
   ,
   тогда уравнение определяет параболу.

Если кривая второго
порядка задана уравнением (12) то, применив
преобразование поворота осей координат
с использованием формул

,
,
(13)

следует при
соответствующем выборе α освободиться
в уравнении от члена с произведением
координат и свести исходное уравнение
к одному из трех вышеперечисленных
типов.

Пример 5.
Привести к каноническому виду уравнение

.

Решение.

1. Преобразуем
данное уравнение, использовав формулы
поворота осей координат:

или

Найдем α из условия
,
т.е. приравняем к нулю коэффициент при.
Получим уравнение.
Отсюда,.

Заметим, что эти
значения
соответствуют двум взаимно перпендикулярным
направлениям. Поэтому, взяввместо,
мы только меняем ролями осии(рис. 9).

Рис. 9

Пусть
,
тогда,;
возьмем положительные значенияsinα
и cosα.
Тогда уравнение принимает вид

или

2. Выражения, стоящие
в скобках, дополним до полных квадратов:

или

.

Приняв за новое
начало точку
,
применим формулы преобразования
координат,
получим

или
(уравнение эллипса).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Hint: When your parabola is written in the form $y=a(x-h)^2+k$ for constants $a,k,h$, the focal length $f$ is related to the constant $a$ by: $a=frac{1}{4f}$.

Your equation is not in this form, but as a further hint I’ll remind you that it’s OK to swap the x’s and the y’s.

---

Alternatively you can learn «the hard way» by using the definition of the parabola with focus and diretrix. According to the definition of the parabola, the points on the parabola are equidistant from the focus and directrix. If you set up an equation to express the distance between a point $(x_0,y_0)$ on the parabola and call the focus $(f,0)$, you should be able to derive:

$$
sqrt{(x_0-f)^2+y_0^2}=x_0+f
$$

Then you would be able to solve this for $f$.

583 Составить уравнение параболы,
вершина которой находится в начале координат,
зная, что: 583.1 парабола
расположена в правой полуплоскости, симметрично
относительно оси Ох и ее параметр р=3; 583.2 парабола
расположена в левой полуплоскости симетрично
относительно оси Ох и ее параметр р=0,5. 583.3 парабола
расположена в верхней полуплоскости симметрично
относительно оси Оу и ее параметр р=1/4. 583.4 парабола
расположена в нижней полуплоскости симметрично
оси Оу и ее параметр р=3. 584 Определить
величину параметра и расположение относительно
координатных осей следующих парабол: 584.1  ; 584.2  ; 584.3  ; 584.4 . 585 Составить
уравнение параболы, вершина которой находится в
начале координат, зная, что: 585.1 парабола
расположена симметрично относительно оси Ох и
проходит через точку А(9; 6); 585.2 парабола
расположена симметрично относительно оси Ох и
проходит через точку В(-1; 3); 585.3 парабола
расположена симметрично относительно оси Оу и
проходит через точку С(1; 1); 585.4 парабола
расположена симметрично относительно оси Оу и
проходит через точку D(4; -8). 586 Стальной трос
подвешен за два конца; точки крепления
расположены на одинаковой высоте; расстояние
между ними равно 20 см. Величина его прогиба на
расстоянии 2 м от точки крепления, считая по
горизонтали, равна 14,4 см. Определить величину
прогиба этого троса в середине между точками
крепления, приближенно считая, что трос имеет
форму дуги параболы. 587 Составить
уравнение параболы, которая имеет фокус Е(0; -3) и
проходит через начало координат, зная, что ее
осью служит ось Оу. 588 Установить, какие
линии определяются следующими уравнениями.
Изобразить эти линии на чертеже. 588.1 ; 588.2 ; 588.3  ; 588.4 ; 588.5 ; 588.6 ; 588.7 ; 588.8  . 589 Найти фокус F и
уравнение директрисы параболы . 590 Вычислить
фокальный радиус точки М параболы , если
абсцисса точки М равна 7. 591 Вычислить
фокальный радиус точки М параболы , если
ордината точки М равна 6. 592 На параболе найти точки, фокальный радиус
которых равен 13. 593 Составить
уравнение параболы, если дан фокус F(-7; 0) и
уравнение директрисы . 594 Составить
уравнение параболы, зная, что ее вершина
совпадает с точкой (; ), параметр равен p, ось параллельна оси
Ох и парабола простирается в бесконечность: 594.1 в положительном
направлении оси Ох; 594.2 в отрицательном
направлении оси Ох. 595 Составить
уравнение параболы, зная, что ее вершина
совпадает с точкой (; ), параметр равен p, ось параллельна оси
Оу и парабола простирается в бесконечность: 595.1 в положительном
направлении оси Оу (т.е. парабола является
восходящей); 595.2 в отрицательном
направлении оси Оу (т.е. парабола являетя
нисходящей). 596 Установить, что
каждое из следующих уравнений определяет
параболу, и найти ее вершины А, величину
параметра р и уравнение директрисы: 596.1 ; 596.2 ; 596.3 ; 596.4 . 597 Установить, что
каждое из следующих уравнений определяет
параболу, и найти координаты ее вершины А и
величину параметра р: 597.1 ; 597.2 ; 597.3 . 598 Установить, что
каждое из следующих уравнений определяет
параболу, и найти ее вершины А и величину
параметра р: 598.1 ; 598.2 ; 598.3 . 599 Установить, какие
линии определяются следующими уравнениями: 599.1 ; 599.2 ; 599.3 ; 599.4 . 600 Составить
уравнение параболы, если даны ее фокус F(4; 3) и
директриса . 601 Составить
уравнение параболы, если даны ее фокус F(4; 3) и
директриса . 602 Составить
уравнение параболы, если даны ее фокус F(2; -1) и
директриса . 603 Даны вершина
параболы А(6; -3) и уравнение ее директрисы . Найти фокус F этой параболы. 604 Даны вершина
параболы А(-2; -1) и уравнение е директрисы . Составить уравнение этой параболы. 605 Определить точки
пересечения прямой и параболы . 606 Определить точки
пересечения прямой и параболы . 607 Определить точки
пересечения прямой и параболы . 608 В следующих случаях
определить, как расположена данная прямая
относительно данной параболы – пересекает ли,
касается или проходит вне ее: 608.1 , ; 608.2 , ; 608.3  , . 609 Определить, при
каких значениях углового коэффициента k прямая : 609.1 пересекает
параболу ; 609.2 касается ее; 609.3 проходит вне этой
параболы. 610 Вывести условие,
при котором прямая касается параболы . 611 Доказать, что к
параболе можно провести одну и
только одну касательную с угловым коэффициентом . 612 Составить
уравнение касательной к параболе в ее
точке М₁(x₁; y₁). 613 Составить
уравнение прямой, которая касается параболы и параллельна прямой . 614 Составить
уравнение прямой, которая касается параболы и перпендикулярна к прямой . 615 Провести
касательную к параболе параллельно
прямой и вычислить расстояние d между этой
касательной и данной прямой. 616 На параболе найти точку М₁, ближайшую к прямой , и
вычислить расстояние d от точки М₁ до этой прямой. 617 Составить
уравнения касательных к параболе , проведенных
из точки А(2; 9). 618 К параболе проведена касательная. Доказать, что
вершина этой параболы лежит посередине между
точкой пересечения касательной с осью Ох и
проекцией точки касания на ось Ох. 619 Из точки А(5; 9)
проведены касательные к параболе . Составить
уравнение хорды, соединяющей точки касания. 620 Из точки Р(-3; 12)
проведены касательные к параболе . Вычислить
расстояние d от точки Р до хорды параболы,
соединяющей точки касания. 621 Определить точки
пересечения эллипса и
параболы . 622 Определить точки
пересечения гиперболы и
параболы . 623 Определить точки
пересечения парабол , . 624 Доказать, что
прямая, касающаяся параболы в некоторой точке М,
составляет равные углы с фокальным радиусом
точки М и с лучом, который, исходя из М, идет
параллельно оси параболы в ту сторону, куда
парабола бесконечно простирается. 625 Из фокуса параболы под острым углом к оси
Ох направлен луч света. Известно, что . Дойдя
до параболы, луч от нее отразился. Составить
уравнение прямой, на которой лежит отраженный
луч. 626 Доказать, что две
параболы, имеющую общую ось и общий фокус,
расположенный между ее вершинами, пересекаются
под прямым углом. 627 Доказать, что если
две параболы со взаимно перпендикулярными осями
пересекаются в четырех точках, то эти точки лежат
на одной окружности.

Парабола: определение, свойства, построение

Параболой называется геометрическое место точек плоскости, равноудаленных от заданной точки и заданной прямой , не проходящей через заданную точку. Это геометрическое определение выражает директориальное свойство параболы.

Директориальное свойство параболы

Точка называется фокусом параболы, прямая — директрисой параболы, середина перпендикуляра, опущенного из фокуса на директрису, — вершиной параболы, расстояние от фокуса до директрисы — параметром параболы, а расстояние от вершины параболы до её фокуса — фокусным расстоянием (рис.3.45,а). Прямая, перпендикулярная директрисе и проходящая через фокус, называется осью параболы (фокальной осью параболы). Отрезок , соединяющий произвольную точку параболы с её фокусом, называется фокальным радиусом точки . Отрезок, соединяющий две точки параболы, называется хордой параболы.

Для произвольной точки параболы отношение расстояния до фокуса к расстоянию до директрисы равно единице. Сравнивая директориальные свойства эллипса, гиперболы и параболы, заключаем, что эксцентриситет параболы по определению равен единице .

Геометрическое определение параболы, выражающее её директориальное свойство, эквивалентно её аналитическому определению — линии, задаваемой каноническим уравнением параболы:

Действительно, введем прямоугольную систему координат (рис.3.45,б). Вершину параболы примем за начало системы координат; прямую, проходящую через фокус перпендикулярно директрисе, примем за ось абсцисс (положительное направление на ней от точки к точке ); прямую, перпендикулярную оси абсцисс и проходящую через вершину параболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат оказалась правой).

Составим уравнение параболы, используя её геометрическое определение, выражающее директориальное свойство параболы. В выбранной системе координат определяем координаты фокуса и уравнение директрисы . Для произвольной точки , принадлежащей параболе, имеем:

где — ортогональная проекция точки на директрису. Записываем это уравнение в координатной форме:

Возводим обе части уравнения в квадрат: . Приводя подобные члены, получаем каноническое уравнение параболы

т.е. выбранная система координат является канонической.

Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.51), и только они, принадлежат геометрическому месту точек, называемому параболой. Таким образом, аналитическое определение параболы эквивалентно его геометрическому определению, выражающему директориальное свойство параболы.

---

Уравнение параболы в полярной системе координат

Уравнение параболы в полярной системе координат (рис.3.45,в) имеет вид

где — параметр параболы, а — её эксцентриситет.

В самом деле, в качестве полюса полярной системы координат выберем фокус параболы, а в качестве полярной оси — луч с началом в точке , перпендикулярный директрисе и не пересекающий её (рис.3.45,в). Тогда для произвольной точки , принадлежащей параболе, согласно геометрическому определению (директориальному свойству) параболы, имеем . Поскольку , получаем уравнение параболы в координатной форме:

что и требовалось доказать. Заметим, что в полярных координатах уравнения эллипса, гиперболы и параболы совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( для эллипса, для параболы, для гиперболы).

---

Геометрический смысл параметра в уравнении параболы

Поясним геометрический смысл параметра в каноническом уравнении параболы. Подставляя в уравнение (3.51) , получаем , т.е. . Следовательно, параметр — это половина длины хорды параболы, проходящей через её фокус перпендикулярно оси параболы.

Фокальным параметром параболы, так же как для эллипса и для гиперболы, называется половина длины хорды, проходящей через её фокус перпендикулярно фокальной оси (см. рис.3.45,в). Из уравнения параболы в полярных координатах при получаем , т.е. параметр параболы совпадает с её фокальным параметром.

---

Замечания 3.11.

1. Параметр параболы характеризует её форму. Чем больше , тем шире ветви параболы, чем ближе к нулю, тем ветви параболы уже (рис.3.46).

2. Уравнение (при ) определяет параболу, которая расположена слева от оси ординат (рис. 3.47,a). Это уравнение сводится к каноническому при помощи изменения направления оси абсцисс (3.37). На рис. 3.47,a изображены заданная система координат и каноническая .

3. Уравнение определяет параболу с вершиной , ось которой параллельна оси абсцисс (рис.3.47,6). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36).

Уравнение , также определяет параболу с вершиной , ось которой параллельна оси ординат (рис.3.47,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36) и переименования координатных осей (3.38). На рис. 3.47,б,в изображены заданные системы координат и канонические системы координат .

4. График квадратного трехчлена является параболой с вершиной в точке , ось которой параллельна оси ординат, ветви параболы направлены вверх (при ) или вниз (при ). Действительно, выделяя полный квадрат, получаем уравнение

которое приводится к каноническому виду , где , при помощи замены и .

Знак выбирается совпадающим со знаком старшего коэффициента . Эта замена соответствует композиции: параллельного переноса (3.36) с и , переименования координатных осей (3.38), а в случае еще и изменения направления координатной оси (3.37). На рис.3.48,а,б изображены заданные системы координат и канонические системы координат для случаев и соответственно.

5. Ось абсцисс канонической системы координат является осью симметрии параболы, поскольку замена переменной на не изменяет уравнения (3.51). Другими словами, координаты точки , принадлежащей параболе, и координаты точки , симметричной точке относительно оси абсцисс, удовлетворяют уравнению (3.S1). Оси канонической системы координат называются главными осями параболы.

---

Пример 3.22. Изобразить параболу в канонической системе координат . Найти фокальный параметр, координаты фокуса и уравнение директрисы.

Решение. Строим параболу, учитывая её симметрию относительно оси абсцисс (рис.3.49). При необходимости определяем координаты некоторых точек параболы. Например, подставляя в уравнение параболы, получаем . Следовательно, точки с координатами принадлежат параболе.

Сравнивая заданное уравнение с каноническим (3.S1), определяем фокальный параметр: . Координаты фокуса , т.е. . Составляем уравнение директрисы , т.е. .

---

Общие свойства эллипса, гиперболы, параболы

1. Директориальное свойство может быть использовано как единое определение эллипса, гиперболы, параболы (см. рис.3.50): геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету , называется:

а) эллипсом, если ;

б) гиперболой, если ;

в) параболой, если .

2. Эллипс, гипербола, парабола получаются в сечениях кругового конуса плоскостями и поэтому называются коническими сечениями. Это свойство также может служить геометрическим определением эллипса, гиперболы, параболы.

3. К числу общих свойств эллипса, гиперболы и параболы можно отнести биссекториальное свойство их касательных. Под касательной к линии в некоторой её точке понимается предельное положение секущей , когда точка , оставаясь на рассматриваемой линии, стремится к точке . Прямая, перпендикулярная касательной к линии и проходящая через точку касания, называется нормалью к этой линии.

Биссекториальное свойство касательных (и нормалей) к эллипсу, гиперболе и параболе формулируется следующим образом: касательная (нормаль) к эллипсу или к гиперболе образует равные углы с фокальными радиусами точки касания (рис.3.51,а,б); касательная (нормаль) к параболе образует равные углы с фокальным радиусом точки касания и перпендикуляром, опущенным из нее на директрису (рис.3.51,в). Другими словами, касательная к эллипсу в точке является биссектрисой внешнего угла треугольника (а нормаль — биссектрисой внутреннего угла треугольника); касательная к гиперболе является биссектрисой внутреннего угла треугольника (а нормаль — биссектрисой внешнего угла); касательная к параболе является биссектрисой внутреннего угла треугольника (а нормаль — биссектрисой внешнего угла). Биссекториальное свойство касательной к параболе можно сформулировать так же, как для эллипса и гиперболы, если считать, что у параболы имеется второй фокус в бесконечно удаленной точке.

4. Из биссекториальных свойств следуют оптические свойства эллипса, гиперболы и параболы, поясняющие физический смысл термина «фокус». Представим себе поверхности, образованные вращением эллипса, гиперболы или параболы вокруг фокальной оси. Если на эти поверхности нанести отражающее покрытие, то получаются эллиптическое, гиперболическое и параболическое зеркала. Согласно закону оптики, угол падения луча света на зеркало равен углу отражения, т.е. падающий и отраженный лучи образуют равные углы с нормалью к поверхности, причем оба луча и ось вращения находятся в одной плоскости. Отсюда получаем следующие свойства:

– если источник света находится в одном из фокусов эллиптического зеркала, то лучи света, отразившись от зеркала, собираются в другом фокусе (рис.3.52,а);

– если источник света находится в одном из фокусов гиперболического зеркала, то лучи света, отразившись от зеркала, расходятся так, как если бы они исходили из другого фокуса (рис.3.52,б);

– если источник света находится в фокусе параболического зеркала, то лучи света, отразившись от зеркала, идут параллельно фокальной оси (рис.3.52,в).

5. Диаметральное свойство эллипса, гиперболы и параболы можно сформулировать следующим образом:

– середины параллельных хорд эллипса (гиперболы) лежат на одной прямой, проходящей через центр эллипса (гиперболы);

– середины параллельных хорд параболы лежат на прямой, коллинеарной оси симметрии параболы.

Геометрическое место середин всех параллельных хорд эллипса (гиперболы, параболы) называют диаметром эллипса (гиперболы, параболы), сопряженным к этим хордам.

Это определение диаметра в узком смысле (см. пример 2.8). Ранее было дано определение диаметра в широком смысле, где диаметром эллипса, гиперболы, параболы, а также других линий второго порядка называется прямая, содержащая середины всех параллельных хорд. В узком смысле диаметром эллипса является любая хорда, проходящая через его центр (рис.3.53,а); диаметром гиперболы является любая прямая, проходящая через центр гиперболы (за исключением асимптот), либо часть такой прямой (рис.3.53,6); диаметром параболы является любой луч, исходящий из некоторой точки параболы и коллинеарный оси симметрии (рис.3.53,в).

Два диаметра, каждый их которых делит пополам все хорды, параллельные другому диаметру, называются сопряженными. На рис.3.53 полужирными линиями изображены сопряженные диаметры эллипса, гиперболы, параболы.

Касательную к эллипсу (гиперболе, параболе) в точке можно определить как предельное положение параллельных секущих , когда точки и , оставаясь на рассматриваемой линии, стремятся к точке . Из этого определения следует, что касательная, параллельная хордам, проходит через конец диаметра, сопряженного к этим хордам.

6. Эллипс, гипербола и парабола имеют, кроме приведенных выше, многочисленные геометрические свойства и физические приложения. Например, рис.3.50 может служить иллюстрацией траекторий движения космических объектов, находящихся в окрестности центра притяжения.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Кривые второго порядка — определение и построение с примерами решения

Содержание:

Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру — значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными х и у записывается в виде

1. Если точка М(а,Ь) принадлежит фигуре Ф, то координаты (а,Ь) являются решениями уравнения
2. если пара чисел (c,d) является решением уравнения F(x,y) = 0, то точка N(c,d) принадлежит фигуре Ф.

Это определение в более компактной записи выглядит следующим образом. Уравнение называется уравнением фигуры, если , то есть (а, b) — решение уравнения F(x,y) = 0.

Из определения уравнения фигуры следует, что фигура Ф состоит только из тех точек плоскости, координаты которых являются решениями уравнения , т.е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

1. дано уравнение и надо построить фигуру Ф, уравнением которой является ;
2. дана фигура Ф и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения и решается, чаще всего, методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

1. Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
2. Записать в координатах условие, сформулированное в первом пункте.

Эллипс

Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек , есть величина постоянная (большая, чем расстояние между ).

Точки называются фокусами эллипса. Обозначив расстояние между фокусами через 2с, а сумму расстояний от точек эллипса до фокусов через 2а, имеем с b. В этом случае а называется большой полуосью, a b — малой.

Если а =Ь, то уравнение (7.3) можно переписать в виде:

(7.5)

Это уравнение окружности с центром в начале координат. Эллипс (3) можно получить из окружности (4) сжатием плоскости к оси Ох. Пусть на плоскости выбрана прямоугольная система координат Оху. Тогда преобразование, переводящее произвольную точку М(х,у) в точку координаты которой задаются формулами будет окружность (4) переводить в эллипс, заданный соотношением

Число называется эксцентриситетом эллипса. Эксцентриситет характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении становится более вытянутым

Фокальными радиусами точки М эллипса называются отрезки прямых, соединяющие эту точку с фокусами . Их длины и задаются формулами Прямые называются директрисами эллипса. Директриса называется левой, а — правой. Так как для эллипса и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая — правее правой вершины.

Директрисы обладают следующим свойством: отношение расстояния г любой точки эллипса от фокуса к ее расстоянию d до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.

Гипербола

Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек есть величина постоянная (не равная нулю и меньшая, чем расстояние между ).

Точки называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 2с. Модуль расстояний от точек гиперболы до фокусов обозначим через а. По условию, а 0) (рис. 9.7). Ось абсцисс проведём через фокус F перпендикулярно директрисе. Начало координат расположим посередине между фокусом и директрисой. Пусть А — произвольная точка плоскости с координатами (х, у) и пусть . Тогда точка А будет лежать на параболе, если r=d, где d- расстояние от точки А до директрисы. Фокус F имеет координаты .

Тогда А расстояние Подставив в формулу r=d, будем иметь. Возведя обе части равенства в квадрат, получим

или

(9.4.1)

Уравнение (9.4.1)- каноническое уравнение параболы. Уравнения также определяют параболы.

Легко показать, что уравнение , определяет параболу, ось симметрии которой перпендикулярна оси абсцисс; эта парабола будет восходящей, если а > 0 и нисходящей, если а О. Для этого выделим полный квадрат:

и сделаем параллельный перенос по формулам

В новых координатах преобразуемое уравнение примет вид: где р — положительное число, определяется равенством .

Пример:

Пусть заданы точка F и прямая у =-1 (рис. 9.8). Множество точек Р(х, y) для которых расстояние |PF| равно расстоянию, называется параболой. Прямая у = -1 называется директрисой параболы, а точка F — фокусом параболы. Чтобы выяснить, как располагаются точки Р, удовлетворяющие условию, запишем это равенство с помощью координат: , или после упрощения . Это уравнение геометрического места точек, образующих параболу (рис. 9.8).

Кривые второго порядка на плоскости

Кривой второго порядка называется фигура на плоскости, задаваемая в прямоугольной системе координат уравнением второй степени относительно переменных х и у:

где коэффициенты А, В и С не равны одновременно нулю

Любая кривая второго порядка на плоскости принадлежит к одному из типов: эллипс, гипербола, парабола, две пересекающиеся прямые, 2 параллельные прямые, прямая, точка, пустое множество.

Кривая второго порядка принадлежит эллиптическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют одинаковые знаки: АС>0.

Кривая второго порядка принадлежит гиперболическому типу, если коэффициент В равен нулю: В=0, а коэффициенты А и С имеют противоположные знаки: АС 2с. Точка М(х,у) принадлежит эллипсу тогда и только тогда, когда ее координаты удовлетворяют уравнению

которое называют каноническим уравнением эллипса.

Число а называют большей полуосью эллипса, число — мень-

шей полуосью эллипса, 2а и 2b — соответственно большей и меньшей осями эллипса. Точки называют вершинами эллипса, а — его фокусами (рис. 12).

Координатные оси являются осями симметрии эллипса, а начало координат — его центром симметрии. Центр симметрии эллипса называется центром эллипса.

Замечание. Каноническое уравнение эллипса можно рассматривать и в случае b>а. Оно определяет эллипс с большей полуосью b, фокусы которого лежат на оси Оу.

В случае а=b каноническое уравнение эллипса принимает вид и определяет окружность радиуса а с центром в начале координат.

Эксцентриситетом эллипса называется отношение фокусного расстояния к длине большей оси.

Так, в случае а>b эксцентриситет эллипса выражается формулой:

Эксцентриситет изменяется от нуля до единицы и характеризует форму эллипса. Для окружности Чем больше эксцентриситет, тем более вытянут эллипс.

Пример:

Показать, что уравнение

является уравнением эллипса. Найти его центр, полуоси, вершины, фокусы и эксцентриситет. Построить кривую.

Решение:

Дополняя члены, содержащие х и у соответственно, до полных квадратов, приведем данное уравнение к каноническому виду:

— каноническое уравнение эллипса с центром в точке большей полуосью а=3 и меньшей полуосью

Найдем эксцентриситет эллипса:

Для вычисления вершин и фокусов удобно пользовать новой прямоугольной системой координат, начало которой находится в точке а оси параллельны соответственно осям Ох, Оу и имеют те же направления (осуществили преобразование параллельного переноса). Тогда новые координаты точки будут равны ее старым координатам минус старые координаты нового начала, т.е.

В новой системе координат координаты вершин и фокусов гиперболы будут следующими:

Переходя к старым координатам, получим:

Построим график эллипса.

Задача решена.

Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.

Так же, как и для эллипса, геометрическое свойство точек гиперболы выразим аналитически. Расстояние между фокусами назовем фокусным расстоянием и обозначим через 2с. Постоянную величину обозначим через 2а: 2а

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Фокальный радиус вектор параболы

Глава 20. Парабола

Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

(1)

Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

.

Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле

.

Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

(2)

В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

(3)

если она лежит в верхней полуплоскости (рис.), и

(4)

если в нижней полуплоскости (рис.)

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Аналитическая геометрия
• Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.

Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Эллипс.

Эллипс с каноническим уравнением $frac+frac=1, ageq b>0,$ и меет форму изображенную на рисунке.

Параметры $a$ и $b$ называются полуосями эллипса (большой и малой соответственно). Точки $A_1(-a, 0),$ $A_2(a, 0), $ $B_1(0, -b), $ и $B_2(0, b), $ его вершинами. Оси симметрии $Ox$ и $Oy$ — главными осями а центр симметрии $O -$ центром эллипса.

Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами эллипса векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей эллипсу. В частном случае $a=b$ фокусы $F_1$ и $F_2$ совпадают с центром, а каноническое уравнение имеет вид $frac+frac=1,$ или $x^2+y^2=a^2,$ т.е. описывает окружность радиуса $a$ с центром в начале координат.

Прямые $D_1: x=-a/e$ и $D_2: x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами эллипса.

Теорема. ( Директориальное свойство эллипса)

Эллипс является множеством точек, отноше ние расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$

Примеры.

2.246. Построить эллипс $9x^2+25y^2=225.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.

Приведем уравнение эллипса к каноническому виду:

а) Находим полуоси $a=5,$ $b=3.$

б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$

$c=sqrt<5^2-3^2>=sqrt<16>=4Rightarrow F_1(-4, 0),qquad F_2(4, 0).$

г) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Ответ: а) $a=5,$ $b=3;$ б) $ F_1(-4, 0),qquad F_2(4, 0);$ в) $e=frac<4><5>;$ г) $D_1: x=-frac<25><4>$ и $D_2: x=frac<25><4>.$

2.249 (a). Установить, что уравнение $5x^2+9y^2-30x+18y+9=0$ определяет эллипс, найти его центр $C,$ полуоси, эксцентриситет и уравнения директрис.

Приведем уравнение эллипса к каноническому виду, для этого выделим полные квадраты:

Это уравнение эллипса. Центр имеет координаты $C=(x_0, y_0)=(-3, -1);$ полуоси $a=3,$ $b=sqrt 5.$

Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-frac<3><2/3>=-frac<9> <2>$ и $D_2: x=frac<3><2/3>=frac<9><2>.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$

Ответ: $C=(x_0, y_0)=(-3, -1);$ $a=3,$ $b=sqrt 5;$ $ e=frac<2><3>.$ $D_1:2x+3=0, $ $D_2: 2x-15=0.$

2.252. Эллипс, главные оси которого совпадают с координатными осми, проходят через точки $M_1(2, sqrt 3)$ и $M_2(0, 2).$ Написать его уравнение, найти фокальные радиусы точки $M_1$ и расстояния этой точки до директрис.

Решение.

Поскольку оси эллипса совпадают с координатными осями, то центр эллипса совпадает с началом координат. Следовательно, из того, что точка $(0, 2)$ принадлежит эллипсу, можно сделать вывод, что $b=2.$

Далее, чтобы найти $a,$ подставим найденное значение $b$ и координаты точки $M_1(2, sqrt 3)$ в каноническое уравнение эллипса $frac+frac=1:$

Таким образом, уравнение эллипса $frac<16>+frac<4>=1.$

Далее найдем координаты фокусов:

$c=sqrt=sqrt<16-4>=2sqrt 3Rightarrow F_1(-2sqrt 3, 0),,,, F_2(2sqrt 3, 0).$

Отсюда находим $overline =(2+2sqrt 3, sqrt 3),$ $overline=(2-2sqrt 3, sqrt 3).$

Чтобы найти расстояния от точки $M_1$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$

Таким образом, расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_1: sqrt 3 x+8=0$

расстояние от точки $M_1(2, sqrt 3)$ до прямой $D_2: sqrt 3 x-8=0$

Параметры $a$ и $b$ называются полуосями гиперболы. Точки $A_1(-a, 0),$ $A_2(a, 0) — $ ее вершинами. Оси симметрии $Ox$ и $Oy$ — действительной и мнимой осями а центр симметрии $O -$ центром гиперболы.

Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrtgeq 0,$ называются фокусами гиперболы, векторы $overline$ и $overline -$ фокальными радиус-векторами, а числа $r_1=|overline|$ и $r_2=|overline| -$ фокальными радиусами точки $M,$ принадлежащей гиперболе.

Прямые $D_1: x=-a/e$ и $D_2:x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами гиперболы.

Теорема. (Директориальное свойство гиперболы).

Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей дирек трисы постоянно и равно $e.$

Примеры.

2.265. Построить гиперболу $16x^2-9y^2=144.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.

Приведем уравнение гиперболы к каноническому виду:

а) Находим полуоси $a=3,$ $b=4.$

б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=sqrt:$

$c=sqrt<3^2+4^2>=sqrt<25>=5Rightarrow F_1(-5, 0),qquad F_2(5, 0).$

г) Асимптоты гиперболы находим по формулам $y=pmfracx:$

д) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Ответ: а) $a=3,$ $b=4;$ б) $ F_1(-5, 0),qquad F_2(5, 0);$ в) $e=frac<5><3>;$ г) $y=pmfrac<4><3>x;$ д ) $D_1: x=-frac<9><5>$ и $D_2: x=frac<9><5>.$

2.269 (a). Установить, что уравнение $16x^2-9y^2-64x-54y-161=0$ определяет гиперболу, найти ее центр $C,$ полуоси, эксцентриситет, уравнения асимптот и директрис.

Приведем заданное уравнение к каноническому виду, для этого выделим полные квадраты:

Это уравнение гиперболы. Центр имеет координаты $C=(x_0, y_0)=(2,-3);$ полуоси $a=3,$ $b=4.$

Асимптоты гиперболы c центром в начале координат, находим по формулам $y=pmfracx,$ а с центром в точке $C=(x_0, y_0) -$ по формуле $y-y_0=pmfrac(x-x_0),$

$$y+3=frac<4><3>(x-2)Rightarrow 3y+9=4x-8Rightarrow 4x-3y-17=0.$$

$$y+3=-frac<4><3>(x-2)Rightarrow 3y+9=-4x+8Rightarrow 4x+3y+1=0.$$

Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-frac<3><5/3>=-frac<9> <5>$ и $D_2: x=frac<3><5/3>=frac<9><5>.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$

Ответ: $C=(2, -3);$ $a=3,$ $b=4;$ $ e=frac<5><3>,$ $4x-3y-17=0,$ $4x+3y+1=0,$ $D_1:5x-1=0, $ $D_2: 5x-19=0.$

2.272. Убедившись, что точка $M(-5, 9/4)$ лежит на гиперболе $frac<16>-frac<9>=1,$ найти фокальные радиусы этой точки и расстояния этой точки до директрис.

Решение.

Проверим, что заданная точка лежит на гиперболе:

Следовательно, точка $M(-5, 9/4)$ лежит на гиперболе $frac<16>-frac<9>=1.$

Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы:

$c=sqrtRightarrow c=sqrt<16+9>=sqrt <25>=5$ Следовательно, фокусы имеют координаты $F_1(-5, 0), F_2(5, 0).$

Фокальные радиусы точки, можно найти по формулам $r_1=|overline|$ и $r_2=|overline|.$

Чтобы найти расстояния от точки $M$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-frac<4><5/4>Rightarrow x=-frac<16><5>Rightarrow 5x+16=0;$

$D_2: x=frac<4><5/4>Rightarrow x=frac<16><5>Rightarrow 5x-16=0;$

Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=left|frac<sqrt>right|.$$

Таким образом, расстояние от точки $M(5, 9/4)$ до прямой $D_1: sqrt 5x+16=0$

расстояние от точки $M(5, 9/4)$ до прямой $D_2: sqrt 5x-16=0$

Ответ: $r_1=9/4,$ $r_2=frac<41><4>;$ $d_1=frac<41><5>;$ $d_2=frac<9><5>.$

2.273. Найти точки гиперболы $frac<9>-frac<16>=1,$ находящиеся на расстоянии $7$ от фокуса $F_1.$

Решение.

Из уравнения гиперболы находим полуоси: $a=3, , b=4.$ Следовательно, $c=sqrtRightarrow c=sqrt<9+16>=sqrt <25>=5.$

Отсюда находим $F_1=(-5, 0).$

Геометрическое место точек, расположенных на расстоянии $7$ от фокуса $F_1,$ это окружность с центром в точке $F_1=(-5, 0)$ и радиусом $r=7:$

Чтобы н айти точки гиперболы $frac<9>-frac<16>=1,$ находящиеся на расстоянии $7$ от фокуса $F_1,$ решим систему уравнений

Решим уравнение $5x^2+18x-72=0:$

Находим соответствующие координаты $y:$ $y_1=pmsqrt<24-2,4^2-10cdot 2,4>=sqrt<-5,76>$ — нет корней .

Ответ: $(-6, pm4sqrt 3).$

Парабола.

Парабола с каноническим уравнением $y^2=2px, p>0,$ и меет форму изображенную на рисунке.

Число $p$ называется параметром параболы. Точка $O -$ ее вершиной, а ось $Ox$ — осью параболы.

Точка $Fleft(frac

<2>, 0right)$ называется фокусом параболы, вектор $overline -$ фокальным радиус-векторам, а число $r=|overline| -$ фокальным радиусом точки $M,$ принадлежащей параболе.

Прямая $D: x=-p/2$ перпендикулярная оси и проходящая на расстоянии $p/2$ от вершины параболы, называется ее директрисой.

Примеры.

2.285 (а). Построить параболу $y^2=6x$ и найти ее параметры.

Решение.

Параметр $p$ параболы можно найти из канонического уравнения $y^2=2px: $

$$y^2=6xRightarrow y^2=2cdot 3xRightarrow p=2.$$

Ответ: $p=3.$

2.286 (а). Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси $Ox$ и $p=1/2.$

Решение.

Поскольку парабола расположена в левой полуплоскости, симметрично относительно оси $Ox,$ то уравнение параболы будет иметь вид $y^2=-2px.$ Подставляя заданное значение параметра, находим уравнение параболы:

Ответ: $y^2=-x.$

2.288 (а). Установить, что уравнение $y^2=4x-8$ определяет параболу, найти координаты ее вершины $A$ и величину параметра $p.$

Решение.

Уравнение параболы, центр которой сдвинут в точку $(x_0, y_0),$ имеет вид $(y-y_0)^2=2p(x-x_0)^2.$

Приведем заданное уравнние к такому виду:

Таким образом, $y^2=4(x^2-2)$ — парабола с центром в точке $(0, 2).$ Параметр $p=2.$

Ответ: $C(0, 2),$ $p=2.$

2.290. Вычислить фокальный параметр точки $M$ параболы $y^2=12x,$ если $y(M)=6.$

Решение.

Чтобы найти фокальный параметр точки $M,$ найдем ее координаты. Для этого подставим в уравнение параболы координату $y:$ $$6^2=12xRightarrow 36=12xRightarrow x=3.$$

Таким образом, точка $M$ имеет координаты $(3, 6).$

Из уравнения параболы $y^2=12x$ находим параметр параболы: $y^2=2cdot 6xRightarrow p=6.$ Следовательно фокус параболы имеет координаты $F(3, 0).$

Далее находим фокальный параметр точки:

Ответ: $6.$

2.298. Из фокуса параболы $y^2=12x$ под острым углом $alpha$ к оси $Ox$ направлен луч света, причем $tgalpha=frac<3><4>.$ Написать уравнение прямой, на которой лежит луч, отраженный от параболы.

Решение.

Найдем координаты фокуса. Из канонического уравнения параболы $y^2=2px$ находим параметр: $y^2=12x=2cdot 6xRightarrow p=6.$

Координаты фокуса $F(p/2, 0)Rightarrow F(3,0).$

Далее находим уравнение прямой, которая проходит через точку $(3, 0)$ под углом $alpha: tgalpha=frac<3><4>$ к оси $OX.$ Уравнение ищем в виде $y=kx+b,$ где $k=tgalpha=frac<3><4>.$

Чтобы найти $b,$ в уравнение прямой подставим координаты точки $(3, 0):$

$0=frac<3><4>cdot 3+bRightarrow b=-frac<9><4>.$ Таким образом, уравнение луча, направленного из фокуса $y=frac<3><4>x-frac<9><4>.$

Далее, найдем точку пересечения найденной прямой с параболой:

Поскольку по условию луч падает под острым углом, то мы рассматриваем только положительную координату $y=18.$ Соответствующее значение $x=frac<18^2><12>=frac<324><12>=27.$

Таким образом, луч пересекает параболу в точке $(27, 18).$

Далее найдем уравнение касательной к параболе в найденной точке $(27, 18)$ по формуле $(y-y_0)=y'(x_0)(x-x_0):$

Подставляем все найденные значения в уравнение касательной:

$y-18=frac<1><3>(x-27)Rightarrow 3y-54=x-27Rightarrow x-3y+27=0.$

Далее, найдем угол $beta$ между лучем $y=frac<3><4>x-frac<9><4>$ и касательной $x-3y+27=0.$ Для этого оба уравнения запишем в виде $y=k_1x+b_1$ и $y=k_2+b_2$ угол вычислим по формуле $tg(L_1, L_2)=frac<1+k_1cdot k_2>$

$$L_2: x-3y+27=0Rightarrow y=frac<1><3>x+9Rightarrow k_2=frac<1><3>.$$

Легко увидеть, что угол между лучем $L_1,$ направленным из фокуса и его отражением равен $pi-2beta,$ а угол между отраженным лучем и осью $Ox$ $pi-(pi-2beta)-alpha=2beta-alpha.$

Зная $tgbeta=frac<1><3>$ и $tgalpha=k_1=frac<3><4>$ и вспоминая формулы для двойного угла тангенса и тангенс разности, находим $tg(2beta-alpha):$

$$tg(2beta-alpha)=frac<1+tg2beta tgalpha>=frac<frac<3><4>-frac<3><4>><1+frac<3><4>frac<3><4>>=0.$$ Следовательно, прямая, содержащая отраженный луч параллельна оси $Ox.$ Так как она проходит через точку $(27, 18),$ то можно записать ее уравнение $y=18.$

источники:

http://a-geometry.narod.ru/problems/problems_20.htm

http://mathportal.net/index.php/analiticheskaya-geometriya/ellips-giperbola-parabola-direktorialnoe-svojstvo-ellipsa-i-giperboly