Фо́кусное
расстоя́ние —
физическая характеристика оптической
системы.
Для центрированной оптической системы,
состоящей из сферических поверхностей,
описывает способность собирать лучи в
одну точку при условии, что эти лучи
идут из бесконечности параллельным
пучком параллельно оптической
оси.
Для
системы линз, как и для простой линзы конечной
толщины, фокусное расстояние зависит
от радиусов кривизны поверхностей,
показателей преломления стёкол и толщин.
Определяется
как расстояние от передней главной
точки до переднего
фокуса (для
переднего фокусного расстояния), и как
расстояние от задней главной точки
дозаднего
фокуса (для заднего
фокусного расстояния).
При этом, под главными точками
подразумеваются точки пересечения
передней (задней) главной
плоскости соптической
осью.
Величина заднего
фокусного расстояния является
основным параметром, которым принято
характеризовать любую оптическую
систему.
Парабола (или параболоид вращения)
фокусирует параллельный пучок лучей в
одну точку
Фо́кус (от лат. focus —
«очаг») оптической (или работающей с
другими видами излучения)
системы — точка, в которой пересекаются
(«фокусируются»)
первоначально параллельные лучи после
прохождения через собирающую систему
(либо где пересекаются их продолжения,
если система рассеивающая). Множество
фокусов системы определяет её фокальную
поверхность. Главный фокус системы
является пересечением её главной оптической
оси и
фокальной поверхности. В настоящее
время[1],
вместо термина главный
фокус (передний
или задний) используются термины задний
фокус и передний
фокус.
Опти́ческая
си́ла —
величина, характеризующая преломляющую
способность осесимметричных линз и
центрированных оптических
систем из
таких линз. Измеряется оптическая сила
в диоптриях (в СИ):
1 дптр=1 м-1.
Обратно
пропорциональна фокусному
расстоянию системы:
где —
фокусное расстояние линзы.
Оптическая
сила положительна у собирающих систем
и отрицательна в случае рассеивающих.
Оптическая
сила системы, состоящей из двух находящихся
в воздухе линз с оптическими силами и
,
определяется формулой[1]:
где —
расстояние между задней главной
плоскостью первой линзы и передней
главной плоскостью второй линзы. В
случае тонких линзсовпадает
с расстоянием между линзами.
Обычно
оптическая сила используется для
характеристики линз, используемых
в офтальмологии,
в обозначениях очков и для упрощённого
геометрического определения траектории
луча.
Для
измерения оптической силы линз используют
диоптриметры[2],
которые позволяют проводить измерения
в том числе астигматических и контактных
линз.
18. Формула сопряжённых фокусных расстояний. Построение изображения линзой.
Сопряжённое
фо́кусное расстоя́ние —
расстояние от задней главной
плоскости объектива до
изображения объекта, когда объект
расположен не в бесконечности, а на
некотором расстоянии от объектива.
Сопряженное фокусное расстояние всегда
большефокусного
расстояния объектива и
тем больше, чем меньше расстояние от
объекта допередней
главной плоскости объектива .
Эта зависимость приведена в таблице, в
которой расстоянияи
выражены
в величинах.
|
Изменение |
|
|
Расстояние |
Расстояние |
|
4f |
1,33f |
|
2f |
2f |
|
1,5f |
3f |
|
1,2f |
6f |
|
1,1f |
11f |
Для линзы эти
расстояния связаны отношением,
непосредственно следующим из формулы
линзы:
или,
если d и R выразить в величинах фокусного
расстояния :
б) Построение
изображения в линзах.
Для
построения хода луча в линзе применяются
те же законы, что и для вогнутого зеркала.
Луч, параллельный
оси,
проходит через фокус и наоборот.
Центральный луч (луч, идущий через
оптический центр линзы) проходит через
линзу без
отклонения;
в толстых
линзах
он немного смещается параллельно самому
себе (как в плоскопараллельной пластинке,
см. рис. 214). Из обратимости хода лучей
следует, что каждая линза имеет два
фокуса, которые находятся на одинаковых
расстояниях от линзы (последнее верно
лишь для тонких линз). Для тонких
собирающих линз и центральных лучей
справедливы следующие законы
построения изображений:
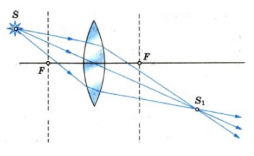
g >2F; изображение
обратное, уменьшенное,
действительное, b >F (рис.221).
g = 2F; изображение
обратное, равное, действительное, b = F.
F <g < 2F;
изображение обратное, увеличенное,
действительное, b > 2F.
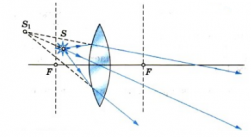
g < F; изображение
прямое, увеличенное, мнимое, — b > F.
При g < F лучи
расходятся, на продолжении пересекаются
и дают мнимое
изображение.
Линза действует как увеличительное
стекло (лупа).
Изображения
в рассеивающих линзах всегда мнимые,
прямые и уменьшенные (рис.223).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Мы уже познакомились с явлением преломления света на границе двух плоских сред. Но на практике особый интерес представляет явление преломления света на сферических поверхностях линз.
Определение
Линза — прозрачное тело, ограниченное сферическими поверхностями.
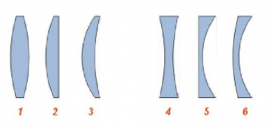
Какими бывают линзы?
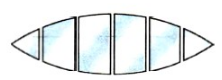
По форме различают следующие виды линз:
- Выпуклые — линзы, которые посередине толще, чем у краев.
- Вогнутые — линзы, которые посередине тоньше, чем у краев.
Выпуклые линзы тоже имеют разновидности:
- Двояковыпуклая — линза, ограниченная с обеих сторон выпуклыми сферическими поверхностями (СП). Такая линза изображена ниже на рисунке 1.
- Плосковыпуклая — линза, ограниченная выпуклой СП с одной стороны и плоской поверхностью с другой (рис. 2)
- Вогнуто-выпуклая — линза, ограниченной с одной стороны вогнутой СП, а с другой — выпуклой СП (рис. 3).
Разновидности вогнутых линз:
- Двояковогнутая — линза, ограниченная с обеих сторон вогнутыми СП (рис. 4).
- Плосковогнутая — линза, ограниченная вогнутой СП с одной стороны и плоской поверхностью с другой (рис. 5)
- Выпукло-вогнутая — линза, ограниченной с одной стороны выпуклой СП, а с другой — вогнутой СП (рис. 6).
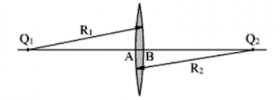
Тонкая линза
Мы будем говорить о линзах, у которых толщина l = AB намного меньше радиусов сферических поверхностей этой линзы R1 и R2. Такие линзы называют тонкими.
Определение
Тонкая линза — линза, толщина которой пренебрежимо мала по сравнению с радиусами сферических поверхностей, которыми она ограничена.
Главная оптическая ось тонкой — прямая, проходящая через центры сферических поверхностей линзы (на рисунке она соответствует прямой O1O2).
Оптический центр линзы – точка, расположенная в центре линзы на ее главной оптической оси (на рисунке ей соответствует точка О). При прохождении через оптический центр линзы лучи света не преломляются.
Побочная оптическая ось — любая другая прямая, проходящая через оптический центр линзы.
Изображение в линзе
Подобно плоскому зеркалу, линза создает изображения источников света. Это значит, что свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в точку (изображение) независимо от того, какую часть линзы прошли лучи.
Определение
Оптическое изображение — картина, получаемая в результате действия оптической системы на лучи, испускаемые объектом, и воспроизводящая контуры и детали объекта.
Практическое использование изображений часто связано с изменением масштаба изображений предметов и их проектированием на поверхность (киноэкран, фотоплёнку, фотокатод и т. д.). Основой зрительного восприятия предмета является его изображение, спроектированное на сетчатку глаза.
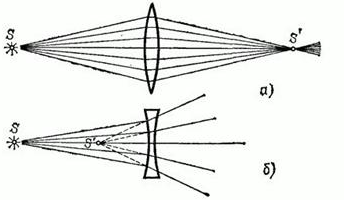
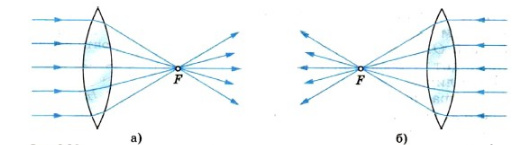
Изображения разделяют на действительные и мнимые. Действительные изображения создаются сходящимися пучками лучей в точках их пересечения (см. рисунок а). Поместив в плоскости пересечения лучей экран или фотоплёнку, можно наблюдать на них действительное изображение.
Если лучи, выходящие из оптической системы, расходятся, но если их мысленно продолжить в противоположную сторону, они пересекутся в одной точке (см. рисунок б). Эту точку называют мнимым изображением точки-объекта. Она не соответствует пересечению реальных лучей, поэтому мнимое изображение невозможно получить на экране или зафиксировать на фотоплёнке. Однако мнимое изображение способно играть роль объекта по отношению к другой оптической системе (например, глазу или собирающей линзе), которая преобразует его в действительное.
Собирающая линза
Обычно линзы изготавливают из стекла. Все выпуклые линзы являются собирающими, поскольку они собирают лучи в одной точке. Любую из таких линз условно можно принять за совокупность стеклянных призм. В воздухе каждая призма отклоняет лучи к основанию. Все лучи, идущие через линзу, отклоняются в сторону ее главной оптической оси.
Если на линзу падают световые лучи, параллельные главной оптической оси, то при прохождении через нее они собираются на одной точке, лежащей на оптической оси. Ее называют главным фокусом линзы. У выпуклой линзы их два — второй главный фокус находится с противоположной стороны линзы. В нем будут собираться лучи, которые будут падать с обратной стороны линзы.
Главный фокус линзы обозначают буквой F.
Определение
Фокусное расстояние — расстояние от главного фокуса линзы до их оптического центра. Оно обозначается такой же букой F и измеряется в метрах (м).
В однородных средах главные фокусы собирающих линз находятся на одинаковом расстоянии от оптического центра.
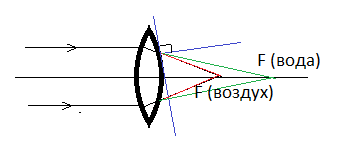
Пример №1. Что произойдет с фокусным расстоянием линзы, если ее поместить в воду?
Вода — оптически более плотная среда, поэтому преломленные лучи будут располагаться ближе к перпендикуляру, восстановленному к разделу двух сред. Следовательно, фокусное расстояние увеличится. На рисунке лучам, выходящим из линзы в воздухе, соответствуют красные линии. Лучам, выходящим из линзы в воде — зеленые. Видно, что зеленые линии больше приближены к перпендикуляру, восстановленному к разделу двух сред, что соответствует закону преломления света.
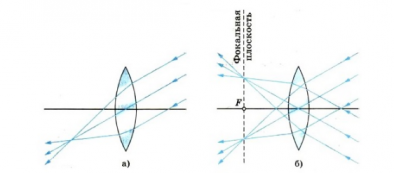
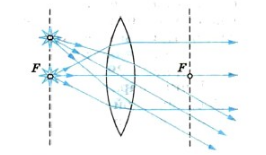
Направим три узких параллельных пучка лучей от осветителя под углом к главной оптической оси собирающей линзы. Мы увидим, что пересечение лучей произойдет не в главном фокусе, а в другой точке (рисунок а). Но точки пересечения независимо от углов, образуемых этими пучками с главной оптической осью, будут располагаются в плоскости, перпендикулярной главной оптической оси линзы и проходящей через главный фокус (рисунок б). Эту плоскость называют фокальной плоскостью.
Поместив светящуюся точку в фокусе линзы (или в любой точке ее фокальной плоскости), получим после преломления параллельные лучи.
Если сместить источник дальше от фокуса линзы, лучи за линзой становятся сходящимися и дают действительное изображение.
Когда же источник света находится ближе фокуса, преломленные лучи расходятся и изображение получается мнимым.
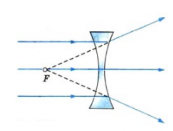
Рассеивающая линза
Вогнутые линзы обычно являются рассеивающими (лучи, выходя из них, не собираются, а рассеиваются). Это бывает если, поместить вогнутую линзу в оптически менее плотную среду по сравнению с материалом, из которого изготовлена линза. Так, стеклянная линза в воздухе является рассеивающей.
Если направить на вогнутую линзы световые лучи, являющиеся параллельными главной оптической оси, то образуется расходящийся пучок лучей. Если провести их продолжения, то они пересекутся в главном фокусе линзы. В этом случае фокус (и изображение в нем) является мнимым. Этот фокус располагается на фокусном расстоянии, равном F.
Другой мнимый фокус находится по другую сторону линзы на таком же расстоянии при условии, что среда по обе стороны линзы одинаковая.
Оптическая сила линзы
Оптическая сила линзы — величина, характеризующая преломляющую способность симметричных относительно оси линз и центрированных оптических систем, состоящих из таких линз.
Обозначается оптическая сила линзы буквой D. Единица измерения — диоптрий (дптр). Оптической силой в 1 дптр обладает линза с фокусным расстоянием 1 м.
Оптическая сила линзы равна величине, обратной ее фокусному расстоянию:
D=±1|F|
D > 0, если линза собирающая, D < 0, если линза рассеивающая. Чем ближе к линзе ее фокусы, тем сильнее линза преломляет лучи, собирая или рассеивая их, и тем больше оптическая сила линзы.
Пример №2. Найти фокусное расстояние линзы, если ее оптическая сила равна –5 дптр.
Так как оптическая силы линзы отрицательная, речь идет о рассеивающей линзе. Следовательно, будем использовать формулу:
D=−1|F|
Отсюда:
|F|=−1D=−1−5=0,2 (м)
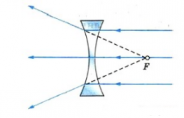
Задание EF18041
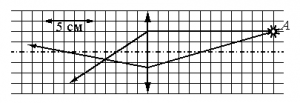
Ответ:
а) 14 дптр
б) 20 дптр
в) 17 дптр
г) 33 дптр
Алгоритм решения
1.Записать формулу для нахождения оптической силы линзы.
3.Найти точку на главной оптической оси точку главного фокуса линзы.
4.Вычислить фокусное расстояние и перевести его в СИ.
5.Вычислить оптическую силу линзы.
Решение
Оптическая сила линзы определяется формулой:
D=1F
На рисунке видно, что 5 клеток = 5 см. Следовательно, 1 клетка = 1 см. После прохождения сквозь линзу лучи света, параллельные главной оптической оси, фокусируются в главном фокусе, который лежит на этой оси. Значит, фокус находится в точке пересечения этой оси и луча. От него до линзы 3 клетки. Следовательно, фокусное расстояние равно 3 см, или 0,03 м.
Отсюда:
D=10,03≈33 (дптр)
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17706
Стеклянную линзу (показатель преломления стекла nстекла = 1,54), показанную на рисунке, перенесли из воздуха (nвоздуха = 1) в воду (nводы = 1,33). Как изменились при этом фокусное расстояние и оптическая сила линзы?
Ответ:
а) Фокусное расстояние уменьшилось, оптическая сила увеличилась.
б) Фокусное расстояние увеличилось, оптическая сила уменьшилась.
в) Фокусное расстояние и оптическая сила увеличились.
г) Фокусное расстояние и оптическая сила уменьшились.
Алгоритм решения
1.Установить характер преломления лучей линзой при ее перемещении из воздуха в воду.
2.Выяснить, как от этого зависят фокусное расстояние и оптическая сила линзы.
Решение
Чтобы узнать, что произойдет с лучами света при прохождении их сквозь линзу, погруженную воду, найдем относительные показатели преломления:
nвоздух−стекло=nстеклоnвоздух=1,541=1,54
nвода−стекло=nстеклоnвода=1,541,33≈1,16
Видно, что относительный показатель преломления уменьшился. Значит, преломленный линзой луч будет менее отклоняться от нормали, проведенной в точке падения на линзу. Следовательно, чтобы достигнуть главной оптической оси, ему придется пройти большее расстояние. Это говорит о том, что фокусное расстояние линзы увеличится.
Оптическая сила линзы — величина, обратная ее фокусному расстоянию. Если оно увеличится, то оптическая сила уменьшится.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18076
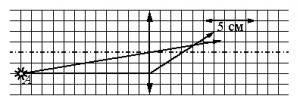
Какова приблизительно оптическая сила этой линзы?
Ответ:
а) –33,3 дптр
б) 7,7 дптр
в) 25,0 дптр
г) 33,3 дптр
Алгоритм решения
1.Записать формулу для нахождения оптической силы линзы.
2.Рассчитать длину 1 клетки.
3.Найти точку на главной оптической оси точку главного фокуса линзы.
4.Вычислить фокусное расстояние и перевести его в СИ.
5.Вычислить оптическую силу линзы.
Решение
Оптическая сила линзы находится по формуле:
D=1F
На рисунке видно, что 5 соответствуют 5 см. Следовательно, 1 клетка равна 1 см. После прохождения сквозь линзу лучи света, параллельные главной оптической оси, фокусируются в фокусе, который лежит на этой оси. Из рисунка видно, фокус находится в точке пересечения этой оси и луча, параллельного ей. Эту точку и линзу разделяют 3 клетки. Следовательно, фокусное расстояние равно 3 см, или 0,03 м.
Отсюда:
D=10,03≈33,3 (дптр)
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.9k
Лабораторная работа
ОПРЕДЕЛЕНИЕ ФОКУСНЫХ
РАССТОЯНИЙ СОБИРАЮЩИХ И
РАССЕИВАЮЩИХ ЛИНЗ
Цель работы: научиться определять
фокусные расстояния собирающих и рассеивающих линз.
Приборы и
принадлежности: набор линз; осветитель; экран.
Теоретическая часть
Оптические линзы
представляют собой тела из прозрачного вещества (стёкла, прозрачные кристаллы,
пластмассы и т. д.), ограниченные двумя сферическими поверхностями, вершины
которых лежат на одной оси, называемой оптической осью (рис.1).
а
б
в
г
д
е
 |
Для тонких линз
имеет место соотношение:
,
(1)
где b – расстояние от линзы до изображения; а – расстояние от
линзы до предмета; f – фокусное расстояние
линзы. Знаки расстояний, входящих в формулу (1), можно определять по простому правилу:
если расстояние отсчитывается от линзы по ходу луча, то ему приписывают знак
«+», в противном случае — « — ».
На рисунке 1
показаны различные типы собирающих и рассеивающих линз: а) двояковыпуклая; б)
плосковыпуклая; в) выпукло-вогнутая; г) двояковогнутая; д) плосковогнутая; е)
вогнуто-выпуклая. Около соответствующих рисунков показаны характеристики линз:
радиусы кривизны и фокусы. К собирающим линзам относят типы а, б, в, к
рассеивающим — г, д, е. У первых середина линзы толще, чем края, у вторых края
толще, чем середина.
Описание экспериментальной установки
Установка для
измерения фокусных расстояний собирающих и рассеивающих линз представлена на
рис. 2.
Установка состоит
из источника света 1 с наклеенной на нем стрелкой, играющей роль предмета.
Источник света 1 установлен на основании 2. Экран 6, на котором получается
изображение, установлен на основании 4. Основания 2 и 4 скрепляются между собой
при помощи стержней, по которым могут перемещаться одна или несколько
исследуемых линз 3. Вертикальность расположения установки можно регулировать
при помощи ножек 7.Установка снабжена метровой шкалой, позволяющей определить
положение линз в каждом из опытов. Каждая из линз может быть независимо удалена
из оптического тракта.
Выполнение работы
Рассмотрим
методику измерений при работе на установке, изображенной на рисунке 2. В данном
случае фокусное расстояние собирающих линз можно определить тремя способами:
1) по расстояниям от предмета до
линзы и от изображения до линзы;
2) по величине предмета и
изображения;
3) способом Бесселя.
Определение фокусного расстояния
собирающей линзы по расстоянию от предмета до линзы и по расстоянию от
изображения до линзы
В этом случае фокусное расстояние
определяется непосредственно из формулы тонкой линзы. Для этого необходимо:
1. Устанавить в
оптический тракт установки исследуемую собирающую линзу.
2. Отрегулировать
положение осветителя, линзы и экрана по высоте (получаемое изображение должно
получаться неизогнутым).
3. Включить
осветитель и получить четкое увеличенное или уменьшенное изображение на экране.
4. По
измерительному устройству отмерить расстояние от линзы до экрана и от линзы до
предмета.
5. По измеренным
расстояниям от линзы до предмета и от линзы до изображения исходя из формулы (1)
определить фокусное расстояние.
6. Определить
погрешность измерения фокусного расстояния данным методом.
7. Результаты
измерения занести с таблицу 1.
Таблица.1
|
№ |
a , м |
b , м |
f |
fср |
Df |
Данным способом необходимо измерить
фокусное расстояние не менее 3 раз.
Определение фокусного расстояния по
величине предмета и
изображения
Построим геометрическое изображение
предмета в собирающей линзе:
Рис. 3. Схема построения изображения
предмета в собирающей линзе
Исходя из данного
геометрического построения получим:

Тогда с учетом
формулы тонкой линзы 

Производя
простейшие преобразования формулы (3), получаем:
. (4)
Из (4) следует,
что фокусное расстояние собирающей линзы можно определить по высотам предмета и
изображения. Для измерения до фокусного расстояния данным способом необходимо:
1. Получить четкое уменьшенное или
увеличенное изображение предмета.
2. Измерить при
помощи линейки высоту линейки, высоту предмета и высоту изображения (высота
предмета считается известной h=2.5 см).
3. Измерить расстояние
от предмета до линзы.
4. Полученные
результаты подставить в формулу и найти величину фокусного расстояния.
5. Измерения
повторить не менее 3 раз и результаты занести в таблицу 2.
6. Определить
погрешность нахождения данным способом.
Таблица 2
|
№ |
H , м |
h , м |
a , м |
f |
fср |
Df |
Способ Бесселя
Данный способ
основан на том, что при расстоянии между предметом и экраном, превышающим 4F, одна и та же собирающая линза может давать как
увеличенное, так и уменьшенное изображение предмета. Поясним это, исходя из
формулы тонкой линзы:

(5)
,
(6)
где L – расстояние от предмета до экрана.
Выразим из (6) b и подставим полученное выражение в
формулу тонкой линзы:

После
преобразования получаем квадратное уравнение:
. (8)
Исходя из решения
данного квадратного уравнения, получаем:

Если расстояние
между двумя положениями линзы обозначить через k, то получим:


Таким образом, в способе Бесселя
достаточно измерить расстояние между предметом и экраном и расстояние между
двумя положениями линзы, при которых она дает четкие изображения. Порядок
измерения в этом случае следующий:
1. Получить четкое увеличенное
изображение предмета и отметить положение линзы при помощи карандаша.
2. Получить четкое уменьшенное
изображение предмета и отметить положение линзы при помощи карандаша
3. Измерить расстояние между этими
двумя этими положениями линзы.
4. Измерить расстояние между
предметом и экраном.
5. Вычислить фокусное расстояние.
6. Определить погрешность.
7. Полученные
результаты занести в таблицу 3.
Таблица 3
|
№ |
L , м |
k, м |
f |
fср |
Df |
Определение фокусного
расстояния рассеивающей линзы
Для того чтобы
определить фокусное расстояние рассеивающей линзы, нужно взять собирающую
линзу с известным фокусным расстоянием, оптическая сила которой больше по
модулю, чем у рассеивающей линзы. Далее эти линзы сдвигаются вплотную друг с
другом. Оптическая сила такой системы складывается из оптических сил каждой из
линз:
,
(12)
или
.
(13)
Здесь f, f1 и f2 – соответственно фокусные
расстояния системы первой и второй линзы. Таким образом, оптическая система из
двух таких линз является собирающей, и ее фокусное расстояние можно определить
как для обычной тонкой собирающей линзы, а затем из формулы (13) найти фокусное
расстояние рассеивающей линзы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие линзы называются
тонкими?
2. Дайте
определения главных фокусов.
3.
Что такое оптическая сила линзы?
4.
Может ли двояковыпуклая линза иметь отрицательную оптическую силу?
5. Покажите, что
если расстояние между предметом и экраном превышает 4 F, то изображение на экране может быть
получено при двух различных положениях линзы. Что будет, если это расстояние
будет 4 F?
8. В каких случаях получаются
действительные изображения, а в каких -мнимые? Чем действительное изображение
отличается от мнимого? При каких условиях изображение переносится в
бесконечность?
9. Что произойдет
с изображением, если половина линзы закрыта непрозрачным экраном?
10. Как построить
изображение точки, лежащей на главной оптической оси?
11. Постройте
график зависимости координаты точки изображения от координаты точечного
источника для тонкой собирающей (рассеивающей) линзы.
12. Восстановите падающий луч по
известному преломленному лучу.
13. Покажите
построением, что все лучи, исходящие из произвольной точки объекта,
находящегося в фокальной плоскости лупы, будут при выходе из лупы параллельны
друг другу.
14. Покажите
построением, что два произвольных параллельных луча, входящих в систему из двух
линз, расположенных так, что задний фокус первой линзы совпадает с передним
фокусом второй линзы, на выходе системы также будут параллельны.