3.4.3. Фокусы и эксцентриситет гиперболы
Ввиду неравенства , фокусы гиперболы лежат «внутри» её ветвей и только
там. Координаты фокусов определяются следующим образом:
Если гипербола задана каноническим уравнением , то РАССТОЯНИЕ от центра
симметрии до каждого из фокусов рассчитывается по формуле:
, и, соответственно, фокусы имеют координаты
.
Для нашей гиперболы , таким образом:
(см. рис. выше).
Если гиперболу переместить / повернуть, то фокусы, естественно, мигрируют вместе с ней и их координаты изменятся.
Эксцентриситетом гиперболы называют отношение .
Так как расстояние от центра до фокуса больше расстояния от центра до вершины: , то эксцентриситет гиперболы всегда больше «единицы»:
.
Для нашего примера: .
По аналогии с эллипсом, зафиксируйте значение и проведите самостоятельный анализ и проверку следующих фактов:
При увеличении эксцентриситета ветви гиперболы «распрямляются» к оси . В предельном случае
они стремятся занять положение двух прямых, проходящих через точки
параллельно оси ординат.
Если же значение эксцентриситета приближается к единице, то ветви гиперболы «сплющиваются» к оси .


| Оглавление |
Автор: Aлeксaндр Eмeлин
-
Гипербола и её форма.
Начать изучение
-
Фокусы, эксцентриситет и директрисы гиперболы.
Начать изучение
-
Точки гиперболы и их свойства.
Начать изучение
-
Уравнение касательной к гиперболе.
Начать изучение
Гипербола и её форма.
Гиперболой мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=1.label{ref9}
$$
Из этого уравнения видно, что для всех точек гиперболы (|x| geq a), то есть все точки гиперболы лежат вне вертикальной полосы ширины (2a) (рис. 8.6). Ось абсцисс канонической системы координат пересекает гиперболу в точках с координатами ((a, 0)) и ((-a, 0)), называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. Таким образом, гипербола состоит из двух не связанных между собой частей. Они называются ее ветвями. Числа (a) и (b) называются соответственно вещественной и мнимой полуосями гиперболы.
Утверждение.
Для гиперболы оси канонической системы координат являются осями симметрии, а начало канонической системы — центром симметрии.
Доказательство.
Доказательство аналогично доказательству соответствующего утверждения для эллипса.
Для исследования формы гиперболы найдем ее пересечение с произвольной прямой, проходящей через начало координат. Уравнение прямой возьмем в виде (y=kx), поскольку мы уже знаем, что прямая (x=0) не пересекает гиперболу. Абсциссы точек перечения находятся из уравнения
$$
frac{x^{2}}{a^{2}}-frac{k^{2}x^{2}}{b^{2}}=1.
$$
Поэтому, если (b^{2}-a^{2}k^{2} > 0), то
$$
x=pm frac{ab}{sqrt{b^{2}-a^{2}k^{2}}}.
$$
Это позволяет указать координаты точек пересечения ((ab/v, abk/v)) и ((-ab/v, -abk/v)), где обозначено (v=(b^{2}-a^{2}k^{2})^{1/2}). В силу симметрии достаточно проследить за движением первой из точек при изменении (k) (рис. 8.7).
Числитель дроби (ab/v) постоянен, а знаменатель принимает наибольшее значение при (k=0). Следовательно, наименьшую абсциссу имеет вершина ((a, 0)). С ростом (k) знаменатель убывает, и (x) растет, стремясь к бесконечности, когда (k) приближается к числу (b/a). Прямая (y=bx/a) с угловым коэффициентом (b/a) не пересекает гиперболу, и прямые с большими угловыми коэффициентами ее тем более не пересекают. Любая прямая с меньшим положительным угловым коэффициентом пересекает гиперболу.
Если мы будем поворачивать прямую от горизонтального положения по часовой стрелке, то (k) будет убывать, (k^{2}) расти, и прямая будет пересекать гиперболу во все удаляющихся точках, пока не займет положения с угловым коэффициентом (-b/a).
К прямой (y=-bx/a) относится все, что было сказано о (y=bx/a): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из приведенных рассуждений вытекает, что гипербола имеет вид, изображенный на рис. 8.7.
Определение.
Прямые с уравнениями (y=bx/a) и (y=-bx/a) в канонической системе координат называются асимптотами гиперболы.
Запишем уравнения асимптот в виде (bx-ay=0) и (bx+ay=0). Расстояния от точки (M(x, y)) до асимптот равны соответственно
$$
h_{1}=frac{|bx-ay|}{sqrt{a^{2}+b^{2}}}, h_{2}=frac{|bx+ay|}{sqrt{a^{2}+b^{2}}}.nonumber
$$
Если точка (M) находится на гиперболе, то (b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2}), и
$$
h_{1}h_{2}=frac{|b^{2}x^{2}-a^{2}y^{2}|}{a^{2}+b^{2}}=frac{a^{2}b^{2}}{a^{2}+b^{2}}.nonumber
$$
Утверждение.
Произведение расстояний от точки гиперболы до асимптот постоянно и равно (a^{2}b^{2}/(a^{2}+b^{2})).
Отсюда следует важное свойство асимптот.
Свойство.
Если точка движется по гиперболе так, что ее абсцисса по абсолютной величине неограниченно возрастает, то расстояние от точки до одной из асимптот стремится к нулю.
Доказательство.
Действительно, хотя бы одно из расстояний (h_{1}) или (h_{2}) при этих условиях должно неограниченно возрастать, и, если бы предложение было неверно, произведение не было бы постоянно.
Фокусы, эксцентриситет и директрисы гиперболы.
Определение.
Введем число (c), положив
$$
c^{2}=a^{2}+b^{2}label{ref10}
$$
и (c > 0). Фокусами гиперболы называются точки (F_{1}) и (F_{2}) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат.
Отношение (varepsilon=c/a), как и для эллипса, называется эксцентриситетом. У гиперболы (varepsilon > 1).
Утверждение 9.
Расстояния от произвольной точки (M(x, y)) на гиперболе до каждого из фокусов следующим образом зависят от ее абсциссы (x):
$$
r_{1}=|F_{1}M|=|a-varepsilon x|, r_{2}=|F_{2}M|=|a+varepsilon x|.label{ref11}
$$
Доказательство.
Доказательство этого утверждения почти дословно совпадает с доказательством аналогичного утверждения для эллипса.
Заметим, что равенства eqref{ref11} можно подробнее записать так:
- для правой ветви гиперболы ((x geq a))
$$
r_{1}=varepsilon x-a, r_{2}=varepsilon x+a;nonumber
$$ - для левой ветви гиперболы ((x leq -a))
$$
r_{1}= a-varepsilon x, r_{2}=-varepsilon x-a;nonumber
$$
Итак, для правой ветви (r_{2}-r_{1}=2a), а для левой ветви (r_{1}-r_{2}=2a). В обоих случаях
$$
|r_{2}-r_{1}|=2a.label{ref12}
$$
Директрисами гиперболы называются прямые, задаваемые в канонической системе координат уравнениями
$$
x=frac{a}{varepsilon}, x=-frac{a}{varepsilon}.label{ref13}
$$
Директрисы лежат ближе к центру, чем вершины, и, следовательно, не пересекают гиперболу. Директриса и фокус, лежащие по одну сторону от центра, считаются соответствующими друг другу.
Точки гиперболы и их свойства.
Утверждение 10.
Для того чтобы точка (M) лежала на гиперболе, необходимо и достаточно, чтобы разность ее расстояний до фокусов по абсолютной величине равнялась вещественной оси гиперболы (2a).
Доказательство.
Необходимость условия уже доказана. Для доказательства достаточности условия его нужно представить в виде
$$
sqrt{(x-c)^{2}+y^{2}}=pm 2a+sqrt{(x+c)^{2}+y^{2}}nonumber
$$
Дальнейшее отличается от доказательства соответствующего утверждения для эллипса только тем, что нужно воспользоваться равенством (c^{2}=a^{2}+b^{2}), а не (c^{2}=a^{2}-b^{2}).
Утверждение 11.
Для того чтобы точка лежала на гиперболе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету (varepsilon) (рис. 8.10).
Доказательство.
Доказательство повторяет доказательство предложения 4. Докажем, например, необходимость условия для фокуса (F_{2}(-c, 0)). Пусть (M'(x, y)) — точка гиперболы. Расстояние от (M’) до директрисы с уравнением (x=-a/varepsilon) по формуле (9) § 3 гл. II равно
$$
d’=left|x+frac{a}{varepsilon}right|=frac{1}{varepsilon}|varepsilon x+a|.nonumber
$$
Из формулы eqref{ref11} мы видим теперь, что (r’/d’=varepsilon).
Уравнение касательной к гиперболе.
Уравнение касательной к гиперболе в точке (M_{0}(x_{0}, y_{0})), лежащей на ней, выводится так же, как соответствующее уравнение касательной для эллипса. Оно имеет вид
$$
frac{xx_{0}}{a^{2}}-frac{yy_{0}}{b^{2}}=1.label{ref14}
$$
Утверждение 12.
Касательная к гиперболе в точке (M_{0}(x_{0}, y_{0})) есть биссектриса угла между отрезками, соединяющими эту точку с фокусами.
Доказательство.
Доказательство почти не отличается от доказательства соответствующего утверждения для эллипса.
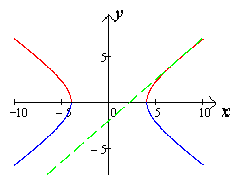
Как найти фокус гиперболы?
Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы: c=√a2+b2⇒c=√16+9=√25=5 Следовательно, фокусы имеют координаты F1(−5,0),F2(5,0). Фокальные радиусы точки, можно найти по формулам r1=|¯F1M| и r2=|¯F2M|.
Как строить гиперболу по уравнению?
Как построить гиперболу?
- Сначала находим асимптоты. …
- Теперь находим две вершины гиперболы, которые расположены на оси абсцисс в точках . …
- Ищем дополнительные точки. …
- Изобразим асимптоты , вершины , дополнительные и симметричные им точки в других координатных четвертях.
Как найти коэффициент К в Гиперболе?
Разберемся, как же определить коэффициент k по графику функции. Из формулы: у = k / x следует, что k = у·х. То есть мы можем взять любую целочисленную точку с удобными координатами и перемножить их – получим k.
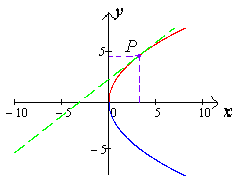
Что такое P в параболе?
Определение параболы. где число p, называемое параметром параболы, есть расстояние от фокуса до директрисы. На чертеже линия параболы — бордового цвета, директриса — ярко-красного цвета, расстояния от точки до фокуса и директрисы — оранжевого.
Как составить уравнение параболы по графику?
Алгоритм построения параболы Уравнение квадратичной функции имеет вид y = ax2 + bx + c. Уравнение квадратичной функции имеет вид y = a * (x — x₀)2 + y₀ Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Что такое фокус параболы?
Пара́бола (греч. παραβολή — приближение) — геометрическое место точек на плоскости, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).
Как найти действительную полуось гиперболы?
Действительная полуось гиперболы — число a = |OA1| = |OA2|. Мнимая полуось гиперболы — число b. В нашем примере: а = 2, b = √5, |А1А2| = 4.
Как определить график функции?
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика. График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Как найти значение k?
Чтобы определить коэффициент k, необходимо выбрать некоторую точку на прямой и вычислить частное ординаты и абсциссы заданной точки. Прямая проходит через точку M(4; 2), следовательно получим 2 4 = 0,5 . Значит, k=0,5, и данная прямая является графиком линейной функции y=0,5x.
Как найти угловой коэффициент k?
Угловой коэффициент равен отношению количества делений на оси Y к количеству делений на оси Х; в нашем примере угловой коэффициент равен 5/7.
Как вычислить директрису параболы?
Чтобы найти эксцентриситет параболы, достаточно воспользоваться следующей формулой из определения эксцентриситета: ε = M F M M d , где точка — точка пересечения перпендикуляра, опущенного из точки c прямой .
Как найти вершину параболы квадратичной функции?
Воспользуйтесь формулой для вычисления значения координаты x вершины. Вершина также является точкой симметрии параболы. Формула для нахождения координаты x параболы: x = -b/2a.
Как найти функцию по графику?
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика. График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Как найти с в параболе?
Воспользуйтесь формулой для вычисления значения координаты x вершины. Вершина также является точкой симметрии параболы. Формула для нахождения координаты x параболы: x = -b/2a. Подставьте в нее соответствующие значения для вычисления x.
Что показывает а в параболе?
a — старший коэффициент, который отвечает за ширину параболы. Большое значение a — парабола узкая, небольшое — парабола широкая. b — второй коэффициент, который отвечает за смещение параболы от центра координат. с — свободный член, который соответствует координате пересечения параболы с осью ординат.
Что такое параболический?
Параболический — прил. Имеющий форму параболы [парабола I 1.]. Толковый словарь Ефремовой.
Как узнать что это парабола?
Пара́бола (греч. παραβολή — приближение) — геометрическое место точек на плоскости, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы). Наряду с эллипсом и гиперболой, парабола является коническим сечением.
Гипербола: определение, свойства, построение
Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек и
есть величина постоянная
, меньшая расстояния
между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.
Фокальное свойство гиперболы
Точки и
называются фокусами гиперболы, расстояние
между ними — фокусным расстоянием, середина
отрезка
— центром гиперболы, число
— длиной действительной оси гиперболы (соответственно,
— действительной полуосью гиперболы). Отрезки
и
, соединяющие произвольную точку
гиперболы с ее фокусами, называются фокальными радиусами точки
. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Отношение , где
, называется эксцентриситетом гиперболы. Из определения
следует, что
.
Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:
(3.50)
Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки
к точке
); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат
оказалась правой).
Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов и
. Для произвольной точки
, принадлежащей гиперболе, имеем:
Записывая это уравнение в координатной форме, получаем:
Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:
где , т.е. выбранная система координат является канонической.
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.
Директориальное свойство гиперболы
Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее (рис.3.41,а). При
, когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.
Гиперболу с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки
(фокуса) к расстоянию до заданной прямой
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
(директориальное свойство гиперболы). Здесь
и
— один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
В самом деле, например, для фокуса и директрисы
(рис.3.41,а) условие
можно записать в координатной форме:
Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса
и директрисы
:
Уравнение гиперболы в полярной системе координат
Уравнение правой ветви гиперболы в полярной системе координат (рис.3.41,б) имеет вид
, где
— фокальный параметр гиперболы.
В самом деле, выберем в качестве полюса полярной системы координат правый фокус гиперболы, а в качестве полярной оси — луч с началом в точке
, принадлежащий прямой
, но не содержащий точки
(рис.3.41,б). Тогда для произвольной точки
, принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем
. Выражаем расстояние между точками
и
(см. пункт 2 замечаний 2.8):
Следовательно, в координатной форме уравнение гиперболы имеет вид
Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:
Выражаем полярный радиус и делаем замены
:
что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( для гиперболы,
для эллипса).
Геометрический смысл коэффициентов в уравнении гиперболы
Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение , находим абсциссы точек пересечения:
. Следовательно, вершины имеют координаты
. Длина отрезка, соединяющего вершины, равна
. Этот отрезок называется действительной осью гиперболы, а число
— действительной полуосью гиперболы. Подставляя
, получаем
. Длина отрезка оси ординат, соединяющего точки
, равна
. Этот отрезок называется мнимой осью гиперболы, а число
— мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.
Замечания 3.10.
1. Прямые ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).
2. Прямые , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).
Для равносторонней гиперболы, описываемой уравнением (т.е. при
), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат
(рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид
(гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).
В самом деле, повернем каноническую систему координат на угол (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами
Подставляя эти выражения в уравнение равносторонней гиперболы и приводя подобные члены, получаем
3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.
Действительно, если точка принадлежит гиперболе
. то и точки
и
, симметричные точке
относительно координатных осей, также принадлежат той же гиперболе.
Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.
4. Из уравнения гиперболы в полярных координатах (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси (
при
).
5. Эксцентриситет характеризует форму гиперболы. Чем больше
, тем шире ветви гиперболы, а чем ближе
к единице, тем ветви гиперболы уже (рис.3.43,а).
Действительно, величина угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника:
. Учитывая, что
и
, получаем
Чем больше , тем больше угол
. Для равносторонней гиперболы
имеем
и
. Для
угол
тупой, а для
угол
острый (рис.3.43,а).
6. Две гиперболы, определяемые в одной и той же системе координат уравнениями и
называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы
приводится к каноническому при помощи переименования координатных осей (3.38).
7. Уравнение определяет гиперболу с центром в точке
, оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение
определяет сопряженную гиперболу с центром в точке
.
Параметрическое уравнение гиперболы
Параметрическое уравнение гиперболы в канонической системе координат имеет вид
где — гиперболический косинус, a
гиперболический синус.
Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству .
Пример 3.21. Изобразить гиперболу в канонической системе координат
. Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.
Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: — действительная полуось,
— мнимая полуось гиперболы. Строим основной прямоугольник со сторонами
с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя
в уравнение гиперболы, получаем
Следовательно, точки с координатами и
принадлежат гиперболе. Вычисляем фокусное расстояние
эксцентриситет ; фокальныи параметр
. Составляем уравнения асимптот
, то есть
, и уравнения директрис:
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Пусть
фокусы гиперболы лежат на оси Ох.
Межфокусное расстояние гиперболы равно
причем
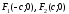
Заметим, что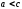
Следовательно,
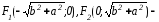
гиперболы. [1.С.109]
5)
Директориальное свойство гиперболы:
Определение
3.4.
Директрисами гиперболы
называются
прямые, параллельные канонической оси
ОУ и отстоящие от этой оси на расстояние
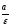
Уравнения
директрис гиперболы имеют вид: ++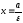
, если
гипербола задана уравнением
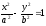
Если
гипербола задана уравнением
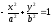
то директрисы определяются уравнениями

6)
Эксцентриситет гиперболы:
Определение
3.5.
Отношение
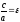
Так как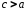
то
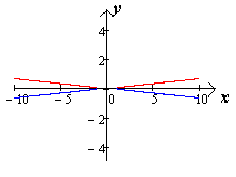
Если
при постоянном значении
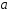
число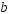
то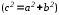
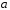
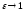
то гипербола будет стремиться к лучам
(чертеж
21.).
Чертеж
21.
Если
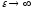
то гипербола будет стремиться к
параллельным прямым (чертеж
22.).
[1.С.109]
Чертеж
22.
7)
Касательная к гиперболе:
Уравнение
касательной к гиперболе
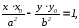
где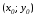
координаты точки касания, а
соответственно действительная и мнимая
полуоси гиперболы (чертеж
23.).
Чертеж
23.

Диаметр гиперболы:
Если
гипербола задана уравнением
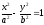
то её диамерт, сопряженный хордам с
угловым коэффициентом k,
определяется уравнением
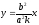
ПАРАБОЛА
Определение
4.1.Парабола-
это геометрическое
множество точек, для каждой из которых
расстояние от некоторой фиксированной
точки, называемой фокусом, равно
расстоянию до некоторой прямой, называемой
директрисой (директриса не проходит
через фокус). [8.С.589]
Общий
вид уравнения
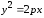
Исследование
свойств параболы
1)
Вершина параболы:
Уравнению
(15) удовлетворяют числа
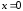
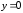
следовательно, парабола проходит через
начало координат.[1.c.109-110]
2)
Симметрия параболы:
Пусть
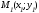
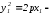
равенство. Точка
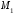
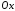
следовательно, парабола симметрична
относительно оси абсцисс. [1.С.110]
-
Эксцентриситет
параболы:
Определение
4.2. Эксцентриситетом
параболы называется число
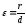
равное единице.
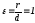
так как по определению параболы

4)
Касательная параболы:
Касательная
к параболе в точке касания
определяется
уравнением
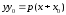
где
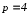
29.)
Чертеж
29.
-
Фокус
параболы:
Если
уравнение параболы имеет вид
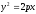
то её фокус
имеет координаты
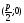
Если
уравнение параболы имеет вид
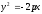
то её фокус будет иметь координаты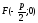
-
Диаметр
параболы:
Если
парабола задана уравнением
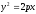
то её диаметр определяется уравнением
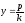
угловой коэффициент.
-
Уравнения
директрис параболы:
Если
уравнение параболы имеет вид
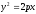
то директриса параболы имеет уравнение:

Если уравнение параболы имеет вид
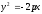
то уравнение директрисы параболы имеет
вид:
Чтобы
обобщить работу по теории линий второго
порядка в элементарной математике и
для удобства использования информации
о линиях при решении задач, заключим
все данные о линиях второго порядка в
таблицу № 1.
Таблица
№1.
Линии второго порядка в элементарной математике
|
Название |
Окружность |
Эллипс |
Гипербола |
Парабола |
|
Характеристические |
|
|
|
|
|
Уравнение |
|
|
|
|
|
Эксцентриситет |
|
|
|
|
|
Уравнение |
|
|
|
|
|
Фокус |
|
|
|
|
|
Диаметры |
|
|
|
|
|
Уравнения |
|
|
|
-
Возможности
использования ИКТ в изучении линий
второго порядка
Сегодня
современные информационные технологии
становятся важнейшим инструментом
модернизации школы в целом – от управления
до воспитания и обеспечения доступности
образования.
Процесс
информатизации, охвативший все стороны
жизни современного общества, имеет
несколько приоритетных направлений, к
которым, безусловно, следует отнести
информатизацию образования. Она является
первоосновой глобальной рационализации
интеллектуальной деятельности человека
за счет использования
информационно-коммуникационных
технологий (ИКТ).
Середина
90-х годов прошлого века и до сегодняшнего
дня, характеризуется массовостью и
доступностью персональных компьютеров
в России, широким использованием
телекоммуникаций, что позволяет внедрять
разрабатываемые информационные
технологии обучения в образовательный
процесс, совершенствуя и модернизируя
его, улучшая качество знаний, повышая
мотивацию к обучению, максимально
используя принцип индивидуализации
обучения. Информационные технологии
обучения являются необходимым инструментом
на данном этапе информатизации
образования.
Информационные
технологии не только облегчают доступ
к информации и открывают возможности
вариативности учебной деятельности,
ее индивидуализации и дифференциации,
но и позволяют по-новому организовать
взаимодействие всех субъектов обучения,
построить образовательную систему, в
которой ученик был бы активным и
равноправным участником образовательной
деятельности.
Формирование
новых информационных технологий в
рамках предметных уроков стимулируют
потребность в создании новых
программно-методических комплексов
направленных на качественное повышение
эффективности урока. Поэтому, для
успешного и целенаправленного
использования в учебном процессе средств
информационных технологий, преподаватели
должны знать общее описание принципов
функционирования и дидактические
возможности программно- прикладных
средств, а затем, исходя из своего опыта
и рекомендаций, «встраивать» их в
учебный процесс.
Изучение
математики в настоящее время сопряжено
с целым рядом особенностей и трудностей
развития школьного образования в нашей
стране.
Появился
так называемый кризис математического
образования. Причины его состоят в
следующем:
—
в изменении приоритетов в обществе и в
науке, то есть в настоящее время идет
рост приоритета гуманитарных наук;
—
в сокращении количества уроков математики
в школе;
—
в оторванности содержания математического
образования от жизни;
—
в малом воздействии на чувства и эмоции
учащихся.
Сегодня
остается открытым вопрос: «Как же
наиболее эффективно использовать
потенциальные возможности современных
информационных и коммуникационных
технологий при обучении школьников, в
том числе, при обучении математике?».
Компьютер
– отличный помощник в изучении такой
темы, как “Квадратичная функция”,
потому что, используя специальные
программы можно строить графики различных
функций, исследовать функцию, легко
определить координаты точек пересечения,
вычислить площади замкнутых фигур и
т.д. Например, на уроке алгебры в 9-м
классе, посвящённом преобразованию
графика (растяжения, сжатия, переносы
координатных осей) можно увидеть лишь
застывший результат построения, а на
экране монитора прослеживается вся
динамика последовательных действий
учителя и ученика.
Компьютер,
как ни одно техническое средство, точно,
наглядно и увлекательно открывает перед
учеником идеальные математические
модели, т.е. то, к чему должен стремиться
ребенок в своих практических действиях.
Сколько
трудностей приходится испытывать
учителю математики для того, чтобы
убедить учеников в том, что касательная
к графику квадратичной функции в точке
касания практически сливается с графиком
функции. На компьютере этот факт
продемонстрировать очень просто-
достаточно сузить интервал по оси Ох и
обнаружить, что в очень маленькой
окрестности точки касания график функции
и касательная совпадают. Все эти действия
происходят на глазах у учеников. Этот
пример дает толчок к активным размышлениям
на уроке.
Для
активизации познавательной деятельности
использование ИКТ может происходить
на всех этапах и при разных типах уроков.
На
вводных уроках важно заинтересовать
ребят яркими, запоминающимися образами,
которые можно создать с помощью библиотеки
электронных наглядных пособий или
образовательных ресурсов сети Интернет.
Увеличения доли информации, представляемой
в визуальной форме, открывает принципиально
новые возможности для усвоения нового
материала, развития внимания и
сообразительности.
При
формировании новых знаний может быть
использовано электронное сопровождение
в виде презентации, на которой отражены
основные понятия, схемы, алгоритм
применения правил.
На
уроках закрепления можно использовать
электронный тренажер или возможности
цифрового образовательного ресурса, с
помощью которых обучающиеся не только
могут применить свои знания в процессе
практической деятельности, но и увидеть
личный результат.
Использование
цифровых образовательных ресурсов на
уроке контроля позволяет организовать
проверочную работу, при которой ученик
не только получает отметку и оценку
своих знаний, но и анализ всего хода
выполнения работы (количество правильных
и неправильных ответов, на какие правила
была допущена ошибка, какой материал
необходимо повторить и т.д.)
Тем
самым использование компьютера возможно
как в ходе объяснения нового материала
на уроке, так и на этапе контроля. При
помощи программ, например «My
Test»,
ученик самостоятельно может проверить
свой уровень знаний по теории, выполнить
теоретико-практические задания. Программа
удобна своей универсальностью. Она
может быть использована и для самоконтроля,
и для контроля со стороны учителя.
Разумная
интеграция математики и компьютерных
технологий позволит богаче и глубже
взглянуть на процесс решения задачи,
ход осмысления математических
закономерностей. Кроме того, компьютер
поможет сформировать графическую,
математическую и мыслительную культуру
учеников, а также с помощью компьютера
можно подготовить дидактические
материалы: карточки, листы опроса, тесты
и др. При этом давать возможность ребятам
самостоятельно разрабатывать тесты по
теме, в ходе чего развивается интерес
и творческий подход.
Грамотное
спользование ИКТ дает возможность:
-
повысить
мотивацию обучения; -
увеличить
индивидуальную активность учащихся; -
сформировать
информационную компетенцию; -
для
свободного творчества; -
для
интерактивность обучения; -
активизировать
познавательную деятельность и повысить
качество успеваемости школьников; -
для
развития навыков самообразования и
самоконтроля; -
повышения
уровня комфортности обучения; -
снизить
дидактически затруднений у учащихся; -
развивать
информационное мышление; -
проводить
уроки на высоком эстетическом уровне; -
индивидуально
подойти к ученику, применяя разноуровневые
задания.
А
для учителя, информационные технологии
способны решать многие педагогические
задачи, предоставляя новые возможности
для творчества, приобретения и закрепления
профессиональных навыков, позволяют
реализовывать принципиально новые
формы и методы обучения.
Таким
образом ИКТ становятся неотъемлемой
частью современного учебного процесса,
способствующей повышению качества
образования. А
значат есть необходимость и возможности
применения компьютера на уроках
математики достаточно широко. Использование
информационных технологий будет
способствовать повышению качества
знаний, расширит горизонты изучения
квадратичной функции, следовательно,
поможет найти новые перспективы для
поддержания интереса учащихся к предмету
и к теме.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

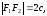

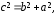
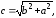
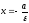

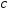

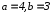
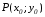
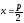
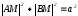
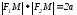
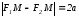
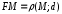


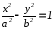
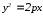
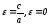
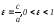
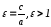
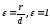
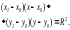
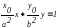
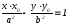
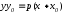

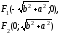
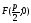 ,
,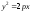 .
.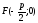 ,
,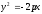
 ,
,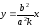 ,
,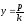 ,
,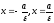 ,
,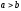 .
.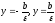 ,
,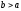
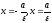 ,
,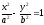 .
.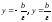 ,
,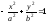 .
.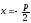 ,если
,если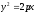 .
.