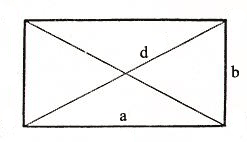
Прямоугольник. Формулы и свойства прямоугольника
Определение.
Прямоугольник — это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую — шириной прямоугольника.
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
AB||CD, BC||AD
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
AC = BD
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d2 = 2a2 + 2b2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника — квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.
Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d2 — b2
b = √d2 — a2
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
3. Формула стороны прямоугольника (длины и ширины прямоугольника) через периметр и другую сторону:
4. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:
a = d sinα
b = d cosα
5. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол β:
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.
Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a2 + b2
2. Формула диагонали прямоугольника через площадь и любую сторону:
| d = | √S2 + a4 | = | √S2 + b4 |
| a | b |
3. Формула диагонали прямоугольника через периметр и любую сторону:
| d = | √P2 — 4Pa + 8a2 | = | √P2 — 4Pb + 8b2 |
| 2 | 2 |
4. Формула диагонали прямоугольника через радиус описанной окружности:
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d = Dо
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S : sin β
Периметр прямоугольника
Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b)
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a2 | = | 2S + 2b2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d2 — a2) = 2(b + √d2 — b2)
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R2 — a2) = 2(b + √4R2 — b2)
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √Do2 — a2) = 2(b + √Do2 — b2)
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.
Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
| S = | Pa — 2a2 | = | Pb — 2b2 |
| 2 | 2 |
3. Формула площади прямоугольника через диагональ и любую сторону:
S = a√d2 — a2 = b√d2 — b2
4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a√4R2 — a2 = b√4R2 — b2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a√Do2 — a2 = b√Do2 — b2
Окружность описанная вокруг прямоугольника
Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:
| R = | √P2 — 4Pa + 8a2 | = | √P2 — 4Pb + 8b2 |
| 4 | 4 |
3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:
| R = | √S2 + a4 | = | √S2 + b4 |
| 2a | 2b |
4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:
5. Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:
6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
Угол между стороной и диагональю прямоугольника
Формулы определения угла между стороной и диагональю
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
Угол между диагоналями прямоугольника
Формулы определения угла между диагоналями прямоугольника
1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:
β = 2α
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:
Загрузить PDF
Загрузить PDF
Прямоугольник — четырехсторонняя фигура с четырьмя прямыми углами, противолежащие стороны которой равны. Все, что нужно сделать для вычисления его площади, — умножить длину на ширину. Хотите знать как это сделать? Читайте дальше.
-
1
Прямоугольник — четырехсторонняя фигура, противолежащие стороны которой равны. Если одна сторона равна 10 см, то и противолежащая будет равна 10 см.
- Любой квадрат также является прямоугольником. Площадь квадрата находится по той же формуле.
-
2
Выучите формулу нахождения площади прямоугольника: S = a * b, где S — площадь, a — длина, b — ширина, то есть, площадь равна произведению сторон.
Реклама
-
1
Найдите длину прямоугольника. Как правило, она указана в задаче, но если нет — найдите ее с помощью линейки.
- Двойные отметки на длинных сторонах означают, что их длины равны.
-
2
Так же найдите ширину прямоугольника.
- Отметки на узких сторонах означают, что их ширины равны.
-
3
Запишите длину и ширину. В нашем примере длина — 5 см, ширина — 4 см.
-
4
Умножьте длину на ширину. Длина — 5 см, ширина — 4 см, вставьте эти числа в формулу S = a * b и вы найдете площадь.
- S = 4 cm * 5 cм
- S = 20 cм^2
-
5
Запишите ответ в квадратных единицах. Ответ: 20 см^2, что означает «двадцать квадратных сантиметров».
- Ответ можно записать как 20 кв. см, так и 20 см^2.
Реклама
-
1
Научитесь использовать теорему Пифагора — она позволяет найти длину стороны прямоугольного треугольника, если известны длины двух других сторон. Можно использовать ее для нахождения гипотенузы, самой длинной из сторон треугольника, а также длины и ширины, образующих прямой угол.
- Прямоугольник имеет четыре прямых угла, и его диагональ образует два прямоугольных треугольника, так что мы можем использовать теорему Пифагора.
- Теорема Пифагора звучит так: квадрат гипотенузы равен сумме квадратов катетов, то есть a^2 + b^2 = c^2, где a и b — стороны (катеты) прямоугольного треугольника, а с — гипотенуза, самая длинная сторона.
-
2
Используйте теорему Пифагора для нахождения другой стороны треугольника. К примеру, прямоугольник имеет сторону длиной 6 см и диагональ длиной 10 см. Одна сторона — 6 см, другая — b, гипотенуза — 10 см. Вставьте значения в теорему и решите. Вот, как это делается:
- Пример: 6^2 + b^2 = 10^2
- 36 + b^2 = 100
- b^2 = 100 — 36
- b^2 = 64
- квадратный корень (b) = квадратный корень (64)
- b = 8
- Длина другой стороны треугольника, которая также является другой стороной прямоугольника, — 8 см.
-
3
Найдите площадь прямоугольника. Поскольку для нахождения длины и ширины мы использовали теорему Пифагора, все, что нам нужно, — это помножить длину на ширину:
- Пример: 6 cм * 8 cм = 48 cм^2
-
4
Запишите окончательный ответ в квадратных единицах: 48 cм^2 или 48 кв. см.
Реклама
Советы
- Все квадраты — прямоугольники, но не все прямоугольники — квадраты.
- При нахождении площади ответ всегда нужно записывать в квадратных единицах.
Реклама
Об этой статье
Эту страницу просматривали 279 981 раз.
Была ли эта статья полезной?
Содержание:
- Формула площади прямоугольника
- Формула периметра прямоугольника
Прямоугольник — это четырёхугольник, у которого четыре прямых угла. Размеры прямоугольника задаются длинами его
сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a = b) называется квадратом.
Формула площади прямоугольника
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади прямоугольника выражается числом заключающихся в него квадратных единиц.
1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).
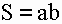
S — площадь прямоугольника
a — длина 1-ой стороны прямоугольника
b — длина 2-ой стороны прямоугольника
См. также: Программа для расчета площади прямоугольника.
Формула периметра прямоугольника
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры.
Периметр имеет ту же размерность величин, что и длина.
1) Периметр прямоугольника равен удвоенной сумме 2-х его смежных сторон (a, b).
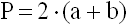
P — периметр прямоугольника
a — длина 1-ой стороны прямоугольника
b — длина 2-ой стороны прямоугольника
См. также: Программа для расчета периметра прямоугольника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Выбирайте формулу, ориентируясь на известные величины.
1. Если известны две соседние стороны
Просто перемножьте две стороны прямоугольника.
- S — искомая площадь прямоугольника;
- a и b — соседние стороны.
2. Если известны любая сторона и диагональ
Найдите квадраты диагонали и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте длину известной стороны на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- d — любая диагональ (напомним: обе диагонали прямоугольника имеют одинаковую длину).
3. Если известны любая сторона и диаметр описанной окружности
Найдите квадраты диаметра и любой стороны прямоугольника.
От первого числа отнимите второе и найдите корень из результата.
Умножьте известную сторону на полученное число.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- D — диаметр описанной окружности.
4. Если известны любая сторона и радиус описанной окружности
Найдите квадрат радиуса и умножьте результат на 4.
Отнимите от полученного числа квадрат известной стороны.
Найдите корень из результата и умножьте на него длину известной стороны.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- R — радиус описанной окружности.
5. Если известны любая сторона и периметр
Умножьте периметр на длину известной стороны.
Найдите квадрат известной стороны и умножьте полученное число на 2.
От первого произведения отнимите второе и разделите результат на 2.
- S — искомая площадь прямоугольника;
- a — известная сторона;
- P — периметр прямоугольника (равен сумме всех сторон).
6. Если известны диагональ и угол между диагоналями
Найдите квадрат диагонали.
Разделите полученное число на 2.
Умножьте результат на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- d — любая диагональ прямоугольника;
- α — любой угол между диагоналями прямоугольника.
7. Если известны радиус описанной окружности и угол между диагоналями
Найдите квадрат радиуса окружности, описанной вокруг прямоугольника.
Умножьте полученное число на 2, а потом на синус угла между диагоналями.
- S — искомая площадь прямоугольника;
- R — радиус описанной окружности;
- α — любой угол между диагоналями прямоугольника.
Читайте также 🎓❓📐
- ТЕСТ: Умеете ли вы считать в уме?
- Как легко и быстро считать проценты в уме
- Как найти площадь любого треугольника
- ТЕСТ: Сколько центнеров в тонне? А сантиметров в дециметре? Проверьте, умеете ли вы переводить единицы измерения
- Как освоить устный счёт школьникам и взрослым
Формулы. Площадь. Формула площади прямоугольника.
В математике существуют буквенные выражения, которые определяют зависимость между физическими величинами. Такая зависимость называется формулой.
Физические величины – это путь, время, скорость, периметр, площадь и другие.
Если обозначить каждую величину определенной буквой, то для них можно записать формулы.
Обозначим скорость буквой v,
Время – t,
Путь – S,
Периметр – P,
Площадь – S.
Пусть скорость постоянна. Чтобы найти путь, нужно скорость умножить на время. Соответствующая формула: S=vt.
Следовательно, чтобы найти скорость, нужно путь разделить на время: v=S:t. А чтобы найти время, нужно путь разделить на скорость: t=S:v.
Периметр – это сумма всех сторон фигуры. У квадрата четыре одинаковые стороны, значит, его периметр можно найти по формуле P=a+a+a+a=4a, где a – длина стороны. У прямоугольника две пары одинаковых сторон, значит, его периметр можно найти по формуле P=a+a+b+b=2a+2b=2(a+b), где a и b – длины соседних сторон.
Площадь прямоугольника – это произведение длин двух соседних сторон. Формула S=a*b. Так как у квадрата все стороны одинаковы, его площадь можно найти по формуле S=a*a=a2.
Две фигуры называются равными, если они совпадают при наложении. Площади и периметры равных фигур равны.
Площадь всей фигуры равна сумме площадей ее частей.
С помощью формул можно решать разные задачи.
Задача 1. Велосипедист едет со скоростью 15 км/ч. Какое расстояние он проедет за 4 ч?
Решение: S=v*t=15*4=60 км.
Задача 2. Автомобиль движется со скоростью 60 км/ч. За какое время он пройдет путь в 600км?
Решение: t=S:v=600:60=10 ч.
Задача 3. С какой скоростью должен идти человек, чтобы пройти 24 км за 4 ч?
Решение: v=S:t=24:4=6 км/ч
Задача 4. Длина прямоугольника 4 дм, ширина 3 дм. Найдите периметр прямоугольника.
P=2a+b=24+3=2*7=14 дм.