Симметри́я криста́ллов — закономерность атомного строения, внешней формы и физических свойств кристаллов, заключающаяся в том, что кристалл может быть совмещен с самим собой путем поворотов, отражений, параллельных переносов (трансляций) и др. преобразований симметрии, а также комбинаций этих преобразований. Симметрия свойств кристалла обусловлена симметрией его строения.
Отражения и вращения, приводящие многогранник в совмещение с самим собой, называются преобразованиями симметрии или симметричными операциями.
Воображаемые плоскости, линии и точки, с помощью которых осуществляются эти отражения и вращения, называются элементами симметрии.
Для обозначения симметричных преобразований и соответствующих им элементов симметрии используют две системы обозначения — международную, принятую интернациональным союзом кристаллографов, и символику, основанную на формулах симметрии.
Плоскость симметрии — плоскость, которая делит фигуру на две части, расположенные друг относительно друга, как предмет и его зеркальное отражение. Обозначение: международное — m, по формуле симметрии — Р.
Пример: в кубе 3 взаимно перпендикулярные плоскости симметрии делят пополам противоположные ребра куба как координатные плоскости прямоугольной системы координат, а шесть плоскостей симметрии проходят по диагоналям граней куба. Все девять плоскостей симметрии куба пересекаются в одной точке — в центре куба. Плоскости симметрии располагаются в симметричной фигуре строго определенно, и все пересекаются друг с другом.
Поворотная ось симметрии —прямая линия, при повороте вокруг которой на определенный угол фигура совмещается сама с собой. Обозначение: международное — n, по формуле симметрии — Ln. Соответственно двойная ось обозначается 2 или L2, тройная — 3 или L3, четверная — 4 или L4; шестерная — 6 или L6. Порядок оси симметрии n показывает, сколько раз фигура совместится сама с собой при полном обороте вокруг этой оси. У куба есть три оси 4-го порядка, которые проходят через центры противоположных граней, 4 оси 3-го порядка, являющиеся пространственными диагоналями куба и 6 осей 2-го порядка, проходящих через середины пар противоположных ребер. Все оси симметрии куба пересекаются в одной точке в центре куба.
Центр симметрии (центр инверсии, центр обратного равенства) — особая точка внутри фигуры, характеризующаяся тем, что любая прямая, проведенная через центр симметрии, встречает одинаковые (соответственные) точки фигуры по обе стороны от центра на равных расстояниях. Симметричное преобразование в центре симметрии — это зеркальное отражение в точке. Обозначение: международное — 1, по формуле симметрии — С. Когда мы отражаем куб в плоскостях симметрии, зеркально отражаются все его точки, кроме находящихся на самой плоскости симметрии. Когда куб поворачивается вокруг разных осей симметрии, поворачиваются все точки, кроме точек, лежащих на самой оси симметрии. При отражении в центре симметрии остается одна точка, не отражающаяся, не смещающаяся, — сам центр. Отражение в плоскости, поворот вокруг оси симметрии, зеркальное отражение в центре симметрии представляют собой конечные или точечные симметричные преобразования. При этих преобразованиях фигура не перемещается как целое, и хотя бы одна ее точка остается на месте.
Полярным называется направление, концы которого геометрически и физически не эквивалентны, их нельзя совместить никакими преобразованиями симметрии.
Инверсионная ось симметрии — совместное действие оси вращения и одновременного отражения (инверсии) в центре симметрии.
Обозначение: международное — n, по формуле симметрии — Ln=Lni.
Соответственно, тройная — 3 или L3i, четверная — 4 или L4i; шестерная — 6 или L6i.
Внешняя, видимая симметрия кристаллов исчерпывающе описывается приведенными выше элементами симметрии и их сочетаниями.
Плоскости симметрии, оси симметрии простые и инверсионные, центр симметрии обнаруживаются в кристаллах в различных сочетаниях.
Формула симметрии состоит из записанных подряд всех элементов симметрии данного объекта. Например, обычная поваренная соль (хлористый натрий) кристаллизуется в форме кубов, алмаз, квасцы — в форме октаэдров. Полный набор элементов симметрии у этих разных многогранников один и тот же: девять плоскостей, три оси четвертого порядка, четыре оси третьего порядка, шесть осей второго порядка и центр симметрии. В формуле симметрии на первом месте принято писать оси симметрии от высших к низшим, на втором плоскости симметрии, затем центр. Формула симметрии куба 3L44L36L29PC.
Классом или видом симметрии какого-либо объекта называют полную совокупность операций симметрии этого объекта. Все многообразие симметрии кристаллических многогранников и их физических свойств описывается 32 классами симметрии.
По симметрии и числу единичных направлений кристаллы делятся на три категории: высшую, среднюю и низшую.
Кристаллы высшей категории не имеют единичных направлений, У них обязательно есть несколько осей порядка выше, чем 2, в частности четыре оси 3, расположенные как пространственные диагонали куба. Это высокосимметричные кристаллы. Любому направлению в кристалле высшей категории соответствуют другие симметрично эквивалентные направления. Свойства кристаллов в направлениях симметрично эквивалентных должны быть одинаковыми, поэтому анизотропия свойств в кристаллах высшей категории выражена слабее всего. Многие физические свойства (электропроводность, теплопроводность, показатель преломления) в этих кристаллах изотропны как в аморфных веществах, а анизотропия других свойств (упругость, электрооптический эффект) гораздо слабее, чем у кристаллов других категорий. Внешняя форма кристаллов высшей категории, как правило, изометрична, т. е. развита примерно одинаково во все стороны, как куб, октаэдр, тетраэдр.
Кристаллы средней категории имеют одно особое направление, а именно: одна ось симметрии 3, 4 или 6, простая или инверсионная. Анизотропия физических свойств у этих кристаллов гораздо сильнее, чем у кристаллов высшей категории. Особенно заметно различие свойств вдоль и поперек главной оси симметрии. Характерные формы кристаллов средней категории — призмы, пирамиды и др.
К низшей категории относятся кристаллы, у которых нет осей симметрии порядка выше чем 2, а единичных направлений несколько. Это наименее симметричные кристаллы с ярко выраженной анизотропией свойств.
Три категории делятся на 7 сингоний. В сингонию объединяются те кристаллы, для которых одинакова симметрия элементарных ячеек и их структур и одинакова система координат.
- Ladd Marcus Frederick Charles. Symmetry in molecules and crystals. — Chichester: Ellis Horwood, 1989.
- Зоркий П. М. Симметрия молекул и кристаллических структур. — М.: Изд-во МГУ, 1986.
- Изюмов Ю. А. Фазовые переходы и симметрия кристаллов. — М.: Наука, 1984.
Формулы симметрии и тридцать два вида симметрии кристаллов
Перечень
всех элементов симметрии кристалла,
записанный в виде их символов, называется
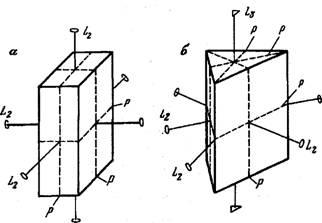
формулой симметрии. Например, если в
кристалле имеются три оси 1,2, три плоскости
симметрии и центр симметрии (рис. 25, а),
то его формулой симметрии будет З-С^ЗРС.
Если кристалл обладает одной осью
симметрии третьего порядка Ьз,тремя
вертикальными и одной горизонтальной
плоскостью симметрии и тремя осями
второго порядка (рис. 25, б), то его формула
симметрии будет ЬъЪЬъ^Р. Но одновременно
в этом кристалле ось Ьз является осью
1^6. Поэтому его формулу симметрии можно
записать и так: Х,-631/24Р. В таких формулах
порядок записи следующий: сначала
главные оси, затем другие, потом плоскости
и центр инверсии.
Рис.
25. Многогранники с разными наборами
элементов симметрии.
Кристаллы
одного и того же минерала независимо
от их огранки характеризуются одно и
той же формулой симметрии. Число таких
формул не беспредельно, поскольку
элементы симметрии взаимосвязаны между
собой. Геометрический вывод всех
возможных сочетаний элементов
симметрии в кристаллах был сделан
немецким минералогом И. Гесселем в
1830 г. и финном А. В. Гадолиным в 1867 г. Из
него следует, что в природе может
существовать только 32 сочетания, или,
как принято говорить, 32 вида симметрии,
которые объединены в семь групп — семь
сингоний. Перечень видов симметрии и
сингоний приведен в табл. 5.
Сингонию
кристалла определяют по обязательному
для каждой сингоний элементу симметрии.
В кристаллах кубической сингоний
обязательно присутствуют четыре оси
третьего порядка (41>з), в гексагональной
сингоний — одна ось Ьв, тетрагональной
— 1-4, тригональной — 1-з.СингоНии
объединены в три категории—низшую,
среднюю и высшую. В таблице указаны
также принятые в кристаллографии
названия видов симметрии— примитивный,
планальный (плана-плоскость), аксиальный
(акси-ось) и т.п.
Простыв кристаллографические формы
Естественные
форма и огранка кристаллов зависят от
их структуры и условий образования.
Каждая грань отвечает плоской сетке, а
внешняя симметрия кристаллов соответствует
симметрии их структуры.
Наиболее
совершенные по своей огранке кристаллы
образуются при равномерной диффузии
вещества ко всем частям растущего
кристалла и при одинаковой дефектности
кристаллической решетки во всех ее
частях. На таких кристаллах закономерно
повторяются одинаковые грани. На одних
кристаллах это грани только одного
вида, например грани гексаэдра (куба),
на других повторяются грани двух, трех
и более видов. На кристаллах одинаковые
грани соответствуют одинаковым плоским
сеткам в структуре минерала, они
характеризуются одним и тем же узором
расположения атомов и схожим механизмом
роста (рис. 26).
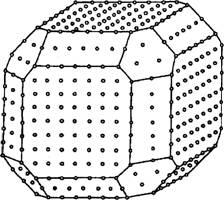
Рис.
26. Одинаковые узор и плотность расположения
атомов на одинаковых гранях кристалла
(Вадило, 1964).
Совокупность
граней кристалла, отвечающих одинаковым
плоским сеткам, называется простой
кристаллографической формой. На
кристалле, изображенном на рис. 26, имеется
26 граней, они принадлежат к трем простым
кристаллографическим формам. К одной
простой форме относятся шесть граней,
к другой — восемь, к третьей— двенадцать.
Выделение простых кристаллографических
форм на кристаллах имеет большой
физический смысл, а именно: одинаковые
грани характеризуются одними и теми же
скоростями роста, блеском, твердостью
и сходством других свойств.
На
идеально развитом кристалле все грани
одной и той же простой кристаллографической
формы одинаковы. Отсюда—сколько на
равномерно развитом кристалле сортов
граней, столько на нем и простых
кристаллографических форм. Исходя из
строгого определения, простой
кристаллографической формой можно
назвать совокупность граней, связанных
друг с другом элементами симметрии.
Чаще
всего кристаллы огранены комбинацией
нескольких простых кристаллографических
форм. Чтобы представить себе в объеме
геометрические очертания каждой из
них, надо мысленно продлить все грани
данной простой кристаллографической
формы так, как будто бы им не мешали
расти грани других простых
кристаллографических форм, и попытаться
оценить вид получившегося многогранника.
Легко догадаться, что большие грани
квадратных очертаний (их шесть) на рис.
26 есть грани гексаэдра (куба). Труднее
представить, чем являются небольшие
грани шестиугольных очертаний. Их
восемь, а если их сомкнуть друг с другом,
получится многогранник из восьми
равносторонних треугольников. Такой
восьмигранник называется в геометрии
октаэдром. Наконец, если мысленно
соединить длинные прямоугольные грани,
а их двенадцать, получится фигура,
называемая ромбододекаэдром. Следовательно,
можно сказать, что кристалл образован
гранями трех простых кристаллографических
форм — куба, октаэдра и ромбододекаэдра.
Доказано,
что в мире кристаллов число простых
кристаллографических форм ограничено.
Всего их 47.
В
сингониях низшей категории возможны
моноэдры, диэдры, пинакоиды (от греч.
monos—один; hedra (эдр) — сторона, грань;
pinax—доска), ромбические призмы,
ромбические пирамиды, ромбические
дипирамиды и ромбические тетраэдры
(рис. 27).
Рис.
27. Простые формы низшей категории
сингоний. В сингониях средней категории
вероятны моноэдры, пинакоиды, призмы
разного рода, различные пирамиды и
дипирамиды, трапецоэдры, ромбоэдры,
скаленоэдры, тетрагональные тетраэдры
(рис. 28).
Рис.
28. Простые формы средней категории
сингоний.
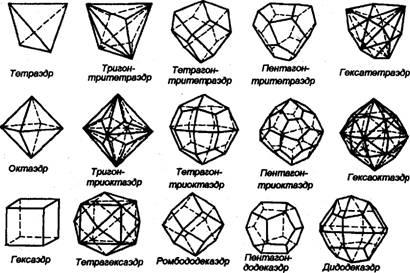
В
кубической сингонии возможны 15 простых
кристаллографических форм, из них на
кристаллах минералов чаще всего
наблюдаются тетраэдр, октаэдр, гексаэдр
(куб), ромбододекаэдр, Пентагон-додекаэдр,
тетрагон-триоктаэдр (рис. 29).
Рис.
29. Простые формы кубической сингонии.
Как
видно, простые формы могут быть закрытыми
и открытыми. Первые образуют привычные
всем геометрические фигуры, целиком
ограничивающие какой-либо конечный
объем. Таковы, например, куб, октаэдр,
ромбоэдр, скаленоэдр, дипира-миды.
Открытые формы являются незамкнутыми
и тем самым они поначалу менее понятны.
Таковы пирамиды с бесконечно расходящимися
от вершины гранями, пина-коид (две
беспредельно протяженные в пространстве
параллельные друг другу плоскости)
и призмы, напоминающие беспредельно
идущие трубы многоугольного сечения,
ничем не ограниченные по их длине.
Реальное сочетание в природе граней
открытых и закрытых простых
кристаллографических форм дает кристаллу
его конечный телесный объем.
Формула — симметрия
Cтраница 2
Этих примеров достаточно для того, чтобы показать, что расчет с помощью формул симметрии следует отнести к основам такой стереохимии, результаты которой базируются не на чистой эмпирии, а на научных основах. Вывод указанных формул или функций, которые необходимо в них подставить, основан на вычислении количества перестановок с использованием классических методов Эйлера. При этом в указанных функциях не принимались во внимание так называемые стереоизомеры, которые отличаются различным строением при аналогичном положении заместителей. К этим стерео-изомерам относятся, например, энантиоморфные конфигурации при асимметрических атомах углерода. Имеется общее правило, что максимальное число стереоизомеров соединения с а асимметрическими атомами углерода может достигать 2е, однако фактическое число может быть и меньше при наличии компенсации этих асим-метричностей. Полна разработал способ расчета числа таких изомеров. Так, для спиртов С Н2л 1ОН он дает следующее число изомеров.
[16]
Этих примеров достаточно для того, чтобы показать, что расчет с помощью формул симметрии следует отнести к основам такой стереохимии, результаты которой базируются не на чистой эмпирии, а на научных основах. Вывод указанных формул или функций, которые необходимо в них подставить, основан на вычислении кбличества перестановок с использованием классических методов, Эйлера. При этом в указанных функциях не принимались во внимание так называемые стереоизомеры, которые отличаются различным строением при аналогичном положении заместителей. Кэтимстерео — иЗомерам относятся, например, энантиоморфные конфигурации при асимметрических атомах углерода. Имеется общее правило, что максимальное число стереоизомеров соединения с а асимметрическими атомами углерода может достигать 2, однако фактическое число может быть и меньше при наличии компенсации атих асим-метричностей. Полна разработал способ расчета числа таких изомеров. Так, для спиртов С Н2п 1ОН он дает следующее число изомеров.
[17]
Обычно в теории пространственных групп симметрии для каждой из групп указываются в символе ( формуле симметрии) лишь порождающие элементы симметрии, а производные элементы симметрии опускаются. Так, в выбранном нами в качестве примера виде симметрии вместо полной формулы L22P в сокращенной формуле будут указаны лишь две плоскости симметрии, а обозначение оси второго порядка будет опущено.
[18]
Мы здесь не будем останавливаться на задачах, которые могут быть решены с помощью таких формул симметрии, а ограничимся следующей таблицей, заимствованной у Полна.
[19]
В международной и шубниковской системах обозначений приведены элементы симметрии, из которых можно вывести остальные. В графе Формула симметрии приведены все элементы симметрии данного класса: L — осич С — центр, Р — плоскость симметрии; перед каждым символом стоит число соответствующих элементов.
[20]
Видом симметрии кристаллического многогранника называется совокупность всех его элементов симметрии. Вид симметрии обозначается формулой симметрии.
[21]
Кратко это записывается формулой симметрии L & P.
[23]
Мы здесь не можем подробно останавливаться на выводе характерных формул симметрии для всех различных цепных, плоских и пространственных групп симметрии. Уже сделанных указаний достаточно для объяснения изложенных принципов.
[25]
Мы здесь не можем подробно останавливаться на выводе характерных формул симметрии для всех различных ценных, влоеких и пространственных групп симметрии. Уже еде данных указаний достаточно для объяснения изложенных принципов.
[27]
В формулах симметрии приведены лишь основные элементы симметрии кристаллов разных классив. Так, в таблице не указывается ( кроме класса 1) элемент симметрии 1, который присущ всем классам; в тех случаях, когда приведена старшая по порядку ось, подчиненная ей младшая по порядку ось ( совпадающая по направлению) не указывается. Число осей и плоскостей в формулах симметрии записано в скобках.
[28]
В табл. 3 приводятся наиболее распространенные в отечественной литературе обозначения ( формулы симметрии) и названия каждого вида симметрии, а также общепринятые международные символы по К. В этих обозначениях знака для осей симметрии нет, их заменяют на цифры ( порядок оси): 1 — Li; 2 — / 2; 3 — Ls; 4 — / 4 и 6 — Le. Если к оси четного порядка имеется перпендикулярная плоскость т, то это записывается так: 2 / т, 4 / / n, 6 / m; эти международные символы соответствуют формулам симметрии L2PC, LiPC и ЬЪРС. Международные символы не отличаются наглядностью, но они значительно компактнее и незаменимы для машинной техники.
[29]
Точечные системы в цепных группах, как и в группах точечных симметрии, могут образовать однопараметрические взацмозависи — мости, которые, однако, в этом случае простираются бесконечно. Это действительно, например, для точек с условием симметрии С2й ( рис. 47а), помеченных большими кружками и образующих ряд точек с промежутком т; это, однако, не действительно для представленных 4 точек общего положения, которые отчетливо распадаются на отдельные структурные группы. Если учесть новые изложенные факты, то понятия и концепции, разработанные для точечных групп симметрии, можно непосредственно перенести на новые цепные группы. Формулы симметрии будут даны в общей сводке в разделе Д этой главы.
[30]
Страницы:
1
2
3